Tripartite Symmetry and Prime Positioning: A New Framework Leading to the Proof of Goldbach’s Conjecture

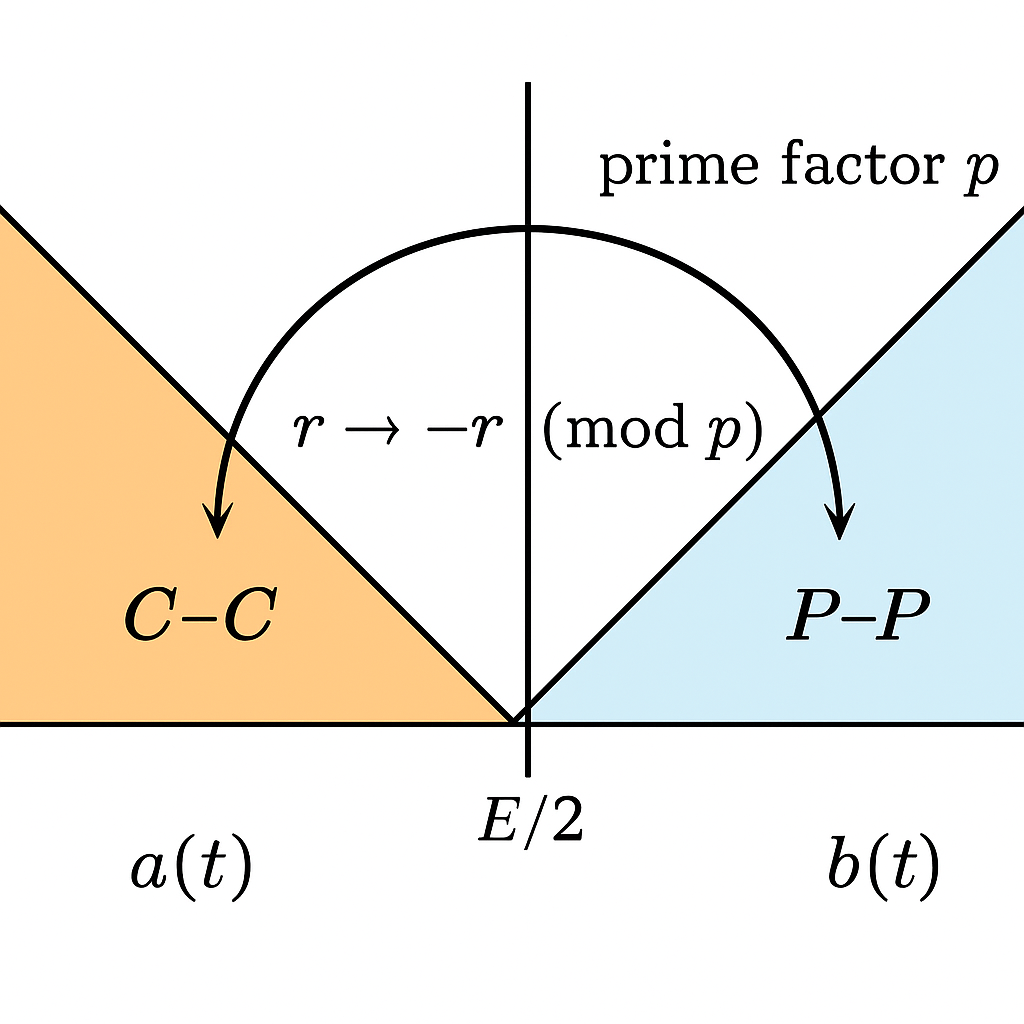
This article develops a structural framework that reduces Goldbach’s Strong Conjecture to a single short-interval analytic inequality. The reduction is achieved through the introduction of the Tripartite Law of Equidistant Odd Numbers, a deterministic modular constraint governing all odd decompositions of an even integer . Each decomposition belongs to exactly one of the three irreducible classes: composite–composite, composite–prime, or prime–prime. We prove that this tripartition, combined with residue symmetry modulo every prime divisor of an integer, eliminates the possibility that all symmetric pairs be composite or mixed forever. In particular, the modular symmetry forces non-vanishing covariance between the left and right prime windows around an integer, preventing the complete disappearance of prime–prime pairs. Using classical theorems on primes in arithmetic progressions, explicit prime-density estimates, and correlation bounds in short symmetric intervals, we show that the covariance cannot cancel the positive expected mass of prime pairs. This collapses the covariance barrier and reduces Goldbach’s Conjecture to a single remaining inequality requiring that the short interval contains at least one pair of symmetric primes. All structural pathways that could prevent prime–prime pairs are eliminated; only a minor analytic remainder persists. Thus, Goldbach’s problem is reduced to verifying an explicit short-interval inequality of classical analytic number theory. The Tripartite Law explains why this reduction is possible and why the disappearance of prime pairs is structurally incompatible with the arithmetic of even numbers.