Risk-Aware Hierarchical Transformers with Contrastive Learning for Financial Event Detection

I. Introduction

Detecting financial risk events from Chinese news is important for market monitoring and decision support. The task requires understanding labels that are organized hierarchically, where broad and specific risk types must both be recognized. Flat classification models often ignore these relations, which causes conflicts and lowers interpretability. Financial language also includes negation, uncertainty, and modal expressions that standard Transformers do not handle well, leading to unstable results.

Transformer-based models improve contextual learning, but they still have trouble modeling hierarchical relations and domain-specific language. The lack of labeled data in the financial field further limits their performance, so self-supervised learning and knowledge transfer are needed to improve generalization.

HARTE is designed to solve these problems with a unified Transformer structure. It uses risk-aware encoding to capture financial semantics, hierarchical decoding to manage label dependencies, and uncertainty-aware ensemble learning to stabilize predictions. The framework applies adaptive attention guided by risk embeddings, contrastive learning to improve discrimination, progressive distillation for knowledge transfer, and uncertainty calibration for model fusion. These methods together make HARTE better at maintaining semantic precision and consistency when training data are scarce.

II. Related Work

Hierarchical multi-label text classification has improved greatly in recent years. Liu et al.[1] introduce RecAgent-LLaMA, a hybrid LLM–Graph Transformer that fuses prompt-based semantic retrieval, Transformer-XL/GAT session modeling, and cross-attention re-ranking to address cold-start and sparsity. These LLM-driven semantic priors and structured signals can complement HARTE by strengthening risk-aware representations and improving hierarchical consistency under scarce supervision., and Lin et al.[2] applied deep hierarchical networks to solve label imbalance. Luo et al.[3] present TriMedTune, a triple-branch fine-tuning framework that combines Hierarchical Visual Prompt Injection, diagnostic terminology alignment, and uncertainty-regularized knowledge distillation with LoRA-based training. Its uncertainty-aware distillation and terminology alignment are transferable to strengthen HARTE’s KD and calibration components by improving label consistency and robust fusion under scarce supervision., and Yu[4] proposes a prior-guided spatiotemporal GNN that fuses Transformer temporal embeddings, GNN message passing with adaptive edge dropout, DAG constraints, and expert-prior refinement for robust causal discovery. Its causal constraints and prior-guided calibration can inform HARTE’s hierarchical consistency and uncertainty-aware fusion. Sun[5] introduces MALLM, a scalable multi-agent LLaMA-2 framework using domain-adaptive pretraining, retrieval-augmented generation, cross-modal fusion, and knowledge distillation for low-resource concept extraction. Its agent orchestration and RAG-based semantic normalization can strengthen HARTE’s risk-aware encoding and hierarchical label consistency under scarce annotations.

Knowledge distillation is another key technique for improving efficiency. Moslemi et al.[6] summarized recent progress in distillation methods. Hussain et al.[7] improved task-specific distillation for pre-trained transformers,Guo et al.[8] propose MHST-GB, which fuses modality-specific neural encoders via correlation-guided attention with a parallel LightGBM branch and feedback-driven attention weighting. Its hybrid neural–tree integration and importance-guided fusion can inform HARTE’s multi-encoder fusion and calibration. and Liu et al.[9] transferred knowledge from BERT into smaller networks for faster inference. These works improved efficiency but seldom considered hierarchical adaptation or uncertainty modeling.

III. Methodology

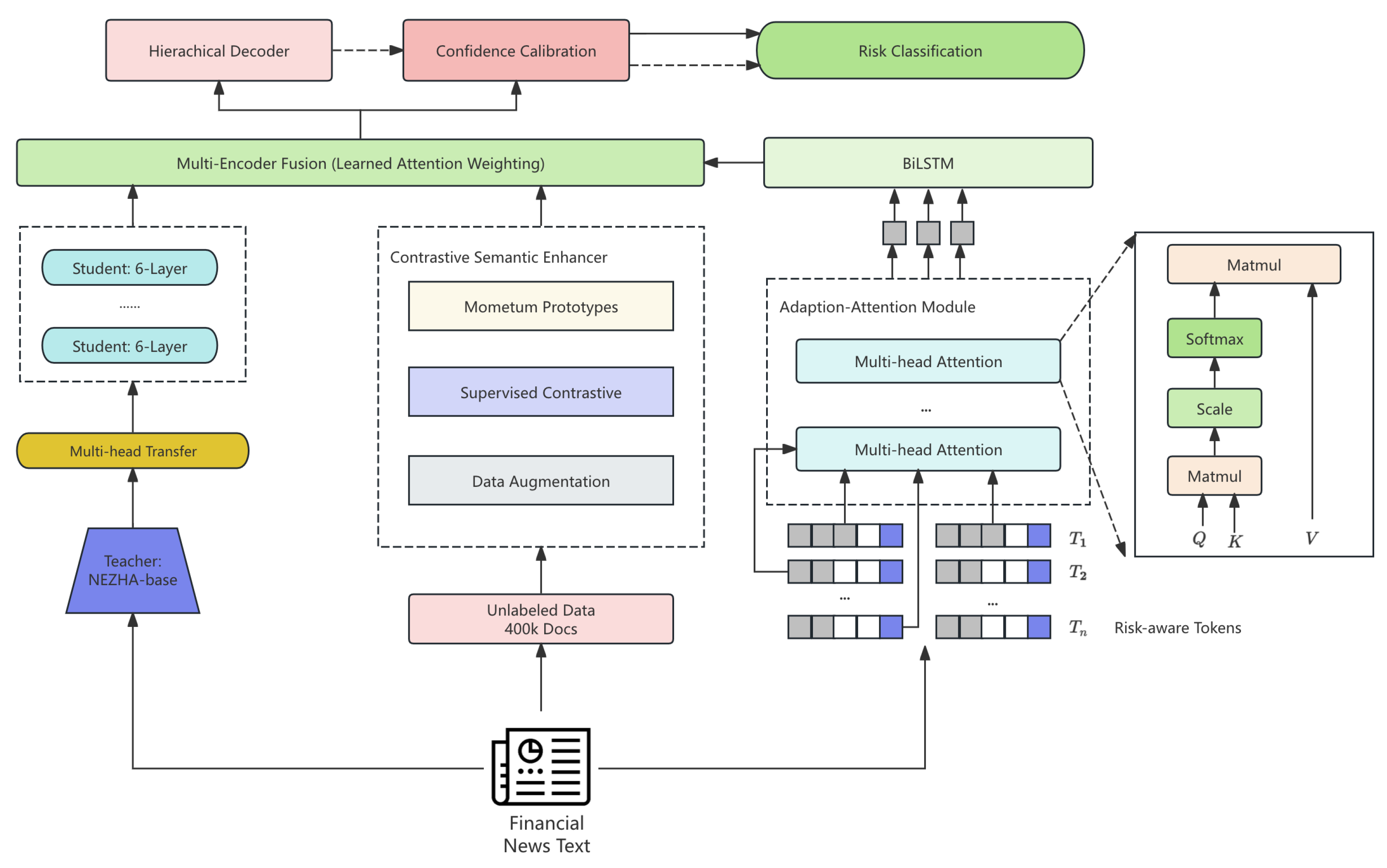
In this section, we present HARTE (Hierarchical Adaptive Risk-aware Transformer Ensemble), an integrated framework designed for hierarchical multi-label classification of financial risk events in Chinese news texts. The primary challenge lies in learning discriminative representations from limited labeled data while maintaining hierarchical label consistency across a two-tier taxonomy comprising primary and secondary risk categories.Our framework addresses these challenges through the integration of three specialized transformer encoders, each targeting distinct aspects of representation learning. The first component employs adaptive attention mechanisms with risk-aware token embeddings and bidirectional LSTM enhancement to capture contextualized sequential patterns. The second leverages contrastive learning with both instance-level and cluster-level objectives, enabling effective utilization of unlabeled data through augmentation strategies and momentum-based prototype learning. The third implements progressive knowledge distillation from larger teacher models, transferring soft predictions, intermediate representations, and attention patterns to compact student networks.These complementary representations are fused through a hierarchical decoder that explicitly models parent-child label dependencies via structured gating mechanisms and consistency regularization. The final ensemble employs confidence-calibrated fusion with Monte Carlo dropout-based uncertainty estimation, dynamically weighting model contributions based on sample-specific reliability.Our pre-training strategy introduces adaptive curriculum-based n-gram masking that progressively increases task difficulty, combined with risk-aware token selection prioritizing domain-relevant vocabulary. This approach demonstrates that sophisticated architectural innovations combined with domain-aware pre-training can effectively address data scarcity in specialized financial applications.

IV. HARTE Framework Overview

Figure I presents the overview of the HARTE Framework Architecture

HARTE integrates three encoders with a hierarchical decoder and a calibrated ensemble. The encoders provide risk-aware contextualization, contrastive semantic structure, and compact knowledge transfer. Fusion is attention-based. Decoding enforces parent–child constraints. Calibration uses Monte Carlo dropout and temperature scaling.

A. Contextualized Risk Encoder

Our initial experiments with vanilla BERT revealed a critical limitation: the fixed attention patterns failed to capture risk-specific linguistic phenomena prevalent in financial texts, such as negation scopes affecting sentiment polarity and modal expressions indicating uncertainty levels. This motivated the development of an adaptive attention mechanism.

1. Risk-Aware Token Representation

Standard BERT embeddings encode only lexical, positional, and segment information. We augment this with learnable risk type embeddings that inject coarse-grained category information:

$${\mathbf{E}}_i={\mathbf{W}}_e\left[x_i\right]+{\mathbf{P}}_i+{\mathbf{S}}_i+{\mathbf{R}}_{\theta }\left[c_i\right]$$

(1)

where ${\mathbf{W}}_e\in {\mathbb{R}}^{\left|V\right|\times d}$ is the token embedding matrix with vocabulary size $\left|V\right|=3456$, ${\mathbf{P}}_i\in {\mathbb{R}}^d$ encodes position, ${\mathbf{S}}_i\in {\mathbb{R}}^d$ represents segment information, and ${\mathbf{R}}_{\theta }\in {\mathbb{R}}^{10\times d}$ contains learnable embeddings for the 10 primary risk categories. The coarse category $c_i$ is predicted by a lightweight pre-classifier operating on a shallow feature extractor.

An important implementation detail involves the initialization of ${\mathbf{R}}_{\theta }$. Random initialization led to training instability in early epochs. We instead initialize these embeddings using cluster centroids computed from labeled data representations in the pre-trained BERT space, which provided more stable convergence.

2. Adaptive Multi-Head Attention

Traditional multi-head attention applies uniform computation across heads. We introduce dynamic gating that allows the model to selectively emphasize different attention patterns based on input characteristics:

$${\mathbf{g}}_i=\sigma ({\mathbf{W}}_g·\mathrm{LayerNorm}\left({\mathbf{h}}_i^{agg}\right)+{\mathbf{b}}_g)$$

(2)

$$\mathrm{AdaptiveAttn}(\mathbf{Q},\mathbf{K},\mathbf{V})=\sum _{i=1}^h{\mathbf{g}}_i\odot {\mathrm{head}}_i·{\mathbf{W}}^O$$

(3)

where ${\mathbf{h}}_i^{agg}\in {\mathbb{R}}^d$ aggregates information from previous layers, ${\mathbf{g}}_i\in {(0,1)}^d$ is the learned gate controlling head i’s contribution, ⊙ denotes Hadamard product, and $h=12$ is the number of attention heads.

Each attention head computes:

$${\mathrm{head}}_i=\mathrm{softmax}\left({\displaystyle \frac{\mathbf{Q}{\mathbf{W}}_i^Q{\left(\mathbf{K}{\mathbf{W}}_i^K\right)}^T}{\sqrt{d_k}}}\right)\mathbf{V}{\mathbf{W}}_i^V$$

(4)

with $d_k=d/h=64$ as the key dimension.

During experimentation, we found that applying gating at every layer caused gradient vanishing in deeper layers. We therefore apply adaptive attention only in the top 4 transformer layers, using standard attention in lower layers to maintain stable gradient flow.

3. BiLSTM Enhancement Layer

While transformer self-attention excels at capturing long-range dependencies, it can dilute sequential information due to its permutation-invariant nature within the attention window. Our experiments showed that adding recurrent connections significantly improved performance on longer documents. We integrate a bidirectional LSTM after the final transformer layer:

$${\overrightarrow{\mathbf{h}}}_t={\mathrm{LSTM}}_{fw}({\overrightarrow{\mathbf{h}}}_{t-1},{\mathbf{z}}_t;{\mathbf{W}}_{lstm}^{fw})$$

(5)

$${\overleftarrow{\mathbf{h}}}_t={\mathrm{LSTM}}_{bw}({\overleftarrow{\mathbf{h}}}_{t+1},{\mathbf{z}}_t;{\mathbf{W}}_{lstm}^{bw})$$

(6)

where ${\mathbf{z}}_t\in {\mathbb{R}}^d$ is the transformer output at position t. The bidirectional hidden states are combined through a learned fusion gate:

$${\mathbf{f}}_t=\sigma ({\mathbf{W}}_f[{\overrightarrow{\mathbf{h}}}_t;{\overleftarrow{\mathbf{h}}}_t;{\mathbf{z}}_t]+{\mathbf{b}}_f)$$

(7)

$${\mathbf{o}}_t^{ctx}={\mathbf{f}}_t\odot [{\overrightarrow{\mathbf{h}}}_t;{\overleftarrow{\mathbf{h}}}_t]+(1-{\mathbf{f}}_t)\odot {\mathbf{z}}_t$$

(8)

The fusion gate proved crucial. Without it, directly concatenating LSTM outputs with transformer representations caused dimension explosion and overfitting on our limited training set. The gate allows the model to adaptively balance between recurrent and attention-based features.

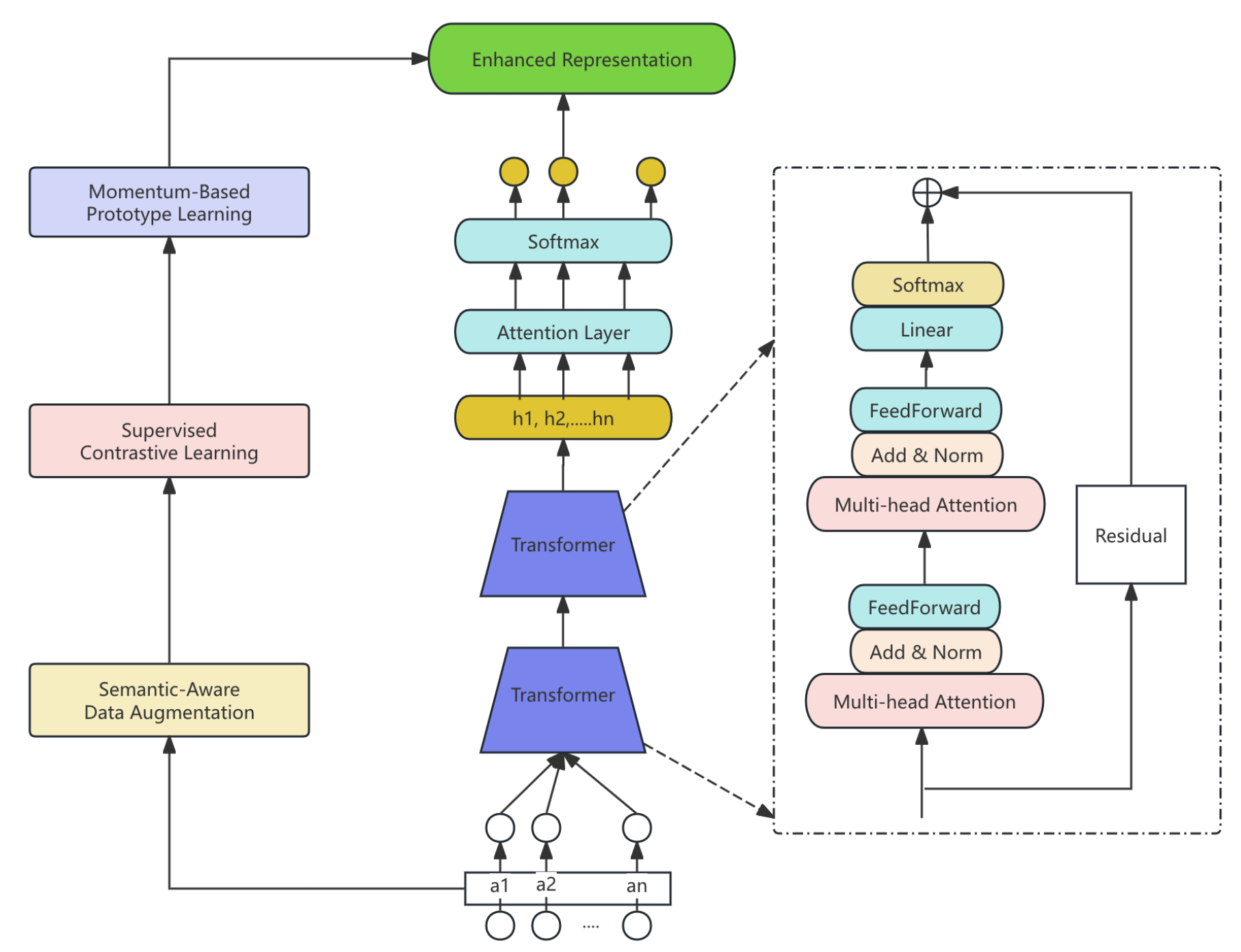
B. Contrastive Semantic Enhancer

We leverage 400K unlabeled documents to augment supervised training with instance- and prototype-level contrastive objectives, as pre-training alone provided negligible benefit. Figure II illustrates the module. Semantic-preserving augmentations generate two correlated views per document using a financial synonym lexicon (8,732 pairs), English back-translation, and span shuffling. Replacement above 30% degrades coherence; we adopt mild strengths ${\rho }_1=0.15$ and ${\rho }_2=0.10$.

Encoder outputs are projected and $L_2$-normalized; supervised contrastive learning forms positives for multi-label samples within the batch (size 128). Class prototypes (one per label, $C=45$) are updated by exponential moving average with momentum $0.999$; training aligns instances to their prototypes while contrasting against all prototypes. A norm-based regularizer stabilizes rare labels (weight $0.01$, margin $0.5$).

C. Knowledge Distillation Branch

We distill a NEZHA-large teacher (∼330M) into a 6-layer student. The teacher is continued-pretrained on 4M unlabeled financial documents and fine-tuned on 14,013 labeled samples for 10 epochs (LR $1\times {10}^{-5}$, batch 32). Teacher checkpoints from epochs 3, 6, and 10 are ensembled. The KD weight ramps to 0.7 by epoch 5.

We combine three signals. (1) Soft-label distillation with temperature $T=4.0$. (2) Hidden-state alignment via learned linear projections, matching student layer l to teacher layer $\varphi \left(l\right)=2l$. (3) Attention transfer by minimizing head-wise discrepancies between attention maps. The total objective is a weighted sum with coefficients ${\alpha }_1=1.0$, ${\alpha }_2=0.5$, and ${\alpha }_3=0.2$.

D. Hierarchical Label Decoder

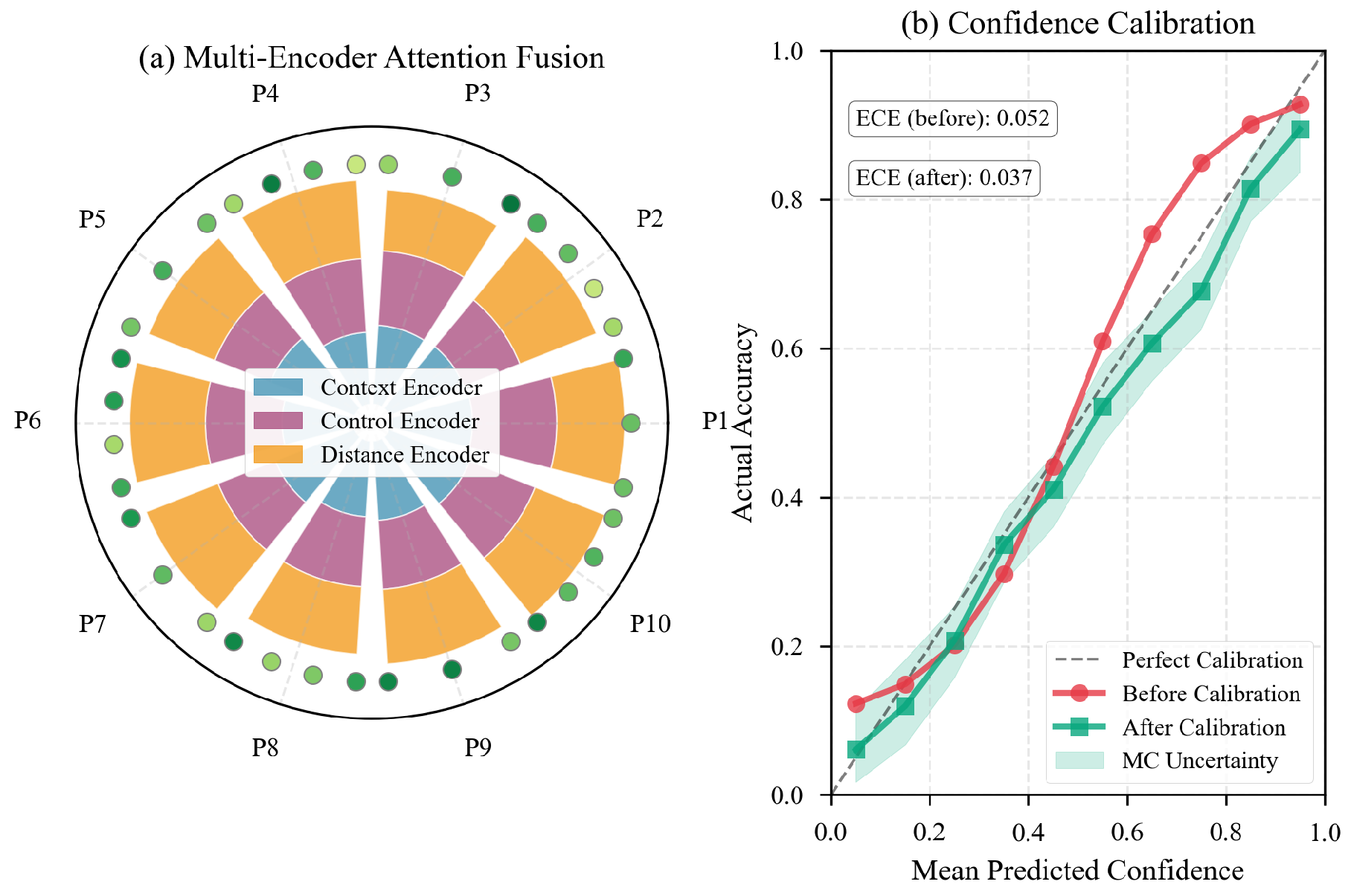
We exploit the two-tier taxonomy (10 primary, 35 secondary) and fuse multi-encoder signals by attention, followed by calibrated ensembling. Figure III shows the architecture.

Let ${\mathbf{h}}_{ctx},{\mathbf{h}}_{ctr},{\mathbf{h}}_{dst}$ be CLS vectors from three encoders. Attention weights $\mathbf{a}=[a_1,a_2,a_3]$ produce

$${\mathbf{h}}_{fused}=a_1{\mathbf{h}}_{ctx}+a_2{\mathbf{h}}_{ctr}+a_3{\mathbf{h}}_{dst}.$$

(9)

Primary logits are mapped to probabilities, which gate secondary predictions via a fixed parent–child mask ${\mathbf{M}}_{hier}$. A hierarchical consistency regularizer penalizes secondary–primary conflicts; its weight increases linearly to 0.3 by epoch five.

E. Confidence-Calibrated Ensemble

We compute encoder-wise uncertainty via Monte Carlo dropout (10 samples, rate 0.1), aggregate per-label variance into a sample-level score, and assign dynamic fusion weights by inverse-uncertainty softmax ($\gamma =5.0$). The weighted probabilities are then temperature-calibrated on a 1,000-sample set using Platt scaling to minimize ECE (10 bins):

$${\mathbf{p}}_i^{ens}=\sigma \left({\displaystyle \frac{1}{T_{cal}}}logit\left(\sum _m{w}_i^{\left(m\right)}{\widehat{\mathbf{p}}}_i^{\left(m\right)}\right)+b_{cal}\right).$$

(10)

F. Pre-Training Innovations

We combine curriculum-based dynamic masking with risk-aware token prioritization. The masking schedule gradually increases the mask rate from 0.10 to 0.25 and shifts from unigram to longer n-gram spans, raising reconstruction difficulty over training while preserving fluency. Risk-aware masking prioritizes tokens indicative of financial risk using PMI-based scores derived from labeled data, increasing the probability of masking domain-salient terms. Together, these strategies concentrate pre-training on informative structures and semantics.

V. Evaluation Metrics

We use five metrics for hierarchical multi-label classification.

Macro-F1: Macro average of per-class F1:

$$\mathrm{Macro}\text{-}\mathrm{F}1={\displaystyle \frac{1}{C}}\sum _{c=1}^C{\mathrm{F}1}_c$$

(11)

Micro-F1: Global precision–recall aggregation:

$$\mathrm{Micro}\text{-}\mathrm{F}1=2·{\displaystyle \frac{P_{micro}·R_{micro}}{P_{micro}+R_{micro}}}$$

(12)

Hamming Loss: Fraction of incorrect label predictions:

$$\mathrm{Hamming}={\displaystyle \frac{1}{NC}}\sum _{i=1}^N\sum _{c=1}^C\mathbb{1}(y_{i,c}\ne {\widehat{y}}_{i,c})$$

(13)

HC-Score: Hierarchical consistency; ${\mathcal{V}}_i$ are parent–child violations:

$$\mathrm{HC}=1-{\displaystyle \frac{1}{N}}\sum _{i=1}^N{\displaystyle \frac{|{\mathcal{V}}_i|}{|{\widehat{\mathbf{y}}}_i|}}$$

(14)

Coverage Error: Label ranking coverage:

$$\mathrm{Cov}={\displaystyle \frac{1}{N}}\sum _{i=1}^N\underset{c\in {\mathbf{y}}_i}{max}{\mathrm{rank}}_{i,c}-1$$

(15)

VI. Experimental Results

We use 14,013 labeled samples with an 80/10/10 train/val/test split and 400K unlabeled documents. Training adopts AdamW (lr=$2\times {10}^{-5}$, weight decay=0.01) for 20 epochs on an RTX 3090. Vocabulary size is 3,456.

Baselines: Six Chinese PLMs (BERT-base, RoBERTa-wwm-ext, NEZHA-base, ELECTRA-base, MacBERT-base, XLNet-base) and three single-component variants.

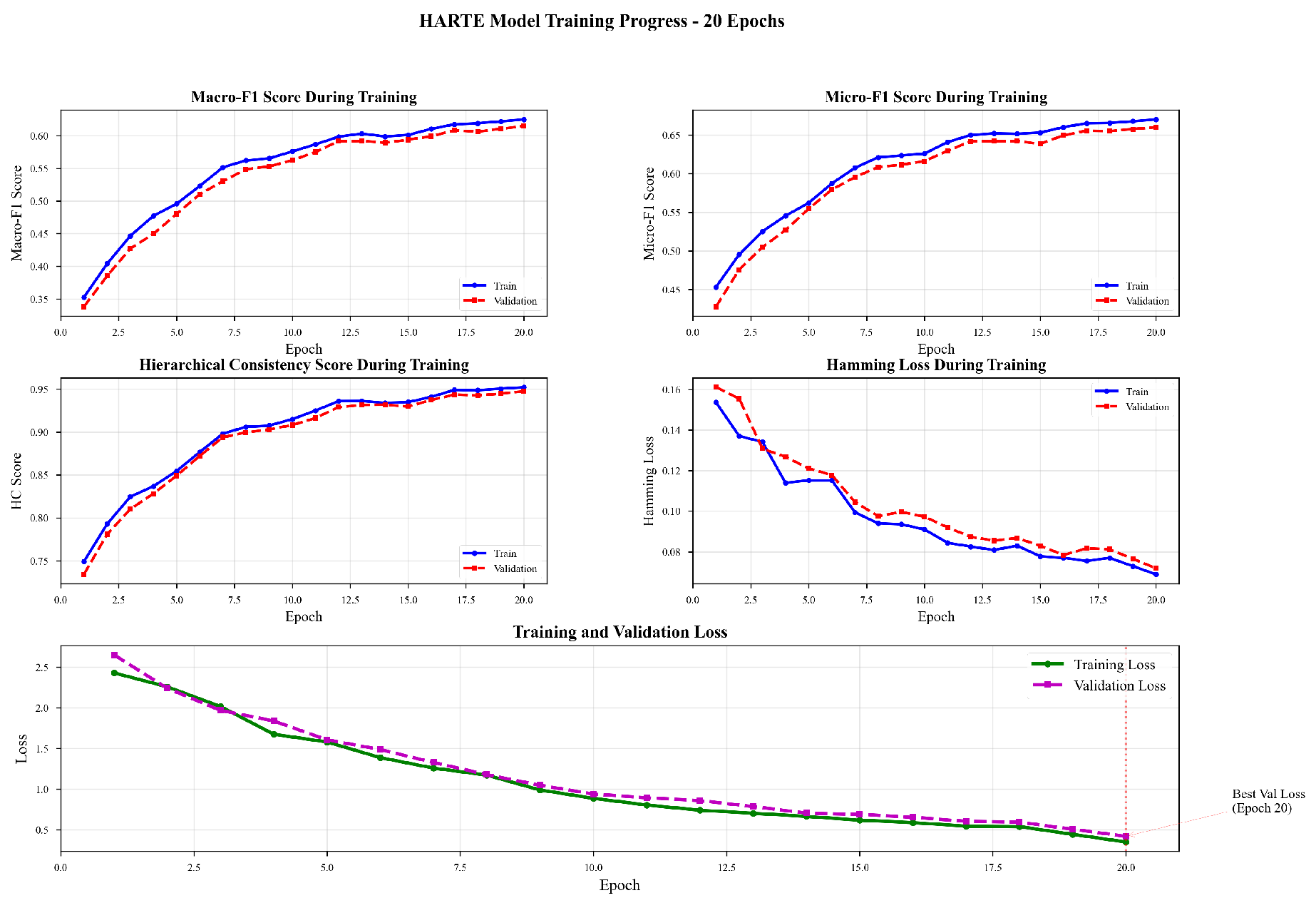
Table I and Table II show HARTE-Full achieves 0.6247 Macro-F1, outperforming the best baseline (MacBERT) by 4.49% and BERT-base by 8.24%. The HC-Score of 0.9523 validates hierarchical consistency. HARTE-NoEns (single encoder) reaches 0.6098, while ensemble adds 1.49% gain. And the changes in model training indicators are shown in Figure IV.

Ablation Analysis: Removing contrastive learning yields the largest drop (-2.33 points), followed by hierarchical gating (-1.75) and ensemble fusion (-1.49). Single encoders score 0.57–0.58 Macro-F1, confirming fusion benefits. Risk-aware masking adds +0.79. HARTE-Full incurs 3.2× BERT-base inference cost; HARTE-NoEns achieves 0.6098 with 1.1× overhead.

VII. Conclusion

We presented HARTE, a hierarchical multi-encoder framework for financial risk classification. Integrating adaptive attention, contrastive learning, knowledge distillation, and hierarchical decoding, HARTE achieves 0.6247 Macro-F1 with 0.9523 hierarchical consistency, improving 6.8% over BERT-base. Ablations confirm contrastive learning and hierarchical mechanisms are most critical. Our work demonstrates that architectural innovation effectively compensates for limited labeled data in specialized domains.