1. Introduction
Environmental degradation, particularly air pollution, ranks among the foremost threats to global health [
1]. This crisis is primarily driven by the rapid expansion of urban industrial activity, a growing global transportation network, and large-scale biomass burning, which together emit a complex mixture of hazardous particulate matter and gaseous pollutants. These insidious emissions significantly degrade air quality, leading to a marked increase in a wide range of diseases, from acute respiratory infections to chronic cardiovascular conditions and cancer. The most devastating impacts are concentrated in densely populated megacities, where intense emission sources and widespread human exposure converge with dangerous consequences. Consequently, the development and implementation of comprehensive, intelligent air quality monitoring (AQM) systems have become an indispensable tool for public health protection. The key challenge lies not only in obtaining reliable data but also in ensuring its timeliness, broad geographic coverage, and continuous operation [
2,
3]. The data from these systems provide the essential foundation for effective environmental policies, proactive public health advisories, and rigorous regulatory measures. Ultimately, this systematic and technologically advanced approach is vital for safeguarding populations, guiding sustainable urban development, and securing a healthier quality of life for the millions of people in the world’s ever-expanding urban centers.
Traditional air pollution monitoring, which relies on fixed stations and temporary laboratories, is often hampered by high costs and an inability to provide dense spatial coverage. Modern systems overcome these limitations by deploying extensive networks of low-cost wireless sensors. A notable advancement is the integration of mobile sensors mounted on vehicles or drones, enabling dynamic, real-time data collection along transport routes and identifying pollution hotspots that fixed stations inevitably miss [
4]. These pervasive sensor networks are a significant application of the Internet of Things (IoT), forming a core component of the smart city infrastructure [
5]. Mobile air quality sensors transmit a continuous data stream to decision-making centers, enabling the creation of highly detailed, real-time pollution maps. This capability facilitates intelligent urban management, including adaptive traffic control to reduce congestion-related emissions and the delivery of personalized air quality alerts to citizens. However, due to constraints from limited resources, these monitoring networks require careful optimization. A systematic review of the methods employed for this purpose is provided in [
6]. An attractive optimization strategy is to cluster sensors into normal and polluted zones. This enables a dynamic transmission policy as follows. Sensors in polluted zones intensify operation for high-resolution data, while those in clean zones reduce reporting rates and send summaries to conserve energy and alleviate network load. A significant challenge, however, arises from the fuzzy and unstable boundaries of these clusters.
The distribution and concentration of air pollutants, including particles, volatile organic compounds, and microorganisms, are largely dependent on stochastic and highly dynamic meteorological factors [
7,
8,
9]. Urban structure, specifically building density, green spaces, and the shape and size of buildings contributes to air pollution patterns by either facilitating or inhibiting the dispersion of pollutants [
10,
11]. This is exemplified by the urban canyon effect, where tall buildings along narrow streets trap emissions, creating localized pockets of dangerously high pollution concentrations [
12,
13]. The concentration of pollutants like particulate matter (PM
2.5), nitrogen dioxide (NO₂), and ozone (O₃) is characterized by pronounced spatiotemporal heterogeneity. Moreover, this variability is further compounded by vertical dynamics [
14]. Therefore, from a geometric perspective, the spatiotemporal distribution of pollutant concentrations forms a heterogeneous and fluid patchwork. Transitions between “polluted” and “clean” zones can be undefined. Sensors located just a few meters apart can detect significantly different pollutant levels. This dynamic and stochastic nature of pollution makes it unrealistic to divide mobile sensors into strictly polluted and unpolluted clusters, rendering the use of hard clustering algorithms impractical.
This paper presents a probabilistic clustering approach for air quality sensors based on the Expectation-Maximization (EM) algorithm. Its practical application is a dynamic data transmission policy that uses soft cluster membership probabilities to intelligently allocate network resources. This policy achieves significant energy savings in clean zones by reducing transmission frequency and volume, while simultaneously enhancing monitoring resolution in polluted areas through more intensive data collection. This intensification of operation in polluted zones is driven by several factors. It enables high-frequency tracking of pollution dynamics and provides more detailed data for pollution source identification and analysis. Furthermore, the volume of transmitted data can be increased to ensure reliable transmission of critical environmental data.
This paper presents a probabilistic clustering framework for sensor networks based on the Expectation-Maximization (EM) algorithm. The potential practical contribution is a dynamic data transmission policy, driven by soft cluster membership probabilities, which intelligently allocates network resources. This policy yields achieves significant energy savings in clean zones by curtailing data transmission frequency and volume, while simultaneously enhancing the monitoring resolution in polluted areas through intensified sensor operation. This intensification of operation in polluted zones is driven by several factors. It enables high-frequency tracking of pollution dynamics and provides more detailed data for pollution source identification and analysis. Furthermore, the volume of transmitted data can be increased to ensure reliable transmission of critical environmental data [
15]. Consequently, powering down sensors in clean zones becomes a strategically justified mechanism for energy conservation. Informed by the insights from our prior work [
16], this paper introduces an efficient and problem-specific realization of the EM clustering algorithm. To the best of our knowledge, this constitutes the first implementation of EM clustering in this context.
The rest of this paper is organized as follows. The paper proceeds with a review of related work in
Section 2.
Section 3 details the proposed methodology, providing a comprehensive description of the Expectation-Maximization algorithm, the specification of the probabilistic air pollution model, and the specific implementation of the EM clustering.
Section 4 presents a performance analysis, and Section 5 provides concluding remarks.
2. Related Work
The escalating challenge of urban air quality has intensified the focus on advanced pollution monitoring systems. Current research utilizes a heterogeneous mix of stationary reference stations, mobile laboratories, and pervasive networks of wireless sensors [
16,
17,
18]. A foundational review in this domain [
17] systematically evaluates the deployment of Wireless Sensor Networks (WSNs) for urban atmospheric sensing. It underscores the critical integration of geospatial data, IoT architectures, and solid-state sensor technologies. The analysis prioritizes key network performance metrics, including energy efficiency, nodal lifetime, packet delivery latency, and network throughput, which are paramount for sustainable large-scale deployment. Building on these principles, a practical implementation is demonstrated in [
19], which details an industrial air quality monitoring system embedded within smart city infrastructure. This architecture co-opts the city’s street lighting grid to serve as a backbone for sensor placement and data backhaul. By utilizing streetlights as powered, elevated nodes, the system facilitates real-time data acquisition from distributed sensors, forwarding telemetry to aggregation points for processing and enabling dynamic public health alerts. The paper [
20] presents a technical analysis of the latest advances in air pollution detection with a focus on air pollutants, sensor technologies, and IoT frameworks.
The review by [
21] analyzes the application of advanced artificial intelligence (AI) in environmental research, covering both machine learning (ML) and deep learning (DL). It notes the current dominance of ML, highlighting the Random Forest method for achieving accuracies up to 98.2%. The study by [
22] asserts that low-cost air monitoring sensors can achieve high effectiveness when paired with modern ML methods. The authors emphasize that while sensor accuracy depends on factors like gas sensitivity and environmental conditions, ML models can capture complex interdependencies in sensor responses to correct readings. Their research demonstrates that even simple models like multiple linear regression, when implemented on a microcontroller, significantly enhance the performance of low-cost CO, O₃, and CO₂ sensors. To enhance calibration model performance, a low-cost, multi-parameter air quality monitoring system utilizing various machine learning algorithms is presented in [
23]. The work in [
24] describes a methodology that employs machine learning to predict air quality. The approach first applies a decision tree algorithm to extract direct rules for real-time detection, followed by a process-mining algorithm to model changes in air conditions.
Optimizing data transmission in air pollution monitoring is essential for balancing system reliability with operational costs, primarily by reducing power consumption and network congestion [
25,
26]. This can be achieved through strategies such as optimized transmission scheduling, controlling the volume of transmitted data, reducing packet sizes, rational choice of the number of sensors, and adopting energy-efficient communication protocols [
16,
27]. While frequent data collection improves the accuracy of air quality measurements, it significantly increases the load on both the sensor network and the data processing center.
Efficient transmission scheduling is crucial for balancing monitoring reliability with communication costs [
28,
29]. In areas with dense sensor deployment, transmission frequency can be reduced for select nodes to minimize data redundancy. Conversely, in regions with rapidly fluctuating pollutant concentrations, schedules can prioritize higher transmission rates for more accurate tracking. For battery-powered sensors, longevity is a primary constraint, making energy conservation a key objective. One strategy to this end [
28] involves neighboring nodes exchanging data exclusively upon detecting critical events. Dual-prediction strategies offer further efficiency: both the sensor and base station maintain a shared model to predict readings, triggering a transmission only when the actual measurement deviates beyond a predefined threshold. This selective communication paradigm significantly reduces redundant data transfer, thereby conserving energy and extending the operational network lifespan.
A principal strategy for reducing the substantial data volume transmitted in WSNs-based monitoring systems is the application of data compression. The paper [
30] proposes an optimization algorithm based on spatial and temporal data compression for solving monitoring problems in underground tunnels. The authors introduce spatial and temporal correlation functions for data compression and recovery.
Previous studies have proposed various models for air quality analysis. For example, Markov process theory was used to model environmental pollution dynamics [
31], and unsupervised learning, specifically the EM algorithm, was used to estimate the parameters of an air quality model in the suburbs of Paris [
32]. In [
33], DL technique is used to predict air quality, using the EM algorithm to impute missing data. The authors conclude that approaches based on training datasets are insufficient.
The performance optimization of environmental monitoring systems is a widely researched field, with methodologies spanning various approaches [
29,
34]. The authors of [
34] focus on optimizing sensor network design for pollution monitoring, specifically to identify atmospheric carbon dioxide hotspots. Their analysis of LoRaWAN-based wireless sensor networks employs a combined modeling and physical implementation approach, evaluated using packet loss metrics. Shifting to network design under uncertainty, the paper [
29] tackles the challenge of designing AQM networks in coal ports, considering operational efficiency and uncertain wind conditions. Their proposed method formulates the deterministic AQM network design as a maximum-weight location problem, solving it with a progressive coverage model that incorporates a cooperative strategy.
3. Methodology
3.1. Expectation–Maximization Algorithm
The power of EM clustering lies in its probabilistic interpretation. Each data point does not belong rigidly to a single cluster but is instead described by a distribution of memberships. This reflects uncertainty in the data and aligns well with re-al-world situations where boundaries between groups are diffuse rather than sharp. Moreover, EM provides a mathematically principled way to handle over-lapping clusters, noisy measurements, and dynamic changes in the data distribution. These characteristics make it particularly well-suited for modeling air quality monitoring data, where pollutant concentrations exhibit smooth gradients, temporal fluctuations, and heterogeneous spatial distributions.
The EM algorithm is a maximum likelihood estimation framework for models involving latent (unobserved) variables. In clustering problems, the latent variable is the cluster membership of each data point, which is not directly observed. Unlike hard clustering methods that assign each data point to exactly one cluster, EM adopts a probabilistic model in which every observation may belong to each cluster with some probability. This approach is especially powerful when data are generated from a mixture of probability distributions, and the goal is to estimate both the mixture parameters and the soft cluster assignments.
Let us introduce the formalism of the EM algorithm [
35,
36]. Let the dataset be
, and assume the data are drawn from a mixture of
distributions, where the probability mass function (pmf) or probability density function (pdf) of the
-th distribution is denoted by
. Thus, each distribution is parameterized by
(individual parameter or set of parameters), and each cluster
k has a mixing proportion
, with
The pdf/pmf of the mixture model is
where
The notion of cluster membership is formalized through the introduction of a set of latent variables
, one for each observation. Each
is a
K-dimensional binary random vector indicating which component generated the corresponding data point
. This vector uses a one-hot encoding, meaning
Assuming the data points are independent and identically distributed, the complete-data likelihood for the full dataset is then
For computational simplicity, the model parameters are estimated by maximizing the expected value of the complete-data log-likelihood function:
Since the latent variables are unobserved, the function cannot be optimized directly. Instead, the EM algorithm maximizes its expected value, taken with respect to the posterior distribution of Z given the observed data X and the current parameter estimates . Thus, the EM algorithm proceeds iteratively in two steps as follows.
Compute the posterior probabilities, often referred to as responsibilities, that each data point that each data point belongs to each cluster, given the current parameter estimates
. This responsibility, denoted
, is the conditional expectation of the latent variable
given the observed data and the current parameters:
An application of Bayes’ theorem provides the closed-form expression for the posterior responsibility, quantifying the probability that component
k generated observation
:
These probabilities express the degree of membership of point
in cluster
. Each point is thus softly assigned to all clusters, with weights summing to 1 across clusters. This expression can be further simplified by substituting into it a probability mass (or density) function of practical interest. Next, since
is a function of the unobserved latent variables Z, it is necessary to consider its expectation conditional on the observed data
and current parameter estimates
which defines the
Q-function:
The M-step involves maximizing the
Q-function, computed in the previous E-step, with respect to the model parameters
to obtain an updated estimate:
The
Q-function can be separated into two independent parts: one relating to the mixture weights and the other to the parameters of the probability distributions. This separation allows us to address each optimization problem individually. Therefore, taking (1) into account and applying the method of Lagrange multipliers, we derive the update rules for the mixture parameters:
The update rules for the distribution parameters are derived by maximizing the corresponding term of the
Q-function:
In other words, the parameters of each component distribution are re-estimated by weighted maximum likelihood, where the weights are the posterior probabilities . The E-step and M-step are alternated until convergence, typically measured by changes in the log-likelihood function or in the parameter set Θ. Furthermore, an iteration limit can be imposed with the goal of keeping the algorithm’s runtime within acceptable bounds. The algorithm is guaranteed to converge to at least a local maximum of the likelihood function.
3.2. Model Specification
Extending our prior work [
16], we consider air pollution monitoring through a sensor network capable of mobility. A mobile air quality sensor traverses a geographic region containing both areas of normal background air quality and zones with elevated pollution levels. The sensor is equipped to detect a specific pollutant and generates a message upon each significant detection event. The message generation process is modeled as a Poisson process, where the transmission rate is a function of the sensor’s location. Specifically, the message generation rate
is low when the sensor is outside the polluted zone, but it switches to a higher rate
(
) upon entering the polluted area. The Poisson distribution is a foundational model for data transmission and event count analysis in diverse systems including communication networks. For example, in a typical scenario, the time to detect a critical event with a reusable mobile air quality sensor follows an exponential distribution [
16]. The parameter
of this distribution is determined by the specific characteristics of the sensor, including its mobility and performance. Consequently, the number of critical events detected within a fixed time interval,
T, is described by a Poisson distribution with a rate parameter
. The probability of observing exactly
t events in this interval is given by the Poisson pmf:
here
is a random variable representing the number of events.
3.3. Refinement of EM Clustering
In the context of air quality monitoring, we consider the problem of distinguishing between regular background activity and air pollution events based on the number of alerts, , recorded by a sensor over a fixed time interval. The observed dataset , represents the count of alerts from all sensors in the monitoring area. We model these data as a mixture of two Poisson distributions, where the first component (), parameterized by , models the low-rate Poisson process of normal background activity, and the second component (), parameterized by (where >), models the high-rate process of alert generation characteristic of a pollution event. This approach accounts for the fundamental uncertainty in attributing any individual observation with a high count to either a rare extreme value in the normal state or to a genuine pollution incident. The primary goal of applying the EM algorithm is to compute the responsibility for each sensor reading based on the estimated parameters (the mixing probabilities and the rates , ) thereby allowing each sensor’s reading to be probabilistically classified as either originating from a “polluted zone” or from the “normal state.” The properties of the Poisson distribution allow the update equations for the EM algorithm to be derived in a closed analytical form.
Therefore, we consider a mixture of two Poisson distributions parameterized by a mixing probability
, such that an observation belongs to class 1 with probability
and to class 2 with probability
. Following the structure of the general mixture model in (2), the specific probability mass function for a single data point
under a two-component Poisson mixture model is defined as
where
.
Substituting the Poisson probability mass function (12) into the responsibility formula and simplifying, we obtain the responsibility of cluster 1
The responsibility of cluster 2 is consequently
From a computational perspective, it is methodologically advantageous to structure the calculations in the following manner:
The inverse responsibility calculation is more numerically stable because it avoids underflow errors that arise when directly processing extremely small probability values. It structures the computation to work with larger, more manageable numbers instead of perilously tiny ones. This method is also more computationally efficient as it reduces the number of complex exponential calculations required per data point. The resulting speedup can be crucial for processing large datasets effectively in real time.
The performance of the EM algorithm is highly sensitive to its initial parameter values [
37]. In our case, if the initial values for the rate parameters
and
are identical, the model enters a symmetric state from which it cannot escape. This leads the algorithm to converge immediately to a degenerate solution where the parameter estimates for both components remain equal. Consequently, the model fails to recover the underlying mixture structure. To ensure a robust start, the initial values of Poisson distribution parameters are instead derived from the empirical data,
X, with the smaller parameter set to the dataset’s lower quartile and the larger one to the upper quartile.
Within the framework of the EM algorithm for a two-class mixture model, the computation defined by Formula (10) reduces to
The optimization problem (11) for finding parameter estimates of the distribution in this case reduces to the form:
The term
can be safely ignored in the optimization problem because it is a constant additive term with respect to the model parameters
, and therefore its removal does not change the location of the extremum of the objective function. Therefore, to find
we maximize the following function:
Set the derivative equal to zero to find the critical point:
Solving this equation yields the update rule for the parameter:
Let us check the second derivative to confirm that this critical point is a maximum.
A negative second derivative at the critical point confirms a maximum. The second derivative is always negative (unless all or are zero, which is a degenerate case). This conclusively proves that the obtained critical point is a global maximum for the function with respect to .
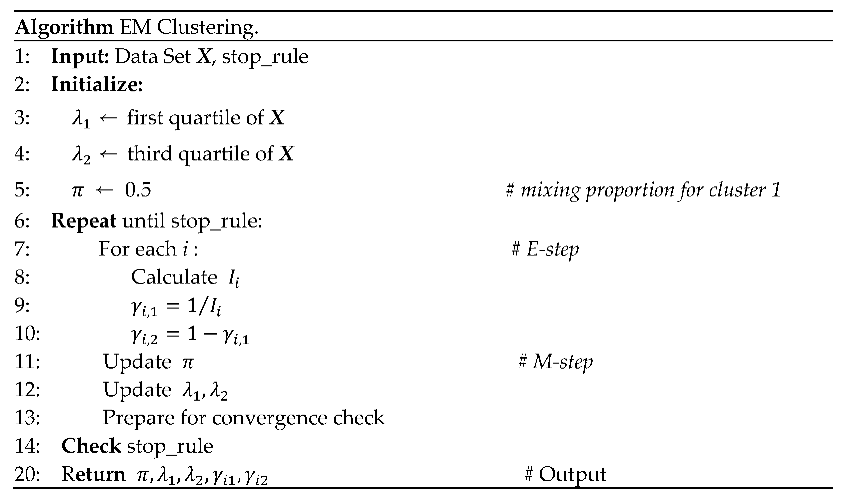
For completeness, we provide a compact pseudocode of the used EM clustering algorithm.
While the EM clustering algorithm does not have a definitive, universally optimal stopping rule, convergence is typically assessed by monitoring the relative increment in the observed data’s log-likelihood between iterations. The algorithm terminates once this change falls below a specified threshold, which indicates parameter stabilization near a local maximum. Additionally, a hard limit on the number of iterations can be set to prevent unnecessary computations should convergence be slow.
4. Performance Analysis
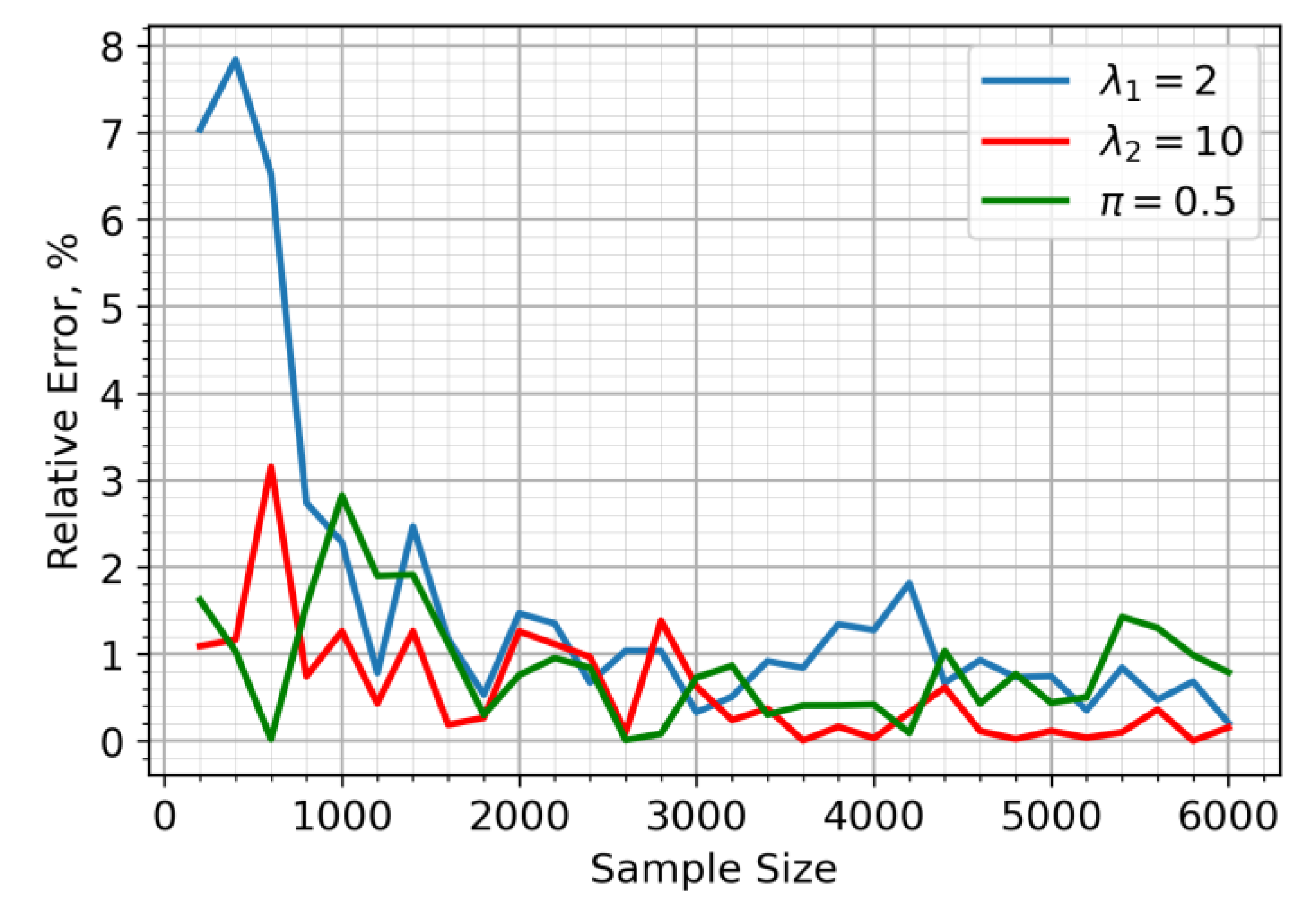
This section presents the results of a simulation-based performance evaluation of the EM algorithm for the soft clustering of air sensors. The objective is to evaluate the algorithm’s ability to correctly classify sensors into “normal air” or “pollution” clusters, under the assumption that the rate of detection for events of interest differs for each case. Our experimental procedure involves generating separate samples for two air quality scenarios using pseudorandom number generators for the Poisson distribution with different parameters. To generate a sample corresponding to observations in the normal situation, we use parameter , and for a sample corresponding to air pollution, we use parameter , where . These samples are combined and randomly shuffled to create a dataset with an unknown underlying structure, simulating data from a real sensor network. The EM algorithm is applied to this combined sample to estimate the mixture parameters and calculate the cluster membership probabilities (responsibilities). To evaluate the algorithm’s performance, the results are analyzed separately for each of the original samples.
The EM clustering algorithm demonstrates a strong ability to accurately estimate the underlying mixture components:
and
. As illustrated in
Figure 1, the relative error for each parameter remains low, generally not exceeding a few percent across the tested sample sizes. However, as the sample size grows, the error does not follow a monotonic decreasing trend but demonstrates fluctuations. This non-monotonic behavior is expected because the EM algorithm converges to a local maximum of the likelihood function. The specific random sample drawn for a given size can slightly bias the initial conditions or the convergence path, leading to minor variations in the final estimates. Consequently, while larger samples provide more stable estimates on average, the stochastic nature of both the data generation and the EM optimization process results in natural fluctuations in accuracy.
In
Figure 1, it is assumed that the sensors have an equal probability of being in either the clean or polluted air zones (
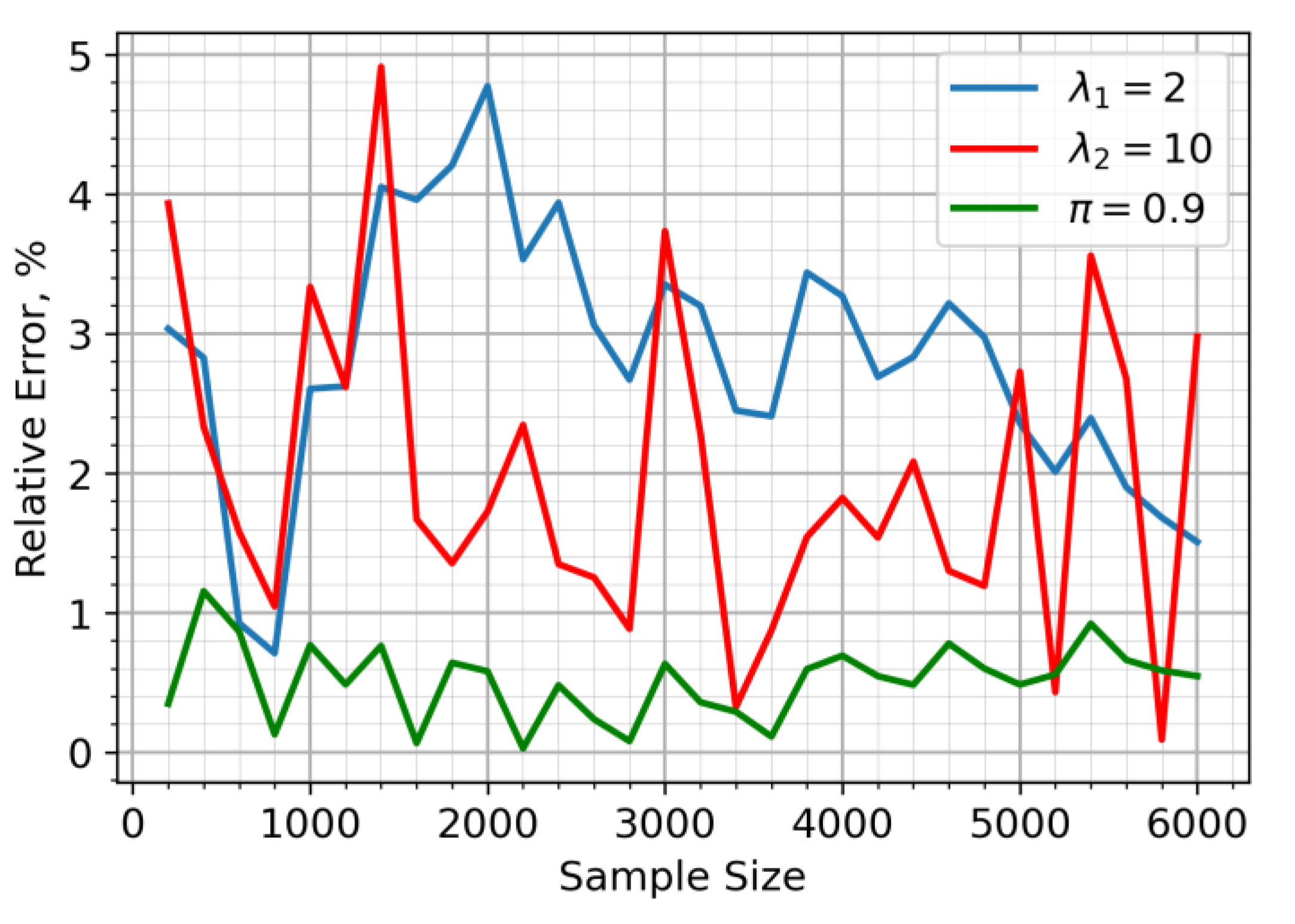
). The relative error of the parameter estimates, for the situation in which 90% of sensors are within the air pollution zone (
), is illustrated in
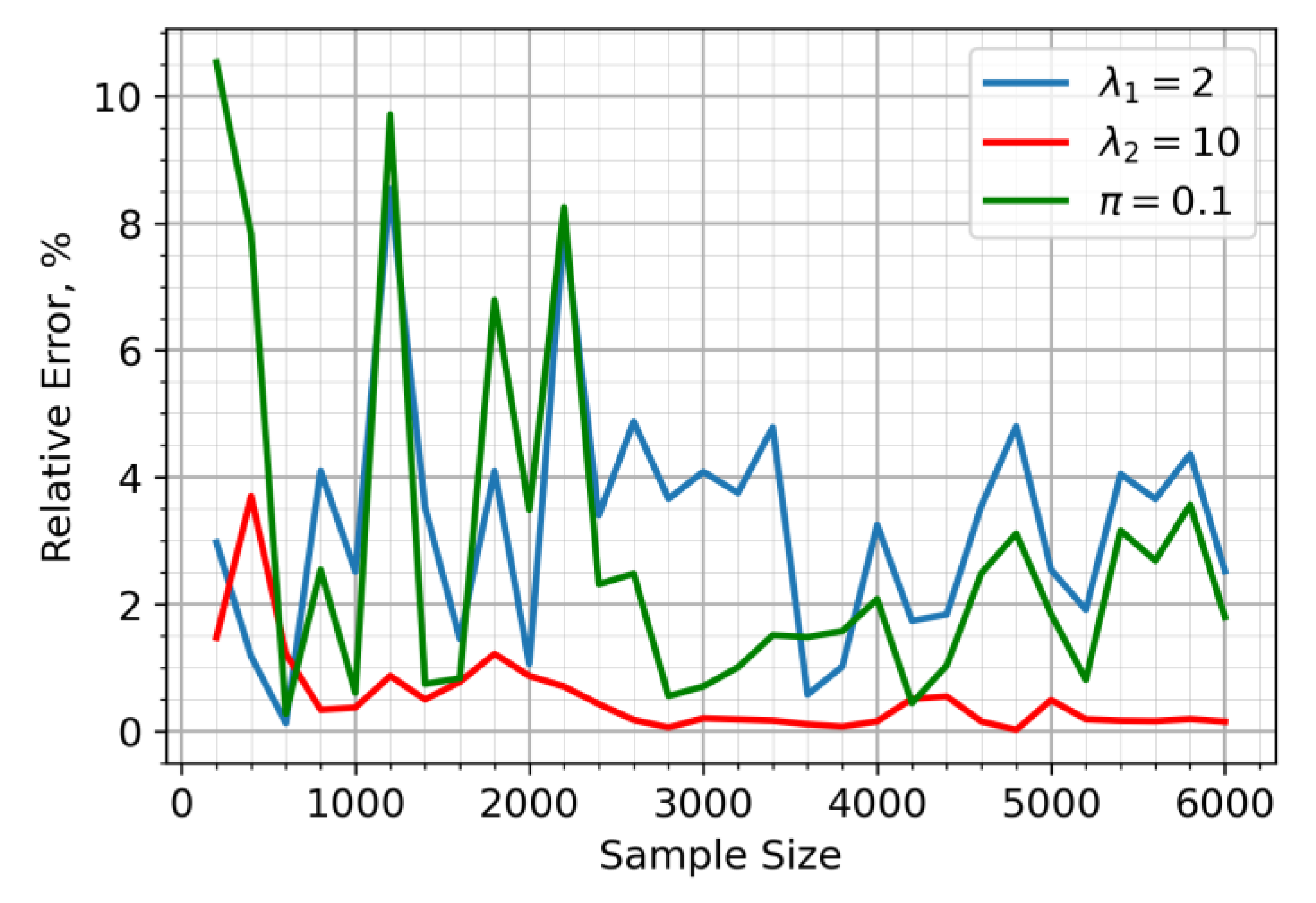
Figure 2. The proposed approach yielded a highly accurate and stable estimate for the λ₂ parameter, corresponding to sensor data from the pollution zone. While the accuracy of the λ₁ estimate decreased compared to the equal sample size scenario, this only impacted a minor portion of the sample (10%).
Figure 3 depicts the case where the majority of sensors (90%) are in unpolluted zones (
). As expected, the parameter estimates show noticeable fluctuations in accuracy, though these consistently stay within a 5% margin.
In all cases considered, the EM algorithm correctly assigns sensors to their corresponding class with near certainty (responsibilities are very close to 1).
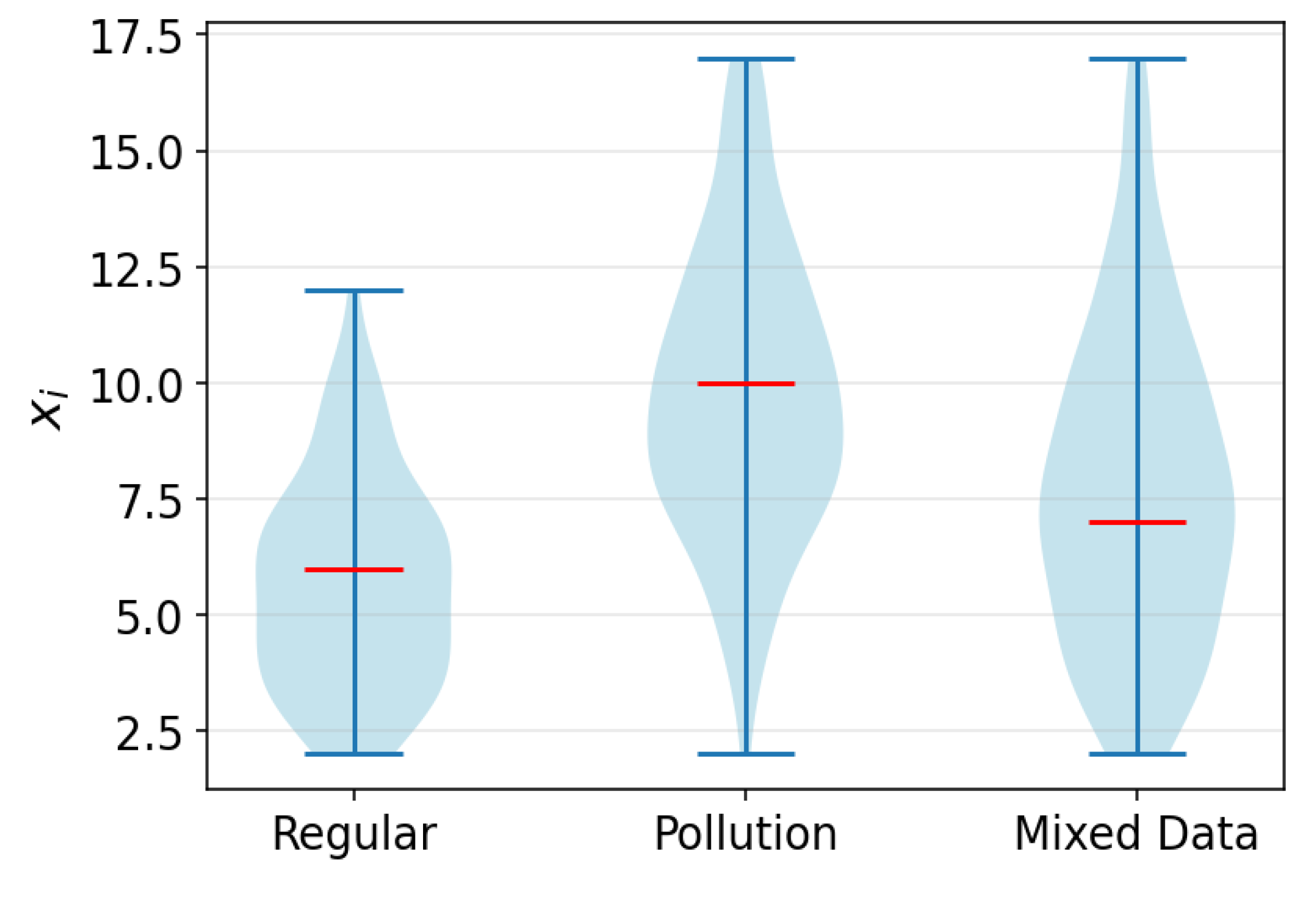
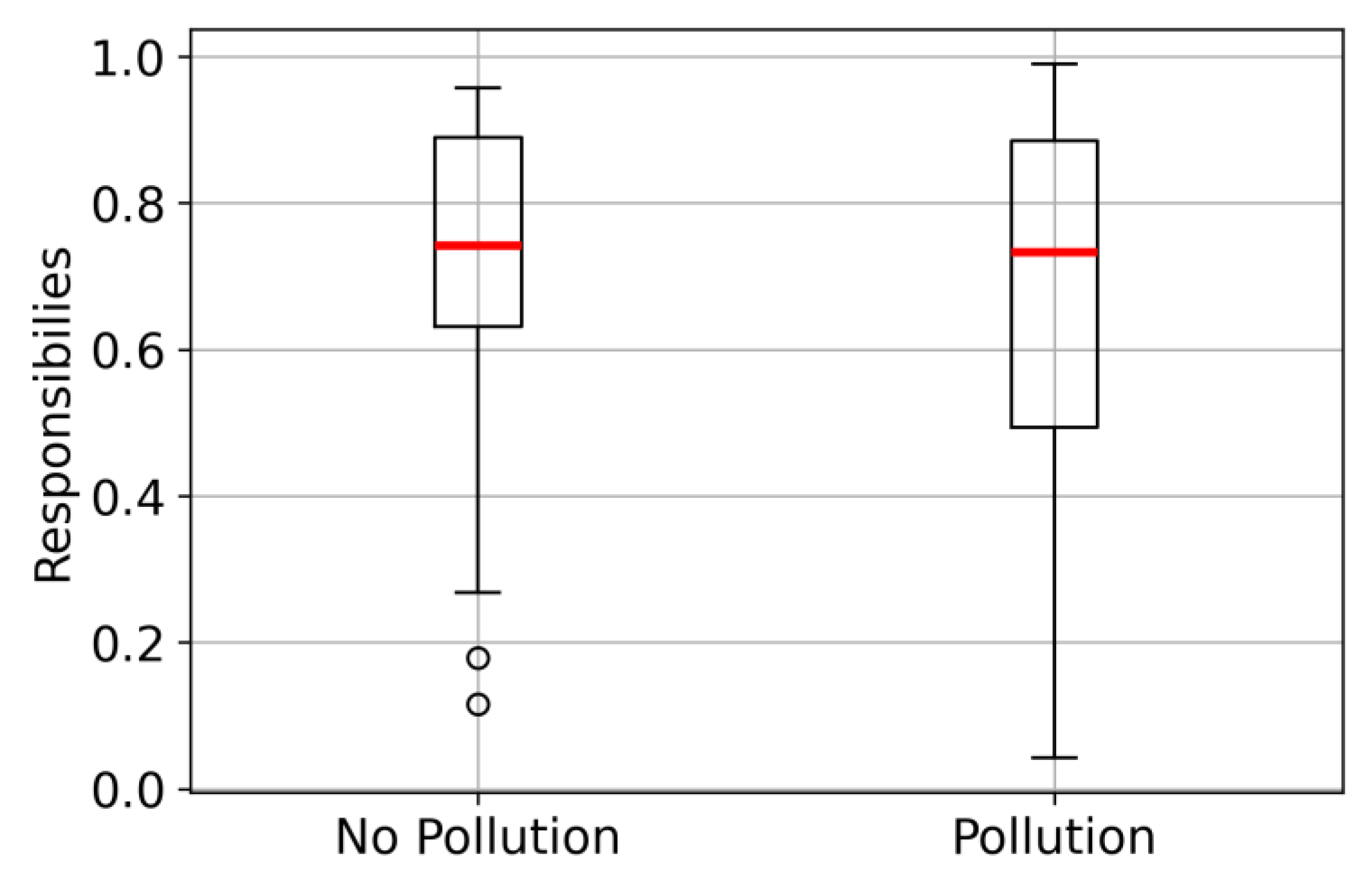
Let us consider an extreme scenario with a modest sample size (
N = 200) and relatively close detection intensities (
). The dataset generated for this situation is presented in
Figure 4 as a violin plot. This violin plot illustrates the smoothed density of data distribution, where its width shows the frequency of values, and the inner red line indicates the median. The result of EM clustering for
is shown in
Figure 5. A shift in
improves the estimation accuracy for the predominant subsample.
In this scenario, гunlike hard clustering approaches (e.g., k-means), which would disable over 30% of sensors in the pollution zone, probabilistic clustering enables the involvement of all these sensors in intensive and detailed air pollution monitoring via parameterized data transmission policies. Even a simple activation policy, triggering intensive operation or a switch to energy-saving mode when a sensor’s probability exceeds a 0.5 threshold, ensures that a significant majority of sensors are correctly assigned an operational state commensurate with their true status.
To reduce the inherent volatility of the EM algorithm when applied to small sample sizes, a reasonable strategy is to initialize the procedure from a set of random starting points, thereby protecting against spurious convergence to an unrepresentative local optimum and providing more reliable parameter estimates.
8. Conclusions
This paper has addressed the critical challenge of data aggregation in large-scale air pollution monitoring networks, where the volume and stochastic nature of sensor data can lead to significant communication overhead. This paper investigates the application of unsupervised machine learning, a branch of artificial intelligence, for enhancing the performance of air quality monitoring systems. We proposed and validated a modified Expectation-Maximization algorithm for the soft clustering of sensors. By modeling sensor alert signals as a mixture of Poisson distributions, our method probabilistically distinguishes between normal background activity and pollution events, assigning each sensor a cluster membership probability. The power of this approach lies in its probabilistic foundation, which naturally handles the uncertainty and diffuse boundaries inherent in environmental data. Unlike hard clustering techniques, our model provides a nuanced view of the monitoring landscape, enabling the implementation of dynamic data transmission policies. Simulation results confirm the high efficiency of this method, demonstrating that the cluster membership probability serves as a robust mechanism for controlling the fundamental trade-off between data redundancy and monitoring accuracy. The provided results can be used to open promising avenues for future research into more sophisticated, self-organizing data aggregation protocols for environmental sensing and other distributed monitoring applications.
Author Contributions
Conceptualization, V.S. and O.D.; methodology, V.S.; software, V.S.; validation, V.S. and O.D.; formal analysis, V.S.; investigation, V.S.; resources, V.S. and O.D.; data curation, V.S.; writing—original draft preparation, V.S. and O.D.; writing—review and editing, V.S. and O.D.; visualization, V.S.; supervision, V.S.; project administration, V.S. and O.D.; funding acquisition, V.S. and O.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a grant for research centers, provided by the Ministry of Economic Development of the Russian Federation in accordance with the subsidy agreement with the Novosibirsk State University dated April 17, 2025 No. 139-15-2025-006: IGK 000000C313925P3S0002.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors have no conflicts of interest to declare.
Abbreviations
The following abbreviations are used in this manuscript.
| AQM |
Air Quality Monitoring |
| WSNs |
Wireless sensor networks |
| IoT |
Internet of Things |
| EM |
Expectation-Minimization |
| pmf |
probability mass function |
| pdf |
probability density function |
| ML |
Machine Learning |
| DL |
Deep Learning |
References
- Campbell, L.D.; Pruss, U.A. Climate change, air pollution and noncommunicable diseases. Bull. World Health Organ. 2019, 97, 160–161.
- Sun, C.; Li, V.O.; Lam, J.C.; Leslie, I. Optimal Citizen-Centric Sensor Placement for Air Quality Monitoring: A Case Study of City of Cambridge, the United Kingdom. IEEE Access 2019, 7, 47390–47400.
- Sokolova, O.; Yurgenson, A.; Shakhov, V. Development of Air Quality Monitoring Systems: Balancing Infrastructure Investment and User Satisfaction Policies. Sensors 2025, 25, 875.
- Zarrar, H.; Dyo, V. Drive-by air pollution sensing systems: Challenges and future directions. IEEE Sens. J. 2023, 23, 23692.
- Pamula, A.S.P.; Ravilla, A.; Madiraju, S.V.H. Applications of the Internet of Things (IoT) in Real-Time Monitoring of Contaminants in the Air, Water, and Soil. Eng. Proc. 2022, 27, 26.
- Verghese, S.; Nema, A.K. Optimal design of air quality monitoring networks: A systematic review. Stoch. Environ. Res. Risk Assess 2022, 2022 36, 2963–2978.
- Xiong, J.; Li, J.; Gao, F.; Zhang, Y. City Wind Impact on Air Pollution Control for Urban Planning with Different Time-Scale Considerations: A Case Study in Chengdu, China. Atmosphere 2023, 14, 1068.
- Nakyai, T.; Santasnachok, M.; Thetkathuek, A.; Phatrabuddha, N. Influence of Meteorological Factors on Air Pollution and Health Risks: A Comparative Analysis of Industrial and Urban Areas in Chonburi Province, Thailand. Environ. Adv. 2025, 19, 100608.
- Kumar, P.G.; Lekhana, P.; Musini, T.; Chandrakala, S. Effects of Vehicular Emissions on the Urban Environment - A State of the Art. Mater. Today Proc. 2020, 45, 738–745.
- Wang, F.; Dong, M.; Ren, J. et al. The impact of urban spatial structure on air pollution: empirical evidence from China. Environ Dev Sustain 2022, 24, 5531–5550.
- Rodríguez, M. C.; Dupont-Courtade, L.; Oueslati, W. Air pollution and urban structure linkages: Evidence from European cities. Renewable and Sustainable Energy Reviews 2016, 53, 1–9.
- Miao, Ch.; Yu, Sh.; Hu, Y.; Bu, R.; Qi, L.; He, X.; Chen, W. How the morphology of urban street canyons affects suspended particulate matter concentration at the pedestrian level: An in-situ investigation. Sustainable Cities and Society 2020, 55. 102042.
- Montalvo, M.; Horna, D. A Numerical Investigation of the Relationship Between Air Quality, Topography, and Building Height in Populated Hills. Buildings 2025, 15, 2145.
- Naizabayeva, L.; Kolesnikova, K.; Khrutba, V. Simulation-Based Assessment of Urban Pollution in Almaty: Influence of Meteorological and Environmental Parameters. Appl. Sci. 2025, 15, 6391.
- Shakhov, V.; Migov, D.; Chen, H.; Mishchenko, P.; Koo, I. Toward Reliability of Long Wireless Sensor Networks. IEEE Access 2024, 12, 124506-124516.
- Shakhov, V.; Materukhin, A.; Sokolova, O.; Koo, I. Optimizing Urban Air Pollution Detection Systems. Sensors 2022, 22, 4767.
- S., S.R.; Aburukba, R.; El Fakih, K. Wireless Sensor Networks for Urban Development: A Study of Applications, Challenges, and Performance Metrics. Smart Cities 2025, 8, 89.
- Christakis, I.; Tsakiridis, O.; Kandris, D.; Stavrakas, I. Air Pollution Monitoring via Wireless Sensor Networks: The Investigation and Correction of the Aging Behavior of Electrochemical Gaseous Pollutant Sensors. Electronics 2023, 12, 1842.
- Wang, L. Design industrial 5.1 air quality monitoring system and develop smart city infra-structure, Measurement: Sensors 2024, 35, 101292.
- Shahid, S.; Brown, D.J.; Wright, P.; Khasawneh, A.M.; Taylor, B.; Kaiwartya, O. Innovations in Air Quality Monitoring: Sensors, IoT and Future Research. Sensors 2025, 25, 2070.
- Chadalavada, S.; Faust, O.; Salvi, M.; Seoni, S.; Raj, N.; Raghavendra, U.; Gudigar, A.; Barua, P.D.; Molinari, F.; Acharya, R. Application of artificial intelligence in air pollution monitoring and forecasting: A systematic review. Environ. Model. Softw. 2025, 185, 106312.
- Colléaux, Y.; Willaume, C.; Mohandes, B.; Nebel, J.-C.; Rahman, F. Air Pollution Monitoring Using Cost-Effective Devices Enhanced by Machine Learning. Sensors 2025, 25, 1423.
- Wang, G.; Yu, C.; Guo, K.; Guo, H.; Wang, Y. Research of low-cost air quality monitoring models with different machine learning algorithms. Atmos. Meas. Tech. 2024, 17, 181–196.
- Liu, Y.; Yu, W.; Zhai, X.; Zhang, B.; McDonald-Maier, K.D.; Fasli, M. Multi-level CEP rules automatic extraction approach for air quality detection and energy conservation decision based on AI technologies. Applied Energy 2024, 372, 123724.
- Bogdanffy, L.; Lorinț, C.R.; Nicola, A. Development of a Low-Cost Traffic and Air Quality Monitoring Internet of Things (IoT) System for Sustainable Urban and Environmental Management. Sustainability 2025, 17, 5003.
- Yin, P.-Y. Scheduling and Routing of Device Maintenance for an Outdoor Air Quality Monitoring IoT. Sustainability 2025, 17, 6522.
- Przystupa, K.; Bernatska, N.; Dzhumelia, E.; Drzymała, T.; Kochan, O. Ensuring Energy Efficiency of Air Quality Monitoring Systems Based on Internet of Things Technology. Energies 2025, 18, 3768.
- Lewandowski, M.; Płaczek, B. Data Transmission Reduction in Wireless Sensor Network for Spatial Event Detection. Sensors 2021, 21, 7256.
- Brito, T.; Azevedo, B.F.; Mendes, J.; Zorawski, M.; Fernandes, F.P.; Pereira, A.I.; Rufino, J.; Lima, J.; Costa, P. Data Acquisition Filtering Focused on Optimizing Transmission in a LoRaWAN Network Applied to the WSN Forest Monitoring System. Sensors 2023, 23, 1282.
- He, B.; Li, Y. Big Data Reduction and Optimization in Sensor Monitoring Network. J. Appl. Math. 2014, 2014, 294591.
- Bogalecka, M. Probabilistic approach to modelling, identification and prediction of environmental pollution. Environ. Model. Assess. 2023, 28, 1–14.
- Cheam, A.S.M.; Marbac, M.; McNicholas, P.D. Model-Based Clustering for Spatiotemporal Data on Air Quality Monitoring. Environmetrics 2017, 28, e2437.
- Fu, L.; Li, J.; Chen, Y. An innovative decision making method for air quality monitoring based on big data-assisted artificial intelligence technique. J. Innov. Knowl. 2023, 8, 100294.
- Sabando-Bravo, K.E.; Navia, M.; Zambrano-Martinez, J.L. Optimizing CO2 Monitoring: Evaluating a Sensor Network Design. J. Sens. Actuator Netw. 2025, 14, 93.
- Meng, X.L.; Van Dyk, D. The EM algorithm—An old folk-song sung to a fast new tune. J. R. Stat. Soc. Ser. B. Stat. Methodol. 1997, 59, 511–567.
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data Via the EM Algorithm. J. R. Stat. Soc. 1977, 39, 1–38.
- Panić, B.; Klemenc, J.; Nagode, M. Improved Initialization of the EM Algorithm for Mixture Model Parameter Estimation. Mathematics 2020, 8, 373.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).