Homotopy Type Theory as a Framework for Geometric Equality: The Case of Triangles

1. Introduction

In classical Euclidean geometry, the notion of “equality” for geometric figures is multifaceted, often leading to pedagogical and formal confusion. When are two triangles “the same”? Are they “equal,” “congruent,” or “similar”? While mathematicians understand the distinct definitions of these terms, the language used can be imprecise. For instance, “equal triangles” is often used colloquially to mean congruent triangles, yet two triangles at different locations are not strictly identical. This ambiguity becomes a significant hurdle in formal systems, such as automated theorem provers and CAD software, where a precise understanding of equality is paramount.

Homotopy Type Theory (HoTT) offers a novel and powerful language to address these foundational issues. HoTT enriches Martin-Löf type theory with concepts from homotopy theory, where types are interpreted as spaces and the equality between two elements is a type of "paths" between them. The identity type, ${\mathrm{Id}}_A(a,b)$, captures all the ways in which a and b can be identified. This "proof-relevant" nature of equality allows us to distinguish between different notions of sameness.

This paper proposes a formal framework using HoTT to clarify these different notions of equality for triangles. We define a type for triangles and then formalize what it means for two triangles to be equal, congruent, and similar, all within a single foundational system. The univalence axiom, a cornerstone of HoTT, is central to our approach, as it formally equates equivalence between types with identity in a universe of types.

Our contribution is a rigorous, foundational account of geometric equality that is both conceptually clear and formally specified. This has the potential to impact several areas:

• Geometry Education: Providing a precise language to help students better understand the nuances of geometric relations.
• Automated Theorem Proving: A formal HoTT definition of geometric objects can lead to more robust automated provers for geometry.
• Computer-Aided Design (CAD): Expressive logic for defining and manipulating geometric objects and their relationships.
• Robotics and AI: Formalizing the sophisticated understanding of shape and space required for AI systems that reason about the physical world.

The paper is structured as follows. Section 2 reviews key concepts from HoTT. Section 3 develops our formal framework for triangles. Section 4 presents a detailed case study of triangle equalities. Section 5 explores applications. Section 6 situates our work within the context of related formalizations of geometry. Finally, Section 7 concludes and outlines future directions.

2. Background on Homotopy Type Theory

We briefly review the key concepts from HoTT essential for this paper. For a comprehensive introduction, we refer the reader to “The HoTT Book” [5].

2.1. Types as Spaces and Identity as Paths

In HoTT, a type A is viewed as a space, and its elements $a,b:A$ as points. The identity type ${\mathrm{Id}}_A(a,b)$ is the type of paths from a to b. The existence of an element $p:{\mathrm{Id}}_A(a,b)$ is a proof that a and b are equal. Crucially, there can be multiple distinct paths between two points, representing different proofs of equality. For any $a:A$, there is a canonical path ${\mathrm{refl}}_a:{\mathrm{Id}}_A(a,a)$ representing reflexivity. This interpretation allows us to distinguish types by their “homotopy level”: a type is a set if there is at most one path between any two points.

2.2. Higher Inductive Types (HITs)

Higher Inductive Types (HITs) generalize inductive types by allowing constructors not only for points but also for paths and higher paths. This enables the direct definition of types with specified topological structures. For example, the circle $S^1$ is a HIT with a point constructor $\mathrm{base}:S^1$ and a path constructor $\mathrm{loop}:{\mathrm{Id}}_{S^1}(\mathrm{base},\mathrm{base})$. HITs are essential for defining quotient types and moduli spaces, where we want to identify certain points via paths.

2.3. Precise Geometric Definitions

To formalize triangles, we must first define their components. We assume a type Point for points in the Euclidean plane, equivalent to ${\mathbb{R}}^2$.

Definition 1

(Segment). For two points $A,B:$ Point, the type of segments between them is the identity type itself:

$$\mathit{Segment}(A,B):\equiv {\mathit{Id}}_{\mathit{Point}}(A,B)$$

In the context of ${\mathbb{R}}^2$, where Point is a set, this type is inhabited if and only if A and B are the same point. For distinct points, we use a different notion, such as the set of points on the line segment, but for specifying the edges of a located triangle, the vertices suffice.

Definition 2

(Non-Collinear). Three points $A,B,C:$ Point are non-collinear if the type representing their collinearity is empty. Assuming $\mathit{Point}={\mathbb{R}}^2$, collinearity can be expressed as the existence of a scalar $k:\mathbb{R}$ such that the vector from A to C is a multiple of the vector from A to B.

$$\mathit{IsCollinear}(A,B,C):\equiv \sum _{k:\mathbb{R}}{\mathit{Id}}_{{\mathbb{R}}^2}(C-A,k·(B-A))$$

Thus, the property of being non-collinear is the proposition:

$$\mathit{NonCollinear}(A,B,C):\equiv \neg \mathit{IsCollinear}(A,B,C):\equiv \left(\mathit{IsCollinear}\right(A,B,C)\to \perp )$$

2.4. The Univalence Axiom

The univalence axiom states that for any two types A and B, the canonical map from their identity type to the type of equivalences between them is itself an equivalence:

$$\mathrm{ua}:\left({\mathrm{Id}}_{\mathrm{Type}}(A,B)\right)\simeq (A\simeq B)$$

Essentially, equivalent types are equal. This axiom allows us to treat isomorphic structures as identical, which is crucial for defining spaces of shapes where congruent figures are identified.

3. A Formal Framework for Geometric Equality

We now construct a formal type for triangles in HoTT.

3.1. The Type of Triangles

A specific, located triangle is defined by its three vertices and a proof that they are not collinear. We use a dependent pair type ($\Sigma$-type) for this.

Definition 3

(Type of Triangles). The type of triangles is defined as:

$$\mathit{Triangle}:\equiv \sum _{v_1,v_2,v_3:\mathit{Point}}\mathit{NonCollinear}(v_1,v_2,v_3)$$

An element $T:\mathit{Triangle}$ is a pair $((v_1,v_2,v_3),p)$, where $(v_1,v_2,v_3)$ are the vertices and p is the proof of non-collinearity.

3.2. Equality of Triangles as Paths

The identity type ${\mathrm{Id}}_{\mathrm{Triangle}}(T_1,T_2)$ formalizes the strictest notion of equality. Let $T_1=((v_{11},v_{12},v_{13}),p_1)$ and $T_2=((v_{21},v_{22},v_{23}),p_2)$. By the definition of identity for $\Sigma$-types, a path in ${\mathrm{Id}}_{\mathrm{Triangle}}(T_1,T_2)$ consists of paths between corresponding vertices:

• $q_1:{\mathrm{Id}}_{\mathrm{Point}}(v_{11},v_{21})$
• $q_2:{\mathrm{Id}}_{\mathrm{Point}}(v_{12},v_{22})$
• $q_3:{\mathrm{Id}}_{\mathrm{Point}}(v_{13},v_{23})$

and a proof that $p_1$ is equal to $p_2$ when transported along these paths. Since Point is a set, the paths $q_i$ only exist if the vertices are identical. Thus, ${\mathrm{Id}}_{\mathrm{Triangle}}(T_1,T_2)$ is inhabited if and only if $T_1$ and $T_2$ have the exact same vertices in the same order—they are the same object.

4. Case Study: Equalities of Triangles

We now formalize the distinct notions of sameness for triangles.

4.1. Strict Equality

As defined above, two triangles $T_1,T_2:\mathrm{Triangle}$ are strictly equal if ${\mathrm{Id}}_{\mathrm{Triangle}}(T_1,T_2)$ is inhabited. This corresponds to perfect identity.

4.2. Congruence

Congruence relates two triangles that have the same side lengths and angles, regardless of their position.

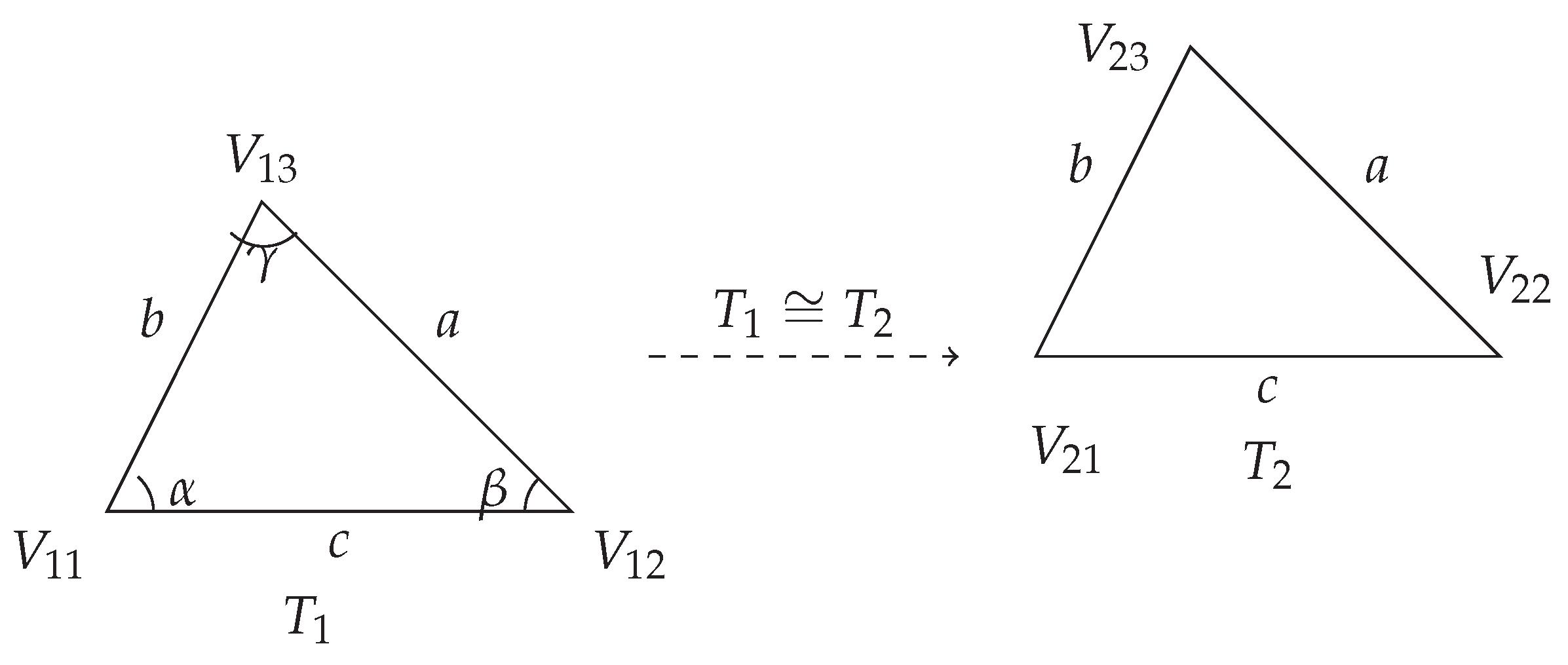
Definition 4

(Congruence). Let $T_1$ and $T_2$ be two triangles with vertices $(v_{11},v_{12},v_{13})$ and $(v_{21},v_{22},v_{23})$. A congruence $T_1\cong T_2$ is a record consisting of:

• A permutation σ of $\{1,2,3\}$.
• Equalities of corresponding side lengths:

  –

  ${\mathit{Id}}_{\mathbb{R}}(\mathit{dist}(v_{11},v_{12}),\mathit{dist}(v_{2,\sigma \left(1\right)},v_{2,\sigma \left(2\right)}))$

  –

  ${\mathit{Id}}_{\mathbb{R}}(\mathit{dist}(v_{12},v_{13}),\mathit{dist}(v_{2,\sigma \left(2\right)},v_{2,\sigma \left(3\right)}))$

  –

  ${\mathit{Id}}_{\mathbb{R}}(\mathit{dist}(v_{13},v_{11}),\mathit{dist}(v_{2,\sigma \left(3\right)},v_{2,\sigma \left(1\right)}))$

This definition captures the Side-Side-Side (SSS) criterion directly. An element of the type $T_1\cong T_2$ is a proof of their congruence.

Figure 1. Congruent triangles $T_1$ and $T_2$ have identical side lengths ($a,b,c$) and angles ($\alpha ,\beta ,\gamma$), but different vertex locations.

Figure 1. Congruent triangles $T_1$ and $T_2$ have identical side lengths ($a,b,c$) and angles ($\alpha ,\beta ,\gamma$), but different vertex locations.

4.3. Similarity

Similarity relates triangles with proportional side lengths and equal angles.

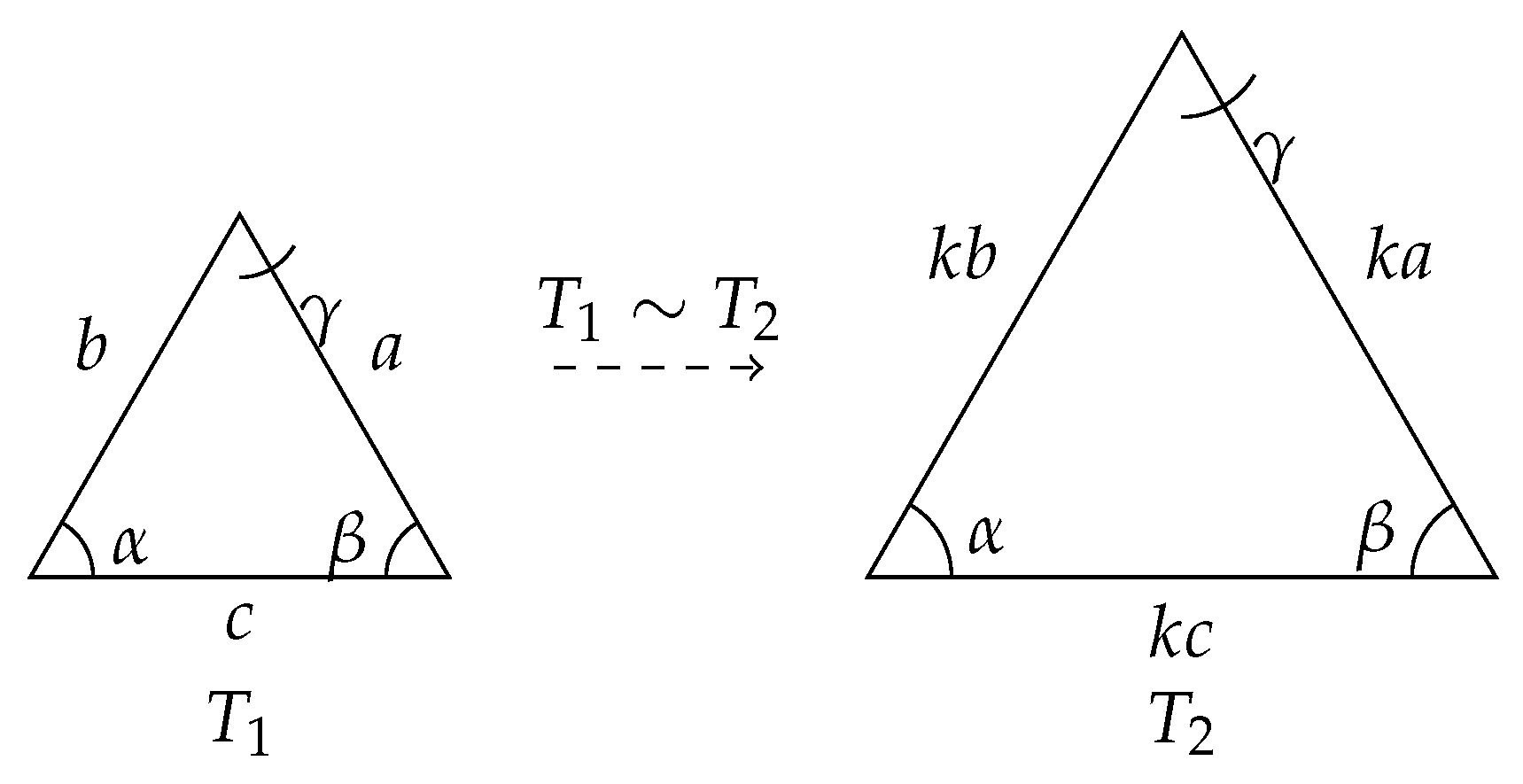
Definition 5

(Similarity). A similarity $T_1\sim T_2$ is a record consisting of:

• A permutation σ of $\{1,2,3\}$.
• A positive scale factor $k:{\mathbb{R}}^{+}$.
• Equalities of proportional side lengths:

  –

  ${\mathit{Id}}_{\mathbb{R}}(k·\mathit{dist}(v_{11},v_{12}),\mathit{dist}(v_{2,\sigma \left(1\right)},v_{2,\sigma \left(2\right)}))$

  –

  etc. for the other two sides.

Figure 2. Similar triangles $T_1$ and $T_2$ have equal angles but proportional side lengths.

Figure 2. Similar triangles $T_1$ and $T_2$ have equal angles but proportional side lengths.

4.4. The Moduli Space of Triangles

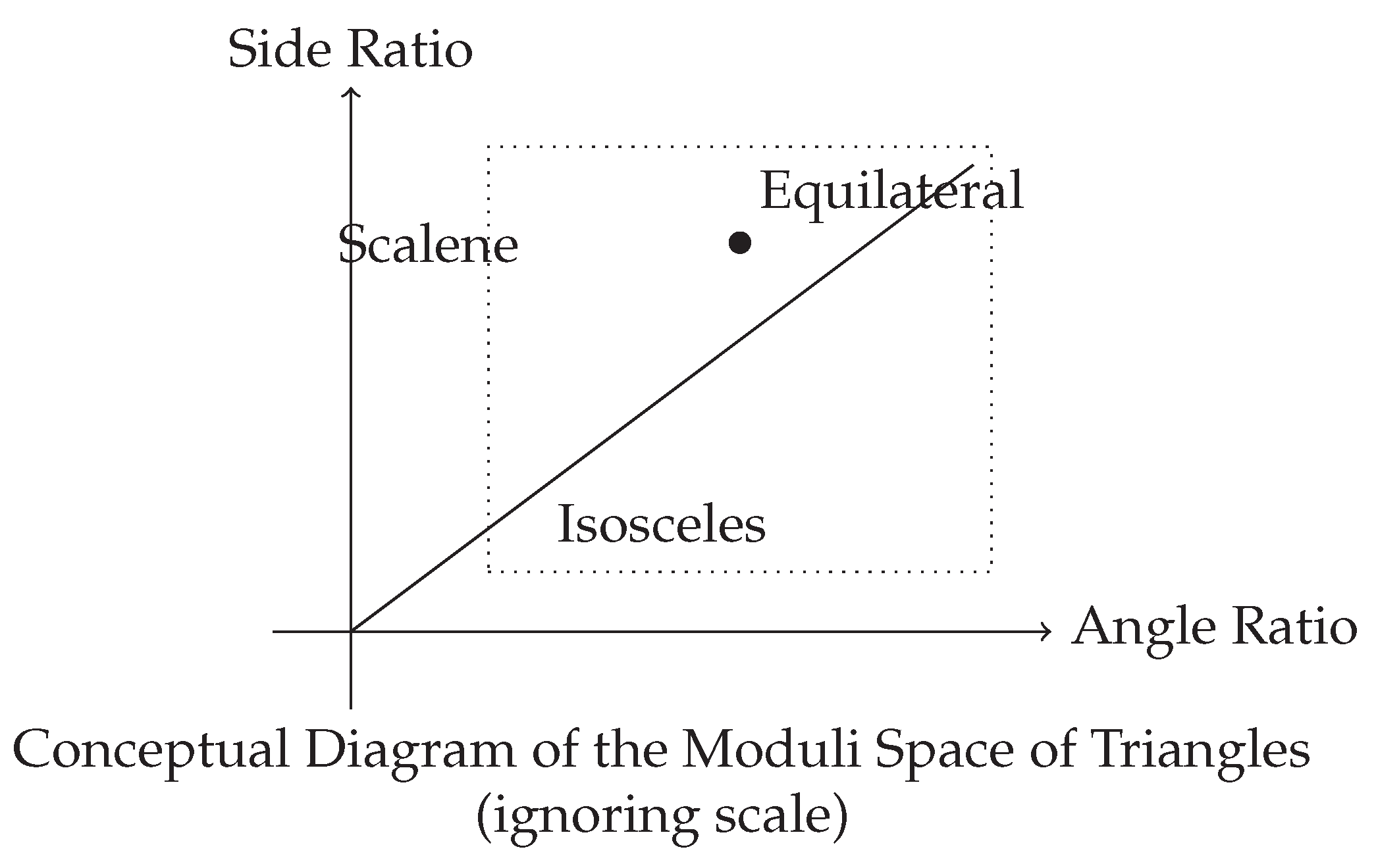
To capture the idea that congruent triangles represent the same “shape,” we define a new type, ‘TriangleShape’, as a Higher Inductive Type. This type is the quotient of ‘Triangle’ under the congruence relation.

Definition 6

(TriangleShape HIT). The type TriangleShape is the HIT generated by:

• A point constructor shape: Triangle → TriangleShape.
• A path constructor that turns any congruence into a path: for any $T_1,T_2$: Triangleand any congruence proof $c:T_1\cong T_2$, there is a path

  $$\mathit{cong}\_\mathit{to}\_\mathit{path}\left(c\right):{\mathit{Id}}_{\mathit{TriangleShape}}(\mathit{shape}\left(T_1\right),\mathit{shape}\left(T_2\right))$$

This definition effectively “glues” together all congruent triangles in the new space ‘TriangleShape’, which can be thought of as the moduli space of triangles.

Theorem 1.

For any two triangles $T_1,T_2$: Triangle, the type of congruences between them is equivalent to the identity type between their shapes.

$$(T_1\cong T_2)\simeq {\mathit{Id}}_{\mathit{TriangleShape}}(\mathit{shape}\left(T_1\right),\mathit{shape}\left(T_2\right))$$

Proof Sketch .

The map from left to right is given by the ‘$\mathit{cong}\_\mathit{to}\_\mathit{path}$’ constructor. The map from right to left is constructed using the induction principle of the ‘TriangleShape’ HIT. The fact that these maps are inverses of each other also follows from the induction principle and the computation rules of the HIT. The univalence axiom is the underlying principle that ensures such a quotient construction is well-behaved, identifying the equivalence of congruence with genuine path equality in the higher type. □

Figure 3. A conceptual diagram of the moduli space of triangles. Each point represents a unique triangle shape (an equivalence class of congruent triangles). Specific points or lines correspond to shapes with special properties like being equilateral or isosceles.

Figure 3. A conceptual diagram of the moduli space of triangles. Each point represents a unique triangle shape (an equivalence class of congruent triangles). Specific points or lines correspond to shapes with special properties like being equilateral or isosceles.

5. Applications

Our formal framework has several potential applications:

5.1. Geometry Education

A HoTT-based curriculum could introduce geometric concepts with greater precision:

• Equality (Id type): Being the very same object in the same location.
• Congruence (≅): An equivalence preserving distance, identified with a path in the space of shapes.
• Similarity (∼): An equivalence preserving angles but not distances.

This formally separates an object from its intrinsic properties (its shape).

5.2. Automated Theorem Proving

Formalizations of geometry in proof assistants like Coq, Lean, or Agda could benefit from this framework. Theorems about “all triangles” can be proven once for the type ‘TriangleShape’, and the results apply to all concrete triangles by transport.

5.3. CAD Systems and AI

In CAD, managing constraints between parts of a design can be represented in a principled way using paths and equivalences. For an AI agent, recognizing an object regardless of its position and orientation is a problem of identifying congruence. Our framework naturally captures the distinction between a specific object instance and its abstract shape.

6. Related Work

The formalization of geometry has a rich history. Early efforts focused on synthetic approaches, formalizing axiom systems like those of Hilbert or Tarski. The GeoCoq project is a major effort in this direction, formalizing a large portion of Euclidean geometry in Coq based on Tarski’s axioms. Other work in Coq has focused on Hilbert’s axioms and specific geometric algorithms.

In recent years, the Lean proof assistant and its mathematical library, Mathlib, have become prominent. Mathlib contains extensive development of Euclidean geometry from an analytic perspective (based on normed vector spaces). Projects like LeanGeo build on this to formalize competition-level geometry problems.

Work in Agda has also explored synthetic geometry, often with a constructive flavor or connections to cubical type theory.

The novelty of our paper lies not in formalizing a large body of geometric theorems, but in using the unique features of HoTT—specifically identity types, HITs, and the univalence axiom—to provide a new foundational perspective on the meaning of geometric equality itself. While other systems can define congruence and similarity as equivalence relations, HoTT allows us to state that congruent triangles are literally equal in the type of shapes. This provides a unified language for equality that other formal systems lack, offering a new tool for conceptual clarity in mathematics and its applications.

7. Conclusion

We have presented a novel framework using Homotopy Type Theory to formally distinguish and relate the concepts of strict equality, congruence, and similarity in Euclidean geometry. By defining triangles as a type and leveraging identity types as paths, we provided a precise meaning for each notion of sameness. The introduction of ‘TriangleShape’ as a Higher Inductive Type, whose paths are congruences by definition, demonstrates the power of HoTT to model abstract mathematical concepts like moduli spaces directly.

The primary contribution of this work is the conceptual clarity it brings to the foundations of geometry, showing that different equivalences are not just ad-hoc relations but are intrinsic to the rich structure of identity in HoTT. This has profound implications for education and for the design of formal systems in automated reasoning and AI.

Limitations of this work include its focus on triangles and its informal presentation. Future research should pursue several directions:

• Full Formalization: Implementing this framework in a HoTT-compatible proof assistant like Cubical Agda to formally verify congruence theorems (e.g., SAS, ASA) as constructions of paths in ‘TriangleShape’.
• Generalization: Extending the framework to polygons, circles, and 3D objects, which will require more complex HITs to define their respective moduli spaces.
• Connections to Physics: Exploring how this framework for geometric invariance connects to the role of symmetry and transformation groups in physics, for which HoTT seems a natural language.

Ultimately, HoTT offers a powerful new perspective on the foundations of geometry, aligning formal mathematics more closely with the intuitions of mathematicians.