Energy-Constrained Motion Planning and Scheduling for Autonomous Robots in Complex Environments

Zhichao Ma; Zheyu Zhang; Zijun Gao; Aijia Sun; Yinuo Yang; Hao Liu

doi:10.20944/preprints202509.1316.v1

Submitted:

15 September 2025

Posted:

16 September 2025

You are already at the latest version

Abstract

Autonomous robots increasingly operate in complex and dynamic environments where energy resources are limited. Effective motion planning and scheduling strategies are critical to achieving mission objectives while minimizing energy consumption. This paper proposes an energy-constrained motion planning framework that jointly considers path optimization and task scheduling under limited energy budgets. We integrate an energy consumption model with a task-priority-based scheduling algorithm to ensure efficient execution of tasks while maintaining safety and mission performance. The proposed approach is validated in simulated complex environments with varying obstacle distributions and energy constraints, demonstrating improved performance compared to baseline greedy and shortest path-only planners. The results highlight the importance of coupling energy-aware planning with adaptive scheduling to enhance the autonomy of resource-constrained robotic systems.

Keywords:

reinforcement learning

;

proximal policy optimization

;

motion planning

;

robot navigation

Subject:

Computer Science and Mathematics - Robotics

I. Introduction

Autonomous mobile robots have been increasingly deployed in real-world scenarios such as warehouse logistics, search and rescue, and environmental monitoring, where they are often required to perform multiple prioritized tasks in cluttered or partially known environments[1]. However, these robots are typically limited by their onboard energy capacity, which poses significant challenges for mission success[2]. In such energy-constrained situations, the robot must carefully balance task completion performance, path safety, and energy consumption, to ensure that high-value tasks are completed before battery exhaustion[3]. This challenge becomes even more critical when the robot operates in environments with complex obstacle distributions and dynamic task priorities, where a naive shortest-path planner or a fixed scheduling sequence may quickly fail due to inefficient energy use or unsafe trajectories[4].

Traditional motion planning algorithms, such as A* or RRT, generally aim to minimize distance or travel time but seldom incorporate explicit energy constraints or the priority structure of multiple tasks[5,6]. Likewise, classical scheduling methods often rely on fixed priority rules or static sequences, overlooking the actual energy cost of visiting task sites. As a result, these methods struggle to maximize mission outcomes under realistic conditions with limited energy[7,8]. There is thus a pressing need for a framework that can jointly optimize motion planning and task scheduling while dynamically adapting to changing energy levels and mission priorities[9,10].

Recent advances in deep reinforcement learning (DRL) have shown promising results in high-dimensional decision-making tasks, demonstrating the ability to learn adaptive policies through interaction with the environment[11,12]. In particular, Proximal Policy Optimization (PPO) has achieved a good trade-off between training stability and sample efficiency, making it attractive for robotic decision-making[13,14]. However, if DRL is applied directly to robotic planning without incorporating a physically realistic energy consumption model, the resulting behavior may be impractical or even unsafe[15]. Therefore, combining traditional energy-aware cost modeling with a DRL-based adaptive policy mechanism offers a promising pathway toward more robust and practical solutions[16].

This paper proposes an integrated framework that uses PPO to learn a hybrid action policy capable of making discrete task selection decisions while simultaneously adjusting continuous motion planning parameters, thereby coupling scheduling and energy-aware path planning. The local path planner is based on a modified A* algorithm with a cost function that explicitly accounts for both path length and estimated energy consumption, and the PPO policy dynamically tunes these weights according to the current state and residual battery level. This mechanism enables the robot to prioritize high-value tasks adaptively and to adjust its trajectories based on available energy, achieving a balanced trade-off among mission effectiveness, safety, and energy conservation.

To validate the effectiveness of the proposed method, we conducted a systematic comparison against three representative planning algorithms, including the traditional A* algorithm optimized solely for shortest paths, a fixed-priority scheduling scheme using A*, and an energy-aware A* algorithm that incorporates fixed energy weights in the cost function but lacks adaptive capabilities. The evaluation focused on metrics such as task completion rate, proportion of remaining energy, and the number of safety violation events, in order to comprehensively assess the robot’s task execution performance and behavioral safety under limited energy conditions. The results demonstrate that the proposed hybrid action strategy based on deep reinforcement learning achieves a superior balance in dynamically adjusting task priorities and distributing energy, thereby significantly improving overall performance in multi-task scenarios.

The main contribution of this paper lies in presenting a novel approach for joint task scheduling and motion planning of energy-constrained autonomous robots, which combines a physically grounded energy-aware planning mechanism with the adaptive policy capabilities of deep reinforcement learning. This method offers a promising technical perspective for enabling efficient and reliable decision-making behaviors of autonomous robots operating in complex multi-task environments.

II. Proposed Method

In order to address the problem of energy-constrained motion planning and scheduling for autonomous robots in complex environments, we propose a unified framework that integrates traditional model-based energy evaluation with deep reinforcement learning techniques, specifically employing a Proximal Policy Optimization algorithm for policy adaptation. The fundamental motivation is to maximize the completion of prioritized tasks while respecting strict energy budgets, in scenarios where obstacle distributions and task requirements are uncertain or change dynamically. Let us define the problem formally as a Markov Decision Process (MDP) characterized by a state space

S

., an action space

A

, a transition function

P

, a reward function

r

, and a discount factor

γ

. In this framework, the robot's state at each time step can be written as

s_{t} = [x_{t}, y_{t}, θ_{t}, e_{t}, q_{t}, o_{t}],

(1)

where

(x_{t}, y_{t}, θ_{t})

denotes the robot’s current pose,

e_{t}

the remaining energy,

q_{t}

a vector representing the current priority queue of tasks, and

o_{t}

an observation encoding the local obstacle occupancy grid. The action produced by the policy is hybrid, consisting of both a discrete task selection and a continuous parameter vector for modulating the motion planner’s trade-off, expressed as

a_{t} = (a_{t}^{task}, a_{t}^{planner}),

(2)

with

a_{t}^{task} \in {1, 2, \dots, N}

representing the next task index, and

a_{t}^{planner} \in ℝ^{2}

specifying the planner weight adjustments

(λ_{t}, μ_{t})

. Here,

λ_{t}

controls the relative emphasis on path distance, while

μ_{t}

modulates the penalty for energy expenditure in the cost function of the motion planner.

The robot’s motion planner employs a modified A* algorithm with a cost function defined by

C (p) = λ_{t} d (p) + μ_{t} E_{motion} (p),

(3)

where

d (p)

is the path length along candidate path

p

, and

E_{motion} (p)

denotes the predicted energy consumption along the same path, modeled by:

E_{motion} (p) = α d (p) + β \sum_{k = 1}^{N - 1} |v_{k + 1} - v_{k}|,

(4)

with

α

and

β

as physically calibrated constants. The second term captures the energy penalties induced by acceleration or deceleration, which are particularly important for wheeled robots with non-negligible inertial effects. Each task

i

additionally has a fixed execution energy cost

e_{i}

, resulting in a total mission energy consumption:

E_{total} = \sum_{i = 1}^{n} (E_{motion}^{(i)} + e_{i}),

(5)

which must remain within the initial battery budget

E_{\max}

.

The reward function provided to the reinforcement learning agent is shaped to reflect multiple objectives. Specifically, the instantaneous reward at time

t

is defined as:

\begin{array}{l} r_{t} {= w}_{1} TaskCompletion (t) - \\ w_{2} EnergyUsed (t) - w_{3} CollisionRisk (t), \end{array}

(6)

where

TaskCompletion (t)

is a binary indicator of whether a high-priority task has been completed,

EnergyUsed (t)

measures the amount of energy depleted during that step, and

CollisionRisk (t)

represents the likelihood of violating safety distances to obstacles. The weights

w_{1}

,

w_{2}

, and

w_{3}

balance the trade-off between performance, energy consumption, and safety. The PPO algorithm then optimizes the policy

π_{θ} (a_{t} | s_{t})

to maximize the expected return:

J (θ) = E_{π_{θ}} [\sum_{t = 0}^{T} γ^{t} r_{t}],

(7)

using the clipped surrogate objective:

L^{CLIP} (θ) = E [\min (r (θ) A, clipped (r (θ)) A)]

(8)

where the ratio:

r_{t} (θ) = \frac{π_{θ} (a_{t} | s_{t})}{π_{θ_{old}} (a_{t} | s_{t})}

(9)

and clipped constrains the ratio within

[1 - ϵ, 1 + ϵ]

. constrains the policy update size, and

{\hat{A}}_{t}

is the advantage function estimated via generalized advantage estimation (GAE) with

{\hat{A}}_{t} = \sum_{l = 0}^{\infty} {(γ λ)}^{l} (r_{t + l} + γ V (s_{t + l + 1}) - V (s_{t + l})),

(10)

where

V

is the state-value baseline and

λ

the GAE smoothing parameter. To ensure policy stability, we adopt a two-layer feedforward neural network with 256 and 128 neurons respectively, ReLU activations, and separate output heads for the discrete task selector and continuous planner parameters. Training proceeds with the Adam optimizer at a learning rate of

3 \times 10^{- 4}

, batch size of 2048 samples, discount factor

γ = 0.99

, clipping parameter

ϵ = 0.2

, and entropy bonus coefficient 0.01 to encourage exploration.

By integrating the adaptive task selection and continuous cost-weight modulation into a unified hybrid action output, the robot can learn to dynamically decide which task to attempt next while also tuning its motion planner in an energy-aware manner. At each planning cycle, the robot updates its state estimate based on newly observed energy levels and obstacle maps, then forwards this state through the policy network to obtain an action, which is then deployed to the path planner and task scheduler. The task scheduler reorders the priority queue according to the discrete choice, while the modified A* planner recalculates the energy-weighted trajectory. This closed-loop feedback cycle proceeds continuously until the robot either completes its mission or exhausts its budget, with the DRL policy learning to balance task importance, energy conservation, and collision avoidance by directly interacting with the environment. Over the course of training, the robot refines its policy to maximize the coverage of high-priority tasks while maintaining a safe, energy-efficient trajectory, thus demonstrating the benefit of coupling classical energy models with modern deep reinforcement learning techniques to achieve robust, adaptive mission planning under realistic constraints.

III. Experiments

In order to verify the effectiveness of the proposed energy-constrained adaptive scheduling and motion planning framework based on deep reinforcement learning, we built a two-dimensional simulation environment using ROS and Gazebo. The simulation area is configured as a

10, m \times 10, m

planar workspace, which contains ten static obstacles whose positions are randomly generated to increase the diversity of the scene. There are eight task locations distributed in the environment, each with a different priority assigned, and each task requires a certain amount of battery energy ranging from

5, Wh

to

8, Wh

. The robot has an initial battery capacity of

100, Wh

, and its physical configuration follows the differential drive model with a maximum linear velocity of

0.5, m / s

and a maximum acceleration of

0.3, {m / s}^{2}

. During the task execution, the robot continuously communicates with the ROS-based scheduler to decide the next action based on the priority, remaining energy, and current state, and verifies the feasibility of the motion instructions through Gazebo's physical simulation.

We compared the proposed PPO-based hybrid action strategy with three representative planning algorithms, including the traditional shortest path A* method (A*-SP), a fixed priority scheduling scheme based on standard A* (Fixed Priority A*), and an energy-aware A* method that includes a fixed energy weight in the cost function but does not use reinforcement learning (Energy-Aware A*). In each experiment, the obstacle layout and task location were generated using different random seeds, and the test was repeated 50 times, recording the metrics at the end of each task or when the energy was exhausted. The evaluation metrics include task completion rate, remaining energy ratio, and the number of safety violation events.

The two sets of experimental results comprehensively evaluate the performance of each method in terms of task execution efficiency and path quality. As shown in Table 1, the proposed method significantly outperforms the baseline approaches in task completion rate (95%), remaining energy (42.0%), and safety (only 2 violation events), demonstrating its overall advantage in energy-aware scheduling and task execution. Furthermore, the path quality comparison in Table 2 shows that the proposed method generates the shortest path (1.24×10³ m) with the lowest average curvature (0.16 rad/m) and maximum curvature (0.58 rad/m), indicating smoother trajectories that facilitate real-world control and execution. These results collectively confirm the proposed method’s superior performance in energy efficiency, safety, and motion controllability.

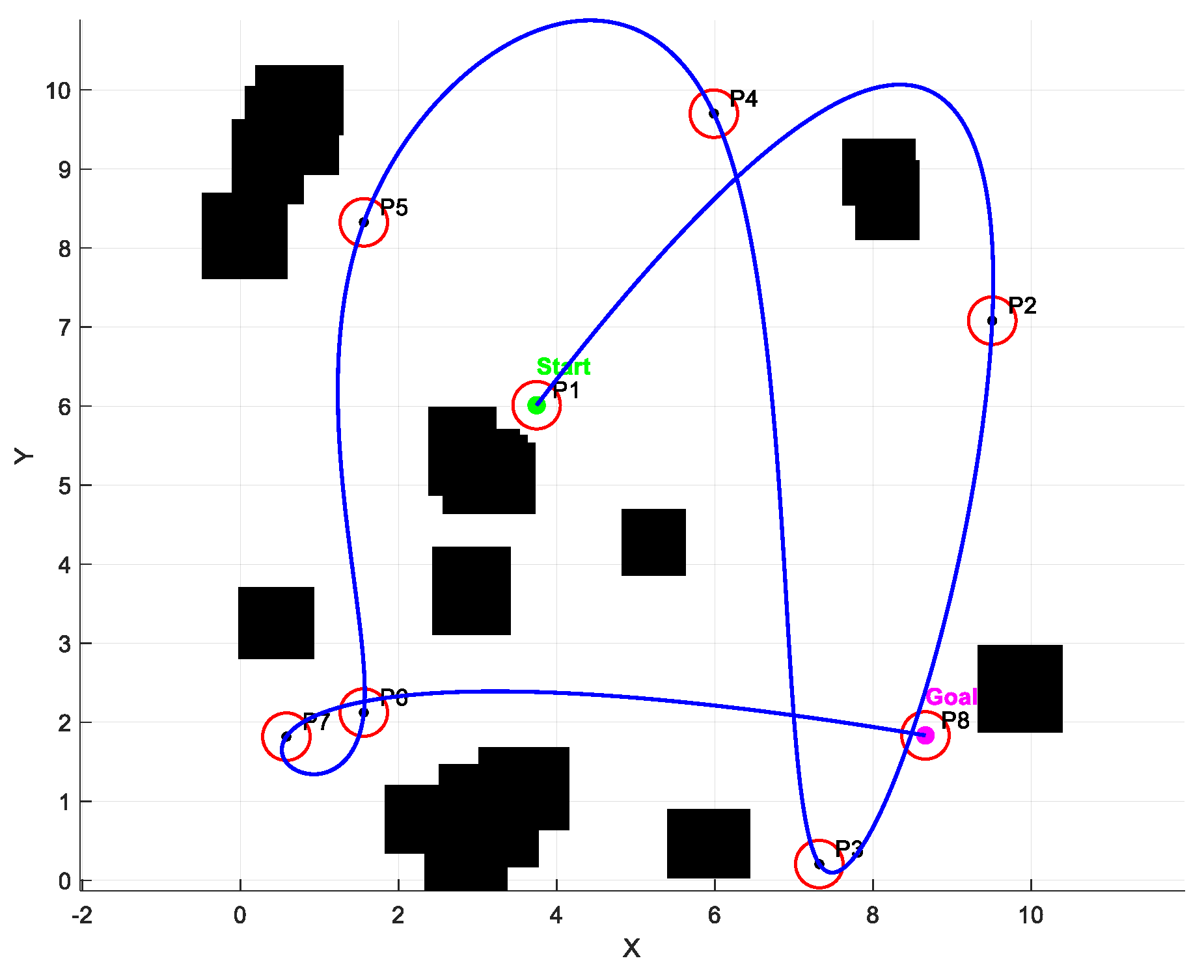
Figure 1 shows the effect of the algorithm in this paper. It can be seen that the generated path is smooth and effectively ensures that it passes through all task locations. In the statistical results of the 50 experiments, the traditional A*-SP method has the lowest task completion rate, with an average of 72.0%, because it completely ignores the energy budget and often runs out of battery power before completing high-priority tasks. It also has very little remaining energy and a significantly higher number of safety violations compared to other methods. The fixed-priority A* scheme improves the task completion rate by enforcing the priority order, but still lacks energy awareness, so the energy efficiency is relatively low and there are safety issues in chaotic environments. The energy-aware A* method can improve energy efficiency and reduce collision risks to a certain extent by adding fixed energy weights to the path cost function, but its static scheduling order is still difficult to flexibly adapt to changing task priorities or remaining energy. In contrast, the proposed PPO-based hybrid action framework dynamically generates discrete scheduling decisions and continuous planning parameters through a learning policy network, enabling the robot to make more intelligent decisions based on the remaining energy and current environmental state. The results show that this method significantly improves the average task completion rate to 95.0%, retains about 42% of the initial energy on average, and reduces safety violations to an average of only 2.

IV. Conclusions

This study presents an integrated framework for energy-constrained motion planning and task scheduling, combining a physically grounded energy model with a PPO-based hybrid action policy. By jointly optimizing discrete task selection and continuous path planning parameters, the method enables autonomous robots to adapt to dynamic environments and energy limitations. Experimental results show that the proposed approach outperforms traditional planners in task completion rate, energy efficiency, and safety, demonstrating its effectiveness and robustness. This work highlights the value of coupling classical energy-aware planning with reinforcement learning to support intelligent, energy-efficient decision-making in complex multi-task scenarios.

References

Zhou, Z., Zhang, J., Zhang, J., He, Y., Wang, B., Shi, T., & Khamis, A. (2024). Human-centric reward optimization for reinforcement learning-based automated driving using large language models. arXiv preprint arXiv:2405.04135. arXiv:2405.04135.
Ding, T., Xiang, D., Rivas, P., & Dong, L. (2025). Neural Pruning for 3D Scene Reconstruction: Efficient NeRF Acceleration. arXiv preprint. arXiv:2504.00950.
Yao, Z., Li, J., Zhou, Y., Liu, Y., Jiang, X., Wang, C., ... & Li, L. (2024). Car: Controllable autoregressive modeling for visual generation. arXiv preprint. arXiv:2410.04671.
Wang, Z., Li, B., Wang, C., & Scherer, S. (2024, October). AirShot: Efficient few-shot detection for autonomous exploration. In 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (pp. 11654-11661). IEEE.
Deng, T., Shen, G., Chen, X., Yuan, S., Shen, H., Peng, G., ... & Chen, W. (2025). MCN-SLAM: Multi-Agent Collaborative Neural SLAM with Hybrid Implicit Neural Scene Representation. arXiv preprint. arXiv:2506.18678.
Yang, C., He, Y., Tian, A. X., Chen, D., Wang, J., Shi, T., ... & Liu, P. (2024). Wcdt: World-centric diffusion transformer for traffic scene generation. arXiv preprint. arXiv:2404.02082.
Wang, J., Zhang, Z., He, Y., Song, Y., Shi, T., Li, Y., ... & He, L. (2024). Enhancing code llms with reinforcement learning in code generation. arXiv e-prints, arXiv-2412.
Zeng, S., Chang, X., Xie, M., Liu, X., Bai, Y., Pan, Z., ... & Wei, X. (2025). FutureSightDrive: Thinking Visually with Spatio-Temporal CoT for Autonomous Driving. arXiv preprint. arXiv:2505.17685.
He, L., Ka, D. H., Ehtesham-Ul-Haque, M., Billah, S. M., & Tehranchi, F. (2024). Cognitive models for abacus gesture learning. In Proceedings of the Annual Meeting of the Cognitive Science Society (Vol. 46).
Ding, T. K., Xiang, D., Qi, Y., Yang, Z., Zhao, Z., Sun, T., ... & Wang, H. (2025, May). NeRF-Based defect detection. In International Conference on Remote Sensing, Mapping, and Image Processing (RSMIP 2025) (Vol. 13650, pp. 368-373). SPIE.
Wei, Y., Gao, M., Xiao, J., Huang, B., Zhang, Y., & Tian, Y. (2025, March). Real-Time Traffic Sign Recognition Based on Threshold Segmentation and Neural Networks. In 2025 10th International Conference on Information and Network Technologies (ICINT) (pp. 80-87). IEEE.
Zhou, Y., Zeng, Z., Chen, A., Zhou, X., Ni, H., Zhang, S., ... & Chen, X. (2024, August). Evaluating modern approaches in 3d scene reconstruction: Nerf vs gaussian-based methods. In 2024 6th International Conference on Data-driven Optimization of Complex Systems (DOCS) (pp. 926-931). IEEE.
Ni, H., Meng, S., Chen, X., Zhao, Z., Chen, A., Li, P., ... & Chan, Y. (2024, August). Harnessing earnings reports for stock predictions: A qlora-enhanced llm approach. In 2024 6th International Conference on Data-driven Optimization of Complex Systems (DOCS) (pp. 909-915). IEEE.
Oehmcke, S., Li, L., Trepekli, K., Revenga, J. C., Nord-Larsen, T., Gieseke, F., & Igel, C. (2024). Deep point cloud regression for above-ground forest biomass estimation from airborne LiDAR. Remote Sensing of Environment, 302, 113968.
Gu, N., Kosuge, K., & Hayashibe, M. (2025). TactileAloha: Learning Bimanual Manipulation with Tactile Sensing. IEEE Robotics and Automation Letters.
Deng, T., Shen, G., Xun, C., Yuan, S., Jin, T., Shen, H., ... & Chen, W. (2025). Mne-slam: Multi-agent neural slam for mobile robots. In Proceedings of the Computer Vision and Pattern Recognition Conference (pp. 1485-1494).

Figure 1. Algorithm performance.

Table 1. Comparison of Experimental Results.

Method	Task Completion Rate (%)	Remaining Energy (%)	Safety Violation Events
A*-SP	72.0	18.0	14
Fixed Priority A*	83.0	25.5	9
Energy-Aware A*	89.0	33.2	6
Proposed	95.0	42.0	2

Table 2. Path length and Curvature.

Method	Path Length (×10³ m)	Avg Curvature (rad/m)	Max Curvature (rad/m)
A*-SP	1.47	0.32	0.95
Fixed Priority A*	1.39	0.28	0.83
Energy-Aware A*	1.32	0.35	0.97
Proposed	1.24	0.16	0.58

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Energy-Constrained Motion Planning and Scheduling for Autonomous Robots in Complex Environments

Abstract

Keywords:

Subject:

I. Introduction

II. Proposed Method

III. Experiments

IV. Conclusions

References

MDPI Initiatives

Important Links

Subscribe