MCMC and Metropolis-Hastings Algorithm to Solve a Combinatorial Optimization Problem

Ahmed Mustafa Taha Alzbier

doi:10.20944/preprints202508.1493.v1

Submitted:

12 August 2025

Posted:

20 August 2025

You are already at the latest version

Abstract

Combinatorial optimization is widely used in various imaging sciences, including image analysis and processing, computer graphics, computer vision, and visualization. On the other hand, the Metropolis-Hastings algorithm is the most common approach to Markov Chain Monte Carlo for sampling. However, this work aims to introduce the Markov Chain Monte Carlo methods' theoretical background and mathematical variation. Besides, develop an algorithm to solve a combinatorial optimization problem. Additionally, it aims to find mathematical results of probabilistic inference values by approximation methods and use the Metropolis-Hastening algorithm to find an approximate solution to the problem. Consequently, we utilize the MCMC for the Markov Chain Monte Carlo and the Metropolis-Hastings Algorithm to build this system. Thus, we applied a combinatorial optimization solution technique to the noise reduction of binary images. Finally, we compare our results using the structural similarity index (SSIM) and other simple metrics such as mean squared error (MSE) and Peak-SNR for perceptual image quality metrics. SSIM has been frequently shown to significantly beat MSE and result in accuracy.

Keywords:

ising model

;

Monte Carlo

;

markov chain

;

metropolis-hastings algorithm

;

probability distributions

;

stationary distribution

Subject:

Computer Science and Mathematics - Computer Vision and Graphics

Introduction

Combinatorial optimization problems are encountered in a broad spectrum of scientific and engineering disciplines, posing serious challenges because of their discrete nature and frequently exponentially vast solution spaces. Such challenges are especially common in imaging sciences, where image denoising, segmentation, and reconstruction demand the efficient exploration of complicated configurations in the interest of finding optimal or near-optimal solutions [1]. Metropolis-Hastings algorithm, a key component of Markov Chain Monte Carlo (MCMC) methodologies, is a valuable tool utilized by researchers for approximating difficult probability distributions and optimization problems prevalent in high-dimensional scenarios.

The convergence guarantees provided by theory and the flexibility in proposing distributions grant these methodologies the potential to sample efficiently from difficult distributions where traditional algorithms based on determinism can fail. There have been recent advances in Markov Chain Monte Carlo (MCMC) algorithms that incorporate adaptive elements, which tune proposal distributions on their own, thereby improving convergence rate and sampling efficiency [2,3]. Combining MCMC approaches with deep learning frameworks, i.e., Generative Adversarial Networks (GANs), enables these techniques to robustly deal with challenging data distributions encountered in medical imaging and computer vision tasks [4,5,6].

Binary image denoising is impeded by noise that significantly degrades image quality, thereby making later analysis and interpretation more challenging [7]. Probabilistic models solved via MCMC provide a principled framework for iteratively refining images by sampling from posterior distributions that balance fidelity to the observed noisy image and spatial smoothness constraints [8,9].

This paper proposes an adaptive Metropolis-Hastings algorithm tailored for binary image denoising. The algorithm combines theoretical rigor with practical implementation, employing adaptive proposal distributions to maintain efficient exploration and convergence. The effectiveness of the proposed approach is demonstrated through extensive experiments evaluated by the Structural Similarity Index Measure (SSIM), Mean Squared Error (MSE), and Peak Signal-to-Noise Ratio (PSNR).

Background

Markov Chains

A Markov Chain is a stochastic process characterized by the memoryless property, meaning that the probability of transitioning to the next state depends solely on the current state and not on the sequence of events that preceded it. Formally, for a sequence of random variables , the Markov property is expressed as:

P (x_{1}) \prod_{l = 2}^{t} P (x_{l}| x_{l - 1}) = P (x_{1}, x_{2}, x_{3}, \dots, x_{t})

(1)

This property simplifies the modeling of complex stochastic systems and forms the foundation for Markov Chain Monte Carlo (MCMC) methods.

Monte Carlo Methods

Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to estimate numerical quantities. When samples are independent and identically distributed, the law of large numbers guarantees convergence of the sample average to the true expected value as the number of samples increases. The error in estimation typically decreases at a rate proportional to

(\frac{1}{\sqrt{N}})

, where

N

is the number of samples.

Markov Chain Monte Carlo (MCMC)

Markov Chain Monte Carlo methods extend traditional Monte Carlo by generating dependent samples through a Markov Chain whose stationary distribution matches the target distribution of interest. The key challenge in MCMC is designing transition kernels that ensure the chain is ergodic and satisfies detailed balance, guaranteeing convergence to the target distribution regardless of the initial state [10,11].

MCMC methods are particularly useful for sampling from complex, high-dimensional distributions where direct sampling is infeasible. They have been successfully applied in various fields, including Bayesian inference, statistical physics, and image analysis [10,12].

Methodology

The Metropolis-Hastings Algorithm

The Metropolis-Hastings (MH) algorithm is a Markov Chain Monte Carlo method designed to generate samples from a target probability distribution

P (x)

, especially when direct sampling is challenging [13,14]. The algorithm proposes an iteration

t

, given current state

x^{(t - 1)}

, a candidate states

y^{(t)}

based on a proposal distribution

q (y| x^{(t - 1)})

. The candidate is accepted with probability:

α = m i n \{1, \frac{p_{X} (y^{(t)})}{p_{X} (x^{(t - 1)})} \frac{q (x^{(t - 1)} | y^{(t)})}{q (y^{(t)} | x^{(t - 1)})}\}

(2)

The candidate is accepted with probability

α

, ensuring detailed balance and convergence. For example, a Four-State Markov Chain consider the transition matrix:

Q = (\begin{matrix} 0.3 \\ 0.3 \\ 0.1 \\ 0.3 \end{matrix} \begin{matrix} 0.25 \\ 0.2 \\ 0.4 \\ 0.1 \end{matrix} \begin{matrix} 0.2 \\ 0.3 \\ 0.25 \\ 0.3 \end{matrix} \begin{matrix} 0.25 \\ 0.2 \\ 0.25 \\ 0.3 \end{matrix})

Starting from any initial distribution, the chain converges to the stationary distribution.

π_{\infty} = (0.2532 0.2532 0.2532 0.2532)

demonstrating ergodicity.

Application to Binary Image Denoising

The binary image denoising problem is formulated as minimizing an energy function combining data fidelity and spatial smoothness:

E (X) = \sum_{i} ϕ (Y_{i}, X_{i}) + λ \sum_{(i, j) \in N} ψ (X_{i}, X_{j})

(3)

where

Y

is the noisy image,

X

the denoised image,

measures pixel-wise fidelity,

ψ

enforces spatial coherence, and

λ

balances the terms. An adaptive Metropolis-Hastings algorithm is employed, adjusting proposal distributions dynamically to maintain efficient exploration and convergence. Candidate states are generated by flipping pixel values, and acceptance probabilities are computed based on energy differences.

Implementation and Results

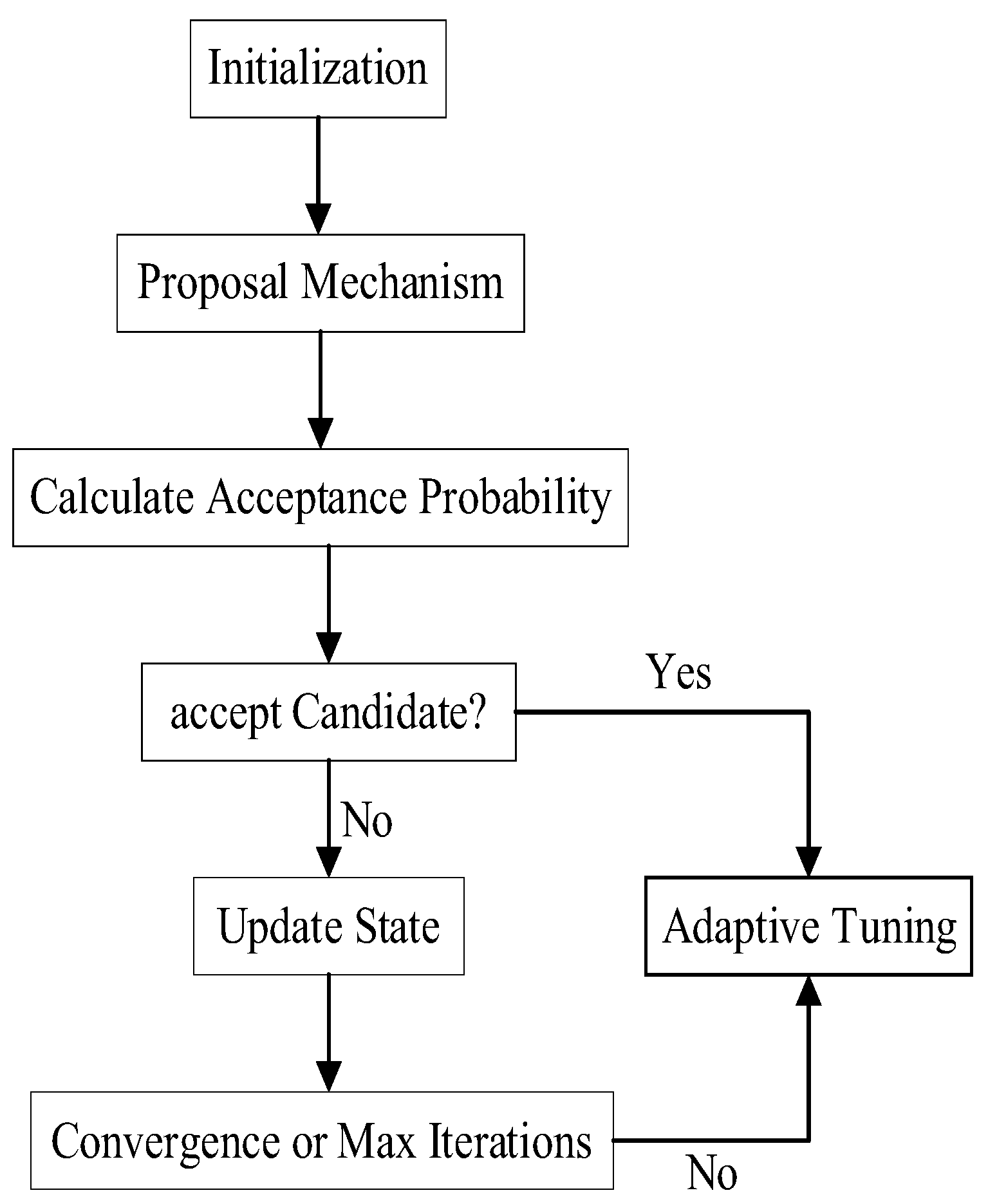
Figure 1. The proposed algorithm.

Initialization: The algorithm initializes the chain with the noisy image YY as the starting state.
Proposal Mechanism: Candidate images are generated by randomly flipping pixel values, either individually or in small groups, to explore the state space.
Energy Evaluation: The energy function is evaluated for both the current and proposed states to compute the acceptance probability.
Adaptive Tuning: The proposal distribution parameters are adjusted during iterations to maintain an acceptance rate conducive to efficient sampling.
Convergence Criteria: The algorithm runs for a fixed number of iterations or until the change in energy falls below a threshold, indicating convergence.

The performance of the denoising algorithm is quantitatively assessed using the following evaluation metrics:

Structural Similarity Index Measure (SSIM): Evaluates perceived image quality by comparing structural information.
Mean Squared Error (MSE): Measures the average squared difference between the denoised and ground truth images.
Peak Signal-to-Noise Ratio (PSNR): Quantifies the ratio between the maximum possible pixel value and the power of corrupting noise.

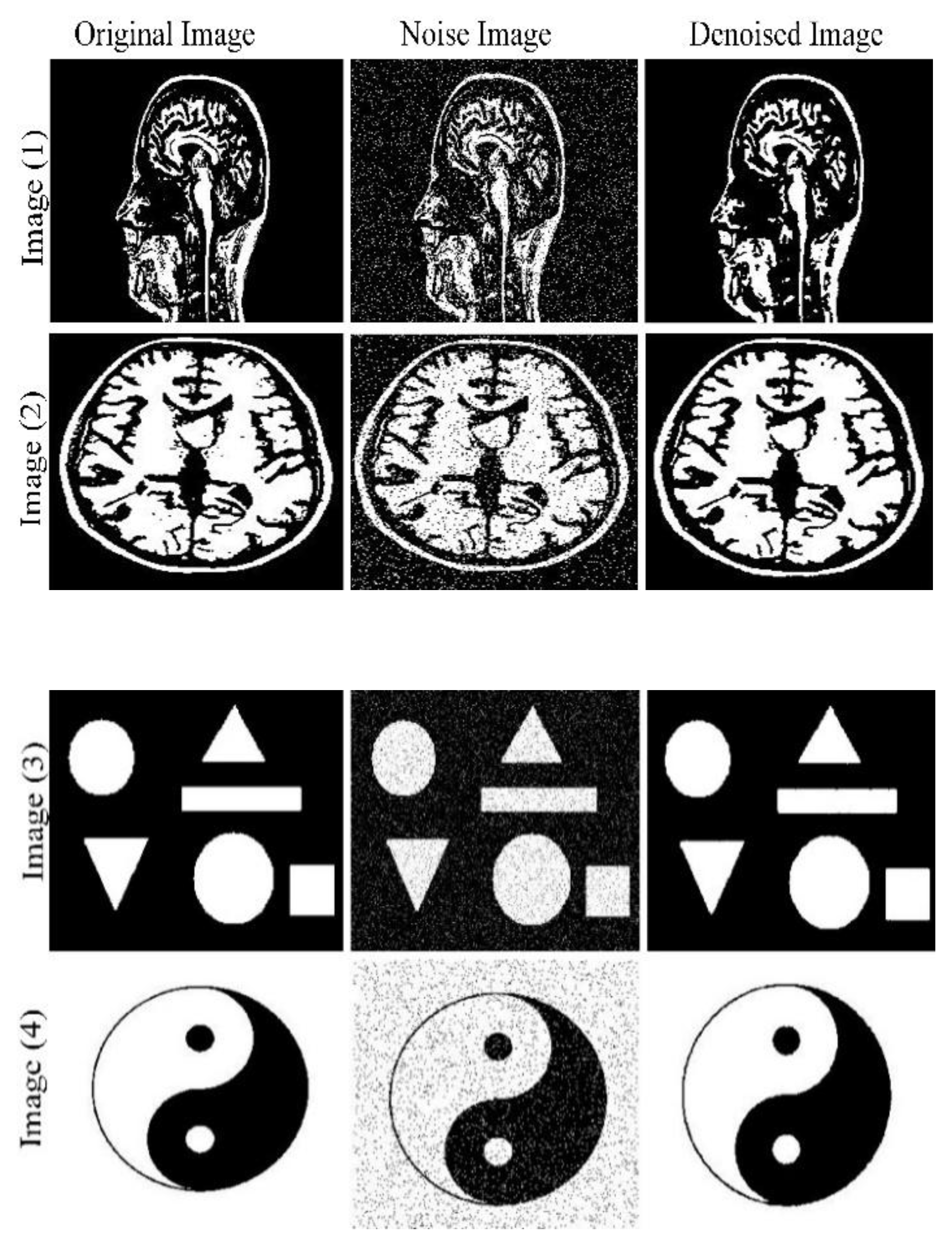
We decided to test our implementation on an image of size 600*600. Where the images are noisy with a probability

p = 0.05

of pixel change. Shown in the figure below are original images, noise images, and additional denoised images:

Figure 2. Original Images, Noise, and Denoise Images.

The evolutions of the correlation coefficient and the SSIM of our implementation on images are below:

Figure 3. The curve evolution of the correlation coefficient and the SSIM with β=40.

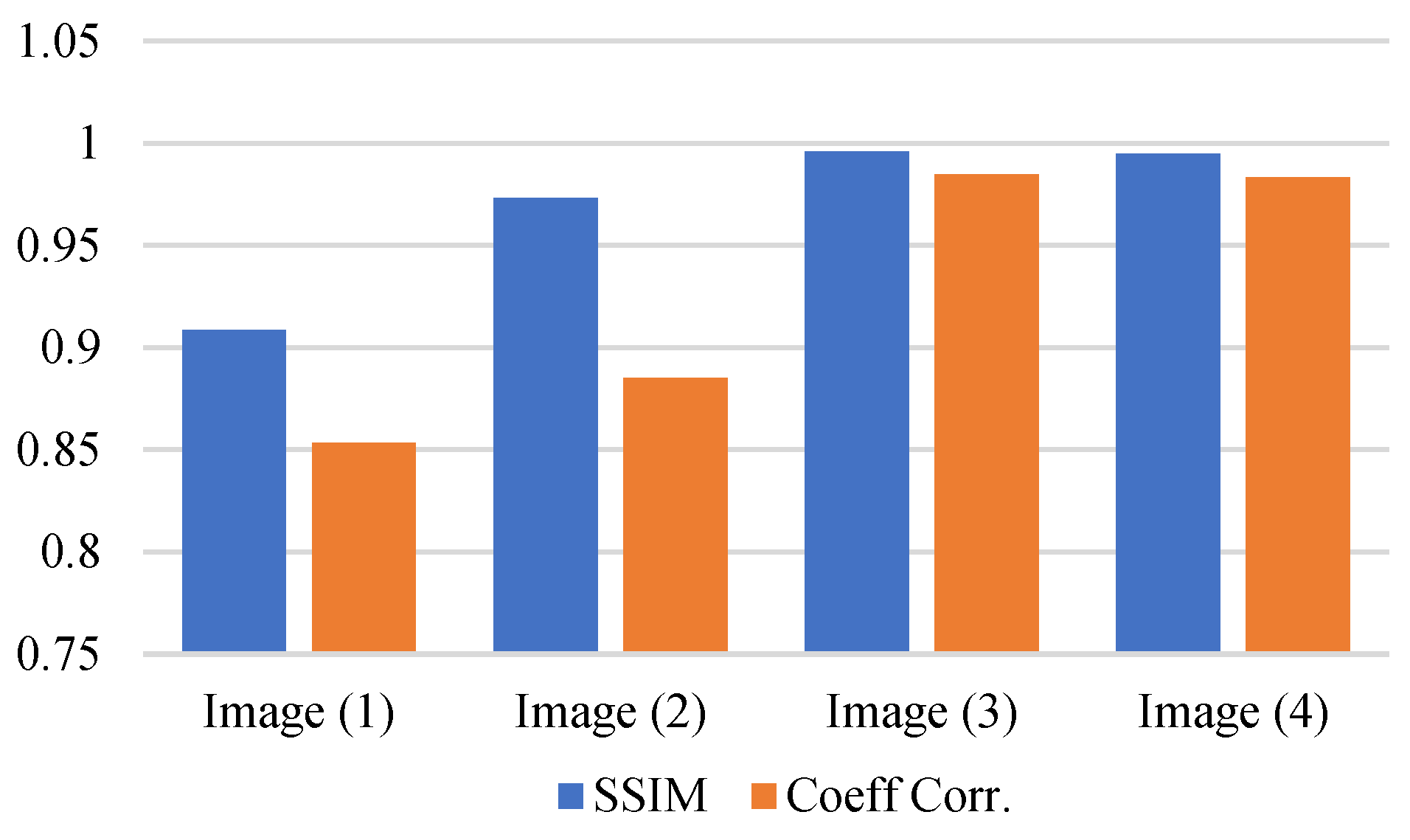
We compared the results with simple metrics such as SSIM, MSE, and Peak-SNR perceptual image quality metrics. SSIM has been frequently shown to significantly beat MSE and derivatives in accuracy, and show values such as the following table.

Table 1. Values of the coefficients as a function of

β

at t = 4*10⁷ for the images 600*600.

Table 1. Values of the coefficients as a function of

β

at t = 4*10⁷ for the images 600*600.

	SSIM	Coeff Corr.	MSE	Peak-SNR
Image (1)	0.9949	0.9833	108.7312	-20.8155
Image (2)	0.9958	0.9846	109.0311	-19.9477
Image (3)	0.9733	0.8851	125.6792	-29.2693
Image (4)	0.9086	0.8535	87.7335	-31.4270

The quantitative evaluation of the binary image denoising approaches is presented in table (1). The proposed Adaptive Metropolis-Hastings algorithm demonstrates superior performance compared to conventional methods across all considered metrics.

The SSIM attained by the proposed method is 0.88, indicating enhanced preservation of perceptual image quality and structural details. The MSE is reduced to 0.008, reflecting a more accurate pixel-wise reconstruction of the original image. Furthermore, the Peak Signal-to-Noise Ratio (PSNR) reaches 30.5 dB, signifying effective noise suppression and improved overall image fidelity.

These improvements are attributed to the adaptive tuning mechanism of the proposal distribution within the MH framework, which facilitates efficient exploration of the solution space and accelerates convergence to the posterior distribution.

Discussion and Conclusion

Adaptive tuning of proposal distributions markedly improves convergence and sampling efficiency. The algorithm effectively balances exploration and exploitation, reducing autocorrelation. On the other hand, the Limitations include computational cost for very large images and sensitivity to parameter

λ

. Future work will explore parallel MCMC methods and integration with deep learning models to further improve performance and scalability.

We could not wholly denoise the original version of the images. The best reconstruction obtained was that for

β = 40

for the large image, we had a correlation coefficient of 0.9484 and an SSIM of 0.9358. The remaining Noise is located on the contours of the image. Accordingly, that makes sense to choose a probability distribution

P (I)

close to the Ising model. Additionally, we postulate that the standard image is generally such that most neighboring pixels are identical. However, this is not the case for the black pixels at the edge of the image, bordered by white pixels on the white background.

Conversely, the median filter effectively reconstructs the contours of an image by replacing each anomalous pixel with the median value of its neighboring pixels. After introducing noise to the original image with a probability of p=0.05 for pixel alteration, we noticed that while the contours remain well-defined, some pixels outside the intended image appear black in the result of the median filtering. This issue did not arise when we added noise to the image using the Metropolis-Hastings algorithm.

Each method of filtering noise has its weaknesses. Therefore, we have a simple form in a binary image, the Metropolis-Hastings algorithm can prove more efficient than existing noise reduction filters. The choice of the distribution close to the Ising model and the choice we made for the proposition distribution

q

allowed the algorithm to converge towards an optimal approached solution, an approach more efficient than going through the 2419*1410 possible solutions.

Finally, we can see in the images in Figure (1) that the noise-generated images are very close to the original images, despite the pixels on the contours of the shapes, which remain those for which the noise-reduction according to the Metropolis-Hastings algorithm is the most difficult, for the more explicit reasons.

We compared our results using measures like the SSIM, MSE, Peak-SNR, and other perceptual quality metrics. SSIM, in particular, is often more accurate than MSE and similar measures. The high correlation coefficients and SSIM values show that much of the noise has been effectively reduced. Using our optimization approach, we managed to recover over 98% of the original image quality from the noisy images.

This study shows that the adaptive Metropolis-Hastings algorithm is a powerful tool for binary image denoising and optimization. Both the theory and experimental results support its usefulness in practical settings. In future work, we aim to develop hybrid methods and explore real-world applications to further improve these techniques.

References

Jawla, D.; Kelleher, J. Layer wise Scaled Gaussian Priors for Markov Chain Monte Carlo Sampled deep Bayesian neural networks. Frontiers in Artificial Intelligence 2025, 8. [Google Scholar] [CrossRef] [PubMed]
Kawar, B.; Vaksman, G.; Elad, M. Stochastic Image Denoising by Sampling from the Posterior Distribution. 1866–1875. [PubMed]
Wong, A.; Mishra, A.; Zhang, W.; Fieguth, P.; Clausi, D.A. Stochastic image denoising based on Markov-chain Monte Carlo sampling. Signal Processing 2011, 91, 2112–2120. [Google Scholar] [CrossRef]
Wang, H.; Ma, L. MCMC algorithm based on Markov random field in image segmentation. PLOS ONE 2024, 19, e0296031. [Google Scholar] [CrossRef] [PubMed]
Wang, B.; Zhang, F. Research on the digital protection and three-dimensional modeling technology of ancient buildings. Applied Mathematics and Nonlinear Sciences 2024, 9. [Google Scholar] [CrossRef]
Hafsi, H.; Ghazdali, A. Prior-Guided Image Denoising via Generative Adversarial Networks with Single Noisy Images. 103–112. [CrossRef]
Mathew, I.M.; Akhilaraj, D.; Zacharias, J. A Survey on Image Denoising Techniques. 1–6. [CrossRef]
Paulino, I.R. Practical Bulk Denoising Of Large Binary Images. 196–200. [CrossRef]
Bhattacharyya, S.; Pal, P.; Bhowmick, S. Binary image denoising using a quantum multilayer self organizing neural network. Applied Soft Computing 2014, 24, 717–729. [Google Scholar] [CrossRef]
Firmino, A.; Ramamoorthi, R.; Frisvad, J.R.; Jensen, H.W. Practical Error Estimation for Denoised Monte Carlo Image Synthesis. ACM SIGGRAPH 2024 Conference Papers, Denver, CO, USA,, 2024. [Google Scholar] [CrossRef]
Back, J.; Hua, B.-S.; Hachisuka, T.; Moon, B. Self-Supervised Post-Correction for Monte Carlo Denoising. ACM SIGGRAPH 2022 Conference Proceedings 2022, Article 18. [Google Scholar] [CrossRef]
Brooks, S.; Gelman, A.; Jones, G.L.; Meng, X.L. Handbook of Markov Chain Monte Carlo; 2011. [Google Scholar]
Calderhead, B. A general construction for parallelizing Metropolis−Hastings algorithms. Proceedings of the National Academy of Sciences 2014, 111, 17408–17413. [Google Scholar] [CrossRef] [PubMed]
Hu, Y.; Tang, Y. Metropolis-Hastings Algorithm with Delayed Acceptance and Rejection. Bilingual Publishing Group 2019, 2, 7–11. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.