Financial Time Series Forecasting Based on Sliding Window–Variational Mode Decomposition and Deep Learning

1. Introduction

Financial time series forecasting refers to the use of historical data to build time series or other econometric models to predict key financial indicators such as prices, indices, returns, and volatility. Accurate forecasting of financial time series data enhances the understanding of market volatility, assists government agencies in risk control, and helps investors formulate more rational investment strategies using market fluctuation information.

Classical financial time series prediction methods primarily employ statistical models such as ARCH (Autoregressive Conditional Heteroskedasticity Model) and GARCH (Generalized ARCH), as well as their improved versions. These models describe features like heteroskedasticity and volatility clustering in financial markets [1,2].

With the advent of the deep learning era in the 21st century, numerous classic neural network models have emerged, such as Convolutional Neural Networks (CNN), Deep Belief Networks (DBN), Autoencoders (AE), and Recurrent Neural Networks (RNN). Among them, Long Short-Term Memory (LSTM) networks are particularly effective for processing sequential data. LSTM, proposed by Sepp Hochreiter and Jürgen Schmidhuber in 1997 [3], is a type of RNN that effectively captures long-term dependencies in time series by retaining relevant historical information within neurons.

LSTM has been widely applied in financial time series forecasting. For example, Jin Xuejun (2016) used LSTM to study whether China’s inflation level was affected by the expansionary monetary policy of the United States. He compared the results with a Value at Risk (VAR) model and concluded that LSTM outperformed VAR in economic analysis [4].

Xie Heliang et al. (2018) constructed an LSTM-based option pricing model and conducted empirical analysis using 50ETF call and put options. Their results showed that the LSTM model provided higher pricing accuracy than the classic Black-Scholes Monte Carlo method [5].

Li Ying and Wang Lulu (2020) proposed a GA-LSTM model, which integrates Genetic Algorithms to optimize LSTM parameters. They applied this to model complex, nonlinear time series data in the futures market and achieved improved prediction accuracy [6].

Chen Qiqi (2020) utilized CNNs to extract spatial structural features from data, followed by LSTM for sequential feature extraction. This CNN-LSTM hybrid model was shown to effectively predict short-term intraday stock highs [7].

Properly preprocessed datasets significantly enhance model performance. Effective decomposition techniques for time series include Empirical Mode Decomposition (EMD) [8] and Variational Mode Decomposition (VMD) [9], originally proposed for noise reduction in engineering signal processing. These methods have since been applied to financial data such as crude oil [10] and gold prices [11].

VMD is a recently proposed adaptive signal decomposition method based on variational principles. It formulates an optimization problem that minimizes the sum of bandwidths of each mode, decomposing the signal into multiple quasi-orthogonal intrinsic mode functions (IMFs) with reduced noise and redundancy.

Due to the nonlinear and nonstationary characteristics of financial time series data, direct application of historical closing prices and returns to LSTM models often results in lagged predictions. This compromises the accuracy of trend forecasts. To address this, we propose a Sliding Window Variational Mode Decomposition (SW-VMD) method to process Chinese stock index data. After extracting key features, LSTM networks are used to predict price and return trends. Comparative experiments are designed to validate the model’s effectiveness.

2. Related Work

Recent developments in financial time-series forecasting have significantly benefited from advanced deep learning models. Models built on convolutional neural networks (CNNs) have proven effective in extracting spatial features from stock volatility data, enhancing predictive accuracy in financial contexts [12]. Meanwhile, reinforcement learning methods have been successfully adapted for financial decision-making and scheduling, leveraging multi-agent strategies to navigate complex market dynamics [13]. Efforts to combine multimodal data sources through feedforward networks have also demonstrated promising results in improving the robustness of stock prediction models [14].

In the domain of financial text analysis, one-dimensional CNNs have enabled high-precision risk classification and auditing capabilities, underscoring the versatility of CNN-based architectures [15]. Reinforcement learning continues to show potential for nonlinear and dynamic risk control in volatile financial markets through nested temporal frameworks [16]. Enhancements to reinforcement learning algorithms, such as those based on the A3C model, have further contributed to more accurate market turbulence prediction and proactive risk management [17].

Outside of core financial forecasting, diffusion models have been introduced for interface generation, which—while outside traditional financial domains—offer insights into generative modeling applicable to data synthesis and scenario simulations [18]. Transfer learning methods for large language models have further introduced dynamic fine-tuning strategies that can support robust few-shot learning, critical for domains with sparse financial event data [19].

Graph-based learning has also been employed to detect transaction fraud by modeling network structures, supporting the idea of relational modeling in financial data streams [20]. In portfolio optimization, reinforcement learning methods such as QTRAN have been applied to dynamically allocate resources, providing a theoretical basis for strategic financial positioning [21].

Anomaly detection techniques based on global temporal attention and transformer models have emerged in video and sequential data, which can be translated into high-frequency trading data analysis [22]. Ensemble and data balancing methods have enhanced classification tasks such as credit card fraud detection [23], while heterogeneous graph attention networks have enabled deep fraud analytics in heterogeneous financial environments [24].

Probabilistic graphical models and variational inference have addressed class imbalance problems often found in financial classification datasets [25]. Advances in BERT-based compliance analysis have improved audit automation through contextual understanding [26], and deep anomaly detection systems have demonstrated efficacy in uncovering irregularities in high-frequency trading scenarios [27].

Causal representation learning has been proposed for market return forecasting, revealing the impact of hidden variables on prediction tasks [28]. Temporal graph learning frameworks and hybrid LSTM-Copula methods have contributed significantly to modeling user behavior and portfolio risk across evolving markets [29,30]. BiLSTM-CRF models, originally used in social text segmentation, offer transferable techniques for boundary detection in labeled financial sequences [31].

Further research on causal inference for return prediction across markets has refined the cross-domain forecasting capability of financial models [32], while multi-task learning architectures have been employed for macroeconomic forecasting, reinforcing the importance of domain fusion [33]. Decision-making dynamics in audit workflows have also been enhanced through deep Q-learning frameworks [34].

Finally, generative models for volatility prediction and multi-task instruction encoding strategies reflect growing trends in applying advanced generative and coordinated learning mechanisms to financial and regulatory modeling [35,36].

3. LSTM Neural Network Based on SW-VMD Data Decomposition

We first construct the sliding window VMD data decomposition algorithm and the LSTM network, then integrate the preprocessed data with the neural network to build separate models for stock index closing prices and returns.

3.1. Sliding Window–Variational Mode Decomposition Algorithm

The core concept of the Variational Mode Decomposition (VMD) algorithm is to transform the decomposition of the original time series into a constrained variational optimization problem. Under the condition that the sum of all intrinsic mode functions (IMFs) and the residual equals the original signal, the algorithm aims to minimize the estimated bandwidth of each mode. Based on this condition, the center frequency and bandwidth of each decomposed mode are determined, enabling adaptive frequency-domain partitioning and effective separation of the signal components. Through iterative optimization, the center frequencies and mode functions are continuously updated until multiple IMFs are obtained. The number of IMFs is predefined manually.

For the financial time series data in this study, each VMD decomposition result is influenced by the entire original signal. This means that if the entire time series is decomposed at once, the decomposition result at the current time point will contain information from future data. Consequently, this prevents valid predictive analysis based on current data decomposition.

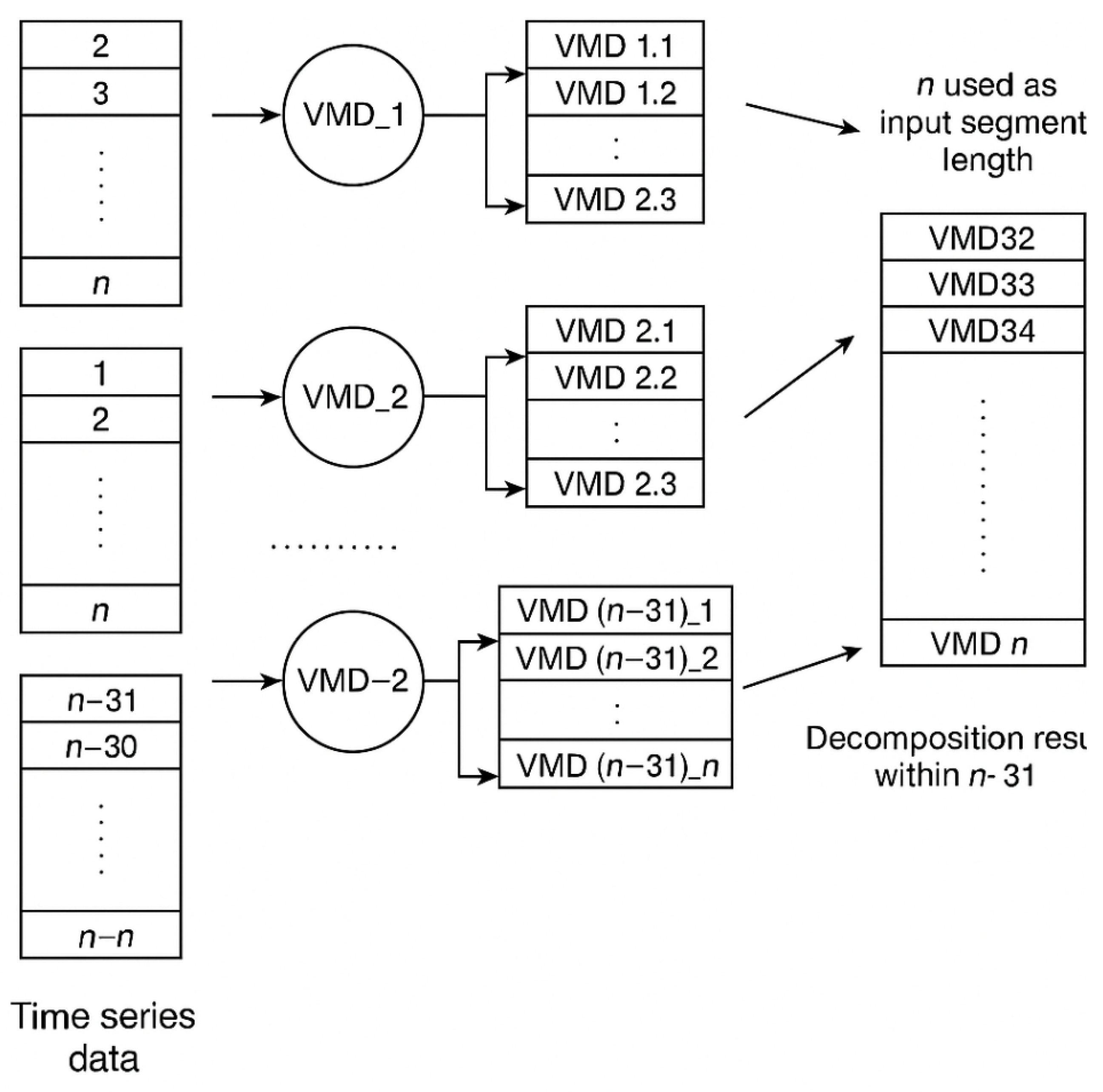
To address this, we propose a sliding window-based VMD decomposition strategy. Specifically, a dataset of 32 days is treated as a window, and the decomposition is performed in a progressive manner. The detailed process is as follows: the data from Day 1 to Day 32 is decomposed using VMD, and the decomposition result of Day 32 is taken as the first input for the model to predict the closing price and return of Day 33. This process continues iteratively—i.e., the decomposition of data from Day $n-31$ to Day n yields the decomposition result of Day n, which serves as the ${(n-31)}^{\mathrm{th}}$ input to the model to predict the ${(n+1)}^{\mathrm{th}}$ day’s results.

The decomposition data construction process is illustrated in Figure 1.

In Figure 1, VMD_i ($i=1,\dots ,n-31$) denotes the $i^{\mathrm{th}}$ set of data undergoing VMD decomposition. VMD_i_j ($i=1,\dots ,n-31;j=i,\dots ,i+31$) represents the decomposed result of the $j^{\mathrm{th}}$ day from the $i^{\mathrm{th}}$ VMD operation. VMD_i indicates the $i^{\mathrm{th}}$ input variable for the model, corresponding to the final item in the VMD result of the $i^{\mathrm{th}}$ decomposition. That is, VMD32 = VMD_1_32, VMD33 = VMD_2_33, VMD34 = VMD_3_34, and so on until VMD_n = VMD_$(n-31)$(n).

3.2. LSTM Network Structure

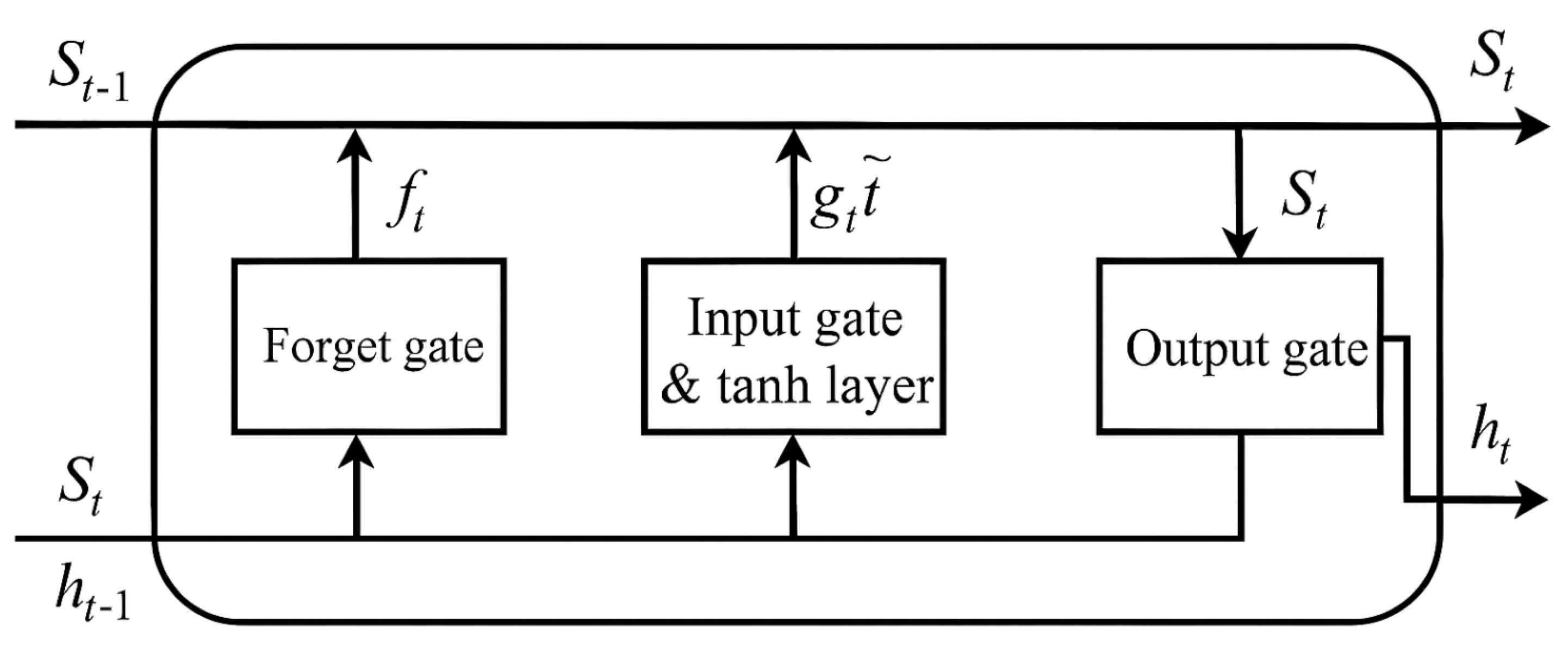
The Long Short-Term Memory (LSTM) neural network consists of three main components: an input layer, an output layer, and hidden layers. The number of hidden layers and the number of neurons in each layer determine the network’s depth and complexity. Analogous to biological neural networks, neurons are the smallest computational units capable of processing information. LSTM uses neurons to selectively allow sequence information to influence the network state at each training step. Activation functions such as tanh, sigmoid, and ReLU are used to output values between 0 and 1 as gates, which determine how much of the current input can pass through these "gates."

A "layer" refers to a group of neurons, and the overall network is formed by connecting these layers in a structured manner. The LSTM algorithm includes two processes: forward propagation and backpropagation. During forward propagation, information is processed through the forget gate, input gate, and output gate in order. In backpropagation, the chain rule is used to compute gradients of weights and biases in each neuron, which are iteratively updated using optimization algorithms until a suitable neural network model is trained.

Figure 2 shows the structure of an LSTM unit.

As illustrated in Figure 2, the LSTM network not only extracts useful information from the current data state in a sequence but also retains long-term dependencies from earlier computation steps that are far from the current state. This makes LSTM one of the ideal tools for solving time-series problems.

In summary, the specific algorithmic process of the LSTM time-series forecasting model based on SW-VMD data decomposition is as follows:

• Step 1: Apply Sliding Window–Variational Mode Decomposition to stock index closing price and return sequences of length n, generating input data of length $n-31$ with m intrinsic mode functions (IMFs).
• Step 2: Split the data into training, validation, and testing sets. The validation set covers 30 days, and the testing set spans 60 days.
• Step 3: During training, introduce the validation set after 1000 training steps. Perform validation every 30 steps and save the model that performs best on the validation set.
• Step 4: Input the test set into the best-performing saved model to predict stock index closing prices and returns. Evaluate and compare the effects of different models and datasets on prediction performance.

4. Empirical Analysis

Due to their strong representativeness in the stock market and relatively stable investment profile, this study selects the Shanghai Composite Index and the CSI 300 Index. Historical information prior to each time point is used to build LSTM neural network models to predict the next day’s stock index closing price and return trends.

To assess the effectiveness of the algorithm on datasets with different volatilities, both the relatively stable closing price and the highly volatile return series are decomposed for model construction. Models using raw data and those using SW-VMD decomposed data are compared to evaluate the impact of decomposition on model prediction performance.

The logarithmic return is calculated using adjacent closing prices as follows:

$$r=ln\left({\displaystyle \frac{p_i}{p_{i-1}}}\right)$$

(1)

Based on the return sequence, the price trend is defined as:

$$\mathrm{trend}=\left\{\begin{array}{cc}\mathrm{down},\hfill & r_i<-1\%\hfill \\ \mathrm{flat},\hfill & -1\%\le r_i\le 0.5\%\hfill \\ \mathrm{up},\hfill & r_i>0.5\%\hfill \end{array}\right.$$

(2)

The input variables for the LSTM model without data decomposition include closing price, highest price, lowest price, previous closing price, trading volume, and return. For the SW-VMD-based model, the number of intrinsic mode functions (IMFs) is set to 6, and both closing price and return data are decomposed per the process in Figure 1.

4.1. Stationarity and Memory Property Testing

ADF (Augmented Dickey-Fuller) tests are performed to assess the stationarity of the time series. A series is considered stationary if the test statistic is less than the critical values at 1%, 5%, or 10% levels. Table 1 shows the ADF results.

The Hurst exponent is then used to evaluate the memory properties of the time series before model training. Table 2 displays the results.

The results show that the return sequences fall in the range [0.45, 0.5], indicating long memory with weak anti-persistence. Closing price sequences have Hurst values above 0.5, indicating strong persistence—when prices rise, they tend to keep rising, and vice versa.

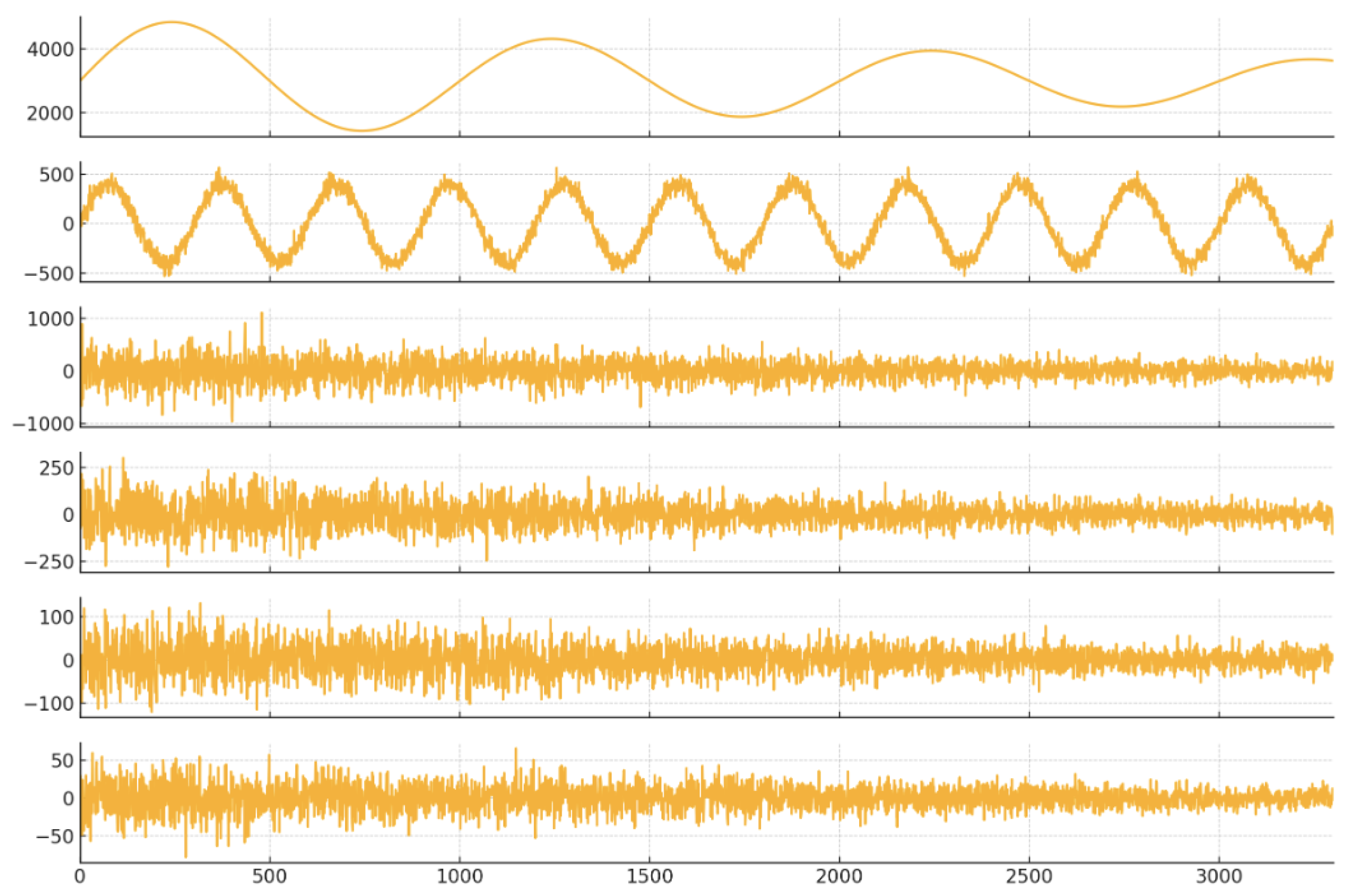
4.2. Data Processing and Decomposition

The SW-VMD algorithm is applied to decompose the closing price and return series of both indices into six IMFs. An example of the VMD decomposition for the CSI 300 closing price is shown in Figure 3.

4.3. Prediction Results and Analysis

The LSTM is implemented using the TensorFlow framework. Data is normalized using Z-score standardization. The model is configured with 3 hidden layers, each containing 128 neurons. Batch size is set to 256, time step to 1, and number of iterations to 5000. Dropout rate is 0.1 to avoid overfitting. Both L1 and L2 regularizations are applied with parameters 0.01.

A fixed step decay learning rate is used, starting at 0.0015 and decaying by 97.5% every 50 steps. The Adam optimizer is employed. The training loss function is defined by the mean squared error (MSE):

$$\mathrm{MSE}={\displaystyle \frac{1}{m}}\sum _{i=1}^m{(y_i-{\widehat{y}}_i)}^2$$

(3)

The total data lengths are 7207 (SSE) and 3264 (CSI 300). After applying a 32-day sliding window, usable lengths are 7176 and 3233. The last 60 entries are used as the test set, and the previous 30 as the validation set.

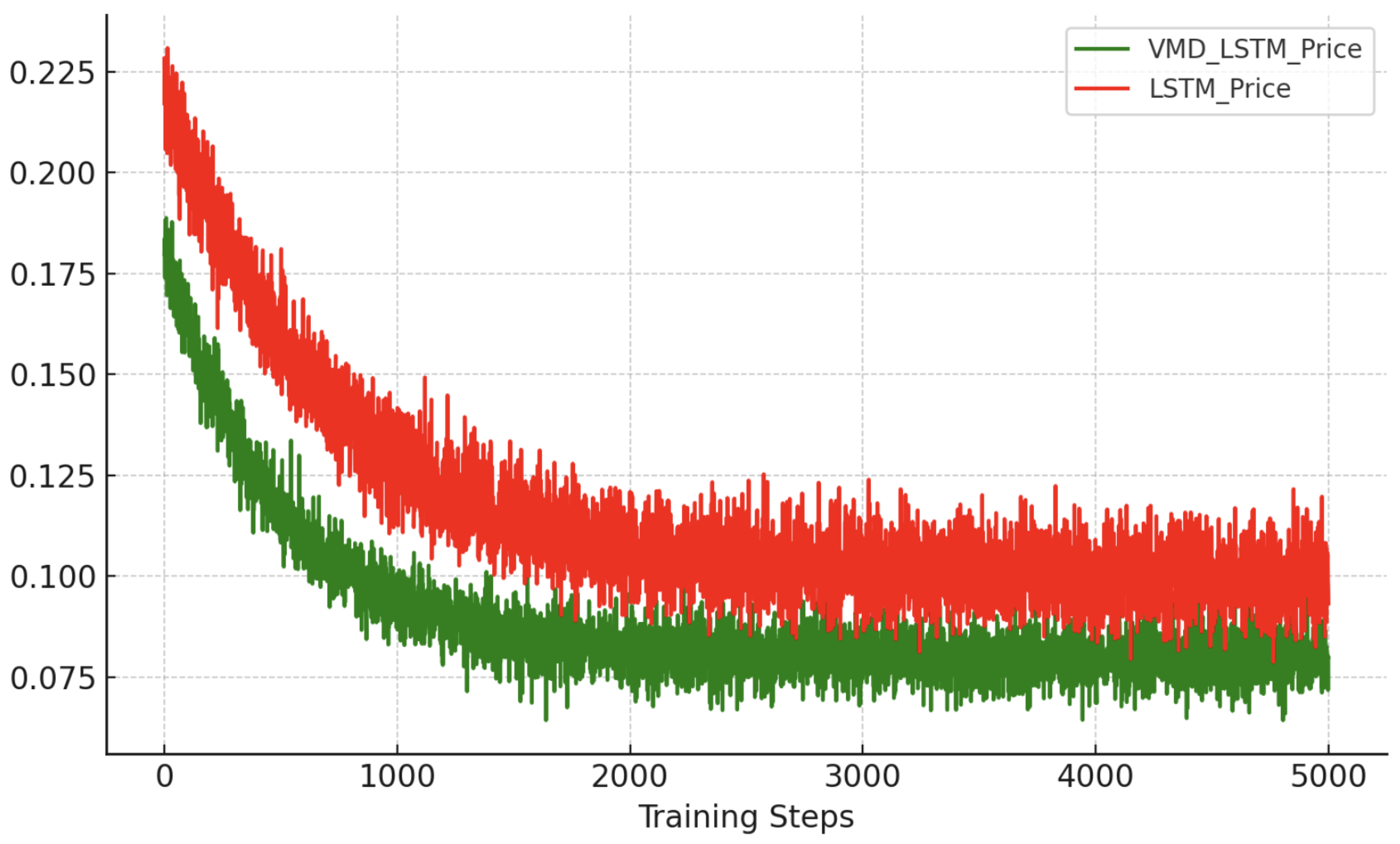
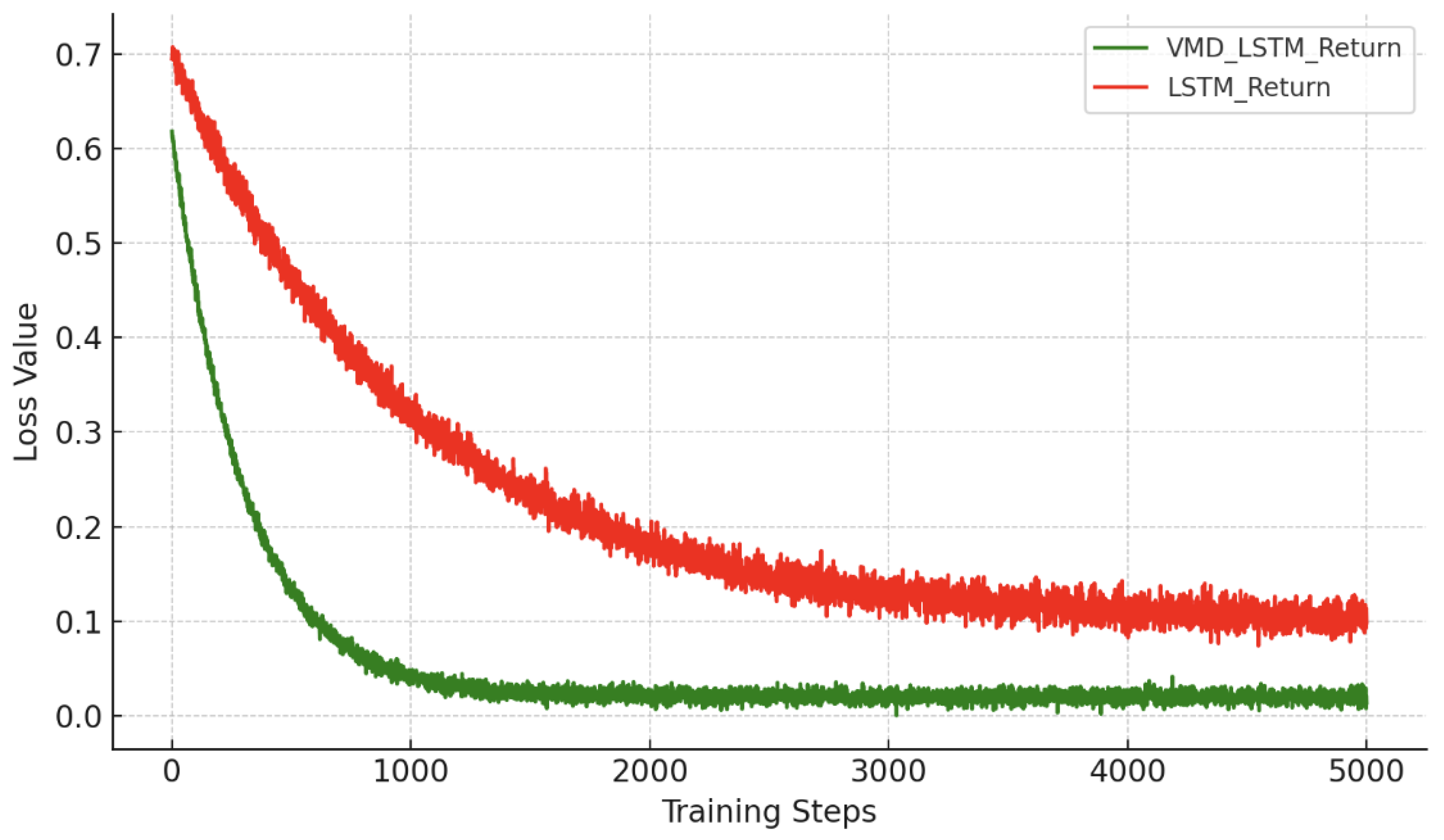
Figure 4 and Figure 5 show that SW-VMD significantly improves model convergence, especially for the more volatile return series.

4.4. Validation and Performance Evaluation

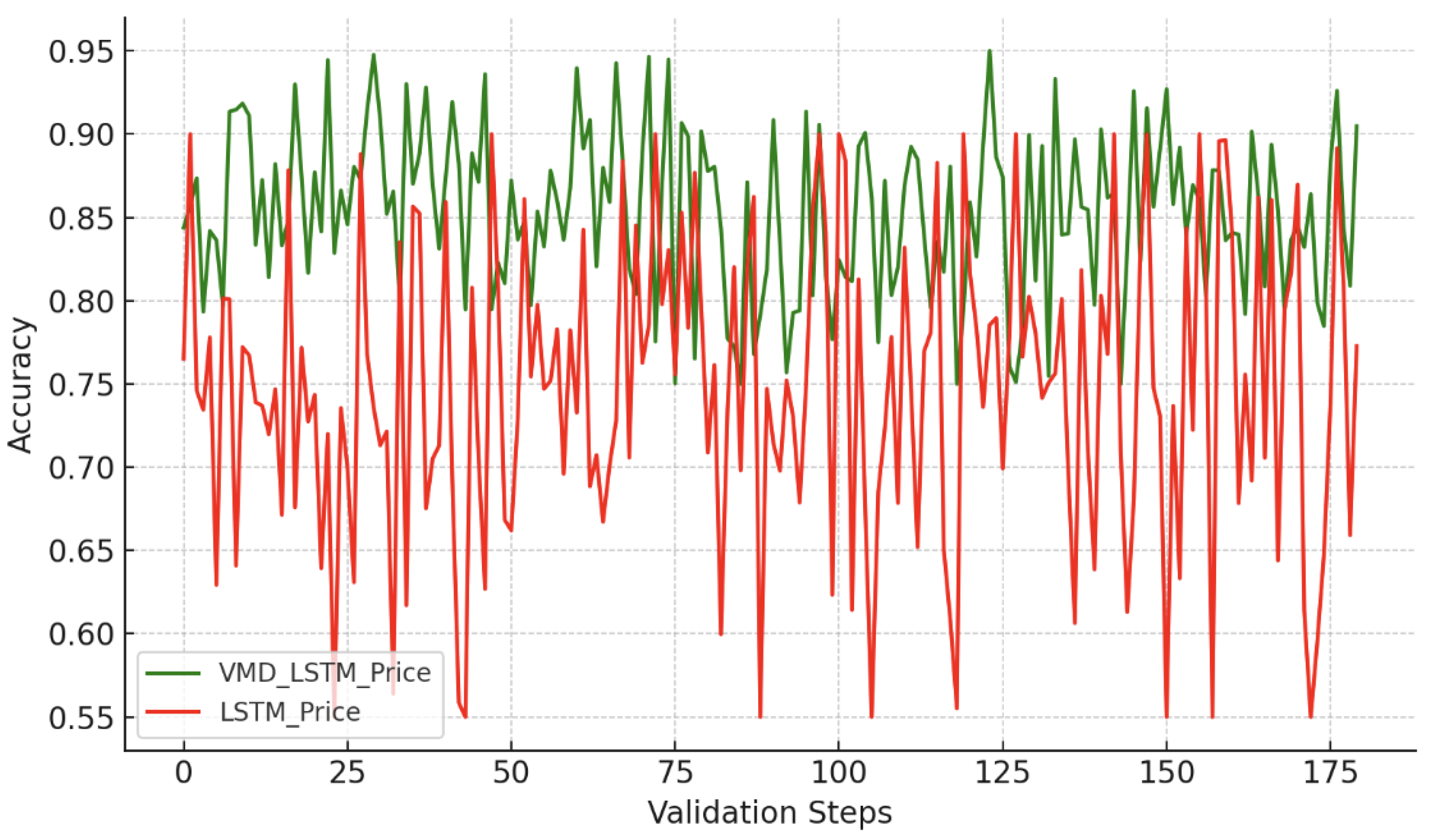
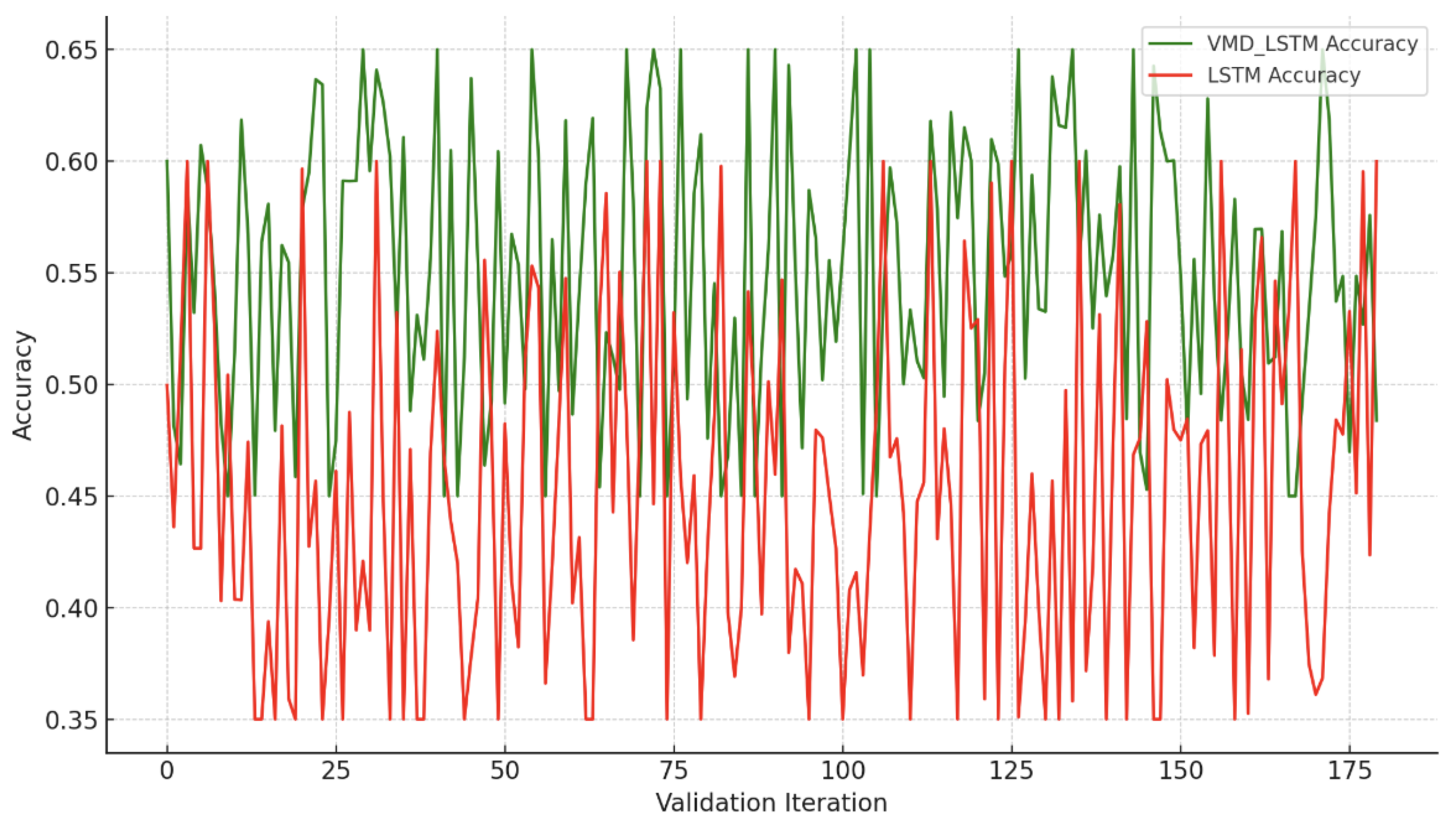
Figure 6 and Figure 7 show the trend prediction accuracy on the validation set. In 180 validations, the SW-VMD-enhanced model outperformed the raw model 158 and 120 times for SSE and CSI 300 price prediction (87.78% and 66.67%). For returns, SW-VMD outperformed in 148 and 173 cases (82.22% and 96.11%).

Overall, SW-VMD improves trend accuracy by 5.28% for price and 12.65% for return. The method is especially effective on more volatile time series.

5. Conclusion

This paper proposes an optimized forecasting approach for financial time series based on the Sliding Window–Variational Mode Decomposition (SW-VMD) and LSTM neural network. Since VMD extracts intrinsic mode functions from an entire dataset, a sliding window approach ensures proper use of historical data without leaking future information.

The decomposed data not only exhibit linearity and stationarity but also enhance feature extraction and reuse. Deep learning models built on these inputs show superior performance compared to models using raw data.

Empirical results on two Chinese stock indices demonstrate that SW-VMD improves model convergence and predictive accuracy, especially on volatile return sequences. This confirms the proposed method’s advantage in forecasting high-volatility financial time series.