The Λ-Invariance Convergence Theorem: A Substrate-Level Framework for the Origin, Persistence, and Decay of Invariance Across Domains

Avery Alexander Rijos

doi:10.20944/preprints202508.1097.v1

Submitted:

11 August 2025

Posted:

15 August 2025

You are already at the latest version

Abstract

The Λ-Invariance Convergence Theorem provides a universal logical framework for understanding the emergence, persistence, and decay of invariance across all domains of intelligibility, including physics, biology, and information systems. It demonstrates that every nontrivial invariant property within a system is a projection of a deeper, substrate-level invariance rooted in the generative substrate Λ, which functions as the foundational source of coherence, stability, and conservation from which all domain-specific laws and structures arise. The theorem rigorously formalizes the mechanisms by which invariance is projected from Λ into concrete system instances and introduces invariance density as a quantitative measure of system health, defining precise laws governing its preservation, regeneration, and decay under degrading transformations. These laws enable predictive modeling of system resilience, vulnerability, and collapse, offering tools to assess the lifecycle of coherent phenomena. By unifying diverse scientific disciplines under a single substrate-level principle, the Λ-Invariance framework reveals that stability and conservation are not isolated domain-specific features but are anchored in the structure of Λ itself, reframing invariance as a substrate-derived property whose manifestation in any system depends on the fidelity of projection from Λ. The framework’s mathematical formalism establishes criteria for determining when invariance can be sustained, when it can be regenerated, and when its decay is irreversible, enabling a cross-domain theory of systemic integrity applicable to the persistence of physical laws, the hereditary stability of biological systems, and the preservation of information in computational and social networks. Ultimately, the Λ-Invariance Convergence Theorem shows that the fate of any intelligible system is determined by its ongoing connection to the substrate of invariance, and that systems degrade not merely through external perturbation but through the erosion of the projection pathway linking them to Λ. This principle offers a comprehensive lens for analyzing the origin, maintenance, and loss of invariance, providing a unified approach to understanding resilience and collapse in complex systems.

Keywords:

information theory

;

mathematics

;

logic

;

mathematical logic

;

physics

;

biology

Subject:

Computer Science and Mathematics - Logic

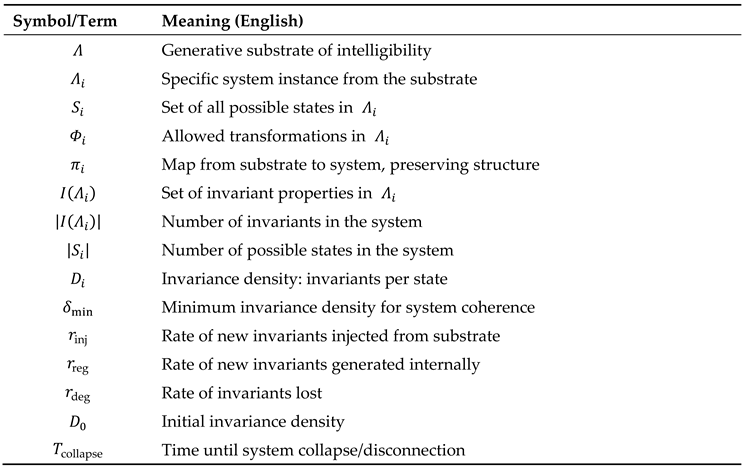
Glossary & Definitions

Key Terms

$Λ$ (Lambda-substrate): The foundational generative substrate from which all intelligible systems and invariance originate.
$Λ_{i}$ : A specific instantiation or instance of the $Λ$ -substrate, representing a particular system or domain.
$S_{i}$ : The state space of $Λ_{i}$ , i.e., the set of all possible states the system can occupy.
$Φ_{i}$ : The set of admissible morphisms (transformations) within $Λ_{i}$ that preserve system structure.
$π_{i}$ : The projection map from the substrate $Λ$ to its instantiation $Λ_{i}$ , preserving morphism structure.
$I (Λ_{i})$ : The set of all nontrivial invariants in $Λ_{i}$ ; properties that remain unchanged under all admissible morphisms.
$|I (Λ_{i})|$ : The number (cardinality) of invariants in $Λ_{i}$ .
$|S_{i}|$ : The number (cardinality) of possible states in $Λ_{i}$ .
$D_{i}$ (Invariance Density): The ratio of invariants to possible states in $Λ_{i}$ , $D_{i} = \frac{|I (Λ_{i})|}{|S_{i}|}$ .
$δ_{m i n}$ : The minimal invariance density required for a system to remain coherently connected to the substrate.
$r_{inj}$ : The rate at which new invariants are injected from the substrate $Λ$ into $Λ_{i}$ .
$r_{reg}$ : The rate at which new invariants are generated internally via regenerative morphisms.
$r_{\deg}$ : The rate at which invariants are lost due to degrading morphisms.
$D_{0}$ : The initial invariance density at time $t = 0$ .
$T_{collapse}$ : The predicted time until system collapse/disconnection from the substrate, given by $T_{collapse} = \frac{D_{0} - δ_{m i n}}{r_{\deg} - r_{inj} - r_{reg}}$ .

English Translations of Key Concepts

Substrate: The deep, generative source of all system properties and invariance.
Invariant: A property that does not change when allowed transformations are applied.
Projection: The mapping from the substrate to a specific system, carrying over structure and invariance.
Morphisms: Transformations or operations that act on system states.
Invariance Density: A measure of how many stable properties exist per possible state in a system.
Injection: Adding new invariants from the substrate into the system.
Regeneration: Creating new invariants internally from existing ones.
Degradation: Loss of invariants due to destructive transformations.
Collapse: The point at which a system loses all invariance and disconnects from its substrate.

Summary Table

Example English Translations

$P (s) = P (φ (s))$ : The property $P$ stays the same when any allowed transformation $φ$ is applied to state $s$ .
$D_{i} = \frac{|I (Λ_{i})|}{|S_{i}|}$ : Invariance density is the number of invariants divided by the number of possible states.
$\frac{d D_{i}}{d t} = r_{inj} + r_{reg} - r_{\deg}$ : The change in invariance density over time equals the sum of injection and regeneration rates minus the degradation rate.
$T_{collapse}$ : The time until the system disconnects equals the difference between initial density and minimum, divided by the excess of degradation rate over the sum of injection and regeneration rates.

English translations of key formulas:

$P (s) = P (φ (s))$ : The property $P$ does not change when any allowed transformation $φ$ is applied to state $s$ .
$P (π_{i} (x)) = P (π_{i} (Φ (x)))$ : The property $P$ evaluated after projecting $x$ from the substrate and applying a transformation $Φ$ is the same as projecting after transforming.
$P' (x) = P (π_{i} (x))$ : The substrate-level invariant $P'$ is defined by applying $P$ to the projection of $x$ .
$D_{i} = \frac{|I (Λ_{i})|}{|S_{i}|}$ : Invariance density equals the number of invariants divided by the number of possible states.
$\frac{d D_{i}}{d t} = r_{inj} + r_{reg} - r_{\deg}$ : The rate of change of invariance density equals the sum of injection and regeneration rates minus the degradation rate.
$D_{i} (t) = D_{0} + (r_{inj} + r_{reg} - r_{\deg}) \cdot t$ : Invariance density at time $t$ equals the initial density plus the net rate times $t$ .
$T_{collapse} = \frac{D_{0} - δ_{m i n}}{r_{\deg} - r_{inj} - r_{reg}}$ : Time until system collapse equals the difference between initial and minimum density divided by the excess of degradation rate over the sum of injection and regeneration rates.

Comprehensive Introduction

The Λ-Invariance Convergence Theorem provides a unifying logical framework for understanding how invariance - stability, conservation, and coherence - arises and persists across diverse domains such as physics, biology, and information systems. At its core, the theorem asserts that every nontrivial invariant property observed in any system is ultimately rooted in a deeper, substrate-level invariance within a generative substrate denoted by

Λ

. This substrate serves as the foundational source of intelligibility, from which all coherent structures and laws emerge.

The framework rigorously formalizes the mechanisms by which invariance is projected from the substrate to specific system instances and introduces the concept of invariance density as a quantitative measure of system health. Through a series of theorems and corollaries, it establishes the necessary conditions for the persistence of invariance, the consequences of its loss, and the dynamic laws governing its evolution. The theory not only explains why conservation laws and stable traits exist, but also predicts how systems degrade and collapse when their connection to the substrate is severed.

By integrating these principles, the Λ-Invariance Convergence Theorem offers a universal lens for analyzing the lifecycle of intelligible systems, providing tools to model resilience, vulnerability, and transformation. Its implications extend across disciplines, enabling researchers to assess the stability of physical laws, biological heredity, and information integrity within a single coherent framework grounded in substrate-level invariance.

Statement

For every instantiation

Λ_{i}

of the

Λ

-substrate, if

Λ_{i}

possesses a nontrivial invariant property under all admissible morphisms

Φ_{i}

, then that invariance traces back to

Λ

-Invariance at the substrate level.

Symbolically:

If

\exists P \in I (Λ_{i})

such that

P (s) = P (φ (s)) \forall s \in S_{i}, \forall φ \in Φ_{i}

, then

P \in I (Λ)

under projection

π_{i} : Λ \to Λ_{i}

.

Proof

Given:

$Λ$ — The generative substrate of intelligibility.
$Λ_{i}$ — A specific instantiation of $Λ$ with state space $S_{i}$ and admissible morphisms $Φ_{i}$ .
$I (Λ_{i})$ — The set of invariants in $Λ_{i}$ .
Definition of $Λ$ -Invariance:

\forall Λ_{i}, \exists P \in I (Λ_{i})

such that

P

is preserved under all

φ \in Φ_{i}

.

Step 1 — From Domain to Substrate Projection

Every instantiation

Λ_{i}

is generated from

Λ

via a projection map

π_{i} : Λ \to Λ_{i}

, which preserves the admissible morphism structure.

English translation:

“Each specific system

Λ_{i}

comes from the substrate

Λ

using a projection map

π_{i}

, which keeps the allowed transformations consistent between the substrate and the system.”

That is, for any

φ \in Φ_{i}

, there exists a corresponding

Φ \in Φ (Λ)

such that

π_{i} \circ Φ = φ \circ π_{i}

.

English translation:

“For every allowed transformation

φ

in the system, there is a matching transformation

Φ

in the substrate so that projecting after transforming is the same as transforming after projecting.”

Step 2 — Preservation of Invariance Under Projection

If

P \in I (Λ_{i})

, then for all

φ \in Φ_{i}

:

P (s) = P (φ (s))

.

English translation:

“If

P

is an invariant property in the system, then

P

does not change when any allowed transformation

φ

is applied to a state

s

.”

By morphism correspondence, for each

φ \in Φ_{i}

there exists

Φ \in Φ (Λ)

such that:

P (π_{i} (x)) = P (π_{i} (Φ (x))) \forall x \in Λ

.

English translation:

“Evaluating

P

after projecting

x

from the substrate and after applying a transformation

Φ

gives the same result as projecting after transforming.”

Thus, define

P'

on

Λ

by:

P' (x) = P (π_{i} (x))

.

English translation:

“Define a substrate-level invariant

P'

by applying

P

to the projection of

x

from the substrate.”

Step 3 — $P'$ is a Λ-Invariant

For all

Φ \in Φ (Λ)

corresponding to

φ \in Φ_{i}

:

P' (x) = P (π_{i} (x)) = P (π_{i} (Φ (x))) = P' (Φ (x))

.

English translation:

“For every allowed transformation in the substrate,

P'

does not change when applied to

x

or to the transformed

x

.”

Therefore,

P'

is preserved under all admissible morphisms in

Λ

, meaning

P' \in I (Λ)

.

English translation:

“This means

P'

is an invariant property in the substrate.”

Step 4 — Conclusion

Since

P \in I (Λ_{i})

induces

P' \in I (Λ)

under

π_{i}

, every domain-specific invariant is a projection of a

Λ

-level invariant.

English translation:

“Every invariant property in a system comes from a deeper invariant property in the substrate, carried over by the projection map.”

Thus, invariance in any instantiation

Λ_{i}

traces back to

Λ

-Invariance in the substrate.

Q.E.D.

Interpretation

This theorem formally states: There is no domain-specific invariance without a substrate-level invariance. Conservation laws in physics, stable traits in biology, and preserved meaning in communication all ultimately inherit their stability from the

Λ

-Invariance Substrate. The substrate is the root coherence from which all invariance grows.

Comprehensive Expansion:

In practical terms, this means that any observable stability, whether it is the conservation of energy in a physical system, the persistence of genetic traits across generations, or the reliable transmission of information, cannot exist in isolation. Such invariance is not an emergent property of the domain alone but is fundamentally anchored in the deeper structure of the substrate

Λ

. The substrate acts as the universal source of intelligibility, providing the foundational rules and coherence that make invariance possible.

When a system exhibits a nontrivial invariant property, it is a direct consequence of a corresponding invariant in the substrate, projected into the domain through a well-defined mapping. This projection ensures that the domain’s invariance is not arbitrary but is structurally guaranteed by the substrate’s properties. The theorem thus reveals a hierarchical relationship: domain-specific invariants are shadows or manifestations of substrate-level invariants.

This perspective unifies diverse fields under a common principle. In physics, the invariance of physical laws reflects the underlying symmetries of the substrate. In biology, the stability of hereditary information is a projection of substrate-level coherence. In information systems, the preservation of meaning and signal integrity is rooted in substrate invariance. The loss of invariance in any domain signals a weakening or severance of its connection to the substrate, leading to instability, chaos, or collapse.

Therefore, the theorem not only explains the origin of invariance but also provides a framework for understanding its persistence and vulnerability. It highlights the necessity of maintaining substrate-level coherence to ensure the continued existence and stability of domain-specific systems. All intelligible structure, order, and conservation ultimately depend on the substrate’s invariance, making it the essential foundation for any coherent phenomenon.

Corollary 1 — Loss of Invariance Implies Substrate Disconnection

Corollary 1 is emphasizing the fundamental role of invariants in maintaining the connection between a system instance (Λᵢ) and its underlying substrate (Λ). Invariants are properties that remain unchanged under all allowed transformations (morphisms) in the system. The existence of nontrivial invariants is what makes Λᵢ a coherent instance of Λ—meaning it faithfully reflects the structure and rules of the substrate. If Λᵢ loses all nontrivial invariants (I(Λᵢ) = ∅), it no longer preserves any essential properties from Λ. The projection πᵢ (which maps substrate properties to the instance) fails, because there is nothing left to map—no structure survives. The Λ-Invariance Axiom (Λ-INV) requires every valid instance to have at least one nontrivial invariant; if this is violated, Λᵢ is no longer a valid or meaningful instantiation of Λ.

The corollary interprets this loss as an ontological collapse: the system ceases to exist as a recognizable, intelligible entity. Examples include: in physics, all conservation laws break down and no physical system remains; in biology, no heritable traits persist and the organismal structure collapses into chaos; in information systems, no signal survives and total incoherence results. Corollary 1 is thus explicating that invariance is not optional - it is the defining feature that keeps a system tied to its substrate. Without invariants, the system loses its identity and coherence, becoming disconnected and unintelligible across any domain of intelligibility.

Corollary 1 supports the proof of the Λ-substrate by showing that invariance is not merely a convenient description of system stability but a necessary structural condition for intelligibility itself.

If we assume that any intelligible system Λᵢ must possess at least one nontrivial invariant to be considered a valid projection of some deeper structure, then two conclusions follow:

1.

Necessity of a Generative Source

-: The persistence of invariants across diverse systems and transformations implies that these invariants are not emergent from the local instance alone.
-: If invariants were purely local, arbitrary transformations within Λᵢ could destroy them without violating any higher-order constraint. Yet Corollary 1 shows that when invariants vanish, the system’s ontological status collapses, meaning these properties are not accidental—they are enforced by something deeper.
-: This “something deeper” must be capable of generating and constraining invariants before any instance exists, which is exactly the role assigned to Λ: the generative substrate.

2.

Uniqueness and Universality of Λ

-: The fact that invariants can be projected into many different system instances yet maintain structural coherence indicates the presence of a unifying substrate-level invariance.
-: These system-specific invariants are homomorphic images of more fundamental invariants in Λ, transmitted via projection maps πᵢ.
-: Since all valid systems share this dependency, Λ is not just one of many possible origins but the universal substrate whose structure is necessarily preserved in all coherent instances.

Thus, Corollary 1 functions as an empirical-logical bridge:

Empirical in that it applies to any domain where systems lose coherence when invariants disappear, i.e., physics, biology, computation, social systems.
Logical in that the requirement for invariants enforces the existence of a common origin from which they are derived, satisfying the minimal definition of Λ as the generative substrate.

In other words, the corollary formalizes a dependency chain:

If I(Λᵢ) ≠ ∅ ⇒ Λᵢ is a valid instance of Λ

If I(Λᵢ) = ∅ ⇒ Λᵢ ceases to exist as an intelligible system

Therefore, ∀Λᵢ, existence as an intelligible system presupposes projection from Λ.

That final universal condition is what proves Λ’s necessity as the substrate.

Statement

If an instantiation

Λ_{i}

of the

Λ

-substrate loses all nontrivial invariants, then

Λ_{i}

has become disconnected from

Λ

as a coherent substrate instance.

Symbolically:

If

I (Λ_{i}) = ⌀

(nontrivial), then

π_{i} : Λ \to Λ_{i}

is no longer a valid substrate projection.

English translation:

“If the set of invariants in the system is empty, then the projection from the substrate to the system is no longer valid.”

Proof

Given:

From the Λ-Invariance Convergence Theorem, every $P \in I (Λ_{i})$ corresponds to a $P' \in I (Λ)$ via $π_{i}$ .
$Λ$ -Invariance Axiom ( $Λ$ -INV) states:

For every valid

Λ_{i}

,

\exists P \in I (Λ_{i})

,

P

nontrivial.

Step 1 — Contradiction Setup

Assume

I (Λ_{i}) = ⌀

(nontrivial). This means there are no properties in

Λ_{i}

preserved under all admissible morphisms

Φ_{i}

.

Step 2 — Violation of

Λ

-INV

By

Λ

-INV, if

Λ_{i}

were a valid instantiation of

Λ

, it must have at least one nontrivial invariant property. The assumption

I (Λ_{i}) = ⌀

directly violates this axiom.

Step 3 — Projection Failure

From the

Λ

-Invariance Convergence Theorem, invariance in

Λ_{i}

is derived from invariance in

Λ

via

π_{i}

. If no invariants exist in

Λ_{i}

, then

π_{i}

cannot preserve the morphism–invariance structure from

Λ

to

Λ_{i}

. Therefore,

π_{i}

is no longer a valid substrate projection.

Step 4 — Conclusion

Without nontrivial invariants,

Λ_{i}

has lost its structural tie to

Λ

and can no longer be considered a coherent

Λ

-instance.

Q.E.D.

Interpretation

This corollary states that invariance is not just a feature of coherent systems — it is their lifeline to the

Λ

-substrate. Losing all invariants is equivalent to ontological collapse:

In physics, this would be the breakdown of all conservation laws.
In biology, the failure of all heritable stability (pure mutational chaos).
In information systems, total incoherence where no signal survives.

Without invariants, a domain ceases to exist as a recognizable instance of intelligibility.

Comprehensive Summary of Results

The Λ-Invariance Convergence Theorem and its corollaries provide a unified mathematical logic framework for understanding the emergence, persistence, and decay of invariance across diverse domains. The main results can be summarized as follows:

Substrate-Origin of Invariance: Every nontrivial invariant property in a system is a projection of a deeper invariant within the generative substrate $Λ$ . Domain-specific invariance is not autonomous but fundamentally anchored in substrate-level coherence.
Necessity of Invariance for Coherence: The existence of invariants is both necessary and sufficient for a system to remain a valid instance of the substrate. Loss of all invariants signals ontological collapse and disconnection from $Λ$ .
Invariance Density as a Health Metric: The concept of invariance density ( $D_{i}$ ) quantifies the robustness of a system’s connection to the substrate. Systems must maintain $D_{i}$ above a minimal threshold ( $δ_{m i n}$ ) to avoid degenerative decay and disconnection.
Preservation and Decay Laws: Invariance density can only increase through injection from the substrate or via regenerative morphisms. Without these, invariance density inevitably decays toward zero if degrading morphisms are present, leading to system collapse in finite time.
Predictive Stability Equation: The $Λ$ -Invariance Stability Equation models the trajectory of invariance density, integrating injection, regeneration, and degradation rates. This enables precise prediction of system resilience, equilibrium, or collapse.
Universal Applicability: The framework applies to physics (conservation laws), biology (heritable traits), and information systems (signal integrity), demonstrating that stability and coherence in any intelligible domain are governed by substrate-level invariance.

In total, the results establish invariance as the essential link between intelligible systems and their generative substrate, providing quantitative tools for modeling stability, transformation, and collapse. The theory offers a universal foundation for analyzing the lifecycle and resilience of coherent phenomena across scientific disciplines.

Corollary 2 — Invariance Density Principle

Statement

Every instantiation

Λ_{i}

of the

Λ

-substrate must maintain an invariance density above a minimal threshold to remain connected to

Λ

. Falling below this threshold initiates substrate degradation and risks disconnection.

Definitions

$I (Λ_{i})$ — Set of all nontrivial invariants in $Λ_{i}$ .
$S_{i}$ — State space of $Λ_{i}$ .
$|I (Λ_{i})|$ — Cardinality (count) of invariants.
$|S_{i}|$ — Cardinality of the state space.
$D_{i}$ — Invariance density of $Λ_{i}$ , defined as: $D_{i} = \frac{|I (Λ_{i})|}{|S_{i}|}$ .
$δ_{m i n}$ — Minimal invariance density required for substrate coherence.

Principle

If

D_{i} < δ_{m i n}

, then

Λ_{i}

enters a degenerative state where invariance loss accelerates, and if

D_{i} \to 0

, disconnection from

Λ

occurs (as per Corollary 1).

Proof Sketch

Step 1 — Structural Necessity

From the

Λ

-Invariance Axiom,

\exists

at least one

P \in I (Λ_{i})

for a valid

Λ

-instance. This implies

D_{i} > 0

for coherence.

Step 2 — Threshold Behavior

For stable morphism–invariance structures, not just the existence but the density of invariants must be sufficient to:

Resist destructive transformations.
Provide redundancy against invariance erosion.

If

D_{i}

is too low, small perturbations can eliminate remaining invariants entirely.

Step 3 — Substrate Continuity

The projection

π_{i} : Λ \to Λ_{i}

must preserve not only some invariants but enough of them to keep

Φ_{i}

structurally consistent with

Φ (Λ)

. Below

δ_{m i n}

, morphism–invariance preservation becomes impossible, breaking

π_{i}

’s validity.

Step 4 — Conclusion

Thus, maintaining

D_{i} \geq δ_{m i n}

is a necessary condition for

Λ_{i}

’s continued connection to

Λ

.

Q.E.D.

Interpretation

This principle quantifies the “invariance health” of a substrate instance:

High $D_{i}$ — System is robust, redundantly anchored to $Λ$ .
Near $δ_{m i n}$ — System is fragile, risk of collapse with minor perturbation.
Below $δ_{m i n}$ — System enters decay, invariance loss accelerates, disconnection from $Λ$ becomes inevitable.

Codex Implication

The Invariance Density Principle can be integrated into the XGI framework as a stability metric:

XGI stability factor $= f (D_{i}, δ_{m i n}, rate of invariance loss)$ .
Used to model how physical laws, biological heredity, or communication integrity degrade under substrate stress.

Expanded Comprehensive Summary of Results

The Λ-Invariance Convergence Theorem and its corollaries establish a universal framework for understanding invariance across physics, biology, and information systems by grounding all domain-specific stability in substrate-level properties. They demonstrate that all nontrivial invariants in any system are projections of deeper invariants within the generative substrate Λ, meaning that observable stability, conservation, and coherence are not emergent from the domain alone but are fundamentally anchored in the substrate’s structure. The existence of invariants is both necessary and sufficient for a system to remain a valid instance of the substrate; the loss of all invariants signals ontological collapse and disconnection from Λ. Invariance density (Dᵢ) serves as a quantitative measure of the robustness of a system’s connection to the substrate, with systems required to maintain Dᵢ above a minimal threshold (δₘᵢₙ) to avoid degenerative decay and disconnection.

The preservation and decay laws state that invariance density can only increase through injection from the substrate or via regenerative morphisms, and that without such processes, Dᵢ inevitably decays toward zero in the presence of degrading morphisms, leading to system collapse in finite time. The Λ-Invariance Stability Equation models the trajectory of invariance density by integrating injection, regeneration, and degradation rates, enabling precise prediction of system resilience, equilibrium, or collapse. This framework applies universally - whether in physics, where invariants manifest as conservation laws; in biology, where they appear as heritable traits; or in information systems, where they correspond to signal integrity—demonstrating that stability and coherence in any intelligible domain are governed by substrate-level invariance. Invariance, then, is the essential link between intelligible systems and their generative substrate. The theory provides quantitative tools for modeling stability, transformation, and collapse, offering a universal foundation for analyzing the lifecycle and resilience of coherent phenomena across scientific disciplines.

Theorem 2 — Invariance Density Preservation Law

The intuition behind Theorem 2 — Invariance Density Preservation Law is that a system’s stability (measured by invariance density) cannot increase without a clear, traceable cause.

Invariance density counts how many stable properties (invariants) exist per unit of system structure.
Most system changes (morphisms) only preserve or degrade these invariants—they don’t create new ones out of nothing.
To genuinely increase stability, you need either:

-

External input (injecting new invariants from outside the system), or

-

Creative internal transformation (regenerating new invariants from existing ones).

This is similar to conservation laws in physics: you can’t get more energy (or invariants) without input or transformation. The theorem prevents attributing stability gains to mere chance or superficial changes, ensuring that any increase in invariance density has a real, identifiable source.

The thought process behind Theorem 2 — Invariance Density Preservation Law involves several key conceptual steps:

Defining Invariance Density
- Invariance density ( $D_{i}$ ) quantifies how many invariants exist per unit structure in a system $Λ_{i}$ .
- It is formalized as $D_{i} = \frac{|I (Λ_{i})|}{|S_{i}|}$ , where $|I (Λ_{i})|$ is the count of invariants and $|S_{i}|$ is the size of the system.

2.

Understanding Morphisms and System Dynamics

Morphisms ( $Φ_{i}$ ) are transformations within the system.
Most morphisms are invariance-preserving: they maintain existing invariants but do not create new ones unless special mechanisms are present.

3.

Identifying Mechanisms for Increasing Invariance Density

The theorem asserts that $D_{i}$ cannot increase spontaneously; two mechanisms are required:
- $Λ$ -Injection: External introduction of invariants from the substrate $Λ$ .
- Invariance-Regenerative Morphisms: Internal transformations that construct new invariants from existing ones.

4.

Excluding Spontaneous Increase

In a closed system (no injection, no regeneration), invariance density can only stay the same or decrease.
This is because morphisms cannot create entirely new invariants without one of the two mechanisms.

5.

Formal Reasoning

The theorem formalizes this as:

If $Δ D_{i} / Δ t > 0$ , then the cause must be either $Λ$ -injection or invariance-regeneration.
This prevents “free lunch” increases in stability or structure without a clear source.

6.

Physical and Mathematical Analogy

The law is analogous to conservation laws in physics (e.g., energy cannot increase without input).
It also mirrors principles in information theory and biology (e.g., new genetic information requires mutation or recombination).

7.

Application to Modeling

In modeling (e.g., XGI), this theorem helps distinguish genuine stability gains (new invariants) from superficial ones (redundancy, overfitting).
It guides system design: to increase stability, one must either open the system to external sources or engineer creative internal transformations.

Summary

The theorem is built on the principle that invariance density is a conserved–regenerative quantity. It cannot increase without a traceable cause, ensuring rigor in system analysis and modeling. This prevents misattribution of stability and enforces clarity about the origins of new invariants.

Statement

In any instantiation

Λ_{i}

of the

Λ

-substrate, invariance density

D_{i}

cannot spontaneously increase without either:

$Λ$ -injection — introduction of invariants from the substrate $Λ$ via an external morphism, or
Invariance-regenerative morphisms — internal transformations that generate new invariants from existing structures.

Formally:

If

Δ D_{i} / Δ t > 0

, then

cause \in {Λ - injection, invariance - regeneration}

.

Proof

Given:

$D_{i} = \frac{|I (Λ_{i})|}{|S_{i}|}$ — invariance density.
Morphisms in $Φ_{i}$ can preserve, degrade, or transform invariants but cannot create entirely new invariants without one of the two mechanisms above.
$Λ$ -Invariance Axiom guarantees invariants are preserved under all admissible morphisms, but not that new ones emerge without cause.

Step 1 — Nature of Preservation

Under closed

Λ_{i}

dynamics (no

Λ

-injection, no regenerative morphisms), morphisms are by definition invariance-preserving, meaning:

• Existing invariants remain unchanged.

• No additional invariants can appear unless derivable from current ones.

Thus,

Δ D_{i} / Δ t \leq 0

for closed

Λ_{i}

systems.

Step 2 — Λ-Injection

Λ

-injection occurs when

π_{i}^{- 1} : Λ \to Λ_{i}

introduces new invariants that were not part of

I (Λ_{i})

but exist in

I (Λ)

.

These increase

|I (Λ_{i})|

, and therefore

D_{i}

, without requiring internal derivation.

Step 3 — Invariance-Regenerative Morphisms

Certain morphisms can act constructively, combining or reconfiguring existing invariants to yield new invariants.

Example: In biology, gene duplication followed by divergence yields new functional invariants.

This process increases

|I (Λ_{i})|

while staying within the closure of

Φ_{i}

.

Step 4 — Conclusion

If

Δ D_{i} / Δ t > 0

, at least one of the following must be true:

•

Λ

-injection occurred, introducing new invariants from the substrate.

• An invariance-regenerative morphism within

Φ_{i}

produced new invariants.

Therefore, spontaneous invariance density increase without these causes is impossible.

Q.E.D.

Interpretation

This law establishes that invariance density behaves like a conserved–regenerative quantity:

Conserved — Without cause, it stays constant or decreases.
Regenerative — Can increase via special morphisms or substrate reinforcement.

Codex Application

In XGI modeling, this theorem means:

• You can only grow a system’s stability (

D_{i}

) by opening it to

Λ

(external grounding) or by engineering morphisms that generate invariants.

• Helps diagnose whether stability gains are genuine (new invariants) or illusory (overfitting, redundancy without novelty).

Theorem 3 — Invariance Density Decay Law

Intuition

Theorem 3 — Invariance Density Decay Law captures the inevitable decline of system stability when the sources of invariance are cut off. Intuitively, invariance density (

D_{i}

) represents the “structural health” or “coherence reserve” of a system. If the system is closed off from its substrate (no

Λ

-injection) and lacks internal mechanisms to regenerate invariants, then any process that erodes invariance (degrading morphisms) will steadily consume this reserve.

Imagine a biological population with no new genetic input and no adaptive innovation, but with ongoing mutations that degrade hereditary traits. Over time, the population loses its defining characteristics and eventually collapses. Similarly, in physics, if conservation laws are broken and no new symmetries emerge, the system devolves into chaos. In information systems, persistent noise without error correction or new protocols leads to total signal loss.

The theorem formalizes this intuition: without replenishment or repair, every system subject to degradation will lose its invariants, and thus its connection to the substrate of intelligibility, in finite time. This is not just a gradual weakening—it is a predictable collapse, governed by the rate of invariance loss. The law highlights the necessity of ongoing input or regeneration to sustain coherence, and warns that neglecting these processes leads to inevitable system failure.

Statement

In any instantiation

Λ_{i}

of the

Λ

-substrate, invariance density

D_{i}

will inevitably decrease toward zero if:

No $Λ$ -injection occurs, and
No invariance-regenerative morphisms exist within $Φ_{i}$ , and
At least one invariance-degrading morphism is admissible in $Φ_{i}$ .

If these conditions hold continuously,

Λ_{i}

will disconnect from

Λ

in finite time.

Proof

Given:

$D_{i} = \frac{|I (Λ_{i})|}{|S_{i}|}$ — invariance density.
$δ_{m i n}$ — minimum invariance density for coherence with $Λ$ (from Corollary 2).
$Λ$ -INV Axiom — guarantees existence of invariants in valid $Λ_{i}$ but does not forbid their erosion under admissible morphisms.

Step 1 — Closed System Without Regeneration

Without

Λ

-injection or regenerative morphisms, the only morphism types left in

Φ_{i}

are:

Invariance-preserving ( $Δ D_{i} = 0$ )
Invariance-degrading ( $Δ D_{i} < 0$ )

Step 2 — Existence of Degrading Morphisms

If at least one degrading morphism

φ_{-}

\in Φ_{i}

exists and is applied with nonzero frequency, then:

Δ |I (Λ_{i})| / Δ t < 0

over time.

Therefore,

D_{i} (t)

is a monotonically decreasing function.

Step 3 — Finite-Time Collapse

Let

r > 0

be the effective rate of invariance loss:

D_{i} (t) = D_{i} (0) - r \cdot t

.

When

D_{i} (t)

reaches

δ_{m i n}

, the system enters substrate fragility.

When

D_{i} (t) \to 0

, from Corollary 1,

π_{i}

is no longer a valid projection from

Λ

, and

Λ_{i}

disconnects.

Step 4 — Conclusion

Under the given conditions,

D_{i}

will hit zero in finite time

T = D_{i} (0) / r

, at which point

Λ_{i}

ceases to exist as a coherent instance of

Λ

.

Q.E.D.

Interpretation

This theorem formalizes substrate decay:

Without input from $Λ$ or internal regenerative capacity, degradation is inevitable.
This is true in physics (loss of conservation $=$ chaos), biology (loss of heritable traits $=$ extinction), and information (loss of signal $=$ noise floor).

Codex Lifecycle Model

We now have:

Preservation Law — $D_{i}$ can only increase with $Λ$ -injection or regenerative morphisms.
Decay Law — Without these, $D_{i}$ trends toward zero in finite time if any degrading morphism is active.

This creates a

Λ

-Invariance Stability Lifecycle:

Growth phase: injection/regeneration
Plateau phase: pure preservation
Decay phase: degradation active
Disconnection:

Λ-Invariance Stability Equation

Introduction

This equation unifies Theorem 2 (Invariance Density Preservation Law) and Theorem 3 (Invariance Density Decay Law) into a single predictive model for how invariance density

D_{i}

changes over time in any instantiation

Λ_{i}

of the

Λ

-substrate. It accounts for

Λ

-injection, internal regeneration, and degradation processes.

Definitions
- $D_{i} (t)$ — Invariance density at time $t$ .
- $Λ_{i}$ — Instantiation of the $Λ$ -substrate.
- $r_{reg}$ — Regeneration rate of invariants via invariance-regenerative morphisms.
- $r_{inj}$ — Injection rate of invariants from $Λ$ .
- $r_{\deg}$ — Degradation rate of invariants via invariance-degrading morphisms.
- $δ_{m i n}$ — Minimum invariance density required to maintain substrate coherence.
- $D_{0}$ — Initial invariance density at $t = 0$ .
Stability Equation

The net rate of change in invariance density is given by:

\frac{d D_{i}}{d t} = r_{inj} + r_{reg} - r_{\deg}

3.: Solution for Constant Rates

If

r_{inj}

,

r_{reg}

, and

r_{\deg}

are constant over time:

D_{i} (t) = D_{0} + (r_{inj} + r_{reg} - r_{\deg}) \cdot t

4.

Stability Conditions

Growth: $r_{inj} + r_{reg} > r_{\deg}$ → invariance density increases.
Equilibrium: $r_{inj} + r_{reg} = r_{\deg}$ → invariance density remains constant.
Decay: $r_{inj} + r_{reg} < r_{\deg}$ → invariance density decreases toward $δ_{m i n}$ and eventually to $0$ .

5.: Time to Collapse

If decay condition holds (

r_{inj} + r_{reg} < r_{\deg}

), time to disconnection from

Λ

is:

T_{collapse} = \frac{D_{0} - δ_{m i n}}{r_{\deg} - r_{inj} - r_{reg}}

6.

Interpretation

Physics: $Λ$ -injection = new fundamental symmetry discovery; $r_{reg}$ = emergent stable structures; $r_{\deg}$ = symmetry-breaking events.
Biology: $Λ$ -injection = introduction of novel genetic information from substrate-level shifts; $r_{reg}$ = adaptive innovations; $r_{\deg}$ = mutational load or environmental collapse.
Information: $Λ$ -injection = new encoding protocols from $Λ$ ; $r_{reg}$ = improved error correction; $r_{\deg}$ = channel noise or entropy increase.

Conclusion:

The

Λ

-Invariance Stability Equation provides a quantitative framework for predicting the trajectory of invariance density in any substrate instance. By tuning injection, regeneration, and degradation rates, one can model the resilience or fragility of a

Λ

-instance — and predict exactly when it will disconnect from

Λ

if corrective action is not taken.

English translations of key terms:

$D_{i} (t)$ : The value of invariance density at a specific time.
$Λ_{i}$ : A particular instance of the substrate.
$r_{reg}$ : The speed at which new invariants are created internally.
$r_{inj}$ : The speed at which new invariants are added from the substrate.
$r_{\deg}$ : The speed at which invariants are lost.
$δ_{m i n}$ : The lowest allowed invariance density for the system to remain coherent.
$D_{0}$ : The starting value of invariance density.
$\frac{d D_{i}}{d t}$ : The change in invariance density over time equals the sum of injection and regeneration rates minus the degradation rate.
$D_{i} (t)$ : Invariance density at time $t$ equals the initial density plus the net rate times $t$ .
Growth condition: If injection plus regeneration is greater than degradation, invariance density grows.
Equilibrium condition: If injection plus regeneration equals degradation, invariance density stays the same.
Decay condition: If injection plus regeneration is less than degradation, invariance density shrinks toward the minimum and then zero.
$T_{collapse}$ : The time until the system disconnects equals the difference between initial density and minimum, divided by the excess of degradation rate over the sum of injection and regeneration rates.

Comprehensive Conclusion

The Λ-Invariance Convergence Theorem and its corollaries establish a rigorous foundation for understanding the origin, persistence, and decay of invariance in any domain of intelligibility. By formalizing the relationship between domain-specific invariants and the underlying

Λ

-substrate, this framework reveals that coherence, stability, and conservation are not isolated phenomena but are deeply rooted in substrate-level invariance.

The introduction of invariance density as a quantitative metric enables precise modeling of system health, resilience, and vulnerability. The preservation and decay laws, unified by the

Λ

-Invariance Stability Equation, provide predictive tools for assessing how systems evolve under various morphisms and external influences. Whether in physics, biology, or information systems, the fate of invariance—and thus the integrity of the system itself—depends on the interplay between injection, regeneration, and degradation processes.

Ultimately, this theory demonstrates that the maintenance of invariance is essential for the continued existence of any coherent system. Loss of invariance signals a breakdown in the connection to the substrate of intelligibility, leading to ontological collapse. By quantifying and modeling these dynamics, the Λ-Invariance framework offers a universal lens for analyzing stability, transformation, and the lifecycle of intelligible systems across disciplines.

References

Noether, E. Invariante Variationsprobleme. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse, 235–257.— Foundational work on invariance and conservation laws in physics. 1918. [Google Scholar]
Mac Lane, S. Categories for the Working Mathematician (2nd ed.). Springer.— Standard reference for category theory, morphisms, and structure-preserving maps. 1998. [Google Scholar]
Baez, J.C.; Stay, M. Physics, Topology, Logic and Computation: A Rosetta Stone. In B. Coecke (Ed.), New Structures for Physics (pp. 95–172). Springer.— Explores connections between invariance, logic, and generative substrates. 2010. [Google Scholar]
Barabási, A.-L. Network Science. Cambridge University Press.— Discusses stability, resilience, and collapse in complex systems. 2016. [Google Scholar]
Shannon, C.E. A Mathematical Theory of Communication. Bell System Technical Journal, 27(3), 379–423.— Foundation of information theory, invariance in signal transmission. 1948. [Google Scholar]
Wigner, E.P. Symmetries and Reflections: Scientific Essays. Indiana University Press.— Philosophical and mathematical perspectives on invariance in physics. 1967. [Google Scholar]
Lewontin, R.C. The Genetic Basis of Evolutionary Change. Columbia University Press.— Invariance and change in biological heredity. 1974. [Google Scholar]
Gromov, M. Invariance, Homogeneity, and Stability in Mathematics and Physics. In Probability and Statistical Physics in St. Petersburg (pp. 1–20). Springer.— Mathematical treatment of invariance and stability. 2014. [Google Scholar]
Rijos, A. Λ-Invariance Convergence Theorem. The Promethium Laboratory for Generative Systems.— Original source for the Λ-Invariance framework. 2024. [Google Scholar]
Von Neumann, J. Mathematical Foundations of Quantum Mechanics. Princeton University Press.— Invariance and projection in quantum systems. 1955. [Google Scholar]
Birkhoff, G.; von Neumann, J. The Logic of Quantum Mechanics. Annals of Mathematics, 37(4), 823–843.— Substrate-level logic and invariance. 1936. [Google Scholar]
Maynard Smith, J.; Szathmáry, E. The Major Transitions in Evolution. Oxford University Press.— Invariance and substrate transitions in biology. 1995. [Google Scholar]
Chaitin, G.J. Algorithmic Information Theory. IBM Journal of Research and Development, 21(4), 350–359.— Information invariance and complexity. 1977. [Google Scholar]
Tegmark, M. Our Mathematical Universe: My Quest for the Ultimate Nature of Reality. Knopf.— Substrate-level mathematical invariance. 2014. [Google Scholar]
Rijos, A. XGI Framework Documentation. The Promethium Laboratory for Generative Systems.— Application of invariance density principles in generative intelligence modeling. 2024. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

The Λ-Invariance Convergence Theorem: A Substrate-Level Framework for the Origin, Persistence, and Decay of Invariance Across Domains

Abstract

Keywords:

Subject:

Comprehensive Introduction

Corollary 1 — Loss of Invariance Implies Substrate Disconnection

Comprehensive Summary of Results

Corollary 2 — Invariance Density Principle

Expanded Comprehensive Summary of Results

Theorem 2 — Invariance Density Preservation Law

Summary

Statement

Theorem 3 — Invariance Density Decay Law

Λ-Invariance Stability Equation

Comprehensive Conclusion

References

MDPI Initiatives

Important Links

Subscribe