A Mathematical Model to Study the Role of Sterile Insect Technique in Crop Pest Control: Dynamics and Optimal Control Study

1. Introduction

The Sterile Insect Technique (SIT) is a powerful and eco-friendly method of pest control pest that involves the release of sterilized insects into the environment [8,9]. These sterile males, developed via radiation or genetic techniques, interfere with wild males during mating, reducing the number of fertile matings. Since they cannot produce viable offspring, the pest population gradually declines over successive generations [10]. SIT has been effectively adopted in numerous agricultural environments to manage pests such as fruit flies, mosquitoes, and moths [11]. By reducing reliance on chemical pesticides, SIT helps maintain ecological balance and prevents resistance development in pest populations. Mathematical models play a crucial role in optimizing SIT strategies by analyzing pest dynamics, determining the ideal release rates of sterile insects, and evaluating long-term population suppression [13,14,15].

The female pest population plays a vital role in the reproductive cycle. New pests are generated through mating between female and fertile male pests, with a fixed proportion of the offspring being female [1]. However, when sterile male pests are introduced into the environment, they compete with fertile males for mating but do not produce viable offspring. This reduces the overall reproductive success of the pest population. The growth of the female population is thus modeled as a function of mating success, which is disrupted by the presence of sterile males. Furthermore, female pests experience natural mortality and additional losses due to sterile mating interference [2,3,4]. Likewise, the male pest population arises from the same mating process, with the remaining fraction of the offspring being male. These males also contribute to future generations through mating, but they too face natural death. The sterile male pests, which are released externally at a constant rate as part of the SIT program, are assumed to be non-reproductive but actively engage in mating competition. Their presence lowers the number of successful fertilization by fertile males, thereby decreasing the pest reproduction rate. Sterile males do not persist indefinitely; they die naturally over time, modeled by a constant mortality term [5,6,7].

Mathematical models for pest control using biopesticides are available [21,22]. But models for pest management using sterile insect technology are few [16,17,18,19]. In [20], a mathematical framework incorporating mating disruption and trapping techniques is used for pest management. Differential equations are used to represent the population dynamics of pest species, including parameters for mating disruption efficiency and trapping effectiveness. The model helped in analyzing the impact of these control strategies on the pest population over time. In [17], a mathematical model for pest control is developed using sterile insects and natural enemies to suppress pest populations. The model typically includes equations describing pest population dynamics, sterile insect release rates, and interactions with natural enemies. Building on this, [18] investigated population models and Knipling’s sterility formulation, emphasizing the biological factors that influence the effectiveness of the Sterile Insect Technique (SIT) program. These factors include residual fertility, mating competitiveness, mating patterns, immigration, density dependence, age structure, population aggregation, and various biotic interactions. The study highlights that combinations of these factors often exhibit synergistic effects, whereas simpler control methods may be more likely to succeed when they account for smaller proportions of overall mortality. In [19], researchers examined mathematical models for the dynamics of interactive wild and sterile insect populations, which can be used as approximations for the Sterile Insect Technique (SIT) and discussed dynamical features and different release methods. Here, we propose a mathematical model for the dynamics of a crop population and its pests (male and female) and release of sterile male pests with a constant rate and applied optimal control theory for cost minimization.

Optimal control theory plays a crucial role in pest management by helping design strategies that minimize both economic costs and ecological damage [23]. It provides mathematical frameworks to determine the best timing, intensity, and methods of intervention—whether through pesticides, biological controls, or habitat modification. By using mathematical models, researchers can predict pest population growth and identify the most effective control measures while considering constraints like environmental impact and long-term sustainability [15]. This approach is particularly useful in integrated pest management (IPM), where the goal is to strike a balance between agricultural productivity and ecosystem health [24,25].

The aim of this study to derive a mathematical model to capture the dynamics of pest populations influenced by the Sterile Insect Technique (SIT). The model incorporates sterilization effects, population interactions to evaluate the effectiveness of SIT in pest management. Using the proposed mathematical model, we study stability switch in the system via Hopf bifurcation. Through optimal control analysis, we determine the best strategies for releasing sterile insects to maximize pest suppression while minimizing economic and ecological costs. Our findings highlight the potential of SIT as a sustainable and effective approach for integrated pest control in agriculture.

The structure of the article is as follows: (i) Section 2 presents the formulation of the mathematical model along with its fundamental properties; (ii) Section 3 analyzes the system dynamics, including equilibrium points, their local and global stability, and the occurrence of Hopf bifurcation; (iii) Section 4 introduces the optimal control problem; (iv) Section 5 provides the sensitivity analysis of the model parameters; (v) numerical simulations are presented in Section 6 to illustrate the model’s behavior; and (v) Section 7 concludes the study with a discussion of the results.

2. Mathematical Model Formulation

We formulate a deterministic mathematical framework to examine the interaction between crop biomass and a pest population consisting of female pests, male pests, and sterile male pests introduced for biological control. This model captures the ecological dynamics of pest management through sterile male techniques and provides a framework to analyze the effectiveness of this control strategy in maintaining crop productivity. The following assumptions are made:

A1: There are four population in the model, namely

(i)

$X\left(t\right)$: crop biomass,

(ii)

$Y\left(t\right)$: number of female pests,

(iii)

$Z\left(t\right)$: number of male pests,

(iv)

$U\left(t\right)$: number of sterile male pests, at time t.

The crop biomass, $X\left(t\right)$, is assumed to follow logistic growth in the absence of pests, governed by a natural growth rate and a carrying capacity that represents the maximum supportable biomass in the environment. However, the presence of pests negatively affects crop growth. Both female and male pests feed on the crop, and this feeding activity reduces the net biomass. This is modeled by incorporating a loss term proportional to the interaction between the crop biomass and the pest population, assuming a Holling type-I functional response. The intensity of damage increases with pest density, capturing the biological reality of overgrazing or infestation pressure.

A2: The crop biomass $X\left(t\right)$ is assumed to follow logistic growth with an intrinsic rate $r_1$ and a carrying capacity $K_1$. However, it is reduced due to damage caused by both female and male pests at a rate $\alpha$, represented by the term $\alpha X(Y+Z)$.

$${\displaystyle \frac{dX}{dt}}=r_{1}X\left(1-{\displaystyle \frac{X}{K_1}}\right)-\alpha X(Y+Z)$$

A3: We consider a pest management approach involving the release of sterile male pests. These males compete with their fertile counterparts for mating opportunities, effectively reducing the production of viable offspring.

Female pests reproduce with the assistance of male pests. We assume that successful reproduction is governed by a rate proportional to the product of the female and male populations, modulated by the crop biomass availability X, since access to crops enhances reproductive success.The consumption rate of female pests is $\alpha$ while that of male pests is $\beta$ where $\beta <\alpha$. Thus, the birth term is modeled as $pc\alpha XYZ\left(1-{\displaystyle \frac{Y+Z}{K_2}}\right)$, where $c\alpha$ is the intrinsic reproduction rate, p is the fraction contributing to the female population, and $K_2$ is the effective pest carrying capacity. Female pests experience natural mortality at a rate $\mu$, and are also affected by sterile males through mating interference modeled by $\beta YU$. Hence, the equation for the female pest population is:

$${\displaystyle \frac{dY}{dt}}=pc\alpha XYZ\left(1-{\displaystyle \frac{Y+Z}{K_2}}\right)-{\displaystyle \frac{\beta YU}{Y+Z}}-\mu Y,$$

A4: The male pest population increases due to reproduction from female–male interactions, but with fraction $(1-p)$, and also follows saturation behavior governed by $K_2$. The corresponding death rate is again $\mu$. The equation for male pests becomes:

$${\displaystyle \frac{dZ}{dt}}=(1-p)c\alpha XYZ\left(1-{\displaystyle \frac{Y+Z}{K_2}}\right)-\mu Z$$

Sterile male pests $U\left(t\right)$ are introduced into the environment continuously at a constant rate ${\Pi }_u$, and decay naturally at rate $\mu$ [19]. These sterile males disrupt normal mating patterns, leading to a reduction in the pest population’s effective reproduction rate.

Based on the above assumptions, the following model is obtained:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dX}{dt}}& =& r_{1}X\left(1-{\displaystyle \frac{X}{K_1}}\right)-\alpha X(Y+Z),\hfill \\ \hfill {\displaystyle \frac{dY}{dt}}& =& p\left(c\alpha X\right)YZ\left(1-{\displaystyle \frac{Y+Z}{K_2}}\right)-{\displaystyle \frac{\beta YU}{Y+Z}}-\mu Y,\hfill \\ \hfill {\displaystyle \frac{dZ}{dt}}& =& (1-p)\left(c\alpha X\right)YZ\left(1-{\displaystyle \frac{Y+Z}{K_2}}\right)-\mu Z,\hfill \\ \hfill {\displaystyle \frac{dU}{dt}}& =& {\Pi }_u-\mu U,\hfill \end{array}$$

(1)

with initial conditions as

$$X\left(0\right)>0,Y\left(0\right)>0,Z\left(0\right)>0,U\left(0\right)>0.$$

(2)

For the plausibility of the model, we study the positive invariance and boundedness of solutions of the model (1).

2.1. Positivity invariance

First equation of system (1) can be rewritten as:

$${\displaystyle \frac{dX}{dt}}=X{f}_1(X,Y,Z),$$

(3)

where,

$$f_1(X,Y,Z)=r_1\left(1-{\displaystyle \frac{X}{K_1}}\right)-\alpha (Y+Z)$$

(4)

Integrating both sides of (4), we get

$$X\left(t\right)=X\left(0\right)exp\left({\int }_0^t{f}_1(X,Y,Z)dt\right)$$

(5)

Since $X\left(0\right)\ge 0$, we have

$$X\left(t\right)\ge 0\mathrm{for}\mathrm{all}t\ge 0.$$

(6)

Using similarly argument as above, we can prove the nonnegativity of $Y\left(t\right)$. For nonnegativity of $Z\left(t\right)$, we rewrite the third equation of system (1) as:

$${\displaystyle \frac{dZ}{dt}}\ge Z{f}_3(X,Y,Z),$$

(7)

where,

$$f_3(X,Y,Z)=(1-p)c\alpha XY\left(1-{\displaystyle \frac{Y+Z}{K_2}}\right)-\mu .$$

(8)

Thus

$$Z\left(t\right)\ge Z\left(0\right)exp\left({\int }_0^t{f}_3(X,Y,Z)dt\right).$$

(9)

Hence, if $Z\left(0\right)\ge 0$, then $Z\left(t\right)\ge 0$ for all t. Finally, for nonnegativity of $U\left(t\right)$, we rewrite the fourth equation of (1) as:

$${\displaystyle \frac{dU}{dt}}\ge -\mu U$$

(10)

Integrating both sides, we get

$$U\left(t\right)\ge U\left(0\right)exp(-\mu t).$$

(11)

Thus, if $U\left(0\right)\ge 0$, then $U\left(t\right)\ge 0$ for all t. Therefore, we conclude that all solutions of the system (1) with initial condition (2) are non-negative for all $t\ge 0$.

2.2. Boundedness of the System

To establish the boundedness of the system, we define

$$W\left(t\right)=X\left(t\right)+Y\left(t\right)+Z\left(t\right)+U\left(t\right),$$

where $X\left(t\right),Y\left(t\right),Z\left(t\right),U\left(t\right)\ge 0$ for all $t\ge 0$.

Differentiating $W\left(t\right)$ with respect to time and using the system equations (1), we get

$$\begin{array}{cc}\hfill {\displaystyle \frac{dW}{dt}}& =r_{1}X\left(1-{\displaystyle \frac{X}{K_1}}\right)-\alpha X(Y+Z)+p\left(\alpha cX\right)YZ\left(1-{\displaystyle \frac{Y+Z}{K_2}}\right)\hfill \\ \hfill & -{\displaystyle \frac{\beta YU}{Y+Z}}-\mu Y+(1-p)\left(\alpha cX\right)YZ\left(1-{\displaystyle \frac{Y+Z}{K_2}}\right)\hfill \\ \hfill & -\mu Z+{\Pi }_u-\mu U.\hfill \end{array}$$

(12)

Combining similar terms, we can rewrite this as follows

$$\begin{array}{cc}\hfill {\displaystyle \frac{dW}{dt}}& =r_{1}X\left(1-{\displaystyle \frac{X}{K_1}}\right)-\alpha X(Y+Z)+pc\alpha XYZ\left(1-{\displaystyle \frac{Y+Z}{K_2}}\right)-\mu (Y+Z+U)\hfill \\ \hfill & -{\displaystyle \frac{\beta YU}{Y+Z}}+{\Pi }_u.\hfill \end{array}$$

We use the fact that the logistic growth term satisfies

$$r_{1}X\left(1-{\displaystyle \frac{X}{K_1}}\right)\le {\displaystyle \frac{r_1{K}_1}{4}}=C.$$

Also, we use the inequality

$$pc\alpha XYZ\le c\alpha {\left({\displaystyle \frac{Y+Z}{2}}\right)}^2={\displaystyle \frac{pc\alpha }{4}}X{(Y+Z)}^2,$$

and also note that

$${(Y+Z)}^2-{\displaystyle \frac{4\mu }{Xc\alpha }}(Y+Z)\le 0,\mathrm{whenever}Y+Z\mathrm{is}\mathrm{sufficiently}\mathrm{large}.$$

The term $pc\alpha XYZ\left(1-{\displaystyle \frac{Y+Z}{K_2}}\right)$ vanishes as $Y+Z\to K_2$, and becomes negative beyond ${\displaystyle \frac{\beta YU}{Y+Z}}\ge 0.$ Hence, for large $W\left(t\right)$, the quadratic terms are dominated by the negative linear term, and we obtain:

$${\displaystyle \frac{dW}{dt}}\le C-\delta W.$$

Thus

$$\underset{t\to \infty }{lim\; sup}W\left(t\right)\le {\displaystyle \frac{C}{\delta }}.$$

(13)

for some constants $C>0$, $\delta >0$. Using Comparison principle, we see that $W\left(t\right)$ is bounded for all $t\ge 0$. Therefore, the solutions $X\left(t\right),Y\left(t\right),Z\left(t\right),U\left(t\right)$ are all uniformly bounded on $[0,\infty )$.

3. Dynamics of the System

We analyze the dimensionless system in this section to determine its equilibrium points (1) and examine the stability of the system in their vicinity.

3.1. Existence of Equilibria

We analyse the system (1). We observe the following one equilibrium points for system (1), the interior equilibrium point $E^{*}(X^{*},Y^{*},Z^{*},U^{*})$, where

$$\begin{array}{ccc}& & U^{*}={\displaystyle \frac{{\Pi }_u}{\mu }},\hfill \\ & & Y^{*}={\displaystyle \frac{K_1{K}_2\mu }{(1-p)c{X}^{*}\left\{(\alpha K_1{K}_2-r_1{K}_1+r_1{X}^{*})\right\}}},\hfill \\ & & Z^{*}={\displaystyle \frac{{\Pi }_u\beta \alpha K_1^2{K}_2}{\mu rpc{X}^{*}(K_1-X^{*})(\alpha K_1{K}_2-r{K}_1+r{X}^{*})}}.\hfill \end{array}$$

(14)

and $X^{*}$ is the positive roots of the following equation:

$$B_0{X}^4+B_1{X}^3+B_2{X}^2+B_{3}X+B_4=0,$$

(15)

where,

$$\begin{array}{ccc}\hfill B_0& =& c\mu p{r}^3(1-p),\hfill \\ \hfill B_1& =& -K_1{K}_2\alpha c\mu p^2{r}^2+K_1{K}_2\alpha c\mu p{r}^2-3K_{1}c\mu p{r}^3+3K_{1}c\mu p^2{r}^3,\hfill \\ \hfill B_2& =& -2K_1^2{K}_2\alpha c\mu p{r}^2+2K_1^2{K}_2\alpha c\mu p^2{r}^2+3K_1^{2}c\mu p{r}^3-3K_1^{2}c\mu p^2{r}^3,\hfill \\ \hfill B_3& =& K_1^3{K}_2\alpha c\mu p{r}^2(1-p)-K_1^{3}c\mu p{r}^3(1-p)+K_1^2{K}_2\alpha {\mu }^{2}pr,\hfill \\ \hfill B_4& =& -K_1^3{K}_2\alpha {\mu }^{2}pr-K_1^3{K}_2{\Pi }_u{\alpha }^2\beta (1-p).\hfill \end{array}$$

Since, $p<1$, thus $(1-p)>0$. This implies, $B_0>0$ and $B_4<0.$ Hence, we conclude that the equation (15) admits at least one positive root, given that its discriminant is positive.

3.2. Local stability analysis

The Jacobian matrix of the system at interior equilibrium point $E^{*}(X^{*},Y^{*},Z^{*},U^{*})$ is given by:

$$J_{E^{*}}=\left[\begin{array}{cccc}{l}_{11}& l_{12}& l_{13}& 0\\ \\ l_{21}& l_{22}& l_{23}& l_{24}\\ \\ l_{31}& l_{32}& l_{33}& 0\\ \\ 0& 0& 0& l_{44}\end{array}\right].$$

Here, $l_{11}=r_1(1-{\displaystyle \frac{2X^{*}}{K_1}})-\alpha (Y^{*}+Z^{*}),l_{12}=-\alpha X^{*},l_{13}=-\alpha X^{*},l_{21}=pc\alpha Y^{*}{Z}^{*}(1-{\displaystyle \frac{Y^{*}+Z^{*}}{K_2}}),l_{22}=pc\alpha X^{*}{Z}^{*}(1-{\displaystyle \frac{z^{*}+2Y^{*}}{K_2}})-{\displaystyle \frac{\beta U^{*}{Z}^{*}}{{(Y^{*}+Z^{*})}^2}}-\mu ,l_{23}=pc\alpha X^{*}{Y}^{*}(1-{\displaystyle \frac{2Z^{*}+Y^{*}}{K_2}})+{\displaystyle \frac{\beta U^{*}{Y}^{*}}{{(Y^{*}+Z^{*})}^2}},l_{24}=-{\displaystyle \frac{\beta Y^{*}}{(Y^{*}+Z^{*})}},l_{31}=(1-p)c\alpha Y^{*}{Z}^{*}(1-{\displaystyle \frac{Y^{*}+Z^{*}}{K_2}}),l_{32}=(1-p)c\alpha X^{*}{Z}^{*}(1-{\displaystyle \frac{Z^{*}+2Y^{*}}{K_2}}),l_{33}=(1-p)c\alpha X^{*}{Y}^{*}(1-{\displaystyle \frac{2Z^{*}+Y^{*}}{K_2}})-\mu ,l_{44}=-\mu .$

At $E^{*}(X^{*},Y^{*},Z^{*},U^{*})$, the characteristic equation is given as

$$\begin{array}{c}\hfill {\rho }^4+A_1{\rho }^3+A_2{\rho }^2+A_3\rho +A_4=0.\end{array}$$

(16)

where,

$$\begin{array}{ccc}\hfill A_1& =& -(l_{11}+l_{22}+l_{33}+l_{44}),\hfill \\ \hfill A_2& =& l_{11}{l}_{22}+l_{11}{l}_{33}+l_{11}{l}_{44}+l_{22}{l}_{33}+l_{22}{l}_{44}+l_{33}{l}_{44}-l_{12}{l}_{21}-l_{13}{l}_{31}-l_{23}{l}_{32},\hfill \\ \hfill A_3& =& -[l_{11}{l}_{22}{l}_{44}+l_{11}{l}_{33}{l}_{44}+l_{22}{l}_{33}{l}_{44}-l_{11}{l}_{23}{l}_{32}-l_{12}{l}_{21}{l}_{44}-l_{12}{l}_{23}{l}_{31}\hfill \\ & & -l_{13}{l}_{31}{l}_{44}-l_{13}{l}_{21}{l}_{32}],\hfill \\ \hfill A_4& =& l_{11}(l_{22}{l}_{33}-l_{23}{l}_{32})l_{44}-l_{12}(l_{21}{l}_{33}-l_{23}{l}_{31})l_{44}+l_{13}(l_{21}{l}_{32}-l_{22}{l}_{31})l_{44}.\hfill \end{array}$$

(17)

By the Routh–Hurwitz criterion, the characteristic equation has all roots with negative real parts if and only if

$$\begin{array}{ccc}\hfill & i)& A_1>0,A_3>0,A_1{A}_2-A_3>0,\hfill \\ & ii)& A_1{A}_2{A}_3-{A_3}^2-{A_1}^2{A}_4>0.\hfill \end{array}$$

(18)

Consequently, we derive the following result.

Theorem 1.

The system is asymptotically stable at the endemic equilibrium $E^{*}$ provided the conditions in (18) are fulfilled.

3.3. Hopf bifurcation analysis

Any parameter in the system can serve as a bifurcation parameter. In this analysis, we consider $\eta$ as a generic bifurcation parameter. We derive the condition under which a Hopf bifurcation occurs at the critical value ${\eta }^{*}$ in a neighborhood of the endemic equilibrium point $E^{*}$.

Let us define a continuously differentiable function, $\Psi :(0,\infty )\to \mathbf{R}$ be the following of $\eta$:

$$\Psi \left(\eta \right):=A_1\left(\eta \right)A_2\left(\eta \right)A_3\left(\eta \right)-A_3^2\left(\eta \right)-A_4\left(\eta \right)A_1^2\left(\eta \right).$$

For a Hopf bifurcation to occur, it is required that the spectrum $\sigma \left(\eta \right)=\{\rho :D(\rho )=0\}$ of the characteristic equation includes a pair of complex conjugate eigenvalues. Specifically, there must exist a critical value ${\eta }^{*}\in (0,\infty )$ such that a pair of complex conjugate eigenvalues $\rho \left({\eta }^{*}\right),\overline{\rho }\left({\eta }^{*}\right)\in \sigma \left(\eta \right)$ satisfy the following conditions:

$$\mathrm{Re}\rho \left({\eta }^{*}\right)=0,\mathrm{Im}\rho \left({\eta }^{*}\right)={\omega }_0>0,$$

along with the transversality condition

$${\left.{\displaystyle \frac{dRe\rho \left(\eta \right)}{d\eta }}\right|}_{{\eta }^{*}}\ne 0$$

Furthermore, all other elements of the spectrum $\sigma \left(\eta \right)$ must possess negative real parts.

Theorem 2.

The system (1) undergoes a Hopf bifurcation at the endemic equilibrium $E^{*}$ when $\eta ={\eta }^{*}\in (0,\infty )$ if and only if the transversality condition $\Psi \left({\eta }^{*}\right)=0$ is satisfied. and

$$A_1^3{A}_2^{\prime }{A}_3(A_1-3A_3)>2(A_2{A}_1^2-2A_3^2)(A_3^{\prime }{A}_1^2-A_1^{\prime }{A}_3^2)$$

(19)

and At the critical value $\eta ={\eta }^{*}$, the eigenvalue $\rho \left(\eta \right)$ is purely imaginary, while all other eigenvalues have negative real parts.

Proof. 

By the condition $\Psi \left({\eta }^{*}\right)=0$, the characteristic equation can be written as

$$\left({\rho }^2+{\displaystyle \frac{A_3}{A_1}}\right)\left({\rho }^2+A_1\rho +{\displaystyle \frac{A_1{A}_4}{A_3}}\right)=0.$$

If it has four roots, say ${\rho }_i$, (i=1,2,3,4) with the pair of purely imaginary roots at $\eta ={\eta }^{*}$ as ${\rho }_1={\overline{\rho }}_2$, then we have

$$\begin{array}{c}\hfill {\rho }_3+{\rho }_4=-A_1,{\omega }_0^2+{\rho }_3{\rho }_4=A_2,{\omega }_0^2({\rho }_3+{\rho }_4)=-A_3,{\omega }_0^2{\rho }_3{\rho }_4=A_4.\end{array}$$

(20)

where ${\omega }_0=\mathrm{Im}{\rho }_1\left({\eta }^{*}\right)$. By dividing the third equation by the first in (20), we obtain ${\omega }_0=\sqrt{A_3{A}_1^{-1}}$. If ${\rho }_3$ and ${\rho }_4$ are complex conjugate eigenvalues, then from (20), it follows that $2\mathrm{Re}\left({\rho }_3\right)=-A_1$. On the other hand, if ${\rho }_3$ and ${\rho }_4$ are real roots, then by (16) and (20), we conclude that ${\rho }_3<0$ and ${\rho }_4<0$. To complete the analysis, it remains to verify the transversality condition.

Now, we proceed to verify the transversality condition.

$${\displaystyle \frac{dRe\left({\rho }_j\left(\eta \right)\right)}{d\eta }}{|}_{\eta ={\eta }^{*}}\ne 0,j=1,2.$$

Since $\Psi \left({\eta }^{*}\right)$ is a continuous function of all its roots, there exists an open interval $\eta \in ({\eta }^{*}-ϵ,{\eta }^{*}+ϵ)$ in which ${\rho }_1$ and ${\rho }_2$ remain complex conjugate for all $\eta$ within this neighborhood. Let us assume that their general forms in this interval are given by:

$$\begin{array}{ccc}\hfill {\rho }_{1,2}\left(\eta \right)& =& \zeta \left(\eta \right)\pm i\nu \left(\eta \right).\hfill \end{array}$$

Substituting ${\rho }_j\left(\eta \right)=\zeta \left(\eta \right)\pm i\nu \left(\eta \right)$, into (16) and differentiating, we have

$$\begin{array}{c}\hfill L_1\left(\eta \right){\zeta }^{\prime }\left(\eta \right)-L_2\left(\eta \right){\nu }^{\prime }\left(\eta \right)+L_3\left(\eta \right)=0,\\ \hfill L_2\left(\eta \right){\zeta }^{\prime }\left(\eta \right)+L_1\left(\eta \right){\nu }^{\prime }\left(\eta \right)+L_4\left(\eta \right)=0,\end{array}$$

(21)

where

$$\begin{array}{ccc}\hfill L_1\left(\eta \right)& =& 4{\zeta }^3-12\zeta {\nu }^2+3A_1({\zeta }^2-{\nu }^2)+2A_2\zeta +A_3,\hfill \\ \hfill L_2\left(\eta \right)& =& 12{\zeta }^2\nu +6A_1\zeta \nu -4{\zeta }^3+2A_2\zeta ,\hfill \\ \hfill L_3\left(\eta \right)& =& A_1{\zeta }^3-3A_1^{\prime }\zeta {\nu }^2+A_2^{\prime }({\zeta }^2-{\nu }^2)+A_3^{\prime }\zeta ,\hfill \\ \hfill L_4\left(\eta \right)& =& 3A_1^{\prime }{\zeta }^2\nu -A_1^{\prime }{\nu }^3+2A_2^{\prime }\zeta \nu +A_3^{\prime }\zeta .\hfill \end{array}$$

Solving (21) for ${\zeta }^{\prime }\left({\eta }^{*}\right)$ we have

$$\begin{array}{c}\hfill {\left[{\displaystyle \frac{dRe\left({\rho }_j\left(\eta \right)\right)}{d\eta }}\right]}_{\eta ={\eta }^{*}}={\zeta }^{\prime }{\left(\eta \right)}_{\eta ={\eta }^{*}}=-{\displaystyle \frac{L_2\left({\eta }^{*}\right)L_4\left({\eta }^{*}\right)+L_1\left({\eta }^{*}\right)L_3\left({\eta }^{*}\right)}{K^2\left({\eta }^{*}\right)+L^2\left({\eta }^{*}\right)}}\\ \hfill ={\displaystyle \frac{A_1^3{A}_2^{\prime }{A}_3(A_1-3A_3)-2(A_2{A}_1^2-2A_3^2)(A_3^{\prime }{A}_1^2-A_1^{\prime }{A}_3^2)}{A_1^4{(A_1-3A_3)}^2+4{(A_2{A}_1^2-2A_3^2)}^2}}>0,\mathrm{using}\left(19\right).\end{array}$$

Hence, the transversality conditions is verified. Thus, Hopf bifurcation occurs at $\eta ={\eta }^{*}$ around $E^{*}$.    □

3.4. Global Stability Analysis

We define the Lyapunov function as follows:

$$\psi (X,Y,Z,U)={\displaystyle \frac{1}{2}}\left[b_1{X}^2+b_2{Y}^2+b_3{Z}^2+b_4{U}^2\right],$$

where $b_i>0$ for $i=1,2,3,4$. $\psi$ is easily seen to be positive definite. Along the trajectory of the system $\dot{P}\left(t\right)=J_{E^{*}}P\left(t\right)$, with $P\left(t\right)={(X\left(t\right),Y\left(t\right),Z\left(t\right),U\left(t\right))}^T$, the derivative of the Lyapunov function $\psi$ is given by:

$$\begin{array}{ccc}\hfill \dot{\psi }& =& b_{1}X\dot{X}+b_{2}Y\dot{Y}+b_{3}Z\dot{Z}+b_{4}U\dot{U},\hfill \\ & =& b_{1}X\left[X{l}_{11}+Y{l}_{12}+Z{l}_{13}\right]+b_{2}Y\left[X{l}_{21}+Y{l}_{22}+Z{l}_{23}+U{l}_{24}\right]\hfill \\ & & +b_{3}Z\left[X{l}_{31}+Y{l}_{32}+Z{l}_{33}\right]+b_{4}U\left[U{l}_{44}\right],\hfill \\ & =& b_1{l}_{11}{X}^2+b_2{l}_{22}{Y}^2+b_3{l}_{33}{Z}^2+b_4{l}_{44}{U}^2+(b_1{l}_{12}+b_2{l}_{21})XY\hfill \\ & & +(b_1{l}_{13}+b_3{l}_{31})XZ+(b_2{l}_{23}+b_3{l}_{32})YZ+b_2{l}_{24}YU.\hfill \end{array}$$

(22)

Thus,we can write the corresponding symmetric matrix to $\dot{\psi }$ is:

$$M={\left[m_{ij}\right]}_{4\times 4}={\displaystyle \frac{1}{2}}\left[\begin{array}{cccc}2b_1{l}_{11}& b_1{l}_{12}+b_2{l}_{21}& (b_1{l}_{13}+b_3{l}_{31})& 0\\ \\ b_1{l}_{12}+b_2{l}_{21}& 2b_2{l}_{22}& b_2{l}_{23}+b_3{l}_{32}& b_2{l}_{24}\\ \\ b_1{l}_{13}+b_3{l}_{31}& b_2{l}_{23}+b_3{l}_{32}& 2b_3{l}_{33}& 0\\ \\ 0& b_2{l}_{24}& 0& 2b_4{l}_{44}\end{array}\right].$$

The local asymptotic stability of the positive equilibrium point $E^{*}$ can be established by verifying that $\dot{\psi }$ is negative definite. This condition is satisfied if the symmetric matrix M, associated with the Lyapunov function, is negative definite. A symmetric matrix is negative definite if all its principal minors of odd order are negative and those of even order are positive. Therefore, the equilibrium point $E^{*}$ is locally stable provided the following conditions hold:

(i)

$2b_1{l}_{11}<0,$

(ii)

$4b_1{b}_2{l}_{11}{l}_{22}-{(b_1{l}_{12}+b_2{l}_{21})}^2>0,$

(iii)

$2b_1{l}_{11}\left[4b_2{b}_3{l}_{22}{l}_{33}-{(b_2{l}_{23}+b_3{l}_{32})}^2\right]-(b_1{l}_{12}+b_2{l}_{21})[2b_3{l}_{33}(b_1{l}_{12}+b_2{l}_{21})-(b_1{l}_{13}+b_3{l}_{31})(b_2{l}_{23}+b_3{l}_{32})]+(b_1{l}_{13}+b_3{l}_{31})[(b_1{l}_{12}+b_2{l}_{21})(b_2{l}_{23}+b_3{l}_{32})-2b_2{l}_{22}(b_1{l}_{13}+b_3{l}_{31})]<0,$

(iv)

$2b_4{l}_{44}\left[\mathrm{LHS}\mathrm{of}\mathrm{inequality}\left(\mathrm{iii}\right)\right]+b_2{l}_{24}\left[\mathrm{Minor}\mathrm{with}\mathrm{respect}{m}_{24}M\right]>0.$

We choose $b_1,b_2,b_3,b_4$ such that

$$\begin{array}{c}\hfill b_2{l}_{23}+b_3{l}_{32}=0,b_1{l}_{12}+b_2{l}_{21}=0,b_1{l}_{13}+b_3{l}_{31}=0.\end{array}$$

(23)

Above, first inequalities hold if $l_{11}<0$ as $b_1>0$. Again, since $b_1>0$, $b_2>0$ and $l_{11}<0$ therefore the second condition holds when $l_{22}<0$. The third inequality holds only for its first is negative. The first term will negative for $l_{33}<0$. In the same way fourth condition automatically satisfy since $l_{44}<0$. Thus, we have

$$\begin{array}{ccc}\hfill & i)& r_1\left(1-{\displaystyle \frac{2X^{*}}{K_1}}\right)-\alpha (Y^{*}+Z^{*})<0,\hfill \\ & ii)& pc\alpha X^{*}{Z}^{*}\left(1-{\displaystyle \frac{Z^{*}+2Y^{*}}{K_2}}\right)-{\displaystyle \frac{\beta U^{*}{Z}^{*}}{{(Y^{*}+Z^{*})}^2}}-\mu <0,\hfill \\ & iii)& (1-p)c\alpha Y^{*}\left(1-{\displaystyle \frac{2Z^{*}+Y^{*}}{K_2}}\right)-\mu <0.\hfill \end{array}$$

(24)

The above results can be summarized in the form of the following theorem :

Theorem 3.

The system (1) is globally asymptotically stable at the equilibrium point $E^{*}$ provided that the conditions specified in (24) are satisfied.

4. The Optimal Control Problem

Here, we formulate an optimal control problem to minimize pests by determining the best time-varying profiles for releasing sterile male pests. The control variables, $c\left(t\right)$ represent the control efforts that regulate the release of sterile male pests. This variable is constrained within the interval $[t_0,t_f]$, with $0<c\left(t\right)<1$. Here, $t_0$ and $t_f$ denote the start and end times of the control period.

Introducing the control parameter, the state system becomes

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dX}{dt}}& =& r_{1}X\left(1-{\displaystyle \frac{X}{K_1}}\right)-\alpha X(Y+Z),\hfill \\ \hfill {\displaystyle \frac{dY}{dt}}& =& pc\alpha XYZ\left(1-{\displaystyle \frac{Y+Z}{K_2}}\right)-{\displaystyle \frac{\beta YU}{Y+Z}}-\mu Y,\hfill \\ \hfill {\displaystyle \frac{dZ}{dt}}& =& (1-p)c\alpha XYZ\left(1-{\displaystyle \frac{Y+Z}{K_2}}\right)-\mu Z\hfill \\ \hfill {\displaystyle \frac{dU}{dt}}& =& (1-c\left(t\right)){\Pi }_u-\mu U,\hfill \end{array}$$

(25)

with $X\left(0\right)>0$, $Y\left(0\right)>0$, $Z\left(0\right)>0$ and $U\left(0\right)>0$ as the initial population size.

Our objective is to derive an optimal control profile of $c\left(t\right)$, denoted by $c^{*}\left(t\right)$, using the maximum principle [26] that minimize the objective function $I\left(c\right(t\left)\right)$ which is defined as

$$\begin{array}{ccc}\hfill I\left(c\right(t\left)\right)& =& {\int }_{t_0}^{t_f}\left[P{c}^2\left(t\right)+QY\left(t\right)+RZ\left(t\right)\right]dt,\hfill \end{array}$$

(26)

The goal of the objective function is to achieve cost-effective pest control by minimizing associated management costs. In this context, $P\ge 0$ represents the weight constants for sterile pests, while $Q,R\ge 0$ denote the penalty multipliers on the benefit of the cost. The term $P{c}_1^2\left(t\right)$ reflects the cost of sterile pests. Mathematically, we rewrite the problem as

$$\begin{array}{ccc}\hfill I\left(c^{*}\left(t\right)\right)& =& min\left\{I\left(c\right(t\left)\right):c\left(t\right)\in U\right\},\hfill \\ & & subjecttothestatesystem\left(\right),where,\hfill \\ \hfill U& =& \left\{c\right(t):cismeasurable,and\hfill \\ & & 0\le c\left(t\right)\le 1,t\in [t_0,t_f]\}.\hfill \end{array}$$

(27)

We derive the following theorem that characterize the optimal system.

Theorem 4.

The objective cost function $I\left(c\right)$ over the control set U attains its minimum at the optimal control $c^{*}$, which corresponds to the interior equilibrium point $(X^{*},Y^{*},Z^{*},U^{*})$. Furthermore, there exist adjoint variables ${\xi }_1,{\xi }_2,{\xi }_3,{\xi }_4$ that satisfy the following system of equations:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d{\xi }_1}{dt}}& =& -{\xi }_1\left[r_1(1-{\displaystyle \frac{2X}{K_1}})-\alpha (Y+Z)\right]-{\xi }_2\left[pc\alpha YZ(1-{\displaystyle \frac{Y+Z}{K_2}})\right]\hfill \\ & & -{\xi }_3\left[(1-p)c\alpha YZ(1-{\displaystyle \frac{Y+Z}{K_2}})\right],\hfill \\ \hfill {\displaystyle \frac{d{\xi }_2}{dt}}& =& -Q+{\xi }_1\alpha X-{\xi }_2\left[pc\alpha XZ(1-{\displaystyle \frac{2Y+Z}{K_2}})-{\displaystyle \frac{\beta UZ}{{(Y+Z)}^2}}-\mu \right]\hfill \\ & & -{\xi }_3\left[(1-p)c\alpha XZ(1-{\displaystyle \frac{2Y+Z}{K_2}})\right],\hfill \\ \hfill {\displaystyle \frac{d{\xi }_3}{dt}}& =& -R+{\xi }_1\alpha X-{\xi }_2\left[pc\alpha XY(1-{\displaystyle \frac{Y+2Z}{K_2}})+{\displaystyle \frac{\beta YU}{{(Y+z)}^2}}\right]\hfill \\ & & -{\xi }_3\left[(1-p)c\alpha XZ(1-{\displaystyle \frac{2Y+Z}{K_2}})\right],\hfill \\ \hfill {\displaystyle \frac{d{\xi }_4}{dt}}& =& {\xi }_2{\displaystyle \frac{\beta Y}{Y+Z}}+{\xi }_4\mu ,\hfill \end{array}$$

(28)

with the boundary condition  ${\xi }_l\left(t_f\right)=0,(l=1,2,3,4).$Moreover, the optimal control is characterized by the following expression

$$\begin{array}{c}\hfill c^{*}\left(t\right)=max\left\{0,min\left\{1,{\displaystyle \frac{{\xi }_4{\Pi }_u}{2P}}\right\}\right\}\end{array}$$

Proof. 

We use Pontryagin Minimum Principle [26] to find the necessary conditions an optimal system. This principle actually converts the optimality system into a problem of minimizing the Hamiltonian function, H. We take the Hamiltonian as follows:

$$\begin{array}{ccc}\hfill H& =& P{c}^2\left(t\right)+QY\left(t\right)+RZ\left(t\right)\hfill \\ & & +{\xi }_1\left\{r_{1}X\left(1-{\displaystyle \frac{X}{K_1}}\right)-\alpha X(Y+Z)\right\}\hfill \\ & & +{\xi }_2\left\{pc\alpha XYZ\left(1-{\displaystyle \frac{Y+Z}{K_2}}\right)-{\displaystyle \frac{\beta YU}{(Y+Z)}}-\mu Y\right\}\hfill \\ & & +{\xi }_3\left\{(1-p)c\alpha XYZ\left(1-{\displaystyle \frac{Y+Z}{K_2}}\right)-\mu Z\right\}\hfill \\ & & +{\xi }_4\left\{(1-c\left(t\right)){\Pi }_u-\mu U\right\}.\hfill \end{array}$$

(29)

According to [26], the optimal controls $c^{*}\left(t\right)$ satisfy

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial H}{\partial c}}\left(t\right)=0\end{array}$$

(30)

which implies,

$$\begin{array}{c}\hfill 2P{c}^{*}-{\xi }_4{\Pi }_u=0\end{array}$$

(31)

To keep the the control bounded between 0 and 1, we use the following compact form of $c^{*}\left(t\right)$

$$\begin{array}{c}\hfill c^{*}\left(t\right)=max\left\{0,min\left\{1,{\displaystyle \frac{{\xi }_4{\Pi }_u}{2P}}\right\}\right\}.\end{array}$$

Pontryagin Minimum Principle says that the adjoint variables should satisfy the following relations:

$$\begin{array}{c}\hfill {\displaystyle \frac{d{\xi }_i}{dt}}=-{\displaystyle \frac{\partial H}{\partial x_i}}\end{array}$$

(32)

where $x_i=(X,Y,Z,U)$ i.e, $x_1=X$, $x_2=Y$ etc.

We use the above relations to find the adjoint equations as given in (28).

The above equations represent the necessary conditions that must be satisfied by the optimal control pair $c\left(t\right)$ and the corresponding state variables of the system. According to the Pontryagin Minimum Principle, the adjoint variables satisfy the transversality conditions ${\xi }_i\left(t_f\right)=0$, for all i.

   □

Remark 1.

The optimal control problem results in an optimality system that constitutes a two point boundary value problem. The state system is an initial value problem, whereas the adjoint system is a terminal (or boundary) value problem. This coupled system is solved numerically using the MATLAB packagebvp4c .

4.1. Uniqueness of the Optimal Control Parameter

Now, we prove that the control variable $u\left(t\right)$ is unique for the system (25). Let us assume that, $(x_1,x_2,x_3,x_4,{\xi }_1,{\xi }_2,{\xi }_3,{\xi }_4)$ and $({\overline{x}}_1,{\overline{x}}_2,{\overline{x}}_3,{\overline{x}}_4,{\overline{\xi }}_1,{\overline{\xi }}_2,{\overline{\xi }}_3,{\overline{\xi }}_4)$ are two set of solutions of the system (25) and (28).

Let us consider $x_i=e^{\lambda t}{p}_i$ and ${\xi }_i=e^{-\lambda t}{q}_i$, for $i=1,2,\dots ,4$. Similarly, ${\overline{x}}_i=e^{\lambda t}{\overline{p}}_i$, and ${\overline{\xi }}_i=e^{-\lambda t}{\overline{q}}_i$, for $i=1,2,\dots ,4$. Then we take the optimal control parameter in the form,

$$\begin{array}{cc}\hfill c\left(t\right)& =max\left(0,min\left(1,{\displaystyle \frac{q_i{e}^{-\lambda t}{\pi }_u)}{2P}}\right)\right),\hfill \\ \hfill \overline{c\left(t\right)}& =max\left(0,min\left(1,{\displaystyle \frac{\overline{q_i}{e}^{-\lambda t}{\pi }_u)}{2P}}\right)\right).\hfill \end{array}$$

(33)

Using the bounds of the control, we can write the inequalities written below:

$${\int }_{t_i}^{t_f}{(c\left(t\right)-\overline{c}\left(t\right))}^{2}dt\le C_2{\int }_{t_i}^{t_f}\left[|q_i-{\overline{q}}_i{|}^2\right]dt.$$

(34)

Putting, $x_i=e^{\lambda t}{p}_i$ and ${\xi }_i=e^{-\lambda t}{q}_i$ (for $i=1,2,\dots ,4$) in (25) and (35), we have:

$$\begin{array}{cc}\hfill {\dot{p}}_i+\lambda p_i& =e^{-\lambda t}{f}_i\left(e^{\lambda t}{p}_i,t\right),i=1,2,\dots ,4,\hfill \\ \hfill {\dot{q}}_i-\lambda q_i& =e^{\lambda t}{F}_i\left(e^{\lambda t}{p}_i,e^{-\lambda t}{q}_i,t\right).\hfill \end{array}$$

(35)

$F_i,(i=1,2,\dots ,4)$ are right hand sides of system (25) and $f_i$ are right hand sides of system (28). As for example, the differential equations of (35), for $i=3$ are given by

$$\begin{array}{ccc}\hfill {\dot{p}}_2+\lambda p_2& =& e^{-\lambda t}\left((1-p)c\alpha p_1{p}_2{p}_3\left(1-{\displaystyle \frac{p_2+p_3}{K_2}}-\mu p_3\right)\right),\hfill \\ \hfill {\dot{q}}_2-\lambda q_2& =& e^{\lambda t}(-R+{\xi }_1\alpha p_1-{\xi }_2[pc\alpha p_1{p}_2(1-{\displaystyle \frac{p_2+2p_3}{K_2}})\hfill \end{array}$$

(36)

$$\begin{array}{ccc}& & +{\displaystyle \frac{\beta p_2{p}_4-{\xi }_3\left[(1-p)c\alpha p_1{p}_3(1-\frac{2p_2+p_3}{K_2})\right]}{{(p_2+p_3)}^2}}\left]\right).\hfill \end{array}$$

(37)

We can get another set of eight equations by substituting ${\overline{x}}_i=e^{\lambda t}{\overline{p}}_i$, ${\overline{\xi }}_i=e^{-\lambda t}{\overline{q}}_i$, for $i=1,2,\dots ,4$.

Now, we subtract the equations for ${\overline{x}}_i$ from $x_i$, and ${\overline{\xi }}_i$ from ${\xi }_i$, for $i=1,2,\dots ,4$. Next, each subtracted equation is multiplied by an appropriate function and then integrated from initial time ($t_0$) to final time ($t_f$).

Thus, we have the following inequalities:

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{2}}{(p_i-{\overline{p}}_i)}^2\left(t_f\right)+\lambda {\int }_{t_0}^{t_f}{(p_i-{\overline{p}}_i)}^{2}dt& \le {\overline{C}}_3{e}^{\lambda t_f}{\int }_{t_0}^{t_f}\left[\sum _{i=1}^4{|p_i-{\overline{p}}_i|}^2\right]dt\hfill \\ \hfill & +{\overline{C}}_4{\int }_{t_0}^{t_f}\left[\sum _{i=1}^4{|q_i-{\overline{q}}_i|}^2\right]dt,\hfill \\ \hfill {\displaystyle \frac{1}{2}}{(q_i-{\overline{q}}_i)}^2\left(t_f\right)+\lambda {\int }_{t_i}^{t_f}{(q_i-{\overline{q}}_i)}^{2}dt& \le {\overline{C}}_5{e}^{\lambda t_f}{\int }_{t_0}^{t_f}\left[\sum _{i=1}^4{|q_i-{\overline{q}}_i|}^2\right]dt.\hfill \end{array}$$

(38)

The constants ${\overline{C}}_1$ to ${\overline{C}}_5$ depend on the coefficients and the bounds of the states and adjoint variables.

Now, adding the above eight inequalities and after some simplification, we finally obtain

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}}\left[\sum _{i=1}^4{(p_i-{\overline{p}}_i)}^2\left(t_f\right)+\sum _{i=1}^4{(q_i-{\overline{q}}_i)}^2\left(t_f\right)\right]+\lambda {\int }_{t_0}^{t_f}\left[\sum _{i=1}^6{(p_i-{\overline{p}}_i)}^2+\sum _{i=1}^4{(q_i-{\overline{q}}_i)}^2\right]dt\\ \hfill \le ({\overline{C}}_6+{\overline{C}}_7{e}^{\lambda t_f}){\int }_{t_0}^{t_f}\left[\sum _{i=1}^4{(p_i-{\overline{p}}_i)}^2+\sum _{i=1}^4{(q_i-{\overline{q}}_i)}^2\right]dt,\end{array}$$

(39)

where, ${\overline{C}}_6$ and ${\overline{C}}_7$ depend on the coefficients and the bounds of $p_i$ and $q_i$, $i=1,2,\dots ,4$. From the above relations we can derive the followings inequalities:

$$\left(\lambda -{\overline{C}}_6-{\overline{C}}_7{e}^{\lambda t_f}\right)·{\int }_{t_0}^{t_f}\left[\sum _{i=1}^4{(p_i-{\overline{p}}_i)}^2+\sum _{i=1}^4{(q_i-{\overline{q}}_i)}^2\right]dt\le 0.$$

(40)

If we choose $\lambda$ such that $\lambda >{\overline{C}}_6+{\overline{C}}_7$ and $t_f<(1/\lambda )ln((\lambda -{\overline{C}}_6)/{\overline{C}}_7)$, then

$$p_1={\overline{p}}_1,p_2={\overline{p}}_2,p_3={\overline{p}}_3,p_4={\overline{p}}_4,q_1={\overline{q}}_1,q_2={\overline{q}}_2,q_3={\overline{q}}_3,q_4={\overline{q}}_4.$$

Therefore, the solution is unique in the time interval $[t_0,t_f]$ and consequently the optimal control function is unique for the optimal system that can minimize the cost.

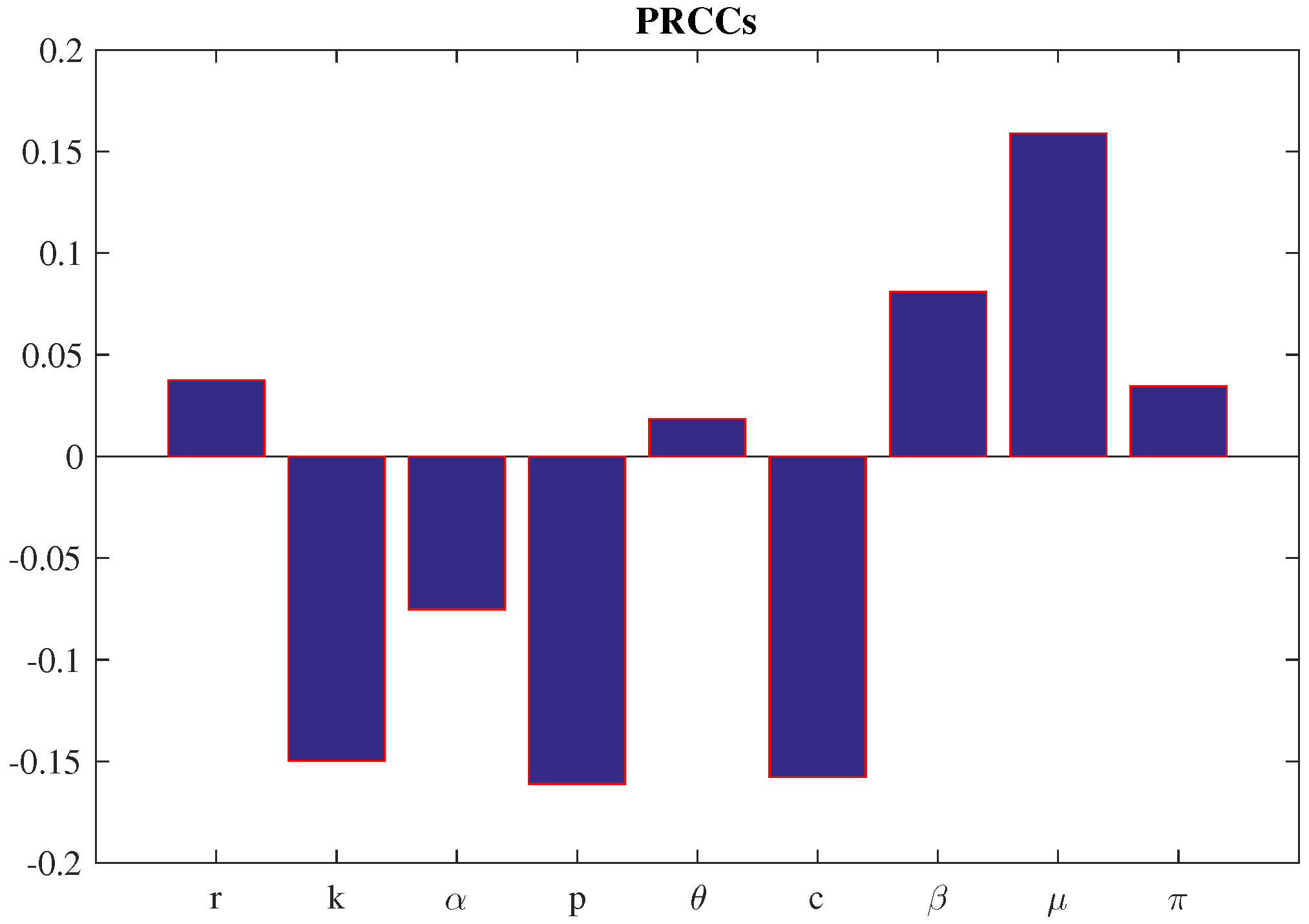
5. Sensitivity Analysis: PRCC

To evaluate how input parameters influence model outcomes, we conduct a sensitivity analysis. This approach helps pinpoint which variables exert the greatest impact on the dynamics of the system [30,31]. Common techniques for sensitivity analysis include Partial Rank Correlation Coefficient (PRCC), extended Fourier Amplitude Sensitivity Test (eFAST). Among these, PRCC is particularly effective for global sensitivity analysis, especially in complex, high-dimensional, and nonlinear models. It accounts for the interdependencies among variables, making it a robust choice for assessing parameter influence [29].

Before applying PRCC, we use Latin Hypercube Sampling (LHS) to generate a diverse and representative set of input values. LHS ensures efficient coverage of the parameter space, which is essential for reliable sensitivity results. Following the methodology outlined by Marino et al. [29], we performed PRCC-based sensitivity analysis on the first and second fish predator populations. This allowed us to clearly assess the relative influence of each predator on the system dynamics.

For crop biomass X, the PRCC results highlight several key parameters: $r,k,\alpha ,\theta ,c,\beta ,\mu ,$ and $\Pi$. Of these, $r,\theta ,\beta ,\mu ,$ and $\Pi$ exhibit positive correlations with biomass, while the remaining parameters show negative associations.

6. Numerical Simulation

This sections contains the detail calculations of analytical results of previous sections using numerical values of the model parameters. The simulated are useful in finding significant results for pest management using sterile insect release technique. First, we study the results that are obtained from the system without optimal control. Then, we discussed the results of the optimal system.

Results from the system without control

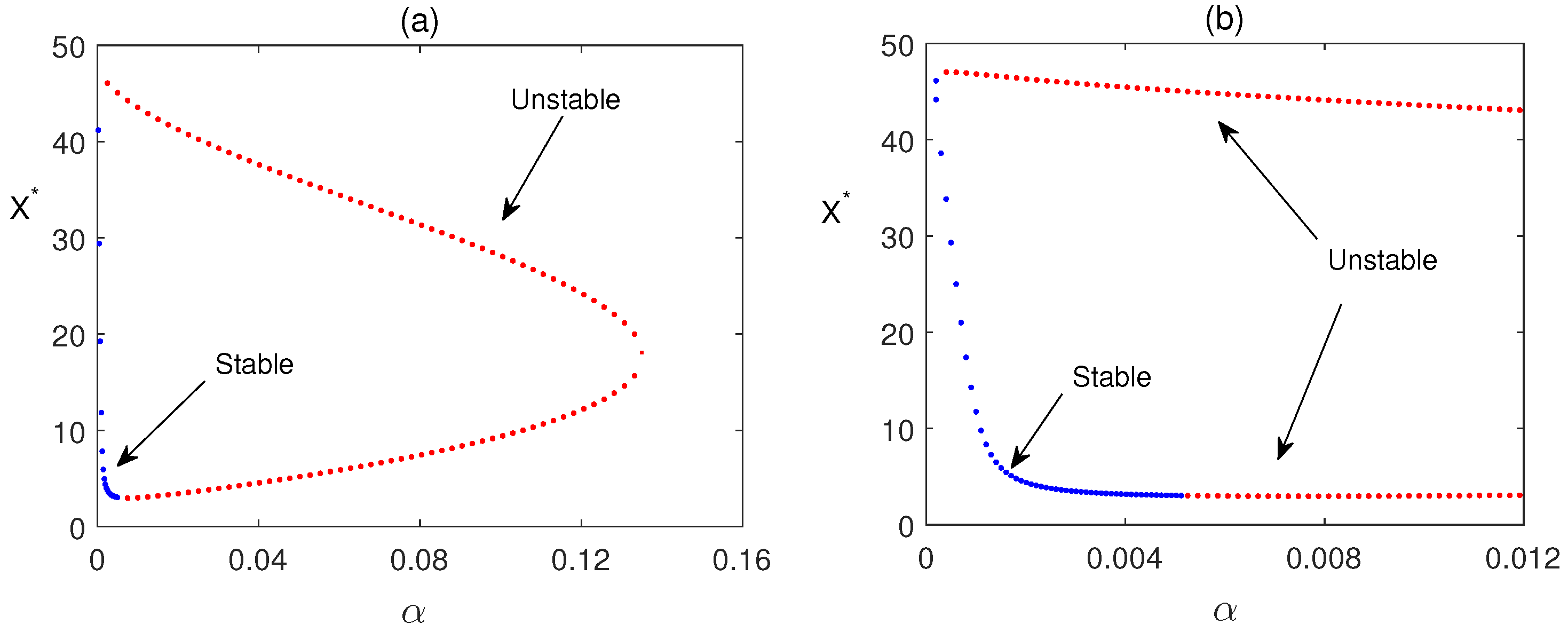
Figure 1 is the analysis of the feasible roots of equation (15). We observe that two feasible interior equilibrium exits but one is stable and another is unstable i.e. bistability does not occur.

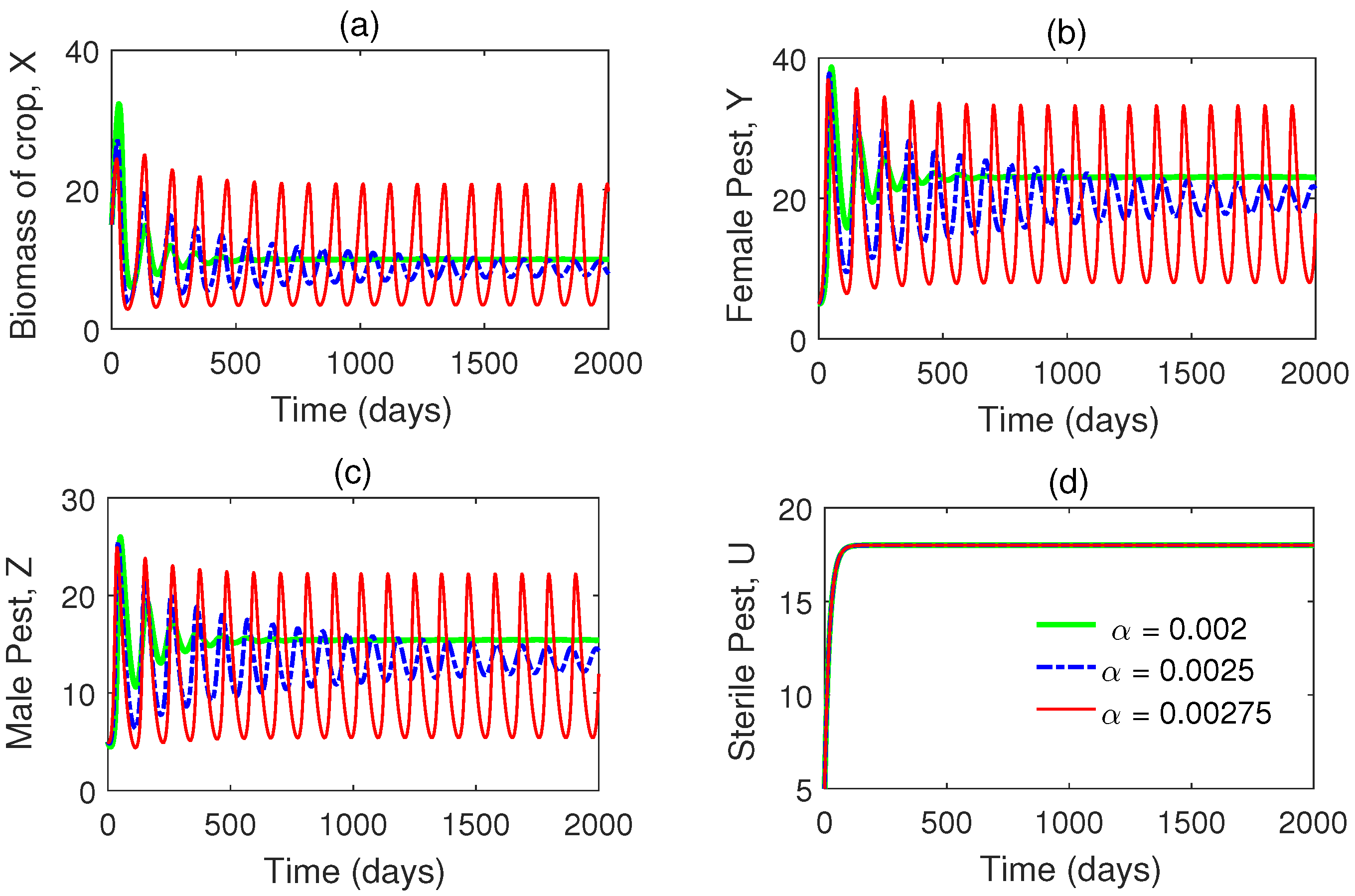
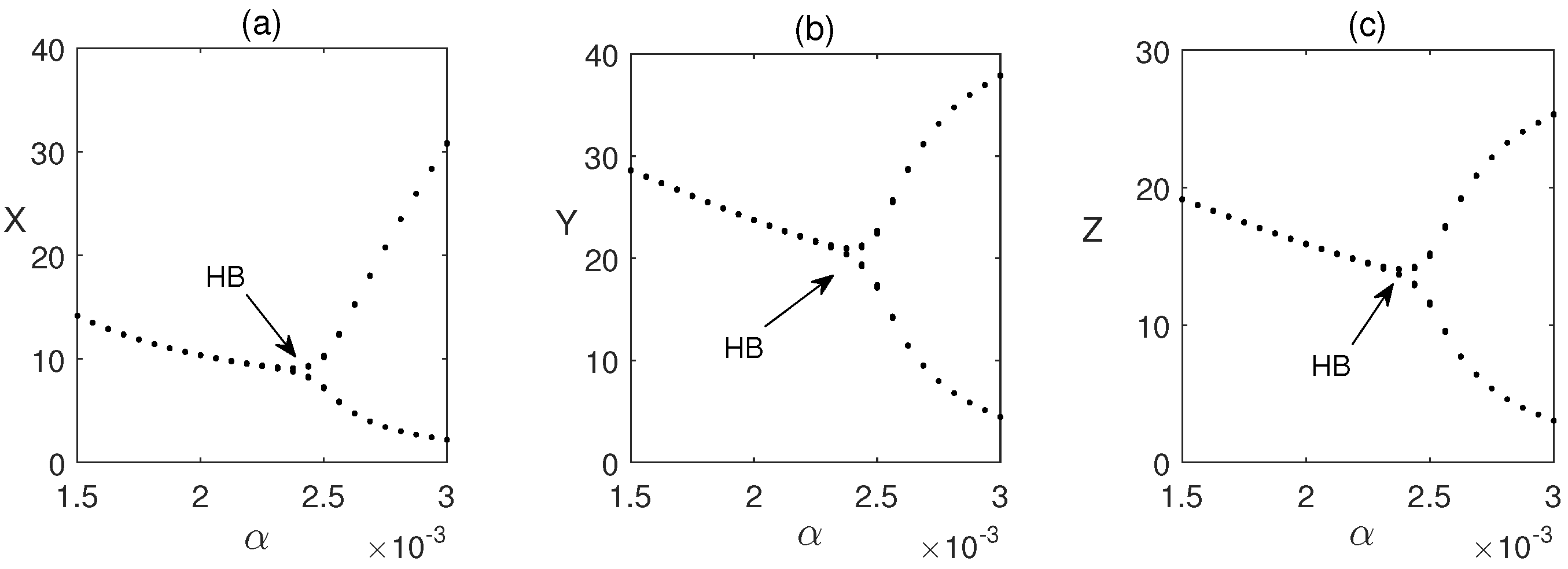
Time series solutions of the system are plotted in Figure 2 for three different values of $\alpha$. It is observed that as the values of $\alpha$ are increased, oscillations in the populations are also increased. Hopf bifurcation is observed in Figure 3 when $\alpha$ passes its critical vale ${\alpha }^{*}=0.002495$ (approx.). In this figure, we have plotted the maximum and minimum values of the periodic solutions with respect to the bifurcation parameter $\alpha$.

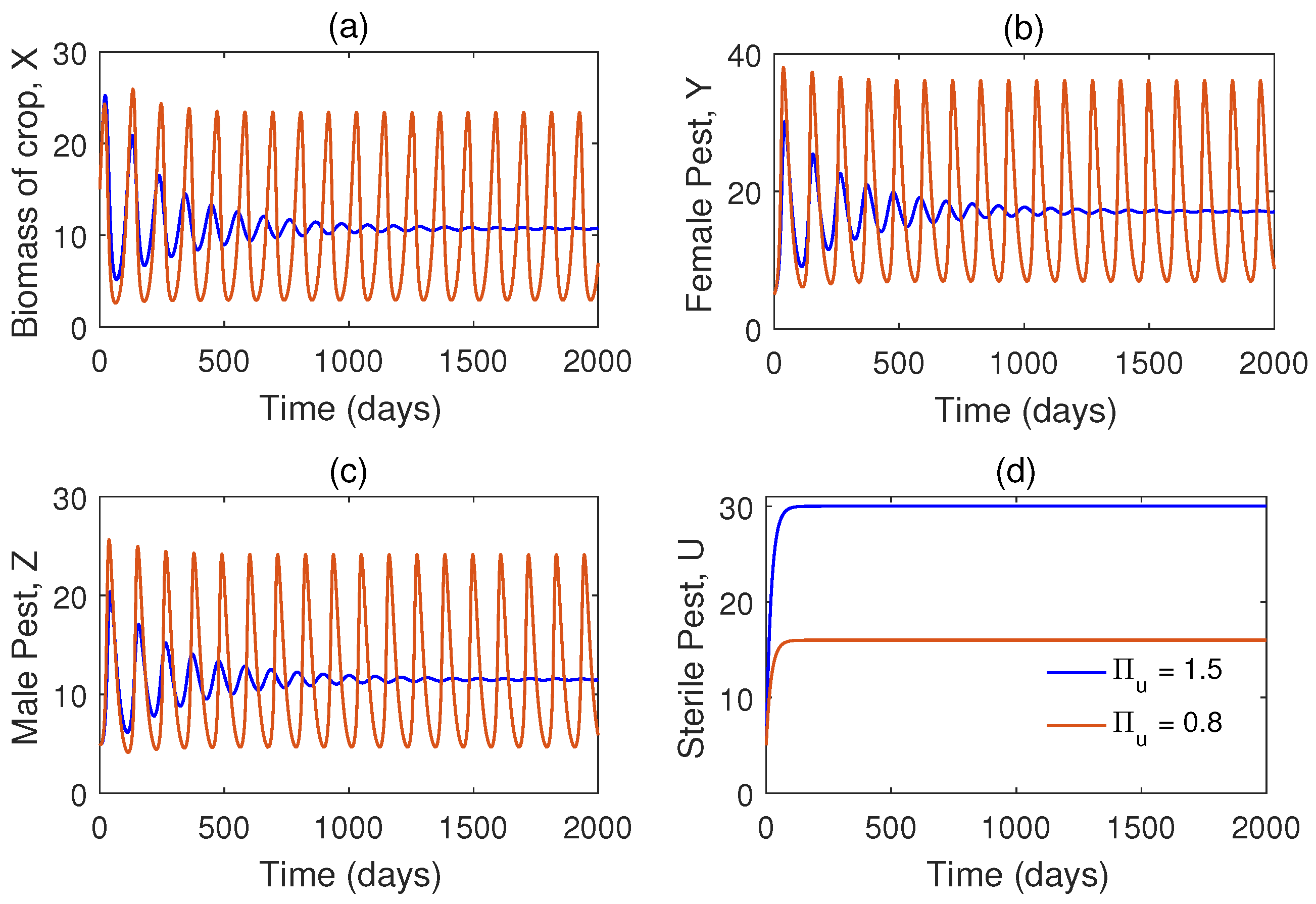
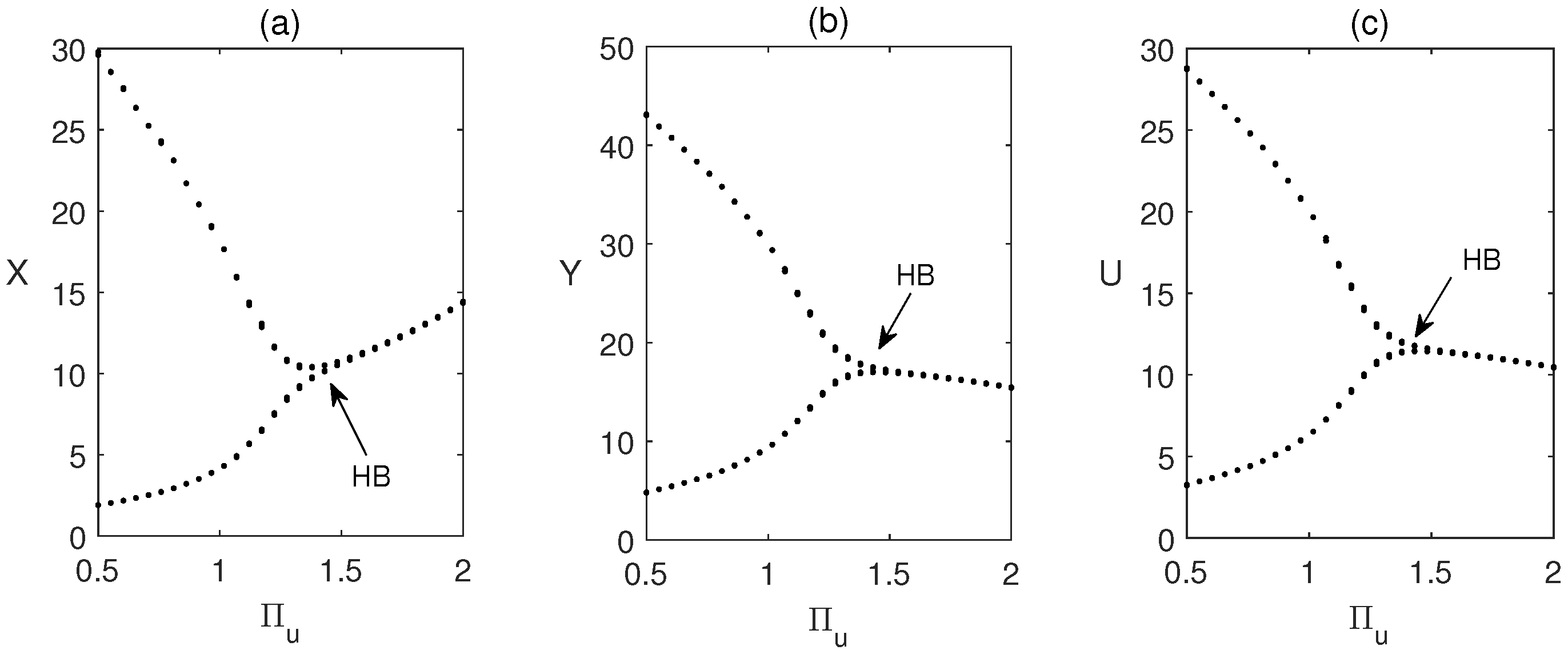
Another time series plot is shown in Figure 4 for different values of the rate of release of sterile male pests, ${\Pi }_u$. We have taken $\alpha =0.0025$ that means there is already periodic oscillation in the system. Now we increase the value of ${\Pi }_u$ and see that the system becomes stable. Thus we conclude that role of ${\Pi }_u$ is to stabilize the system. In Figure 5, we have plotted a Hopf bifurcation diagram for ${\Pi }_u$. Stability switch is observed from unstable to stable when ${\Pi }_u$ is increased from $0.5$ to 2.

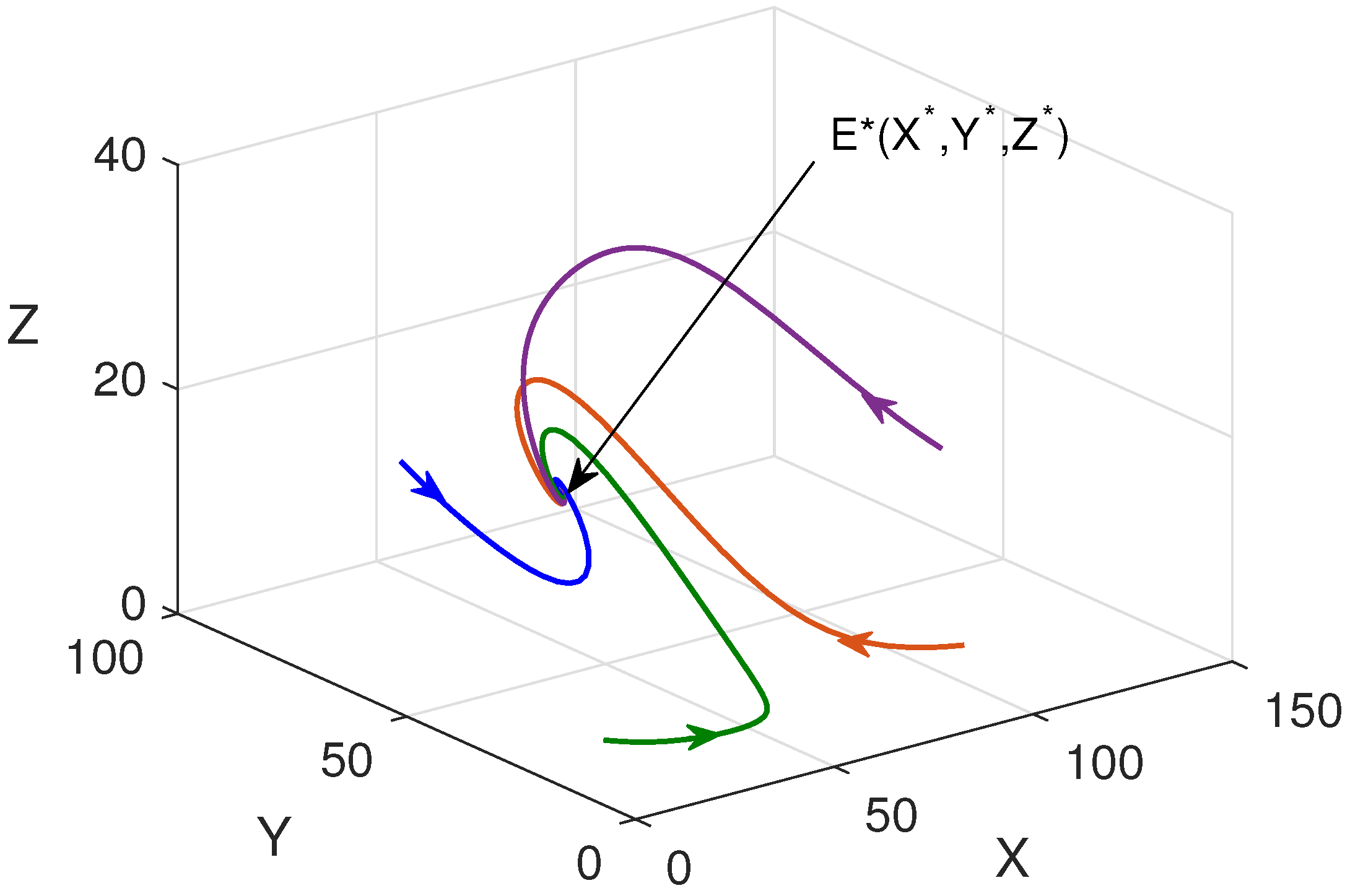
In Figure 6, phase portraits are plotted in different phase planes taking different initial values of the populations. It is observed that all trajectories converge to the same point (interior point, $E^{*}$). This shows that the for the set of parameter values, the system is globally asymptotically stable.

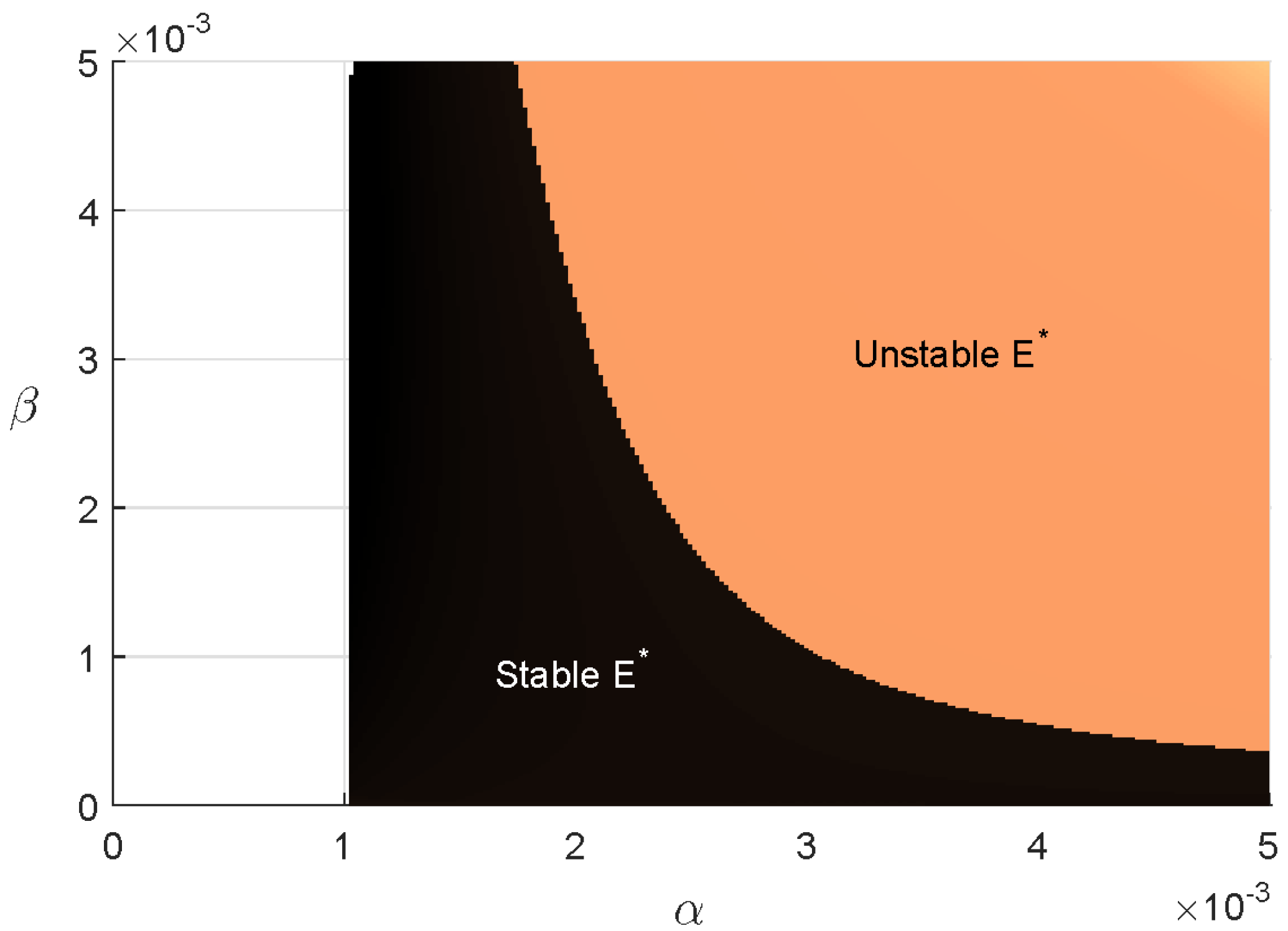
Regions of stability (two parameter bifurcation) of the coexisting equilibrium $E^{*}$ is shown in in $\alpha -\beta$ parameter plane. Figure 7 shows that Region of stability decreases when the parameter values are increased. Note that (15) has two feasible roots. One is always unstable, other one is stable on the green region and unstable in yellow region. This figure also shows that the critical value of $\alpha$ for occurrence of Hopf bifurcation depends on the value of $\beta$.

A Hopf bifurcation occurs when stability of a system shifts due to a change in a parameter values, leading to the emergence of periodic behavior. This phenomenon arises when a pair of complex conjugate eigenvalues cross the imaginary axis of the phase space. Mathematically, it signifies a transition from a stable equilibrium to sustained oscillations. In ecological models, Hopf bifurcation provides insight into how population levels may transition between steady states and cyclical fluctuations as environmental or biological factors vary.

Table 1. Values of the parameters used in numerical simulations [19,22].

Parameters	Definition	Values (Unit)
r	growth rate of plant biomass	0.1 g day−1
$K_1$	maximum plant biomass	50 g m−2
$K_2$	maximum pests	100 (g biomass)−1
$\alpha$	crop consumption rate	0.0025 g pest−1 day−1
$\beta$	contact rate of sterile pest with female pests	0.0005 day−1
$\mu$	mortality rate of pests	0.03 day−1 (g biomass)−1
${\Pi }_u$	Application rate of male sterile pests	0.9 m−2

Table 1. Values of the parameters used in numerical simulations [19,22].

Parameters	Definition	Values (Unit)
r	growth rate of plant biomass	0.1 g day−1
$K_1$	maximum plant biomass	50 g m−2
$K_2$	maximum pests	100 (g biomass)−1
$\alpha$	crop consumption rate	0.0025 g pest−1 day−1
$\beta$	contact rate of sterile pest with female pests	0.0005 day−1
$\mu$	mortality rate of pests	0.03 day−1 (g biomass)−1
${\Pi }_u$	Application rate of male sterile pests	0.9 m−2

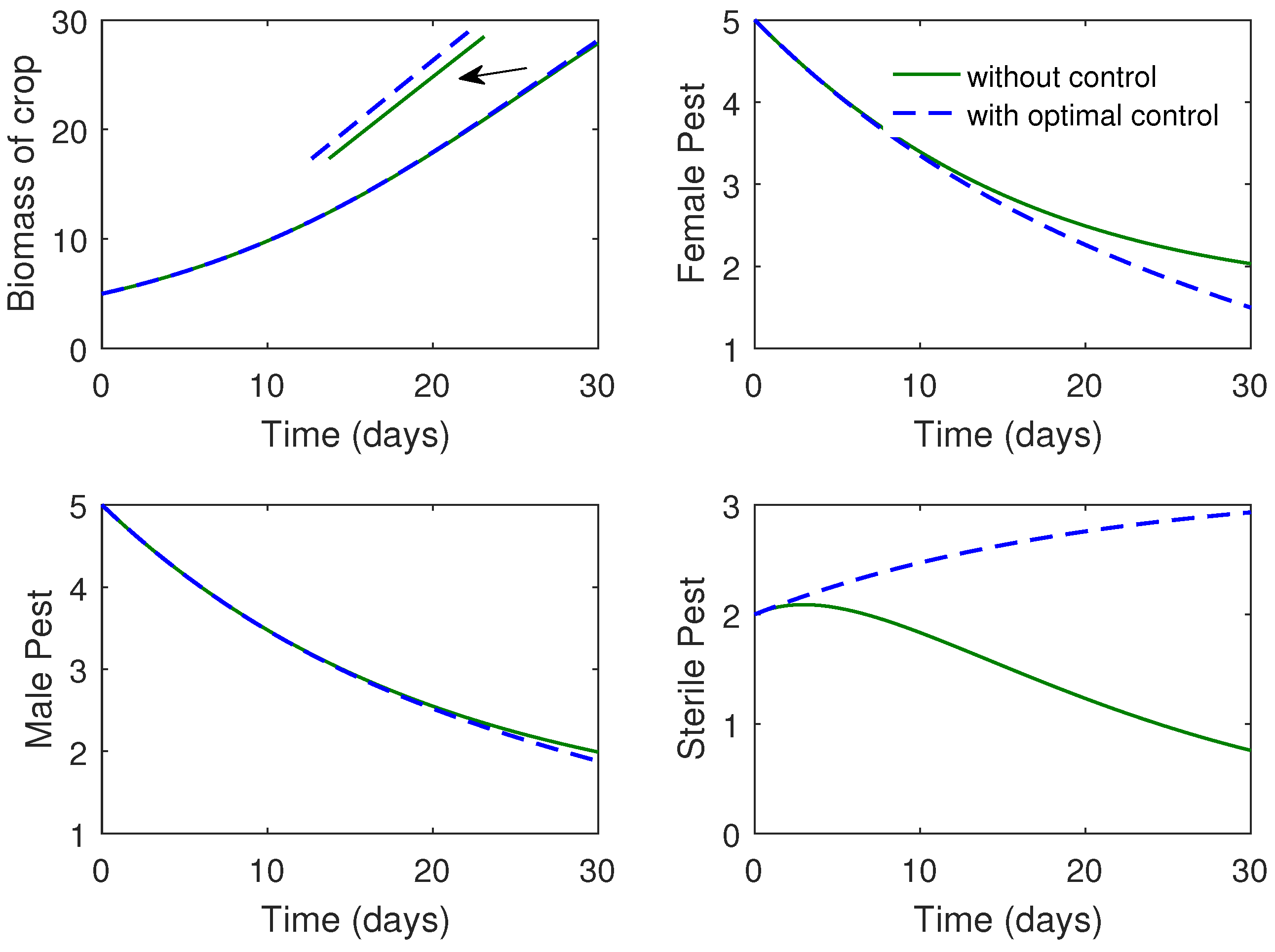
Results from the OCP

The proposed optimal control problem is solved numerically in Matlab using $bvp4c$ solver. Results of the optimal control problem are plotted in Figure 9 and Figure 9. We compare the results between the system with and without control in Figure 9. From Figure 4, we observe that recruitment rate of sterile pests (i.e. ${\Pi }_u$) reduces the total pest population (male and female pests).

Figure 8. PRCCs for the crop biomass, X, with respect to the parameters of the system. Mean values of the parameters are taken from Table 1.

Figure 8. PRCCs for the crop biomass, X, with respect to the parameters of the system. Mean values of the parameters are taken from Table 1.

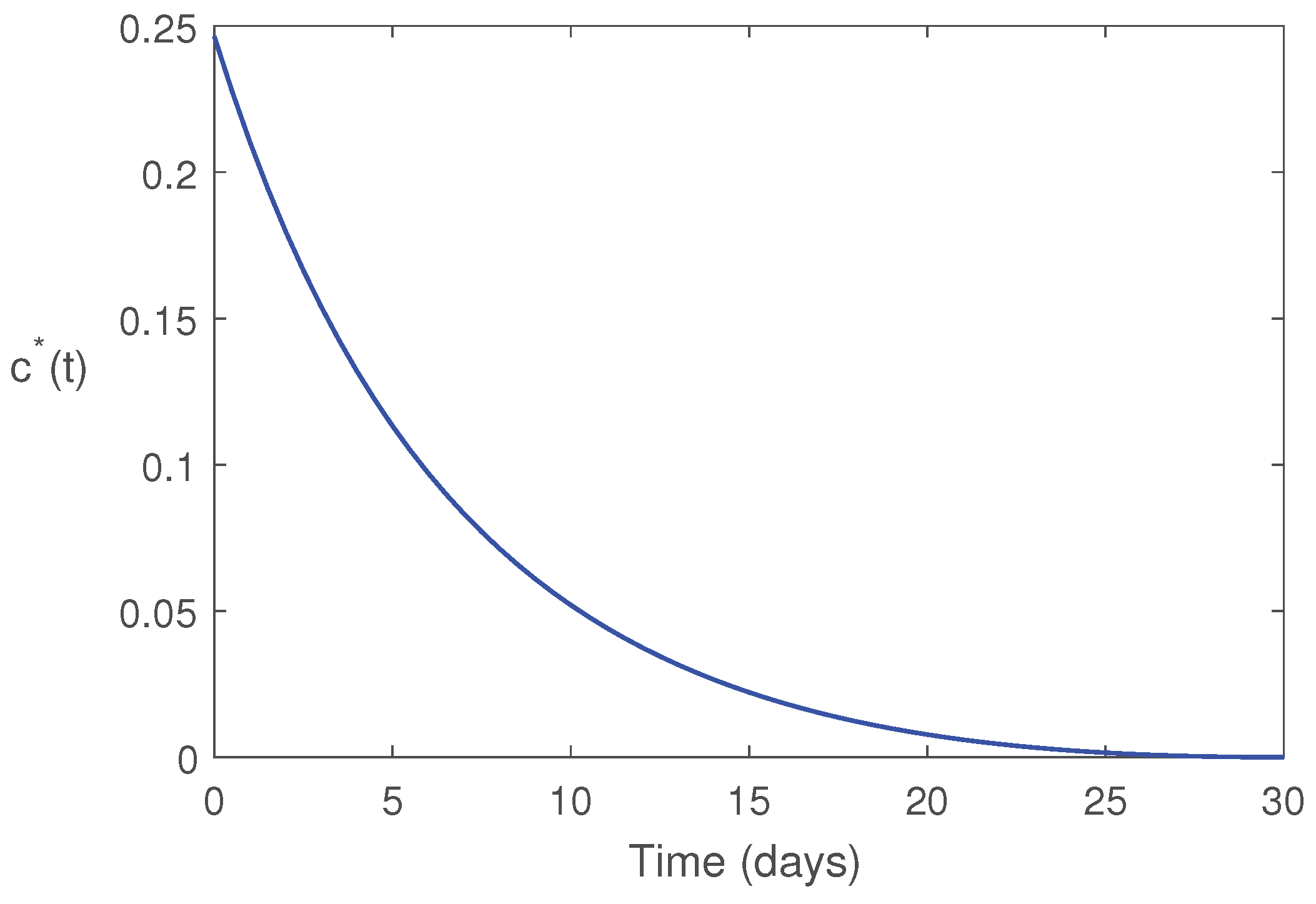
Here, we have shown that optimal use of sterile pests can minimize the pest population with minimum cost (Theorem 4). Optimal profile of the control variable $c^{*}\left(t\right)$ is plotted in Figure 10. This shows that for minimize the cost of pest management, we should follow the trajectory of $c^{*}\left(t\right)$ to release of sterile pests. This figure shows that initially the release rate should be high, then we have to decrease gradually the rate of release as the female pests are decreasing due to this approach.

We can say that constant release is not suitable as cost is higher. But optimal rate of release of sterile pests is significant as it minimizes the costs of pest management.

7. Discussion and Conclusion

The sterile insect technique (SIT) is a biological pest control method that involves the mass release of sterilized insects to reduce the reproductive potential of pest populations. This strategy disrupts pest population growth by preventing fertile matings, thereby suppressing infestations in agricultural systems. In this article, a mathematical model for pest control using SIT is proposed and analysed. the model contains four population: crop biomass, female pest, male pest, and sterile pests.

The proposed model has one equilibrium, the coexisting equilibrium. Stability analysis shows that the point is globally asymptotically stable when the consumption rate $\alpha$ is lower or recruitment rate ${\Pi }_u$ is higher. Hopf bifurcation can be observed when the rate crop consumption by pest, $\alpha$ is higher. The critical value of $\alpha$ depends on the other parameters of the system (Figure 7). The proposed optimal control problem shows that pest can be minimized using sterile male pests into the system when sterile pests are introduced in optimal rate.

SIT represented serves as an effective and eco-friendly method to biologically suppress pest populations. By altering the mating structure within the pest population, SIT indirectly protects the crop biomass from pests. The model helps us explore the long-term behavior of the system, including whether pest populations can be driven to low or stable levels and whether the crop biomass can recover and stabilize.

The proposed model exhibits certain limitations, notably its inability to account for stochastic phenomena such as weather variability and pest immigration, as well as spatial heterogeneity. These factors are essential for accurately representing real-world pest management scenarios.

In conclusion, the sterile insect technology is functional for crop pest management. The results obtained from the proposed mathematical model and from the optimal control problem are significant for real world application.