Submitted:
22 July 2025
Posted:
23 July 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
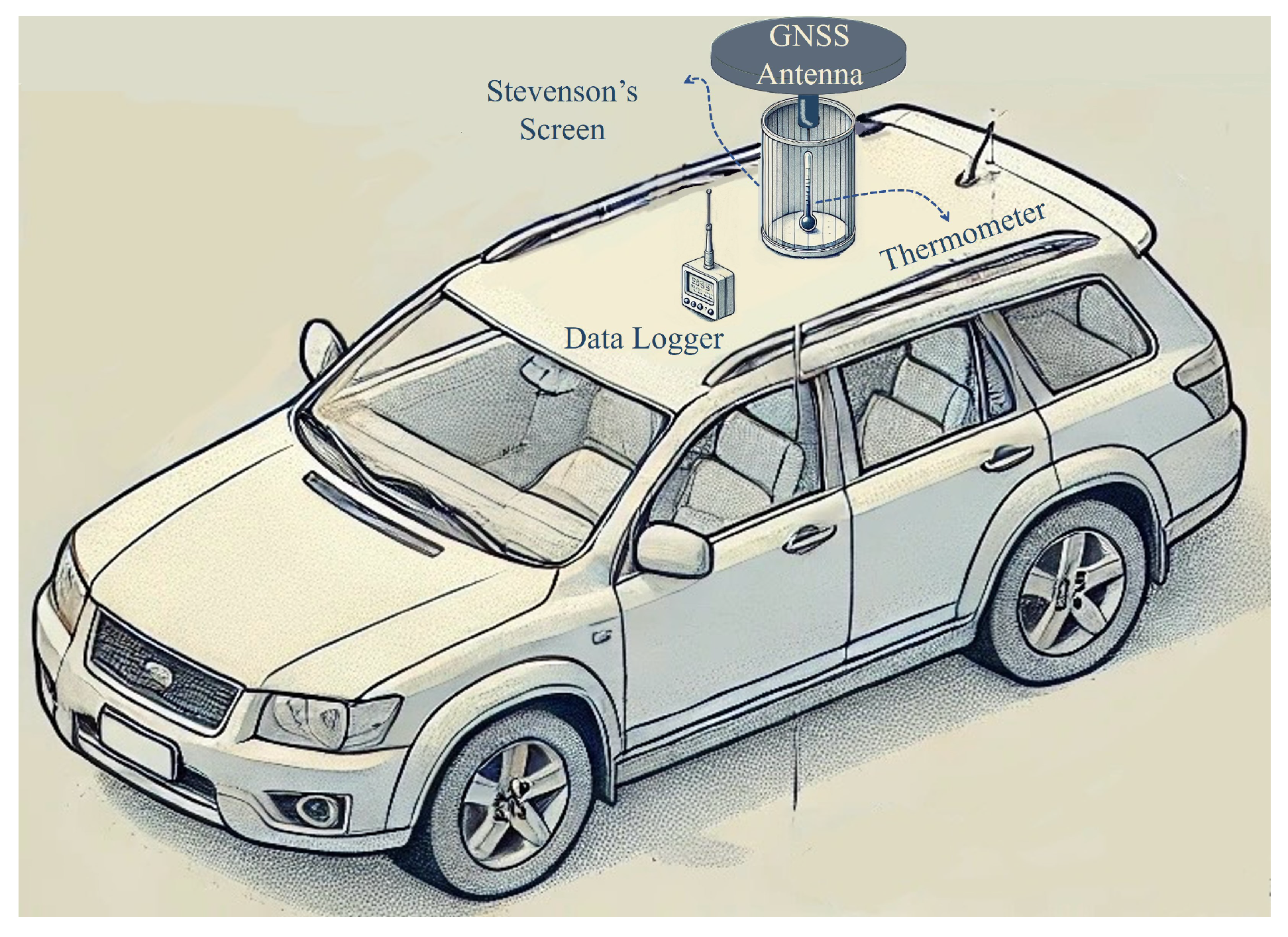
2.1. Data Collection and Sources
2.2. Block Definition and Calculation of Urban Morphology Indicators (UMIs)
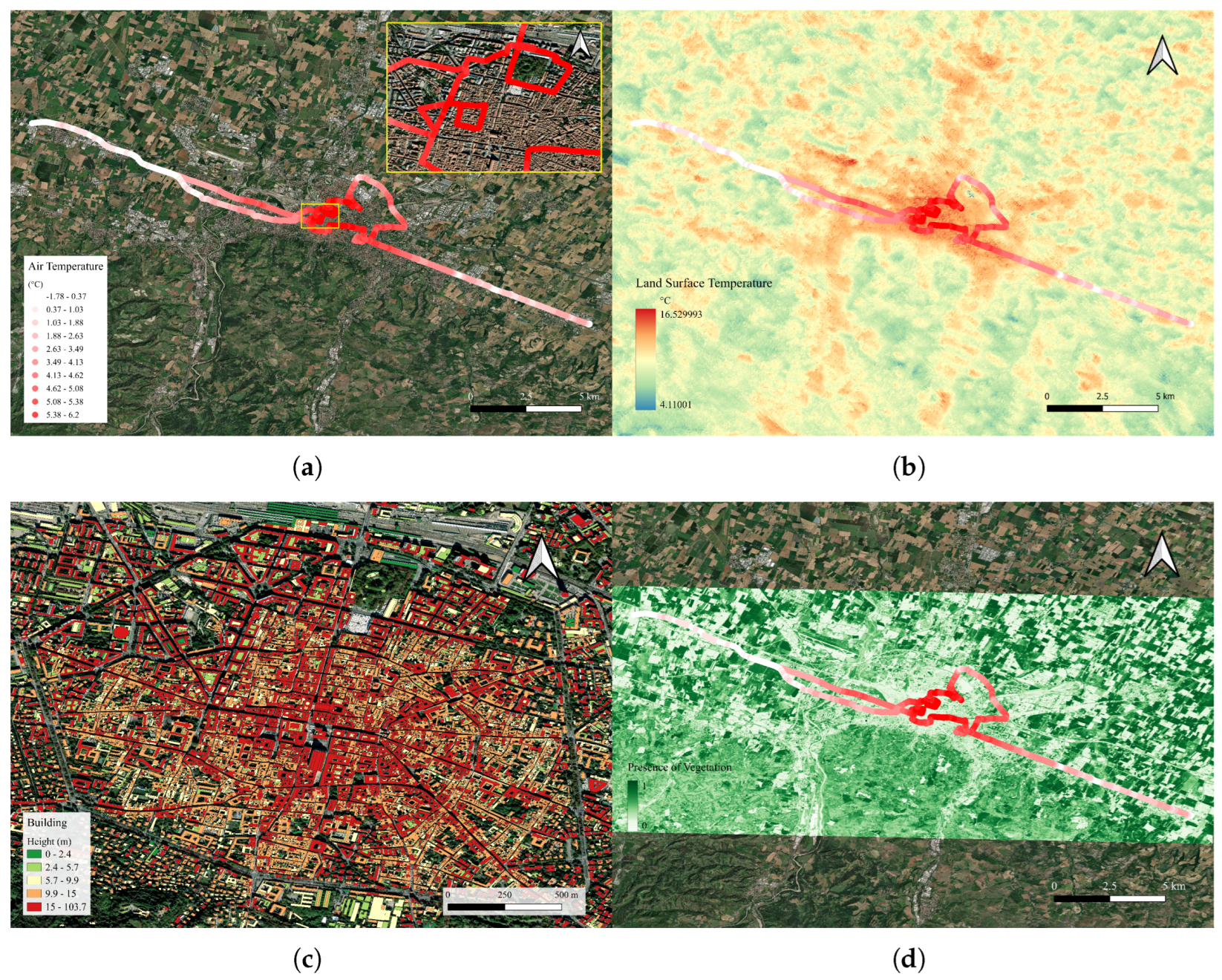
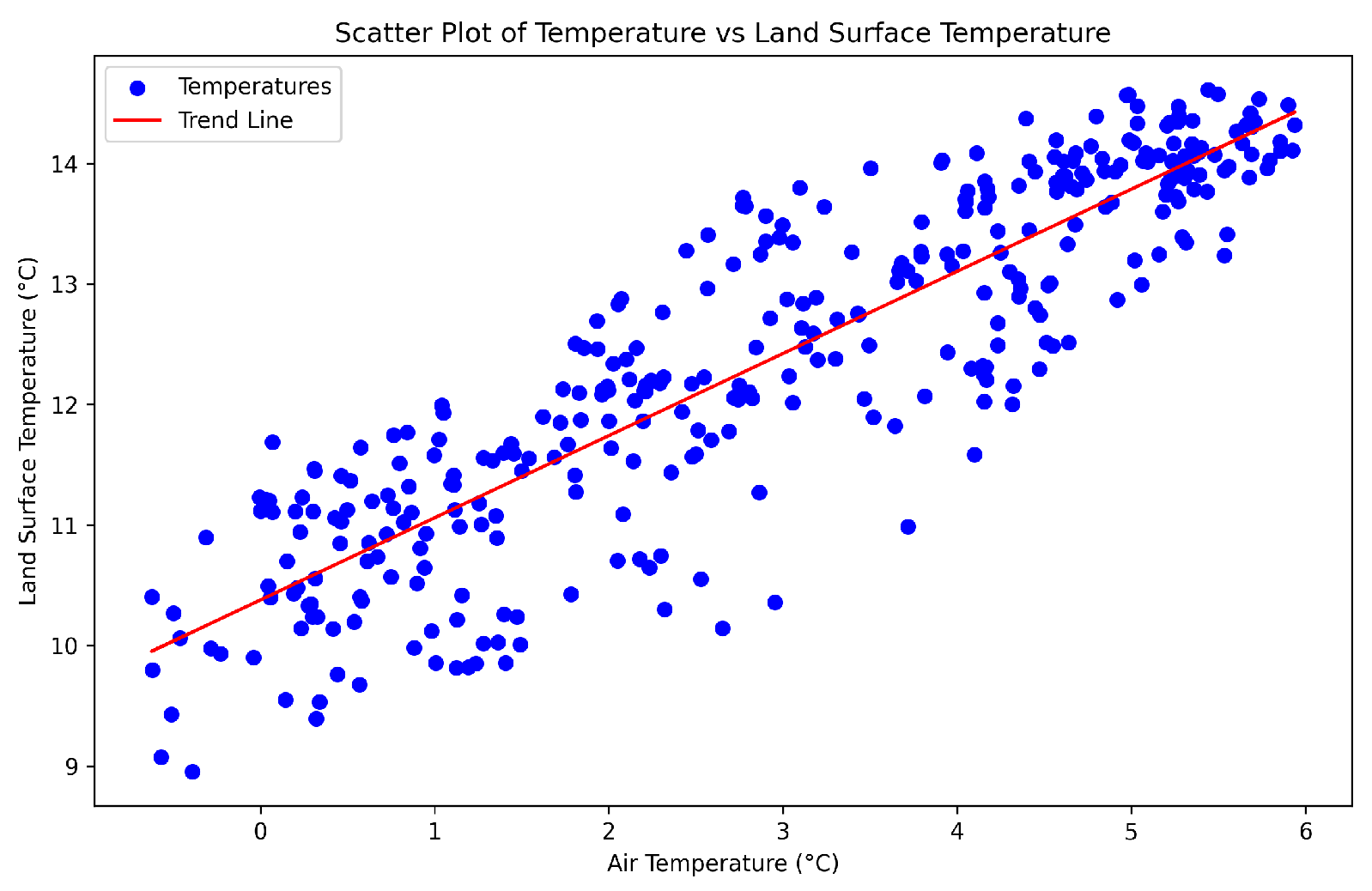
3. Results and Discussion
4. Conclusions
Funding
Abbreviations
| AT | Air Temperature |
| BD | Building Density |
| CUHI | Canopy Urban Heat Island |
| FAR | Floor Area Ratio |
| LCZ | Local Climate Zones |
| LST | Land Surface Temperature |
| MBH | Mean Building Height |
| NDVI | Normalized Difference Vegetation |
| PV | Proportion of Vegetation |
| SFS | Sequential Feature Selection |
| UHI | Urban Heat Island |
| UMIs | Urban Morphology Indicators |
References
- Di Sabatino, D.; Barbano, F.; Brattich, E.; Pulvirenti, B. The multiple-scale nature of urban heat island and its footprint on air quality in real urban environment. Atmosphere 2020, 11, 1186. [Google Scholar] [CrossRef]
- Yang, C.; Yan, F.; Zhang, S. Comparison of land surface and air temperatures for quantifying summer and winter urban heat island in a snow climate city. Journal of environmental management 2020, 265, 110563. [Google Scholar] [CrossRef]
- Rodríguez, L.R.; Ramos, J.S.; Domínguez, S.Á. Simplifying the process to perform air temperature and UHI measurements at large scales: Design of a new APP and low-cost Arduino device. Sustainable Cities and Society 2023, 95, 104614. [Google Scholar] [CrossRef]
- Venter, Z.S.; Chakraborty, T.; Lee, X. Crowdsourced air temperatures contrast satellite measures of the urban heat island and its mechanisms. Science Advances 2021, 7, eabb9569. [Google Scholar] [CrossRef]
- Gawuc, L.; Jefimow, M.; Szymankiewicz, K.; Kuchcik, M.; Sattari, A.; Struzewska, J. Statistical modeling of urban heat island intensity in warsaw, poland using simultaneous air and surface temperature observations. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2020, 13, 2716–2728. [Google Scholar] [CrossRef]
- Li, L.; Zha, Y.; Wang, R. Relationship of surface urban heat island with air temperature and precipitation in global large cities. IEcological Indicators 2020, 117, 106683. [Google Scholar] [CrossRef]
- Mendez-Astudillo, J.; Lau, L.; Tang, Y.-T.; Moore, T. Determination of air urban heat island parameters with high-precision GPS data. Atmosphere 2022, 13, 417. [Google Scholar] [CrossRef]
- Almeida, C.R.; de Teodoro, A.C.; Gonçalves, A. Study of the urban heat island (UHI) using remote sensing data/techniques: A systematic review. Environments 2021, 8, 105. [Google Scholar] [CrossRef]
- Güller, C.; Toy, S. The Impacts of Urban Morphology on Urban Heat Islands in Housing Areas: The Case of Erzurum, Turkey. Sustainability 2024, 16, 791. [Google Scholar] [CrossRef]
- Equere, V.; Mirzaei, P.A. : Riffat, S. Definition of a new morphological parameter to improve prediction of urban heat island. Sustainable Cities and Society 2020, 56, 102021. [Google Scholar] [CrossRef]
- Nardino, M.; Cremonini, L.; Crisci, A.; Georgiadis, T.; Guerri, G.; Morabito, M.; Fiorillo, E. Mapping daytime thermal patterns of Bologna municipality (Italy) during a heatwave: A new methodology for cities adaptation to global climate change. Urban Climate 2022, 46, 101317. [Google Scholar] [CrossRef]
- Nardino, M.; Cremonini, L.; Georgiadis, T.; Mandanici, E.; Bitelli, G. Microclimate classification of Bologna (Italy) as a support tool for urban services and regeneration. International Journal of Environmental Research and Public Health 2021, 18, 4898. [Google Scholar] [CrossRef]
- Zeynali, R.; Bitelli, G.; Mandanici, E. Mobile data acquisition and processing in support of an urban heat island study. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2023, 48, 563–569. [Google Scholar] [CrossRef]
- Zeynali, R.; Mandanici, E.; Sohrabi, A.H.; Trevisiol, F.; Bitelli, G. GIS-Based Urban Heat Island Mapping and Analysis: Experiences in the City of Bologna. Presented at the 2024 IEEE International Workshop on Metrology for Living Environment (MetroLivEnv), IEEE 2024, 230–234.
- Liu, B.; Guo, X.; Jiang, J. How urban morphology relates to the urban heat island effect: A multi-indicator study. Sustainability 2023, 15, 10787. [Google Scholar] [CrossRef]
- Cafaro, R.; Cardone, B.; D’Ambrosio, V.; Di Martino, F.; Miraglia, V. A New GIS-Based Framework to Detect Urban Heat Islands and Its Application on the City of Naples (Italy). Land 2024, 13(8), 1253. [Google Scholar] [CrossRef]
- Lin, A.; Wu, H.; Luo, W.; Fan, K.; Liu, H. How does urban heat island differ across urban functional zones? Insights from 2D/3D urban morphology using geospatial big data. Urban Climate 2024, 53, 101787. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, Y. Urban morphological indicators of urban heat and moisture islands under various sky conditions in a humid subtropical region. Building and Environment 2022, 214, 108906. [Google Scholar] [CrossRef]
- Yang, J.; Ren, J.; Sun, D.; Xiao, X.; Xia, J.C.; Jin, C.; Li, X. Understanding land surface temperature impact factors based on local climate zones. Sustainable Cities and Society 2021, 69, 102818. [Google Scholar] [CrossRef]
- AρρEEARS. Available online: https://appeears.earthdatacloud.nasa.gov/task/area (accessed on 13 November 2024).
- Fisher, J.B.; Lee, B. : Purdy, A.J.; Halverson, G.H.; Dohlen, M.B.; Cawse-Nicholson, K.; Wang, A.; Anderson, R.G.; Aragon, B.; Arain, M.A. ECOSTRESS: NASA’s next generation mission to measure evapotranspiration from the international space station. Water Resources Research 2020, 56, e2019WR026058. [Google Scholar] [CrossRef]
- Hulley, G.C.; Göttsche, F.M.; Rivera, G.; Hook, S.J.; Freepartner, R.J.; Martin, M.A.; Cawse-Nicholson, K.; Johnson, W.R. Validation and quality assessment of the ECOSTRESS level-2 land surface temperature and emissivity product. IEEE Transactions on Geoscience and Remote Sensing 2021, 60, 1–23. [Google Scholar] [CrossRef]
- CARTA TECNICA COMUNALE - Edifici volumetrici. Available online: https://opendata.comune.bologna.it/ (accessed on 13 November 2024).
- Copernicus Data Space Ecosystem. Available online: https://browser.dataspace.copernicus.eu/ (accessed on 13 November 2024).
- Schober, P.; Boer, C.; Schwarte, L.A. Schober, P.; Boer, C.; Schwarte, L.A. Correlation coefficients: appropriate use and interpretation. Anesthesia & analgesia 2018, 126(5), 1763–1768.
- Ogunleye, L.I.; Oyejola, B.A.; Obisesan, K.O. Comparison of some common tests for normality. International Journal of Probability and Statistics 2018, 7, 130–137. [Google Scholar]
- Hauke, J.; Kossowski, T. Comparison of values of Pearson’s and Spearman’s correlation coefficients on the same sets of data. Quaestiones geographicae 2011, 30(2), 87–93. [Google Scholar] [CrossRef]
- Brophy, A.L. An algorithm and program for calculation of Kendall’s rank correlation coefficient. Behavior Research Methods, Instruments, and Computers 1986, 18(1), 45–46.
- Brown, B.L.; Hendrix, S.B. Partial correlation coefficients. Encyclopedia of statistics in behavioral science 2005. [Google Scholar]
- Rückstieß, T.; Osendorfer, C.; Van Der Smagt, P. Sequential feature selection for classification. Presented at the Australasian joint conference on artificial intelligence, Springer 2011, 132–141.
- Sedgwick, P. Spearman’s rank correlation coefficient. Bmj 2014, 349. [Google Scholar] [CrossRef]
- Hu, Y.; Hou, M.; Jia, G.; Zhao, C.; Zhen, X.; Xu, Y. Comparison of surface and canopy urban heat islands within megacities of eastern China. SPRS Journal of Photogrammetry and Remote Sensing 2019, 156, 160–168. [Google Scholar] [CrossRef]
- Schwarz, N.; Schlink, U.; Franck, U.; Großmann, K. Relationship of land surface and air temperatures and its implications for quantifying urban heat island indicators—An application for the city of Leipzig (Germany). Ecological indicators 2012, 18, 693–704. [Google Scholar] [CrossRef]
- Sheng, L.; Tang, X.; You, H.; Gu, Q.; Hu, H. Comparison of the urban heat island intensity quantified by using air temperature and Landsat land surface temperature in Hangzhou, China. Ecological indicators 2017, 72, 738–746. [Google Scholar] [CrossRef]
- Weng, Q.; Lu, D.; Schubring, J. Estimation of land surface temperature–vegetation abundance relationship for urban heat island studies. Remote sensing of Environment 2004, 89, 467–483. [Google Scholar] [CrossRef]
- Zinzi, M.; Agnoli, S. Cool and green roofs. An energy and comfort comparison between passive cooling and mitigation urban heat island techniques for residential buildings in the Mediterranean region. Energy and buildings 2012, 55, 66–76. [Google Scholar] [CrossRef]
- Yuan, F.; Bauer, M.E. Comparison of impervious surface area and normalized difference vegetation index as indicators of surface urban heat island effects in Landsat imagery. Remote Sensing of environment 2007, 106, 375–386. [Google Scholar] [CrossRef]
- Oke, T.R. The energetic basis of the urban heat island. Quarterly journal of the royal meteorological society 1982, 108, 1–24. [Google Scholar] [CrossRef]
- Li, D.; Bou-Zeid, E.; Oppenheimer, M. The effectiveness of cool and green roofs as urban heat island mitigation strategies. Environmental Research Letters 2014, 9, 14. [Google Scholar] [CrossRef]
- Myint, S.W.; Wentz, E.A.; Brazel, A.J.; Quattrochi, D.A. The impact of distinct anthropogenic and vegetation features on urban warming. Landscape ecology 2013, 28, 959–975. [Google Scholar] [CrossRef]
- Schwarz, N.; Lautenbach, S.; Seppelt, R. CExploring indicators for quantifying surface urban heat islands of European cities with MODIS land surface temperatures. Remote Sensing of Environment 2011, 115, 3175–3186. [Google Scholar] [CrossRef]
- Stewart, I.D.; Oke, T.R. Local climate zones for urban temperature studies. Bulletin of the American Meteorological Society 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
- Zhou, B.; Rybski, D.; Kropp, J.P. The role of city size and urban form in the surface urban heat island. Scientific reports 2017, 7, 4791. [Google Scholar] [CrossRef]
- Vavassori, A.; Oxoli, D.; Venuti, G.; Brovelli, M.A.; de Cumis, M.S.; Sacco, P.; Tapete, D. A combined Remote Sensing and GIS-based method for Local Climate Zone mapping using PRISMA and Sentinel-2 imagery. International Journal of Applied Earth Observation and Geoinformation 2024, 131, 1103944. [Google Scholar] [CrossRef]
- Jurato, J.; Galia, T. System and method to calculate the temperature of an external environment air corrected from the radiative error, as well as sensor device usable in such system. Iotopon Srl. U.S. Patent 2022, 11,525,745.
| MBH | BD | FAR | PV | LST | AT | |
|---|---|---|---|---|---|---|
| MBH | 1.00 | 0.89 | 0.81 | -0.55 | 0.77 | 0.76 |
| BD | 0.89 | 1.00 | 0.97 | -0.68 | 0.84 | 0.79 |
| FAR | 0.81 | 0.97 | 1.00 | -0.68 | 0.79 | 0.73 |
| PV | -0.55 | -0.68 | -0.68 | 1.00 | -0.76 | -0.70 |
| LST | 0.77 | 0.84 | 0.79 | -0.76 | 1.00 | 0.89 |
| AT | 0.76 | 0.79 | 0.73 | -0.70 | 0.89 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





