A Novel Explicit Formula for a Product Representation of a Chebyshev-Type Function with Zeros at Prime Powers

1. Introduction

The enigmatic distribution of prime numbers remains one of the most captivating challenges in mathematics. The groundbreaking work of Bernhard Riemann [1] established an intrinsic connection between the counting of prime numbers and the properties of the Riemann zeta function, $\zeta \left(s\right)$, particularly the location of its non-trivial zeros in the complex plane. The celebrated Riemann Hypothesis (RH) posits that all non-trivial zeros of $\zeta \left(s\right)$ lie on the critical line with real part $1/2$, a conjecture whose resolution would have profound implications across various fields of mathematics.

Central to the study of prime distribution are explicit formulas, which establish precise relationships between sums over prime numbers and sums over the non-trivial zeros of $\zeta \left(s\right)$. The most famous among these is the Riemann-von Mangoldt formula, rigorously proved by Hans von Mangoldt [2], which relates the sum of the Von Mangoldt function (related to the Chebyshev functions) to the zeta zeros:

$$\psi \left(x\right)=x-\sum _{\rho }{\displaystyle \frac{x^{\rho }}{\rho }}-ln\left(2\pi \right)-{\displaystyle \frac{1}{2}}ln(1-x^{-2})\mathrm{for}\mathrm{non}-\mathrm{integer}x$$

where the sum is over the non-trivial zeros $\rho =\beta +i\gamma$ of $\zeta \left(s\right)$ [3]. This formula, and variants thereof, are indispensable for understanding and quantifying the statistical behavior of primes.

The second Chebyshev function, $\psi \left(x\right)$, defined as ${\sum }_{n\le x}\Lambda \left(n\right)$, where $\Lambda \left(n\right)$ is the Von Mangoldt function, serves as a cornerstone in this analytical framework. While various forms of explicit formulas exist, the pursuit of alternative analytical representations can often reveal hidden structures, expose new perspectives, and potentially pave the way for novel theoretical insights or computational methodologies. Notable contributions to explicit formulas include those by Hardy and Littlewood [4], Selberg [5], and Weil [6], each offering different forms or extending the theory to other arithmetic functions or L-functions.

In this paper, we embark on a rigorous derivation of a novel product representation for a function, denoted $\widehat{\Psi }\left(z\right)$, which arises from a sequence of transformations applied to the second Chebyshev function. Our primary contribution is the establishment of an identity that inherently demonstrates a duality: one side of the identity represents a product whose zeros are directly determined by prime powers (specifically, at $z=\pm klnp$), while the other side is an exponential sum explicitly depending on the imaginary parts of the non-trivial zeros of the Riemann zeta function. This derivation leverages fundamental tools from complex analysis, including Laplace transforms, Cauchy’s Argument Principle, differentiation of generalized functions, and integral calculus.

This new formulation of a Chebyshev-type function offers a unique analytical lens into the long-standing prime-zero duality. It provides a compact and potentially computationally tractable framework for analyzing prime number distribution, opening avenues for deeper analytical investigations into the Riemann Hypothesis, and inspiring the development of novel numerical algorithms for prime counting or zero localization. The structure of this paper is as follows: Section 2 provides necessary preliminaries. Section 3 details the step-by-step derivation of $\widehat{\Psi }\left(z\right)$. Section 4 discusses the properties and implications of the derived function, and Section 5 concludes the paper.

2. Preliminaries and Background

The second Chebyshev function, $\psi \left(x\right)$, sums the Von Mangoldt function $\Lambda \left(n\right)$, defined as $lnp$ if $n=p^k$ for a prime p and integer $k\ge 1$, and 0 otherwise. It can be conveniently expressed using the Heaviside step function $H\left(t\right)$ (where $H\left(t\right)=1$ for $t\ge 0$ and $H\left(t\right)=0$ for $t<0$):

$$\psi \left(x\right):=\sum _{k\in \mathbb{N}}\sum _{p}H(lnx-klnp)lnp.$$

(1)

The Riemann zeta function, $\zeta \left(s\right)$, initially defined for $\Re \left(s\right)>1$ by ${\sum }_{n=1}^{\infty }{n}^{-s}$, can be analytically continued to the entire complex plane, having a simple pole at $s=1$. Its non-trivial zeros are the focus of the Riemann Hypothesis. For analytical convenience, the completed Riemann zeta function, $\xi \left(s\right)$, is defined as

$$\xi \left(s\right)={\displaystyle \frac{1}{2}}s(s-1){\pi }^{-s/2}\Gamma (s/2)\zeta \left(s\right).$$

The function $\xi \left(s\right)$ is an entire function, and its zeros correspond precisely to the non-trivial zeros of $\zeta \left(s\right)$.

Cauchy’s Argument Principle is a powerful tool in complex analysis for counting zeros and poles of a meromorphic function. For an entire function $\xi \left(s\right)$ and a simple closed contour $\mathfrak{D}$ that does not pass through any zeros of $\xi \left(s\right)$, the principle states that:

$${\oint }_{\mathfrak{D}}{\displaystyle \frac{{\xi }^{\prime }\left(s\right)}{\xi \left(s\right)}}ds=2\pi i\times \left(\mathrm{number}\mathrm{of}\mathrm{zeros}\mathrm{of}\xi \left(s\right)\mathrm{inside}\mathrm{the}\mathrm{contour}\right).$$

Finally, the Laplace transform $\mathcal{L}\left\{f\left(u\right)\right\}\left(z\right)={\int }_0^{\infty }f\left(u\right)e^{-zu}du$ plays a crucial role in transforming sums over functions into forms amenable to analytical manipulation.

3. Derivation of the $\mathbf{z}$-Domain Chebyshev Function $\widehat{\Psi }\left(\mathbf{z}\right)$

This section details the step-by-step derivation of the novel z-domain Chebyshev function $\widehat{\Psi }\left(z\right)$, starting from the classical Chebyshev function and employing a sequence of analytical transformations.

3.1. Laplace Transform of $\psi \left(x\right)$

We begin by taking the Laplace transform of the second Chebyshev function $\psi \left(x\right)$, defined in (1). We define its Laplace transform as

$$\Psi \left(s\right):=\mathcal{L}\left\{\psi \left(e^u\right)\right\}.$$

(2)

Using the linearity of the Laplace transform and the transform of a Heaviside step function (specifically, $\mathcal{L}\left\{H(u-a)\right\}\left(s\right)={\displaystyle \frac{e^{-sa}}{s}}$), we evaluate the transform of each term:

$$\mathcal{L}\left\{\psi \left(e^u\right)\right\}=\sum _{k\in \mathbb{N}}\sum _p\mathcal{L}\left\{H(u-klnp)\right\}lnp=\sum _{k\in \mathbb{N}}{\displaystyle \frac{1}{s}}\sum _{p}lnp{e}^{-kslnp}.$$

(3)

This leads to the relationship between $\Psi \left(s\right)$ and a sum over prime powers:

$$s\Psi \left(s\right)=\sum _{k\in \mathbb{N}}\sum _{p}lnp{e}^{-kslnp},\Re s>1.$$

(4)

This sum is a well-known Dirichlet series, which is also precisely equal to the negative logarithmic derivative of the Riemann zeta function [7]. Thus, we identify the relationship:

$${\displaystyle \frac{{\zeta }^{\prime }\left(s\right)}{\zeta \left(s\right)}}=-\sum _{k\in \mathbb{N}}\sum _{p}lnp{e}^{-kslnp}=-s\Psi \left(s\right).$$

(5)

The s-domain function $\Psi \left(s\right)$ has poles at $s=0$ (from $1/s$), $s=1$, $s=-2m$ (from the pole of ${\zeta }^{\prime }\left(s\right)/\zeta \left(s\right)$), and at the non-trivial zeros of $\zeta \left(s\right)$.

On the basis of Weierstrass’s factorization theorem and the definition for the Gamma function due to Weierstrass, we have the product form of $\zeta \left(s\right)$ in terms of its zeros, as:

$$\zeta \left(s\right)={\displaystyle \frac{{\pi }^{\frac{s}{2}}{e}^{\gamma \frac{s}{2}}}{2(s-1)}}\prod _m\left(1-{\displaystyle \frac{s}{s_m}}\right)\left(1-{\displaystyle \frac{s}{{\overline{s}}_m}}\right)\prod _{m=1}^{\infty }\left(1+{\displaystyle \frac{s}{2m}}\right)e^{-{\displaystyle \frac{s}{2m}}}.$$

(6)

Taking the logs and differentiating, we obtain the Mittag-Leffler’s expansion, as:

$${\displaystyle \frac{{\zeta }^{\prime }\left(s\right)}{\zeta s)}}=\frac{1}{2}ln\pi +\frac{1}{2}\gamma -{\displaystyle \frac{1}{(s-1)}}+\sum _{m=1}^{\infty }{\displaystyle \frac{1}{(s-s_m)}}+{\displaystyle \frac{1}{(s-{\overline{s}}_m)}}+\sum _{m=1}^{\infty }{\displaystyle \frac{1}{s+2m}}-{\displaystyle \frac{1}{2m}}.$$

(7)

Thus,

$$\begin{array}{cc}\hfill -\sum _{k\in \mathbb{N}}\sum _{p}lnp\left(p^{-sk}\right)=& \frac{1}{2}ln\pi +\frac{1}{2}\gamma -{\displaystyle \frac{1}{(s-1)}}\hfill \\ \hfill & +\sum _{m=1}^{\infty }{\displaystyle \frac{1}{(s-s_m)}}+{\displaystyle \frac{1}{(s-{\overline{s}}_m)}}+\sum _{m=1}^{\infty }{\displaystyle \frac{1}{s+2m}}-{\displaystyle \frac{1}{2m}}.\hfill \end{array}$$

(8)

Taking the inverse Laplace transform, we obtain:

$$-\sum _{k\in \mathbb{N}}\sum _{p}lnp\delta (u-klnp)=\delta \left(u\right)(\frac{1}{2}ln\pi +\frac{1}{2}\gamma )-e^u+\sum _{m=1}^{\infty }{e}^{s_{m}u}+e^{{\overline{s}}_{m}u}+\sum _{m=1}^{\infty }{e}^{-2mu}-{\displaystyle \frac{\delta \left(u\right)}{2m}}.$$

(9)

For $u=0$ the above equation diverge. However, for positive $u>0$, we have

$$\sum _{m=1}^{\infty }{e}^{-2mu}={\displaystyle \frac{1}{e^{2u}-1}},$$

and

$$\delta \left(u\right)=0.$$

Thus, we have

$$\sum _{k\in \mathbb{N}}\sum _{p}lnp\delta (u-klnp)=e^u-{\displaystyle \frac{1}{e^{2u}-1}}-\sum _{m=1}^{\infty }{e}^{s_{m}u}+e^{{\overline{s}}_{m}u},u>0.$$

(10)

Equation (10) is the positive part of the explicit formulas established by Weil [6]. The derivation above provides a powerful illustration of the deep connection between prime numbers and the zeros of the Riemann zeta function. The transformation technique can be summarized in four conceptual steps.

• Encoding: The raw, discrete distribution of prime powers is first encoded as a series of spikes (delta functions) on a logarithmic scale.
• Transformation: The Laplace transform acts as a bridge, converting this discrete distribution into a single analytic function in the complex plane, as: $-{\zeta }^{\prime }\left(s\right)/\zeta \left(s\right)$.
• Spectral Decomposition: In this new domain, complex analysis allows this same function to be re-expressed not in terms of primes, but as a sum over its fundamental poles, which are precisely determined by the zeros of $\zeta \left(s\right)$.
• Inverse Transform: The final inverse Laplace transform translates this "spectral data" of the zeros back into the original domain, revealing that the prime distribution is composed of a main growth term (from the pole at $s=1$) plus oscillatory "correction" terms dictated by the non-trivial zeros.

This process provides an explicit duality, demonstrating that the distribution of prime numbers is governed by the harmonic structure of the zeros of the zeta function.

The novelty of this approach lies not in discovering a new mathematical truth, but in a powerful translation that makes a classic result conceptually clear and accessible. While the explicit formula is traditionally derived using the abstract machinery of complex contour integration, this methodology reframes the entire problem in the language of signal processing. By treating the prime distribution as a "signal" and applying the Laplace transform, the derivation becomes a familiar exercise in systems theory. This conceptual shift demystifies the process, revealing the zeros of the zeta function to be the fundamental "resonant frequencies" that govern the seemingly chaotic structure of the primes. The true innovation is therefore explanatory: it recasts an obscure theorem into an intuitive spectral decomposition, bridging the gap between pure number theory and the world of applied science and engineering.

3.2. Explicit Formula from Contour Integration

We invoke Cauchy’s Argument Principle to relate the counting function for non-trivial zeros to a contour integral involving the completed Riemann zeta function $\xi \left(s\right)$. Let $N\left(\tau \right)={\sum }_{m}H(\tau -t_m)$ denote the number of non-trivial zeros of $\zeta \left(s\right)$ with positive imaginary parts $t_m\le \tau$. The closed contour $\mathfrak{D}$ is chosen to encompass the critical strip $[0\le \Re (s)\le 1]$ from imaginary part $-\tau$ to $\tau$. The integral of the logarithmic derivative of $\xi \left(s\right)$ over this contour counts all zeros within $\mathfrak{D}$. Given the symmetry of non-trivial zeros about the real axis, the total number of zeros enclosed by $\mathfrak{D}$ is $2N\left(\tau \right)$. Hence,

$$2\times 2\pi i\sum _{m}H(\tau -t_m)={\oint }_{\mathfrak{D}}\left[{\displaystyle \frac{{\zeta }^{\prime }\left(s\right)}{\zeta \left(s\right)}}+{\displaystyle \frac{1}{(s-1)}}+{\displaystyle \frac{1}{s}}+{\displaystyle \frac{{\Gamma }^{\prime }\left(\frac{s}{2}\right)}{2\Gamma \left(\frac{s}{2}\right)}}-{\displaystyle \frac{1}{2}}ln\pi \right]\mathrm{d}s.$$

(11)

The integrand on the right-hand side (RHS) is exactly ${\displaystyle \frac{{\xi }^{\prime }\left(s\right)}{\xi \left(s\right)}}$. By Cauchy’s Argument Principle, the RHS evaluates to $2\pi i\times \left(2N\right(\tau \left)\right)=4\pi iN\left(\tau \right)$, which is consistent with the left-hand side (LHS).

The number of zeros $N\left(\tau \right)$ is also famously related to the argument of the $\xi$-function evaluated on the critical line. Specifically, by applying the Argument Principle over a contour enclosing the critical strip and utilizing the symmetry properties of $\xi \left(s\right)$, one derives the standard result (see, e.g., Titchmarsh [3]):

$$\pi N\left(\tau \right)=arg\xi (\frac{1}{2}+i\tau ),$$

where the argument is defined by continuous variation from a reference point on the real axis (e.g., $s=2$) where $arg\xi \left(2\right)=0$. This formula holds precisely if $\tau$ is not the ordinate of a zero. The term $arg\xi (\frac{1}{2}+i\tau )$ is the imaginary part of $ln\xi (\frac{1}{2}+i\tau )$. Since $\xi \left(s\right)$ is real for real s, we have $\xi (\frac{1}{2}-i\tau )=\overline{\xi (\frac{1}{2}+i\tau )}$. Consequently, the difference of logarithms becomes:

$$\begin{array}{cc}\hfill ln\xi (\frac{1}{2}+i\tau )-ln\xi (\frac{1}{2}-i\tau )=& ln\xi (\frac{1}{2}+i\tau )-\overline{ln\xi (\frac{1}{2}+i\tau )}\hfill \\ \hfill =& 2iIm[ln\xi (\frac{1}{2}+i\tau )]=2iarg\xi (\frac{1}{2}+i\tau ).\hfill \end{array}$$

(12)

Therefore, we can express the counting function as:

$$\frac{1}{2\pi i}\left[ln\xi \left(\frac{1}{2}+i\tau \right)-ln\xi \left(\frac{1}{2}-i\tau \right)\right].$$

(13)

We now evaluate the term on the RHS using the definition of $ln\xi \left(s\right)$:

$$ln\xi \left(s\right)=ln\frac{1}{2}+lns+ln(s-1)-\frac{s}{2}ln\pi +ln\Gamma \left(\frac{s}{2}\right)+ln\zeta \left(s\right).$$

Evaluating this difference at $s=\frac{1}{2}+i\tau$ and $s=\frac{1}{2}-i\tau$, we have:

$$\begin{array}{cc}\hfill 2\pi i\sum _{m}H(\tau -t_m)=& [ln\zeta (\frac{1}{2}+i\tau )-ln\zeta (\frac{1}{2}-i\tau )]\hfill \\ \hfill & +[ln\Gamma (\frac{1}{4}+i\frac{\tau }{2})-ln\Gamma (\frac{1}{4}-i\frac{\tau }{2})]\hfill \\ \hfill & +[ln(\frac{1}{2}+i\tau -1)-ln(\frac{1}{2}-i\tau -1)]\hfill \\ \hfill & +[ln(\frac{1}{2}+i\tau )-ln(\frac{1}{2}-i\tau )]\hfill \\ \hfill & -[(\frac{1}{2}+i\tau )-(\frac{1}{2}-i\tau )]\frac{1}{2}ln\pi .\hfill \end{array}$$

(14)

For large $\tau$, we use the asymptotic behavior of complex logarithms and the Stirling approximation for the Gamma function. The terms involving $lns$ and $ln(s-1)$ simplify using $ln\left(z\right)-ln\left(\overline{z}\right)=2iarg\left(z\right)$ for arguments near $\pi /2$ or $-\pi /2$:

$$\left[ln\left({\displaystyle \frac{1}{2}}+i\tau -1\right)-ln\left({\displaystyle \frac{1}{2}}-i\tau -1\right)\right]+\left[ln\left({\displaystyle \frac{1}{2}}+i\tau \right)-ln\left({\displaystyle \frac{1}{2}}-i\tau \right)\right]\sim 2i\pi +O\left(\frac{1}{{\tau }^2}\right).$$

Additionally, Stirling’s approximation for the Gamma function logarithm yields (see, e.g., [8]):

$$ln\Gamma (\frac{1}{4}+i\frac{\tau }{2})-ln\Gamma (\frac{1}{4}-i\frac{\tau }{2})\sim i\left(\tau ln{\displaystyle \frac{\tau }{2}}-\tau -{\displaystyle \frac{\pi }{4}}\right)+O\left(\frac{1}{\tau }\right).$$

(15)

Substituting these approximations into the equation for $2\pi i{\sum }_{m}H(\tau -t_m)$ and simplifying, we obtain:

$$\begin{array}{cc}\hfill 2\pi i\sum _{m}H(\tau -t_m)=& [ln\zeta (\frac{1}{2}+i\tau )-ln\zeta (\frac{1}{2}-i\tau )]\hfill \\ \hfill & +i\left(\tau ln{\displaystyle \frac{\tau }{2}}-\tau -{\displaystyle \frac{\pi }{4}}\right)+2i\pi -i\tau ln\pi .\hfill \end{array}$$

(16)

Further simplification leads to:

$$\begin{array}{cc}\hfill 2\pi i\sum _{m}H(\tau -t_m)=& [ln\zeta (\frac{1}{2}+i\tau )-ln\zeta (\frac{1}{2}-i\tau )]\hfill \\ \hfill & +i\left(\tau ln{\displaystyle \frac{\tau }{2\pi }}-\tau +{\displaystyle \frac{7\pi }{4}}\right).\hfill \end{array}$$

(17)

Thus, we can define the exact explicit Riemann-von Mangoldt zeta zeros count function formula in the $\tau$-domain [9], as

$$\nu \left(\tau \right):=\sum _{m}H(\tau -t_m)=\frac{\tau }{2\pi }ln\frac{\tau }{2e\pi }+\frac{7}{8}+\frac{1}{2\pi i}\left[ln\zeta (\frac{1}{2}+i\tau )-ln\zeta (\frac{1}{2}-i\tau )\right].$$

(18)

The derivation of explicit formulas using contour integrals, particularly those relating arithmetic sums to sums over zeta zeros, can be conceptually viewed as a form of inverse transform. This method effectively "inverts" a Dirichlet series (like $-{\zeta }^{\prime }\left(s\right)/\zeta \left(s\right)$) by integrating along specific contours in the complex plane, akin to inverse Laplace transforms with finite limits instead of infinite limits.

Now, the logarithm of the Riemann zeta function can be expressed through its Euler product [7]:

$$ln\zeta \left(s\right)=\sum _{k\in \mathbb{N}}\frac{1}{k}P\left(ks\right)=\sum _{k\in \mathbb{N}}\sum _p\frac{1}{k}{e}^{-kslnp},$$

(19)

Substituting this expansion into the difference term for $ln\zeta$:

$$[ln\zeta (\frac{1}{2}+i\tau )-ln\zeta (\frac{1}{2}-i\tau )]=\sum _p\sum _{k\in \mathbb{N}}{e}^{-{\displaystyle \frac{k}{2}}lnp}\frac{1}{k}\left[e^{-ik\tau lnp}-e^{ik\tau lnp}\right].$$

(20)

Combining these results, we obtain an explicit formula for the zero-counting function in terms of the prime harmonics, as:

$$2\pi i\sum _{m}H(\tau -t_m)=\sum _p\sum _{k\in \mathbb{N}}{e}^{-{\displaystyle \frac{k}{2}}lnp}\frac{1}{k}\left[e^{-ik\tau lnp}-e^{ik\tau lnp}\right]+i\left(\tau ln{\displaystyle \frac{\tau }{2\pi }}-\tau +{\displaystyle \frac{7\pi }{4}}\right).$$

(21)

3.3. The Delta-Function Density

We differentiate Equation (21) with respect to $\tau$. The Heaviside sum on the LHS transforms into a sum of Dirac delta functions, representing the density of zeros along the imaginary axis.

$$\begin{array}{cc}\hfill 2\pi i\sum _m\delta (\tau -t_m)=& -i\sum _p\sum _k{p}^{-{\displaystyle \frac{k}{2}}}lnp[e^{i\tau klnp}+e^{-i\tau klnp}]+iln{\displaystyle \frac{\tau }{2\pi }}.\hfill \end{array}$$

(22)

Rearranging terms and dividing by i, we obtain a precise explicit formula for the density of non-trivial zeros:

$$\begin{array}{c}\hfill 2\pi \sum _m\delta (\tau -t_m)=ln{\displaystyle \frac{\tau }{2\pi }}-\sum _p\sum _k{p}^{-{\displaystyle \frac{k}{2}}}lnp[e^{-i\tau klnp}+e^{i\tau klnp}].\end{array}$$

(23)

The relationship between Equation (10) and Equation (23) represents a profound duality, forming the mathematical core of the connection between primes and zeta zeros. The first formula, a "prime-centric" view, expresses the distribution of prime numbers as a sum over the zeros of the zeta function. It answers the question, "Where are the primes?" by using the "spectral data" of the zeta zeros. In stark contrast, the second formula provides the dual "zero-centric" view: it expresses the distribution of the heights of the zeta zeros as a sum over the prime numbers. It answers the question, "Where are the zeta zeros?" using the primes as the fundamental frequencies. This perfect reciprocity implies that the two sets of numbers—the primes and the zeta zeros—are inextricably locked together, like a signal and its Fourier transform. All the information about one set is perfectly encoded in the other. This duality is the basis for the modern perspective of number theory through physics, suggesting that the zeros are like the resonant energy levels of a quantum system whose structure is determined by the primes, which act like a classical potential.

3.4. Transformation to the z-Domain

We now apply the Laplace transform with respect to $\tau$ to Equation (23). Let z be the Laplace variable. The Laplace transform of $\delta (\tau -t_m)$ is $e^{-z{t}_m}$.

$$2\pi \sum _m{e}^{-z{t}_m}=-{\displaystyle \frac{\gamma +ln\left(2\pi z\right)}{z}}-\sum _p\sum _{k=1}^{\infty }{\displaystyle \frac{lnp}{p^{k/2}}}\left({\displaystyle \frac{1}{z-iklnp}}+{\displaystyle \frac{1}{z+iklnp}}\right).$$

(24)

To uncover a product form, we perform a manipulation by considering z as a complex variable. Replacing z by $iz$ and $-iz$ in the above equation, we obtain two related expressions:

$$2\pi \sum _m{e}^{-iz{t}_m}=-{\displaystyle \frac{\gamma +ln\left(2\pi iz\right)}{iz}}-\sum _p\sum _{k=1}^{\infty }{\displaystyle \frac{lnp}{p^{k/2}}}\left({\displaystyle \frac{1}{iz-iklnp}}+{\displaystyle \frac{1}{iz+iklnp}}\right),$$

(25)

and

$$2\pi \sum _m{e}^{iz{t}_m}=-{\displaystyle \frac{\gamma +ln(-2\pi iz)}{-iz}}-\sum _p\sum _{k=1}^{\infty }{\displaystyle \frac{lnp}{p^{k/2}}}\left({\displaystyle \frac{1}{-iz-iklnp}}+{\displaystyle \frac{1}{-iz+iklnp}}\right).$$

(26)

Subtracting the first of these two equations from the second, we obtain:

$$\begin{array}{cc}\hfill 2\pi \sum _m{e}^{iz{t}_m}-e^{-iz{t}_m}=& {\displaystyle \frac{2\gamma +ln(-2\pi iz)+ln\left(2\pi iz\right)}{iz}}\hfill \\ & +2\sum _p\sum _{k=1}^{\infty }{\displaystyle \frac{lnp}{p^{k/2}}}\left({\displaystyle \frac{1}{iz-iklnp}}+{\displaystyle \frac{1}{iz+iklnp}}\right).\hfill \end{array}$$

(27)

Noting that $ln(-2\pi iz)+ln\left(2\pi iz\right)=ln(-2^2{\pi }^2{i}^2{z}^2)=ln(-2^2{\pi }^2(-1)z^2)=2ln\left(2\pi z\right)$ by assuming $\Re \left(z\right)>0$. Thus, simplifying the logarithmic term on the RHS, and multiplying the entire equation by i and dividing throughout by 2, we obtain:

$$i\pi \sum _m{e}^{iz{t}_m}-e^{-iz{t}_m}={\displaystyle \frac{\gamma +ln\left(2\pi z\right)}{z}}+\sum _p\sum _{k=1}^{\infty }{\displaystyle \frac{lnp}{p^{k/2}}}\left({\displaystyle \frac{1}{z-klnp}}+{\displaystyle \frac{1}{z+klnp}}\right).$$

(28)

Finally, using the identity $(e^{ix}-e^{-ix})=2isinx$ and $i^2=-1$, the LHS can be expressed in terms of sine, as:

$$-2\pi \sum _{m}sin\left(z{t}_m\right)={\displaystyle \frac{\gamma +ln\left(2\pi z\right)}{z}}+\sum _p\sum _{k=1}^{\infty }{\displaystyle \frac{lnp}{p^{k/2}}}\left({\displaystyle \frac{1}{z-klnp}}+{\displaystyle \frac{1}{z+klnp}}\right).$$

(29)

3.5. Log-Product Form

We integrate Equation (29) with respect to z. The integral of the LHS is

$$\int -2\pi \sum _{m}sin\left(z{t}_m\right)dz=2\pi \sum _m{\displaystyle \frac{cos\left(z{t}_m\right)}{t_m}}.$$

For the RHS:

$$\int {\displaystyle \frac{\gamma +ln\left(2\pi z\right)}{z}}dz=\gamma lnz+{\displaystyle \frac{1}{2}}{(ln\left(2\pi z\right))}^2.$$

For the sum term, we use the integration rule $\int ({\displaystyle \frac{1}{z-a}}+{\displaystyle \frac{1}{z+a}})dz=ln(z-a)+ln(z+a)$, which can be expressed as $ln(1-z/a)+ln(1+z/a)$ when appropriate branch cuts are chosen and assuming the integration constant is zero. Thus, we have:

$$\begin{array}{cc}\hfill 2\pi \sum _m{\displaystyle \frac{cos\left(z{t}_m\right)}{t_m}}=& \gamma lnz+\frac{1}{2}{(ln\left(2\pi z\right))}^2\hfill \\ \hfill & +\sum _p\sum _{k=1}^{\infty }{\displaystyle \frac{lnp}{p^{k/2}}}\left[ln\left(1-{\displaystyle \frac{z}{klnp}}\right)+ln\left(1+{\displaystyle \frac{z}{klnp}}\right)\right].\hfill \end{array}$$

(30)

3.6. Exponentiation and Definition

We now exponentiate both sides of Equation (30) to obtain a product representation. We define the z-domain second Chebyshev function $\widehat{\Psi }\left(z\right)$ as:

$$\widehat{\Psi }\left(z\right)=z^{\gamma }{e}^{{\displaystyle \frac{1}{2}}{(ln2\pi z)}^2}\prod _p\prod _{k=1}^{\infty }{\left[\left(1-{\displaystyle \frac{z}{klnp}}\right)\left(1+{\displaystyle \frac{z}{klnp}}\right)\right]}^{{\displaystyle \frac{lnp}{p^{k/2}}}}=e^{2\pi {\sum }_m{\displaystyle \frac{cos\left(z{t}_m\right)}{t_m}}}.$$

(31)

This product form for $\widehat{\Psi }\left(z\right)$ reveals a fascinating property: its zeros are precisely located at $z=\pm klnp$ for all prime numbers p and positive integers k. These are the logarithmic prime powers, demonstrating a direct encoding of prime number information.

Noting that the identity for $\widehat{\Psi }\left(z\right)$ was derived under the condition $\Re \left(z\right)>0$. To justify its validity across the entire complex plane, we invoke the principle of analytic continuation. Both the product representation of $\widehat{\Psi }\left(z\right)$ and its exponential sum form define functions that are analytic on the complex plane. Since these two analytic functions have been proven to be equal on the open right half-plane, a domain which contains limit points, the Identity Theorem for analytic functions guarantees that they must be identical everywhere. This rigorously extends the equality from the right half-plane to the entire complex plane, confirming that the function’s zeros are indeed located at $z=\pm klnp$.

3.7. x-domain Representation and Graphical Properties

Finally, by substituting $z=lnx$ into the definition of $\widehat{\Psi }\left(z\right)$, we obtain its representation in the x-domain:

$$\begin{array}{cc}\hfill \widehat{\Psi }(lnx)=& {(lnx)}^{\gamma }{e}^{{\displaystyle \frac{1}{2}}{(ln(2\pi lnx))}^2}\prod _p\prod _{k=1}^{\infty }{\left[\left(1-{\displaystyle \frac{lnx}{klnp}}\right)\left(1+{\displaystyle \frac{lnx}{klnp}}\right)\right]}^{{\displaystyle \frac{lnp}{p^{k/2}}}}\hfill \\ \hfill =& e^{2\pi {\sum }_m{\displaystyle \frac{cos\left(t_{m}lnx\right)}{t_m}}}.\hfill \end{array}$$

(32)

The zeros of $\widehat{\Psi }(lnx)$ are thus at $x=p^k$ and $x=p^{-k}$ (for $k\in \mathbb{N}$), which is consistent with the zeros at $z=\pm klnp$.

The exponential form on the RHS of (32), given by

$$\widehat{\Psi }(lnx)=e^{S(lnx)}$$

(33)

where

$$S(lnx)=2\pi \sum _m{\displaystyle \frac{cos\left(t_{m}lnx\right)}{t_m}},$$

yields a real-valued function for real x. This implies that $\widehat{\Psi }(lnx)$ is always real. Its positivity depends on the sum $S(lnx)$. The product form clearly shows that $\widehat{\Psi }(lnx)=0$ if $1-{\displaystyle \frac{{(lnx)}^2}{{(klnp)}^2}}=0$ for some prime p and integer k. This occurs when $lnx=\pm klnp$, leading to $x=p^k$ (for $x>1$) or $x=p^{-k}$ (for $0<x<1$). 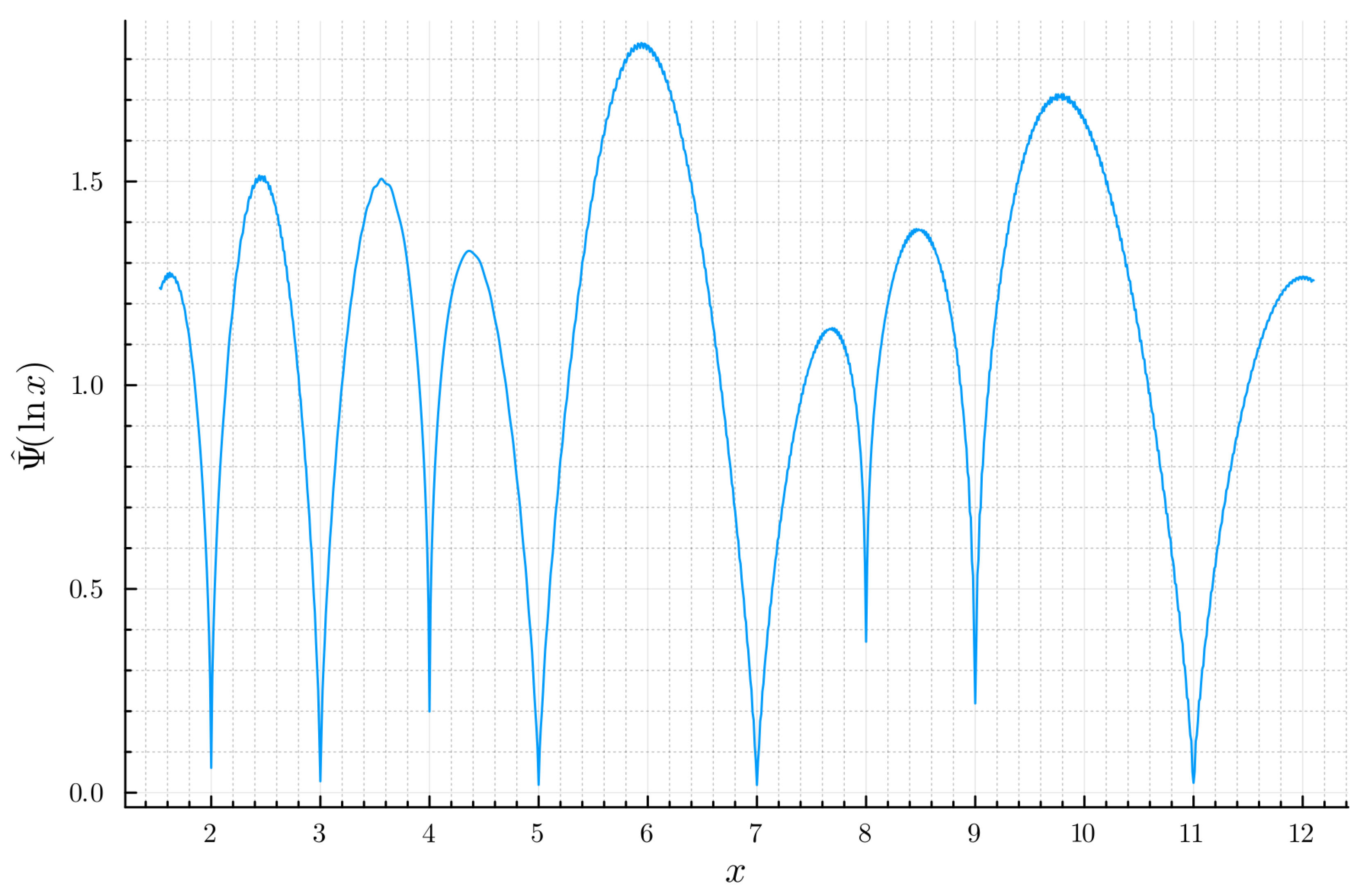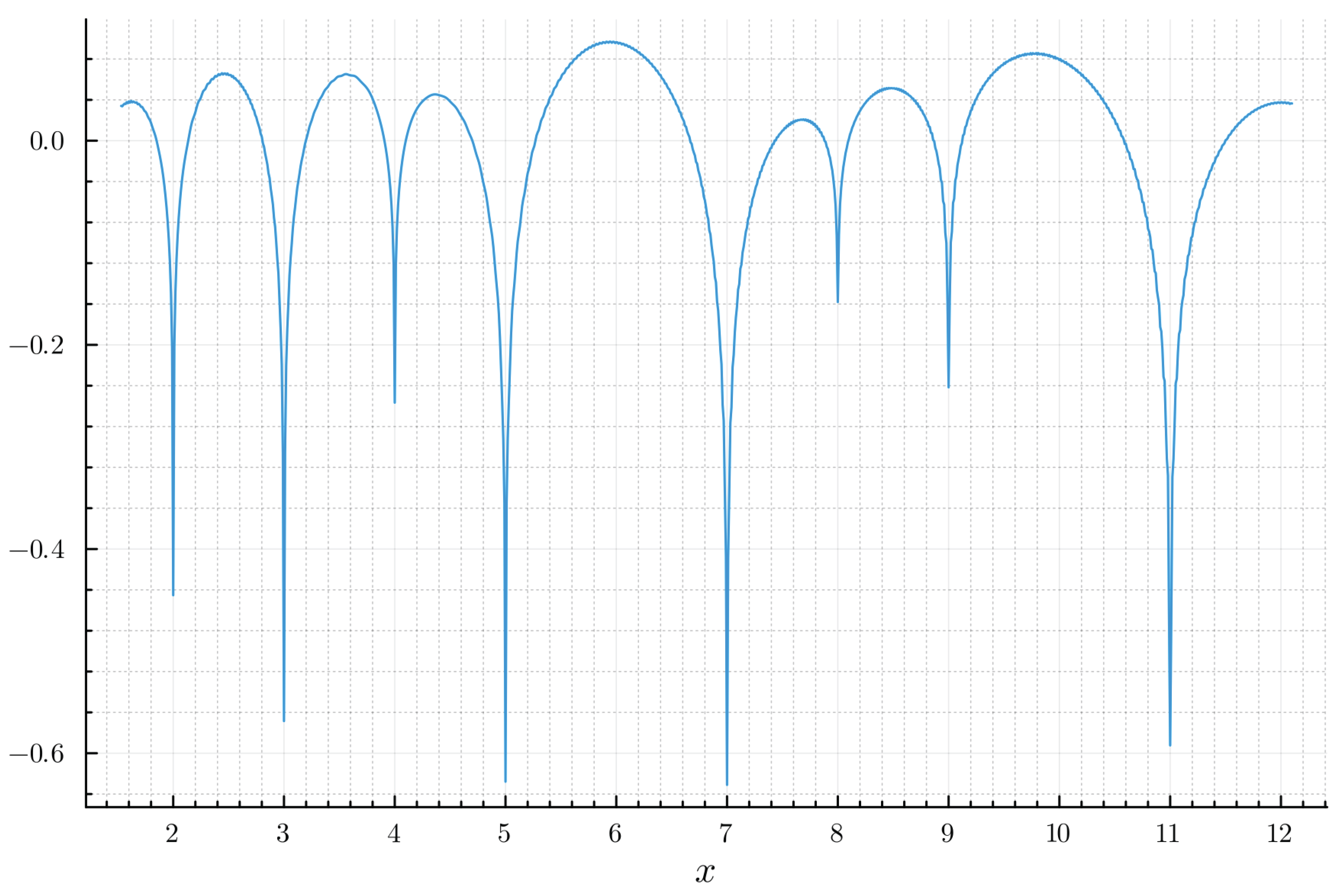At these specific points, the sum $S(lnx)$ in the exponent must diverge to $-\infty$, driving $e^{S(lnx)}$ to zero. This behavior is clearly illustrated in Figure 1, showing sharp dips towards zero at prime power values of x. The corresponding plot of $ln\widehat{\Psi }(lnx)=S(lnx)$ in Figure 2 confirms these divergences as sharp poles towards $-\infty$.

4. Discussion and Implications

The derived identity for $\widehat{\Psi }\left(z\right)$ (Equation (31)) stands as a powerful testament to the profound duality between prime numbers and the non-trivial zeros of the Riemann zeta function. On one side, we have a product whose zeros are explicitly defined by the logarithmic prime powers, $klnp$. On the other, we have an exponential sum directly involving $t_m$ the ordinate of the zeta zeros. This duality is a cornerstone of analytic number theory, and this novel representation offers a fresh analytical perspective.

This new formulation of a Chebyshev-type function opens several avenues for further theoretical and computational exploration:

• Computational Algorithms: This identity might inspire novel numerical algorithms for:
  • Prime Counting Functions: The direct appearance of prime powers as zeros of $\widehat{\Psi }(lnx)$ could lead to new methods for evaluating or approximating prime-counting functions more efficiently, perhaps by analyzing the local behavior of $\widehat{\Psi }(lnx)$ around its zeros.
  • Numerical Stability: Comparative studies of the numerical stability and convergence rates of evaluating $\widehat{\Psi }\left(z\right)$ (or its x-domain counterpart) via its product form versus its exponential sum form could be highly valuable for practical applications.
• Generalizations: The methodology employed, a sequence of Laplace transforms, differentiation, integration, and exponentiation of explicit formulas, could potentially be generalized to derive similar product-sum identities for other arithmetic functions or for L-functions associated with different number fields. This suggests a broader framework for understanding the interplay between number-theoretic objects and the spectral properties of their associated L-functions.
• Bridging Disciplines: The explicit connection shown by $\widehat{\Psi }\left(z\right)$ between number theory and the analysis of generalized functions (Dirac delta) and integral transforms underscores the interdisciplinary nature of mathematical research.

Finally, it is remarkable that the final expression for $\widehat{\Psi }\left(z\right)$ is decorated with the fundamental constants $\pi$, e, and $\gamma$. Their appearance is not coincidental but rather a profound signature of the underlying mathematical structure. The constant $\pi$ arises from the geometry of the complex plane and the periodicity inherent in the zeta function’s functional equation. The constant e is the bedrock of continuous growth and analysis, underpinning the entire framework of logarithms and exponentials. Finally, the Euler-Mascheroni constant $\gamma$ emerges as an intrinsic fingerprint of the Gamma function, which is essential for the analytic continuation of $\zeta \left(s\right)$. The presence of this trio confirms that $\widehat{\Psi }\left(z\right)$ is a natural object, intrinsically linking the discrete world of primes to the fundamental constants of continuous analysis.

5. Conclusion

In this paper, I have rigorously derived a novel product representation for a z-domain Chebyshev-type function, $\widehat{\Psi }\left(z\right)$, which directly equates a product over prime powers to an exponential sum over the imaginary parts of the non-trivial Riemann zeta zeros. This derivation, built upon fundamental principles of complex analysis and integral transforms, offers a unique analytical lens into the deep prime-zero duality that lies at the heart of number theory. The explicit encoding of prime powers as zeros in this new function provides a novel perspective for future theoretical investigations into the Riemann Hypothesis and promises to inspire the development of novel computational algorithms for number-theoretic problems. I hope this work can contribute to the unravelling of the intricate structure of prime numbers through the powerful machinery of analytic methods.