Theory-Trained Deep Neural Networks: Insights, Techniques, and Future Directions

1. Introduction

Deep neural networks (DNNs) have revolutionized a wide array of fields, from computer vision and natural language processing to reinforcement learning and scientific computing. Despite their empirical success, a theoretical understanding of how and why these models work remains elusive [1]. In recent years, the growing interest in bridging the gap between theory and practice has given rise to the concept of Theory-Trained Deep Neural Networks (TT-DNNs)—models designed or informed explicitly by theoretical principles. TT-DNNs represent a promising paradigm shift in the design and training of neural networks [2]. Instead of relying solely on heuristics or massive empirical exploration, this approach incorporates insights from optimization theory, statistical learning, information theory, and approximation theory into the architecture, initialization, and training procedures of DNNs [3]. These theoretically grounded strategies aim to improve generalization, robustness, interpretability, and training efficiency. The goal of this survey is to provide a comprehensive overview of the field of Theory-Trained Deep Neural Networks. We categorize the literature along several dimensions, including theoretical frameworks that guide network training, algorithmic developments that exploit these insights, and practical implementations that demonstrate the effectiveness of theory-informed models [4]. We also highlight open problems and future research directions, emphasizing the interdisciplinary nature of this evolving area. By synthesizing recent advances and organizing them within a unifying framework, this survey aims to serve both as a foundational reference for researchers entering the field and as a roadmap for future theoretical and practical developments in deep learning.

2. Background and Preliminaries

To provide context for Theory-Trained Deep Neural Networks (TT-DNNs), we first review foundational concepts in deep learning and the theoretical frameworks that inform them. This section covers the standard components of deep neural networks, outlines common training procedures, and introduces the mathematical tools often used to analyze and guide neural network design [5].

2.1. Deep Neural Networks

A deep neural network is a parameterized function $f_{\theta }:{\mathbb{R}}^d\to {\mathbb{R}}^k$ composed of multiple layers of affine transformations and nonlinear activations [6]. Formally, a feedforward network with L layers can be expressed as:

$$f_{\theta }\left(x\right)=f_L\circ f_{L-1}\circ \dots \circ f_1\left(x\right),$$

where each layer $f_l\left(x\right)=\sigma (W_{l}x+b_l)$ for weight matrix $W_l$, bias $b_l$, and activation function $\sigma$[7]. Training typically involves minimizing a loss function $\mathcal{L}(f_{\theta }\left(x\right),y)$ over a dataset ${\left\{(x_i,y_i)\right\}}_{i=1}^n$ using stochastic gradient descent (SGD) or its variants [8].

Figure 1. A simple feedforward neural network with one hidden layer [9]. Nodes represent neurons, and arrows indicate weighted connections.

Figure 1. A simple feedforward neural network with one hidden layer [9]. Nodes represent neurons, and arrows indicate weighted connections.

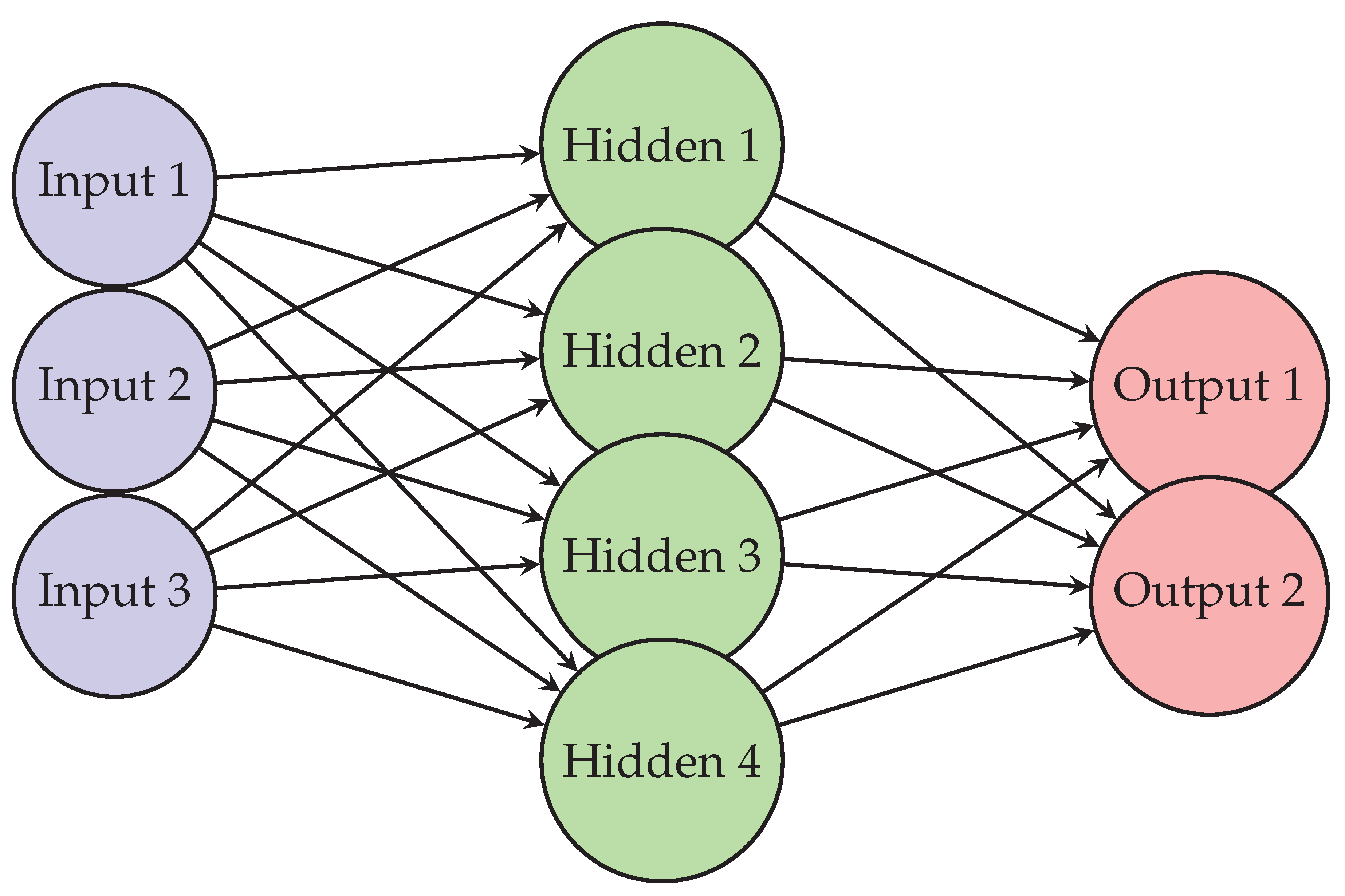
2.2. Theoretical Foundations

Several branches of theory underpin recent advances in TT-DNNs:

-

Optimization Theory: Analyzes the convergence properties of gradient-based methods, particularly in non-convex settings typical of deep networks.

-

Statistical Learning Theory: Provides generalization bounds and capacity measures such as VC-dimension, Rademacher complexity, and uniform stability.

-

Approximation Theory: Studies the expressivity of neural networks, including universal approximation theorems and the role of depth and width [10].

-

Information Theory: Offers tools for understanding compression, mutual information, and the information bottleneck principle in learning dynamics.

2.3. Motivating the Need for Theory-Guided Training

Empirical deep learning often relies on trial-and-error heuristics, large-scale computation, and overparameterization [11]. While successful, this approach lacks principled guarantees and can lead to brittle models. TT-DNNs aim to reduce reliance on brute-force methods by leveraging the above theoretical insights to guide architecture design, training dynamics, and regularization strategies [12]. This can result in models that are more data-efficient, interpretable, and robust to perturbations [13]. The remainder of this survey builds on these foundations to explore how theory can be used not just to analyze but to actively shape the training of deep neural networks.

3. Taxonomy of Theory-Trained Deep Neural Networks

Theory-Trained Deep Neural Networks (TT-DNNs) encompass a diverse set of approaches that integrate theoretical principles into network design and training [14]. To provide clarity and structure, we categorize existing work into four primary classes based on the nature of the theoretical guidance and its role in the training process:

3.1. Optimization-Guided Networks

This category focuses on incorporating optimization theory to design architectures and training algorithms that improve convergence properties and stability. Examples include:

-

Networks trained with provably convergent optimization schemes tailored for non-convex landscapes [15].

-

Methods that exploit gradient flow dynamics or adaptive step sizes inspired by theoretical insights.

3.2. Regularization and Generalization-Driven Networks

These approaches employ statistical learning theory to derive principled regularization techniques and complexity control mechanisms:

-

Architectures designed to enforce low-complexity function classes.

-

Training methods that minimize generalization bounds, such as PAC-Bayes inspired algorithms or margin-based objectives.

3.3. Expressivity-Optimized Networks

Based on approximation theory, these methods design network structures (depth, width, activation choices) to maximize expressive power while maintaining trainability:

-

Networks with theoretically grounded layer designs enabling efficient approximation of target functions [16].

-

Architectures that leverage sparse or structured representations for compactness and interpretability [17].

3.4. Information-Theoretic Training Paradigms

This category leverages information theory to inform training objectives and representations:

-

Models trained using the information bottleneck principle to balance compression and relevance [18].

-

Approaches that quantify and optimize mutual information between layers or between inputs and outputs [19].

3.5. Hybrid Approaches

Many state-of-the-art TT-DNN frameworks combine elements from multiple theoretical domains, resulting in hybrid methods that simultaneously address optimization, generalization, expressivity, and information flow. This taxonomy provides a high-level map of the landscape, helping researchers to identify where their work fits and how different theoretical insights complement each other in advancing the understanding and performance of deep neural networks [20].

4. Theoretical Foundations of Optimization in Deep Neural Networks

Optimization lies at the heart of training deep neural networks. Given a dataset $\mathcal{D}={\left\{(x_i,y_i)\right\}}_{i=1}^n$, the goal is to find network parameters $\theta \in {\mathbb{R}}^p$ that minimize the empirical risk defined by a loss function $\ell :{\mathbb{R}}^k\times {\mathbb{R}}^k\to {\mathbb{R}}_{+}$:

$$\underset{\theta \in {\mathbb{R}}^p}{min}\mathcal{L}\left(\theta \right):={\displaystyle \frac{1}{n}}\sum _{i=1}^n\ell \left(f_{\theta }\left(x_i\right),y_i\right),$$

where $f_{\theta }:{\mathbb{R}}^d\to {\mathbb{R}}^k$ is the neural network parameterized by $\theta$[21]. Due to the non-convex nature of $\mathcal{L}\left(\theta \right)$, classical convex optimization guarantees do not directly apply [22]. However, recent theoretical advances analyze the loss landscape through tools such as the Neural Tangent Kernel (NTK) [23]. The NTK at initialization, denoted ${\Theta }_0$, characterizes the first-order behavior of the network output with respect to parameters:

$${\Theta }_0(x,x^{\prime })={\nabla }_{\theta }{f}_{{\theta }_0}{\left(x\right)}^{\top }{\nabla }_{\theta }{f}_{{\theta }_0}\left(x^{\prime }\right),$$

where ${\theta }_0$ is the initial parameter vector [24]. In the infinite-width limit, training dynamics under gradient descent are approximated by a kernel regression with kernel ${\Theta }_0$, yielding linear convergence rates:

$$\mathcal{L}\left({\theta }_t\right)\le exp(-{\lambda }_{min}\left({\Theta }_0\right)t)\mathcal{L}\left({\theta }_0\right),$$

where ${\lambda }_{min}\left({\Theta }_0\right)$ is the minimal eigenvalue of the NTK Gram matrix. Furthermore, the implicit bias of gradient-based optimization methods can favor solutions with desirable properties [25]. For example, gradient descent on linear models converges to the minimum norm solution. Extending this to deep nonlinear networks remains an active area of research. Understanding these theoretical foundations informs the design of optimization algorithms and initialization schemes that promote faster convergence and better generalization in deep learning.

5. Generalization Theory in Deep Neural Networks

A fundamental question in deep learning is understanding why highly overparameterized neural networks generalize well despite their capacity to perfectly fit training data. Classical learning theory typically bounds the generalization error ${\mathcal{E}}_{\mathrm{gen}}$ by controlling model complexity, but these bounds often fail to explain deep networks’ empirical behavior [26]. Formally, the generalization error is defined as the difference between the expected risk and the empirical risk:

$${\mathcal{E}}_{\mathrm{gen}}\left(\theta \right)={\mathbb{E}}_{(x,y)\sim \mathcal{P}}\left[\ell (f_{\theta }\left(x\right),y)\right]-{\displaystyle \frac{1}{n}}\sum _{i=1}^n\ell \left(f_{\theta }\left(x_i\right),y_i\right),$$

where $\mathcal{P}$ denotes the true data distribution [27]. Recent theoretical advances have introduced norm-based capacity measures that better capture generalization in deep networks. For example, the path norm ${\parallel \theta \parallel }_{\mathrm{path}}$ is defined as the sum of products of weights along all paths from input to output, serving as a complexity measure:

$${\parallel \theta \parallel }_{\mathrm{path}}=\sum _{\pi \in \Pi }\prod _{l=1}^L\parallel W_l^{\left(\pi \right)}\parallel ,$$

where $\Pi$ denotes the set of all paths and $W_l^{\left(\pi \right)}$ are weights along path $\pi$ at layer l[28]. PAC-Bayesian frameworks provide probabilistic bounds on generalization by considering distributions over parameters rather than point estimates. Given a prior distribution P and a learned posterior Q, the PAC-Bayes bound with probability at least $1-\delta$ states:

$${\mathbb{E}}_{\theta \sim Q}\left[{\mathcal{E}}_{\mathrm{gen}}\left(\theta \right)\right]\le \sqrt{{\displaystyle \frac{KL(Q\parallel P)+log\frac{2\sqrt{n}}{\delta }}{2n}}},$$

where $KL(Q\parallel P)$ is the Kullback–Leibler divergence between Q and P. Moreover, margin-based theories argue that the robustness of classification depends on the margin distribution of training samples. For a classifier $f_{\theta }$, the margin of a sample $(x_i,y_i)$ is defined as:

$${\gamma }_i=y_i{f}_{\theta }\left(x_i\right),$$

and maximizing the minimum margin across samples can improve generalization [29]. These theoretical tools collectively contribute to a richer understanding of deep network generalization, guiding the development of regularization techniques and training algorithms that yield more robust models [30].

6. Information-Theoretic Perspectives on Deep Learning

Information theory provides a powerful framework to analyze and understand the learning dynamics of deep neural networks [31]. One of the most influential concepts in this context is the Information Bottleneck (IB) principle, which formalizes the trade-off between compression of the input data and preservation of relevant information for the output task. The IB principle views the learning process as finding a representation T of the input X that maximally compresses the information about X while retaining sufficient information to predict the output Y [32]. Mathematically, this trade-off is formulated as the optimization problem:

$$\underset{p\left(t\right|x)}{min}I(X;T)-\beta I(T;Y),$$

where $I(·;·)$ denotes mutual information and $\beta >0$ is a Lagrange multiplier balancing compression and prediction [33]. Here, $I(X;T)$ measures the amount of information T retains about the input, and $I(T;Y)$ quantifies how informative T is about the output. By minimizing this objective, the network is encouraged to discard irrelevant details from the input while preserving predictive features. This perspective leads to a conceptual interpretation of deep layers as successive representations $T_1,T_2,\dots ,T_L$ that progressively compress the input information, forming a Markov chain:

$$Y\leftrightarrow X\leftrightarrow T_1\leftrightarrow T_2\leftrightarrow \dots \leftrightarrow T_L,$$

where each $T_{\ell }$ ideally contains less redundant information than the previous layer but retains essential characteristics for prediction [34]. Empirical studies have observed phases of fitting and compression during training, lending support to the IB hypothesis [35].

Figure 2. Schematic of the Information Bottleneck framework: input X is transformed through successive representations $T_1,\dots ,T_L$ which compress irrelevant information while preserving predictive content about output Y. The dashed arrow indicates the direct but complex relationship between input and output.

Figure 2. Schematic of the Information Bottleneck framework: input X is transformed through successive representations $T_1,\dots ,T_L$ which compress irrelevant information while preserving predictive content about output Y. The dashed arrow indicates the direct but complex relationship between input and output.

Despite its elegant formulation, computing mutual information terms in high-dimensional neural networks is notoriously challenging due to the intractability of the true distributions involved. This has motivated the development of variational approximations and surrogate objectives such as the Variational Information Bottleneck (VIB), which enables practical implementation by parameterizing distributions with neural networks and optimizing tractable bounds. The information-theoretic perspective also informs the design of regularization techniques, such as noise injection and dropout, which can be interpreted as mechanisms encouraging compression and robustness. Moreover, maximizing mutual information between intermediate representations and the input or output can improve feature quality and interpretability. Overall, viewing deep learning through the lens of information theory provides profound insights into representation learning and generalization, while inspiring novel training strategies that balance expressivity and compression in neural networks.

7. Theory-Informed Training Paradigms

In this section, we review prominent training methodologies that explicitly incorporate theoretical principles to improve the learning process and final model performance [36]. These paradigms demonstrate how theory can guide practical algorithm design, enhancing convergence, generalization, and interpretability.

7.1. Optimization-Theoretic Approaches

Optimization theory has inspired several modifications to standard training algorithms, including:

-

Adaptive Gradient Methods with Theoretical Guarantees: Algorithms such as Adam, AdaGrad, and their variants have been analyzed to better understand convergence rates and stability in non-convex settings [37].

-

Implicit Regularization through Gradient Descent: Recent works show that gradient-based optimization implicitly biases solutions towards simpler models, leading to better generalization without explicit regularization.

-

Optimization in the Overparameterized Regime: Theory-driven approaches leverage the Neural Tangent Kernel (NTK) and mean-field analysis to explain and improve training dynamics when networks are heavily overparameterized [38].

7.2. Regularization and Generalization Techniques

These methods leverage statistical learning theory to enforce constraints that promote better generalization:

-

PAC-Bayesian Training: Training frameworks that optimize PAC-Bayes bounds by incorporating prior distributions over parameters and minimizing expected risk [39].

-

Margin-Based Objectives: Encouraging large margins in the feature space to improve robustness and reduce overfitting.

-

Norm-Based Regularization: Using weight norms or path norms with provable generalization guarantees [40].

7.3. Architecture and Expressivity-Driven Training

Theory-informed choices about network architecture can substantially impact training outcomes:

-

Depth vs [41]. Width Trade-offs: Architectures designed based on universal approximation theorems to optimize representational capacity.

-

Sparse and Structured Networks: Leveraging theoretical sparsity results to build compact, efficient models.

-

Activation Function Design: Theoretical insights guide the choice and modification of activation functions to improve gradient flow and expressivity [42].

7.4. Information-Theoretic Training Strategies

Information theory offers a principled framework to analyze and shape learning dynamics:

-

Information Bottleneck Principle: Training objectives that compress intermediate representations while preserving relevant information about the output [43].

-

Mutual Information Maximization: Methods that maximize mutual information between inputs and learned features to encourage informative representations [44].

-

Entropy-Regularized Training: Introducing entropy constraints to promote robustness and diversity in learned features [45].

Each of these paradigms illustrates how theoretical insights can be directly translated into effective training practices, moving beyond purely empirical approaches towards more principled deep learning methodologies.

8. Applications and Case Studies

Theory-Trained Deep Neural Networks (TT-DNNs) have demonstrated significant benefits across a variety of domains, showcasing the practical value of integrating theoretical insights into model design and training. This section highlights notable applications and case studies that illustrate the impact of theory-informed approaches.

8.1. Computer Vision

In computer vision, theory-driven architectures and training algorithms have led to improved robustness and efficiency:

-

Provably Robust Networks: Models trained with adversarial robustness guarantees using optimization-based regularization and certification methods [46].

-

Efficient Architectures: Sparse and structured networks informed by approximation theory have reduced model size without sacrificing accuracy [47].

8.2. Natural Language Processing

Theoretical frameworks have guided training in NLP tasks to improve generalization and interpretability:

-

Information Bottleneck in Language Models: Using compression-based objectives to enhance representation quality and reduce overfitting [48].

-

Optimization-Guided Fine-Tuning: Adapting optimization schedules based on theoretical analyses to stabilize training of large transformer models [49].

8.3. Scientific Computing and Physics

TT-DNNs are increasingly employed in domains requiring reliable and interpretable models:

-

Physics-Informed Neural Networks (PINNs): Networks trained with PDE constraints that leverage approximation theory to solve complex physical systems.

-

Uncertainty Quantification: PAC-Bayes-based methods providing principled uncertainty estimates in scientific prediction tasks [50].

8.4. Healthcare and Medical Imaging

Theory-trained models contribute to trustworthy AI in sensitive areas:

-

Robust Diagnostic Models: Training with margin-based objectives to improve resistance to data shifts and adversarial attacks [51].

-

Data-Efficient Learning: Leveraging theory-inspired regularization to train with limited annotated medical data.

These case studies underscore how theoretical insights can translate into tangible improvements in real-world systems, driving advances that are not only empirically effective but also principled and reliable.

9. Open Challenges and Future Directions

Despite significant progress in integrating theoretical insights into the training of deep neural networks, several challenges remain unresolved [52]. Addressing these open problems is crucial for advancing the reliability, efficiency, and interpretability of theory-trained models. We highlight some key directions for future research:

9.1. Bridging Theory and Practice

Many theoretical results rely on assumptions or simplified models that do not fully capture the complexities of practical deep learning scenarios [53]. Developing theories that better reflect real-world architectures, datasets, and training dynamics remains an ongoing challenge.

9.2. Scalability of Theory-Informed Methods

While theory-guided algorithms often provide guarantees and interpretability, their computational overhead can be substantial. Designing scalable and efficient implementations that maintain theoretical benefits is a critical research area.

9.3. Understanding Generalization in Overparameterized Regimes

Overparameterized networks defy classical learning theory, yet they generalize remarkably well in practice [54]. Creating refined theoretical frameworks to explain and leverage this phenomenon will deepen our understanding of deep learning [55].

9.4. Robustness and Safety Guarantees

Providing provable robustness against adversarial attacks, distribution shifts, and noisy data is essential for deploying deep networks in safety-critical applications [56]. Developing theory-trained models with rigorous safety guarantees remains a priority [57].

9.5. Interpretable and Explainable Models

Theory-informed design can enhance model interpretability, but creating frameworks that offer clear, actionable explanations without sacrificing performance is still an open challenge [58].

9.6. Unified Theoretical Frameworks

Currently, theoretical insights come from diverse fields such as optimization, information theory, and approximation theory, often in isolation [59]. Integrating these perspectives into unified frameworks could lead to more holistic and powerful theory-trained neural networks.

9.7. Data Efficiency and Transfer Learning

Improving sample efficiency and enabling effective transfer of theory-trained models across tasks and domains are important practical goals that require further theoretical development [60,61]. Addressing these challenges will require interdisciplinary collaboration and continued innovation at the intersection of theory and empirical deep learning. We anticipate that future work in these directions will significantly enhance the capabilities and reliability of deep neural networks [62].

10. Conclusion

Theory-Trained Deep Neural Networks represent a promising frontier in the quest to unify the empirical success of deep learning with rigorous theoretical understanding. By integrating insights from optimization theory, statistical learning, approximation theory, and information theory, TT-DNNs aim to improve model robustness, generalization, interpretability, and training efficiency.

This survey has provided a comprehensive overview of the field, categorizing existing approaches, detailing theory-informed training paradigms, and highlighting key applications where these methods have made significant impact. We also identified open challenges and future directions that will shape the continued evolution of theory-trained models.

As deep learning continues to expand into critical and complex domains, the need for principled, theory-guided methodologies becomes ever more pressing. We believe that ongoing research in theory-trained deep neural networks will not only deepen our fundamental understanding but also drive the development of more reliable, efficient, and transparent AI systems.

We hope this survey serves as a useful resource for researchers and practitioners interested in bridging theory and practice in deep learning, inspiring future innovations at this vibrant intersection.