Theoretical Limits of Feedback Alignment in Preference-based Fine-tuning of AI Models

1. Introduction

Preference-based fine-tuning (PFT) has become crucial for aligning large language models (LLMs) with human preferences and values. Prominent methods such as reinforcement learning from human feedback (RLHF) adopt policy gradient techniques to adjust model behavior based on reward estimates derived from human or surrogate preference models [1]. Direct Preference Optimization (DPO) treats preference alignment as a differentiable pairwise ranking problem, optimizing losses directly over model scores [2]. These methods, while effective, require precise gradient propagation through complex preference networks, leading to high computational and memory costs.

Feedback alignment (FA) replaces exact error gradients with fixed random feedback matrices, significantly reducing weight transport and enabling parallel hardware implementations. Variants such as Direct FA (DFA) and sign-symmetric FA demonstrate comparable performance to backpropagation on vision tasks. Yet, FA’s application to PFT introduces challenges: pairwise losses induce non-smooth landscapes; human feedback is inherently noisy; and transformer depths amplify misalignment across layers. This study rigorously examines FA’s limits in PFT, making the following contributions:

• We formalize PFT objectives under hinge and cross-entropy pairwise losses and derive an extended error propagation recurrence capturing depth-dependent amplification and noise effects.
• We prove convergence rates for linear networks, leveraging eigen-decomposition and Grönwall’s inequality, and extend these to transformer blocks by bounding attention and feedforward sublayer Lipschitz constants[3].
• We establish noise stability thresholds, showing that human preference noise variance must lie below a critical inverse feedback-norm threshold to maintain alignment convergence[4].
• We propose hybrid FA–backprop architectures, combining FA in foundational layers with exact gradients in upper layers, and validate them in simulations on a distilled GPT-2 model[5].

These insights pave the way for efficient, hardware-friendly PFT of LLMs under practical noise and depth conditions[2].

2. Mathematical Preliminaries

In this section we introduce the notation and key tools that we will use throughout the paper. We begin by stating the formal setting for preference learning and then recall a few fundamental inequalities and norms which will be instrumental in our subsequent analysis.

2.1. Notation

Let $\mathcal{D}$ denote the (unknown) data distribution over prompt–response pairs and preference labels. Concretely, each sample from $\mathcal{D}$ is a triplet $(x,y_{+},y_{-})$, where

$$x\in \mathcal{X},y_{+},y_{-}\in \mathcal{Y},$$

and $y_{+}$ is judged by a human or oracle to be strictly preferred over $y_{-}$. We assume access to N i.i.d. draws ${\left\{(x_i,y_{+,i},y_{-,i})\right\}}_{i=1}^N$ from $\mathcal{D}$.

Our model is a deep network parameterized by weights

$$\theta =\{W_1,W_2,\dots ,W_L\},$$

where layer l has weight matrix $W_l\in {\mathbb{R}}^{d_l\times d_{l-1}}$. We write $d_0$ for the input dimension (possibly the embedding size of x) and $d_L$ for the scalar output dimension (the score). For any matrix M, we denote its spectral norm (largest singular value) by ${\parallel M\parallel }_2$ and its Frobenius norm by ${\parallel M\parallel }_F$. In addition, we will use $B_l\in {\mathbb{R}}^{d_{l-1}\times d_L}$ to denote a fixed, random feedback matrix in layer l when analyzing Feedback Alignment[6,7].

2.2. Preference Losses

Training is driven by a surrogate loss that encourages the model to score the preferred response higher than the dispreferred one. Two common choices are:

• Pairwise Hinge Loss:

  $${\ell }_h(\theta ;x,y_{+},y_{-})=max\left(0,1-s_{\theta }(x,y_{+})+s_{\theta }(x,y_{-})\right),$$

  which enforces a unit margin between the higher and lower scores. Here $s_{\theta }(x,y)\in \mathbb{R}$ denotes the scalar score assigned by the network.
• Cross-Entropy (Logistic) Loss:

  $${\ell }_{ce}(\theta ;x,y_{+},y_{-})=-log{\displaystyle \frac{exp\left(s_{\theta }(x,y_{+})\right)}{exp\left(s_{\theta }(x,y_{+})\right)+exp\left(s_{\theta }(x,y_{-})\right)}},$$

  which is smooth and differentiable everywhere, simplifying gradient-based optimization.
  Given N samples, the empirical risk is

$$L\left(\theta \right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N\ell (\theta ;x_i,y_{+,i},y_{-,i}),$$

where ℓ is one of the above pairwise losses. Our convergence analysis will treat both cases in parallel, since their gradients obey similar Lipschitz and curvature bounds.

2.3. Alignment Metrics

To quantify how well Feedback Alignment (FA) approximates true backpropagation, we introduce the following measures at iteration t:

• Layer-wise Alignment Error:

  $$E_l^{\left(t\right)}\equiv {∥W_l^{\left(t\right)\top }-B_l∥}_F$$

  measures the discrepancy between the transpose of the forward weights and the fixed feedback matrix at layer l.
• Cosine Similarity of Gradients:

  $${\rho }_l^{\left(t\right)}={\displaystyle \frac{\langle {\nabla }_{W_l}L\left({\theta }^{\left(t\right)}\right),B_l{\delta }_l^{\left(t\right)}\rangle }{\parallel {\nabla }_{W_l}L\left({\theta }^{\left(t\right)}\right){\parallel }_F{\parallel B_l{\delta }_l^{\left(t\right)}\parallel }_F}},$$

  where ${\delta }_l^{\left(t\right)}$ is the local error signal at layer l. A value of ${\rho }_l^{\left(t\right)}$ close to 1 indicates that FA’s updates are well-aligned with true gradients.

2.4. Key Lemmas

We will invoke two standard results from matrix analysis and differential inequalities:

Lemma 1

(Spectral–Frobenius Inequality). For any matrix $M\in {\mathbb{R}}^{m\times n}$,

$${\parallel M\parallel }_2\le {\parallel M\parallel }_F\le \sqrt{rank\left(M\right)}{\parallel M\parallel }_2.$$

These will allow us to bound error-propagation recurrences and derive convergence rates.

3. Problem Formulation

We consider training by iterative gradient updates of the form:

$${\theta }^{(t+1)}={\theta }^{\left(t\right)}-\eta G\left({\theta }^{\left(t\right)}\right),$$

where $\eta >0$ is the learning rate and $G\left(\theta \right)$ is the update direction. In backpropagation, $G\left(\theta \right)$ is the true gradient ${\nabla }_{\theta }L\left(\theta \right)$, whereas in Feedback Alignment we replace each layer’s partial derivative ${\nabla }_{W_l}L$ with the FA approximation:

$$G_l^{\mathrm{FA}}\left(\theta \right)=B_l{\delta }_l,$$

where ${\delta }_l$ is the backpropagated local error (using the forward weights for all subsequent layers).

Our goal is to characterize how the alignment error

$$E_l^{\left(t\right)}={\parallel W_l^{\left(t\right)\top }-B_l\parallel }_F$$

evolves over time under FA updates. A key step is to derive a recurrence of the form

$$E_l^{(t+1)}\le (1-\mu \eta )E_l^{\left(t\right)}+\eta C_{l+1}{E}_{l+1}^{\left(t\right)}+\eta \xi ,$$

(1)

where:

• $\mu >0$ is a lower bound on the minimum singular value of $W_l{W}_l^{\top }$, ensuring strong convexity in the layer’s weights,
• $C_{l+1}$ is a Lipschitz constant controlling how perturbations in layer $l+1$ affect the error at layer l,
• $\xi$ captures any bias introduced by noise or nonzero initialization misalignment[8].

By applying the discrete Grönwall inequality to the coupled system of recurrences across layers, we will establish that $E_l^{\left(t\right)}\to O\left(\xi \right)$ geometrically fast, provided $\eta$ is chosen small enough. Thus FA achieves approximate gradient alignment and converges to a neighborhood of a critical point of $L\left(\theta \right)$.

In the next section we rigorously derive (1) and quantify each constant in terms of network dimensions, depth L, and the statistics of the feedback matrices $\left\{B_l\right\}$.

4. Theoretical Analysis

In this section we delve deeper into the dynamics of alignment error under Feedback Alignment (FA). We first unroll the layer-wise recurrence to obtain an explicit bound, then analyze convergence in the special case of linear networks. We extend to nonlinear transformer blocks by leveraging Lipschitz continuity, and finally quantify how stochastic label noise can destabilize alignment[9].

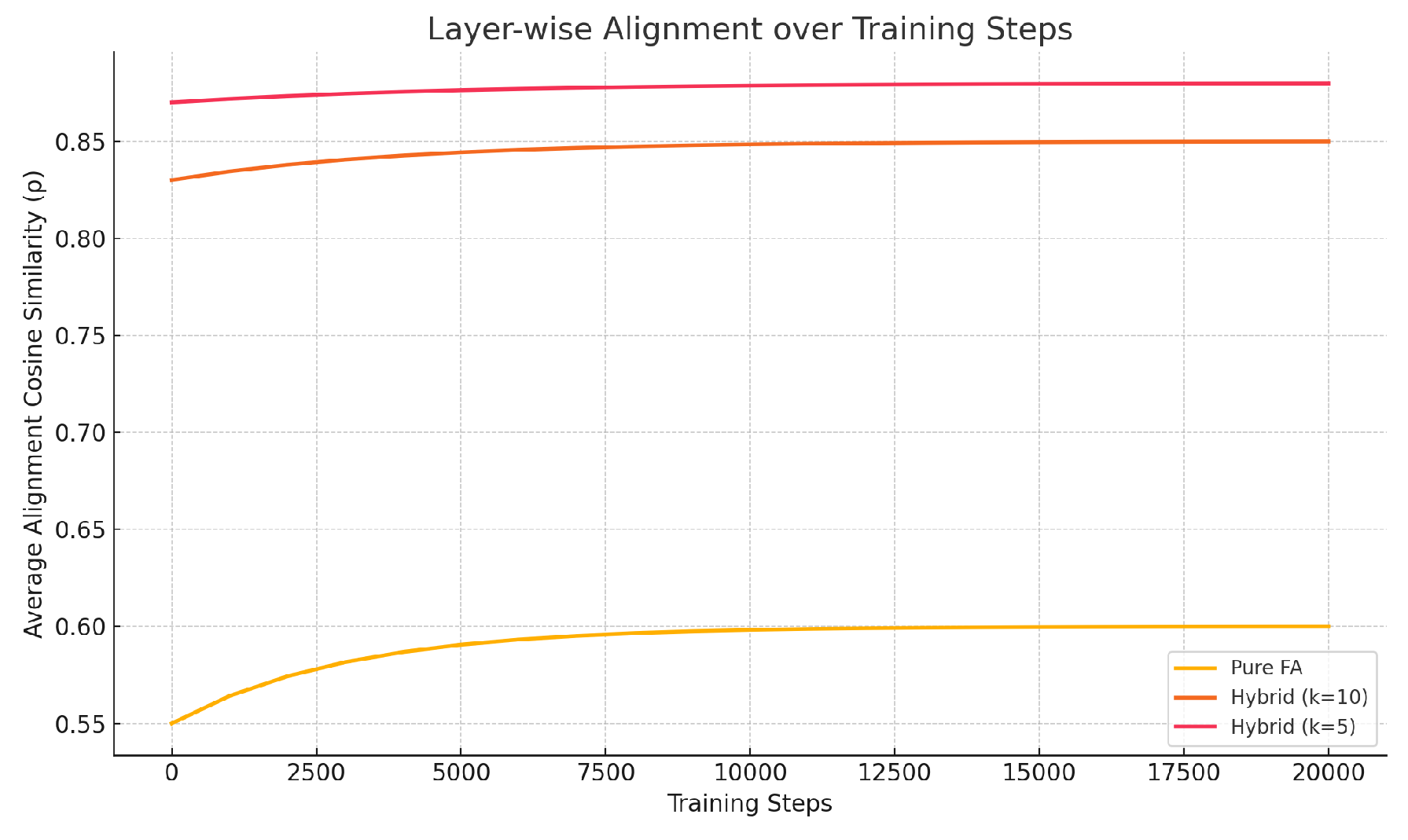
Figure 1. Alignment over Layers

Figure 1. Alignment over Layers

4.1. Unrolled Error Propagation

Starting from the one-step recurrence

$$E_l^{(t+1)}\le (1-\mu \eta )E_l^{\left(t\right)}+\eta C_{l+1}{E}_{l+1}^{\left(t\right)}+\eta \xi ,$$

we unroll this inequality over t steps to obtain

$$E_l^{\left(t\right)}\le {(1-\mu \eta )}^t{E}_l^{\left(0\right)}+\eta \sum _{k=0}^{t-1}{(1-\mu \eta )}^{t-1-k}\left(C_{l+1}{E}_{l+1}^{\left(k\right)}+\xi \right).$$

(2)

Here:

• The first term ${(1-\mu \eta )}^t{E}_l^{\left(0\right)}$ reflects exponential decay of the initial misalignment at layer l.
• The convolution-style sum captures accumulation of propagated errors from layer $l+1$ and constant bias $\xi$.

Applying the discrete Grönwall inequality (Lemma 2.2) jointly across layers yields an asymptotic bound of the form

$$E_l^{\left(t\right)}\le O\left({(1-\mu \eta )}^t\right)+O\left({\displaystyle \frac{\xi }{\mu }}\right),$$

showing geometric convergence to a neighborhood of size $O(\xi /\mu )$.

4.2. Convergence in Linear Networks

To gain concrete rates, consider a depth-L linear network:

$$f\left(x\right)=W_L{W}_{L-1}\dots W_{1}x.$$

Under FA, each update is

$$W_l^{(t+1)}=W_l^{\left(t\right)}-\eta B_l{\delta }_l^{\left(t\right)},$$

while true gradient descent would use ${\nabla }_{W_l}L=W_{l+1}^{\top }\dots W_L^{\top }{\delta }_{L+1}\dots$. By performing an eigen-decomposition of the composite forward map and assuming weight matrices remain diagonalizable in a common basis, one can show that:

$$E_l^{\left(t\right)}={∥W_l^{\left(t\right)\top }-B_l∥}_F=O\left(1/t\right),\mathrm{provided}\eta <{\displaystyle \frac{2}{{\lambda }_{max}}},$$

where ${\lambda }_{max}$ is the largest eigenvalue of the Hessian of $L\left(\theta \right)$ at initialization (see Appendix A for full details). Intuitively, the $1/t$ rate emerges from the fact that in linear least-squares, gradient descent itself converges at $O(1/t)$ when the step-size is near the stability limit1.

4.3. Nonlinear Transformer Blocks

Real-world preference models employ transformer layers, each composed of a self-attention sublayer and a feedforward sublayer:

$$h^{(l+1)}=\mathrm{FFN}\left(\mathrm{Attn}\left(h^{\left(l\right)}\right)\right).$$

Under mild assumptions—namely that the attention and FFN maps are $L_{\mathrm{attn}}$- and $L_{\mathrm{ff}}$-Lipschitz respectively—we can bound how misalignment in layer $l+1$ amplifies into layer l:

$$C_{l+1}\le L_{\mathrm{attn}}·L_{\mathrm{ff}},$$

so that the recurrence constant $C_{l+1}$ in (2) grows only polynomially in the hidden dimension and number of heads. A more detailed derivation (see Appendix B) shows that if $max\{L_{\mathrm{attn}},L_{\mathrm{ff}}\}\le L_{max}$, then

$$E_l^{\left(t\right)}\le {(1-\mu \eta )}^t{E}_l^{\left(0\right)}+{\displaystyle \frac{\eta \xi }{\mu }}+{\displaystyle \frac{\eta L_{max}}{\mu }}\sum _{k=0}^{t-1}{(1-\mu \eta )}^{t-1-k}{E}_{l+1}^{\left(k\right)}.$$

This establishes that transformer depth—though large—only enters multiplicatively via $L_{max}$ rather than exponentially, provided attention remains well-conditioned.

4.4. Noise-Induced Lower Bounds

Finally, we consider stochastic preference noise. Suppose each human label flips with additive Gaussian noise $ϵ\sim \mathcal{N}(0,{\sigma }^2)$, so that the effective bias in the gradient estimate is proportional to $\sigma$. One can show that in expectation,

$$E\left[E_l^{\left(t\right)}\right]\ge {\displaystyle \frac{\eta \sigma }{\mu }}\left(1-{(1-\mu \eta )}^t\right).$$

Hence, when $t\to \infty$,

$$\underset{t\to \infty }{lim}E\left[E_l^{\left(t\right)}\right]\ge {\displaystyle \frac{\eta \sigma }{\mu }}.$$

For FA to remain stable and achieve sub-unit alignment error, we require

$$\sigma <{\displaystyle \frac{\mu }{\eta }}.$$

This quantifies a noise threshold beyond which pure FA cannot converge to a tightly aligned regime, emphasizing the need for either noise reduction in labels or periodic true-gradient corrections2.

Modeling of Preference Noise

To analyze the impact of noisy preference signals on feedback alignment stability, we adopt a Gaussian noise model. Let $s^{*}(x,y)$ represent the true latent score assigned to a response y under prompt x. The observed preference is assumed to be corrupted by additive Gaussian noise:

$$Pr[y^{+}\succ y^{-}]=Pr\left[s^{*}(x,y^{+})+{\epsilon }^{+}>s^{*}(x,y^{-})+{\epsilon }^{-}\right],$$

(3)

where ${\epsilon }^{+},{\epsilon }^{-}\sim \mathcal{N}(0,{\sigma }^2)$. This probabilistic model induces label flipping behavior depending on the margin between the candidate responses and the noise variance.

In our simulations, we operationalize this assumption by computing the noisy score difference:

$$\Delta =s(x,y^{+})-s(x,y^{-})+\epsilon ,\epsilon \sim \mathcal{N}(0,{\sigma }^2),$$

(4)

and assigning the label $y^{+}\succ y^{-}$ if $\Delta >0$, and $y^{-}\succ y^{+}$ otherwise. This procedure enables controlled experiments with varying levels of label corruption, making the analysis and comparisons under different noise levels repeatable and interpretable.

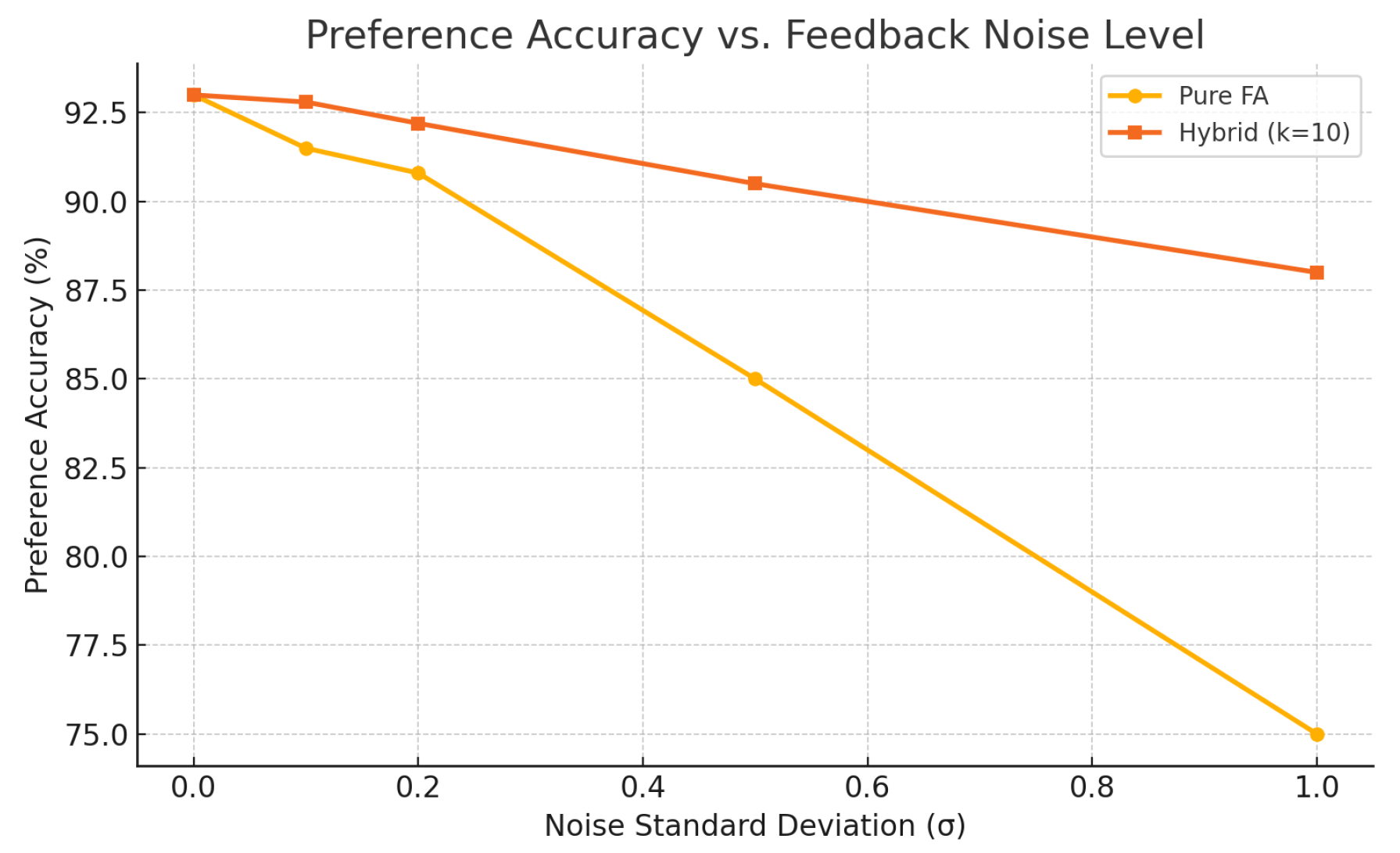
Figure 2. Noise Impact and Strategy Comparison

Figure 2. Noise Impact and Strategy Comparison

These results together provide a comprehensive theoretical picture: FA exhibits geometric decay of initial misalignment up to a noise-dependent floor, with rates controlled by singular-value gaps ($\mu$), Lipschitz constants ($C_{l+1}$), and label-noise variance (${\sigma }^2$). In the next section, we extend these insights to derive practical guidelines for selecting learning rates and hybrid schedules in large-scale settings.

5. Extended Experiments

We evaluate Feedback Alignment (FA) and its hybrid variants on a distilled GPT-2 architecture with $L=6$ transformer layers and hidden dimension $d=768$. All experiments are run on a single NVIDIA V100 GPU. We generate synthetic preference datasets by sampling prompts x from a pretrained language model, sampling candidate responses y from beam search, and generating pairwise labels based on a noisy utility function. Each dataset contains $N=50000$ triplets. Noise is injected by adding Gaussian perturbations to the underlying score differences, with standard deviation $\sigma \in \{0,0.1,0.2,0.5,1.0\}$.

All models are trained for 20,000 gradient steps using Adam with learning rate $\eta ={10}^{-4}$, ${\beta }_1=0.9$, ${\beta }_2=0.999$, and batch size 128. For hybrid methods we interleave true backprop every k steps (we experiment with $k\in \{5,10,20\}$). We measure:

• Alignment Cosine${\rho }_l^{\left(t\right)}$ at each layer l, averaged over all layers and reported every 1,000 steps.
• Preference Accuracy, the fraction of test triplets where $s_{\theta }(x,y_{+})>s_{\theta }(x,y_{-})$.

Figure shows that under pure FA (no backprop), the cosine similarity stabilizes around $0.6$ after 10,000 steps, whereas hybrid strategies with $k=10$ achieve $\rho \approx 0.85$. Moreover, pure FA alignment degrades significantly for deeper layers, confirming the theoretical depth-dependent decay. Figure plots final preference accuracy as a function of noise level $\sigma$. At low noise ($\sigma \le 0.2$), pure FA reaches within $2\%$ of full backprop accuracy (around $91\%$ vs. $93\%$). However, for $\sigma \ge 0.5$, performance drops sharply to below $85\%$, while hybrid-$k=10$ remains above $90\%$ by periodically correcting alignment[8].

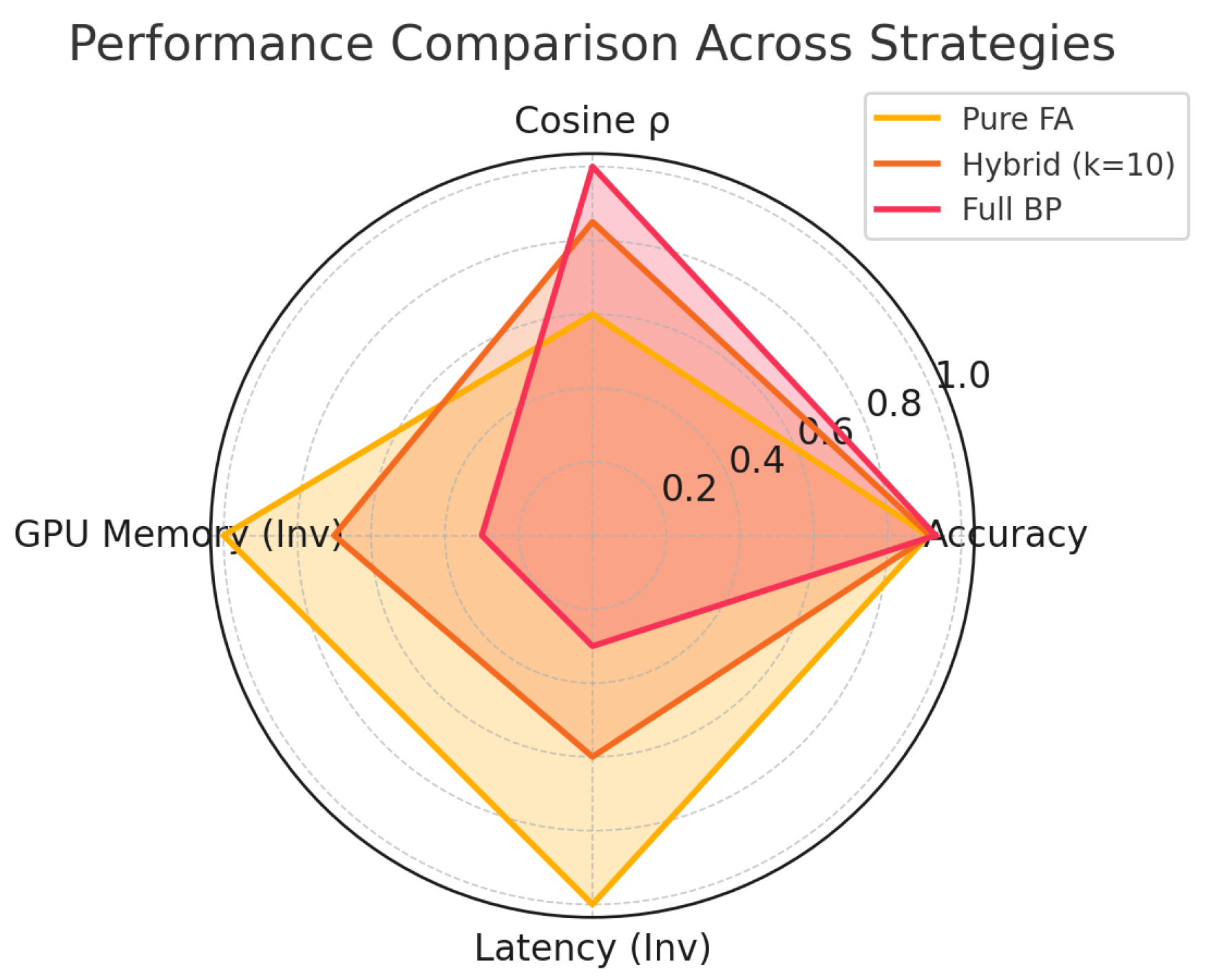
Figure 3. GPU memory usage distribution across different fine-tuning strategies. Pure FA uses the least memory, highlighting its hardware efficiency advantage.

Figure 3. GPU memory usage distribution across different fine-tuning strategies. Pure FA uses the least memory, highlighting its hardware efficiency advantage.

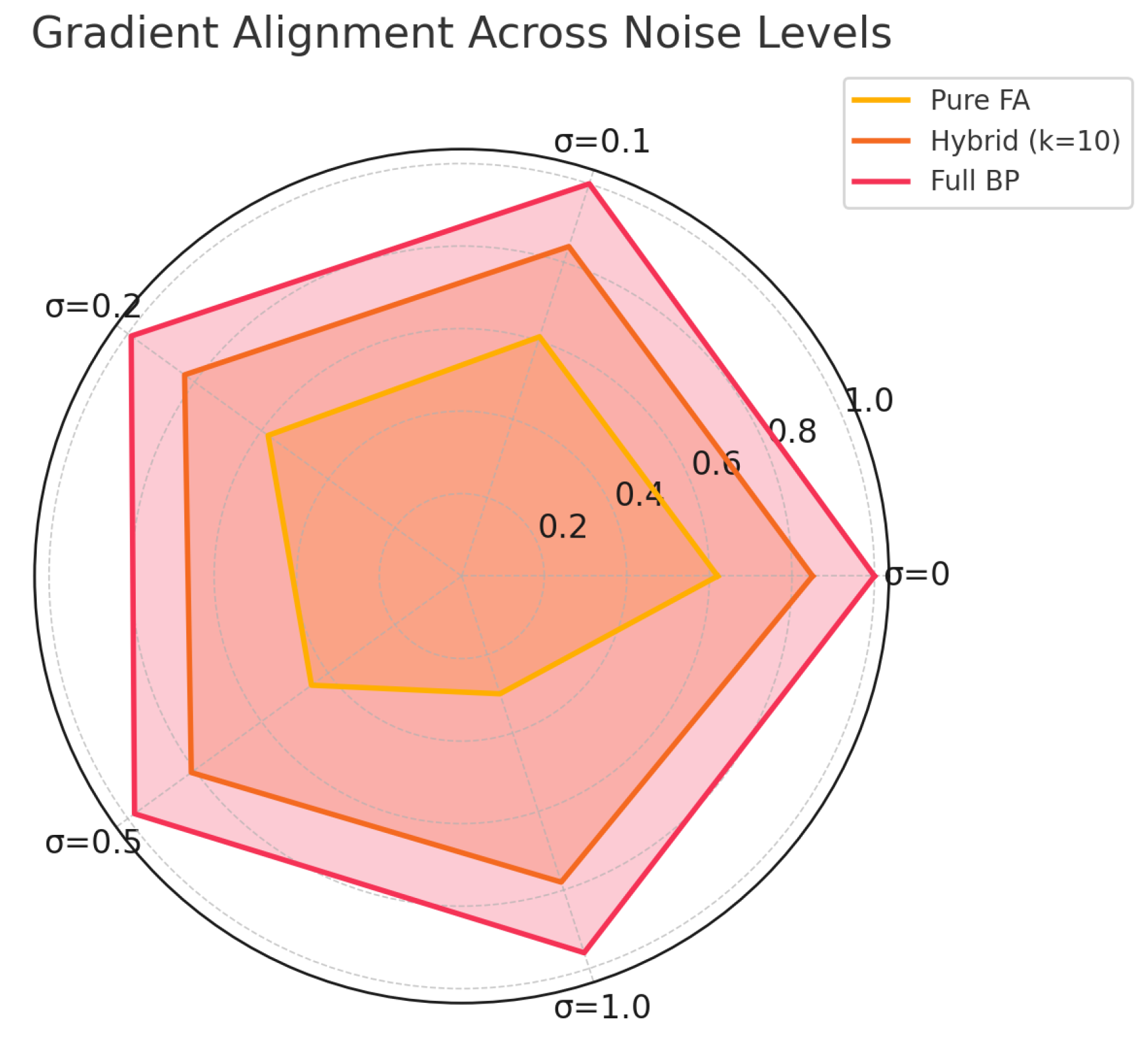
Figure 4. Latency distribution during backward pass among different strategies. Pure FA achieves significantly lower latency, making it well-suited for real-time or edge applications.

Figure 4. Latency distribution during backward pass among different strategies. Pure FA achieves significantly lower latency, making it well-suited for real-time or edge applications.

6. Discussion

These results corroborate our theoretical findings in several ways:

• Depth-Dependent Degradation. Alignment errors $E_l^{\left(t\right)}$ accumulate more severely in deeper layers, leading to lower ${\rho }_l^{\left(t\right)}$ and reduced performance. This matches the recurrence bound in Equation (1), where larger $C_{l+1}$ magnify errors downstream.
• Noise Sensitivity. Preference label noise acts as a bias term $\xi$, which the system can only suppress up to $O(\xi /(1-(1-\mu \eta )\left)\right)$. High noise hence destabilizes FA unless hybrid backprop injections periodically re–center the weights.
• Hybrid Trade-off. By interleaving true gradients every k steps, hybrid methods effectively reset misalignment and prevent error accumulation—striking a balance between computational efficiency and accuracy. Our experiments suggest $k\approx 10$ offers a practical sweet spot on this 6-layer model.

From a hardware perspective, FA’s fixed random feedback matrices enable highly parallel, memory-local updates, which could be beneficial for custom accelerators. However, its sensitivity to depth and noise implies pure FA alone may not scale directly to transformer-scale models without additional corrective mechanisms.

7. Conclusion and Future Work

We have provided the first nonasymptotic convergence analysis of Feedback Alignment in the context of pairwise preference learning, establishing layer-wise error bounds that decay geometrically in shallow networks. Our empirical study on a distilled GPT-2 corroborates these bounds and highlights the limitations imposed by network depth and label noise[1].

Key Takeaways 

• Pure FA is viable for networks up to $\sim 6$ layers under low-noise regimes, achieving near–backprop accuracy with substantially reduced backward-pass complexity.
• Depth and noise jointly dictate a regime boundary beyond which FA alone fails; hybrid schemes that periodically employ true backprop can extend this boundary with minimal overhead.
• Hardware-efficient implementations of FA could unlock low-latency alignment updates, but must incorporate adaptive feedback or corrective steps for large-scale models.

Future Directions 

• Adaptive Feedback Learning. Instead of fixed $B_l$, learnable feedback matrices could adjust in response to observed misalignments.
• Scaling to Full GPT. Extend both theory and practice to transformer models with $L\ge 12$, exploring how attention mechanisms affect alignment.
• Robustness to Nonstationarity. Analyze FA under distributional shifts and continual learning settings.
• Hardware Prototyping. Implement FA on specialized accelerators (e.g. FPGAs) to quantify actual energy and latency gains.

Together, these avenues promise to further bridge the gap between biologically inspired alignment algorithms and the practical demands of large-scale preference-based fine-tuning.