Submitted:
05 June 2025
Posted:
09 June 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Methods
3. Results
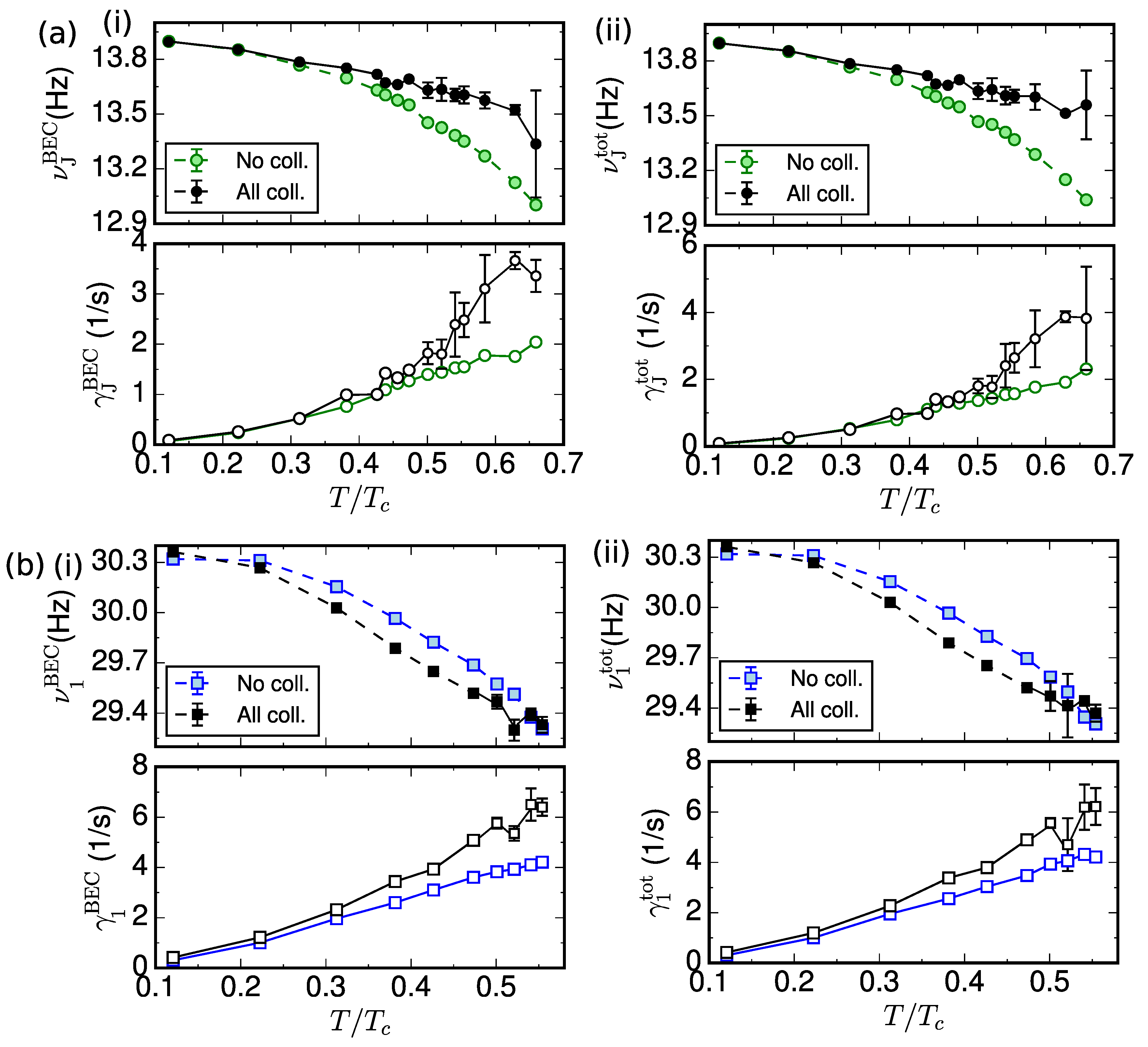
3.1. Effect of Collisions on the Frequency and Damping of Dominant Modes in the Josephson Plasma and Vortex-Induced Dissipative Regimes
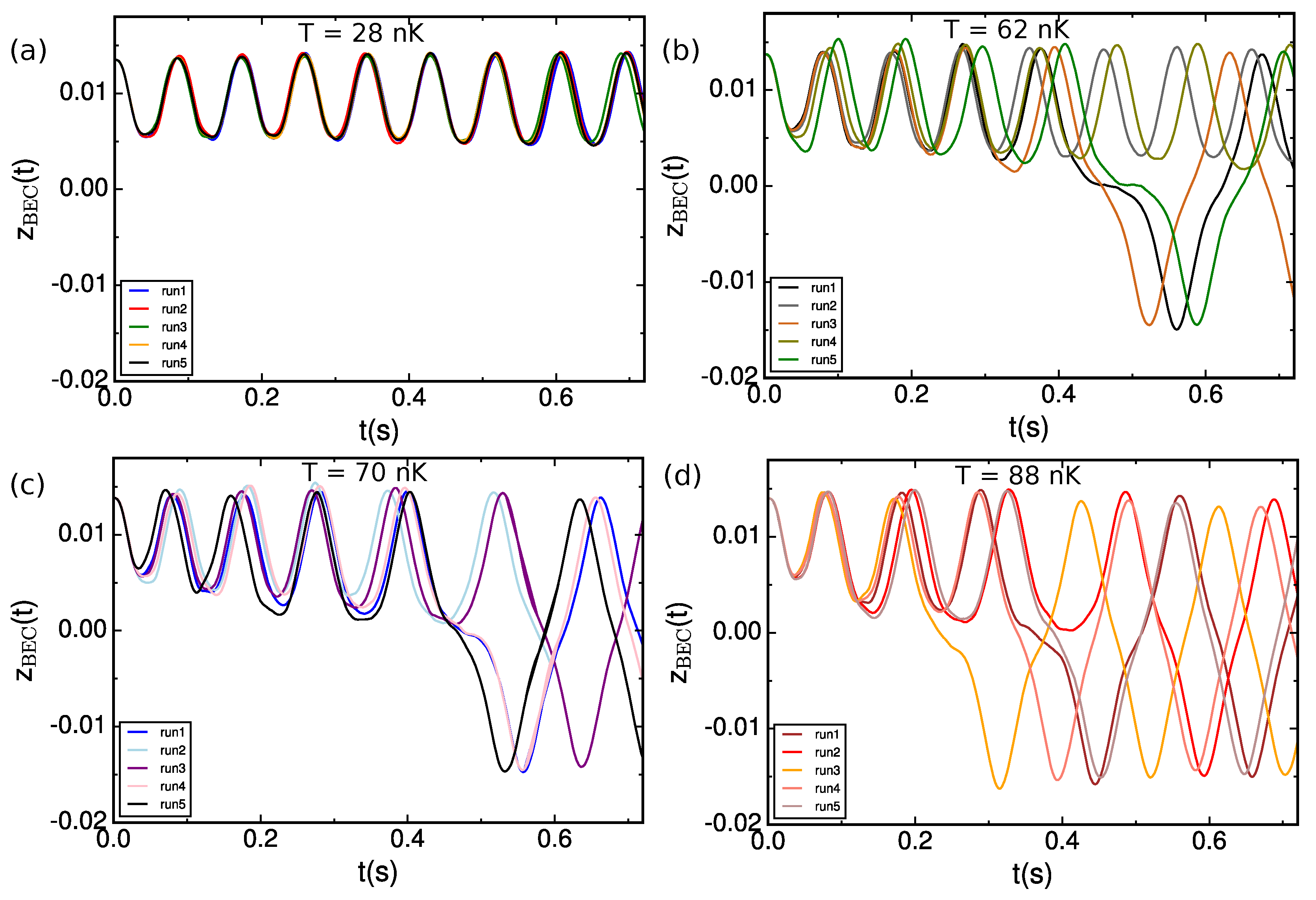
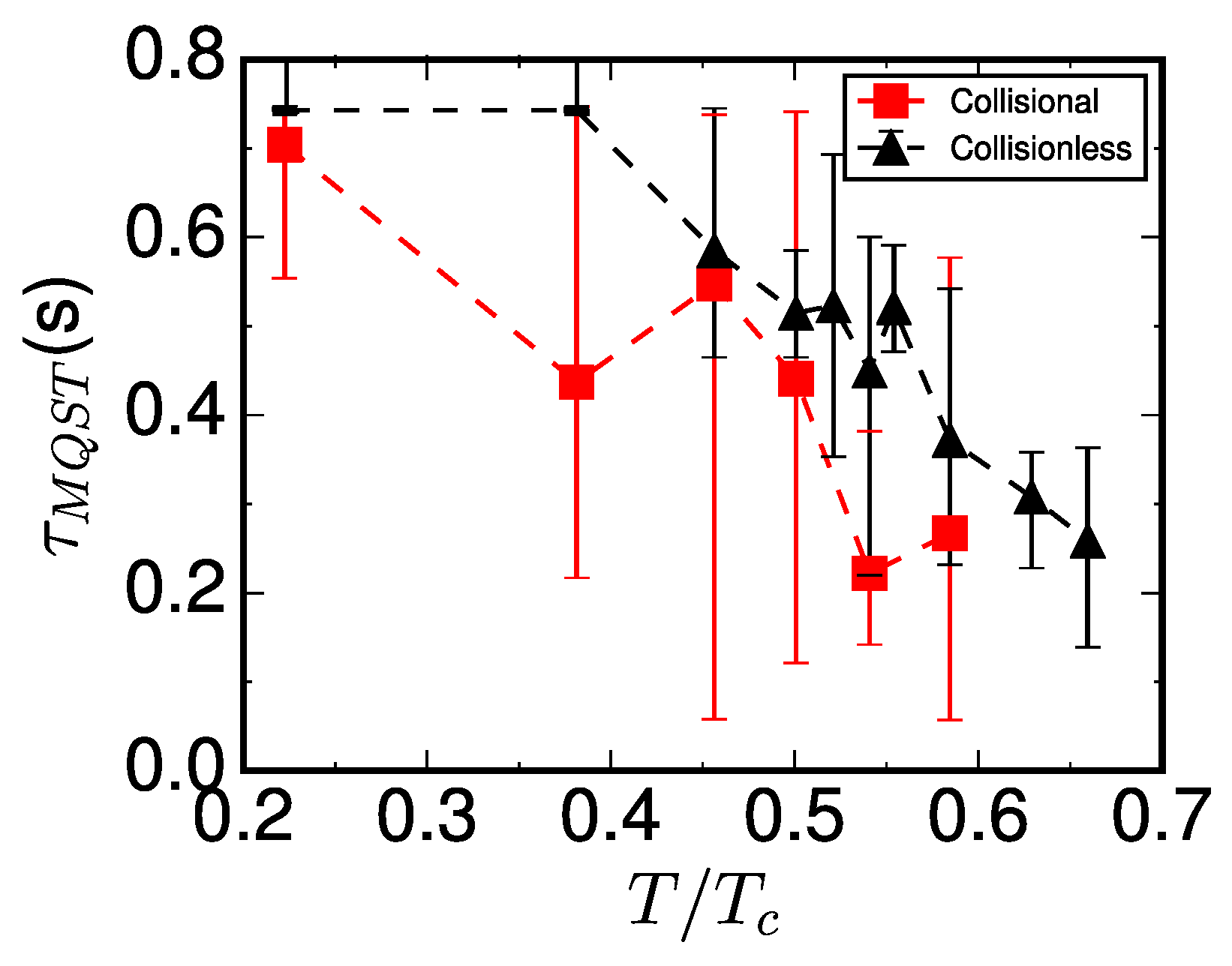
3.2. Role of Collisions on the Macroscopic Quantum Self-Trapping
4. Conclusions
Author Contributions
Data Availability Statement
Conflicts of Interest
Abbreviations
| BEC | Bose-Einstein condensate |
| GPE | Gross-Pitaevskii equation |
| ZNG | Zaremba-Nikuni-Griffin |
| JP | Josephson Plasma |
| VID | Vortex-Induced Dissipation |
| MQST | Macroscopic Quantum Self-Trapping |
References
- Avenel, O.; Varoquaux, E. Josephson effect and quantum phase slippage in superfluids. Phys. Rev. Lett. 1988, 60, 416–419. [Google Scholar] [CrossRef]
- Davis, J.C.; Packard, R.E. Superfluid 3He Josephson weak links. Rev. Mod. Phys. 2002, 74, 741–773. [Google Scholar] [CrossRef]
- Sato, Y.; Hoskinson, E.; Packard, R. Josephson Effects in Superfluid Helium. In Fundamentals and Frontiers of the Josephson Effect; Tafuri, F., Ed.; Springer, Cham, 2019; Vol. 286.
- Hoskinson, E.; Sato, Y.; Hahn, I.; Packard, R.E. Transition from phase slips to the Josephson effect in a superfluid 4He weak link. Nat. Phys. 2006, 2, 23–26. [Google Scholar] [CrossRef]
- Anderson, B.P.; Kasevich, M. Macroscopic quantum interference from atomic tunnel arrays. Science 1998, 282, 1686. [Google Scholar] [CrossRef]
- Cataliotti, F.S.; Burger, S.; Fort, C.; Maddaloni, P.; Minardi, F.; Trombettoni, A.; Smerzi, A.; Inguscio, M. Josephson Junction Arrays with Bose-Einstein Condensates. Science 2001, 293, 843–846. [Google Scholar] [CrossRef]
- Albiez, M.; Gati, R.; Fölling, J.; Hunsmann, S.; Cristiani, M.; Oberthaler, M.K. Direct Observation of Tunneling and Nonlinear Self-Trapping in a Single Bosonic Josephson Junction. Phys. Rev. Lett. 2005, 95, 010402. [Google Scholar] [CrossRef]
- Anker, T.; Albiez, M.; Gati, R.; Hunsmann, S.; Eiermann, B.; Trombettoni, A.; Oberthaler, M.K. Nonlinear Self-Trapping of Matter Waves in Periodic Potentials. Phys. Rev. Lett. 2005, 94, 020403. [Google Scholar] [CrossRef]
- Schumm, T.; Hofferberth, S.; Andersson, L.M.; Wildermuth, S.; Groth, S.; Bar-Joseph, I.; Schmiedmayer, J.; Krüger, P. Matter-wave interferometry in a double well on an atom chip. Nature Physics 2005, 1, 57–62. [Google Scholar] [CrossRef]
- Shin, Y.; Saba, M.; Pasquini, T.A.; Ketterle, W.; Pritchard, D.E.; Leanhardt, A.E. Atom Interferometry with Bose-Einstein Condensates in a Double-Well Potential. Phys. Rev. Lett. 2004, 92, 050405. [Google Scholar] [CrossRef]
- Levy, S.; Lahoud, E.; Shomroni, I.; Steinhauer, J. The a.c. and d.c. Josephson effects in a Bose–Einstein condensate. Nature 2007, 449, 579–583. [Google Scholar] [CrossRef]
- Spagnolli, G.; Semeghini, G.; Masi, L.; Ferioli, G.; Trenkwalder, A.; Coop, S.; Landini, M.; Pezzè, L.; Modugno, G.; Inguscio, M.; et al. Crossing Over from Attractive to Repulsive Interactions in a Tunneling Bosonic Josephson Junction. Phys. Rev. Lett. 2017, 118, 230403. [Google Scholar] [CrossRef] [PubMed]
- LeBlanc, L.J.; Bardon, A.B.; McKeever, J.; Extavour, M.H.T.; Jervis, D.; Thywissen, J.H.; Piazza, F.; Smerzi, A. Dynamics of a Tunable Superfluid Junction. Phys. Rev. Lett. 2011, 106, 025302. [Google Scholar] [CrossRef]
- Valtolina, G.; Burchianti, A.; Amico, A.; Neri, E.; Xhani, K.; Seman, J.A.; Trombettoni, A.; Smerzi, A.; Zaccanti, M.; Inguscio, M.; et al. Josephson effect in fermionic superfluids across the BEC-BCS crossover. Science 2015, 350, 1505–1508. [Google Scholar] [CrossRef]
- Burchianti, A.; Scazza, F.; Amico, A.; Valtolina, G.; Seman, J.A.; Fort, C.; Zaccanti, M.; Inguscio, M.; Roati, G. Connecting Dissipation and Phase Slips in a Josephson Junction between Fermionic Superfluids. Phys. Rev. Lett. 2018, 120, 025302. [Google Scholar] [CrossRef]
- Kwon, W.J.; Del Pace, G.; Panza, R.; Inguscio, M.; Zwerger, W.; Zaccanti, M.; Scazza, F.; Roati, G. Strongly correlated superfluid order parameters from dc Josephson supercurrents. Science 2020, 369, 84–88. [Google Scholar] [CrossRef]
- Luick, N.; Sobirey, L.; Bohlen, M.; Singh, V.P.; Mathey, L.; Lompe, T.; Moritz, H. An ideal Josephson junction in an ultracold two-dimensional Fermi gas. Science 2020, 369, 89–91. [Google Scholar] [CrossRef]
- Del Pace, G.; Kwon, W.J.; Zaccanti, M.; Roati, G.; Scazza, F. Tunneling Transport of Unitary Fermions across the Superfluid Transition. Phys. Rev. Lett. 2021, 126, 055301. [Google Scholar] [CrossRef]
- Josephson, B.D. Possible new effects in superconductive tunnelling. Phys. Lett. 1962, 1, 251–253. [Google Scholar] [CrossRef]
- Anderson, P.W.; Rowell, J.M. Probable Observation of the Josephson Superconducting Tunneling Effect. Phys. Rev. Lett. 1963, 10, 230–232. [Google Scholar] [CrossRef]
- Barone, A.; Paterno, G. Physics and Applications of the Josephson Effect; John Wiley: New York, 1982. [Google Scholar]
- Milburn, G.J.; Corney, J.; Wright, E.M.; Walls, D.F. Quantum dynamics of an atomic Bose-Einstein condensate in a double-well potential. Phys. Rev. A 1997, 55, 4318–4324. [Google Scholar] [CrossRef]
- Smerzi, A.; Fantoni, S.; Giovanazzi, S.; Shenoy, S.R. Quantum Coherent Atomic Tunneling between Two Trapped Bose-Einstein Condensates. Phys. Rev. Lett. 1997, 79, 4950–4953. [Google Scholar] [CrossRef]
- Zapata, I.; Sols, F.; Leggett, A.J. Josephson effect between trapped Bose-Einstein condensates. Phys. Rev. A 1998, 57, R28–R31. [Google Scholar] [CrossRef]
- Raghavan, S.; Smerzi, A.; Fantoni, S.; Shenoy, S.R. Coherent oscillations between two weakly coupled Bose-Einstein condensates: Josephson effects, π oscillations, and macroscopic quantum self-trapping. Phys. Rev. A 1999, 59, 620–633. [Google Scholar] [CrossRef]
- Ruostekoski, J.; Walls, D.F. Bose-Einstein condensate in a double-well potential as an open quantum system. Phys. Rev. A 1998, 58, R50–R53. [Google Scholar] [CrossRef]
- Meier, F.; Zwerger, W. Josephson tunneling between weakly interacting Bose-Einstein condensates. Phys. Rev. A 2001, 64, 033610. [Google Scholar] [CrossRef]
- Paraoanu, G.S.; Kohler, S.; Sols, F.; Leggett, A.J. The Josephson plasmon as a Bogoliubov quasiparticle. Journal of Physics B: Atomic, Molecular and Optical Physics 2001, 34, 4689–4696. [Google Scholar] [CrossRef]
- Kohler, S.; Sols, F. Chemical potential standard for atomic Bose–Einstein condensates. New Journal of Physics 2003, 5, 94. [Google Scholar] [CrossRef]
- Sakellari, E.; Leadbeater, M.; Kylstra, N.J.; Adams, C.S. Josephson spectroscopy of a dilute Bose-Einstein condensate in a double-well potential. Phys. Rev. A 2002, 66, 033612. [Google Scholar] [CrossRef]
- Sakellari, E.; Proukakis, N.P.; Leadbeater, M.; Adams, C.S. Josephson tunnelling of a phase-imprinted Bose–Einstein condensate in a time-dependent double-well potential. New Journal of Physics 2004, 6, 42–42. [Google Scholar] [CrossRef]
- Zou, P.; Dalfovo, F. Josephson oscillations and self-trapping of superfluid fermions in a double-well potential. J Low Temp. Phys. 2014, 177, 240. [Google Scholar] [CrossRef]
- Abad, M..; Guilleumas, M..; Mayol, R..; Piazza, F..; Jezek, D. M..; Smerzi, A.. Phase slips and vortex dynamics in Josephson oscillations between Bose-Einstein condensates. EPL 2015, 109, 40005. [Google Scholar] [CrossRef]
- Bidasyuk, Y.M.; Weyrauch, M.; Momme, M.; Prikhodko, O.O. Finite-temperature dynamics of a bosonic Josephson junction. J. Phys. B 2018, 51, 205301. [Google Scholar] [CrossRef]
- Polo, J.; Ahufinger, V.; Hekking, F.W.J.; Minguzzi, A. Damping of Josephson Oscillations in Strongly Correlated One-Dimensional Atomic Gases. Phys. Rev. Lett. 2018, 121, 090404. [Google Scholar] [CrossRef]
- Polo, J.; Dubessy, R.; Pedri, P.; Perrin, H.; Minguzzi, A. Oscillations and Decay of Superfluid Currents in a One-Dimensional Bose Gas on a Ring. Phys. Rev. Lett. 2019, 123, 195301. [Google Scholar] [CrossRef]
- Xhani, K.; Neri, E.; Galantucci, L.; Scazza, F.; Burchianti, A.; Lee, K.L.; Barenghi, C.F.; Trombettoni, A.; Inguscio, M.; Zaccanti, M.; et al. Critical Transport and Vortex Dynamics in a Thin Atomic Josephson Junction. Phys. Rev. Lett. 2020, 124, 045301. [Google Scholar] [CrossRef]
- Xhani, K.; Galantucci, L.; Barenghi, C.F.; Roati, G.; Trombettoni, A.; Proukakis, N.P. Dynamical phase diagram of ultracold Josephson junctions. New Journal of Physics 2020, 22, 123006. [Google Scholar] [CrossRef]
- Xhani, K.; Proukakis, N.P. Dissipation in a finite-temperature atomic Josephson junction. Phys. Rev. Res. 2022, 4, 033205. [Google Scholar] [CrossRef]
- Wlazłowski, G.; Xhani, K.; Tylutki, M.; Proukakis, N.P.; Magierski, P. Dissipation Mechanisms in Fermionic Josephson Junction. Phys. Rev. Lett. 2023, 130, 023003. [Google Scholar] [CrossRef]
- Furutani, K.; Tempere, J.; Salasnich, L. Quantum effective action for the bosonic Josephson junction. Phys. Rev. B 2022, 105, 134510. [Google Scholar] [CrossRef]
- Bardin, A.; Lorenzi, F.; Salasnich, L. Quantum fluctuations in atomic Josephson junctions: the role of dimensionality. New Journal of Physics 2024, 26, 013021. [Google Scholar] [CrossRef]
- Ji, S.C.; Schweigler, T.; Tajik, M.; Cataldini, F.; Sabino, J.a.; Møller, F.S.; Erne, S.; Schmiedmayer, J. Floquet Engineering a Bosonic Josephson Junction. Phys. Rev. Lett. 2022, 129, 080402. [Google Scholar] [CrossRef] [PubMed]
- Pace, G.D.; Hernández-Rajkov, D.; Singh, V.P.; Grani, N.; Fernández, M.F.; Nesti, G.; Seman, J.A.; Inguscio, M.; Amico, L.; Roati, G. Shapiro steps in strongly-interacting Fermi gases, 2024, [arXiv:cond-mat.quant-gas/2409.03448].
- Bernhart, E.; Röhrle, M.; Singh, V.P.; Mathey, L.; Amico, L.; Ott, H. Observation of Shapiro steps in an ultracold atomic Josephson junction, 2024, [arXiv:cond-mat.quant-gas/2409.03340].
- Gauthier, G.; Szigeti, S.S.; Reeves, M.T.; Baker, M.; Bell, T.A.; Rubinsztein-Dunlop, H.; Davis, M.J.; Neely, T.W. An atomtronic oscillator circuit for quantum gases. arXiv e-prints 2019, p. arXiv:1903.04086, [arXiv:cond-mat.quant-gas/1903.04086].
- Pigneur, M.; Berrada, T.; Bonneau, M.; Schumm, T.; Demler, E.; Schmiedmayer, J. Relaxation to a Phase-Locked Equilibrium State in a One-Dimensional Bosonic Josephson Junction. Phys. Rev. Lett. 2018, 120, 173601. [Google Scholar] [CrossRef]
- Furutani, K.; Salasnich, L. Interaction-induced dissipative quantum phase transition in a head-to-tail atomic Josephson junction. Phys. Rev. B 2024, 110, L140503. [Google Scholar] [CrossRef]
- Saha, A.K.; Dubessy, R. Dynamical phase diagram of a one-dimensional Bose gas in a box with a tunable weak link: From Bose-Josephson oscillations to shock waves. Phys. Rev. A 2021, 104, 023316. [Google Scholar] [CrossRef]
- Momme, M.R.; Bidasyuk, Y.M.; Weyrauch, M. Collective excitations and tunneling dynamics in long bosonic Josephson junctions. Phys. Rev. A 2019, 100, 033601. [Google Scholar] [CrossRef]
- Labouvie, R.; Santra, B.; Heun, S.; Wimberger, S.; Ott, H. Negative Differential Conductivity in an Interacting Quantum Gas. Phys. Rev. Lett. 2015, 115, 050601. [Google Scholar] [CrossRef] [PubMed]
- Begg, S.E.; Davis, M.J.; Reeves, M.T. Nonequilibrium Transport in a Superfluid Josephson Junction Chain: Is There Negative Differential Conductivity? Phys. Rev. Lett. 2024, 132, 103402. [Google Scholar] [CrossRef]
- Saha, A.K.; Ray, D.S.; Deb, B. Phase diffusion and fluctuations in a dissipative Bose-Josephson junction. Phys. Rev. E 2023, 107, 034141. [Google Scholar] [CrossRef]
- Lagoudakis, K.G.; Pietka, B.; Wouters, M.; André, R.; Deveaud-Plédran, B. Coherent Oscillations in an Exciton-Polariton Josephson Junction. Phys. Rev. Lett. 2010, 105, 120403. [Google Scholar] [CrossRef]
- Adiyatullin, A.F.; Anderson, M.D.; Flayac, H.; Portella-Oberli, M.T.; Jabeen, F.; Ouellet-Plamondon, C.; Sallen, G.C.; Deveaud, B. Periodic squeezing in a polariton Josephson junction. Nature Communications 2017, 8, 1329. [Google Scholar] [CrossRef]
- D’Errico, C.; Abbate, S.S.; Modugno, G. Quantum transport in ultracold atoms. Philos. Trans. Royal Soc. A 2017, 375, 20160425. [Google Scholar]
- Wright, K.C.; Blakestad, R.B.; Lobb, C.J.; Phillips, W.D.; Campbell, G.K. Driving Phase Slips in a Superfluid Atom Circuit with a Rotating Weak Link. Phys. Rev. Lett. 2013, 110, 025302. [Google Scholar] [CrossRef]
- Griffin, A.; Nikuni, T.; Zaremba, E. Bose-Condensed Gases at Finite Temperatures; Cambridge University Press, 2009. [CrossRef]
- Jackson, B.; Zaremba, E. Modeling Bose-Einstein condensed gases at finite temperatures with N-body simulations. Phys. Rev. A 2002, 66, 033606. [Google Scholar] [CrossRef]
- Proukakis, N.P.; Jackson, B. Finite-temperature models of Bose–Einstein condensation. J. Phys. B: At. Mol. Opt. Phys. 2008, 41, 203002. [Google Scholar] [CrossRef]
- Lee, K.L.; Proukakis, N.P. Non-equilibrium atomic condensates and mixtures: collective modes, condensate growth and thermalisation. J. Phys. B: At. Mol. Opt. Phys. 2016, 49, 214003. [Google Scholar] [CrossRef]
- Lee, K.L.; Jørgensen, N.B.; Liu, I.K.; Wacker, L.; Arlt, J.J.; Proukakis, N.P. Phase separation and dynamics of two-component Bose-Einstein condensates. Phys. Rev. A 2016, 94, 013602. [Google Scholar] [CrossRef]
- Blakie, P.B.; Bradley, A.S.; Davis, M.J.; Ballagh, R.J.; Gardiner, C.W. Dynamics and statistical mechanics of ultra-cold Bose gases using c-field techniques. Advances in Physics 2008, arXiv:cond-mat.stat-mech/0809.1487]57, 363–455. [Google Scholar] [CrossRef]
- Proukakis, N.; Gardiner, S.; Davis, M.; Szymańska, M. (Eds.) Quantum Gases: Finite Temperature and Non-Equilibrium Dynamics; Imperial College Press: London, United Kingdom, 2013. [Google Scholar]
- Rooney, S.J.; Allen, A.J.; Zülicke, U.; Proukakis, N.P.; Bradley, A.S. Reservoir interactions of a vortex in a trapped three-dimensional Bose-Einstein condensate. Phys. Rev. A 2016, 93, 063603. [Google Scholar] [CrossRef]
- Proukakis, N.P.; Rigopoulos, G.; Soto, A. Self-Consistent Stochastic Finite-Temperature Modelling: Ultracold Bose Gases with Local (s-wave) and Long-Range (Dipolar) Interactions, 2024, [arXiv:cond-mat.quant-gas/2407.20178].
- Jackson, B.; Proukakis, N.P.; Barenghi, C.F.; Zaremba, E. Finite-temperature vortex dynamics in Bose-Einstein condensates. Phys. Rev. A 2009, 79, 053615. [Google Scholar] [CrossRef]
- Jackson, B.; Proukakis, N.P.; Barenghi, C.F. Dark-soliton dynamics in Bose-Einstein condensates at finite temperature. Phys. Rev. A 2007, 75, 051601. [Google Scholar] [CrossRef]
- Allen, A.J.; Zaremba, E.; Barenghi, C.F.; Proukakis, N.P. Observable vortex properties in finite-temperature Bose gases. Phys. Rev. A 2013, 87, 013630. [Google Scholar] [CrossRef]
- Allen, A.J.; Zuccher, S.; Caliari, M.; Proukakis, N.P.; Parker, N.G.; Barenghi, C.F. Vortex reconnections in atomic condensates at finite temperature. Phys. Rev. A 2014, 90, 013601. [Google Scholar] [CrossRef]
- Arahata, E.; Nikuni, T. Propagation of first and second sound in a highly elongated trapped Bose-condensed gas at finite temperatures. Phys. Rev. A 2013, 87, 033610. [Google Scholar] [CrossRef]
- Märkle, J.; Allen, A.J.; Federsel, P.; Jetter, B.; Günther, A.; Fortágh, J.; Proukakis, N.P.; Judd, T.E. Evaporative cooling of cold atoms at surfaces. Phys. Rev. A 2014, 90, 023614. [Google Scholar] [CrossRef]
- Jackson, B.; Zaremba, E. Quadrupole Collective Modes in Trapped Finite-Temperature Bose-Einstein Condensates. Phys. Rev. Lett. 2002, 88, 180402. [Google Scholar] [CrossRef]
- Jackson, B.; Zaremba, E. Finite-Temperature Simulations of the Scissors Mode in Bose-Einstein Condensed Gases. Phys. Rev. Lett. 2001, 87, 100404. [Google Scholar] [CrossRef]
- Straatsma, C.J.E.; Colussi, V.E.; Davis, M.J.; Lobser, D.S.; Holland, M.J.; Anderson, D.Z.; Lewandowski, H.J.; Cornell, E.A. Collapse and revival of the monopole mode of a degenerate Bose gas in an isotropic harmonic trap. Phys. Rev. A 2016, 94, 043640. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




