Submitted:
05 June 2025
Posted:
05 June 2025
You are already at the latest version
Abstract
Keywords:
1. Reasoning, Logic, and Rationality
2. Reasoning and Reversibility
2.1. Intrapropositional Operations of Thought
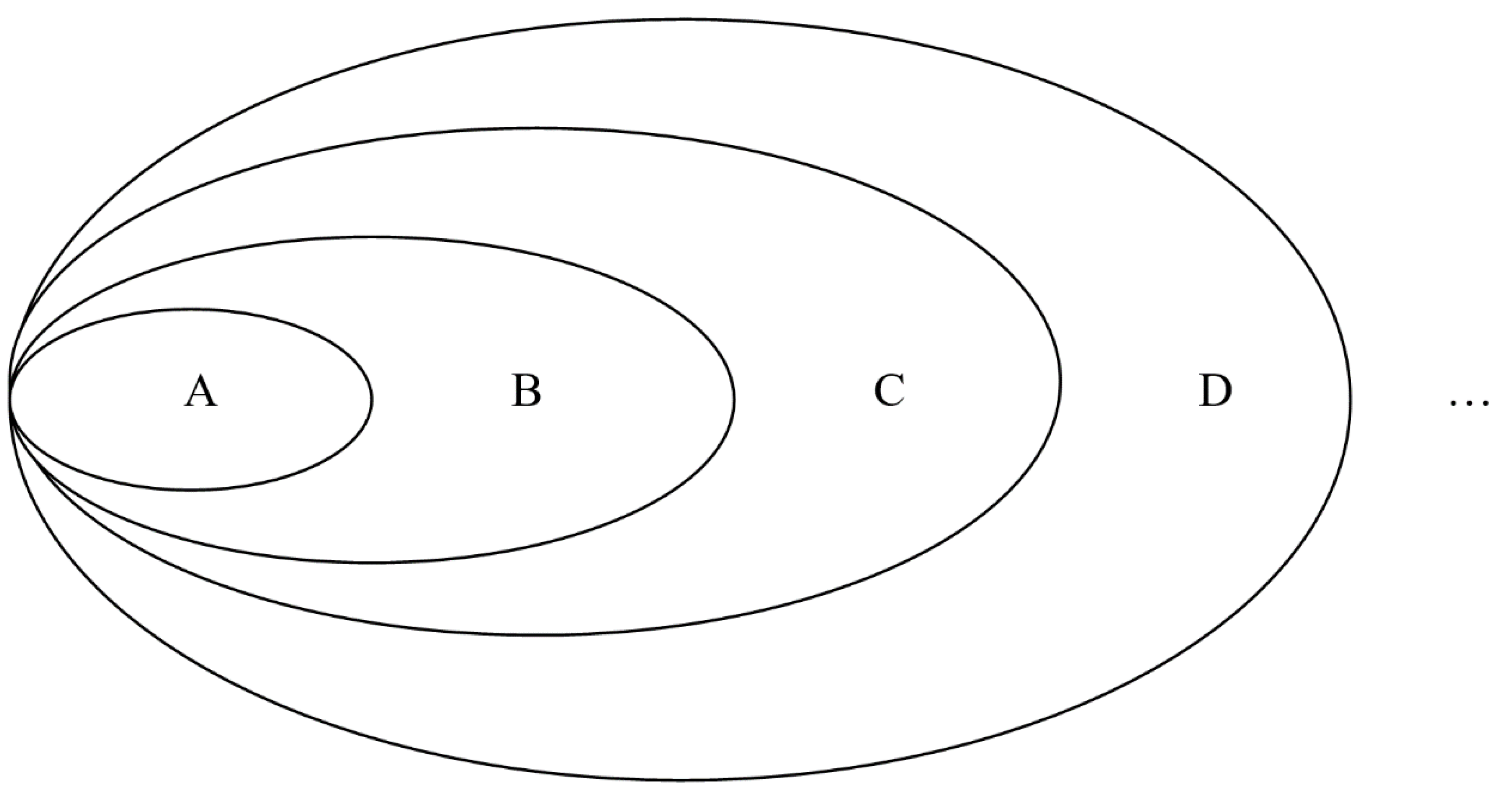
2.1.1. Reasoning with Classes
- The direct operation consists in adding a class ofthe system to another thus forming the union of these classes; for example, , , etc.
- The inverse operation cancels the outcome of thedirect operation by negating a class in a union created by addition so that therelative complement remains; for example, ; ; ; ; etc.
- The general identity operation simultaneously fulfils the following two criteria: (a) composed with an arbitrary element of the grouping, it leaves it invariant; and (b) it is the outcome of the composition of the direct and inverse operations; for example, (a) , , etc.; and (b) ; ; ; etc. [24], see also [23]
2.2. Interpropositional Operations of Thought
2.2.1. Groups of Inversions
2.2.2. Instrumentalization of Structural Possibilities
3. Alternative Strategies in the Rationality Debate
4. Conclusions
Conflicts of Interest
| 1 | "Piaget incorporated the logicist tradition into this theory of cognitive development, proposing that adults eventually developed formal operational thinking on the basis of abstract logical structures” [15] is the way Evans expressed this point almost two decades prior. I believe this is the more accurate formulation, and I hope that I can convince the reader by the end of the paper. |
| 2 | iaget pursued constructivist ends whilst modelling propositional reasoning and found it convenient to use the symbolism of propositional logic; however, he stressed that the symbols do not have the familiar logical meanings [23] ,see also [37]. Piaget used this formalism in Traité de logique, essai de logistique opératoire (1949), his standard work on reasoning; in the second edition, Essai de logique opératoire (1972), it was partially, some might say inadequately, revised to bring it more in line with logical conventions [18,24,38]; nevertheless, I adopt Piaget’s notation for the logical operators to facilitate referencing, although it is partially antiquated and idiosyncratic. |
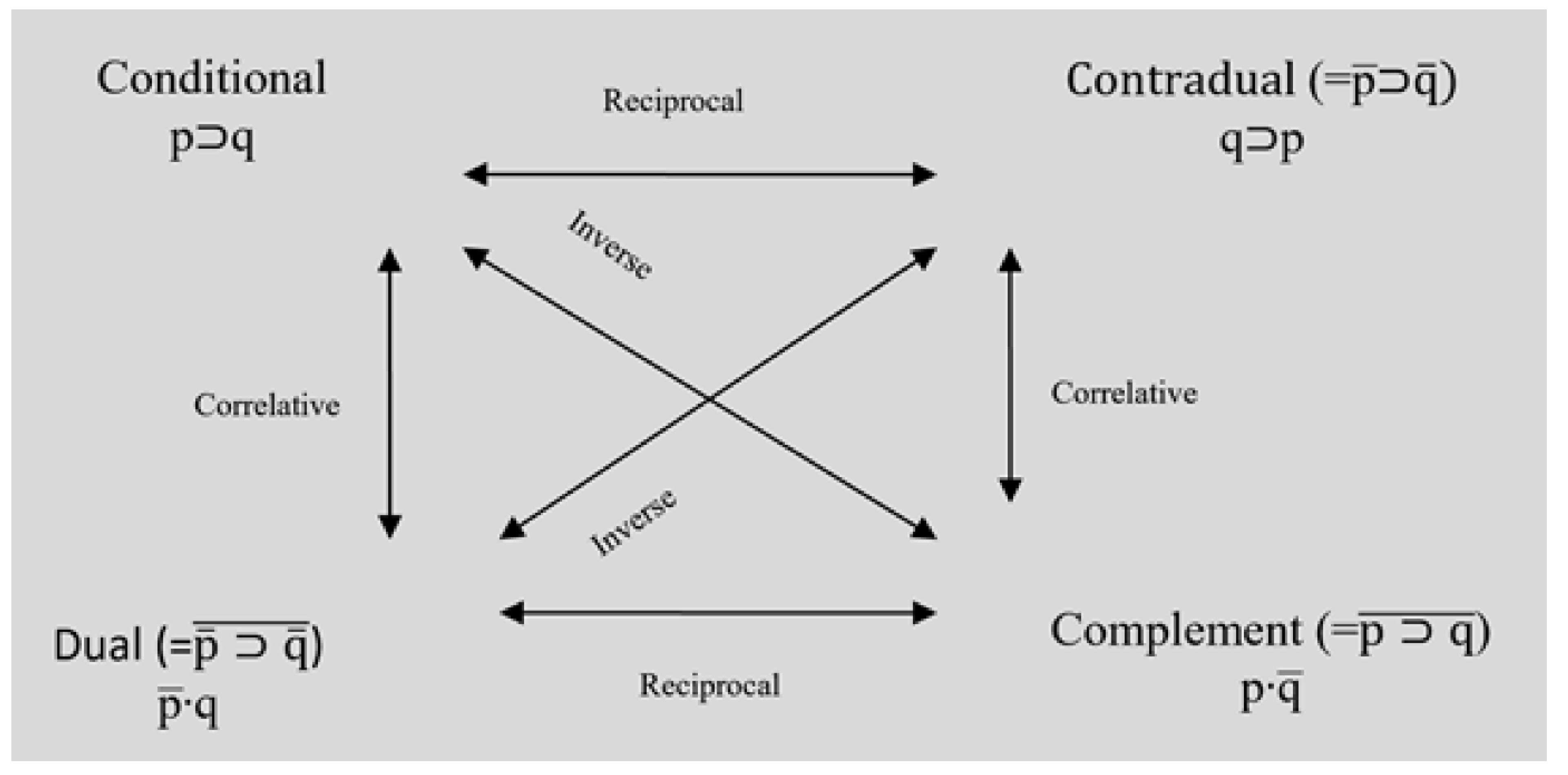
| 3 | ccording to Halmos, confusion surrounds the principle of duality even amongst experienced mathematicians, and it seems as though Piaget was also one of its casualties. The principle of duality actually corresponds to swapping the conjunctions for disjunctions only (in Piaget’s terminology this is the correlative operation). Nevertheless, swapping both is indeed a negation, namely, the complement. |
| 4 | rounds for the designation “reciprocal” come from the way the operation reverses the order of the propositions in the conditional, effectively transforming the conditional into its contradual [24]. |
| 5 | he identity operation is explicitly mentioned in the essential operatory mechanisms characterizing the interpropositional grouping. Complementation, in contrast, is not; however, referring back to Table 1, I have already mentioned that Piaget organised the columns in pairs, and, via disjunctive and conjunctive compositions of the disjunctive normal forms of these column pairs, Piaget showed that they constitute complementaries; column pair 3 and 4, for example, |
| 6 | t might be objected that the interpropositional grouping involving two propositions is not representative of all interpropositional groupings; with respect to non-triviality, however, even the interpropositional grouping involving single propositions has 4 equivalence classes and is therefore non-trivial [24]. |
References
- Wason, P.C. Reasoning. In New Horizons in Psychology; Foss, B.M., Ed.; Penguin Books: Harmondsworth, Middx., 1966; pp. 135–151.
- Wason, P.C.; Johnson-Laird, P.N. Psychology of Reasoning: Structure and Content; Harvard University Press, 1972; Vol. 86.
- Kahneman, D.; Slovic, S.P.; Slovic, P.; Tversky, A. Judgment under Uncertainty: Heuristics and Biases; Cambridge university press, 1982.
- Tversky, A.; Kahneman, D. Extensional versus Intuitive Reasoning: The Conjunction Fallacy in Probability Judgment. Psychological review 1983, 90, 293.
- Samuels, R.; Stich, S.; Faucher, L. Reason and Rationality. In Handbook of epistemology; Springer, 2004; pp. 131–179.
- Samuels, R.; Stich, S. Rationality. In Encyclopedia of Cognitive Science; Nadel, L., Ed.; John Wiley & Sons, Ltd: Chichester, 2006; p. s00171 ISBN 978-0-470-01619-0.
- Evans, J.S.B.T. The Rationality Debate in the Psychology of Reasoning: A Historical Review. 2021. [CrossRef]
- Carruthers, P. Review of Without Good Reason: The Rationality Debate in Philosophy and Cognitive Science; Rationality and Reasoning. The British Journal for the Philosophy of Science 1998, 49, 189–193.
- Brierton, D. Review of Without Good Reason: The Rationality Debate in Philosophy and Cognitive Science. Philosophy 1997, 72, 482–486.
- Galloway, D. Review of Without Good Reason. Philosophy and Phenomenological Research 2000, 60, 234–237. [CrossRef]
- Stein, E. Without Good Reason: The Rationality Debate in Philosophy and Cognitive Science; Clarendon Press, 1996.
- Cohen, L.J. Can Human Irrationality Be Experimentally Demonstrated? Behavioral and Brain Sciences 1981, 4, 317–331. [CrossRef]
- Hanna, R. Rationality and Logic; MIT Press: Cambridge Massachusetts; London England, 2006; ISBN 978-0-262-08349-2.
- Harman, G. Logic and Reasoning. In Foundations: Logic, Language, and Mathematics; Leblanc, H., Mendelson, E., Orenstein, A., Eds.; Springer Netherlands: Dordrecht, 1984; pp. 107–127 ISBN 978-94-017-1592-8.
- Evans, J.St.B.T. Logic and Human Reasoning: An Assessment of the Deduction Paradigm. Psychological Bulletin 2002, 128, 978–996. [CrossRef]
- Parsons, C. Inhelder and Piaget’s the Growth of Logical Thinking†: II. a Logician’s Viewpoint‡. British Journal of Psychology 1960, 51, 75–84. [CrossRef]
- Ennis, R.H. Children’s Ability to Handle Piaget’s Propositional Logic: A Conceptual Critique. Review of Educational Research 1975, 45, 1–41. [CrossRef]
- Seltman, M.; Seltman, P. Piaget’s Logic: A Critique of Genetic Epistemology; George Allen & Unwin: London, 1985; ISBN 0-04-370154-X.
- Johnson-Laird, P.N. How We Reason - Oxford Scholarship Available online: http://www.oxfordscholarship.com/view/10.1093/acprof:oso/9780199551330.001.0001/acprof-9780199551330-chapter-28 (accessed on 10 May 2018).
- Stenning, K.; van Lambalgen, M. Human Reasoning and Cognitive Science; MIT Press: Cambridge Massachusetts; London England, 2008; ISBN 978-0-262-29353-2.
- Piaget, J. Logic and Psychology; Basic Books Inc.: New York, 1957.
- Piaget, J. The Psychology of Intelligence; Routledge Classics; Routledge: London; New York, 2001; ISBN 978-0-415-25401-4.
- Piaget, J.; Beth, E.W. Mathematical Epistemology and Psychology; Synthese Library; Softcover reprint of hardcover 1st edition.; Springer Netherlands: Dordrecht, Holland, 1974; Vol. 12; ISBN 978-90-481-8328-9.
- Piaget, J. Essai de Logique Opératoire; Grize, J.-B., Ed.; Collection sciences du comportement; 2e éd. du Traité de logique, essai de logistique opératoire (1949).; Dunod: Paris, 1972.
- Winstanley, M.A. A Psychological Theory of Reasoning as Logical Evidence: A Piagetian Perspective. Synthese 2021, 199, 10077–10108. [CrossRef]
- Winstanley, M.A. Misconceptions — Johnson-Laird and Piaget on Reasoning. JCS 2022, 23, 1–32. [CrossRef]
- Winstanley, M.A. Logic and Psychology – Minding the Gap with Jean Piaget. History and Philosophy of Logic 2024, 0, 1–31. [CrossRef]
- Kesselring, T. The Mind’s Staircase Revised. In The Cambridge Companion to Piaget; Mueller, U., Carpendale, J.I.M., Smith, L., Eds.; Cambridge University Press: New York, 2009; pp. 372–399 ISBN 978-0-521-89858-4.
- Piaget, J. The Stages of Intellectual Development in Childhood and Adolescence. In The Essential Piaget; Guber, H.E., Vonèche, J.J., Eds.; Basic Books, Inc.: New York, 1977; pp. 814–819.
- Inhelder, B.; Piaget, J. The Psychology of the Child; Basic Books: New York, 1969.
- Smith, L. A Constructivist Interpretation of Formal Operations. Hum Dev 1987, 30, 341–354. [CrossRef]
- Inhelder, B.; Piaget, J. The Growth of Logical Thinking from Childhood to Adolescence; Routledge, Chapman and Hall: London, 1958.
- Halmos, P.R.; Givant, S. Logic as Algebra; The Dolciani Mathematical Expositions; The Mathematical Association of America: Washington D. C, 1998; Vol. 21; ISBN 978-0-88385-327-6.
- Rutherford, D.E. Introduction to Lattice Theory; University Mathematical Monographs; Reprint.; Oliver and Boyd Ltd.: Edinburgh; London, 1966.
- Piaget, J. Structuralism; Basic Books Inc.: New York, 1970; ISBN 465082386.
- Winstanley, M.A. Modelling the Psychological Structure of Reasoning. Euro Jnl Phil Sci 2022, 12. [CrossRef]
- Apostel, L. The Future of Piagetian Logic. Revue Internationale de Philosophie 1982, 36, 567–611.
- Grize, J.-B. Operatory Logic. In Piaget Today; Inhelder, B., de Caprona, D., Cornu-Wells, A., Eds.; Psychology Revivals; Taylor and Francis, 2013; pp. 149–164.
- Hintikka, J.; Sandu, G. What Is Logic? In Philosophy of Logic; Jacquette, D., Ed.; Handbook of the Philosophy of Science; North Holland: Netherlands, 2007; pp. 13–40 ISBN 978-0-444-51541-4.
- Swabey, W.C. The Laws of Thought. The Philosophical Review 1923, 32, 211–221. [CrossRef]
- Halmos, P.R. Algebraic Logic; Dover Edition.; Dover Publications Inc.: Mineola, New York, 2016.
- Winstanley, M.A. “Piaget’s Logic” — An Algebra in Logical Clothing. Manuscript in preparation.
- Stanovich, K.E.; West, R.F. Who Uses Base Rates and P (D/ H)? An Analysis of Individual Differences. Memory & Cognition 1998, 26, 161–179.
 |
| “Ontological” form. | “Logical” form. |
| Identity. | |
| A is A or A = A | (A true proposition is true, or If a proposition is true it is always true.) |
| Non-contradiction. | |
| A cannot both be and not be B. A is not non-A. A is not both B and non-B. | No proposition is both true and false. |
| Excluded Middle. | |
| A is either B or not B. A either is or is not B. | A proposition is either true or false. No proposition is both non-true and non-false. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





