Submitted:
31 May 2025
Posted:
03 June 2025
You are already at the latest version
Abstract
The two major unresolved issues in current mathematics and computer science addressed in this paper are fractal geometry and the P vs. NP problem. Benoît Mandelbrot's pioneering work in fractal geometry provides a mathematical basis for comprehending the complex, self-similar forms common in nature defined by non-integer dimensions. Its uses range from computer graphics to erratic systems across several spheres. On the other hand, the P versus A Millennium Prize Problem, NP problem answers the basic question of whether issues with quickly verifiable answers may also be effectively resolved. Emphasizing their status as important frontiers of knowledge, this article explores the basic ideas of both fields, their current knowledge, and the severe consequences their eventual resolution would have on scientific investigation and technology development.
Keywords:
fractal geometry
; the P vs. NP problem
1. Introduction
Scientific enterprise is defined by the quest of basic truths and the solving of difficult problems. In mathematics and computer science, some open problems are major obstacles since their resolutions might lead to new paradigms of knowledge and competence. This study makes two such issues—the continuous investigation within fractal geometry and the deep P vs. NP problem(Kyritsis, 2023; Vega, 2024). Seemingly unrelated, both fields investigate the essence of complexity: one depicting the intricate complexity of natural forms, the other grappling with the intrinsic limits of computational complexity. The basis of these two important fields of study will be discussed in this paper together with their ongoing relevance and present state of knowledge.
2. Fractal Geometry: Discovering the Complexity of Nature
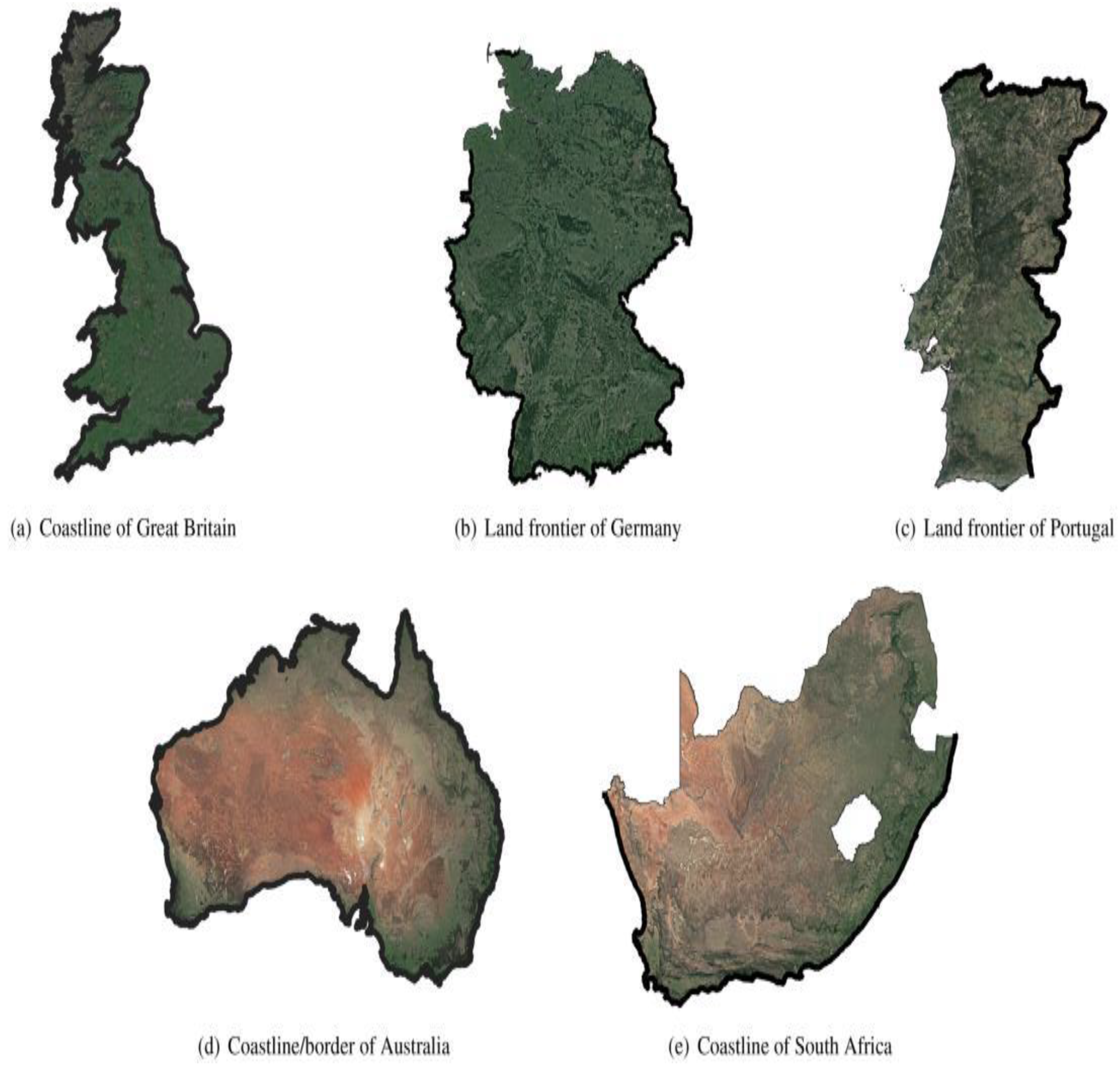
Largely ascribed to Benoît Mandelbrot (Mageed, 2024a; Mageed, 2024b),fractal geometry is a ground-breaking idea that offers a strong mathematical language for characterizing the irregular, broken, and often infinitely detailed forms seen throughout the natural world, as depicted in Figure 1 (c.f., Mageed, 2024a). Unlike conventional Euclidean geometry, which applies only to integer-dimensional entities (such as lines, planes, cubes), fractal geometry (Mageed & Bhat, 2022) welcomes items defined by self-similarity and often has a fraction or fractal dimension.
2.1. Fundamental Ideas
Self-similarity is the distinguishing feature of a fractal; hence, when enlarged, a portion of the object (Mageed & Bhat, 2024) resembles the entirety. As seen in mathematical constructions like the Mandelbrot set or the Koch snowflake(Mageed & Bhat, 2024), this property can be precise; as seen in natural events, it can be statistically Crucially, the idea of fractal dimension defines how entirely a fractal occupies space as its scale varies. Unlike topological dimension—which is always an integer—the fractal dimension can be a non-integer, reflecting the object's complex detail and roughness across all scales (Mageed, 2025). Common approaches for estimating fractal dimension are the box-counting dimension and Hausdorff dimension (Mageed & Bhat, 2024).
2.2. Natural Occurrences and Uses
Nature makes extensive use of fractals(Mageed & Mohamed, 2023). Among the examples are the branching patterns of trees, river networks, and blood vessels; the complex structure of coastlines and mountain ranges; the formation of snowflakes; even the distribution of galaxies (Mageed & Mohamed, 2023; Mageed, 2023a). Apart from defining natural shapes, fractal geometry has seen great use in many scientific and technical fields. Fractals are employed in computer graphics to produce realistic landscapes, textures, and special effects (Linton, 2021). Particularly in chaos theory, where sensitive dependence on initial conditions causes unpredictable, yet often fractally structured, results (Mageed, 2023b), they are also employed in signal processing, data compression (e.g., fractal image compression), and the analysis of complex systems. From neuron branching to protein folding (Strogatz, 2024) the study of fractals has also helped to clarify biological systems.
2.3. Unresolved Issues in Fractal Geometry
Though there have been notable developments, some unresolved issues remain in fractal geometry(Bhat & Mageed, 2023). These comprise a more profound conceptual grasp of the dynamics of complicated fractal sets (Mageed, 2023a), especially those generated from iterative functions in higher dimensionalities. Research on the creation of more robust and computationally efficient approaches for reliably calculating fractal dimensions from noisy, real-world data is currently underway (Mageed, 2024c). Moreover, the full scope of fractal uses in cutting-edge sectors including customized medicine, material science, and network analysis still being investigated (de Anjos et al., 2021). Additionally offering opportunities for future research is the interaction between information theory and fractal geometry (Troscheit, 2022).
3. The P versus NP Problem: The Computation Frontier
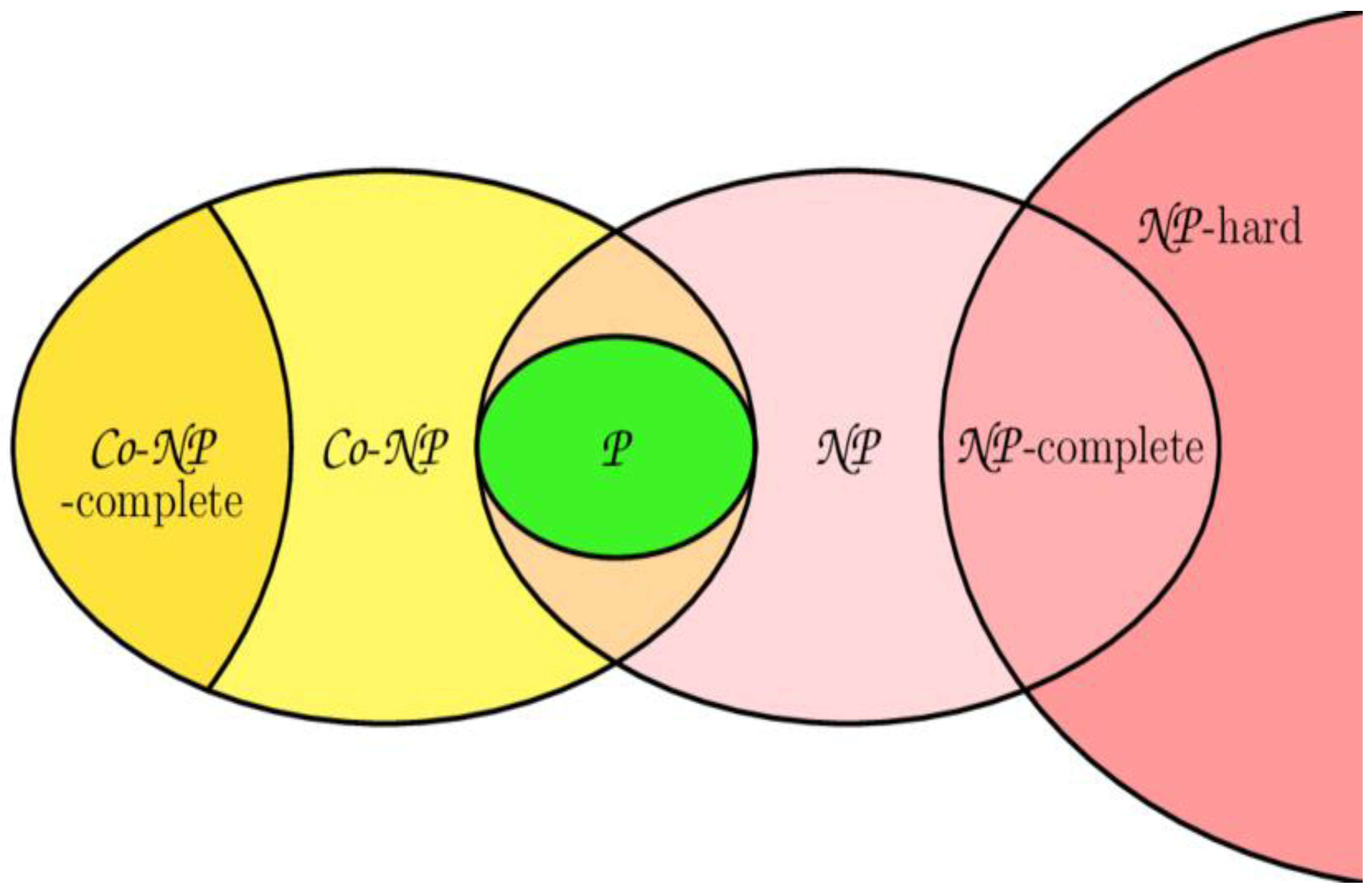
Designated by the Clay Mathematics Institute as a basic challenge in mathematics, one of the seven Millennium Prize Problems is the NP problem with a one million award for its resolution (Germain et al., 2023). It addresses the efficiency limits of algorithms and is central to computational complexity theory(Oliveira, 2023), as in Figure 2 (c.f., Lancini, 2019),
2. Fractal Geometry: Discovering the Complexity of Nature
Largely ascribed to Benoît Mandelbrot (Mageed, 2025), fractal geometry is a ground-breaking idea that offers a strong mathematical language for characterizing the irregular, broken, and often infinitely detailed forms seen throughout the natural world. Unlike conventional Euclidean geometry(Mageed, 2025), which applies only to integer-dimensional entities (such as lines, planes, cubes), fractal geometry welcomes items defined by self-similarity and often has a fraction or fractal dimension.
2.1. Fundamental Ideas
Self-similarity is the distinguishing feature of a fractal; hence, when enlarged, a portion of the object (Mageed, 2025) resembles the entirety. As seen in mathematical constructions like the Mandelbrot set or the Koch snowflake, this property can be precise; as seen in natural events, it can be statistically Crucially(Mageed, 2023a), the idea of fractal dimension defines how entirely a fractal occupies space as its scale varies. Unlike topological dimension—which is always an integer—the fractal dimension can be a non-integer, reflecting the object's complex detail and roughness across all scales (Fraser, 2024). Common approaches for estimating fractal dimension are the box-counting dimension and Hausdorff dimension (Mageed,2025).
2.2. Natural Occurrences and Uses
Nature makes extensive use of fractals. Among the examples are the branching patterns of trees, river networks, and blood vessels; the complex structure of coastlines and mountain ranges; the formation of snowflakes; even the distribution of galaxies (Hussain et al., 2022; Mageed, 2023a). Apart from defining natural shapes, fractal geometry has seen great use in many scientific and technical fields. Fractals are employed in computer graphics to produce realistic landscapes, textures, and special effects (Linton, 2021). Particularly in chaos theory, where sensitive dependence on initial conditions causes unpredictable, yet often fractally structured, results (Mageed, 2023a), they are also employed in signal processing, data compression (e.g., fractal image compression), and the analysis of complex systems. From neuron branching to protein folding (Strogatz, 2024), the study of fractals has also helped to clarify biological systems.
2.3. Unresolved Issues in Fractal Geometry
Though there have been notable developments, some unresolved issues remain in fractal geometry(Mageed, 2024c). These comprise a more profound conceptual grasp of the dynamics of complicated fractal sets (Mageed, 2023a), especially those generated from iterative functions in higher dimensionalities. Research on the creation of more robust and computationally efficient approaches for reliably calculating fractal dimensions from noisy, real-world data is currently underway (Mageed, 2024c). Moreover, the full scope of fractal uses in cutting-edge sectors including customized medicine, material science, and network analysis still being investigated (Mageed, 2025). Additionally offering opportunities for future research is the interaction between information theory and fractal geometry (Troscheit, 2022).
3. The P versus NP Problem: The Computation Frontier
P vs.NP Designated by the Clay Mathematics Institute as a basic challenge in mathematics, one of the seven Millennium Prize Problems is the NP problem with a one million award for its resolution (Germain et al., 2023). It addresses the efficiency limits of algorithms and is central to computational complexity theory(Germain et al., 2023). Though different in their immediate aim, these two domains basically highlight the extent of uncharted intellectual landscape (Mageed, 2024d). They capture the spirit of mathematical and scientific investigation(Mageed, 2025), in which basic problems remain unsolved, motivating many years of scientists to expand the frontiers of knowledge and search for the elusive answers that promises to transform our perspective of complexity, nature, and computation.
Often referred as one of the Millennium Prize Problems (Germain et al., 2023), the P versus NP problem is among the most important unresolved issues in theoretical computer science and mathematics. At its heart, the question asked is if every issue whose answer can be easily checked can also be easily discovered by a computer (Adolfi et al., 2022). This basic question probes the very boundaries of efficient computation.
Decision problems within the class P that a deterministic Turing machine can solve in polynomial time are, these are thought of as tractable or efficiently solvable issues (Chowdhary, 2025). Sorting a list of numbers or doing simple arithmetic operations, for instance, belong under this category (Denning & Tedre, 2021). Problems in P are feasible for larger inputs as their time complexity grows according to a polynomial function of the input size (Okhmatovski & Zheng, 2024).
Conversely, the class NP encompasses decision issues for which a deterministic Turing 1 machine (Cook, 2023) can confirm a suggested answer in polynomial time. The N stands for nondeterministic, which is the hypothetical capacity of a nondeterministic Turing machine to guess the correct answer and then verify it quickly (Widgderson, 2019). A traditional example is the Boolean Satisfiability Problem (SAT), where, given a logical formula, one can easily check whether a particular assignment of truth values satisfies it; nevertheless, discovering such an assignment may be really challenging (Hassan et al., 2024) Other well-known NP challenges include the Traveling Salesperson Problem (TSP) and the Sudoku puzzle, in which finding a solution is simple relative to (Papadimitriou, 2003).
Since every problem solvable in polynomial time can surely be verified in polynomial time, P ⊆ NP is broadly agreed upon (Anand, 2024). Whether P= NP or P ≠ NP is the decisive issue. Most mathematicians and computer scientists vehemently think P ≠ NP (Blum & Blum, 2024). According to this generally accepted theory (Grabowska & Gunia, 2024.), there are issues for which proof is naturally simpler than discovery, therefore suggesting basic computational restrictions. Should it turn out to be true, it would show that some issues are inherently difficult independent of technical progress.
P= NP would have massive consequences. Many presently intractable issues—like breaking contemporary cryptographic systems like RSA—would be implied solved efficiently Matysiak, 2021; Goldwasser et al., 2019). From artificial intelligence, maybe permitting automated theorem proving and creative breakthroughs, to optimization issues in logistics and medicine design, this would revolutionize disciplines enabling effective answers to difficult real-world problems (Facco & Fracas, 2022). On the other hand, it might also undermine several existing security systems.
On the other hand, proving P ≠ NP would confirm the bases of current cryptography and our knowledge of computational complexity (Bossaerts et al., 2019). It would validate that some computational problems are difficult, hence requiring heuristic solutions for numerous optimization problems (Sherry & Thompson, 2021). The P versus Driven by major study on complexity theory and the nature of computation itself (Santha, 2007; Impagliazzo, 1995), NP problem remains one of the most difficult problems in computer science.
Conclusion
Fundamentally, this paper provides a novel fractal exploratory to establish the solution of one of the most complicated Millenium open problems, ever existed. By default, this would be a phenomenal, informed research-based line of inquiry to unlock the P vs NP mystery. Future research includes exploring fractal links with other Millenniums, in pursuit to start the journey of solving the Millenniums one by one.
References
- Kyritsis, K.E., 2023. The Simplest Possible Fully Correct Solution of the Clay Millennium Problem about P vs. NP. A Simple Proof That P≠ NP= EXPTIME. Journal of Computer and Communications, 11(8), pp.181-194.
- Vega, F., 2024. Note for the Millennium Prize Problems.
- Mageed, I.A., 2024a. The Fractal Dimension Theory of Ismail's Third Entropy with Fractal Applications to CubeSat Technologies and Education. Complexity Analysis and Applications, 1(1), pp.66-78.
- Mageed, I.A., 2024b. Fractal Dimension of the Generalized Z-Entropy of The Rényian Formalism of Stable Queue with Some Potential Applications of Fractal Dimension to Big Data Analytics.
- Mageed, I.A. and Bhat, A.H., 2022. Generalized Z-Entropy (Gze) and fractal dimensions. Appl. math, 16(5), pp.829-834.
- Mageed, I.A. and Mohamed, M., 2023. Chromatin can speak Fractals: A review.
- Husain, A., Nanda, M.N., Chowdary, M.S. and Sajid, M., 2022. Fractals: An eclectic survey, part II. Fractal and Fractional, 6(7), p.379.
- Germain, S., Montage, S., Wiles, A. and Applewhite, D., 2023. Picture Credits. The Millennium Prize Problems, p.161.
- Fraser, J.M., 2025. Applications of dimension interpolation to orthogonal projections. Research in the Mathematical Sciences, 12(1), p.10.
- Mageed, I.A., 2025. Fractal Open Problems in Cancer Research, Medicine, Biomedicine, Clinical Sciences, and Dentistry. J of Clin Bio Med Adv, 4 (1), 01-09.
- Mageed, I.A. and Bhat, A.H., 2024. Fractal Dimension of (q, β) Generalized Rényian Entropy, Rq with Potential Fractal Dimension Applications to Smart Cities. J Sen Net Data Comm, 4(2), pp.01-11.
- Mageed, I.A., 2023a, November. Fractal Dimension (Df) of Ismail’s Fourth Entropy with Fractal Applications to Algorithms, Haptics, and Transportation. In 2023 international conference on computer and applications (ICCA) (pp. 1-6). IEEE.
- Lancini, E., 2019. TDIness and multicuts (Doctoral dissertation, Université Paris-Nord-Paris XIII).
- Troscheit, S., 2022. Fractal geometry. Course notes.
- Strogatz, S.H., 2024. Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering. Chapman and Hall/CRC.
- Linton, O., 2021. Fractals. eBook Partnership.
- Mageed, I.A., 2023b, November. Fractal Dimension (Df ) Theory of Ismail’s Second Entropy with Potential Fractal Applications to ChatGPT, Distributed Ledger Technologies (DLTs) and Image Processing (IP). In 2023 international conference on computer and applications (ICCA) (pp. 1-6). IEEE.
- dos Anjos, P.H., Gomes-Filho, M.S., Alves, W.S., Azevedo, D.L. and Oliveira, F.A., 2021. The fractal geometry of growth: Fluctuation–dissipation theorem and hidden symmetry. Frontiers in Physics, 9, p.741590.
- Bhat, A.H. and Mageed, I.A., 2023. Generalised Z-Entropy (Gze) and Fractal Dimensions (FDs). In Fractal Analysis-Applications and Updates. IntechOpen.
- Mageed, I.A., 2024c. Fractal Dimension (Df) Theory of Ismail’s Entropy (IE) with Potential Df Applications to Structural Engineering. Journal of Intelligent Communication, 3(2), pp.111-123.
- Oliveira, I.C., 2025. Meta-mathematics of computational complexity theory. arXiv preprint. arXiv:2504.04416.
- Mageed, I.A., 2024d. A Theory of Everything: When Information Geometry Meets the Generalized Brownian Motion and the Einsteinian Relativity. J Sen Net Data Comm, 4(2), pp.01-22.
- Adolfi, F., Wareham, T. and van Rooij, I., 2022. Computational complexity of segmentation. arXiv preprint. arXiv:2201.13106.
- Chowdhary, K.R., 2025. NP-Completeness. In Theory of Computation: Automata, Formal Languages, Computation and Complexity (pp. 571-597). Singapore: Springer Nature Singapore.
- Denning, P.J. and Tedre, M., 2021. Computational thinking: A disciplinary perspective. Informatics in Education, 20(3), p.361.
- Okhmatovski, V. and Zheng, S., 2024. Theory and Computation of Electromagnetic Fields in Layered Media. John Wiley & Sons.
- Cook, S.A., 2023. The complexity of theorem-proving procedures. In Logic, automata, and computational complexity: The works of Stephen A. Cook (pp. 143-152).
- Hassan, S.M., Hussain, S. and Samad, A., 2024. Reducibility among NP-Hard graph problems and boundary classes. arXiv preprint. arXiv:2411.14553.
- Papadimitriou CH., 2003. Computational complexity. In Encyclopedia of computer science 2003 Jan 1 (pp. 260-265).
- Anand, B.S., 2024. Why the classes P and NP are not well-defined finitarily. arXiv preprint. arXiv:2401.09478.
- Blum, L. and Blum, M., 2024. AI consciousness is inevitable: a theoretical computer science perspective. arXiv preprint. arXiv:2403.17101.
- Grabowska, A. and Gunia, A., 2024. On quantum computing for artificial superintelligence. European Journal for Philosophy of Science, 14(2), p.25.
- MATYSIAK, L., 2021. Generalized RSA cipher and Diffie-Hellman protocol. Journal of applied mathematics & informatics, 39(1_2), pp.93-103.
- Goldwasser, S., Micali, S. and Rivest, R.L., 2019. A" paradoxical" solution to the signature problem. In Providing Sound Foundations for Cryptography: On the Work of Shafi Goldwasser and Silvio Micali (pp. 265-284).
- Facco, E. and Fracas, F., 2022. De Rerum (Incerta) Natura: A tentative approach to the concept of “quantum-like”. Symmetry, 14(3), p.480.
- Bossaerts, P., Yadav, N. and Murawski, C., 2019. Uncertainty and computational complexity. Philosophical Transactions of the Royal Society B, 374(1766), p.20180138.
- Sherry, Y. and Thompson, N.C., 2021. How fast do algorithms improve?[point of view]. Proceedings of the IEEE, 109(11), pp.1768-1777.
Figure 1.
The Great Britain coastline, the German land border, the Portuguese land border, the Australian coastline, and the South African coastline are the locations Mandelbrot cited.
Figure 1.
The Great Britain coastline, the German land border, the Portuguese land border, the Australian coastline, and the South African coastline are the locations Mandelbrot cited.
Figure 2.
A few classes of complexity. Note: P = NP is assumed.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
