Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

A New Real-Time Method for Lung Mass Lesion Detection in CT Images

Submitted:

02 June 2025

Posted:

03 June 2025

You are already at the latest version

Abstract
Detection of lung mass lesion is widely required in the clinic for diagnosis of different pulmonary defects like lung cancer and pulmonary embolism. Due to severe symptoms of such diseases, real-time detection of the lung mass lesion is significant. In this paper, this problem is addressed by a new image segmentation algorithm. Primarily, a Gabor-based filtering algorithm is employed to remove the intensity nonuniformity of the CT image. Then, the holes and discontinuities of the mass lesion are eliminated through morphological operations. Finally, the lesion objects are extracted by using the thresholding and connected-component-analysis. The experimental results demonstrated significantly short CPU time of the proposed algorithm, as 73 milliseconds for each slice on a typical laptop. Also, the solution quality of our method was considerably high, as 91.6%, 85.4%, and 93.3% in terms of accuracy, sensitivity, and specificity, respectively. We further showed that the proposed method provided better solutions compared to six other counterpart algorithms.
Keywords: 
Computed Tomography
;  
Pulmonary Defects
;  
Image Segmentation
Subject: 
Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

I. Introduction

The lung cancer is the (second) most important cancer in men (women) [1]. Today, the high growth of lung cancer requires modern methods for accurate and early diagnosis [2,3]. CT images are always considered as one of the most common and accurate methods for diagnosing suspicious lung glands [4,5]. The lung mass lesion is one of the frequently-observed biomarkers of such diseases in CT images. Hence, real-time detection of those lesions is drastically required in clinic due to high mortality risk of pulmonary diseases.
Generally, the lung mass lesion detection algorithms can be divided into the intensity-based and model-based methods. In the former, the intensity distribution of the mass lesion is used as the biomarker while in the later; its shape is modelled based on the anatomy and prior information [6]. On the other hand, many researchers recently proposed elegant methods based on the convolutional neural networks for nodule detection [7,8,9,10]. Although these methods are significantly elaborate, still naive image processing methods are advantageous for rapid detection. Hereafter, we will focus on this field.
For example, Abdillah et al. [11] proposed a new algorithm for mass lesion detection based on the watershed transform and region growing. In another work, Hashemi et al. [12] took advantage of the region growing for lung region segmentation. They also employed a fuzzy inference system and a multilayer perceptron for cancer type detection. Arya and Gupta [13] employed an elegant method based on the discrete wavelet transform and template matching for mass lesion detection. In another work, Shakeel et al. [14] evaluated a number of classical image processing methods including region growing, global thresholding, fuzzy c-means, Canny and Sobel edge detection, watershed transform, and profuse clustering for mass lesion detection.
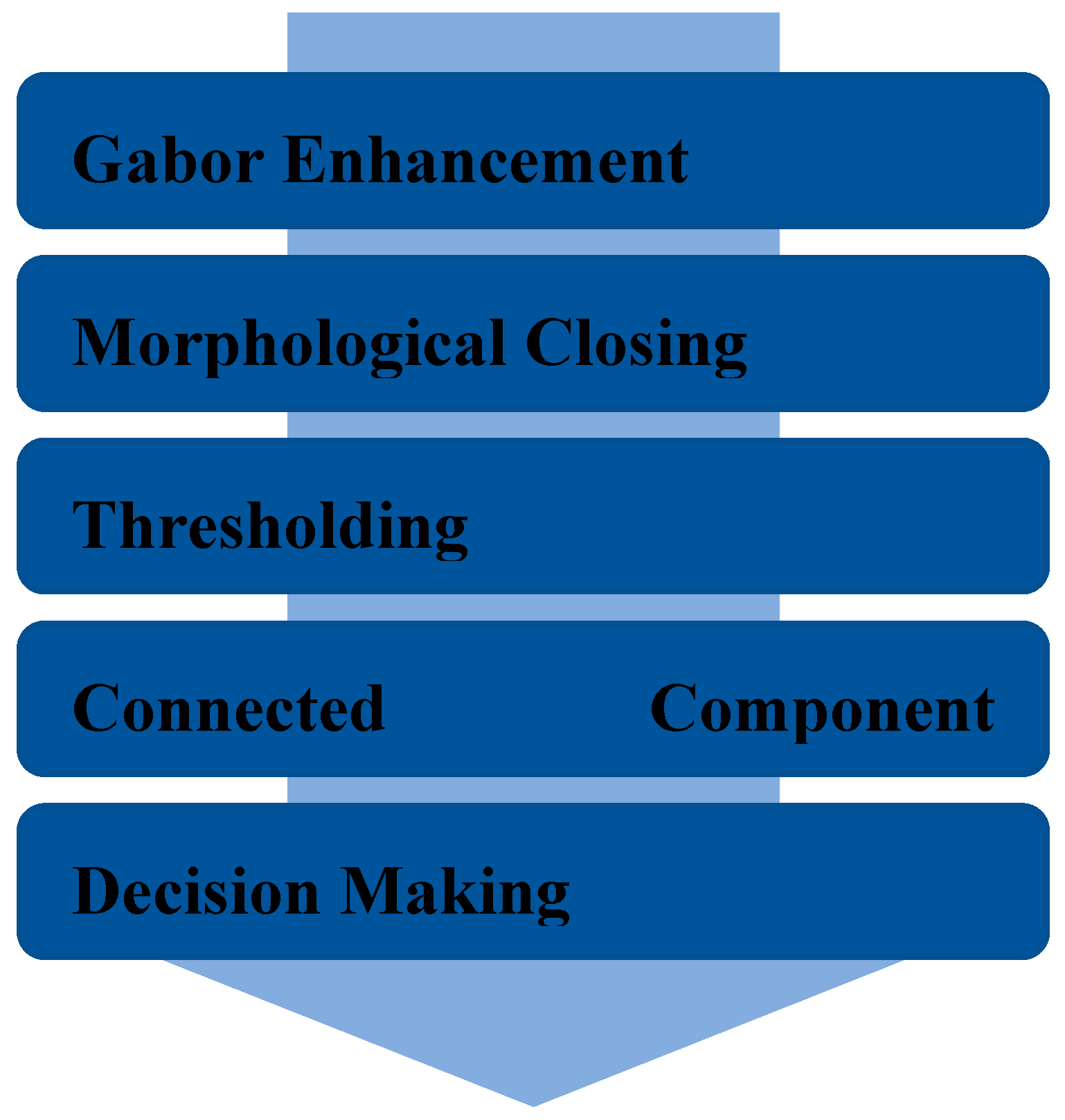
In this paper, we proposed a new real-time accurate method for lung mass lesion detection in CT images. As shown in Figure 1, our proposed method consists of Gabor-based image enhancement, morphological closing, thresholding, and connected component analysis that will be comprehensively stated, in the sequel.

II. The Proposed Method

Our method was originally developed for lung mass lesion detection in 2D CT slices. However, it is worth to cite that for a 3D CT volume, we can separately extract the lesion regions in all the 2D slices. Obviously, by aggregating all the 2D segmented regions, the whole 3D lesion volume can be obtained.
The source CT slices suffer from the intensity nonuniformity which can potentially degrade the detection performance. To overcome this problem, at the first step, we propose an image enhancement algorithm based on the Gabor filter bank. Generally, a Gabor filter supports the directional low-pass filtering in a 2D image by combining a Gaussian filter with a directional sinusoidal function [15], as follows:
ψ k ( x , y ) = 1 2 π σ x σ y exp − 1 2 ( x ˜ 2 σ x 2 + y ˜ 2 σ y 2 ) cos ( 2 π k λ x ˜ + ϕ ) ,     k = 0 , 1 , ... , λ − 1
where σx and σy are STDs of the Gaussian filter and λ and φ adjust the frequency and phase offset of the sinusoidal function, respectively. Also, ( x ˜ , y ˜ ) determines the position of the filter samples after rotation by the angle θ:
x ˜ y ˜ = cos θ sin θ − sin θ cos θ x y , x , y = − r , − r + 1 , ... , r − 1 , r
where r is the radius of the filter domain. For example, Figure 2 illustrates the low-pass Gabor filter bank obtained by λ=4, σx=43, σy= σx/2, and φ=0.
The CT slice f:Ω→R (where Ω is the slice domain) is filtered by using all the given Gabor filters (with σx=4.3) as follows:
g k ( x , y ) = ψ k ∗ f ( x , y ) , k = 1 , 2 , ... , λ
Indeed, the directional low-pass filter ψk degrades noise and small variations along its direction (2πk/λ). Therefore, at each pixel (x,y), we have a vector of λ different coefficients given by all the Gabor filters. Therefore, we compute the norm of that vector as the weighting measure of significant bright variations at each pixel of the CT slice:
η ( x , y ) = ∑ k = 0 λ − 1 g k ( x , y )
Although the source CT image is considerably improved in that last step, still there may remain some discontinuities and holes in the lesion objects. To tackle this problem, at the second step of our algorithm, we perform the morphological closing operator over the image η. It removes dark holes and discontinuities by using a primary dilation and keeps the size of bright objects unchanged through a subsequent erosion operator (with the same structure element) [16]. We experimentally used a square structure element with the side length of 5 mm.
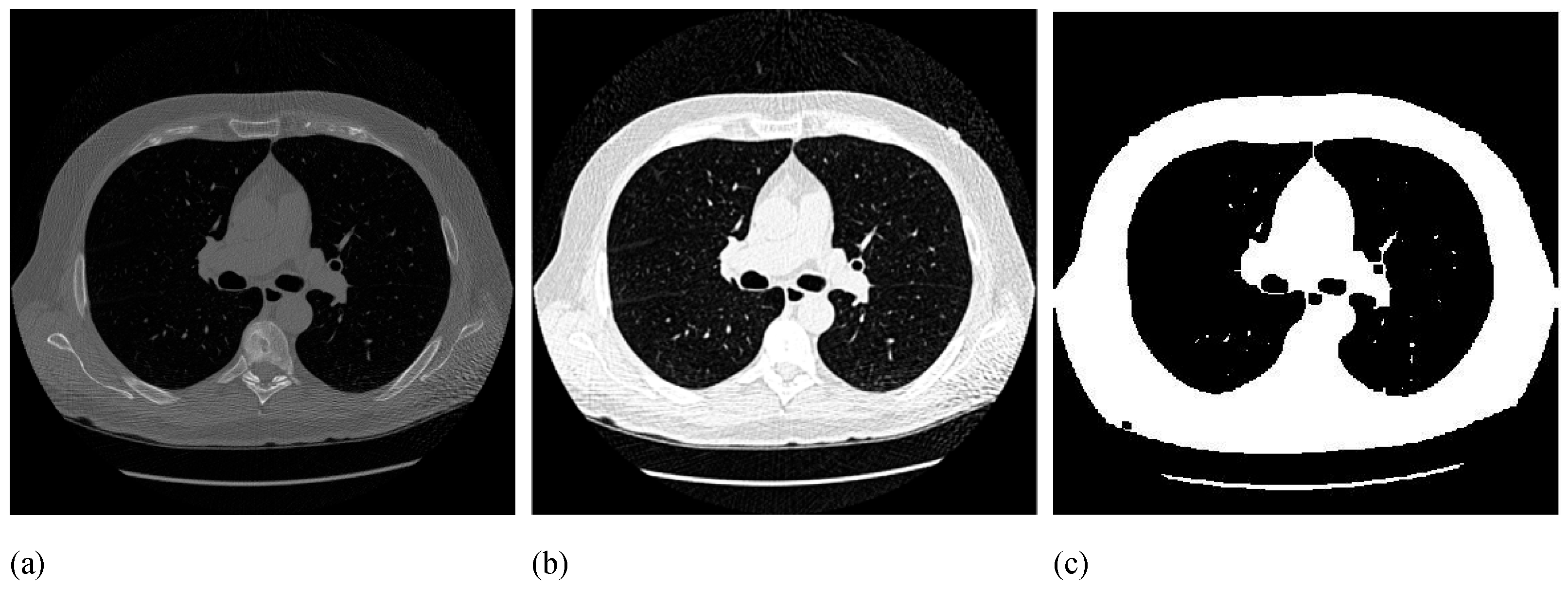
Due to the previously-performed enhancements, the lesion regions are now uniform in the resultant image. Thus, at the third step of our method, we can separate the bright lesion regions from the dark background by using a global thresholding method to obtain the binary foreground image (BFI). We employ the optimal threshold selection method proposed by Otsu [17] due to the robustness against noise and intensity unimodality [18,19]. Figure 3 illustrates the Gabor-based enhancement and thresholding results for a sample CT slice.
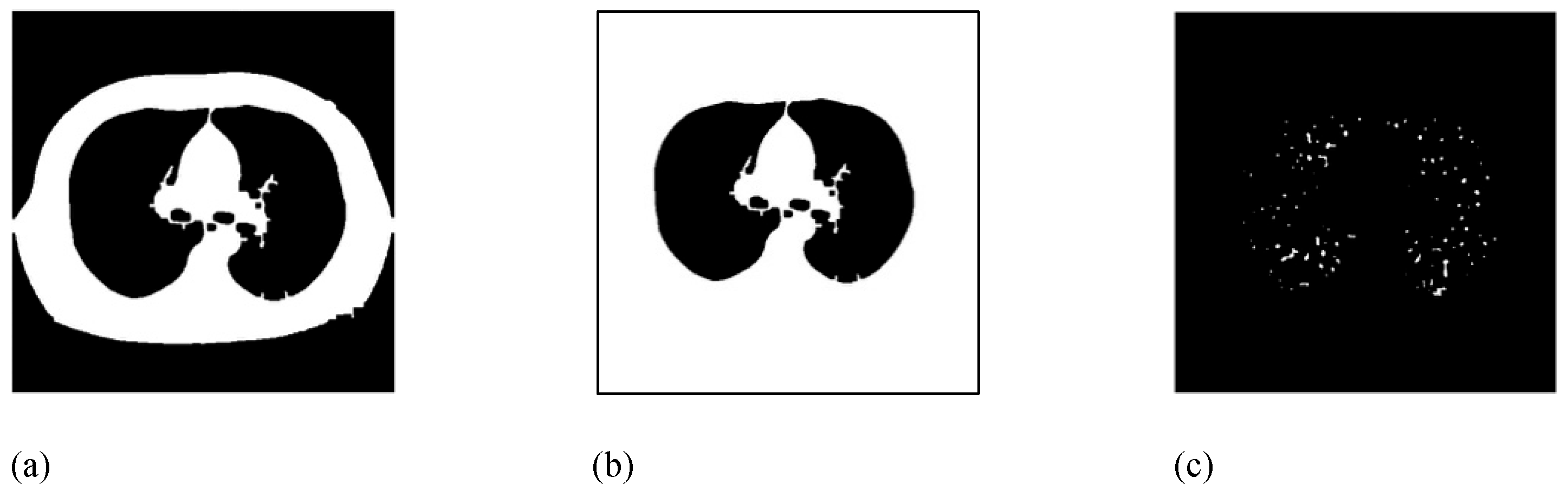
Then, the lesion objects should be extracted from BFI. However, we should primarily remove the large bright region of the chest chamber. For this purpose, the largest connected binary object in BFI is extracted to obtain the binary chest chamber image (CCI) as shown in Figure 4.a. Next, the outer region of the chest chamber is filled in CCI, by using four corners of the image as initial seeds, to obtain the outer chest image (OCI), as illustrated in Figure 4.b. Now, according to the formula MLI=BFI&~OCI (where & and ~ are the binary AND and COMPLEMENT operators), all the foreground pixels of BFI which does not belong to the foreground of OCI are added to the mass lesion image (MLI).
Indeed, MLI includes all the lung bright objects inside the chest chamber. Therefore, a large mass lesion can significantly increase the area of the MLI foreground. Thus, at the last step of our algorithm, the total number of voxels (n) in the LMI foreground (i.e. the possible mass lesion) is counted. Regarding the CT scanning resolution of λx×λy×λz, the total volume of the mass lesion can be computed by vCMI=nλxλyλz. Since the lesion increases the volume of the LMI foreground, the defective lung was distinguished from the healthy by comparing vCMI with a pre-adjusted threshold θ (experimentally regulated as θ=870 mm3 for getting the best performance).

III. Experimental Results

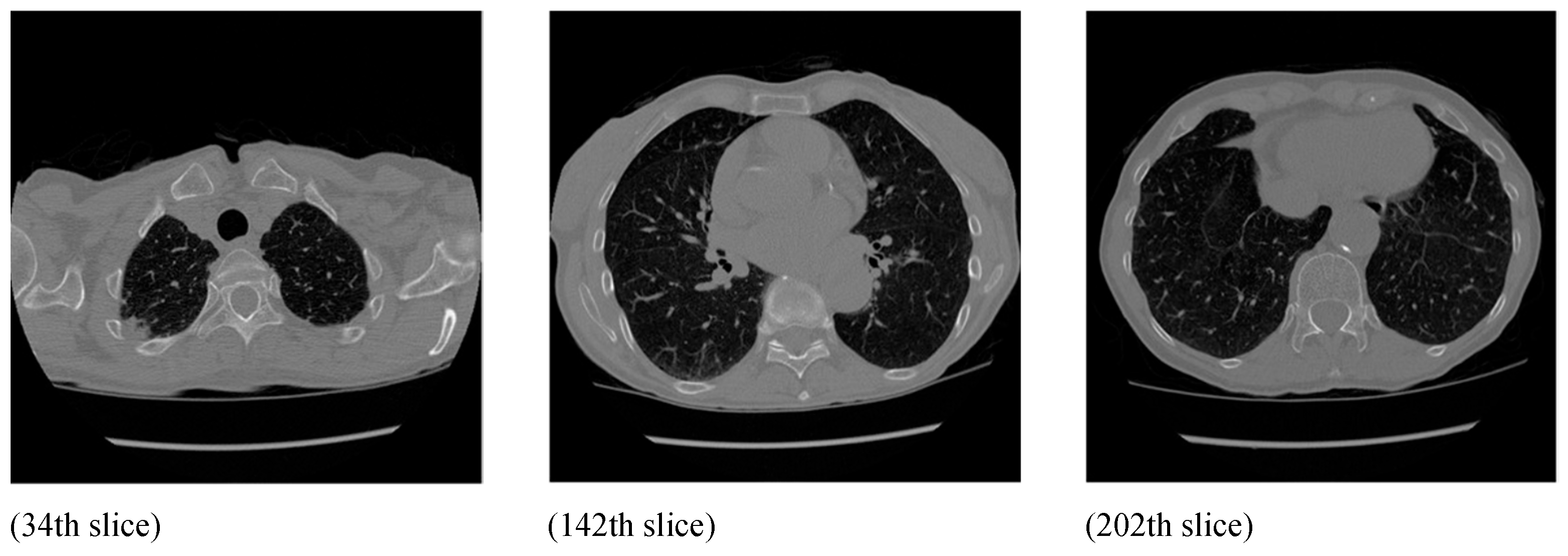
In this work, we chose 50 (36 normal+14 cancer) 3D chest CT volumes (with the voxel size of 0.664×0.662×1.2 mm) from the public VIA and ELCAP databases [20]. Then, 5 2D slices were randomly selected from each volume to make our benchmark dataset. The ground-truth mass lesion regions in each CT slice were delineated by a medical-imaging expert. For example, Figure 4 shows three chosen slices of a sample chest CT volume in our dataset.
We classified all the benchmark images (into healthy and cancer groups) by the proposed method to evaluate its performance in terms of accuracy (with 91.6%), sensitivity (85.4%), and specificity (93.3%) measures. Also, as reported in Table 1, we further compared our method with six different counterpart algorithms in the same category for lung lesion-mass detection. Although different databases were used in evaluations, the proposed approach generally provided the best performance in terms of accuracy and sensitivity while it is located at the second place in terms of specificity.
On the other hand, the average CPU time of the proposed method for a single slice with the size of 512×512 pixel was 0.073 second on a MAC with the CPU of Intel Core-i7 2.8GHz and 8 GB of main memory. Hence, the proposed method provided suitable performance in real time which makes it as appropriate choice for clinical applications.

IV. Conclusion

In this paper, a new fast straightforward method for lung lesion-mass detection in CT images was proposed. It provided short CPU time and, simultaneously, significant solution quality in comparison to a number of counterpart algorithms at the same category. For performance evaluation, we took advantage of a public dataset as the benchmark. However, it would be a good idea to further assess its performance on a local national dataset which requires more efforts to this end.

References

  1. Hosseini, S.H., Monsefi, R. & Shadroo, S (2023) Deep learning applications for lung cancer diagnosis: A systematic review. Multimed Tools Appl. [CrossRef]
  2. R. Gonzalez and V. Ponomaryov, “Automatic lung nodule segmentation and classification in CT images based on SVM,” 9th Int’l Kharkiv Sym. Physics and Engineering of Microwaves, Millimeter and Submillimeter Waves, 2016, pp. 1-4. [CrossRef]
  3. Read and T. Trojan, Human Molecular Genetics. Garland Science: Springer-Verilog, 3rd ed., 2005.
  4. M. S. Brown, J. G. Goldin, R. D. Suh, M. F. McNitt-Gray, J. W. Sayre, and D. R. Aberle, “Lung micronodules: automated method for detection at thin section CT initial experience,” Radiology, vol. 226, no. 1, pp. 256-62, 2003. [CrossRef]
  5. van Ginneken, B. M. Ter Haar Romeny, and M. A. Viergever, “Computer-aided diagnosis in chest radiography: a survey,” IEEE Trans Med Imaging, vol. 20, no. 12, pp. 1228-1241, 2001. [CrossRef]
  6. R. Kleinerman, Z. Wang, J. Lubin, S. Zhang, C. Metayer, and A. Brenner, “Lung cancer and indoor air pollution in rural China,” Ann Epidemiol, vol. 10, no. 7, p. 469, 2000. [CrossRef]
  7. P. Aonpong, Y. Iwamoto, X. H. Han, L. Lin, and Y. W. Chen, “Genotype-guided radiomics signatures for recurrence prediction of non-small cell lung cancer,” IEEE Access, vol. 9, pp. 90244-90254, 2021. [CrossRef]
  8. F. Silva, T. Pereora, J. Morgado, J. Frade, J. Mendes, C. Freitas, E. Negrao, B. Flor de Lima, M. C. D. Silva, A. Madureira, I. Ramos, V. Hespanhol, J. L. Costa, A. Cunha, and H. P. Oliveria, “EGFR assessment in lung cancer CT images: analysis of local and holistic regions of interest using deep unsupervised transfer learning,” IEEE Access, vol. 9, pp. 58667-58676, 2021. [CrossRef]
  9. H. Yu, Z. Zhou, and Q. Wang, “Deep learning assisted predict of lung cancer on computed tomography images using the adaptive hierarchical heuristic mathematical model,” IEEE Access, vol. 8, pp. 86400-86410, 2020. [CrossRef]
  10. O. Ozdemir, R. L. Russell, and A. A. Berlin, “A 3D probabilistic deep learning system for detection and diagnosis of lung cancer using low-dose CT scans,” IEEE Trans. Medical Imaging, vol. 39, no. 5, pp. 1419-1429, May 2020. [CrossRef]
  11. Abdillah, A. Bustamam, and D. Sarwinda, “Image processing-based detection of lung cancer on CT scan images,” Journal of Physics: Conference Series, conf. series 893, no. 012063, 2017. [CrossRef]
  12. A. Hashemi, A. H. Pilevar, and R. Rafeh, “Mass detection in lung CT images using region growing segmentation and decision making based on fuzzy inference system and artificial neural network,” International Journal of Image, Graphics and Signal Processing, vol. 5, no. 6, pp.16-24, 2013.
  13. M. C. Arya and B. Gupta, “Detect mass tissue in lung images using discrete wavelet transformation,” 1st India Int’l Conf. Information Processing, Delhi, 2016, pp. 1-3. [CrossRef]
  14. P. M. Shakeel, M. A. Burhanuddin, M. Ishak Desa, “Lung cancer detection from CT image using improved profuse clustering and deep learning instantaneously trained neural networks,” Measurement, vol. 145, pp. 702-712, 2019. [CrossRef]
  15. H. Abrishami Moghaddam, T. Taghizadeh Khajoie, A. H. Rouhi, and M. Saadatmand-Tarzjan, “Wavelet correlogram: a new approach for image indexing and retrieval,” Pattern Recognition, vol. 38, no. 12, pp. 2506-2518, 2005. [CrossRef]
  16. K. A. M. Said and A. B. Jambek, “A study of image processing using morphological opening and closing processes,” Int’l Journal of Control Theory and Applications, vol. 9, no. 31, pp. 15-21, 2017.
  17. N. Otsu, “A threshold selection method from gray-level histograms,” IEEE Trans. Sys. Man. Cyber., vol. 9, no. 1, pp. 62–66, 1979. [CrossRef]
  18. M. Sezgin M and B. Sankur, “Survey over image thresholding techniques and quantitative performance evaluation,” Journal of Electronic Imaging, vol. 13, no. 1, pp. 146–165, 2004. [CrossRef]
  19. A. H. A. Talab, Z. Huang, F. Xi, and L. Haimng, “Detection crack in image using Otsu method and multiple filtering in image processing techniques,” Optik, vol.127, pp. 1030-1033, 2016. [CrossRef]
  20. ELCAP Public Lung Image Database. Available online: http://www.via.cornell.edu/lungdb.
Preprints 162032 g001
Figure 1. The steps of the proposed lung lesion-mass detection algorithm.
Figure 1. The steps of the proposed lung lesion-mass detection algorithm.
Preprints 162032 g001
Preprints 162032 g002
Figure 2. An illustration of the Gabor filter bank with λ=4, σx=43.4, σy= σx/2, and φ=0.
Figure 2. An illustration of the Gabor filter bank with λ=4, σx=43.4, σy= σx/2, and φ=0.
Preprints 162032 g002
Preprints 162032 g003
Figure 3. (a) A sample CT slice of the lung and the corresponding results of (b) the Gabor-based enhancement algorithm and (c) thresholding (BFI).
Figure 3. (a) A sample CT slice of the lung and the corresponding results of (b) the Gabor-based enhancement algorithm and (c) thresholding (BFI).
Preprints 162032 g003
Preprints 162032 g004
Figure 4. Post processing of the binary image of Figure 2.c: (a) CCI, (b) OCI, and (c) LMI.
Figure 4. Post processing of the binary image of Figure 2.c: (a) CCI, (b) OCI, and (c) LMI.
Preprints 162032 g004
Preprints 162032 g005
Figure 4. The 34th, 142th, and 202th slices of a sample 3D chest CT volume.
Figure 4. The 34th, 142th, and 202th slices of a sample 3D chest CT volume.
Preprints 162032 g005
Table 1. Comparing the solution quality of our method with six other counterpart algorithms in terms of accuracy, sensitivity, and specificity.
Table 1. Comparing the solution quality of our method with six other counterpart algorithms in terms of accuracy, sensitivity, and specificity.
Modality Slice Number Accuracy Sensitivity Specificity
Our Method 2D CT Slice 250 91.6% 85.4% 93.3%
Arya and Gupta [13] 2D X-Ray Radiology 60 86.2% – –
Region Growing [14] 2D CT Slice 5043 73.8% 74.6% 83.0%
Global Thresholding [14] 82.4% 83.5% 95.2%
Fuzzy c-means [14] 88.2% 69.0% 94.3%
Canny Method [14] 86.3% 77.0% 89.0%
Sobel Method [14] 87.4% 83.4% 93.1%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2026 MDPI (Basel, Switzerland) unless otherwise stated