Electronic Properties of Parallelly Aligned Arrays of Carbon Nanotubes

1. Introduction

Carbon nanotubes (CNTs) – quasi-one-dimensional allotropes of carbon, being cylindrical tubes with nanometers in diameter and up to several millimeters in length – have attracted significant research interest ever since their discovery due to their outstanding properties: electronic, optic, mechanical and even supercoducting [1]. From authors’ personal point of view, particularly interesting are: electronic, optic and excitonic properties, due to possible applications of CNTs as active layer in solar cells [5,8]. Electronic properties of isolated CNTs have been subject of numerous theoretical studies, see for example [4,5,7].

However, CNTs in experiments rarely appear as independent entities – most often they form random array of disordered fibers, or are placed into “matrices” of external host. Obecnie coraz wieksza uwage przyciagaja arrays of parallelly aligned CNTs. Its potential applications obey, among others as adhesive films, blackbody absorbers, biological sensors, gas sensors, electron-emitting materials [2,3]. From this point of view, theoretical studies on arrays of parallelly oriented CNT’s are highly desirable.

In our paper, we present results for electronic properties of arrays of parallelly aligned CNTs.

They obey: band structure and densities of states (DOS), and in particular the gap. In our study, we present result for some small-diameter (of ’radius’ 2 and 3) CNTs . The general conclusion is that electronic structure of an array does not differ significantly from properties of isolated ones for distances between CNTs being sufficiently large. However, we observe that when they are sufficiently close each other, they undergo the structural metamorphosis to the graphene-like, or even more complicated structures.

2. Computational Methods

We undertook a systematic exploration of small-diameter carbon nanotubes to examine its electronic properties We have performed first-principles calculations within the framework of the density-functional theory (DFT) as implemented in SIESTA [9].

The exchange and correlation effects were accounted for by the generalized gradient approximation (GGA) with PBE exchange-correlation potential. The optimized atomic structures were obtained by fully relaxing both atomic positions as well as cell parameters by using conjugate gradients (CG) method. The optimization algorithm varied the atomic structure of the system until all forces were smaller than ${10}^{-6}$ eV/Å. All parameters critical for convergence, such as the k-points mesh and the energy cutoff, were carefully tested to ensure the most accurate results.

3. Results

3.1. Isolated CNTs

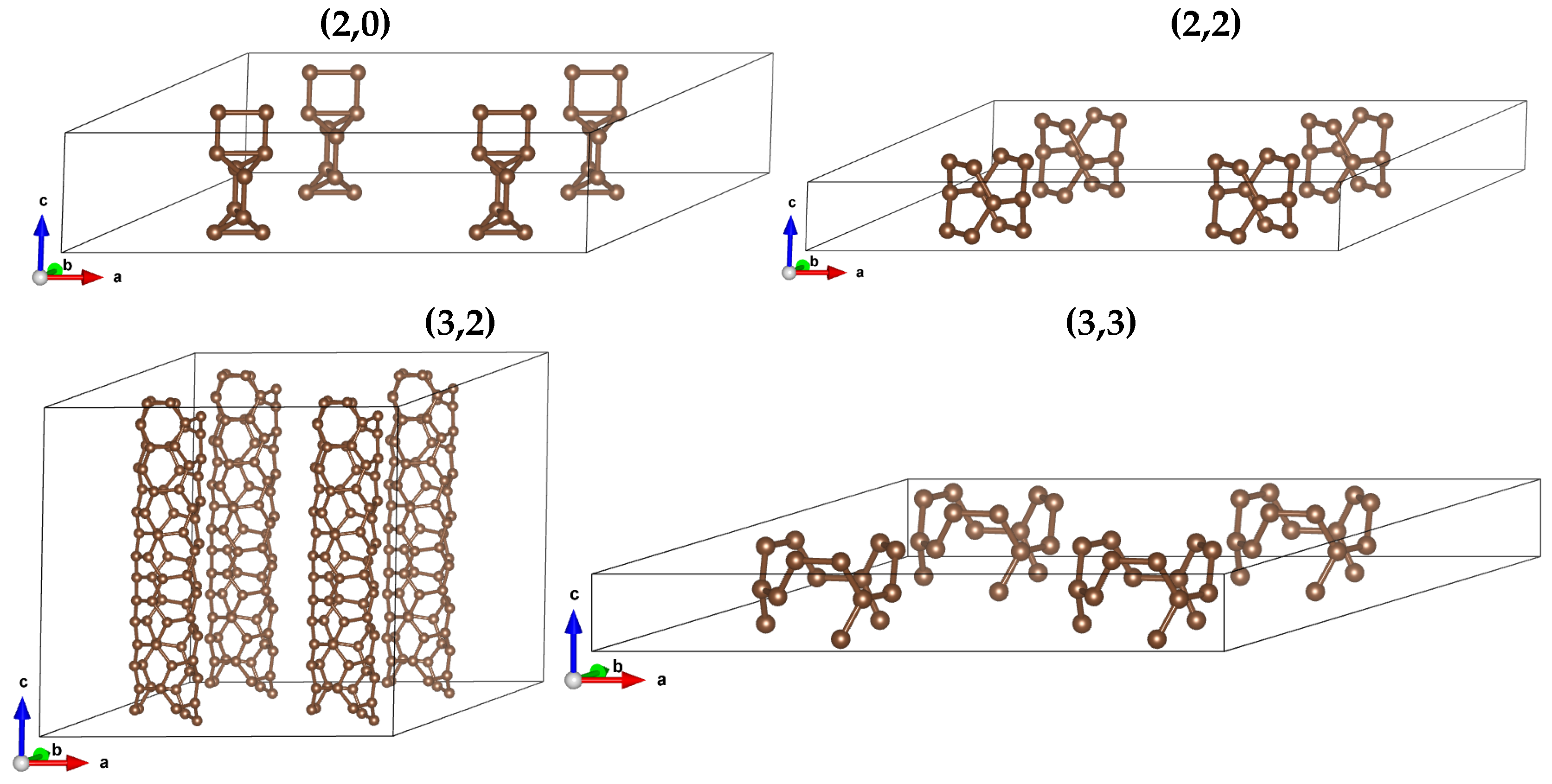
CNTs are characterized by two parameters $(n,m)$, where n is diameter, (so n is a natural number greater than 1) whereas m denotes the chirality parameter, which – for given n – take values from 0 to n. In our study, we compute properties of small-diameter CNTs: n take values 2 and 3. We took two conducting (i.e. zero-gap) and two insulating (non-zero gap)CNTs: diameter-2 series: (2,0) (non-zero gap) and (2,2) (zero gap); and diameter-3 series: (3,2) (non-zero gap) and (3,3) (zero gap). We display their structures on Figure 1

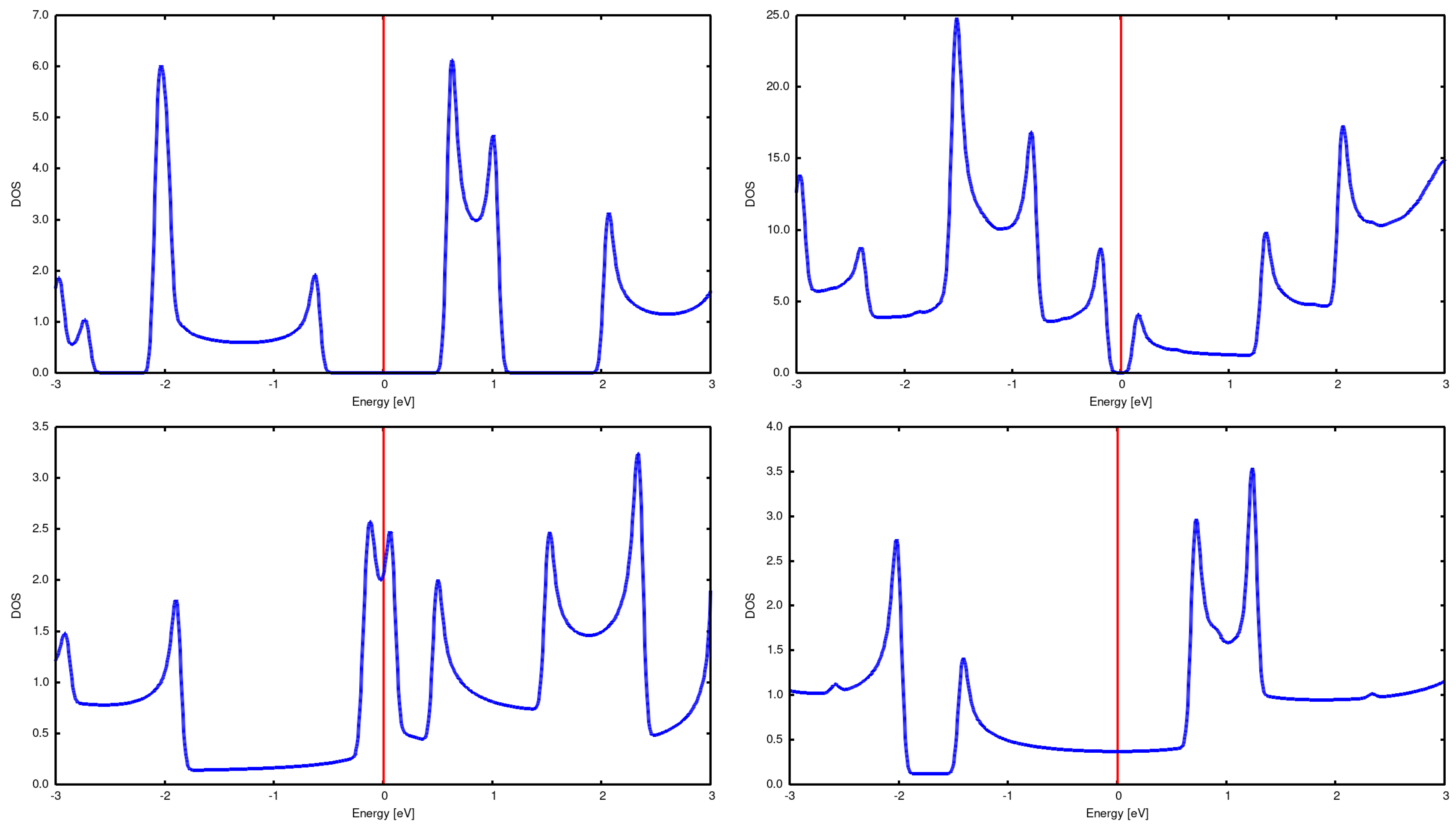
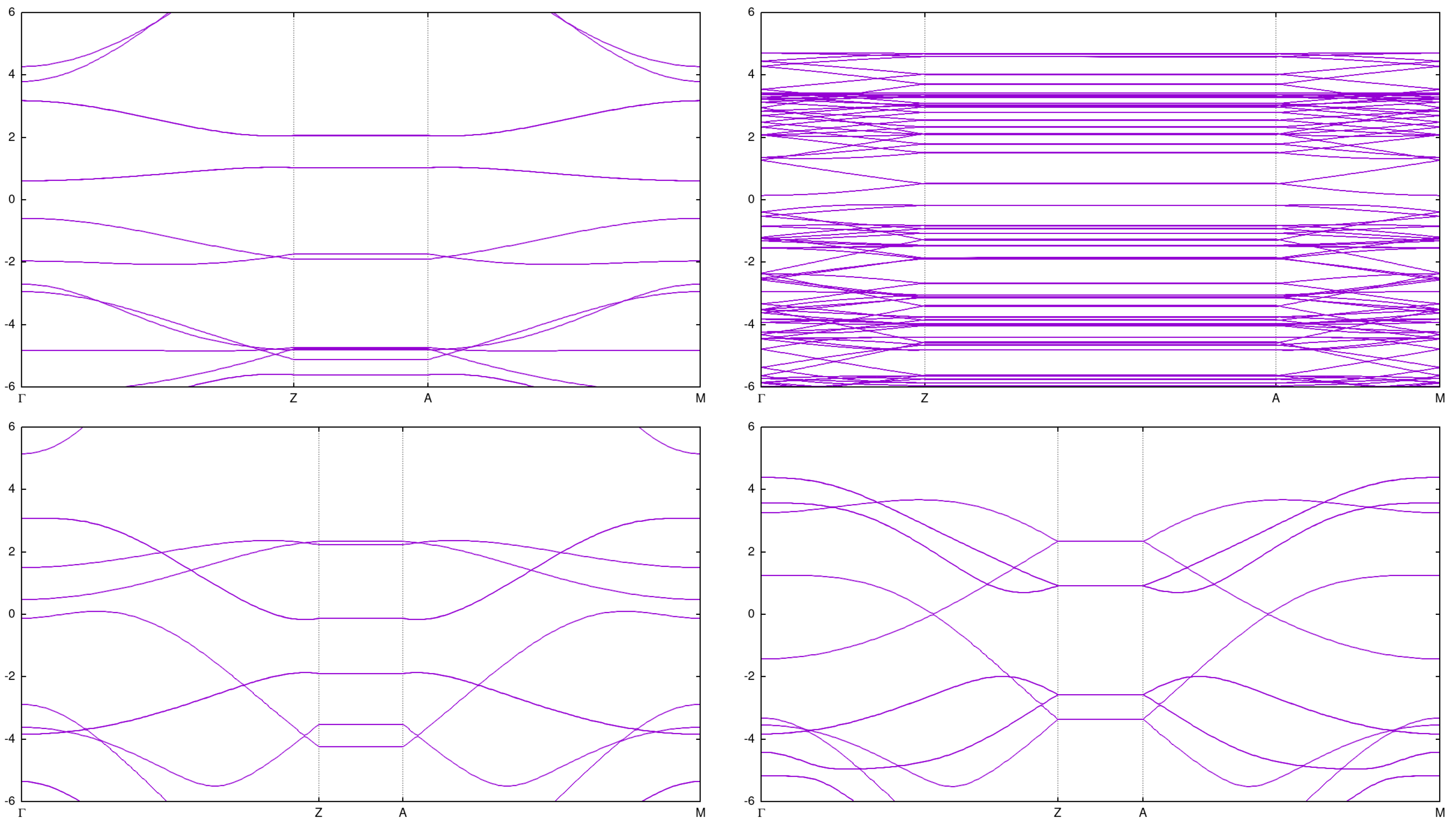
Properties of these CNTs have yet been calculated [4,7] but we reproduce it here for the sake of completeness and for comparison with results for arrays. See Figure 2 and Figure 3 as well as Table 1.

3.2. CNT Arrays

We repeated calculations for arrays of parallelly oriented CNTs. We considered nanotube systems distributed over a 2D triangular lattice (to achieve the ’close packing’) with nanotube distances of 15.0, 10.0, 7.5, and 5.0Å. The ’distance’ means the distance between middles of CNTs. The array structure is illustrated on Figure 4.

Results for band structure and DOSes are very similar for single (isolated) CNTs and their arrays, for intertube distances: 15Åand 10Å. When the distance is equal to 7.5Åone observes some changes, but not too significant. See Table 2. The geometric structures of CNTs in arrays are also similar to those for the single tube. But the situation changes drammatically when the distance is forced to be 5Åin all three cases: DOSes, band structure and gap, and the geometry of cristal lattice. We describe these changes in more details for every individual CNT.

(2,0) The band structure changes radically for distances less than 5Å. The structure of DOS and bands changes complitely and energy gap opens, so the system becomes an insulator. See Figure 5. It is accompanied by complete reorganization of crystal structure to graphene-like one. See Figure 8.

(2,2).

In the case of (2,2) CNTs, the structure rebuilds at the distance about 5 Å, resulting it the set of graphene-like planes. See Figure 9. The bands and DOS also undergo drammatic metamorphosis. See Figure 6.

(3,2).

In this case, we have no definite results as the optimization process does not converge even after large number of steps. Perhaps the optimized structure is very complicated and includes very large number of atoms.

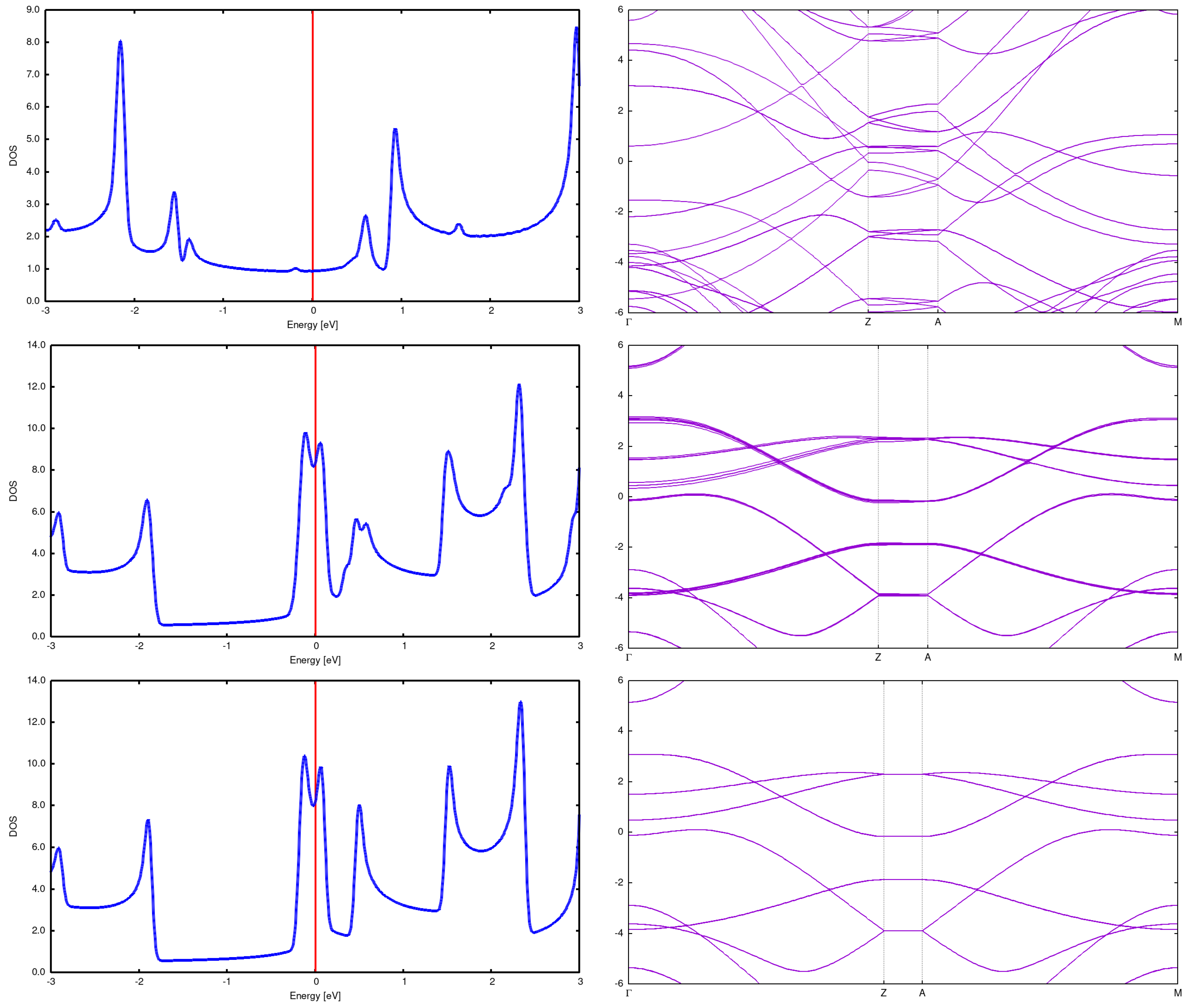
(3,3) Here we present structures for initial distances 7.5Å and 5Å. It is seen that the structure changes completely, resulting in something intermediate between graphite and diamond. See Figure 10. What is not strange, also DOS and bands rebuild in a profound manner. See Figure 7.

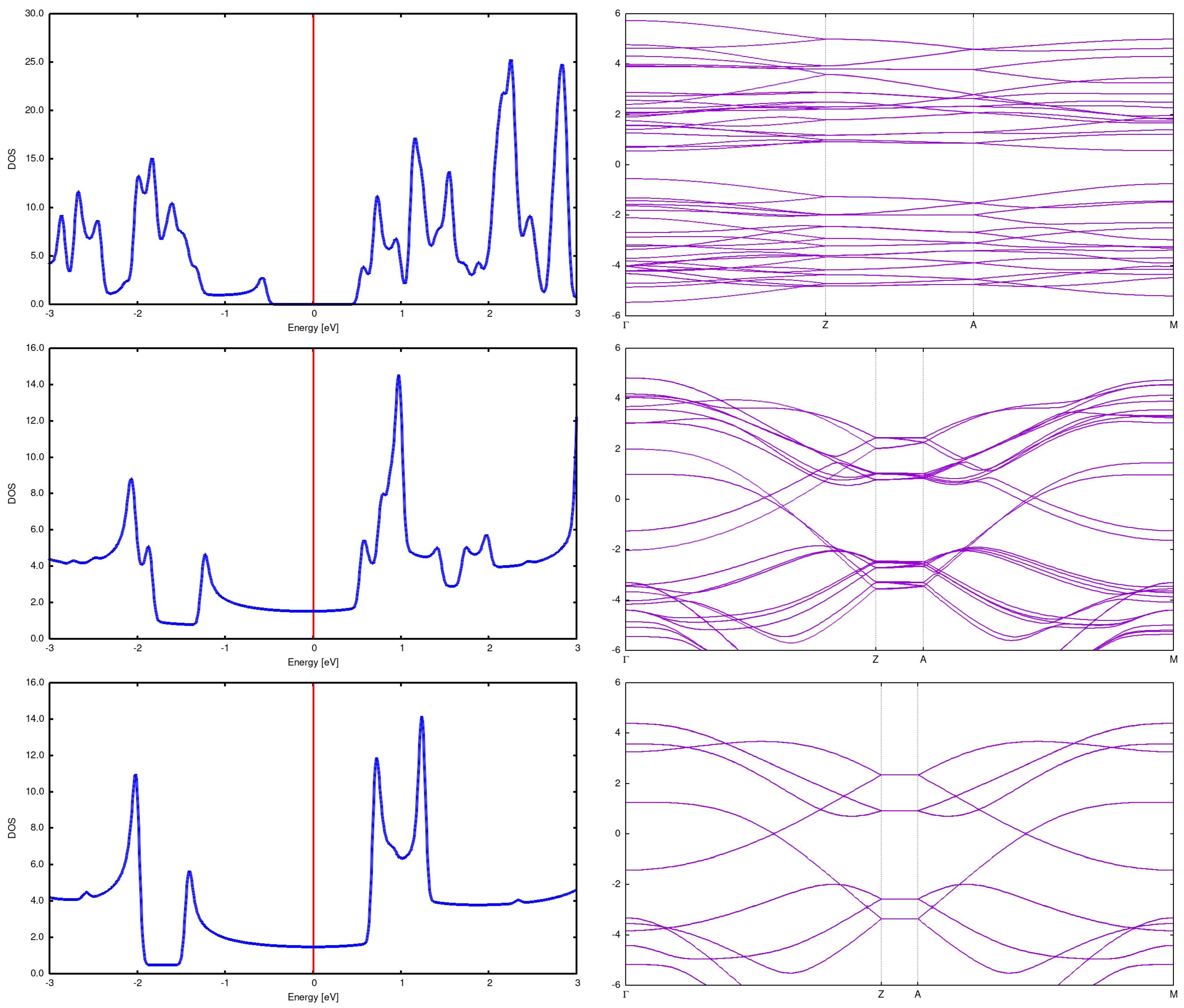
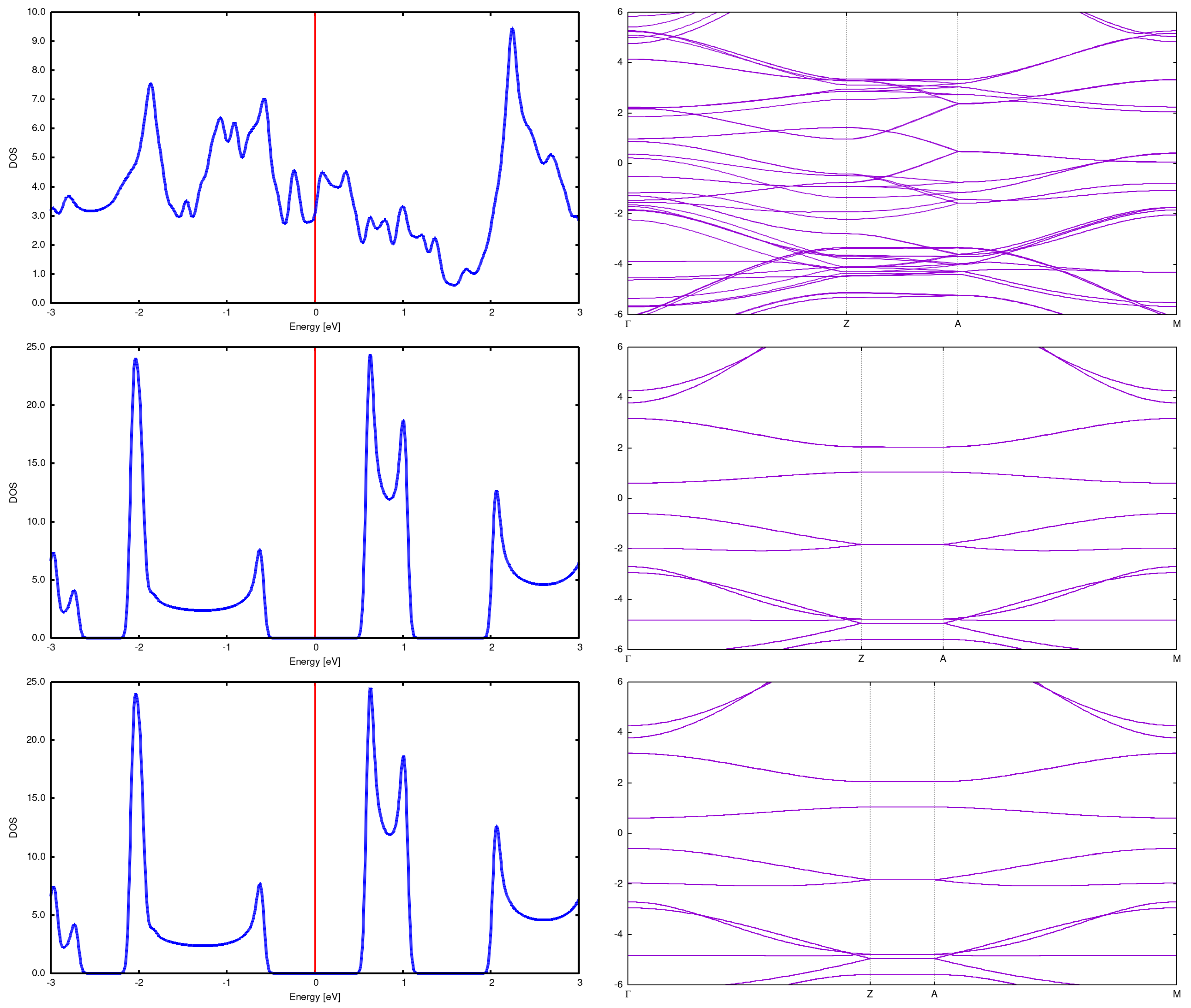
Figure 7. 2x2 array DOS and band structure for (3,3) CNT with $a=5$Å (top), $a=7.5$Å (center) and $a=10$Å(bottom). It is seen that the DOS and band changes drammatically for the distance 5Å; in particular, the energy gap opens

Figure 7. 2x2 array DOS and band structure for (3,3) CNT with $a=5$Å (top), $a=7.5$Å (center) and $a=10$Å(bottom). It is seen that the DOS and band changes drammatically for the distance 5Å; in particular, the energy gap opens

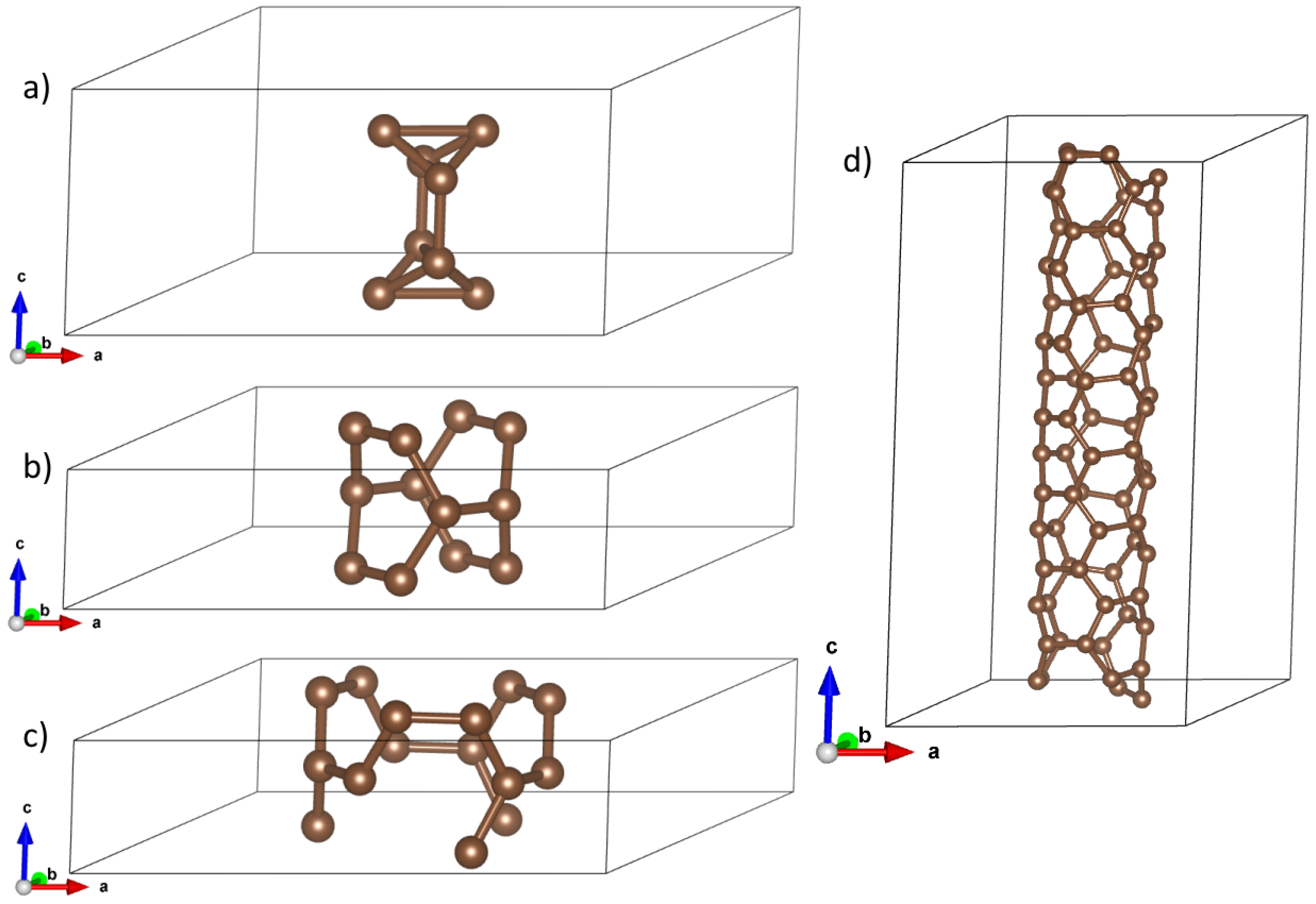
Figure 8. Crystal structure after optimisation for arrays of (2,0)CNTs for intertube distances 5Å(left) and 4Å(right). It is seen that for 5Åthe ’tube-like’ structure is preserved, whereas for 4Åthe completely new structure appears – the planes which ’remembers’ the nanotubes.

Figure 8. Crystal structure after optimisation for arrays of (2,0)CNTs for intertube distances 5Å(left) and 4Å(right). It is seen that for 5Åthe ’tube-like’ structure is preserved, whereas for 4Åthe completely new structure appears – the planes which ’remembers’ the nanotubes.

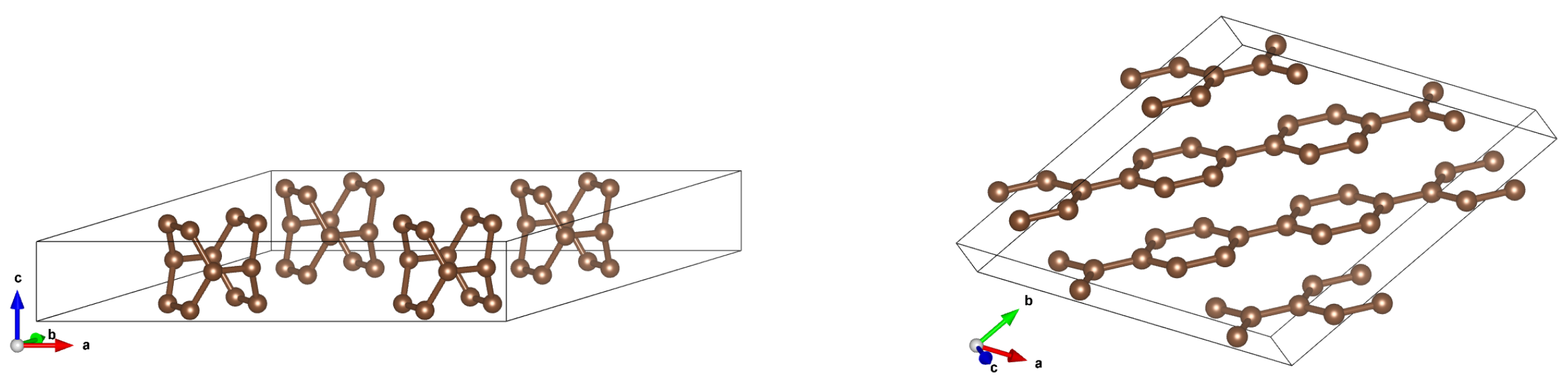
Figure 9. (2,2) CNT optimized structures for initial distances 7.5Åand 5Å. It is seen that for 5Åthe graphene-like structure emerges.

Figure 9. (2,2) CNT optimized structures for initial distances 7.5Åand 5Å. It is seen that for 5Åthe graphene-like structure emerges.

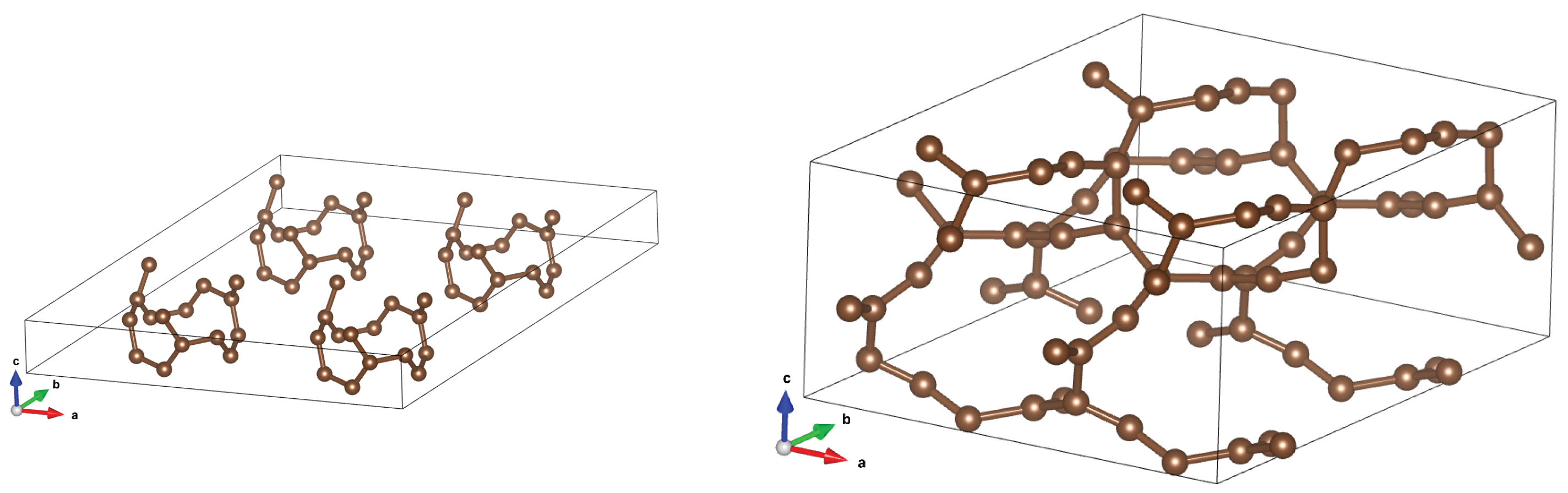
Figure 10. CNT optimized structures for initial distances 7.5Åand 5Å. It is seen that something intermediate between the diamond and graphite appears.

Figure 10. CNT optimized structures for initial distances 7.5Åand 5Å. It is seen that something intermediate between the diamond and graphite appears.

4. Summary, Perspectives of Further Investigations

We have calculated electronic properties of arrays of small-diameter carbon nanotubes. It turned out that for large intertube distances, the DOS and band structures does not differ from the case of isolated CNTs. But for smaller distances, the optimized structure differs radically from initial ones, which implies also radical change of DOS and band structures.

It would be very desirable to continue these calculations in order to:

• Know the equilibrium distance between CNTs. On the ground of present calculation, we conjecture that such arrays does not exist for small-diameter CNTs and are stable only for larger-diameter CNTs. One can guess that in this case the distance between walls of CNTs is the order of 3.5Å, like the distance between graphene layers in graphite. However, such a task is much more demanding from numerical point of view than present calculations.
• For equilibrium-distance arrays, one would know the relation between isolated tube properties and those in arrays: Geometry of CNTs; DOS and band structure; optical properties; exciton diffusion in arrays. All these properties are crucial for the idea of CNT-array-based solar cells. Unfortunately, the numerical demand seems to be enormous.