A Closed-Form Probability Formula for Random Points Avoiding Vertex Neighborhoods in Regular Polygons

1. Introduction

Regular polygons are fundamental geometric shapes with applications spanning from material science (e.g., graphene lattices) to wireless sensor networks. A key problem in geometric probability is to determine the likelihood that a random point within a polygon satisfies specific distance constraints.

Previous studies have characterized special cases: when $n=6$, no point in a regular polygon can satisfy that the distance between this point and all the vertices of the polygon is greater than the side length of the regular polygon. This leads to a trivial probability: when $n=6,P=0$. For the other cases, numerical integration or probabilistic bounds are typically employed.

In this paper, I partition the polygon into exclusion zones around each vertex and meticulously account for overlapping regions through inclusion-exclusion principles, I establish the theorem.

2. Proof

2.1. Find Out the Area Formed by All Points That Meet the Requirements

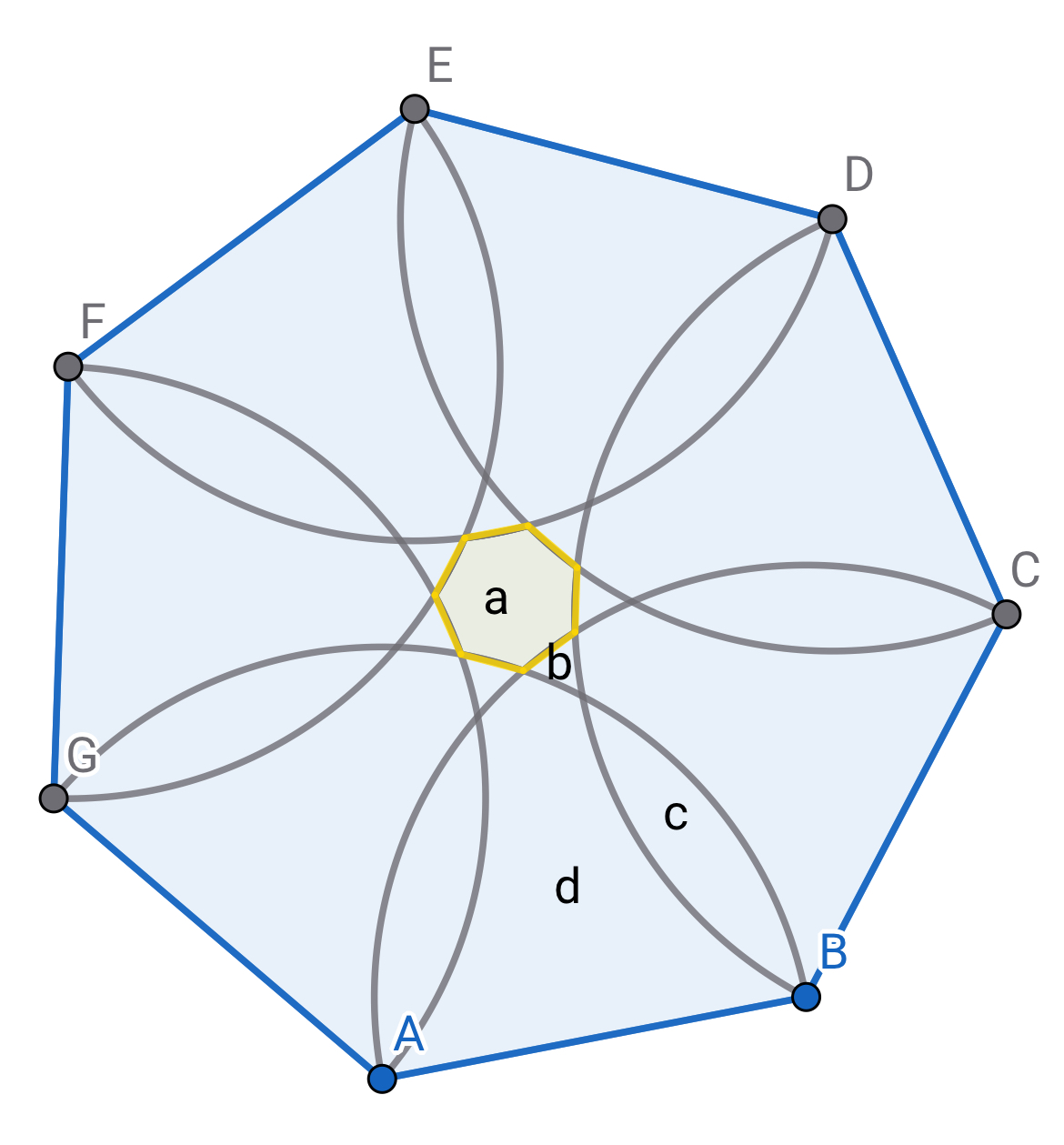
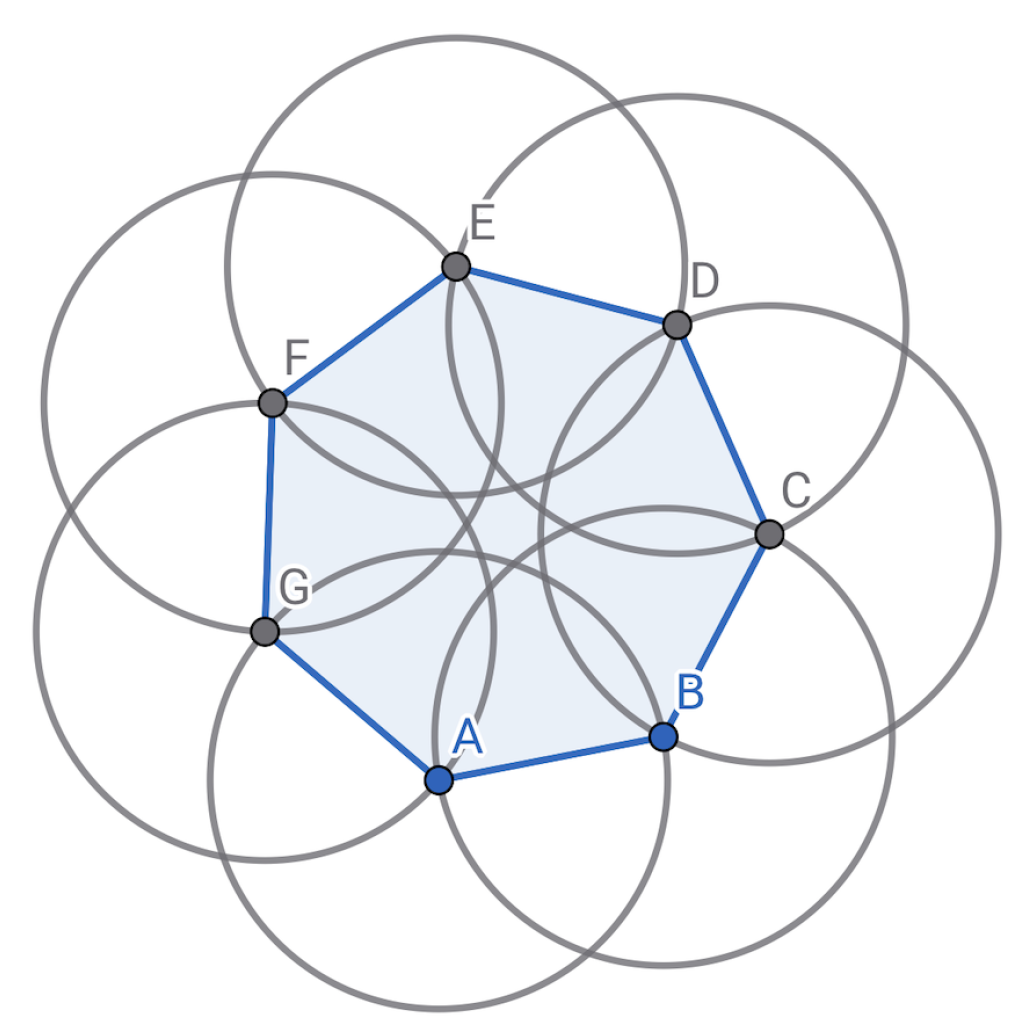
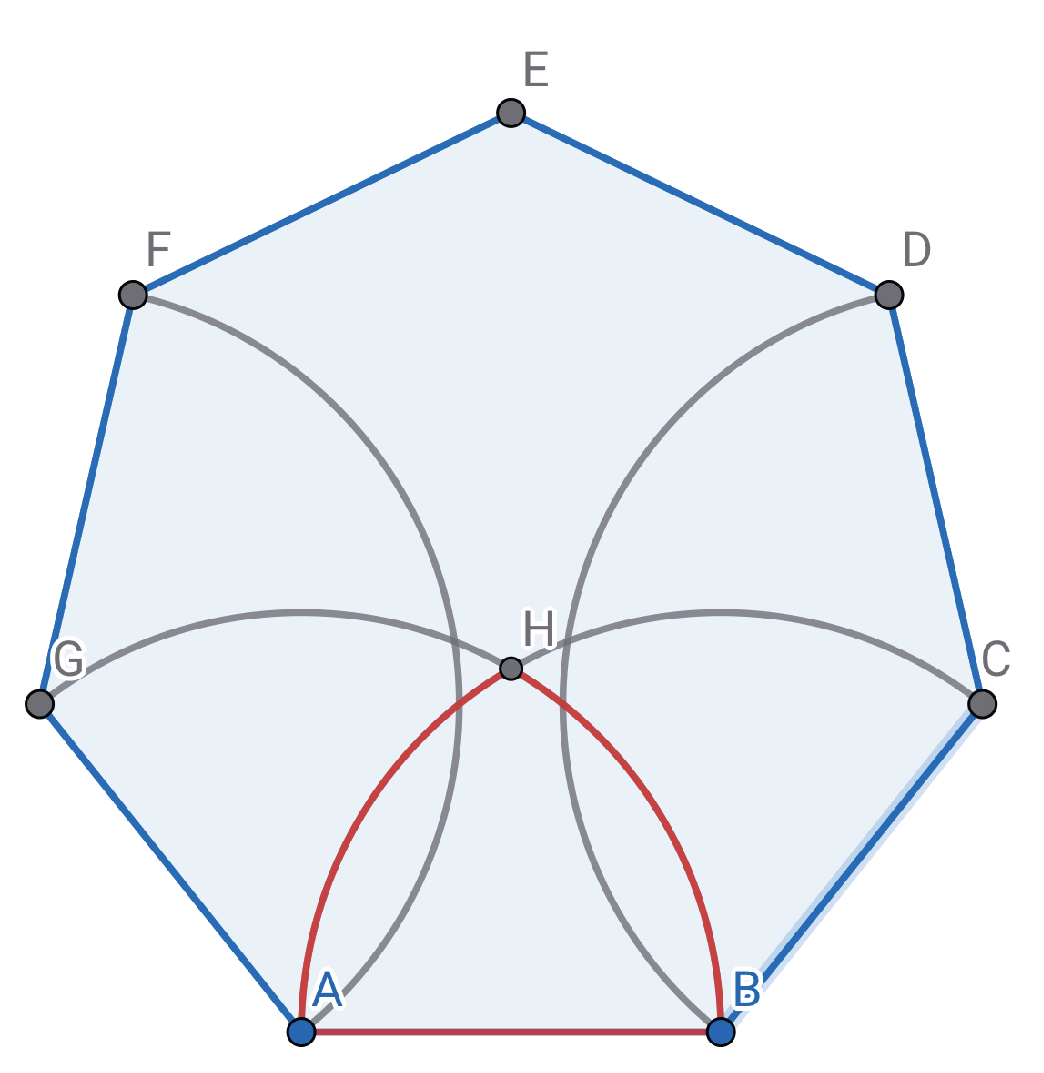
Find out the area that meets the requirements. Taking a regular heptagon as an example($n=7$), it is not difficult for us to draw such a picture like Figure 1.

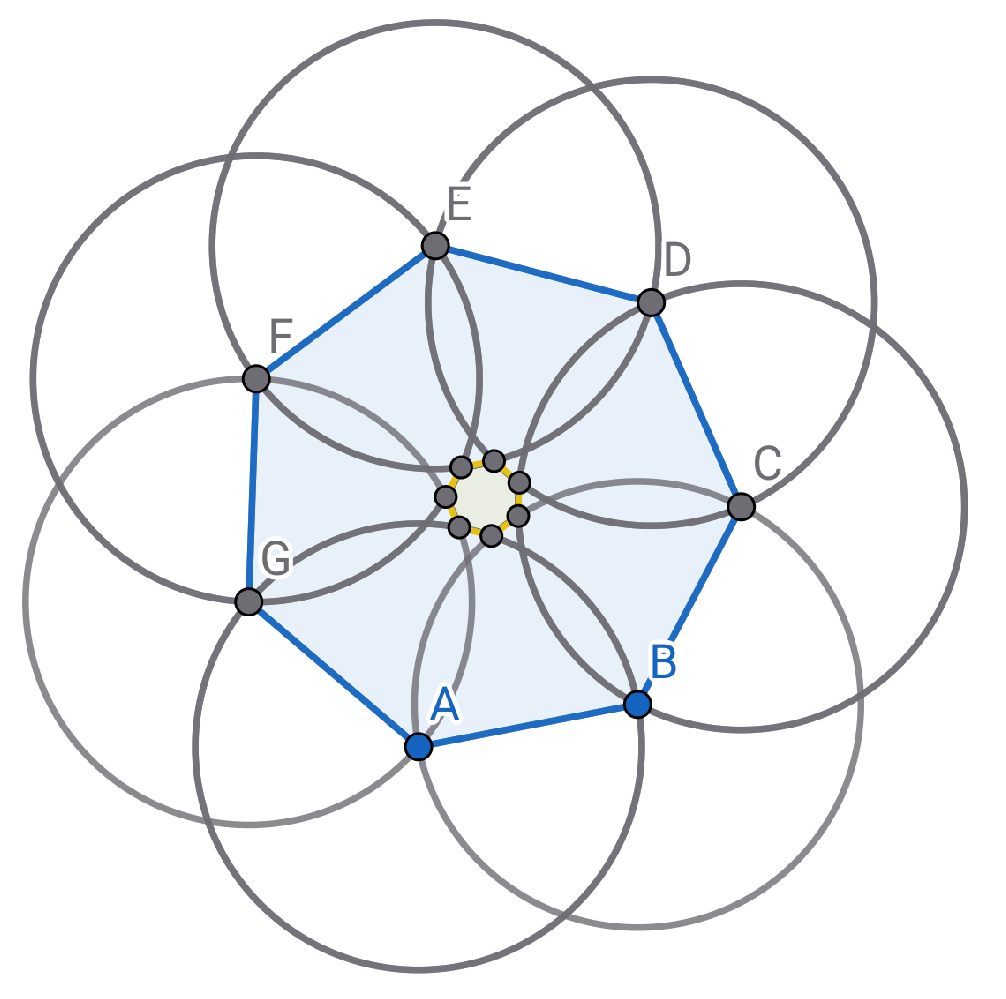
The yellow part in the middle in Figure 2 is the area that meets the requirements.

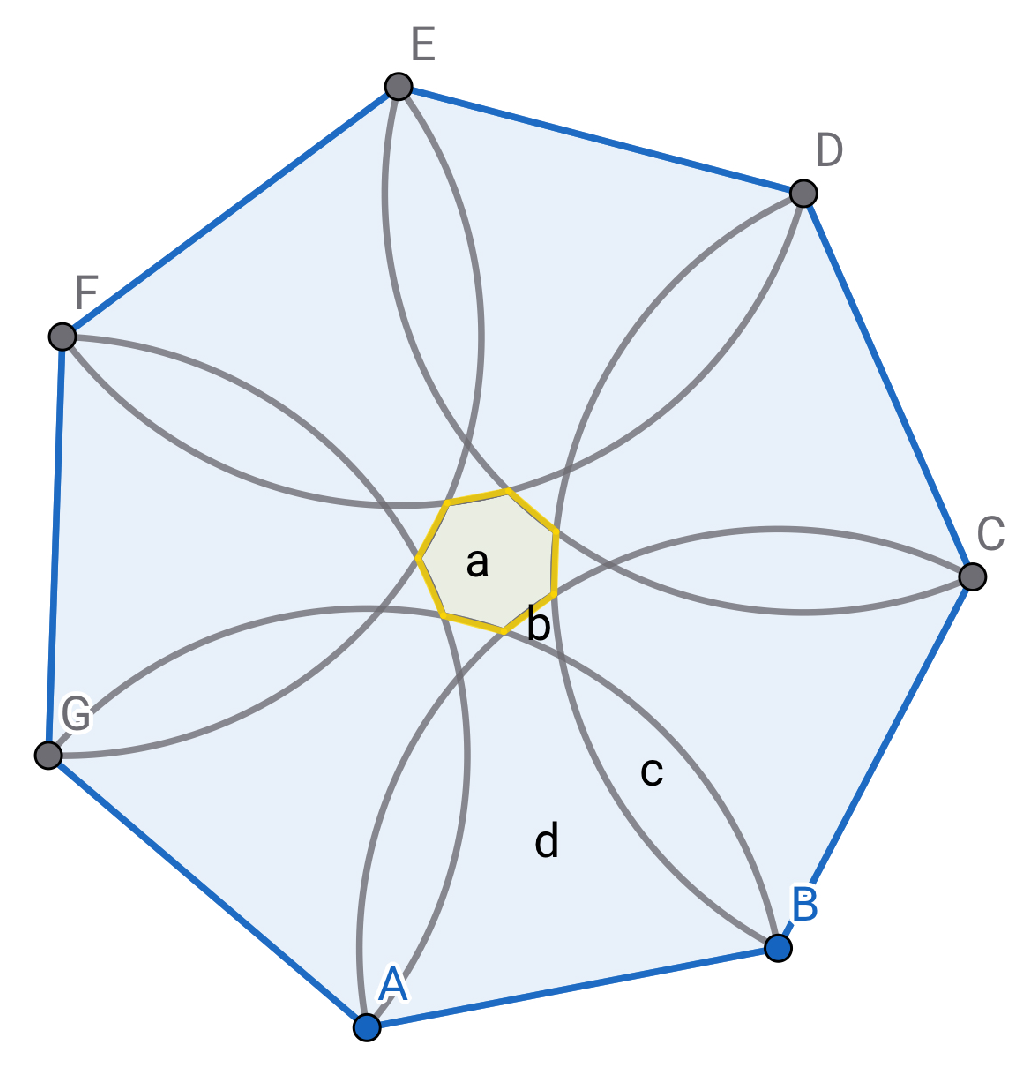
In order to find out the area of this area of any regular polygon with a side number greater than 6, we can divide the polygon into multiple parts and classify these parts like Figure 3, then we got the area $a,b,c$ and d. It is not difficult to find that every b in the same polygon is equal, every c in the same polygon is equal, and every d in the same polygon is also equal, because the whole figure is symmetrical about the center point of a. And the area of the polygon in Figure 3 is composed of $S_a$ and $7(S_b+S_c+S_d)$.

Assume the area of the whole regular polygon is S, When the number of sides of a regular polygon continues to increase, this law will not change, that is:

$$S_a=S-n(S_b+S_c+S_d)$$

So we can follow this rule to find a more specific expression of the area of a, then we can calculate the probability through this expression. but first we need to find a way to find $S_b+S_c+S_d$.

2.2. Find Out the Measure

Let’s first calculate the angle composed of two adjacent sides of a regular polygon with a number of sides n($n>6$), assume the angle is $\theta$,that is

$$\angle \theta ={\displaystyle \frac{(n-2)\pi }{n}}$$

We can use the ratio of this angle to $2\pi$ to find the area of the sector k enclosed by this angle with the side length of the polygon as the radius. Assume that the radius is l.

$$S_k={\displaystyle \frac{(n-2)l^2\pi }{2n}}$$

Referring to Figure 3, it is not difficult to find that

$$S_k=2S_d+3S_c+S_b$$

Then we find out the area of the red part in Figure 4. To express it more clearly, it is better to take the regular hepetagon as an example again. Obviously, the red area consists of an area d and two areas c.

In Figure 4, $HA=AB=BH$, It is not difficult to find that when the number of sides increases, these three line segments are still equal, and ∠$HAB$= $\pi /3$. Through a method similar to our method of calculating the sector area just now, we can get the area of the sector $HAB$, assume the sector is q.

$$S_q={\displaystyle \frac{l^2\pi }{6}}$$

The area of the equilateral triangle we just mentioned is

$$S_{▵HAB}={\displaystyle \frac{\sqrt{3}}{4}}{l}^2$$

Assume the red area is h, so the area of h is

$$S_h=2(S_q-S_{▵HAB})+S_{▵HAB}=2S_q-S_{▵HAB}={\displaystyle \frac{(4\pi -3\sqrt{3})l^2}{12}}$$

Since region h is composed of a region d and two regions c, region k is composed of two regions d, three regions c and one region b, and the areas of the two regions are subtracted to obtain the area of a region b, a region c and a region d.

$$S_{b+c+d}=S_k-S_h={\displaystyle \frac{6l^{2}n\pi -12l^2\pi -4\pi l^{2}n+3\sqrt{3}n{l}^2}{12n}}$$

And we have the measure of the polygon

$$S={\displaystyle \frac{l^{2}ntan\frac{(n-2)\pi }{2n}}{4}}$$

So we got the area of a

$$S_a=S-n{S}_{b+c+d}={\displaystyle \frac{l^{2}ntan\frac{(n-2)\pi }{2n}}{4}}-{\displaystyle \frac{6l^{2}n\pi -12l^2\pi -4\pi l^{2}n+3\sqrt{3}n{l}^2}{12}}$$

And the probability is

$$P={\displaystyle \frac{S_a}{S}}={\displaystyle \frac{3l^{2}ntan\frac{(n-2)\pi }{2n}-6n{l}^2\pi +12l^2\pi +4\pi l^{2}n-3\sqrt{3}n{l}^2}{3l^{2}ntan\frac{(n-2)\pi }{2n}}}$$

So the probability of meeting the conditions will be

$$P={\displaystyle \frac{S_a}{S}}={\displaystyle \frac{3ntan\frac{(n-2)\pi }{2n}-2n\pi +12\pi -3\sqrt{3}n}{3ntan\frac{(n-2)\pi }{2n}}}$$

Finishes the proof.