Information-Theoretic Sequential Framework to Elicit Dynamic High-Order Interactions in High-Dimensional Network Processes

1. Introduction

The complexity of physical, biological, and technological systems arises from the intricate structural and functional interactions among their components. Modern science has shifted away from the reductionist view that the behavior of a networked system—composed of multiple potentially interacting units — can be fully understood by examining each unit in isolation. Additionally, the traditional approach of modelling networked systems through pairwise measures of coupling or causality [1,2] is being increasingly questioned, as it often fails to fully capture the emergent dynamics of the system. Growing evidence indicates that network dynamics cannot be explained solely by pairwise couplings, as Higher-Order Interactions (HOIs) — those involving multiple system components — play a crucial role in shaping the overall behavior [3,4]. As a result, new methods are being developed to incorporate these HOIs into generalized network models [5]. Higher-order relationships involving three or more systems can be redundant (where multiple interacting systems share the same information) or synergistic (where a set of systems holds some information that cannot be seen from any subset). However, implementing such approaches remains challenging, particularly when interactions need to be inferred from data, as is often the case with biological or functional networks that represent the dynamic activity of physical systems.

Information-theoretic measures have been extensively used to assess higher-order interdependences in multivariate dynamical systems across diverse fields including neuroscience [6,7], finance [8,9], physiology [10,11,12], and climatology [13] where redundancies and synergies have been found to play meaningful roles [14,15,16,17,18]. The Partial Information Decomposition (PID) framework has emerged as a prominent tool for analyzing complex higher-order statistical interdependencies [14,19]. PID is able to quantify as separate quantities the synergistic and the redundant information terms together with the unique information that is held by each source but not by the others. Several approaches have been proposed relying on the PID concept and can be divided into two families: directed approaches that decompose information provided by source systems about a target and, undirected methods disentangle shared information among stochastic processes without assigning distinct roles, capturing the interplay between redundancy and synergy while remaining invariant under permutations [20,21]. Despite the advantages of PID approaches, a key limitation is the super-exponential growth of its atoms, making full decomposition impractical for large systems. To mitigate this challenge, coarse-grained PID metrics have been introduced, which bypass the computation of individual atoms by focusing on their linear combinations [22,23,24]. However, this approach still struggles with scalability as the number of processes in the network increases. Another approach recently introduced by Stramaglia et al. [25] proposes method, based on partial conditioning in multivariate data sets a [26], for decomposing Transfer Entropy (TE) [27]; the method is very versatile, as it has been extended to assess feature importance in explainable artificial intelligence [28]. Specifically, this approach bridges dyadic and polyadic methodologies, providing a complementary perspective to those focused on assessing HOIs [14,22,29]. While these methods aim to decompose the total information about the target from multiple sources, the proposed framework focuses on analyzing how the environment modifies the TE between two processes of interest.

This work builds upon [25] by introducing a stepwise strategy to identify, starting from a target node in a complex network, groups of nodes (multiplets) that maximize either redundant or synergistic HOIs. Measures traditionally applied to static analyses of random variables — such as Interaction Information (II) [30], the Redundancy-Synergy Index (RSI) [31], and O-information (OI) [22] — are herein extended to the analysis of stochastic processes. Specifically, the proposed method incorporates the Interaction Information Rate (IIR), the Redundancy-Synergy Index Rate (RSIR), and the O-information Rate Gradient ($\Delta \mathrm{OIR}$) to enable the dynamic analysis of these interactions. The approach is validated through simulations of interaction mechanisms that generate HOIs, including cascade effects, common driver motifs, and common target motifs. Finally, its feasibility is demonstrated through the analysis of a real-world climate network that captures the large-scale climate pattern of the El Niño-Southern Oscillation (ENSO), a key driver of global climate variability [32,33,34].

2. Sequential Method for Quantifying Higher-Order Interactions

This section outlines the methodology of the information-theoretic approach used to identify and quantify HOIs in complex networks. The Matlab Toolbox implementing the greedy approach proposed in this work is freely available for download from the repository https://github.com/helderpinto97/GS-HOIs.

2.1. Sequential Procedure Outline

Let us consider a set consisting of M processes, $\mathit{X}=\{X_1,\dots ,X_M\}$. This approach aims to identify, in a computationally efficient manner, a subset of processes within $\mathit{X}$ that form an informational circuit which is the most redundant or synergistic. To achieve this, the algorithm involves the following steps:

• Given the set $\mathit{X}$, first identify the triplet that exhibits the highest level of redundancy or synergy according to a predefined metric.
• Expand the selected triplet iteratively by adding one process at a time, ensuring that its inclusion results in the maximal statistically significant increase in the overall redundancy or synergy of the joint multiplet according to the chosen metric. Repeat this until no additional inclusion produces a statistically significant increase in redundancy or synergy.

The measures employed in this study to evaluate the prevalence of redundancy or synergy within a subset of processes are as follows: (i) the Interaction Information Rate (IIR) [12], calculated here in its conditional form; (ii) the Redundancy-Synergy Index (RSI) [35], extended in this work to its rate form (RSIR); and (iii) the O-information rate gradient $(\Delta \mathrm{OIR})$[12]. Importantly, the RSIR and $\Delta \mathrm{OIR}$ measures reduce to the IIR when applied to scenarios involving $M=3$ processes.

Therefore, the IIR serves as the basic measure used in this work to implement Step 1 of our algorithm. The IIR for the triplet of processes ${\mathbf{X}}_{\mathbf{1}}=\{X_{i_1},X_{i_2},X_{i_3}\}$, is defined as [12]:

$$\begin{array}{cc}\hfill I_{{\mathit{X}}_1}=I_{X_{i_1};X_{i_2};X_{i_3}}& =I_{X_{i_1};X_{i_2}}+I_{X_{i_1};X_{i_3}}-I_{X_{i_1};X_{i_2},X_{i_3}}\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill & =I_{X_{i_1};X_{i_2}}-I_{X_{i_1};X_{i_2}|X_{i_3}},\hfill \end{array}$$

(2)

where $I_{(·);(·)}$ is the Mutual Information Rate (MIR) which quantifies the information shared between the two processes per unit of time [36], and $I_{(·);(·)\left|\right(·)}$ is the conditional MIR (cMIR). The IIR $I_{X_{i_1};X_{i_2};X_{i_3}}>0$ indicates the prevalence of redundancy, while $I_{X_{i_1};X_{i_2};X_{i_3}}<0$ indicates the prevalence of synergy. Specifically, in the former case, the knowledge of $X_{i_3}$ reduces the information shared by $X_{i_1}$ and $X_{i_2}$, indicating that the statistical dependence between $X_{i_1}$ and $X_{i_2}$ is suppressed when $X_{i_3}$ is observed. Conversely, in the latter case, the knowledge of $X_{i_3}$ increases the information shared by $X_{i_1}$ and $X_{i_2}$, indicating that the statistical dependence between $X_{i_1}$ and $X_{i_2}$ emerges when $X_{i_3}$ is observed. Accordingly, step 1—identifying the most redundant or synergistic triplet—involves finding the maximum or minimum values of the IIR measure across all possible triplets within the set $\mathit{X}$ respectively. The maximally redundant and maximally synergistic triplets identified in this way are denoted as ${\mathit{X}}_1^{\mathrm{M}}$ and ${\mathit{X}}_1^{\mathrm{m}}$, respectively.

The algorithm proceeds iteratively selecting, for each step k ($k\ge 2$), the process $X_{i_{k+2}}^m$ such that

$$X_{i_{k+2}}^m=\underset{X_j\in {X}\setminus {{X}}_{k-1}}{arg\; min}{\mathsf{\Phi }}_{X_j}$$

(3)

in the case of a search for synergy, and selecting the process $X_{i_{k+2}}^M$ such that

$$X_{i_{k+2}}^M=\underset{X_j\in {X}\setminus {{X}}_{k-1}}{arg\; max}{\mathsf{\Phi }}_{X_j}$$

(4)

in the case of a search for redundancy. If the measure ${\mathsf{\Phi }}_{X_j}$ is statistically significant, the process satisfying either Equations (3) or (4) is retained, updating the multiplet to ${\mathbf{X}}_k^m=\{{\mathbf{X}}_{k-1}^m,X_{i_{k+2}}^m\}$ or ${\mathbf{X}}_k^M=\{{\mathbf{X}}_{k-1}^M,X_{i_{k+2}}^M\}$, respectively, and the procedure proceeds to the next step. If ${\mathsf{\Phi }}_{X_j}$ is not statistically significant, the procedure terminates, resulting in the final multiplet: ${\mathbf{X}}^m={\mathbf{X}}_{k-1}^m$ in the case of redundancy, or ${\mathbf{X}}^M={\mathbf{X}}_{k-1}^M$ in the case of synergy. The statistical significance of ${\mathsf{\Phi }}_{X_j}$ is assessed using the surrogate-based approach [25]. Processes are added one at a time to the current multiplet to construct a set that either maximizes or minimizes ${\mathsf{\Phi }}_{X_j}$. The greedy search stops when any observed change in ${\mathsf{\Phi }}_{X_j}$ can reasonably be attributed to chance. To determine this, the probability is estimated that the observed increase (or decrease) in ${\mathsf{\Phi }}_{X_j}$ is smaller (or bigger) than what would result from adding a process with similar individual statistical properties but not coupled with the current multiplet ${\mathbf{X}}_{k-1}$.

The function ${\mathsf{\Phi }}_{(·)}$ applied to a process $X_j\in \mathbf{X}\setminus {\mathbf{X}}_1$ is the objective function of the minimization (or maximization), and is chosen in three different ways as follows. In the case (i), the conditional IIR (cIIR) is employed, where for the step $k=2$:

$${\mathsf{\Phi }}_{X_j}^{\mathrm{IIR}}=I_{{\mathit{X}}_1|X_j},$$

(5)

and for $k\ge 3$:

$${\mathsf{\Phi }}_{X_j}^{\mathrm{IIR}}=I_{{\mathit{X}}_1|X_{i_4},\dots ,X_{i_{k+1}},X_j}.$$

(6)

In the case (ii), the RSIR is employed, which, at step k is defined as [35,37]:

$${\mathsf{\Phi }}_{X_j}^{\mathrm{RSIR}}=\sum _{X_i\in {\mathit{X}}_{k-1}}{I}_{X_j;X_i}-I_{X_j;{\mathbf{X}}_{k-1}}.$$

(7)

Finally, analogously, in case (iii), $\Delta \mathrm{OIR}$ is used [12,38]:

$${\mathsf{\Phi }}_{X_j}^{\Delta \mathrm{OIR}}=\sum _{X_i\in {\mathit{X}}_{k-1}}{I}_{X_j;{\mathbf{X}}_{k-1}\setminus X_i}-k{I}_{X_j;{\mathbf{X}}_{k-1}}.$$

(8)

In both Equations (7) and (8), $I_{(.);(.)}$ as previously denotes the MIR.

In case (i), adding processes to the conditional vector can either increase or decrease the cIIR, revealing how the added processes interact in a synergistic or redundant way with the initial triplet ${\mathbf{X}}_1$. For this specific measure the final multiplets ${\mathbf{X}}^M$ and ${\mathbf{X}}^m$ is obtained appending the initial triplet ${\mathbf{X}}_1$ to the conditioning vector. Regarding cases (ii) and (iii), Equations (7) and (8), the RSIR [35,37] and $\Delta \mathrm{OIR}$[12,38], quantify how the tested process $X_j$ contributes to the balance between redundant and synergistic interdependencies with the current multiplet ${\mathbf{X}}_{k-1}$.

Before delving into the technical details regarding the estimation of these information measures, it is essential to highlight that each objective function — ${\mathsf{\Phi }}_{X_j}^{\mathrm{IIR}}$, ${\mathsf{\Phi }}_{X_j}^{\mathrm{RSIR}}$, and ${\mathsf{\Phi }}_{X_j}^{\Delta \mathrm{OIR}}$ — used to identify the most synergistic or redundant multiplets can be expressed as a sum of MIR terms. In particular, for ${\mathsf{\Phi }}_{X_j}^{\mathrm{RSIR}}$ and ${\mathsf{\Phi }}_{X_j}^{\Delta \mathrm{OIR}}$, this follows directly from Equations (7) and (8). Conversely, the cIIR measure can be expressed as a sum of cMIR terms. For instance, for $k=2$, Equation (5) can be decomposed as:

$$I_{{\mathbf{X}}_{\mathbf{1}}\mid X_j}=I_{X_{i_1};X_{i_2}\mid X_j}+I_{X_{i_1};X_{i_3}\mid X_j}-I_{X_{i_1};X_{i_2},X_{i_3}\mid X_j}.$$

(9)

Moreover, each cMIR term can be expressed in terms of MIR [11], leading to the following reformulation:

$$I_{{\mathbf{X}}_{\mathbf{1}}\mid X_j}=I_{X_{i_1};X_{i_2},X_{i_3},X_j}-I_{X_{i_1};X_{i_2},X_j}-I_{X_{i_1};X_{i_3},X_j}+I_{X_{i_1};X_j}.$$

(10)

The same reasoning applies at each step k. Therefore, for each step, it suffices to estimate only MIR terms to compute the functions ${\mathsf{\Phi }}^{\mathrm{IIR}},$${\mathsf{\Phi }}^{\mathrm{RSIR}}$ and ${\mathsf{\Phi }}^{\Delta \mathrm{OIR}}$. For this purpose, a parametric approach based on the Vector AutoRegressive (VAR) model [39] is employed to estimate the MIR terms involve in the estimation of the three measures, which the details are presented in the next section.

Another key point to emphasize is that, when analyzing real-world complex systems, the focus is often on a specific process and its interaction with the surrounding environment — particularly how other processes influence this target process, either synergistically or redundantly. This consideration can be integrated into Step 1 of the algorithm, where the selected triplet must include the predefined target process.

2.2. Linear Parametric Estimation of Higher-Order Interaction Information Measures

Consider a general system of M units, $\mathcal{S}=\{{\mathcal{S}}_1,\dots ,{\mathcal{S}}_M\}$ and focus on the two units $\mathcal{X}={\mathcal{S}}_i$ and $\mathcal{Y}={\mathcal{S}}_j$ while collecting the remaining $M-2$ units in the group $\mathcal{Z}=\mathcal{S}\setminus \{\mathcal{X},\mathcal{Y}\}$. Since the system $\mathcal{S}$ exhibits dynamic behavior, it is best described as a vector random process $S_n=[S_{1,n},\dots ,S_{M,n}]$, where the temporal dependence is indicated by the time index n, and $S_{i,n}$ represents the sampled value of the $i^{\mathrm{th}}$ process at time step n ($i=1,\dots ,M$, $n\in \mathbb{Z}$ for discrete-time processes). The equivalent notation evidencing the dynamics of the units $\{\mathcal{X},\mathcal{Y},\mathcal{Z}\}$ is $S_n=\left[X_n,Y_n,{\mathbf{Z}}_n\right]$. A widely used method to model the dynamics of $\mathbf{S}=\{X,Y,\mathbf{Z}\}$ is the linear Vector AutoRegressive (VAR) model [39], given by:

$${\mathbf{S}}_n=\sum _{k=1}^p{\mathbf{A}}_k{\mathbf{S}}_{n-k}+U_n$$

(11)

where ${\mathbf{S}}_n$ and ${\mathbf{S}}_{n-k}$ represent M-dimensional variables that capture the state of the process at the current time step n and k steps in the past, respectively. The matrix ${\mathbf{A}}_k$ is an $M\times M$ coefficient matrix, while $U_n$ denotes an independent and identically distributed (i.i.d.) innovation process, with an $M\times M$ covariance matrix ${\Sigma }_U$. Given the full model, represented in Equation (11), restricted models can be used to describe the dynamics of any given subset of processes. Specifically, the dynamics of processes X, Y, and their joint dynamics in the multivariate process $\mathbf{W}=\{X,Y\}$ are represented by:

$$\begin{array}{cc}\hfill X_n& =\sum _{k=1}^q{A}_k^{\left(x\right)}{X}_{n-k}+U_{x,n}\hfill \\ \hfill Y_n& =\sum _{k=1}^q{A}_k^{\left(y\right)}{Y}_{n-k}+U_{y,n}\hfill \\ \hfill {\mathbf{W}}_n& =\sum _{k=1}^q{\mathbf{A}}_k^{\left(w\right)}{\mathbf{W}}_{n-k}+{\mathbf{U}}_{w,n}\hfill \end{array}$$

(12)

where q is the model order (theoretically $q\to \infty$). The parameters $A_k^{\left(x\right)},A_k^{\left(y\right)},{\mathbf{A}}_k^{\left(w\right)}$, and the residual covariances ${\Sigma }_{U_x},{\Sigma }_{U_y},{\Sigma }_{U_w}$, can be derived from the full model parameters ${\mathbf{A}}_k$ and ${\Sigma }_U$ by solving the Yule-Walker equations and reorganizing the covariance structure of $\mathbf{S}$ to relate it to X, Y, or $\mathbf{W}$[40]. Assuming joint Gaussianity of the overall process $\mathbf{S}$, the MIR can be directly determined from the covariances of the residuals of the restricted models:

$$I_{X;Y}={\displaystyle \frac{1}{2}}log{\displaystyle \frac{{\Sigma }_{U_x}·{\Sigma }_{U_y}}{\left|{\Sigma }_{U_w}\right|}}.$$

(13)

The aforementioned procedure can be iterated to construct restricted models that characterize the dynamics of the vector process $\mathbf{Z}$ and the joint processes $\mathbf{V}=\{X,\mathbf{Z}\}$ and $\mathbf{R}=\{Y,\mathbf{Z}\}$. These models are formulated using VAR representations, as outlined in Equation (12), enabling the derivation of expressions for the MIR terms $I_{X;\mathbf{Z}}$ and $I_{X;Y,\mathbf{Z}}=I_{X;\mathbf{R}}$:

$$I_{X;\mathbf{Z}}={\displaystyle \frac{1}{2}}log{\displaystyle \frac{{\Sigma }_{U_x}\left|{\Sigma }_{U_z}\right|}{\left|{\Sigma }_{U_v}\right|}},$$

(14)

$$I_{X;Y,\mathbf{Z}}=I_{X;\mathbf{R}}={\displaystyle \frac{1}{2}}log{\displaystyle \frac{{\Sigma }_{U_x}\left|{\Sigma }_{U_r}\right|}{\left|{\Sigma }_U\right|}}.$$

(15)

Then, the formulations presented in Equations (13)-(15) are directly applied in Equations (10), (7), and (8) to compute ${\mathsf{\Phi }}^{\mathrm{IIR}}$, ${\mathsf{\Phi }}^{\mathrm{RSIR}}$, and ${\mathsf{\Phi }}^{\Delta \mathrm{OIR}}$, respectively, at each step of the algorithm. In practical analyses, these metrics are computed from synchronous time series realizations of the processes X, Y, and $\mathbf{Z}$. The parameters of the full model (11) are estimated using least squares [39], and these estimates are used to derive the covariance matrices of the residuals from the restricted models [40]. These covariance matrices are then employed in Equations (13), (14) and (15) to estimate the MIR terms. The order p of the full model is selected using the Akaike Information Criterion (AIC) [41], while the order q of the restricted models is set to a high value (specifically, $q=22$ in this work) to capture the decay of correlations at increasing lags.

After estimation, the statistical significance of the measures is assessed at each step of the algorithm. Surrogate realizations of the candidate process for the multiplet are generated using the Iterative Amplitude-Adjusted Fourier Transform (IAAFT) method, which destroys cross-correlation while preserving autocorrelation and the power spectrum [42,43,44]. Depending on whether redundancy or synergy is being evaluated, the process is retained if the corresponding probability is above or bellow a predefined threshold, respectively. In this work, the 95% and 5% percentiles of the surrogates distribution are used as thresholds.

3. Simulation Studies

The proposed sequential method for detecting and quantifying HOIs in a network of interacting processes is validated using theoretical examples based on simulated VAR models. In these simulations, various interaction measures are computed directly from the theoretical model parameters, ensuring the evaluation of the proposed method. These simulations demonstrate how our approach can effectively identify processes that interact in a redundant or synergistic manner with respect to a predefined target process.

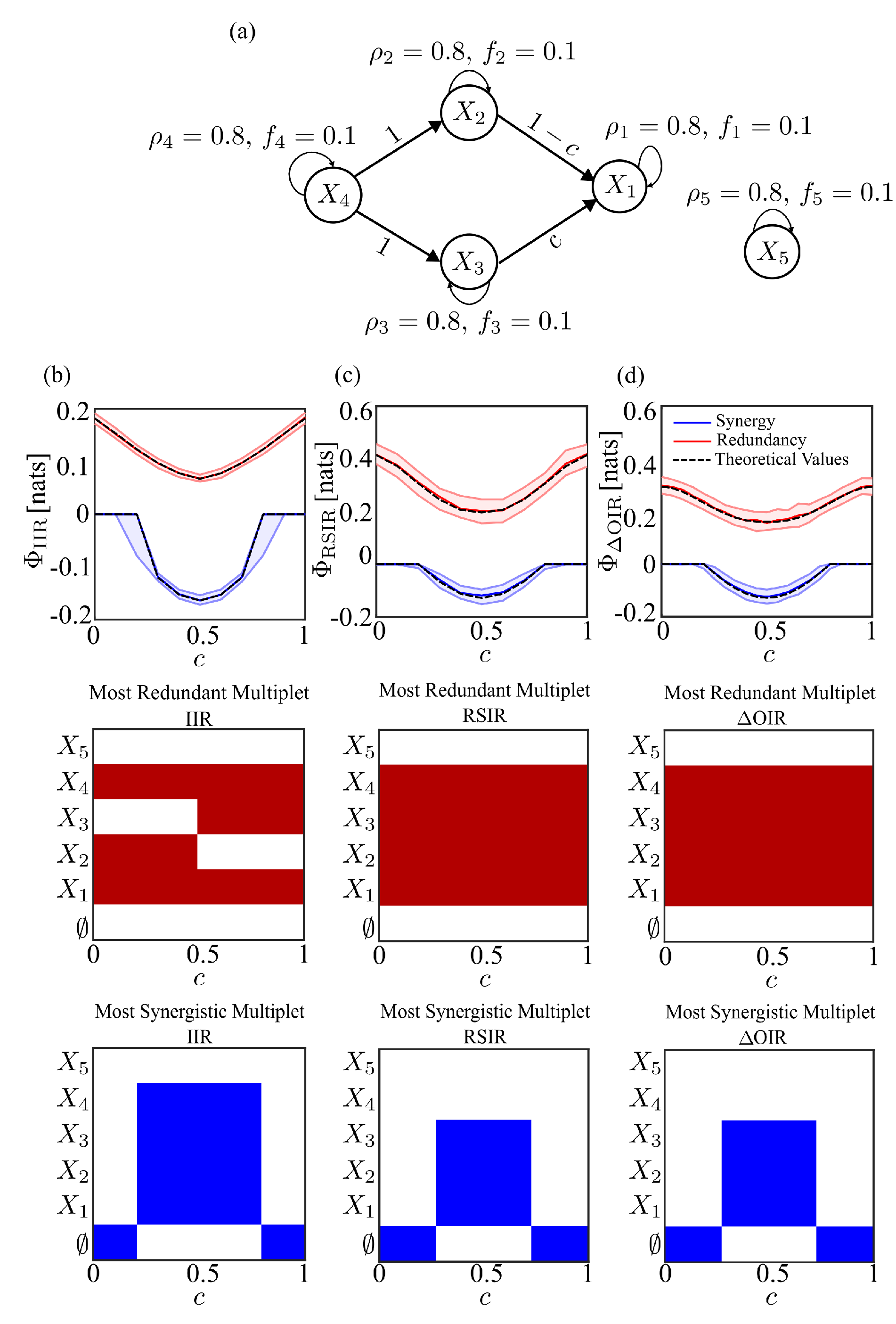
3.1. Five-Dimensional VAR Model

First, the proposed method is evaluated using a five-variate VAR model of order 2, defined by the following equations [7]:

$$\begin{array}{cc}\hfill & X_{1,n}=2{\rho }_{1}cos\left(2\pi f_1\right)X_{1,n-1}-{\rho }_1^2{X}_{1,n-2}+\left(1-c\right)X_{2,n-1}+c{X}_{3,n-2}+U_{1,n},\hfill \\ \hfill & X_{2,n}=2{\rho }_{2}cos\left(2\pi f_2\right)X_{2,n-1}-{\rho }_2^2{X}_{2,n-2}+X_{4,n-1}+U_{2,n},\hfill \\ \hfill & X_{3,n}=2{\rho }_{3}cos\left(2\pi f_3\right)X_{3,n-1}-{\rho }_3^2{X}_{3,n-2}+X_{4,n-2}+U_{3,n},\hfill \\ \hfill & X_{4,n}=2{\rho }_{4}cos\left(2\pi f_4\right)X_{4,n-1}-{\rho }_4^2{X}_{4,n-2}+U_{4,n},\hfill \\ \hfill & X_{5,n}=2{\rho }_{5}cos\left(2\pi f_5\right)X_{5,n-1}-{\rho }_5^2{X}_{5,n-2}+U_{5,n},\hfill \end{array}$$

(16)

where ${\mathbf{U}}_n={\left[U_{1,n},\dots ,U_{5,n}\right]}^{\top }$ represents a zero-mean white Gaussian noise with covariance matrix ${\Sigma }_U$. The node $X_5$ represents an isolated node which does not interact with other processes in the network. The graphical representation of the model (16) is presented in Figure 1(a). The parameter design in the set of equations (16) is chosen to enable autonomous oscillations in all five processes. This is achieved by placing complex-conjugate poles in the complex plane representation of the transfer function of the vector process, with amplitudes ${\rho }_1,{\rho }_2,{\rho }_3,{\rho }_4,{\rho }_5$ and normalized frequency $f_1,f_2,f_3,f_4,f_5$. Causal interactions between processes $X_2$ and $X_1$ are controlled by the coupling parameter $1-c$, while interactions between $X_3$ and $X_1$ are modulated by the parameter c. Specifically, the parameters were set as ${\rho }_1={\rho }_2={\rho }_3={\rho }_3={\rho }_5=0.8$, ${\displaystyle \frac{f_1}{f_s}}={\displaystyle \frac{f_2}{f_s}}={\displaystyle \frac{f_3}{f_s}}={\displaystyle \frac{f_4}{f_s}}={\displaystyle \frac{f_5}{f_s}}=0.1$, which results in oscillatory activity at 0.1 Hz when the sampling frequency $f_s=1$ is considered. The parameter c was allowed to vary freely between 0 and 1.

The median and the 5^th–95^th percentile range of ${\mathsf{\Phi }}_{\mathrm{IIR}}$, ${\mathsf{\Phi }}_{\mathrm{RSI}}$, and ${\mathsf{\Phi }}_{\Delta \mathrm{OIR}},$ considering the process $X_1$ as target, are shown in Figure 1(a), (b), and (c), respectively, along with the most frequently observed redundant (red) and synergistic (blue) multiplets across the 100 generated realizations. In these heatmaps, each cell is colour-coded to indicate whether the process was part of the corresponding multiplet or not. The three information measures used in the ${\mathsf{\Phi }}_{(.)}$ function exhibit a similar pattern: increasing c enhances synergy up to $c=0.5$, after which it declines. Redundancy follows the opposite trend, decreasing until $c=0.5$ and then increasing. This behavior is expected, as low c values lead to redundancy dominance due to the cascade $X_4\to X_2\to X_1$[7]. At intermediate c, synergy and redundancy coexist, with synergy peaking at $c=0.5$ due to the common child structure $X_2\to X_1\leftarrow X_3$, while redundancy reaches its minimum but persists due to the cascades $X_4\to X_2\to X_1$ and $X_4\to X_3\to X_1$. Beyond this point, redundancy increases while synergy declines to zero, driven by the dominance of $X_4\to X_3\to X_1$. This trend is captured by all three measures, though differences arise in the multiplets they identify. ${\mathsf{\Phi }}_{\mathrm{IIR}}$ clearly detects the shift between the cascades $X_4\to X_2\to X_1$ and $X_4\to X_3\to X_1$ as c increases. Meanwhile, ${\mathsf{\Phi }}_{\mathrm{RSIR}}$ and ${\mathsf{\Phi }}_{\Delta \mathrm{OIR}}$ identify $[X_1,X_2,X_3,X_4]$ as the most redundant multiplet, capturing both cascades and the common driver structure $X_2\leftarrow X_4\to X_3$. Regarding synergy, notable differences are observed among the ${\mathsf{\Phi }}_{\mathrm{IIR}}$, ${\mathsf{\Phi }}_{\mathrm{RSIR}}$, and ${\mathsf{\Phi }}_{\Delta \mathrm{OIR}}$ multiplets. In all three measures, the common empty multiplet appears at both low and high values of c, as expected, since synergy is absent in these cases and the network is dominated by cascade effects. However, at intermediate values of c, the multiplet identified by ${\mathsf{\Phi }}_{\mathrm{IIR}}$ differs from those found using ${\mathsf{\Phi }}_{\mathrm{RSIR}}$ and ${\mathsf{\Phi }}_{\Delta \mathrm{OIR}}$. The latter two measures consistently identify the multiplet $[X_1,X_2,X_3]$, revealing the common child structure $X_2\to X_1\leftarrow X_3$. In contrast, ${\mathsf{\Phi }}_{\mathrm{IIR}}$ also includes the process $X_4$ in the multiplet. Specifically, for this measure, the final multiplet is formed by extending the initial triplet with the conditioning vector (see Section 2), where $X_4$ is part of the conditioning vector. By incorporating $X_4$ into the conditioning vector, the visibility of the structure $X_2\to X_1\leftarrow X_3$ is enhanced. Thus, the knowledge of $X_4$ helps clarify the interactions between $X_1$, $X_2$, and $X_3$. This distinction can explain the differences observed in the multiplets identified for redundancy when using IIR when compared to RSIR and $\Delta \mathrm{OIR}$. In RSIR and $\Delta \mathrm{OIR}$, where a new process is added to the multiplet at each step, both methods detect three redundant motifs: the two cascade structures and the common driver structure $X_2\leftarrow X_4\to X_3$. However, since IIR is formulated in terms of conditioning, it selects processes that enhance the visibility of the interaction detected in the initial triplet rather than simply adding a new process at each step. For instance, for lower values of c, IIR identifies the dominant cascade effect $X_4\to X_2\to X_1$. However, no additional process is included in the conditioning vector because neither $X_3$ nor $X_5$ contains information relevant to the cascade effect detected in the first step. A similar reasoning applies to higher values of c.

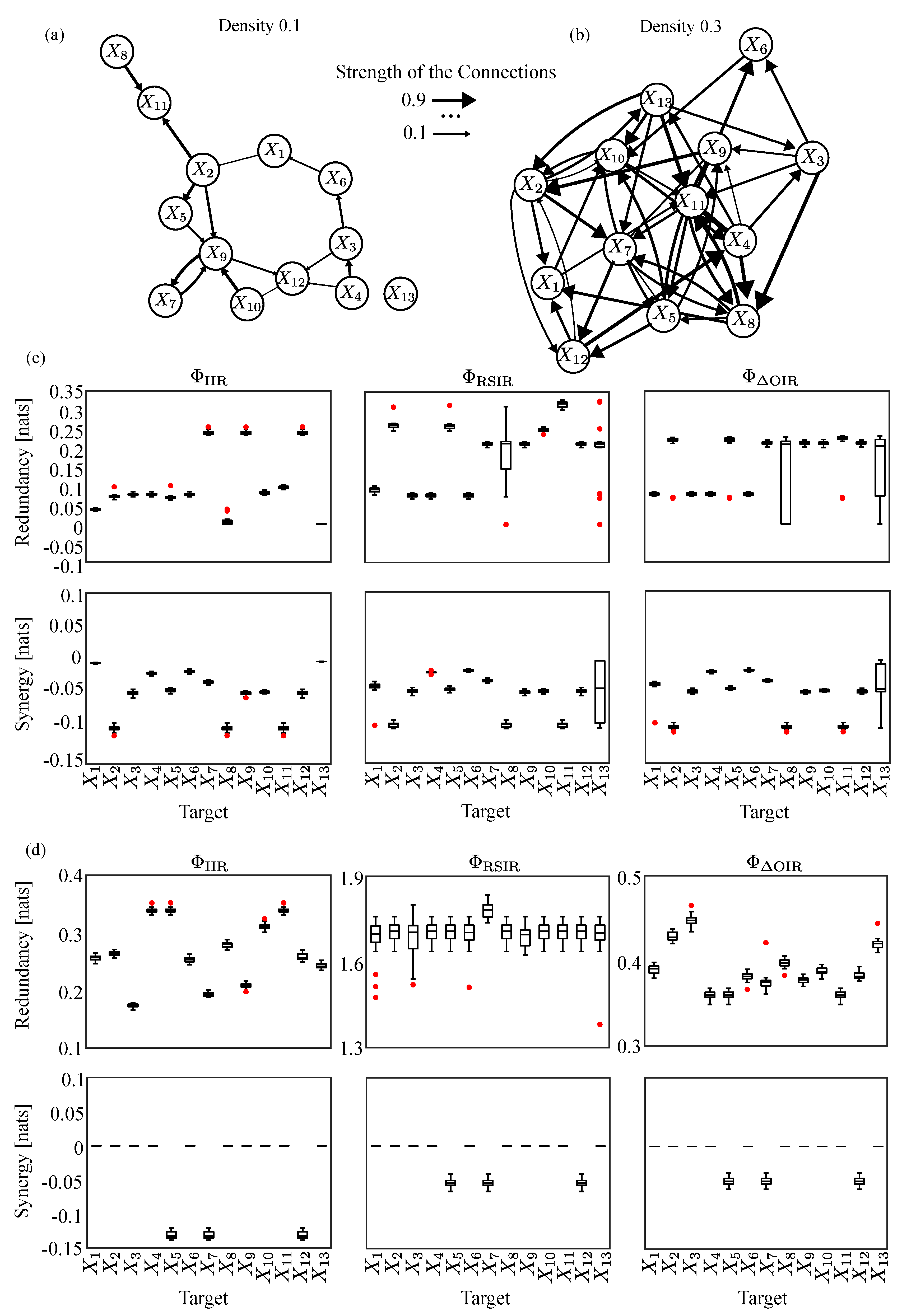
3.2. Randomly Connected Networks

The simulated data-sets were generated according to different ground-truth networks by means of an VAR model used as a generator filter [45,46]. The simulated multivariate time series ($M=13$) were generated as realizations of a VAR process of order $p=3$ fed by Gaussian noise with variance equal to 1. Two different matrices of AR parameters were generated by the SEED-G software according with a predefined network density of 10% and 30% (16 and 48 out of 156 possible connections). The parameters were randomly assigned in the range $[1,p]$ and their values were selected in the interval $[-0.9,0.9]$. This value is imposed only at one lag among the possible p lags, randomly selected.

Figure 2(a) and (b) illustrate a randomly generated network with 13 nodes, featuring edge densities of 10% and 30%, respectively. The increase in density enhances connectivity, which can influence both the structural and dynamic properties of the network. Figure 2(c) presents the distribution of redundancy and synergy, computed using ${\mathsf{\Phi }}_{\mathrm{IIR}}$, ${\mathsf{\Phi }}_{\mathrm{RSIR}}$, and ${\mathsf{\Phi }}_{\Delta \mathrm{OIR}}$, based on 20 realizations of the network shown in Figure 2(a). These distributions are evaluated for all possible target nodes, $X_1,\dots ,X_{13}$. Similarly, Figure 2(d) displays the redundancy and synergy distributions for the same three measures, obtained from 20 realizations of the denser network in Figure 2(b), again considering all possible target processes, $X_1,\dots ,X_{13}$. For the network with 10% density (Figure 2(c)), the results show a predominance of redundancy over synergy across all information measures used in the function ${\mathsf{\Phi }}_{(·)}$. However, notable synergy peaks for the three measures — ${\mathsf{\Phi }}_{\mathrm{IIR}}$, ${\mathsf{\Phi }}_{\mathrm{RSIR}}$, and ${\mathsf{\Phi }}_{\Delta \mathrm{OIR}}$ — are observed when $X_2$, $X_8$, and $X_{11}$ are considered as target nodes. This can be explained by the common child structure $X_2\to X_{11}\leftarrow X_8$, as seen in Figure 2(a).

Increasing the network density parameter to 0.3 results in a greater number of connections, as shown in Figure 2(b). Additionally, Figure 2(d) illustrates an increase in redundancy across all three measured parameters compared to the lower-density network, which is summarized in Figure 2(c). Furthermore, as shown in Figure 2(d), synergy arises when $X_5$, $X_7$, and $X_{12}$ are considered as target processes, which can be explained by the common child structure $X_5\to X_{12}\leftarrow X_7$. Alternatively, this can be explained by comparing the prevalence of synergistic structures involving these three nodes with that of redundant structures. All three measures considered — ${\mathsf{\Phi }}_{IIR}$, ${\mathsf{\Phi }}_{RSIR}$, and ${\mathsf{\Phi }}_{\Delta \mathrm{OIR}}$ — identified the same initial triplet $[X_5,X_7,X_{12}]$. However, while RSIR and $\Delta \mathrm{OIR}$ retained this triplet as the final multiplet, IIR included additional processes, $X_2$ and $X_{13}$, in the conditioning vector (result not shown for simplicity). Although these two processes are associated with redundancy, as they follow the cascade $X_{13}\to X_2\to X_{12}$, their inclusion provides valuable insight into the synergistic interactions within the initial triplet. Another important observation is that the estimated values of redundancy and synergy, calculated for the three measures across both random networks, show minimal bias when compared to the theoretical values, presented as Table 1.

Overall our simulations show that increasing network density leads to a significant rise in HOIs, as expected, because a denser network offers more connections, which helps collective behaviours to emerge. Specifically, we found that more densely connected networks exhibit a predominance of redundant interactions, which can obscure underlying synergistic effects. This behavior can be explained by the presence of common-child structures, whereas redundant interactions are more strongly linked to cascade and common-driver effects — a finding consistent with prior studies [7,12].

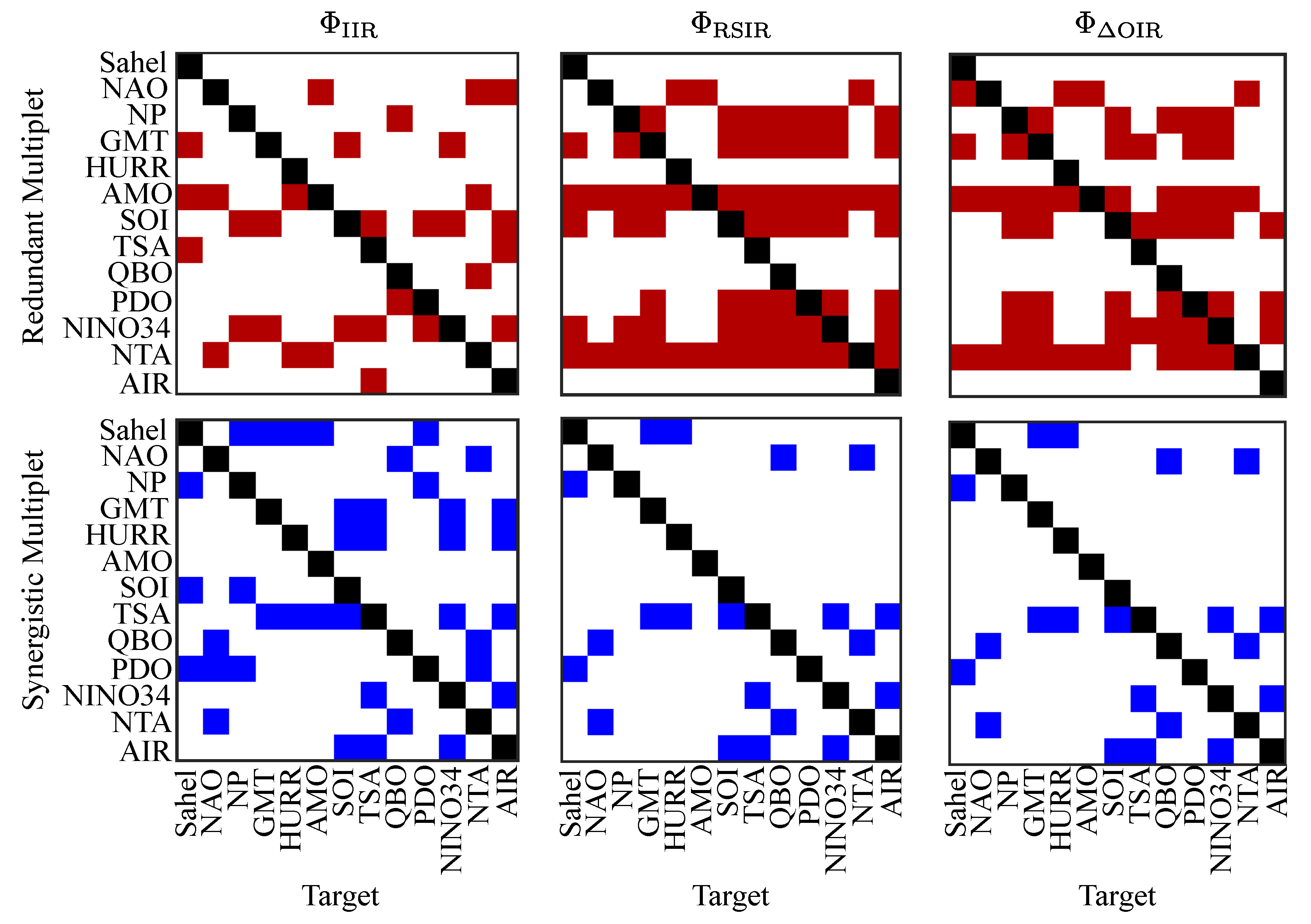
4. Application to a Climate Network

The feasibility of the proposed framework is demonstrated through an exemplary case study in climate science, i.e. the network of interactions among the most representative indices descriptive of El Niño and the Southern Oscillation (ENSO) [33,34]. El Niño and the ENSO is a climate pattern involving periodic warming (El Niño) and cooling (La Niña) of the central and eastern Pacific Ocean, affecting global weather patterns through atmospheric pressure shifts [32]. ENSO is considered the most prominent form of interannual climate variability on Earth [33]. Since the exact mechanisms triggering ENSO warm and cool events are not fully understood, analyzing the statistical relationships among climate variables is crucial. The resulting network of interactions is tightly connected through various feedback loops that influence climate patterns over multiple years [34,47]. This highlights the need to study HOIs using a broader, dynamic approach.

The network considered was composed by 13 time series publicly available [34]: NINO34 (the East Central Tropical Pacific sea surface temperature anomal), SOI (Southern Oscillation Index), AIR (All Indian Rainfall), AMO (Atlantic Multidecadal Oscillation), GMT (Global Mean Temperature anomaly), HURR (total number of hurricanes or named tropical storms per month in the Atlantic region), NOA (North Atlantic Oscillation of pressure anomalies over the Atlantic), NP (North Pacific pattern of sea level pressure), NTA (North Tropical Atlantic), PDO (Pacific Decadal Oscillation), QBO (Quasi-Biennial Oscillation), Sahel (Sahel Standardized Rainfall), and TSA (Tropical Southern Atlantic Index). The time series were detrended and deseasonalized [34], covering the period of 66 years from 1950 to 2016. It is important to note that these variables may not represent entirely distinct processes, as underlying latent factors could influence multiple indices simultaneously. This highlights the necessity of an analytical approach that accounts for shared information and potential interdependencies among the variables, like the one presented in this work.

Figure 3 summarizes the redundant multiplets (first row in red) and synergistic multiplets (second row in blue) for all possible target processes, considering ${\mathsf{\Phi }}_{\mathrm{IIR}}$, ${\mathsf{\Phi }}_{\mathrm{RSIR}}$, and ${\mathsf{\Phi }}_{\Delta \mathrm{OIR}}$. First, we focus on one of the most important processes in the network: the Southern Oscillation Index (SOI). A key observation is that the initial triplet identified for all three measures, regarding redundancy, was the same: $[\mathrm{SOI},\mathrm{GMT},\mathrm{NINO}34]$. This corroborates in some extent the results presented in [34], where authors found that SOI may act as a common driver influencing both NINO34 and GMT. For ${\mathsf{\Phi }}_{\mathrm{IIR}}$, no additional redundant processes were included in the multiplet. However, for ${\mathsf{\Phi }}_{\mathrm{RSIR}}$ and ${\mathsf{\Phi }}_{\Delta \mathrm{OIR}}$, the final multiplet expanded significantly to $[\mathrm{SOI},\mathrm{GMT},\mathrm{NINO}34,\mathrm{NTA},\mathrm{AMO},\mathrm{NP},\mathrm{PDO}]$. This expansion suggests that RSIR and $\Delta \mathrm{OIR}$ capture a broader set of redundant motifs, potentially uncovering cascading effects such as $\mathrm{NINO}34\to \mathrm{AMO}\to \mathrm{SOI}$ and $\mathrm{NINO}34\to \mathrm{NTA}\to \mathrm{SOI}$, as observed in [34]. Furthermore, this finding supports that the triplet $[\mathrm{NINO}34,\mathrm{PDO},\mathrm{SOI}]$ interacts in a redundant manner, consistent with the results reported in [48] using the Partial Information Rate Decomposition framework. Regarding synergy, for all three measures, the initial triplet that contributed to the final multiplet was the same regardless of the considered approach: $[\mathrm{SOI},\mathrm{TSA},\mathrm{AIR}]$. This finding supports the presence of a common child structure, where SOI is influenced by the joint effects of AIR and TSA, potentially indicating an underlying atmospheric teleconnection pattern: $[\mathrm{AIR},\mathrm{TSA}]\to \mathrm{SOI}$[34]. These results also partially align with the findings of [25], where the authors observed that the pair NTA and TSA contribute to the synergy in the pairwise interaction $\mathrm{NINO}34\to \mathrm{SOI}$. The differences observed in this study could be attributed to the methodological approaches: the measures used in the greedy framework presented here are undirected and capture HOIs in a more general sense, whereas [25] employed the conditioning of TE [27], a pairwise causality measure, to infer the presence of HOIs.

Interestingly, the HURR process was not present in any redundant or synergistic multiplet for any target considered, suggesting that this process does not play a role in the emergence of higher-order effects. This could be related with the fact is strongly influenced by ENSO, but it is generally considered an outcome rather than an active interacting variable in redundancy or synergy analyses but more as a pairwise interaction [49,50].

From Figure 3 and Table 2, it is clear that redundant interactions dominate the system behaviours over synergistic ones. This trend holds across all measures considered — ${\mathsf{\Phi }}_{\mathrm{IIR}}$, ${\mathsf{\Phi }}_{\mathrm{RSIR}}$, and ${\mathsf{\Phi }}_{\Delta \mathrm{OIR}}$ — where synergy values remained consistently close to zero. Given the higher density of connections in the climate network [34], this result aligns with the results of the simulation studies as discussed in Section 3.2, showing that the number of pairwise connections influences the presence of HOIs, particularly redundancy.

5. Conclusions

This study introduces a novel sequential approach based on the measures IIR, RSIR, and $\Delta \mathrm{OIR}$ to detect and quantify HOIs in complex, high-dimensional networks. The proposed method iteratively identifies multiplets that interact redundantly or synergistically with a predefined target process. By doing so, it circumvents the computational explosion associated with exhaustively considering all possible combinations, as seen in the approaches presented in [14,22,37], which scale exponentially with the number of network nodes. This makes the method particularly well-suited for analyzing large-scale systems, such as biological and climate networks, where understanding HOIs is crucial for uncovering emergent behaviours and collective dynamics.

The simulations confirm that the proposed method effectively detects and quantifies both redundancy and synergy in complex networks. In a simple five-node network simulation, discussed in Section 3.1, the method successfully identified simultaneous redundancy and synergy, with the detected multiplets aligning closely with theoretical predictions. Extending the analysis to simulations of random network, presented in Section 3.2, revealed that higher connection density led to an increased presence of HOIs, particularly strengthening redundancy. This finding suggests that as network density grows, redundancy becomes the dominant contributor to overall interactions, surpassing cooperative or synergistic effects between nodes.

The proposed greedy approach was applied to a climate network to analyze the interplay between ENSO climate variables, revealing significant high-order effects, with redundancy prevailing over synergy. Particularly, the results indicate that SOI and NINO34 interact redundantly possible reflecting the driver role of this process in the network. Regarding synergistic effects, the multiplet [SOI, TSA, AIR] was identified, suggesting that SOI is influenced by the combined effects of AIR and TSA, potentially indicating an underlying atmospheric teleconnection pattern: $[\mathrm{AIR},\mathrm{TSA}]\to \mathrm{SOI}$.

The sequential framework presented here offers an alternative to PID for quantifying HOIs in complex systems. PID becomes computationally challenging as the number of atoms increases exponentially with the number of sources. In contrast, our approach addresses this issue by starting with a predefined target process and identifying other processes in the network that interact redundantly or synergistically with it. Additionally, the proposed methodology is computationally efficient, particularly when using a greedy search strategy to identify the optimal multiplets that maximize redundancy or synergy, without the need for exhaustive calculations. The measures herein proposed, $\mathrm{IIR}$, $\mathrm{RSIR}$ and $\Delta \mathrm{OIR}$ differ in they nature with IIR being particularly distinct from the other two. Specifically, when RSIR and $\Delta \mathrm{OIR}$ are considered, at each step, a process is added to a multiplet while in the case of IIR, after the identification of the first triplet, additional processes are incorporated through a conditioning vector. We showed that the processes added to the conditioning vector are those that enhance the visibility of redundancy or synergy within the initial triplet. This methodological difference explain the discrepancies observed between IIR and the other two measures, RSIR and $\Delta \mathrm{OIR}$.

The sequential framework proposed in this work demonstrates the ability to efficiently handle intricate networks with a large number of interacting processes at relatively low computational cost. This capability opens new perspectives for investigating complex biological systems and their interactions. In particular, the methodology offers promising perspectives for the study of physiological networks — such as cardiovascular and respiratory interactions [11,51,52] — as well as brain networks [53] and brain–heart interactions [54,55,56].