Reinforcement Learning-Controlled Subspace Ensemble Sampling for Complex Data Structures

1. Introduction

In recent years, with the advent of the big data era, massive, multidimensional, and high-dimensional data have been continuously accumulated across industries such as finance, computer vision, and UI interface generation [1,2,3,4]. The complexity and heterogeneity of data have become increasingly prominent. Against this background, efficiently and accurately mining valuable patterns from complex data has become a core issue in data mining research. However, practical applications often face challenges such as the curse of dimensionality, feature redundancy, noise interference, and class imbalance [5]. These problems severely restrict the performance of traditional mining algorithms. In particular, when dealing with high-dimensional sparse and imbalanced datasets, mainstream methods frequently suffer from limited generalization ability and poor adaptability. There is an urgent need for a more robust and intelligent algorithmic framework to cope with dynamically changing data distributions in complex environments.

In response to these challenges, subspace mining has emerged as an effective technique to address high-dimensional issues and has become a research hotspot. By exploring and combining feature subspaces within high-dimensional data, subspace methods can significantly enhance the perception of local patterns and show strong adaptability in filtering redundant features and suppressing noise. However, traditional subspace methods often rely on static strategies for feature selection and combination. These approaches struggle to adapt to nonlinear structural changes in dynamic data environments. Especially in tasks involving data drift or non-stationary class relationships, fixed subspace construction strategies are prone to information loss or pattern shift, making them inadequate to meet the dual demand for high robustness and strong generalization in complex data scenarios [6].

Meanwhile, the rapid development of reinforcement learning has introduced new solutions to the above problems. Reinforcement learning, through its trial-and-error feedback optimization mechanism, can adjust strategies without prior knowledge to adapt to dynamic environments and evolving goals. When incorporated into subspace mining, reinforcement learning enables the dynamic generation and combination of subspaces. It also captures nonlinear interactions among data features in an adaptive manner, facilitating more effective knowledge integration and pattern recognition across a broader space. This environment-driven strategy evolution empowers traditional static methods with intelligent adjustment capabilities and significantly improves the model's adaptability and robustness when handling high-dimensional heterogeneous data [7].

However, in real-world mining tasks, data often exhibits significant imbalance. Minority classes, though typically more informative, are easily overshadowed by dominant classes, causing learning to be biased toward the majority. To address this, ensemble sampling mechanisms are widely used to rebalance data distributions. These combine under-sampling and over-sampling techniques to enhance the model's sensitivity to minority classes. Nevertheless, existing methods mostly rely on static sampling strategies and lack the ability to perceive distributional shifts. As a result, they fail to optimize sampling configurations dynamically from a global perspective. Integrating ensemble sampling with reinforcement learning allows the sampling process to adjust sample weights dynamically based on reward feedback. This endows the system with adaptivity and environment awareness, which is critical for improving both minority class mining quality and overall model performance [8].

Therefore, this study proposes a reinforcement learning-controlled adaptive subspace ensemble sampling algorithm. It aligns with current trends in processing high-dimensional and complex data and offers a methodological foundation for building robust and adaptive data mining systems. The proposed method bridges subspace modeling, sample redistribution, and policy control, enabling multi-level and multi-granular information extraction and mining. It serves as a theoretical and practical bridge between foundational research and real-world applications. This work has significant theoretical value and practical relevance for advancing intelligent data analysis and high-performance learning systems and provides a generalizable paradigm for complex data modeling across various industries.

2. Related Work

Recent developments in deep and reinforcement learning have laid the groundwork for intelligent systems capable of handling structural complexity and data imbalance. A reinforcement learning-based mechanism for scheduling in dynamic systems [9] showcases how policy-driven adaptability can be harnessed for real-time optimization. This approach underscores the potential of reinforcement learning in dynamically guiding decision-making processes—an idea extended in this paper to control subspace construction and adaptive sampling.

Sequence modeling architectures incorporating bidirectional LSTMs and attention mechanisms [10] demonstrate efficient multi-scale dependency learning. Their capacity to extract salient temporal patterns aligns with this work’s objective of enhancing subspace representation in high-dimensional spaces. Similarly, combining convolutional and recurrent neural networks to capture both local and sequential dependencies [11] provides a foundation for designing feature-aware subspace learning modules in our framework. Techniques from self-supervised learning have proven effective for extracting robust representations without explicit supervision. Vision transformers applied under self-supervised settings [12] validate the value of unsupervised feature encoding, especially when dealing with sparse or noisy inputs. Further, the integration of contrastive and variational approaches [13] offers a structural perspective on how representation learning can remain adaptive under non-stationary distributions, contributing to the adaptive sampling design in this study.

In scenarios characterized by distributional shifts or structural sparsity, attention-based mechanisms have emerged as critical components. The application of spatial-channel attention in modeling cross-domain interactions [14] and the use of graph attention for handling sparse structural data [15] both emphasize flexible architectural designs—concepts embedded within the adaptive subspace and sampling configuration proposed here. The integration of graph neural networks and transformers in time series tasks [16] provides a methodological bridge for combining spatial and temporal modeling, a strategy that parallels the policy-driven feature composition and sample dynamics control employed in our framework.

Reinforcement learning applied in distributed environments through trust-aware strategies [17] illustrates how policy learning can be tailored to heterogeneous conditions. This principle is particularly relevant to the dynamic sample reweighting strategy adopted in our ensemble sampling module. Additionally, structured reasoning techniques leveraging probabilistic modeling [18] offer a nuanced method for addressing classification imbalance. These insights inform the probabilistic underpinnings of the ensemble sampling component, enabling more robust treatment of minority classes and preserving distributional integrity.

Together, these contributions converge to support the framework presented in this study. The reinforcement learning-controlled subspace ensemble sampling algorithm benefits from these diverse methodological innovations, enabling an adaptive and generalizable solution for complex, high-dimensional, and imbalanced data mining scenarios.

3. Method

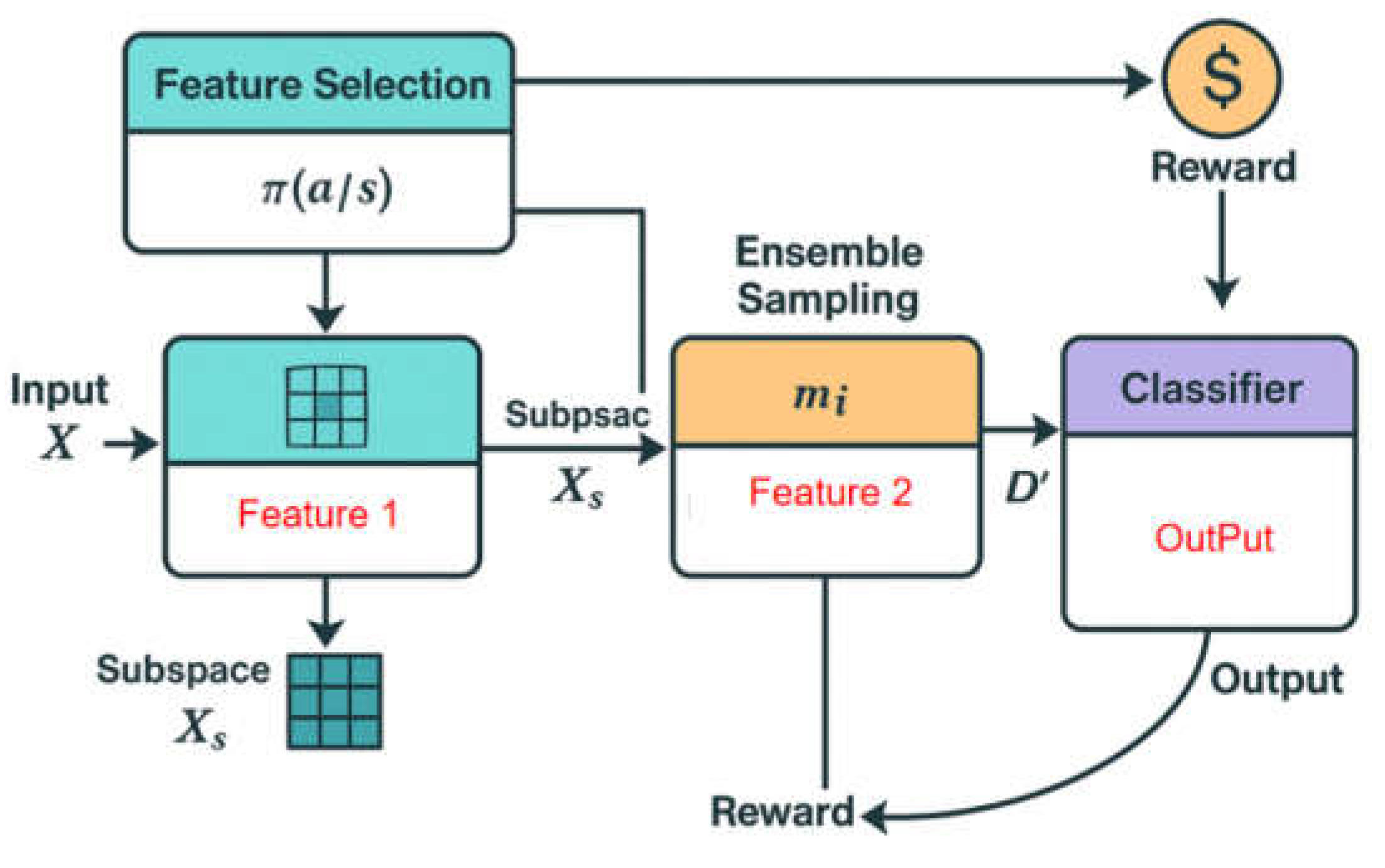
The subspace ensemble sampling adaptive mining method proposed in this study establishes a three-layer nested framework orchestrated by a reinforcement learning (RL) controller. This hierarchical structure comprises feature subspace selection, ensemble-based sample redistribution, and final classification optimization. The reinforcement learning component dynamically guides the subspace selection strategy based on real-time feedback from classification performance, enabling adaptive dimensionality reduction and more targeted feature extraction. This design draws inspiration from the context-aware subspace tuning mechanism introduced in Huang et al., where deep Q-networks were used to enhance intelligent data acquisition [19]. Furthermore, the sample redistribution layer combines under-sampling and over-sampling strategies within an ensemble scheme to mitigate class imbalance, aligning with the nested RL architecture proposed by Yao for temporal adaptation in complex, nonlinear environments [20]. Finally, the optimization layer leverages classification feedback to refine the upper-layer decisions in a closed-loop fashion, a principle using Q-learning variants, as discussed by Xu et al. [21]. The complete architectural flow of the method is illustrated in Figure 1.

The network architecture is driven by a reinforcement learning strategy [22]. First, the input features are subspace selected and the optimal subspace $X_s$ is dynamically constructed through the policy function. Then, the integrated sampling module adjusts the distribution of subspace samples to minimize the inter-class deviation and generate a new training set $D\text{'}$. Finally, the classifier is trained under sample weighting and subspace embedding, and the error feedback is transmitted back as a reward signal to achieve end-to-end policy optimization and adaptive adjustment [23].

In the feature subspace construction phase, the state space is defined as the currently selected feature subset, and the action space is defined as the set of selectable feature indexes. The reinforcement learning agent determines the subspace expansion strategy for each step through the policy function $\pi (a_t|s_t)$. In each round of interaction, the state transition is controlled by environmental feedback. The constructed subspace can be represented as a feature matrix $X_s\subseteq X$, which corresponds to a set of sub-dimensions in the original feature matrix that have been selected by the strategy. Its goal is to maximize the expected cumulative reward:

$${\max }_{\pi }{E}_{\pi }[{\displaystyle \sum _{t=0}^T{\gamma }^t{R}_t}]$$

Where $\gamma$ is the discount factor and $R_t$ is the immediate reward at the tth step, which measures the improvement of the current subspace in classification performance.

In the sample sampling process, a dynamic weighted integration strategy is introduced, combining undersampling and oversampling mechanisms to alleviate the interference of data imbalance on the model. To this end, the sample selection probability distribution $P(y_i)$ is defined, the sampling probability is updated according to the category label $y_i$ and the sample importance weight $w_i$, and the sampling tendency of each type of sample is adjusted through the reinforcement learning agent, so that the distribution is approximately balanced in the newly generated training subset $D\text{'}={\{x_i,y_i\}}_{i=1}^n$. The sampling adjustment goal is to minimize the distribution deviation after resampling:

$${\min }_w{\displaystyle \sum _{i=1}^n{(P\text{'}(y_i)-\frac{1}{C})}^2}$$

Where $P\text{'}(y_i)$ represents the adjusted sample distribution and $C$ is the number of categories.

$$L=-{\displaystyle \sum _{i=1}^n{w}_i\cdot \log p_{\theta }(y_i|x_i^{(s)})}$$

$x_i^{(s)}$ represents the sample input in the current subspace, $p_{\theta }$ is the predicted probability of the model, and $\theta$ is the model parameter. The adaptive mining process constructed by the above mechanism not only realizes dynamic modeling in the feature dimension, but also realizes intelligent adjustment of the sampling strategy at the sample level, thereby improving the generalization ability and robustness of the model as a whole.

4. Experiment

4.1. Datasets

This study uses the KDD Cup 1999 dataset, which is widely applied in network intrusion detection and classification model evaluation tasks. The data originates from real network environments and consists of TCP connection records. It includes both normal behaviors and various types of attacks, categorized into four main classes: DoS, R2L, U2R, and Probe. The dataset contains a total of 41 feature fields, covering basic connection features, content features, and statistical features based on time or host.

The entire dataset is divided into a training set and a test set according to the task objectives. The training set is highly imbalanced, with a significant disparity between the number of normal and attack samples. This reflects a severely skewed class distribution, making it particularly suitable for evaluating algorithm performance under complex sample structures and imbalanced data conditions. After standardization and one-hot encoding, the data is used for generating feature subspaces and learning sampling strategies within the model.

In addition, the dataset provides clear labels and class definitions. This enables the reinforcement learning mechanism to generate accurate reward signals based on prediction accuracy. As a result, the subspace selection strategy and sampling weight configuration can be dynamically optimized. This setup offers strong support for validating the adaptive learning capabilities of the proposed method in complex data scenarios.

4.2. Experimental Results

This paper first gives a performance comparison experiment between this method and the classic imbalanced classification algorithm. The experimental results are shown in Table 1.

In terms of overall accuracy (ACC), the proposed method outperforms all baseline algorithms, achieving a value of 0.9824. This is significantly higher than traditional sampling methods and ensemble strategies, indicating a stronger overall discriminative ability when handling complex and imbalanced data distributions. Especially in scenarios with blurred class boundaries or strong feature interference, the reinforcement learning-guided subspace construction and sampling mechanism effectively enhance the model's understanding of the main structural patterns.

For Precision and Recall, the method achieves 0.9561 and 0.9483 respectively, also ranking at the top. These results demonstrate that the proposed approach balances both accuracy and coverage in identifying minority classes, avoiding the bias commonly found in previous methods. In comparison, traditional techniques such as ADASYN and RUSBoost show some improvement in Recall but suffer from a noticeable drop in Precision, which increases the risk of false positives due to noisy samples.

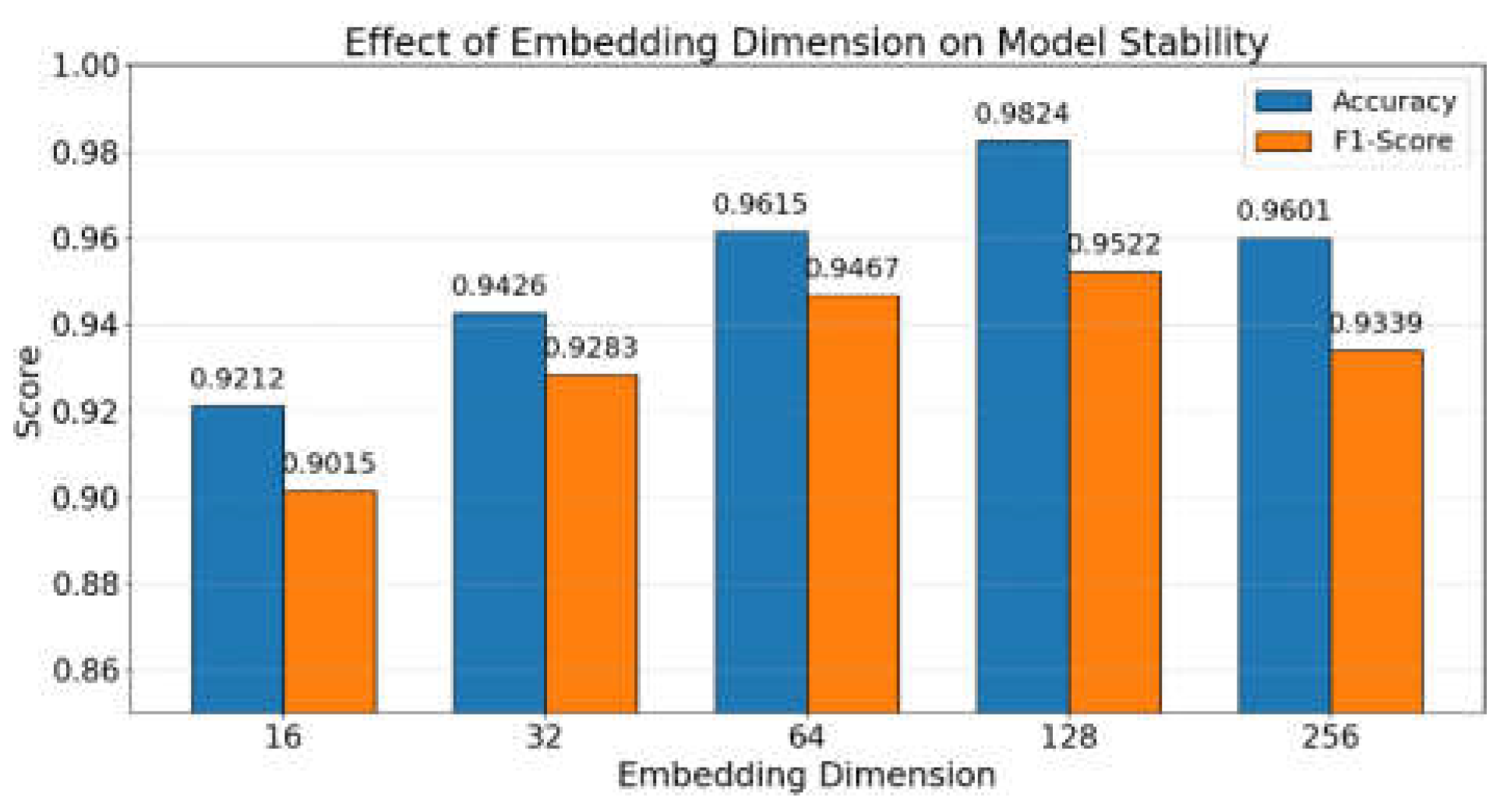
Moreover, when compared to representative methods like EasyEnsembleV2 and Borderline-SMOTE, it is clear that although they partially alleviate class imbalance, their lack of a dynamic strategy adjustment mechanism limits their ability to adapt to the interaction between local features and global structure. In contrast, the proposed method leverages a reinforcement learning mechanism to guide subspace selection and update sampling weights. This enables end-to-end optimization at the strategy level, significantly improving the model's stability and generalization performance. Furthermore, this paper presents a comparative experiment on the effect of subspace embedding dimension change on model stability, aiming to analyze how variations in the dimensionality of the subspace representation impact the consistency and reliability of the model's performance. By systematically adjusting the embedding dimensions and observing corresponding fluctuations in model output, the experiment provides insight into the sensitivity and robustness of the subspace design. The experimental results are comprehensively illustrated in Figure 2.

As shown in the figure, with the increase of subspace embedding dimensions, the overall model performance exhibits an initial rise followed by a slight decline. When the dimension is set to 128, the model achieves optimal results in both Accuracy and F1-Score, reaching 0.9824 and 0.9522 respectively. This indicates that the feature representation at this level is sufficiently expressive, which helps the model identify underlying data structures and class boundaries more effectively. The results suggest that while increasing dimensionality can enhance the richness of representation, exceeding an optimal threshold may introduce redundancy or noise, thereby slightly hindering performance. At lower dimensions (e.g., 16 or 32), the model's performance drops due to limited feature representation capacity. It struggles to capture complex patterns, resulting in reduced effectiveness. When the dimension increases to 256, although more features are retained, the inclusion of redundant information may increase the risk of overfitting. This leads to a decline in F1-Score, suggesting that higher embedding dimensions are not always beneficial.

This paper also conducted a generalization ability comparison experiment based on subspace and non-subspace models, aiming to evaluate the robustness and adaptability of the proposed approach across different representation strategies. By comparing the performance of models that utilize subspace-based representation with those that do not, the experiment assesses how well the learned knowledge can transfer to new, unseen scenarios. The detailed experimental results and comparative analysis are illustrated in Figure 3.

The experimental results in the figure illustrate the generalization performance of subspace-based and non-subspace models over consecutive training epochs. It can be observed that the subspace model achieves higher accuracy in the early stages of training and consistently outperforms the baseline in subsequent epochs. This indicates faster convergence and stronger adaptability. The trend suggests that the subspace mechanism effectively extracts informative features at an early stage, thereby improving learning efficiency.

As training progresses, the performance of the subspace model continues to improve steadily. By the 10th epoch, it reaches an accuracy of 0.980, while the non-subspace model only achieves 0.945. The performance gap remains significant throughout. This demonstrates that traditional full-dimensional modeling suffers from feature redundancy and local optima, which limits the model's generalization ability. Overall, the experiment confirms the clear advantages of introducing a subspace strategy when dealing with complex data structures. It not only improves overall prediction performance but also exhibits strong robustness and adaptability to unseen data distributions. This provides an effective approach for building classification models with enhanced generalization capability.

5. Conclusions

This paper proposes a reinforcement learning-controlled subspace ensemble sampling adaptive mining algorithm to address the challenges posed by data imbalance and structural variation in high-dimensional complex datasets. The method introduces reinforcement learning strategies at both the subspace construction and sample selection levels, enabling dynamic optimization of feature subsets and sample distributions. Through policy feedback mechanisms, the model's sensitivity to local feature structures and its generalization ability to global patterns are effectively enhanced, significantly mitigating the bias issues commonly seen in traditional approaches under imbalanced scenarios. Across multiple comparative experiments, the proposed method outperforms mainstream imbalance-handling algorithms in terms of Accuracy, F1-Score, and other evaluation metrics, demonstrating superior stability and adaptability. In particular, it shows clear advantages in embedding dimension regulation and generalization improvement by combining structural flexibility with policy robustness. The results confirm the effectiveness of the policy-driven subspace sampling mechanism in real-world data mining tasks, providing a more adaptive path for high-dimensional sample modeling.

This study not only broadens the perspective of joint research on subspace mining and sampling mechanisms from an algorithmic standpoint but also introduces a new paradigm for structural control using reinforcement learning in data-driven tasks. With an end-to-end optimization pipeline, the method exhibits strong scalability and transferability, making it applicable to various heterogeneous data environments and dynamic scenarios. It offers both theoretical and practical support for building intelligent mining systems. Future research may further explore the application of this method in multimodal data, online learning systems, and incremental mining settings. By integrating self-supervised learning and adversarial strategies, it is possible to construct a more robust sampling control framework. The approach also holds strong potential for deployment in high-risk data environments such as financial risk management, network security, and medical prediction, driving the evolution of data mining from static modeling toward dynamic and intelligent development.