1. Introduction
Sampling methods are employed when it is impractical to collect data from an entire population. For statistical inferences to be valid, the selected sample must be obtained through probability-based sampling techniques. One of the most commonly used probability sampling methods is simple random sampling. The population mean for a variable of interest, denoted by, is typically estimated using the sample mean , where n is the sample size. This estimator is known to be unbiased. A primary objective in sampling theory is to improve the efficiency of such estimators.
In many cases, the estimation efficiency can be enhanced by utilizing an auxiliary variable that is correlated with the variable of interest. When both variables exhibit a high positive correlation, the ratio estimator, which incorporates the auxiliary variable’s mean, is widely adopted. Numerous studies have proposed improvements to the ratio estimator in the context of simple random sampling. For example, Sisodia and Dwivedi [
1] introduced a modified ratio estimator based on the coefficient of variation of the auxiliary variable. Singh and Tailor [
2] proposed an estimator that incorporates the population correlation coefficient between the target and auxiliary variables. Yadav et al. [
3] developed ratio-cum-product estimators, while Jerajuddin and Kishun [
4] enhanced ratio estimators by considering sample size. Soponviwatkul and Lawson [
5] proposed further refinements by incorporating the coefficient of variation, correlation coefficient, and regression coefficient.
However, in situations where the population is both rare and clustered, simple random sampling may be suboptimal. To address this, Thompson [
6] introduced adaptive cluster sampling (ACS) in 1990. In ACS, an initial sample is selected using simple random sampling without replacement. If a unit in this initial sample satisfies a pre-specified condition for the variable of interest, its neighboring units are added to the sample. This expansion continues iteratively until no additional units meet the condition. The collection of initial and subsequently added units forms a network. Units that do not meet the condition are referred to as edge units. The union of a network and its edge units constitutes a cluster. If the initial unit fails to satisfy the condition, it remains a singleton network. For this study, neighborhoods are defined as the four orthogonally adjacent units (up, down, left, and right), with mutual neighborhood relationships assumed.
Thompson also proposed an estimator and demonstrated that ACS yields improved efficiency in clustered populations. Analogous to simple random sampling, incorporating auxiliary variable information in ACS can further improve estimator performance. Chao [
7] introduced a ratio estimator for ACS, while Dryver and Chao [
8] introduced modified ratio estimators. Chutiman and Kum-phon [
9] presented a ratio estimator using two auxiliary variables. Chutiman[
10] and Yadav et al. [
11] proposed ratio estimators based on population parameters, including the coefficient of variation, kurtosis, skewness, and correlations with auxiliary variables. Chaudhry and Hanif [
12,
13] proposed generalized exponential-type estimators, while Bhat et al. [
14] developed a generalized class of ratio-type estimators.
Increasing the auxiliary variable information is the primary focus of the development of the parameter estimators discussed above. This study presents the development of Chao's ratio-type estimator in adaptive cluster sampling, which uses the Jackknife method to leverage data from a single auxiliary variable, specifically the auxiliary variable's mean.
Section 2 outlines relevant estimators in ACS,
Section 3 introduces the proposed Jackknife-based estimators,
Section 4 presents simulation results, and
Section 5 concludes the study.
2. Adaptive Cluster Sampling
In adaptive cluster sampling, an initial sample of units is selected using simple random sampling without replacement.
Let represent the initial sample size and be the final sample size. Let denote the network that includes unit , and let represent the number of units in that network.
Let be the average of the y-value in the network that includes the initial sample unit , that is, .
The Hansen-Hurwitz estimator of the population mean for the variable of interest is [
15]:
The mean square error (MSE) of
is:
where and .
Let
be the auxiliary variable. The population mean of
is
and
is the average of the auxiliary variable in the network that includes the initial sample unit
, that is,
. The modified Hansen-Hurwitz estimator of the population mean of the auxiliary variable is:
Let
be the population ratio between
and
,
. Chao [
7] introduced the ratio estimator of the population mean, which is
where
is a biased estimator of
. The bias of
is:
where , , , and .
The mean square error (MSE) of
is:
3. Proposed Estimators in Adaptive Cluster Sampling Using the Jackknife Method
Motivated by Banerjee and Tiwari [
16], Quenouille’s Jackknife method [
17] was applied to propose the estimators. The sample network of size
is randomly partitioned into two groups, each of size m = n/2.
The proposed estimators are:
1) , (7)
where and , where and are the sample means based on group of size , for the y-variable and x-variable, respectively.
2) , where . (8)
3) , (9)
where is the ratio estimator of the population mean for the y-variable in the delete network , and , are the modified Hansen-Hurwitz estimators of the population mean in the delete network for the y-variable and x-variable, respectively.
The bias and MSE of each estimator are as follows:
The first estimator:
Let and .
Assuming
, the term
can be expanded as an infinite series.
Therefore, .
The bias of
is given by:
where
,
Therefore, .
The bias of
is derived in the same way as that of
, and the
is equal to the
.
Therefore, the bias of
is:
For the MSE of
,
where
The second estimator: , where
From
and
, it follows that
, and
is an unbiased estimator of
to the first order of approximation (based on Banerjee and Tiwari [
15]).
where
,
Therefore, The MSE of
is
The Third estimator:
Let and .
Assuming
, the term
can be expanded as an infinite series.
The bias of
is given by:
where , , ,
and
.
The bias of
is derived in the same way as that of
, and the
is equal to the
. Therefore, the bias of
is:
where and .
Therefore, the MSE of
is :
4. Simulation Study and Discussion
The populations for both the auxiliary variable and the variable of interest, as used in Chao [
7], were generated using a linked-pairs process in conjunction with a bivariate Poisson cluster process. The resulting population comprised a 20 × 20 grid, yielding a total of 400 units. The mean of the variable of interest (
y) in the population was 0.635, and the Pearson correlation coefficient between the auxiliary variable (
x) and
y was 0.707035. For each simulation iteration, initial sample units were selected via simple random sampling without replacement. The expansion criterion for adaptive cluster sampling was defined by the condition
. A total of 10, 000 iterations were conducted for each estimator under investigation. The number of initial networks
n was varied across the values 4, 8, 10, 16, 20, 26, 30, 40, 50, 100, and 200. The expected final sample size
was computed as follows:
.
The estimated absolute relative bias was defined as:
The estimated mean square error of the estimator was defined as:
The percentage relative efficiency of the proposed estimator, compared with
, was defined as:
.
The estimated absolute relative bias, estimated mean square error (MSE), and percentage relative efficiency of the estimators are presented in
Table 1,
Table 2 and
Table 3.
Discussion
Based on the data studied, the variable of interest is positively correlated with the auxiliary variable. The results from the simulation data are presented as follows:
Table 1 presents the estimated absolute relative bias of the biased estimators, namely
,
, and
. It can be observed that as the sample size increases, the estimated absolute relative bias for all estimators decreases and approaches zero.
Table 2 shows that the estimators incorporating auxiliary variable information—given the positive correlation with the variable of interest—consistently yield lower MSEs compared to estimators that do not use such information. Notably,
achieves a lower MSE than the traditional ratio estimator
when the network sample size is small. Among all estimators,
provides the lowest MSE across all network sample sizes. Although the estimator
is unbiased, its MSE is higher than that of
despite being lower than estimators that do not use auxiliary information.
Table 3 presents the percentage relative efficiency of each estimator compared to
. The estimator
consistently exhibits the highest percentage relative efficiency. Moreover, as the sample size increases, the efficiency of
converges with that of the traditional ratio estimator
.
5. Conclusions
Adaptive cluster sampling (ACS) is particularly effective for studying rare and spatially clustered populations. This research proposed three enhanced ratio-type estimators for ACS, building on Chao’s [
7] original ratio estimator and employing the Jackknife method to reduce bias and improve efficiency. Analytical derivations of bias and MSE were provided for each estimator, and their performance was evaluated through extensive simulation. The simulation results demonstrated that all three proposed estimators outperformed conventional estimators that do not utilize auxiliary variable information. Specifically,
proved to be more efficient than Chao’s estimator for small network sample sizes, while
exhibited superior efficiency for both small and moderate sample sizes. In large-sample settings, the efficiency of
became comparable to that of the traditional ratio estimator. Although
is an unbiased estimator, its efficiency was the lowest among the estimators that incorporate auxiliary variable information.
Author Contributions
Conceptualization, S.W and N.C.; methodology, S.W.; software, N.C. and P.G; investigation, A.N.; writing—original draft preparation, N.C. and A.N.; writing—review and editing, P.G and S.W..; funding acquisition, N.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research project was financially supported by Mahasarakham University.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to thank the editor and the referees for their valuable feedback and insightful suggestions.
Conflicts of Interest
The authors have no conflicts of interest to declare that are relevant to the
content of this article.
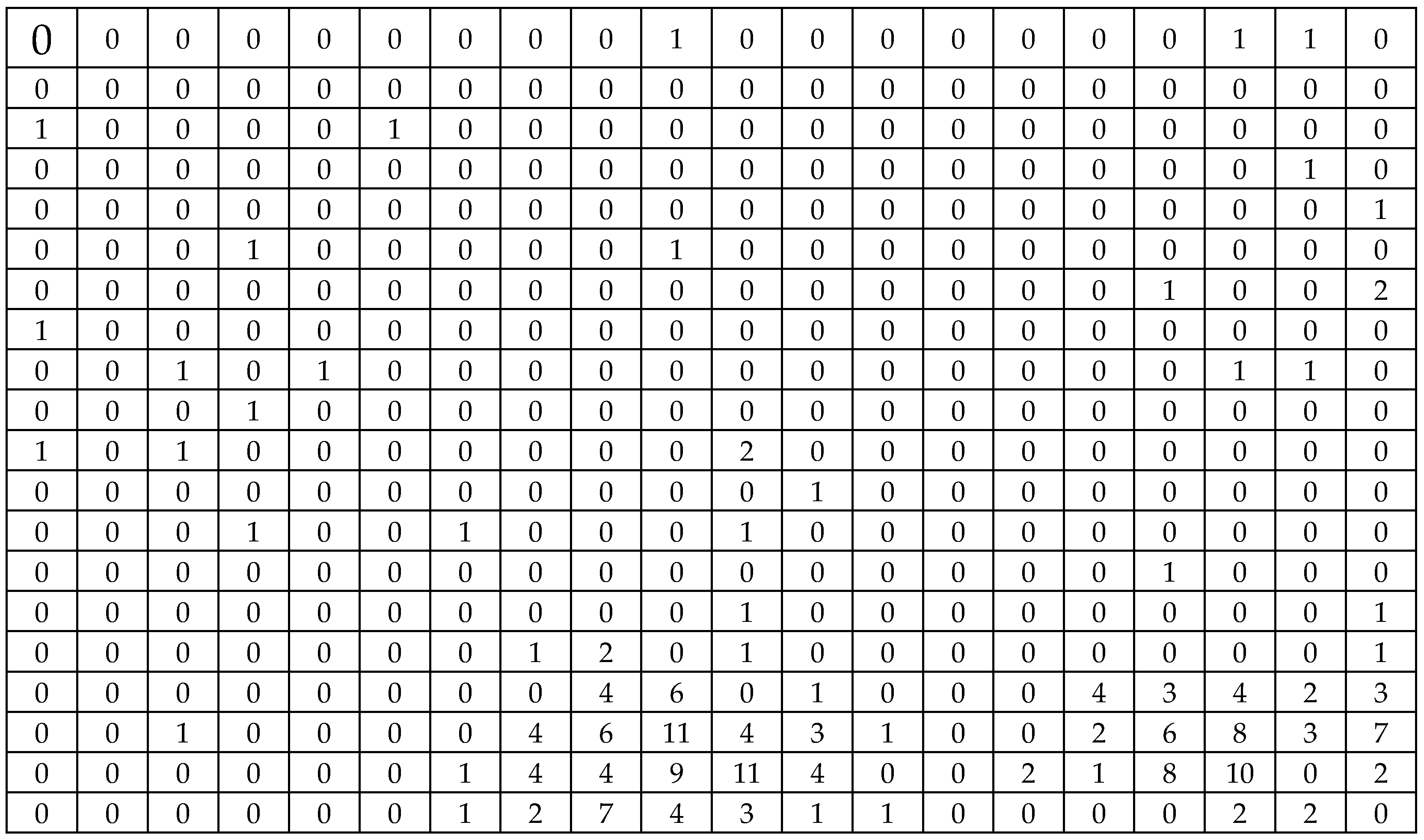
Appendix A
Figure A1 and
Figure A2 display the population distributions for the variable of interest and the auxiliary variable
, respectively
, as generated according to Chao [
7].
Figure A1.
The population of the variable of interest
Figure A1.
The population of the variable of interest
Figure A2.
The population of the auxiliary variable
Figure A2.
The population of the auxiliary variable
References
- Sisodia, B. V. S.; Dwivedi, V. K. A. Modified ratio Estimator Using Coefficient of Variation of Auxiliary Variable. Journal of Indian Society Agricultural Statistics, 1981, 33, 13–18. [Google Scholar]
- Singh, H. P.; Tailor, R. Use of Known Correlation Coefficient in Estimating the Finite Population Mean. Statistics in Transition, 2003, 6, 555–560. [Google Scholar]
- Yadav, S. K.; Subramani, J.; Mishra, S. S.; Shukla, A. K. Improved Ratio-Cum- Product Estimators of Population Mean Using Known Population Parameters of Auxiliary Variables. American Journal of Operational Research, 2016, 6, 48–54. [Google Scholar] [CrossRef]
- Jerajuddin, M.; Kishun, J. Modified Ratio Estimators for Population Mean Using Size of the Sample, Selected from Population. International Journal of Scientific Research in Science, Engineering and Technology, 2016, 2, 10–16. [Google Scholar]
- Soponviwatkul, K.; Lawson, N. New Ratio Estimators for Estimating Population Mean in Simple Random Sampling using a Coefficient of Variation, Correlation Coefficient and a Regression Coefficient. Gazi University Journal of Science, 2017, 30, 610–621. [Google Scholar]
- Thompson, S.K. Adaptive cluster sampling. J. Am. Statist. Assoc. 1990, 85, 1050–1059. [Google Scholar] [CrossRef]
- Chao, C.T. Ratio estimation on adaptive cluster sampling. Journal of Chinese Statistical Association 2004, 42, 307–27. [Google Scholar] [CrossRef]
- Dryver, A.L.; Chao, C.T. Ratio estimators in adaptive cluster sampling. Environmetric 2007, 18, 607–620. [Google Scholar] [CrossRef]
- Chutiman, N.; Kumphon, B. Ratio estimator using two auxiliary variables for adaptive cluster sampling. Thailand Statistician 2008, 241–256. [Google Scholar]
- Chutiman, N. Adaptive cluster sampling using auxiliary variable. Journal of Mathematics and Statistics 2013, 9, 249–255. [Google Scholar] [CrossRef]
- Yadav, S.K.; Misra, S.; Mishra, S. Efficient estimator for population variance using auxiliary variable. American Journal of Operational Research 2016, 6, 9–15. [Google Scholar] [CrossRef]
- Chaudhry, M. S.; and, M. Hanif. Generalized exponential-cum-exponential estimator in adaptive cluster sampling. Pakistan Journal of Statistics and Operation Research 2015, 11, 553–574. [Google Scholar] [CrossRef]
- Chaudhry, M. S.; Hanif, M. Generalized difference-cum-exponential estimator in adaptive cluster sampling. Pakistan Journal of Statistics, 2017, 33, 335–367. [Google Scholar]
- Bhat, A.A.; Sharma, M.; Shah, M.; Bhat, M. Generalized ratio type estimator under adaptive cluster sampling. Journal of Scientific Research 2023, 67, 46–51. [Google Scholar] [CrossRef]
- Thompson, S.K. Sampling, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, New Jersey, 2012; pp. 319–337. [Google Scholar]
- Banerjie, J.; Tiwari, N. Improved ratio type estimator using jack-knife method of estimation. Journal of Reliability and Statistical Studies 2011, 4, 53–63. [Google Scholar]
- Quenouille, M. H. Notes on Bias in Estimation. Biometrika, 1956, 43, 353–360. [Google Scholar] [CrossRef]
Table 1.
The estimated absolute relative bias of the estimators for the population mean of the variable of interest.
Table 1.
The estimated absolute relative bias of the estimators for the population mean of the variable of interest.
|
|
|
|
|
| 4 |
6.8705 |
0.5291 |
0.7104 |
0.6129 |
| 8 |
12.8042 |
0.3045 |
0.5526 |
0.3550 |
| 10 |
15.8498 |
0.2046 |
0.4560 |
0.2390 |
| 16 |
24.8431 |
0.0651 |
0.2804 |
0.0790 |
| 20 |
30.9154 |
0.0254 |
0.1957 |
0.0332 |
| 26 |
38.9001 |
0.0337 |
0.1386 |
0.0354 |
| 30 |
43.8715 |
0.0263 |
0.0997 |
0.0278 |
| 40 |
56.7309 |
0.0077 |
0.0389 |
0.0084 |
| 50 |
68.5383 |
0.0100 |
0.0274 |
0.0103 |
| 100 |
120.1685 |
0.0018 |
0.0083 |
0.0019 |
| 200 |
215.1886 |
0.0031 |
0.0004 |
0.0003 |
Table 2.
The estimated MSE of the estimators for the population mean of the variable of interest.
Table 2.
The estimated MSE of the estimators for the population mean of the variable of interest.
|
|
Estimators that do not use auxiliary variable information |
Estimators use auxiliary variable information |
|
|
|
|
|
|
| 4 |
6.8705 |
10.8216 |
1.1305 |
0.2777 |
0.2730 |
0.3777 |
0.2625 |
| 8 |
12.8042 |
10.8059 |
0.5291 |
0.2115 |
0.1986 |
0.3679 |
0.1929 |
| 10 |
15.8498 |
10.7229 |
0.4623 |
0.1792 |
0.1705 |
0.3361 |
0.1649 |
| 16 |
24.8431 |
9.6113 |
0.2606 |
0.1158 |
0.1149 |
0.2407 |
0.1102 |
| 20 |
30.9154 |
9.2723 |
0.2122 |
0.0990 |
0.0962 |
0.2040 |
0.0938 |
| 26 |
38.9001 |
7.7315 |
0.1790 |
0.0873 |
0.0863 |
0.1665 |
0.0856 |
| 30 |
43.8715 |
6.9521 |
0.1315 |
0.05270 |
0.0521 |
0.0906 |
0.0517 |
| 40 |
56.7309 |
5.9159 |
0.1004 |
0.04060 |
0.0495 |
0.0651 |
0.0401 |
| 50 |
68.5383 |
4.7074 |
0.0717 |
0.02520 |
0.0322 |
0.0292 |
0.0215 |
| 100 |
120.1685 |
1.5727 |
0.0238 |
0.0078 |
0.0091 |
0.0080 |
0.0078 |
| 200 |
215.1886 |
0.2266 |
0.0076 |
0.0023 |
0.0027 |
0.0024 |
0.0023 |
Table 3.
The percentage relative efficiency of the estimators compared with
Table 3.
The percentage relative efficiency of the estimators compared with
|
|
The PRE of the estimators compared with |
|
|
|
|
|
| 4 |
6.8705 |
100 |
407.1231 |
414.1172 |
299.2905 |
430.7640 |
| 8 |
12.8042 |
100 |
250.1418 |
266.3881 |
143.8358 |
274.2445 |
| 10 |
15.8498 |
100 |
257.9432 |
271.0884 |
137.5487 |
279.4969 |
| 16 |
24.8431 |
100 |
224.9978 |
226.8193 |
108.2551 |
236.5163 |
| 20 |
30.9154 |
100 |
214.2381 |
220.6093 |
103.9796 |
226.1834 |
| 26 |
38.9001 |
100 |
205.0630 |
207.3911 |
107.5389 |
209.2577 |
| 30 |
43.8715 |
100 |
249.4971 |
252.5163 |
145.1634 |
254.5208 |
| 40 |
56.7309 |
100 |
247.4008 |
203.0738 |
154.3736 |
250.6114 |
| 50 |
68.5383 |
100 |
284.5574 |
222.8856 |
245.8162 |
333.5505 |
| 100 |
120.1685 |
100 |
306.0567 |
260.4167 |
296.5044 |
306.0567 |
| 200 |
215.1886 |
100 |
324.7863 |
284.6442 |
323.4043 |
324.7863 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).