Synthesis of a Non-Bridge Circuit with Module Balancing Designed to Measure the Dielectric Loss Factor Tan δ

1. Introduction

The assessment of the quality of insulation materials is of significant importance in modern technology. It is very important, for example, in the energy industry and automotive technology. The quality of insulation determines the trouble-free operation of electrical installations and devices, as well as, which is very important, the safety of their use.

Various indicators are used to assess the quality of electrical insulation materials. One of them is the dielectric loss factor tan δ. The dielectric loss factor is a relative quantity defined for real capacitors filled with dielectric material, and an insulating system can generally be treated in this way. This coefficient is determined as the ratio of the power losses in the tested capacitor to the power stored on it. In typical electrical insulation systems, it takes values of 10^-1 to 10^-5, which means that power losses in insulation are at the level of fractions of a percent to even 10%. In the assessment of the quality of insulation, the value of the dielectric loss coefficient itself is less important, the changes in this coefficient are more important, indicating the degradation of the insulation of the tested device or installation. In the measurement of the dielectric loss factor, high requirements for measurement accuracy are not set.

It can be seen that the dielectric loss factor is the tangent of a certain phase angle, by which the phase shift angle between the voltage and current of the tested capacitor decreases due to the flow of the active component of the current through it. For this reason, the dielectric loss factor is often referred to as tan δ. Its value is also a relation of the corresponding impedance components. Analog and digital measurement methods are used to measure the coefficient in question.

Measurements of impedance components and their mutual relations (such as the dielectric loss factor of lossy capacitors) are commonly performed in science and technology. Measurement circuits require the tested object to be supplied with a voltage or sinusoidal current. The measurement signals are the voltage and current of the object being tested. These signals are generally processed in non-zero or zero measurement circuits. In non-zero circuits, the output non-zero signal of the circuit is a function of the measured parameters, in zero circuits the circuit is driven to the equilibrium state, which usually means reaching the zero value of the selected signal, and then the values of the measured quantities are determined on the basis of the parameters of the measurement circuit. An example of such circuits are balanced bridge circuits [1,2,3].

Measurement circuits often use digital processing of measurement signals to measure impedance components [4,5,6,7,8,9,10]. Signal processing is sometimes carried out in the form of electronic circuits and in the form of a software chain of measurement signal processing. The measurement algorithm performs operations that are equivalent to electrical connections between blocks of measurement circuits. Such implementations are called virtual instruments. For the design of virtual instruments, software packages can be used, which significantly facilitate modeling, simulations, and finally testing of the measurement circuit [11].

Circuits for measuring impedance components are usually easy to digitize. Operations on measurement signals are not complicated and changing the parameters of the system is easy. However, some difficulties may be caused by the need to derive the equations for the processing of the circuits.

The synthesis process of a system to measure the dielectric loss factor based on the equations of an AC bridge system with double modular balancing designed to measure the dielectric loss factor tan δ [12] will be presented below. The bridge was first introduced over 60 years ago. At that time, the implementation of such a system was problematic due to the properties of most voltmeters of the time. These were usually analog devices that were characterized by low input resistances. This, in turn, disrupted the flow of currents and the distribution of voltages in the bridge, making it practically impossible to implement it.

The parameters of modern measuring instruments enable the implementation of the system in question. This system is characterized by extraordinary simplicity of design and lack of convergence problems characteristic of typical balanced bridge systems.

The synthesis process of a system for measuring the dielectric loss factor based on the equations of an AC bridge system with double modular balancing designed to measure the dielectric loss factor tan δ [12] will be presented below. The bridge was first introduced more than 60 years ago. At that time, the implementation of such a system was problematic due to the properties of most voltmeters of the time. These were usually analog devices that were characterized by low input resistances. This, in turn, disrupted the flow of currents and the distribution of voltages in the bridge, making it practically impossible to implement it.

2. Measuring Method

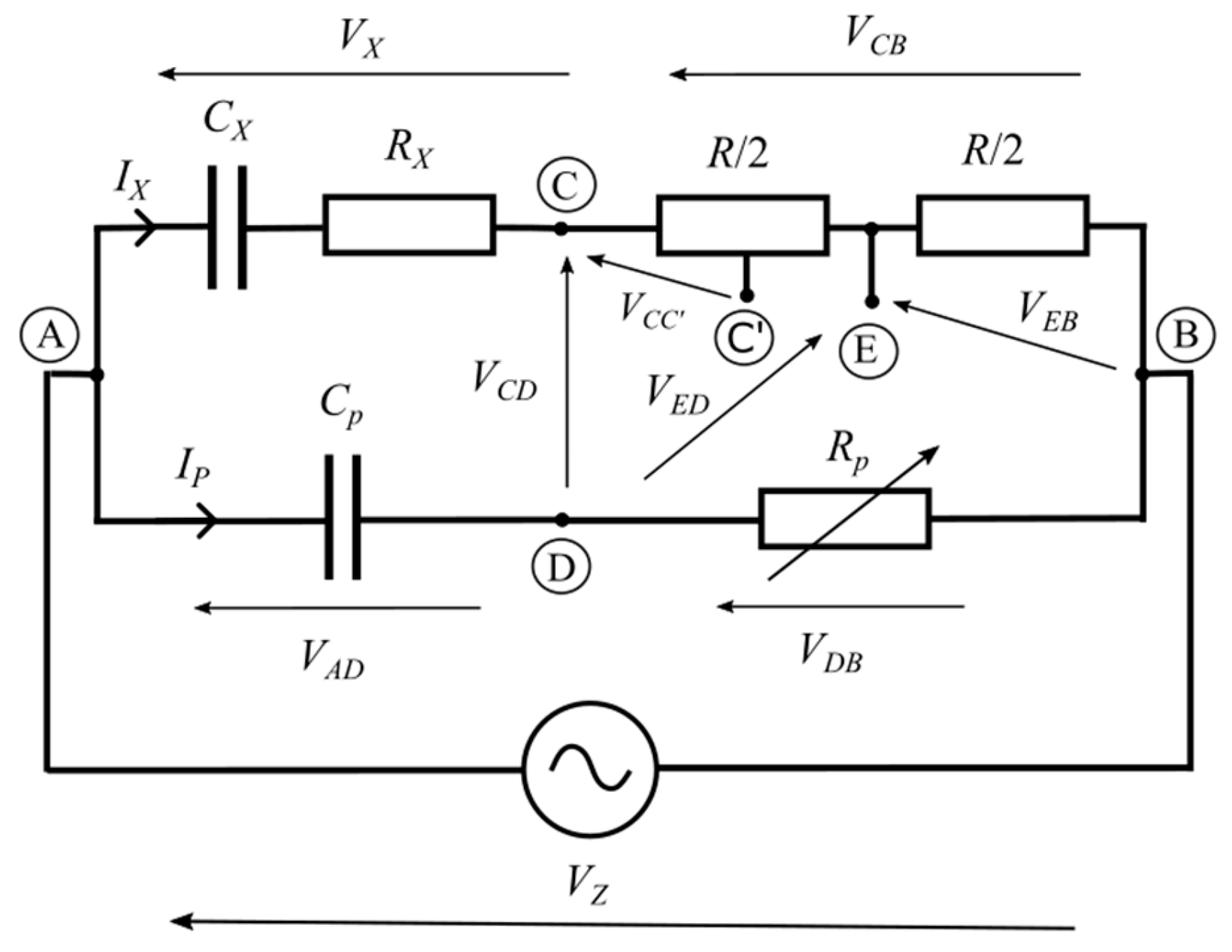
The bridge that is the basis of the synthesis is shown in Figure 1. It is designed to measure the dielectric loss factor tan δ.

The concept of this bridge was presented in the paper [12]. The principle of operation of the bridge is presented in an extremely concise way, making the analysis of the system somewhat difficult. Figure 2 shows the entire original work.

The object of the research here is a lossy capacitor, which has been modeled in a simplified way as a branch consisting of C_X capacitance and R_X resistance connected in series. For such a model, the dielectric loss factor can be expressed as follows:

$$\tan \delta =\omega {R_{X}C}_X$$

(1)

The bridge has two adjustable elements: the R_P resistor and the R_CC’ resistor. The resistors in the CB branch have equal resistances equal to R/2, while the R_CC' resistor is part of the resistor switched on between the CE points and in practice can be implemented as a potentiometer, in which the C' point is attached to the slider. The resistance of this resistor can take values from 0 to R/2. The system has two measurement steps in which two balancing of the system is performed.

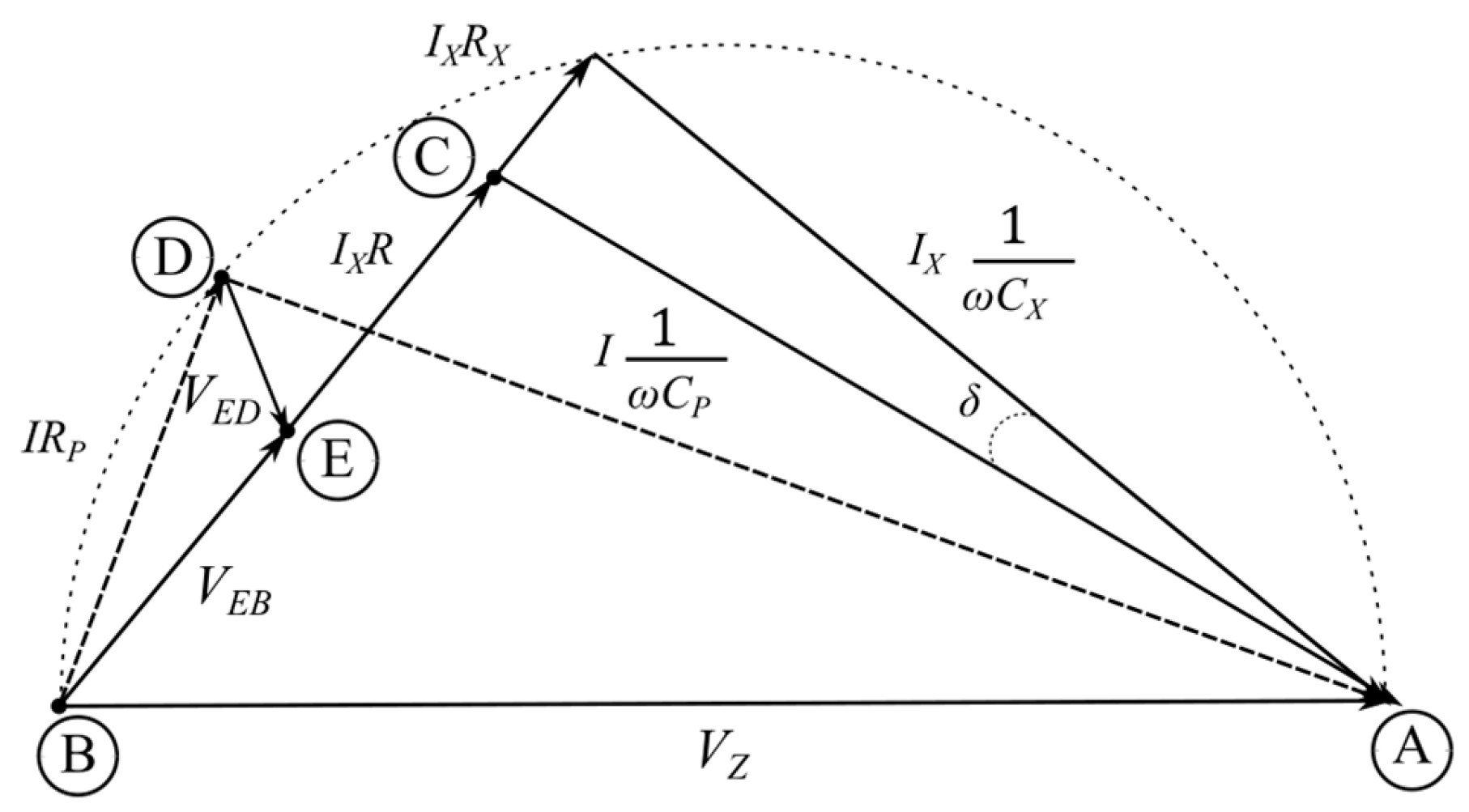
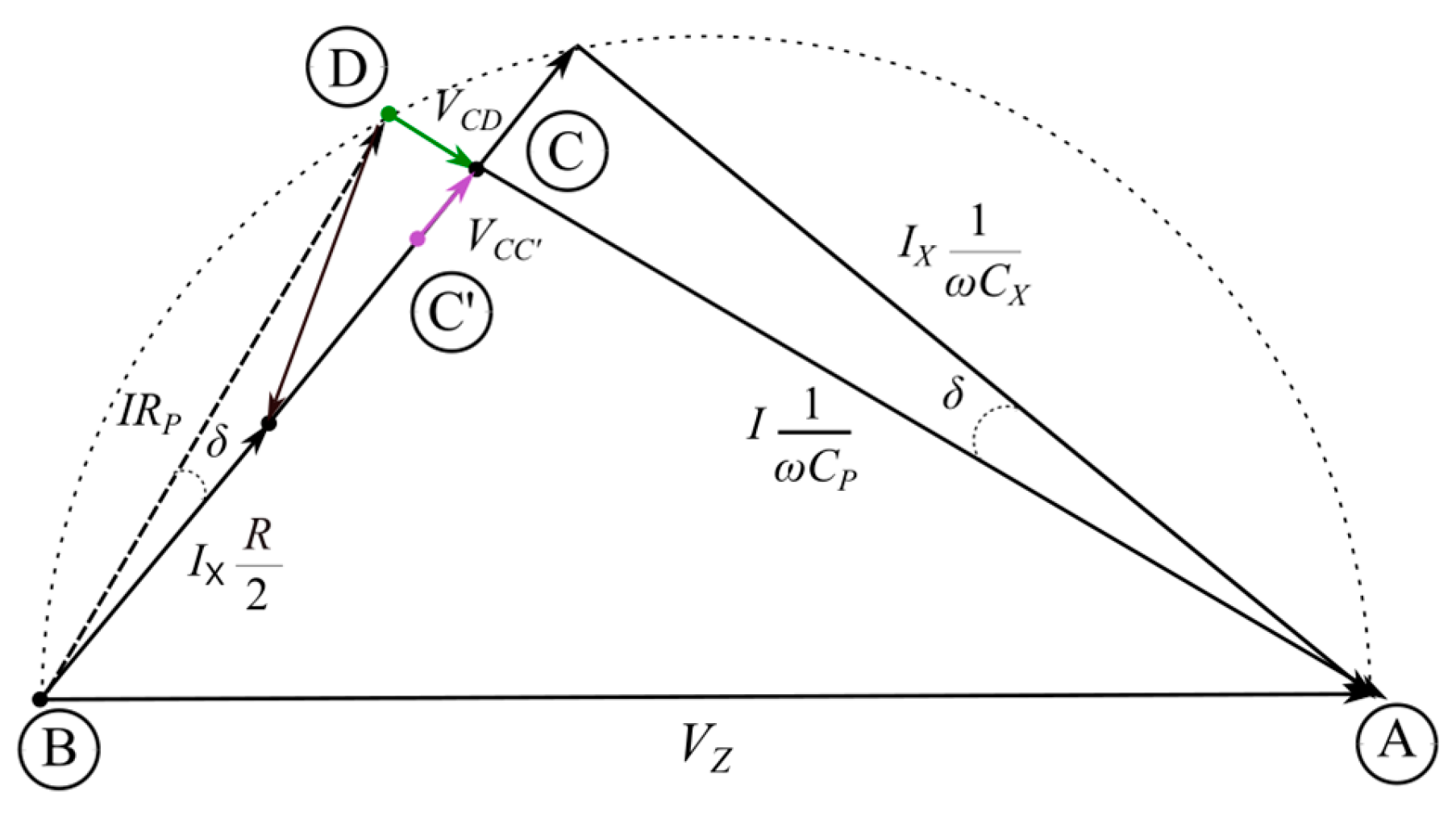
Figure 3 shows a vector diagram of bridge voltages. When constructing the diagram, it was assumed that the supply voltage has a zero phase. The method of constructing graphs using the homographic function (Möbius transformation) presented in [2] was used. Note that points A, B, C, and D are loci on the Gaussian plane of the potentials of the corresponding bridge points from Figure 1.

The bridge requires two measurement steps. In the first measurement step, the R_P resistor is the adjustable element. In this step, the V_EB and V_ED voltage modules are compared. Such a comparison can be made, for example, by comparing the RMS values of the voltages. Note that in this balancing step, the current I_X does not change during the measurement, which means that the V_EB voltage remains unchanged throughout the measurement. The locus of points C and E do not change. Changing the R_P resistor setting results in the D point moving along the ADB semicircle.

The measurement step completes the state in which the voltage preference lengths V_EB and V_ED are equal to each other. This means that the V_ED voltage module is equal to the V_EB voltage module:

$$\left|V_{ED}\right|=\left|V_{EB}\right|.$$

(2)

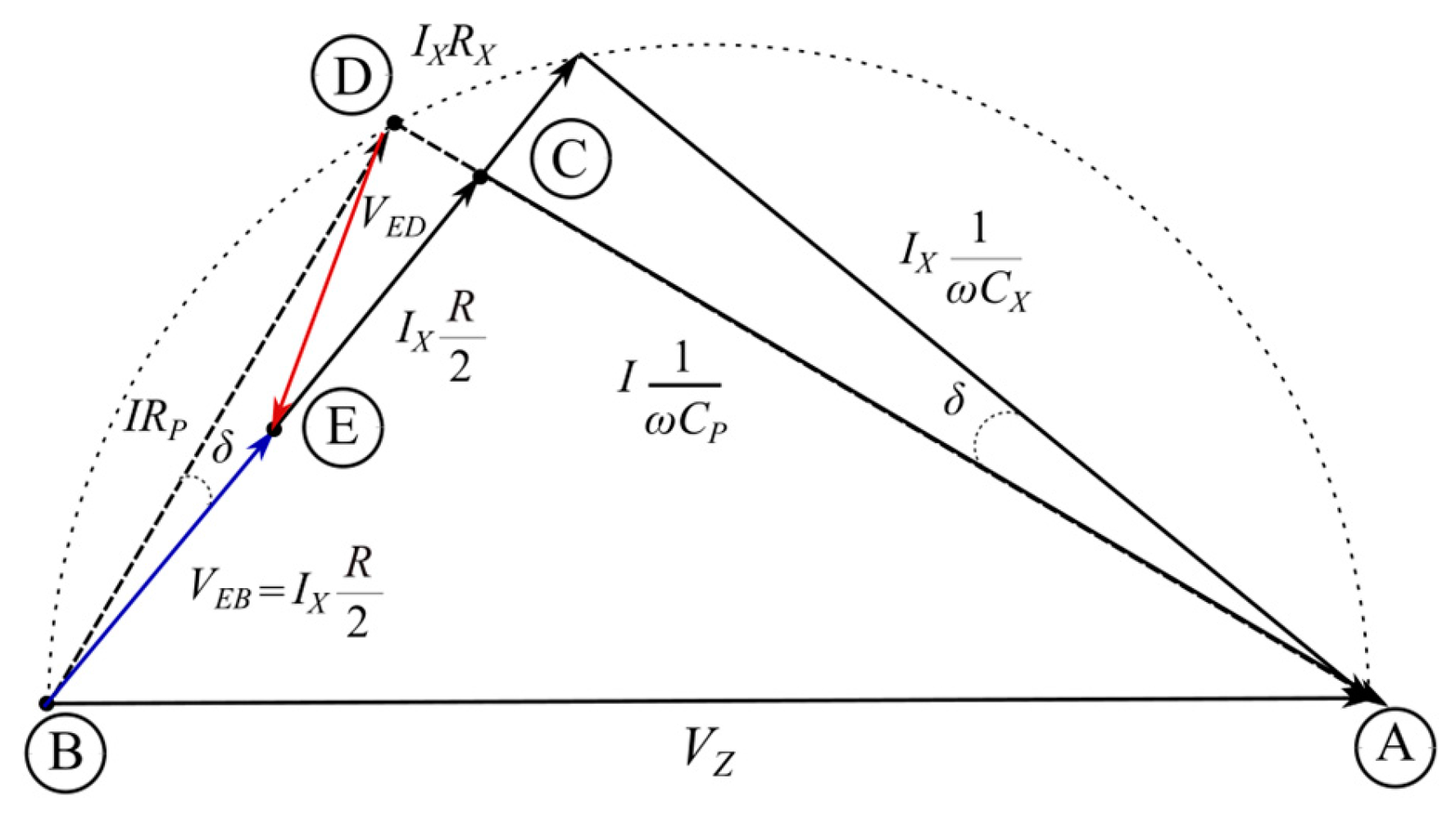
Figure 4 shows the phasor chart after the first balancing step is completed. On the diagram it can be seen that due to the similarity of the triangles, the angle between the V_DB and V_BC voltages is equal to the angle δ the object under control. You can also notice that the V_AC voltage is in phase with the V_AD.

Analyzing the above diagram, it can be seen that it is possible to determine the sine of the angle δ as a voltage relationship between V_CD and V_CB. The author of the paper [12] suggested another way to measure this relationship, as the resistance relationship R_CC' and R. A second measurement step can be performed for this purpose. In the step, the adjustable element is the R_CC' resistor. The value of the R_P resistance from the first step is maintained. The V_CD and V_CC' voltage modules are compared. The bridge is brought to a state in which the voltage module V_CD is equal to the voltage module V_CC':

$$\left|V_{CD}\right|=\left|V_{CC\prime }\right|.$$

(3)

A phasor diagram after completing this step is shown in Figure 5.

From the phasor diagram in this condition, it follows that the sine of the angle δ can be calculated as follows:

$$\sin \delta ={\displaystyle \frac{R_{CC\prime }}{R}}\mathrm{a}=1$$

(4)

From the sine, the tangent of the angle δ can be calculated as:

$$\tan \delta ={\displaystyle \frac{\sin \delta }{\sqrt{1-{\left(\sin \delta \right)}^2}}}={\displaystyle \frac{\frac{R_{CC\prime }}{R}}{\sqrt{1-{\left(\frac{R_{CC\prime }}{R}\right)}^2}}}$$

(5)

For low-loss capacitors, equation (5) can be written in approximate form as:

$$\tan \delta \approx {\displaystyle \frac{R_{CC\prime }}{R}}$$

(6)

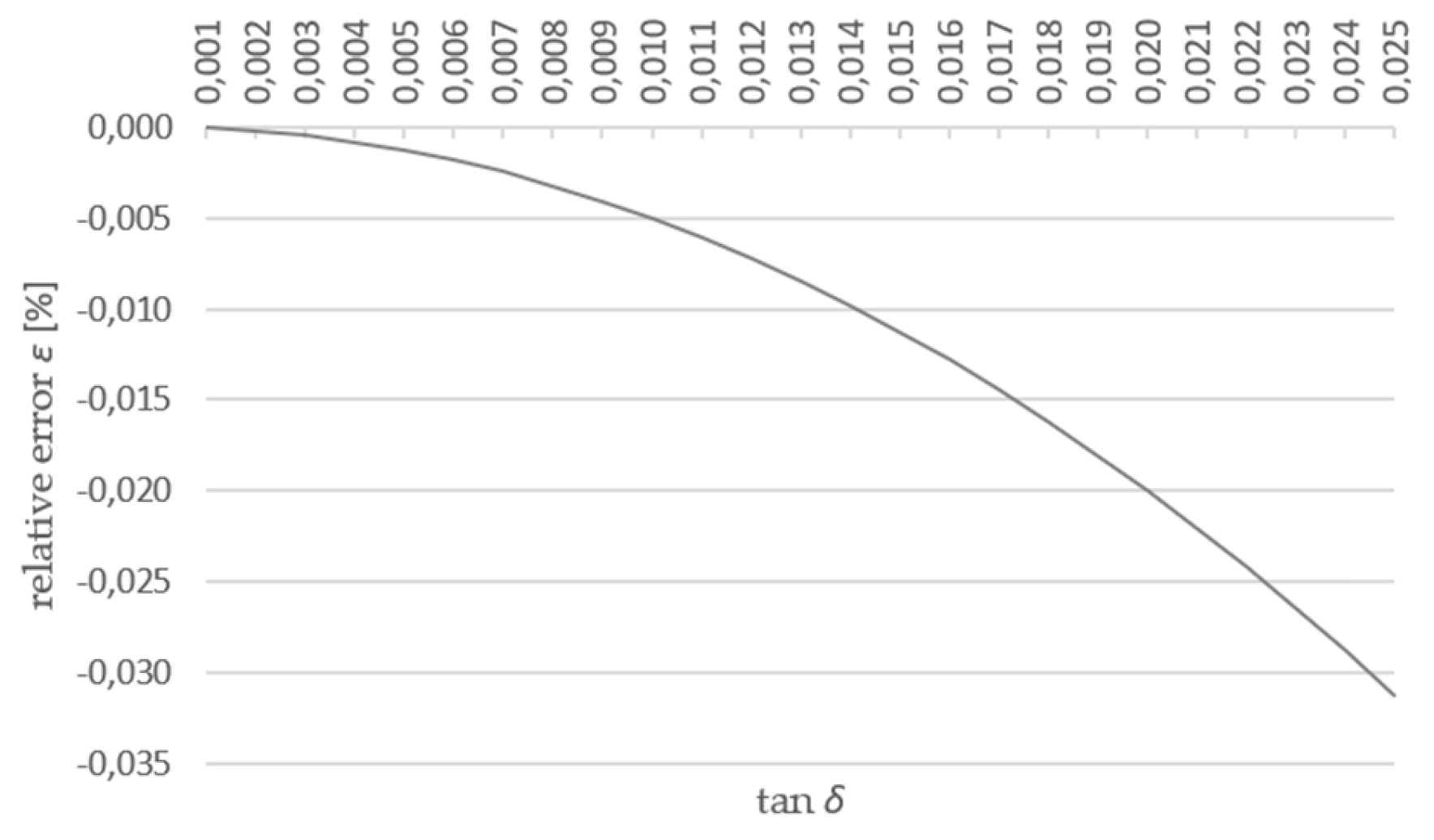
The relative error ε of the approximation (6) can be determined as follows:

$$\epsilon ={\displaystyle \frac{\sin \delta -\tan \delta }{\tan \delta }}=\cos \delta -1$$

(7)

Figure 5 shows the dependence of error (7) on the measured dielectric loss factor tan δ.

Figure 6. Relative error ε vs dielectric loss factor tan δ.

Figure 6. Relative error ε vs dielectric loss factor tan δ.

From the assessment of the approximation error, it appears that for typical dielectric loss factors tan δ the approximation error (6) is vanishingly small.

The analysis of the system shows that the second balancing step is actually used to determine the relationship (4). It allows you to determine the sine (or tangent) of the loss angle as a relation of two resistances. Perhaps the author of the concept intended this to facilitate the measurement by, for example, scaling the potentiometer in tan δ values. The measured dielectric loss factor can also be determined as a relationship of modules or values of effective voltages V_CD and V_CB, which can be easily implemented today. We should remember that voltage measurements in the period when the idea of the bridge was born were difficult due to the relatively low input resistance of the devices and their low accuracy. The author states that voltmeter errors are eliminated because it is used only to determine the equality of voltages. However, it does not take into account the impact on the error of module equality detection on the measurement result.

3. Synthesis of a Non-Bridge System

In this bridge circuit, two signals from the impedance under study are processed: voltage V_X and current I_X. These signals require the application of the V_Z supply voltage. In the case of digital processing, the I_X signal should be converted to voltage, e.g. at a resistor, which acts as a shunt. Note that the supply voltage V_Z together with the branch containing the impedance under test Z_X and resistor R is half of the bridge in Figure 1. The other half can be realized in a different way using transducers that allow the construction of a non-bridge system.

In the case of building a non-bridge equivalent of a bridge, the second measurement step can be omitted. In this case, the measurement will require only one measurement step. The bridge signals subject to detection are V_EB and V_ED. In a non-bridge system, these will be the voltages marked as w₁ and w₂ described by the equations:

$$w_1=V_{EB}={\displaystyle \frac{V_{CB}}{2}}={\displaystyle \frac{R}{2}}{I}_X.$$

(8)

The w₁ signal can be realized by dividing the voltage drawn from resistor R by 2.

The w₂ signal can be written with a dependency:

$$w_2=V_{EB}-{\displaystyle \frac{\left(V_X+V_{EB}\right)}{Z_P}}{R}_P,$$

(9)

where the impedance Z_P is equal to:

$$Z_P=R_P-j{\displaystyle \frac{1}{\omega C_P}}=R_P-j{X}_P,$$

(10)

After the transformations of equation (9), the following relation is obtained:

$$w_2={\displaystyle \frac{R}{2}}\left(1-{\displaystyle \frac{R_P}{Z_P}}\right)I_X-\left({\displaystyle \frac{R_P}{Z_P}}\right)V_X.$$

(11)

The w₂ signal can be obtained by multiplying the voltage and current signals by the appropriate coefficients. Notice that both coefficients contain the relation R_P to Z_P, which can be written as follows:

$${\displaystyle \frac{R_P}{Z_P}}={\displaystyle \frac{R_P}{\left(R_P-j{X}_P\right)}}$$

(12)

In relation (12) there is the setting parameter R_P and the constant X_P which is the reactance of the capacitor C_P. This relation is a complex number. In an analog measurement system, the multiplication by an imaginary unit j means a phase shift of 90°. This can be accomplished using a phase shifter. In digital realization, the multiplication by an imaginary unit can be accomplished by shifting the signal by the number of samples corresponding to 1/4 of the period.

After omitting the second measurement step, the measured dielectric loss factor can be determined from the voltage relation:

$$\tan \delta ={\displaystyle \frac{\left|V_{CD}\right|}{\left|V_{CB}\right|}},$$

(13)

The corresponding voltages depending on (13) are equal to:

$$V_{CB}=R{I}_X$$

(14)

and

$$V_{CD}=V_{CB}-V_{DB},$$

(15)

The V_CD voltage can be written definitively as:

$$V_{CD}=R{I}_X-{\displaystyle \frac{\left(V_X+R{I}_X\right)}{Z_P}}{R}_P=R{I}_X\left(1-{\displaystyle \frac{R_P}{Z_P}}\right)-V_X{\displaystyle \frac{R_P}{Z_P}}.$$

(16)

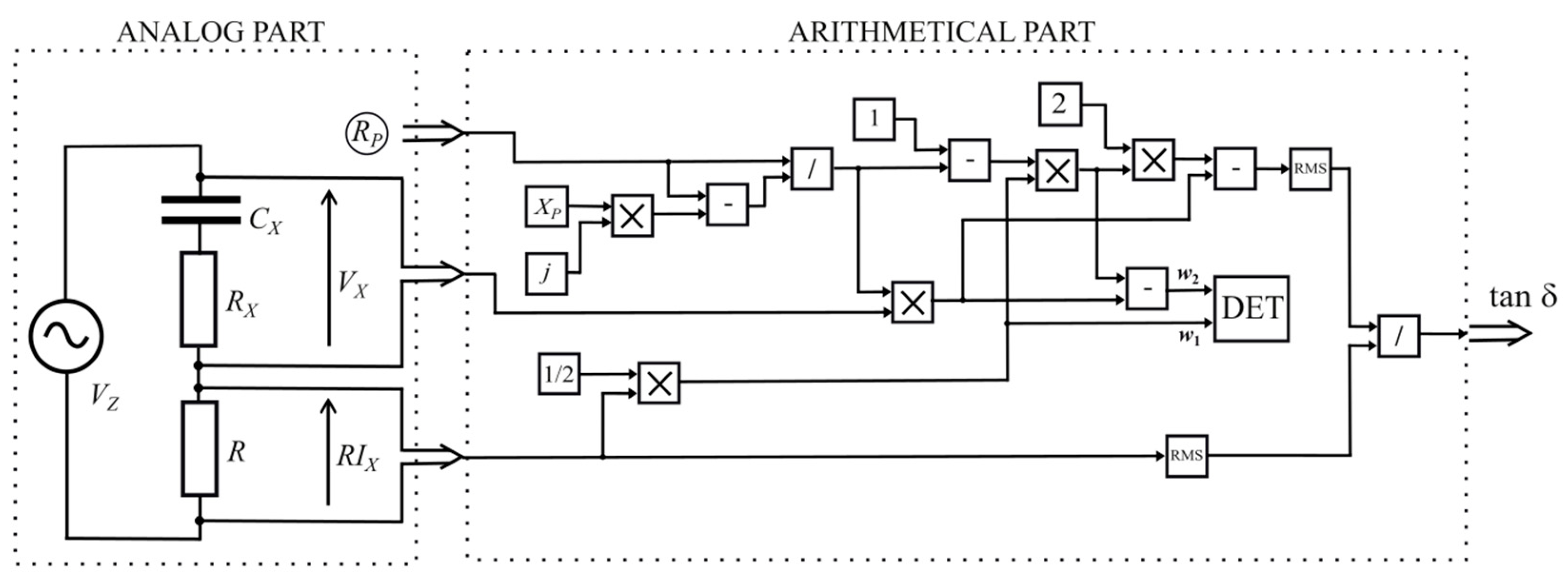
Figure 7 shows the structure of a non-bridge system for measuring the dielectric loss coefficient tan δ derived from the equations describing the bridge in Figure 1. The non-bridged system consists of two parts. The analog part contains the power source, the Z_X impedance undertest, and the R resistor of a known value. The output signals of the analog part are the voltage Z_X and the voltage proportional to the current I_X of the impedance under test. The second part of the system is the arithmetic part, in which the appropriate voltages subject to detection w₁ and w₂ are determined according to equations (8) and (11), respectively. The modules or RMS values of the w₁ and w₂ signals are compared in the DET detector. In the equilibrium state, to which the system is reduced by changing the R_P parameter, the measured tan δ is determined by dividing the modules, or the RMS values of the signals of the system according to the relationship (13).

The arithmetic part of the circuit can be implemented in analog form. The problem in such a project is the need to build analog multiplication and division circuits as well as circuits determining the module or RMS value of the signals subject to detection. In the case of digital implementation, the input signals will be processed in analog-digital circuits and then processed by software. Operations that are difficult for analog signals are much simpler here.

4. Errors and Uncertainties

In the solution discussed, several sources of error and measurement uncertainty can be indicated. One source of uncertainty is the uncertainty of determining the measured dielectric loss factor from equation (13). This coefficient is determined in the equilibrium state as a relationship of the values of the voltage modules V_CD and V_CB, but this relation can be determined as the ratio of the effective values of the voltages in question. Thus, the relative measurement uncertainty of the dielectric loss factor tan δ, denoted as u_rel (tan δ), can be estimated as:

$$u_{rel}\left(\tan \delta \right)=\sqrt{{\left(u_{rel}\left(V_{CD}\right)\right)}^2+{u_{rel}\left(V_{CB}\right)}^2},$$

(17)

where u_rel(V_CD) and u_rel(V_CB) are the uncertainty of determining the RMS value of V_CD and V_CB voltages, respectively.

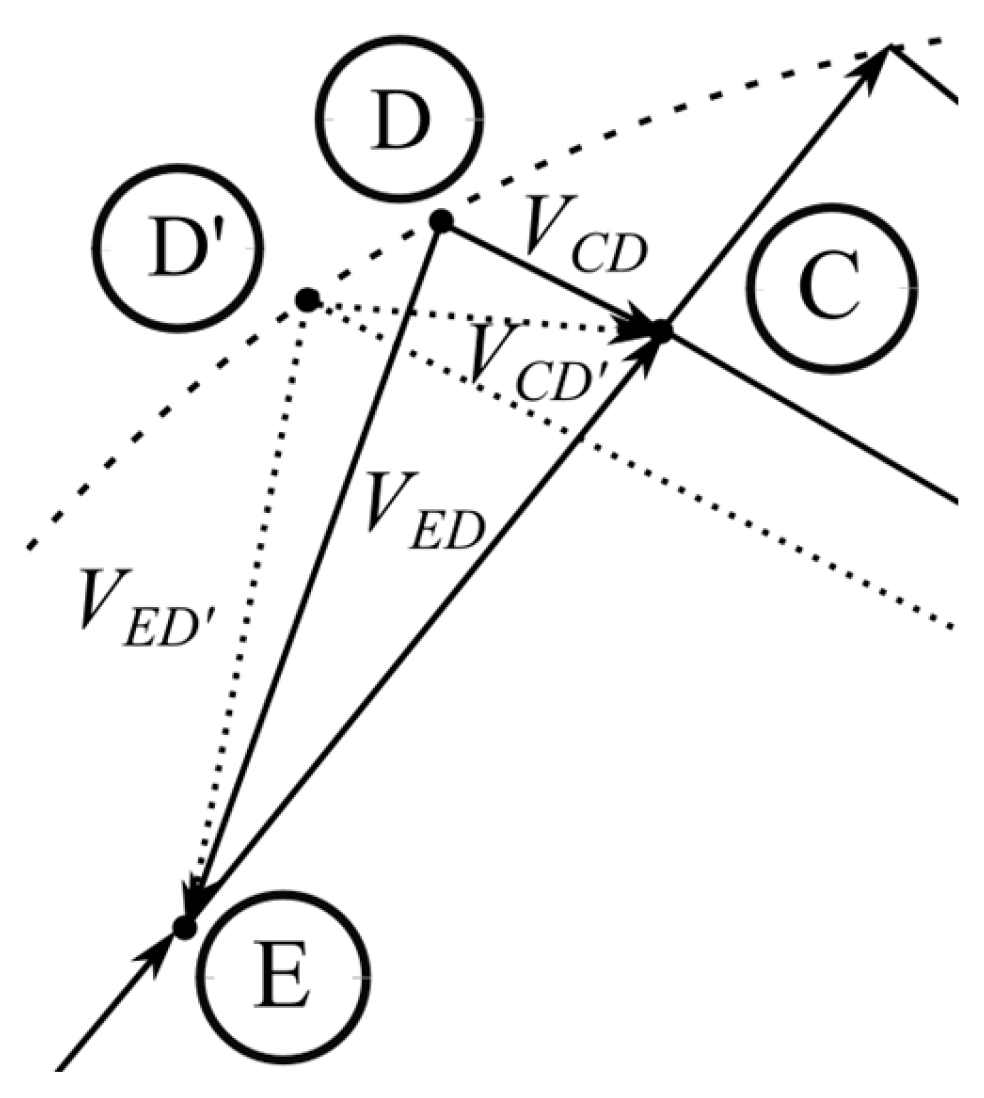
Other sources of error in the system in question are related to the incorrect position of the D point during the measurement. This can be caused by an error in the detection of equilibrium and a loss of the C_P capacitor. In the first case, the equilibrium state of the bridge means the equality of the modules, and thus the values of the effective voltages V_EB and V_ED. The inequality of the mentioned voltages, caused by the incorrect detection of their equality, results in the adoption of an equilibrium state despite the inequality of the V_EB and V_ED voltage modules. Then, on the phasor diagram, the point D' is taken as the potential of the point D, which results in a change in the value of the voltage V_CD to the value of V_CD'. Figure 8 shows an illustration of the loci of points D and D' on the Gaussian plane. For readability, a fragment of the phasor chart is presented.

As a result of the incorrect position of the locus D, the dielectric loss coefficient tan δ determined from equation (13) will have the value tan δ' equal to:

$$\tan {\delta }^{\prime }={\displaystyle \frac{\left|V_{CD\prime }\right|}{\left|V_{CB}\right|}}$$

(18)

The absolute error in determining the dielectric loss coefficient Δ tan δ_D, caused by the shift of the point D, will have the following value:

$$∆\tan {\delta }_D={\displaystyle \frac{\left|V_{CD\prime }\right|}{\left|V_{CB}\right|}}-{\displaystyle \frac{\left|V_{CD}\right|}{\left|V_{CB}\right|}}={\displaystyle \frac{\left|V_{CD\prime }\right|-\left|V_{CD}\right|}{\left|V_{CB}\right|}}.$$

(19)

The analytical calculation of this error is complicated. This is due to the need to calculate the modules of complex voltages. However, the error in determining the dielectric loss factor can be estimated by analyzing the phasor diagram shown in Figure 8. On the diagram it can be seen that the difference of voltage modules V_CD and V_CD' is, for a small difference in voltage modules subject to detection V_ED and V_ED', approximately equal to this difference:

$$\left|V_{DD\prime }\right|=\left|V_{CD\prime }\right|-\left|V_{CD}\right|\approx \left|V_{ED}\right|-\left|V_{ED\prime }\right|$$

(20)

The error equation (19) can then be written as:

$$∆\tan {\delta }_D\approx {\displaystyle \frac{\left|V_{C{D}^{\prime }}\right|}{\left|V_{CB}\right|}}-{\displaystyle \frac{\left|V_{CD}\right|}{\left|V_{CB}\right|}}={\displaystyle \frac{\left|V_{ED}\right|-\left|V_{E{D}^{\prime }}\right|}{\left|V_{CB}\right|}}={\displaystyle \frac{\left|∆V_{ED}\right|}{\left|V_{CB}\right|}}$$

(21)

The difference between V_ED and V_ED' voltage modules, denoted as ∆V_ED, is an absolute error of modular detection.

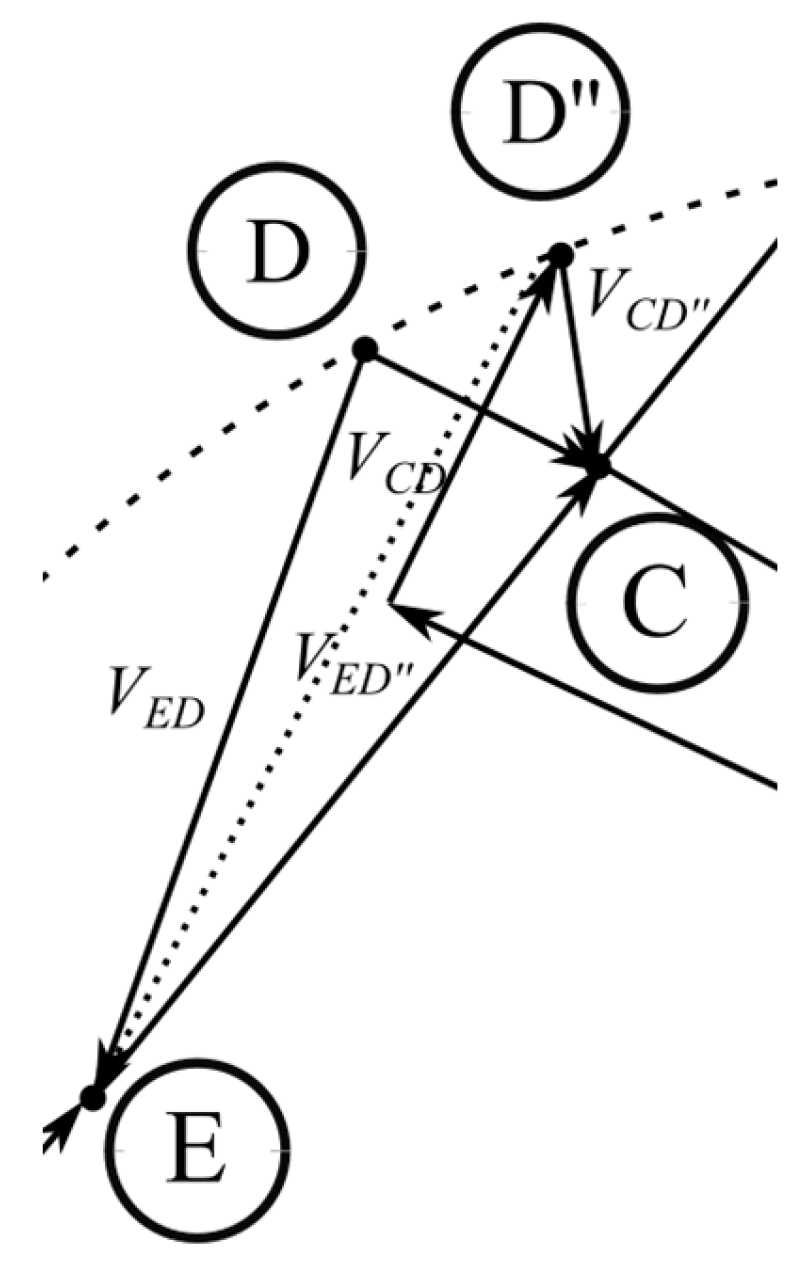
In the same way, the error related to the loss of the C_P capacitor can be determined. In this case, the displacement of the D point will involve a change in the phase angle of the voltage across the lossy capacitor.

This offset can be estimated as the V_DD' voltage from equation (20). The error due to the loss of Δ tan δ_L can then be estimated as:

$$∆\tan {\delta }_L={\displaystyle \frac{\left|V_{CD\prime \prime }\right|}{\left|V_{CB}\right|}}-{\displaystyle \frac{\left|V_{CD}\right|}{\left|V_{CB}\right|}}={\displaystyle \frac{\left|V_{CD\prime }\right|-\left|V_{CD}\right|}{\left|V_{CB}\right|}}$$

(22)

and thus

$$∆\tan {\delta }_L\approx {\displaystyle \frac{\left|V_{DD\prime \prime }\right|}{\left|V_{CB}\right|}}.$$

(23)

The vector of the voltage drop across the real component of the capacitor presented in Figure 9 has been significantly scaled for the readability of the drawing. In fact, it is many times smaller. The modulus of the voltage across the capacitor C_P can be approximated as equal to the voltage module V_DD’’. Then the error caused by the capacitor's loss factor can be estimated as:

$$∆\tan {\delta }_L\approx \tan {\delta }_{CP}$$

(24)

where tan δ_CP is the loss factor of the capacitor C_P.

In a passive bridge circuit, the dielectric loss factor tan δ_CP should be much (several orders) lower than the measured dielectric loss factor tan δ. In a non-bridge circuit, the discussed error related to the quality of the C_P capacitor does not occur. In these circuits, the source of the analogous error will be the realization of the multiplication by the imaginary unit j. In the analog circuit, the source of this error will be the inappropriate phase shift of the shifting switch, different from 90^o. On the other hand, in a system that performs digital signal processing, this source will be the realization of the shift of the vector of measurement signal samples by a time corresponding to 1/4 of the waveform period.

5. Discussion and Conclusions

This evaluation allowed us to develop the concept of a non-bridge measurement system designed to measure the dielectric loss coefficient of a real lossy capacitor modeled by a series connection of RC elements.

For the purpose of synthesis of a non-bridge system, it is necessary to derive equations describing the signals to be detected. In a bridge system, the measurement process requires bringing two selected bridge voltages to a state in which their modules are equal. This state also means the equality of the effective values of these tensions. In the paper [12], the derivation of the equation for the measured tan δ was based on the geometric analysis of the phasor diagram. When signals subject to detection using the symbolic method, in which they are complex numbers, it can be seen that the determination of modules or effective values is very complex, and thus the determination of the processing equation is also complex.

Using the derived equations for the signals subject to detection, the structure of a non-bridge system was developed. It was also noted that the method proposed by the author of the bridge required two balancing steps. In the second step, the purpose of balancing was to determine the voltage relation, which could be determined as a resistance relation. However, it turned out that this method unnecessarily complicates the measurement process. It would also require the use of an adjustable resistor, the design of which would be very troublesome. It seems much easier to determine the measured coefficient from the voltage relations of the circuit. The presented structure of a non-bridge circuit requires taking the voltage of the tested lossy capacitor and the voltage proportional to the current of this capacitor. This voltage can be taken from the appropriate shunt. As you can see, the design of the analog part is very simple and consists only of a supply voltage generator and a shunt. Further signal processing can be done by analogue or digital. The digital implementation is simpler and allows for trouble-free setting of parameter values corresponding to the values of the bridge elements. The operations carried out on the signals in the processing chain are also very simple. Only the operations of shifting by 1/4 of the period corresponding to multiplication by the imaginary unit and the operation of determining modulus or rms values can be slightly more complex, which can be simplified to the procedure of finding the maximum in the set of samples taken for the period.

The errors and uncertainties of the system were also assessed. Here, too, the analytical determination of the value of errors and uncertainty poses considerable difficulties. However, it is possible to make an approximate estimate, indicating the possibility of using the proposed system in practice, eg, measuring tan δ in the assessment of the degradation of insulation materials.

A significant advantage of this system is the constant maximum convergence. The balance process is much simpler than in typical bridge systems. Only one control element is used to reach equilibrium, which in a non-bridged system means a change in the value of only one parameter.