Laplacian Controllability and Observability of Multi-Agent Systems: Recent advances in Tree Graphs

Gianfranco Parlangeli

doi:10.20944/preprints202503.1438.v1

Preprint

Article

Laplacian Controllability and Observability of Multi-Agent Systems: Recent advances in Tree Graphs

This version is not peer-reviewed.

Gianfranco Parlangeli^*

This version is not peer-reviewed.

Downloads

Views

Comments

Submitted:

12 March 2025

Posted:

19 March 2025

You are already at the latest version

Abstract

Laplacian controllability and observability of a consensus network is a widely studied topic in the area of multi-agent systems, complex networks and large-scale systems. In this paper, this problem is afforded when the communication among nodes is described through a starlike tree topology. After a brief description of the mathematical setting of the problem, which is widely adopted for a wide number of multi-agent systems engineering applications, some novel results are drawn based on node positions within the network only. The resulting methods are graphical, thus effective and exempt from numerical errors, and the final algorithm is provided to perform the analysis by machine computation. Several examples are provided to show the effectiveness of the algorithm proposed.

Keywords:

Laplacian controllability

;

leader selection

;

starlike tree graphs

;

Laplacian spectrum

;

eigenvectors

Subject:

Computer Science and Mathematics - Computer Networks and Communications

1. Introduction

In the last decades, the recent advancements of technology pushed a notable thrust of research into the area of complex systems made of an interconnection of locally interacting devices [1]. A brand new paradigm arose in the modern design of engineering complex systems, namely interconnected components of a general system that can be synchronized and controlled towards collective objectives to optimize global performances. In the last decades, such framework has been modeled through multi-agent systems, so that the cross-field of systems theory, multi-agent systems and graph theory has been deeply investigated; a wide and careful description together with examples of engineering applications are reported in [1].

Motivated by their intrinsic adaptability and flexibility, decentralized architectures of components achieving global tasks through distributed algorithms were more and more studied. From this standpoint, an ever-increasing importance has been gained by the underlying communication graph topology and, more precisely, the effect of connection types on the system dynamical properties, and the associated spectral properties of the graph-related matrices [2,3,4].

Within this framework, a significant research field is devoted to the ability of a node to drive the evolution of the team, thus giving rise to the topic of network controllability [5]. Network controllability has been largely investigated in the last decade, providing exciting and unexpected novel insights, motivated by a better understanding of complex self-organized systems operating and functioning [5].

A different yet related key property within the above framework of complex systems made of an interconnection of locally interacting devices is the ability of a single node or a small subset of nodes to infer global information of the network through an appropriate elaboration of local data, which is referred to as network observability [6]. Based on this concept of systems theory applied to complex networks, many fundamental algorithms have been designed to achieve a higher level of security and robustness, as for example monitoring the eventuality of edge faults or disconnections, compensating the detrimental effects of faults and errors on the global performances, or the ability of selecting sensor positioning within the network nodes to get the best global performances in network estimation problems [6].

Surprisingly, these two properties are strongly related from a mathematical perspective. Indeed they are dual problems in the framework of systems theory [7], and they coincide in the case of a symmetric dynamical matrix. In the framework of multi-agent systems, this condition is a common feature when dealing with unweighted bidirectional communication, so that it is often verified.

For this reason, they are usually studied together, for the twofold goal of a deeper understanding of the functioning of complex networks of self-organized locally interacting nodes on one hand, and design ability on the necessary sensors and actuators (in terms of number and positioning) to get some prescribed performance on the other [4,8]. Moreover, the above analysis allows us to get a strong insight into the mechanism of controlling remote nodes and many results can be extended, separately, for the analysis of controllability and observability of multiagent systems connected through a directed communication graph.

A common mathematical tool to properly analyze and understand complex network behavior and its features is the crossfield between systems theory and graph theory. Considering both of the above-mentioned structural properties, the spectrum and the eigenstructure of some graph-related matrices (such as the Adjacency matrix or the Laplacian matrix) are the fundamental mathematical backbones [3,9], and their connections with topological substructures, so that graph topology has also been thouroghly investigated [4].

1.1. Literature Review And Paper Contribution

Controllability and observability are topics of interest to a broad community, and they have been studied over the years using several different tools, which have led to different approaches and results. In this Section, we review the several main methodologies available in the literature for the analysis and design of controllability and observability of a network. This topic has been widely discussed in recent years, the interested reader may also refer to the survey papers [10,11]. A careful and thorough overview of the approaches for the analysis of observability of network systems is [12].

One milestone paper that gave rise to the ideas of most of the further literature and approaches on this topic is [13]. In this paper, the authors introduce and motivate the controllability property of a multi-agent system, and they derive some basic fundamental results using several different approaches that have been largely investigated over the years.

One main direction stemming from this paper is the use of equitable partitions to detect uncontrollable graph topologies [14,15]. However, this method is proved to be only sufficient (and thus it provides only necessary conditions for controllability and observability). Moreover, the investigation of the existence of equitable partitions in large graphs may be difficult.

Other research directions exploring several different facets of controllability are the so-called structural controllability, namely the controllability analysis for almost all edge weights [16], and gramian-based controllability, where energy-based analysis is adopted to study the impact of control [17,18].

In the paper [19], a brand new approach was introduced for the class of path and cycle graphs, considering the position of the control/measured nodes within the network, and necessary and sufficient conditions were derived based on simple modular algebra. This approach stimulated several reserch activities; in [20] the results of [19] were more and more deepened and fully exploited.

The approach of [21] is based on the definition of minimal perfect critical set. This method is adequate to capture the minimum set of leaders for the controllability of undirected graphs, and it is applied to two different class of bipartite networks, namely deterministic scale-free networks and Cayley trees.

In the paper [22], path graphs and star graphs are considered, and the idea exploited is to also use second-order neighbors to improve controllability properties.

In this paper, we extend the results of [19] to a wider class of graphs, namely the class of tree graphs having one node of degree larger than 2, which are also known as starlike graphs [23,24] or spider graphs [25]. It is worth noting that, despite their simple and special topology, such a class of graphs has been recently very considered also among mathematicians for their interesting peculiar properties [23,26,27,28].

The contribution of this paper is to extend the results of [19] to get a deeper insight into the more general case of acyclic graphs. More in detail, the contribution of this paper with respect to the above literature is threefold. First, we provide a complete characterization of node selection, in terms of minimal number and appropriate location within the network, of the class of starlike graphs. The main result is in terms of length of some sub-paths, so that the use of such results does not suffer from numerical errors when the number of participants grows, as opposed to most of the available results. As a second result, we provide deeper insights into the multiplicity of Laplacian eigenvalues of tree graphs, which is still an open problem within the mathematics community. Finally, but not least, the third contribution is to achieve design ability in the construction of networks by connecting ’atom’ subgraphs and node selection to guarantee that the structural properties of network controllability and observability are ensured to hold.

Laplacian spectrum and eigenvector structure of tree graphs have been recently explored by the author also in [29,30]. We believe that the results achieved in this paper can be directly applied to several multi-agent systems and robotic network applications, as those provided for example in Section 2, and, moreover, they concur to have a thorough additional insight into the spectral properties of a Laplacian matrix of tree graphs.

1.2. Notation

In the following,

N

R

R_{\geq 0}

R_{+}

denote the natural, real, non-negative real numbers, and positive real numbers, respectively. Vectors are denoted in bold letters.

0_{d}

and

1_{d}

d \in N

, denote resp. the vector of dimension d with components respectively all equal to 0 or to 1, and

0_{d_{1} \times d 2_{2}}

d_{1}, d_{2} \in N

, the matrix with

d_{1}

rows and

d_{2}

columns with zero entries. For

i \in N

e_{i}

is the i-th element of the canonical basis, e.g.

e_{1} = {[\begin{matrix} 1 & 0 & . . . & 0 \end{matrix}]}^{⊤}

. For a matrix

A \in R^{d_{1} \times d_{2}}

, we denote

{[A]}_{i j}

the

(i, j)

-th element , while

{[A]}_{i}

denotes its i-th column. For a vector

v \in R^{d}

we denote

{(v)}_{i}

the ith component of

v

so that

v = {[{(v)}_{1} . . . {(v)}_{d}]}^{⊤}

Let

M \in R^{n \times n}

, we denote its characteristic polynomial as the polynomial computed though

p_{A} (s) : = det (s I_{n} - A)

. We denote the spectrum of

A \in R^{n \times n}

, namely the set of its eigenvalues, by

Λ (A)

, For an eigenvalue

λ

, the algebraic multiplicity

m_{a} (λ)

λ

is its multiplicity as zero of

p_{A} (s)

, while the geometric multiplicity

m_{g} (λ)

is defined as

m_{g} (λ) = dim [ker (A - λ I_{n})]

. The linear subspace of

R^{n}

given by

ker (A - λ I_{n})

is called eigenspace associated to

λ

and it is denoted by

V_{λ} = ker (A - λ I_{n})

In general, it holds that

1 \leq m_{g} (λ) \leq m_{a} (λ)

; if

m_{a} (λ) = 1

then

λ

is called simple eigenvalue of A, while if

m_{g} (λ) = m_{a} (λ)

for a

λ \in C

such that

m_{a} (λ) > 1

, then

λ

is called semi-simple [31].

1.2.1. Preliminaries from Graph Theory

A graph

G

is a pair

G = (V, E)

with

V = {1, 2, . . ., n}

and

E \subset V \times V

; it is called undirected when

(j, i) \in E

if and only if

(i, j) \in E

. The neighbors set of a node

i \in V

N_{i} = {j \in V | (i, j) \in E}

. The degree of a node

i \in V

d (i)

is the number of incident edges, so that

d (i) = \sum_{j \in N_{i}} 1

. A node

i \in V

is called a pendant node or a leaf node if it holds

d (i) = 1

A sequence of edges

{(j_{ℓ},_{ℓ + 1})}_{|_{ℓ \in [1, k]}} \in E

is a path of length k connecting vertex

j_{1}

with

j_{k + 1}

j_{1} \neq j_{k + 1}

, otherwise it is called a cycle. A graph is connected if for every pair of distinct vertices

i, j \in V

there is a path connecting i and j. An undirected graph

T

with no cycles is called a tree if it is connected, otherwise it is called forest. A path graph

P_{n}

is a graph with

V = {1, \dots, n}

nodes and

E = {(i, i + 1), i = 1, \dots, n - 1}

. A star graph

S

is a graph having one node connected to all the others, and all the others are pendant nodes. A starlike tree graph, denoted by

S (a_{1}, . ., a_{s})

, is a tree graph having

| V | = \sum_{i = 1}^{s} a_{i} + 1

nodes with only one node, say node 1, having

d (1) > 2

, and:

S (a_{1}, . ., a_{s}) - {1} = P_{a_{1}} \cup P_{a_{2}} \cup \dots \cup P_{a_{s}} .

(1)

Parameters

a_{1}

, ..,

a_{n}

determine the starlike tree graph up to isomorphism. We say that the starlike tree

S (a_{1}, . ., a_{s})

has s branches, the lengths of which are

a_{1}

, ..,

a_{n}

Let

G = (V, E)

be an undirected graph; the associated adjacency matrix

A_{G} \in R^{n \times n}

is defined as

{[A]}_{i j} = 1

(i, j) \in E

and

{[A]}_{i j} = 0

(i, j) \notin E

, and the corresponding Laplacian matrix is

{[L_{G}]}_{i j} = - {[A_{G}]}_{i j}

i \neq j

and

{[L_{G}]}_{i i} = \sum_{j = 1, i \neq j}^{n} {[A_{G}]}_{i j}

. If the graph

G

is clear from the context, then the subindex

G

is omitted.

Set one node, say node ℓ, as a grounded node; removing the ℓ-th row and column of L produces the so called grounded Laplacian matrix (also known as a Dirichlet Laplacian matrix) denoted by

L^{(ℓ)}

;. In the following we choose

ℓ = 1

if not otherwise specified.

By costruction the Laplacian is a symmetric positive semidefinite matrix and it has zero row sum, so that it holds

L_{G} 1 = 0

for any

G

, and hence the polynomial

p_{w} (s) = det [s I - L_{w}]

can be written as

p_{w} (s) = s (s - λ_{2}) (s - λ_{3}) \dots (s - λ_{n})

where

λ_{i} \in R_{\geq 0}

we choose the numbering such that

λ_{i} \geq λ_{i - 1}

and, if

G

is connected,

λ_{i} \neq 0

for any

i = 2, . ., n

2. Problem Setting and Preliminary Results

In this Section, we introduce and then properly state the problem afforded in this paper.

Several distributed algorithms for multi-agent systems and robotic networks are designed according to the abstract mathematical framework described in the following, which we refer to as nearest-neighbor distributed averaging multi-agent system. Consider a set of N agents, each holding a continuous time scalar variable

x_{i} (t)

for each node

i \in V

with update rule as:

{\dot{x}}_{i} (t) = v_{i} (t) .

Two neighbor agents are able to communicate between themselves and exchange their values (namely, node i receives

x_{j} (t)

from node j and vice versa), and each node i sets its own input accoding to the agreed protocol

v_{i} (t) = \sum_{j \in N_{i}} (x_{j} (t) - x_{i} (t)) .

(2)

Under this protocol, the evolution of the overall dynamics can be effectively described through an overall vector

x \in R^{N}

built as

{(x)}_{i} (t) = x_{i} (t)

whose time update is compactly expressed by:

\dot{x} (t) = - L_{G} x (t),

(3)

G

denoting the topology of communication among agents.

Assume now that a subset of nodes

V_{i} = {i_{1}, \dots, i_{ℓ}}

, inject an additional input

u_{i} (t)

to the agreed protocol(2) with the intent of controlling the team evolution [13]. In this setting, the resulting system dynamics takes the form:

\begin{matrix} \dot{x} (t) & = - L_{G} x (t) + e_{i_{1}} u_{i_{1}} (t) + e_{i_{2}} u_{i_{2}} (t) + \dots + e_{i_{ℓ}} u_{i_{ℓ}} (t) = \\ = - L_{G} x (t) + B u (t) \end{matrix}

(4)

with

u (t) = {[\begin{matrix} u_{i_{1}} (t) & \dots & u_{i_{ℓ}} (t) \end{matrix}]}^{⊤}

and

B = [\begin{matrix} e_{i_{1}} & w i d t h & \dots & w i d t h & e_{i_{ℓ}} \end{matrix}]

. In the following, we refer to

i_{1}, \dots, i_{ℓ}

as the control nodes, or equivalently leader nodes.

Analogously, consider the case when it is desired to monitor the system evolution of (3), and the value of a subset of nodes

V_{o} = {i_{o_{1}}, \dots, i_{o_{ℓ}}}

is collected with the goal of reconstructing the whole system evolution. In such scenario, nodes

i_{o_{1}}, \dots, i_{o_{ℓ}}

are called observation nodes or measured nodes, and their values

y_{i} (t) = x_{i} (t) = e_{i}^{⊤} x (t)

are exploited for supervision and surveillance of the whole system. In this case, the overall system dynamics is expressed by:

\begin{matrix} \dot{x} (t) & = - L_{G} x (t) \\ y (t) & = C x (t) . \end{matrix}

(5)

with

C = {[\begin{matrix} e_{o_{1}} & w i d t h & \dots & w i d t h & e_{o_{ℓ}} \end{matrix}]}^{⊤}

The above framework is widely adopted in several modern engineering applications in the area of distributed control systems and robotic networks [32,33,34].

Considering the above setting (4), one main analysis is focused on the states that can be achieved through a suitable choice of

u (t)

, which are called controllable or reachable states and they constitute a subspace of of the state space

R^{N}

called reachable subspace and it is denoted by

X_{R}

. The reachable subspace can be obtained computing the image of the reachability matrix:

R = [\begin{matrix} B & w i d t h & L_{G} B & w i d t h & \dots & w i d t h & L_{G}^{N - 1} B \end{matrix}],

(6)

and if

R

has full rank, system (4) is called completely controllable. As regards the state estimation framework based on the knowledge of some measured nodes described by Equation (5), the system-theoretic analysis based on the intial state values that produce an identically zero measured vector, which are called unobservable states. The set of unobservable states is a subspace of

R^{N}

that can be computed as the kernel of the observability matrix:

O = [\begin{matrix} C \\ C L_{G} \\ \dots \\ C L_{G}^{N - 1} \end{matrix}] .

(7)

Remark 1.

Some multi-agent processes are better described by discrete updates of a local quantity, namely

x (t + 1) = (I - γ L_{G}) x (t)

, where

γ \in R_{+}

is calledcoupling factorand it should be chosen sufficiently small to keep the system stable [34], and analogously in this case one gets the following system evolution:

\begin{matrix} x (t + 1) & = (I - γ L_{G}) x (t) + e_{i_{1}} u_{i_{1}} (t) + e_{i_{2}} u_{i_{2}} (t) + \dots + e_{i_{ℓ}} u_{i_{ℓ}} (t) = \\ = (I - γ L_{G}) x (t) + B u (t), \end{matrix}

(8)

with

u (t)

and B defined as in (4) in the case of control problems, oranalogously in the case of observability. However, it is possible to prove, and it is left to the reader, that the reachability analysis for (4) and (8) are equivalent, and the same holds for observability. For this reason, for the sake of coinciseness, we will refer without loss of generality to (4) and (5).

2.1. Problem Statement

Inspired by the applications discussed in the previous paragraph, we are now ready to state the Problem that we afford in the following of this paper. However, considering the discussion in the previous Section 1.1 regarding paper contributions, we provide two problem statements that are equivalent between themselves, considering the a twofold facet (mathematical/engineering) of the same investigation. Here we give the genuine statement as it is stated in [13]. After a brief discussion on the spectral methods for the analysis of reachability and observability, we rephrase the problem in a mathematical fashion, which is related to the eigenstructure investigation afforded in [23,24,25,26,27,28,29,30,31,32,33,34,35].

Problem Statement 1. Given a Laplacian-based multi-agent dynamical system as in Equation (3) with

G

being a starlike tree graph

S (a_{1}, \dots, a_{n})

, find a set of control nodes

V_{i}

such that (4) is completely controllable, or equivalently a set of measured nodes

V_{o}

such that (5) is completely observable.

2.2. Spectral Methods for Controllability and Observability Analysis

Considering the significance of the above properties in the analysis of dynamical systems, several results and technical tools have been developed to get an accurate and thorough investigation of a dynamical system. Among the others, the Popov-Belevich-Hautus polynomial approach has been one of the most adopted methods for its effectiveness [7]. Its use in the context of Laplacian-based multi agent system provides fundamental tools for such analysis.

Proposition 1.

System (4) is completely controllable if and only if:

rank [L_{G} - λ I w i d t h B] = n \forall λ \in C,

(9)

and system (5) is completely observable if and only if:

rank [\begin{matrix} L_{G} - λ I \\ C \end{matrix}] = n \forall λ \in C .

(10)

We now specialize this criterion considering some peculiarities of (4)-(5). Considering that the Laplacian matrix is symmetric, all its eigenvalues are real and semi-simple, so that

m_{a} (λ) = m_{g} (λ)

for any

λ \in C

[31].

Condition (9) is violated if there exist a nonzero vector

v \in R^{N}

such that:

v^{⊤} [L_{G} - λ I w i d t h B] = 0,

and this is equivalent to say:

\{\begin{matrix} L_{G}^{⊤} v & = λ v, \\ e_{i}^{⊤} v & = 0 \forall i \in V_{i}, \end{matrix}

(11)

and, in turn, this means that there should exist an eigenvector having zero value along all the components corresponding to the control nodes. Whenever this condition holds, we call

λ

v

an unreachable eigenvalue and eigenvector. System complete reachability require that such eigenvectors do not exist.

Remark 2

(Minimal set of control nodes for complete controllability). From the above discussion, the number of control/measured nodes must be larger or at least equal to the maximum multiplicity of eigenvectors

m_{g} (λ)

. Moreover for the second condition of (11), it is fundamental to understand the zero-nonzero pattern of each eigenvector.

It is possible to derive an analogous condition for observability, requiring that:

\begin{matrix} L_{G} v & = λ v, \\ e_{i}^{⊤} v & = 0 \forall i \in V_{o} \end{matrix}

(12)

namely, there should exist an eigenvector having zero components along the observation nodes. Also in this case, when this condition holds,

λ

v

are called unobservable eigenvalue and eigenvector, and system complete observability require that such eigenvectors do not exist.

Clearly, in the case of observability, analogous considerations as in Remark 2 hold. However, considering again the symmetry of matrix

L_{G}

, a system is reachable through a set of control nodes if and only if it is observable from the same set of measured nodes, and for this reason we deduce that the controllability problem and the observability problem are indeed equivalent for systems evolving with Laplacian dynamics, as (4) and (5).

In view of the above investigation, the previous Problem Statement can be equivalently rephrased in terms of zero pattern of each eigenvactor, thus translating the problem in a more mathematical fashion. More precisely, we are interested in solving the following problem.

Problem Statement-2. Given a starlike tree graph

S (a_{1}, \dots, a_{n})

, give a complete characterization of the zero-nonzero pattern of each eigenvector of the Laplacian matrix of

S (a_{1}, \dots, a_{n})

, together with the multiplicity

m_{g} (λ)

for each

λ \in Λ_{S (a_{1}, \dots, a_{n})}

3. Laplacian Controllability and Observability Of Starlike Graphs

In this Section, we derive a set of results which constitute the complete theoretical characterizaton of node selection for controllability and observability for the class of starlike tree graphs.

It is worth mentioning that Laplacian eigentructure of starlike graphs have been widely studied also by mathematicians in the recent years for their peculiar features. As for example, on one hand Path Graphs have always simple Laplacian eigenvalues, on the other starlike graphs Laplacian eigenvalue multiplicity may range from 1 to

n - 2

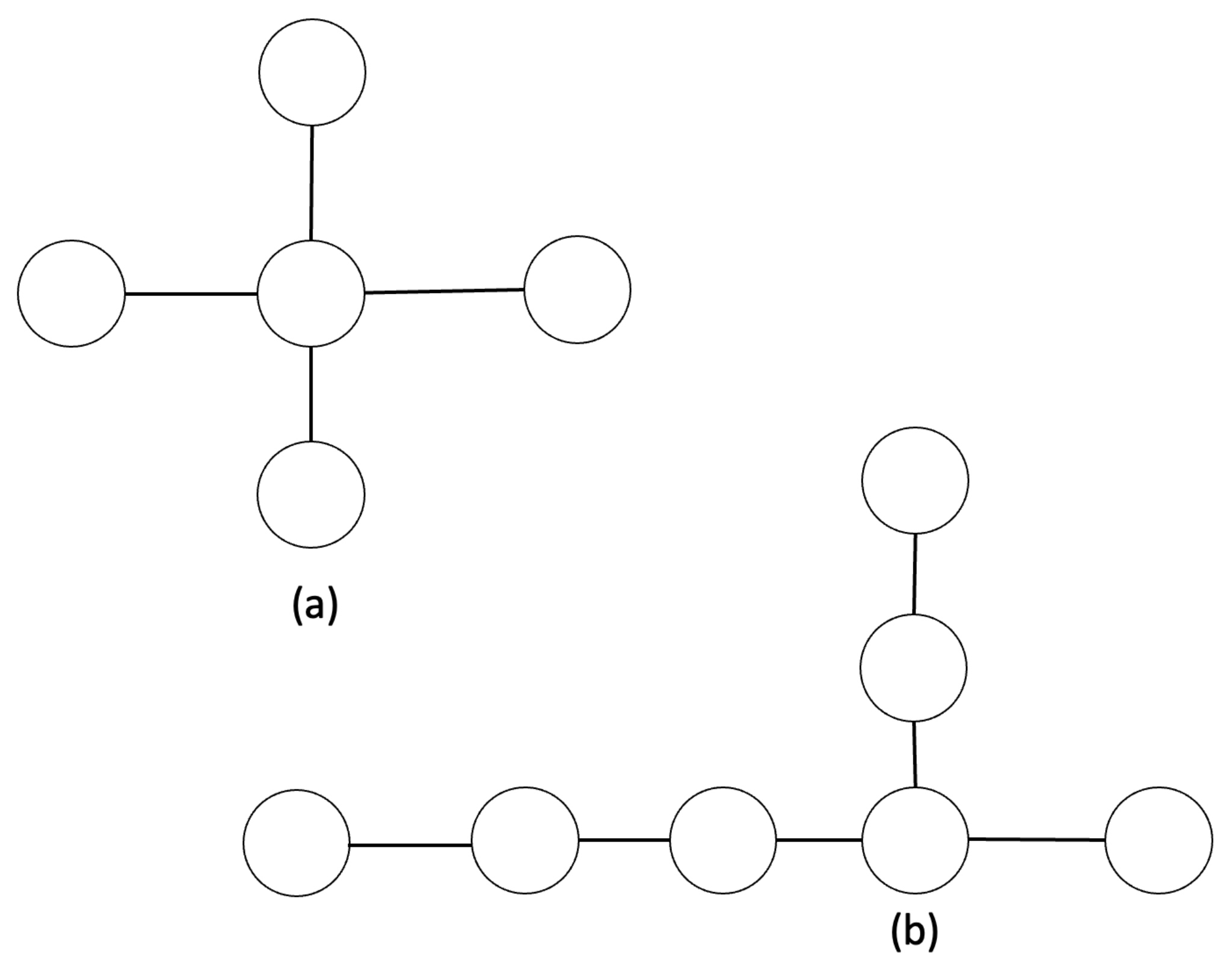
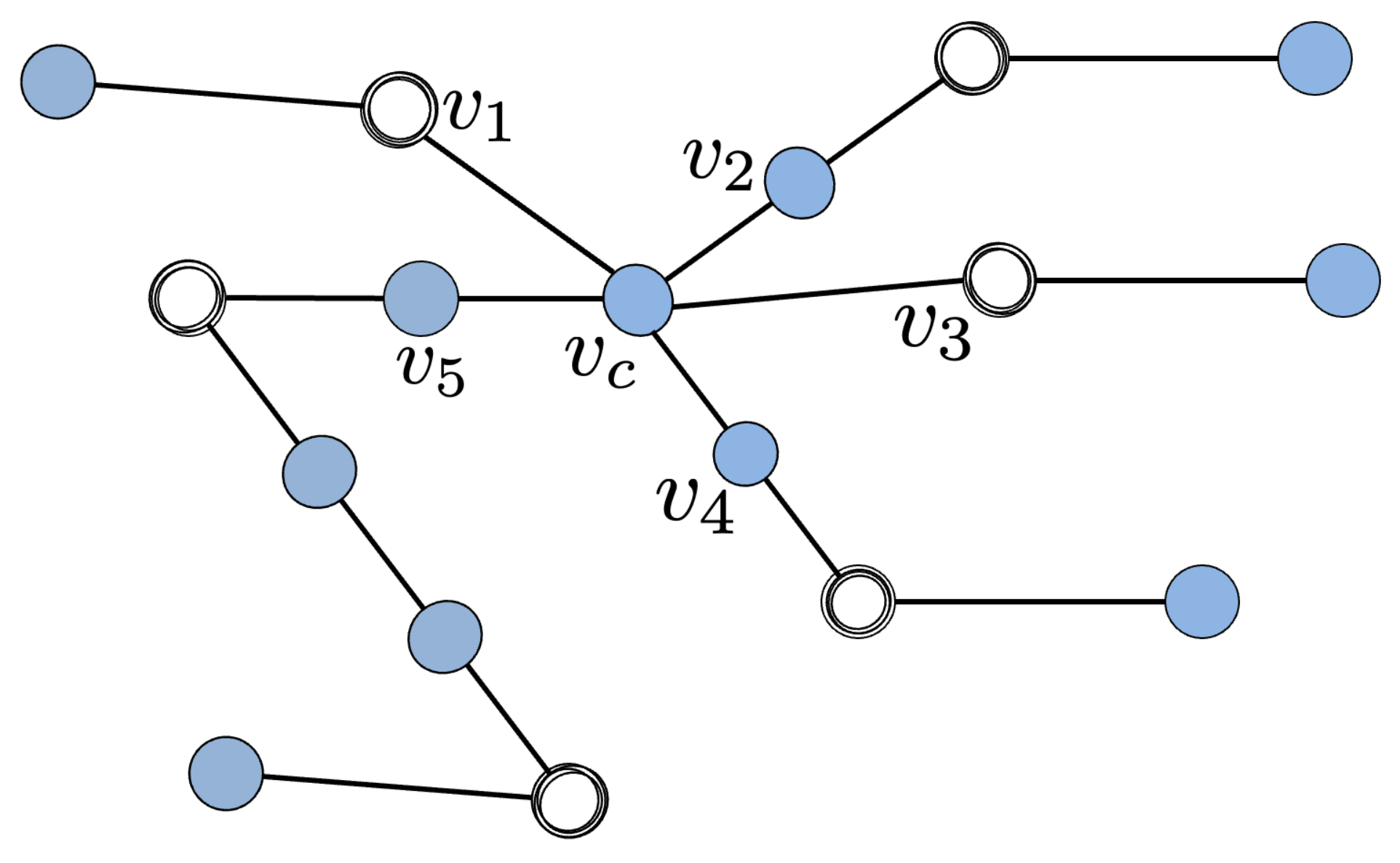
. As for example, consider the two starlike graphs in Figure 1. Graph (a) has

Λ_{a} = {0, 1, 1, 1, 5}

, so that

m_{g} (1) = 3

, and at least 3 nodes must be selected to achieve reachability. Graph (b) has

Λ_{b} = {0, 0.26, 0.62, 1.4, 2.27, 3.1, 4.3}

, and hence all eigenvalues are simple. Considering the problem of interest, the minimum number of nodes necessary to achieve complete controllability and observability in case of Graph (a) is 3 in the first case (and hence, more than half of the nodes constituting the whole network), while in the case of (b), it is possible to have complete reachability and observability by properly selecting only 1 node. We show later that the differences between the two graphs are even more evident, indeed in case (a) such nodes must be chosen joudiciously, while in case (b) rechability and observability is achieved by choosing any node of the network.

3.1. Starlike Trees With Simple Eigenvalues - Preliminary Results

We start the analysis focusing on starlike graphs having simple eigenvalues only. It is worth mentioning that, for trees, integer Laplacian eigenvalues larger than 1 are necessarily simple [36]. In contrast to this, Laplacian eigenvalue

λ = 1

is often present in tree Laplacian spectrum, and its occurrence and multiplicity has been longly studied by mathematicians [37].

In the following of the paper, we adopt the labeling described next. The central node, namely the only node having degree larger than 2, is usually denoted by subindex c and it put as first entry of vector

x (t)

. Then,

{(x)}_{i} (t)

i = 2, . ., a_{1} + 1

are the values of nodes starting from the neighbor of the central node, to the pendant node of branch 1. The other branches are labeled sequentially and they follow the same ordering logic.

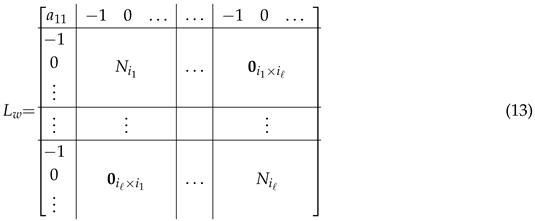
Considering this labeling, the general form of a starlike graph is: Preprints 152153 i001

where

a_{11} = s

, namely the number of branches starting from the central node. Matrices

N_{i}

are some fundamental matrices for the forthcoming analysis, and they are defined and characterized as follows.

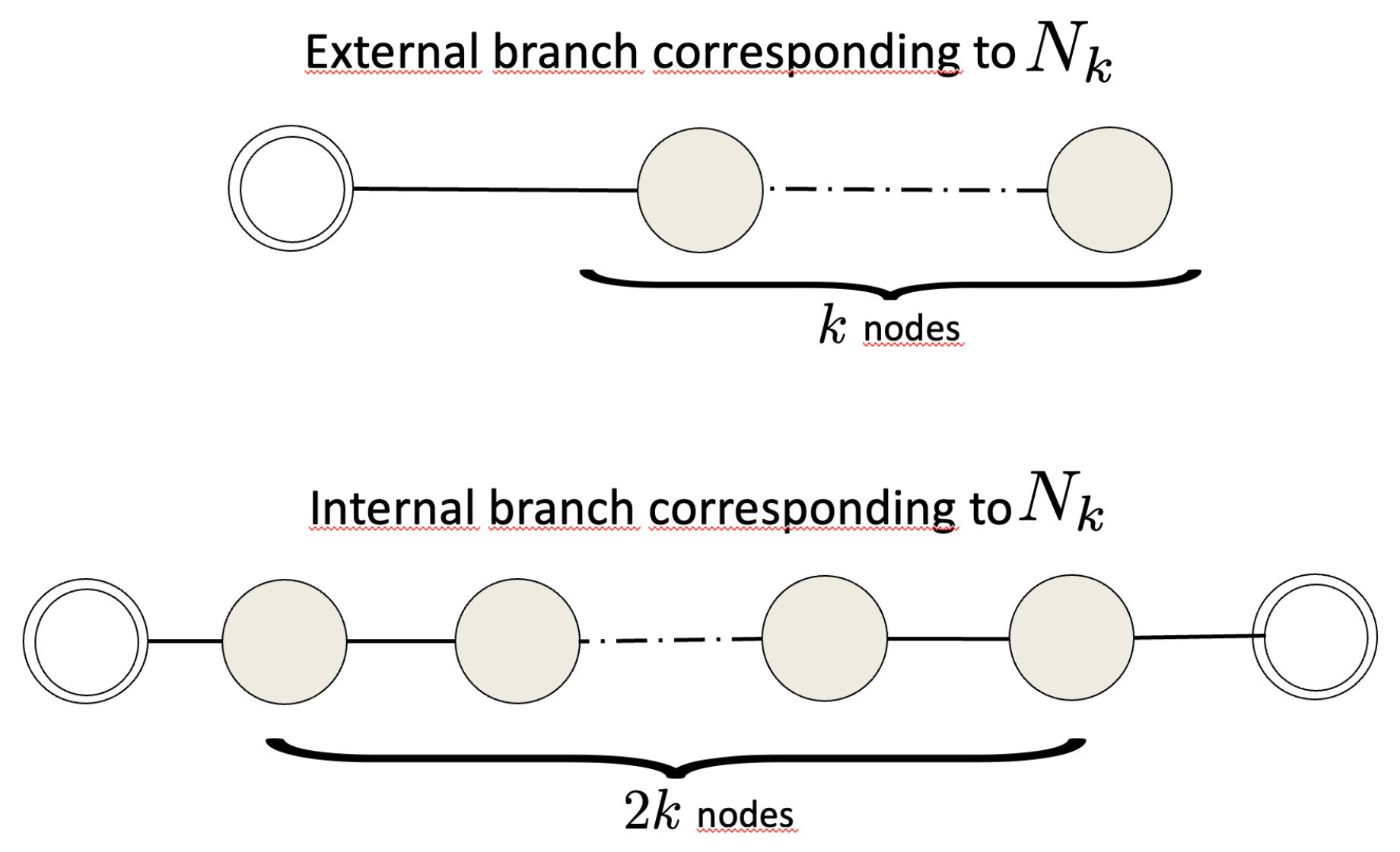
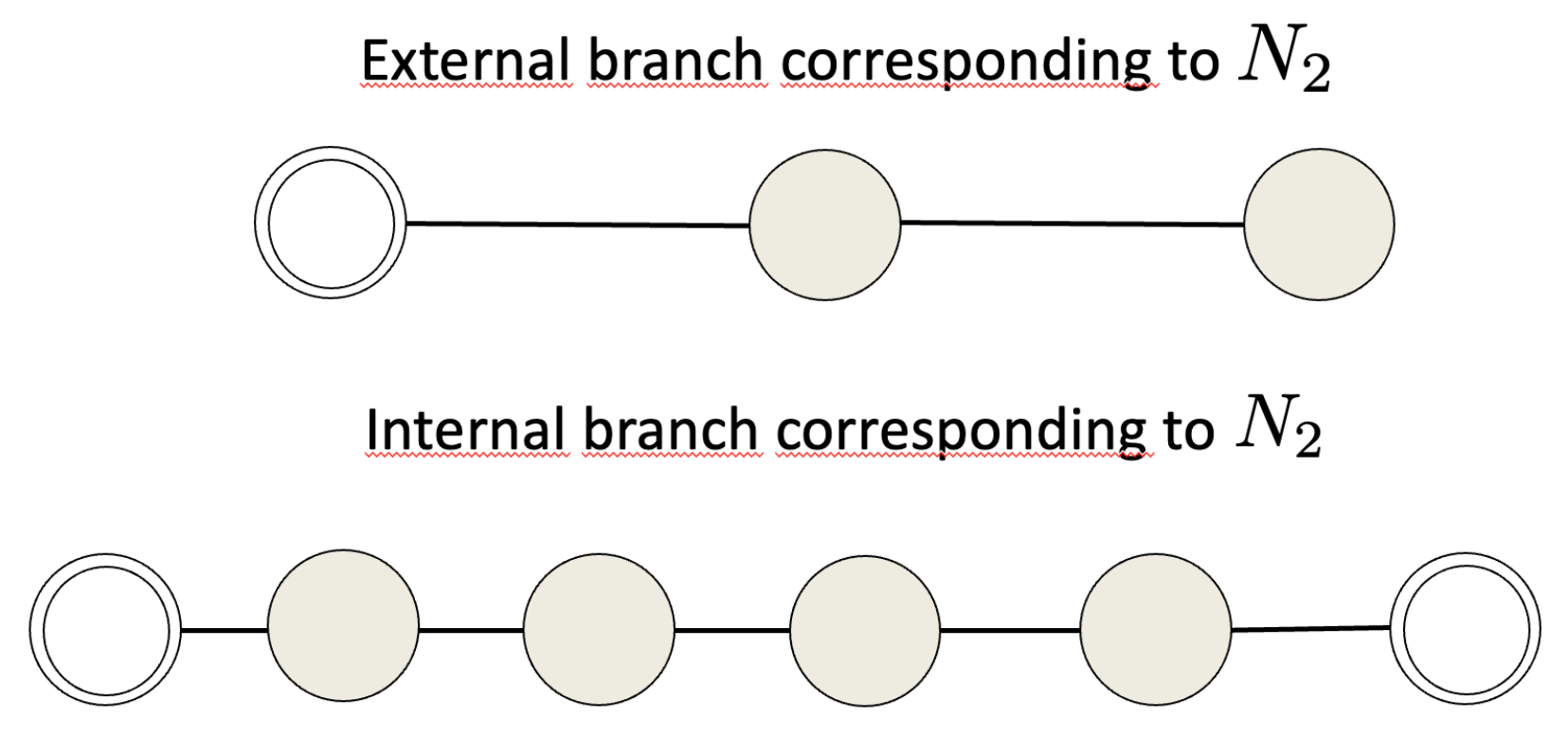
We refer to an external branch of p nodes as the path with one grounded external node, with grounded Laplacian matrix:

N_{p} = [\begin{matrix} 2 & - 1 & 0 \\ - 1 & 2 \\ 0 & ⋱ & - 1 \\ 0 & - 1 & 1 \end{matrix}],

(14)

and to an internal branch of q nodes as:

M_{q} = [\begin{matrix} 2 & - 1 & 0 \\ - 1 & 2 \\ 0 & ⋱ & - 1 \\ 0 & - 1 & 2 \end{matrix}],

(15)

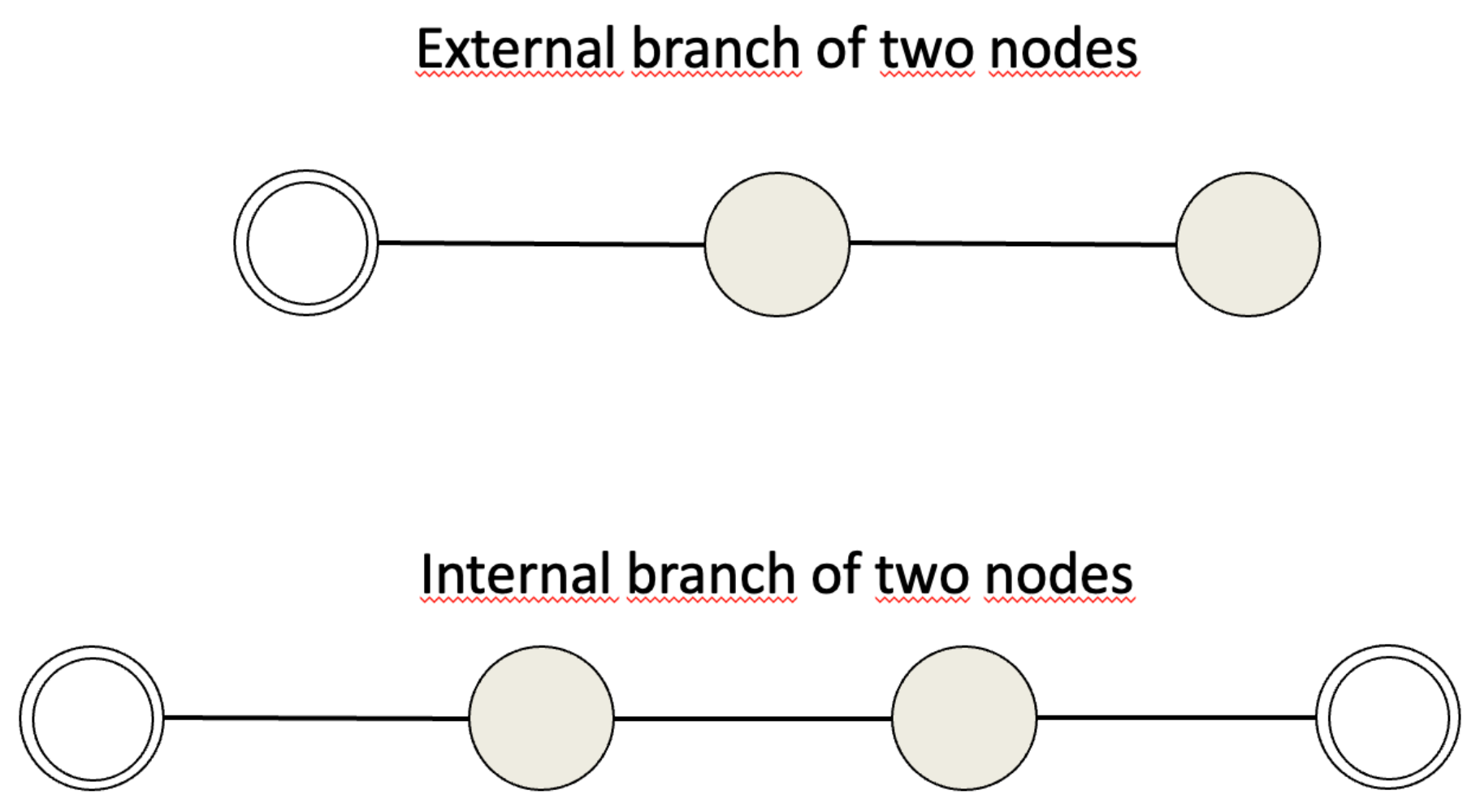
Figure 2 shows an example of an external branch of two nodes (upper side of the figure) and one internal branch of two nodes. The associated grounded Laplacians are:

N_{2} = [\begin{matrix} 2 & - 1 \\ - 1 & 1 \end{matrix}],

(16)

and

M_{2} = [\begin{matrix} 2 & - 1 \\ - 1 & 2 \end{matrix}] .

(17)

The grounded nodes are graphically denoted with a double circle.

In the following, we characterize the Laplacian spectrum of Path graphs, of the two class of matrices

N_{i}

M_{j}

, and their relations. Laplacian spectrum and eigenstructure of Path graphs has been widely considered and studied. Here we briefly give the formulas that characterize it for the sake of completeness. Let

P_{n} = (V, E)

be a Path graph, namely assume that

V = {1, \dots, n}

and

E = {(a, a + 1) : 1 \leq a < n}

. The complete set of eigenvalues of the Laplacian of

P_{n}

can be written as:

λ_{P_{n}}^{j} = 2 (1 - cos (π j / n)), j = 0, . ., n - 1

(18)

and associated eigenvectors:

{(v_{P_{n}}^{j})}_{κ} = cos (\frac{2 π κ j}{n}) κ, j = 0, . ., n - 1 .

(19)

Considering the two class of matrices

N_{p}

and

M_{q}

, their eigenvalues and eigenvectors are respectively [19]:

\{\begin{matrix} λ_{N_{p}} & = 2 - 2 cos [(2 k - 1) \frac{π}{2 p + 1}], j = 1, \dots, p, \\ {(v_{k})}_{j} & = sin [\frac{(p + j) (2 k - 1) π}{2 p + 1}], k = 1, \dots, p, \end{matrix}

(20)

and:

\{\begin{matrix} λ_{M_{q}} & = 2 - 2 cos (k \frac{π}{q + 1}), j = 1, \dots, q, \\ {(w_{k})}_{j} & = sin (\frac{j k π}{q + 1}), k = 1, \dots, q . \end{matrix}

(21)

For the sake of clarity of the following of the paper, we remark that there are some relations among the eigenvalues and eigenvectors of

L_{n}

N_{p}

and

M_{q}

Proposition 2.

For any

p \in N

q \in N

, the following relations hold:

(P1): $Λ_{M_{q}} = Λ_{L_{P_{q + 1}}} - {0}$ ;
(P2): $Λ_{N_{p}} \subset Λ_{L_{P_{2 p + 1}}}$ and, more precisely, considering the numbering of Equation (18), $λ_{N_{p}}^{j} = λ_{P_{2 p + 1}}^{2 j + 1}$ , $j = 1, . ., p$ , namely, eigenvalues of $N_{p}$ can be computed by selecting the odd values of index j of $L_{P_{2 p + 1}}$ from (18).

Proof.

As regards

P 1

, through standard determinant computation using the Laplace formula, it is possible to get:

det (s I - L_{P_{n}}) = s \cdot det (s I - M_{n - 1}),

so that

λ_{L_{n}} = λ_{M_{n - 1}}

plus the zero eigenvalue. As for

P 2

, by comparing (20) with (18), it is possible to prove by direct computation that all the eigenvalues of

N_{p}

are contained in the spectrum of

L_{2 p + 1}

, and it is possible to get them by selecting from (18) the values corresponding to the odd values, from 1 to

2 p - 1

, of (18). □

Considering again the Example depicted in Fig.1, it is easy to compute from (20)

λ_{N_{2}} = \frac{3 \pm \sqrt{5}}{2}

and from (21)

λ_{M_{2}} = 3

and

λ_{M_{2}} = 1

. Moreover, it is left to the reader to verify that

\frac{3 \pm \sqrt{5}}{2}

are also the eigenvalues of

L_{5}

using Equation (18) for

j = 1

and

j = 3

and, finally, that the eigenvalues of

M_{2}

are indeed coicident with those of

L_{3}

(but the zero eigenvalue).

A first simple yet important result follows. It is focused on an eigenvector condition that ensures controllability/observability from any node, namely having a nonzero value in each entry. It turns out a special condition on eigenvalues, namely that only eigenvalues associated to subpaths of the branches can be unreachable.

3.2. Starlike Eigenvalues Associated with Nowhere Zero Eigenvactors

One interesting and surprising result follows. It basically states that loss of reachability and observability may occur only for those eigenvalues characterizing the grounded Laplacians of the constitutive branch paths. It implies that integer eigenvalues different from 1 have nowhere zero eigenvectors and hence they can be controlled by any node.

Proposition 3.

Let

Λ_{S} = {λ \in C | det (λ I - L_{s})}

be the spectrum of a star graph

S (i_{1}, . ., i_{s})

, and define

Λ_{P_{S}} = ⋃_{i = 1}^{s} Λ_{L_{P_{2 i + 1}}}

, where, for each branch,

i = 1, . ., a_{i}

. Any eigenvalue belonging to the set

Λ_{S} - Λ_{P_{S}}

(where − stands for set difference) is always reachable and observable from any node.

Proof.

Suppose to compute an eigenvector with one zero component. Consider the eigenvalue equation built on a laplacian matrix as (13) and an eigenvector having zero in any position, namely:

[\begin{array}{c} a_{11} - λ & \begin{matrix} - 1 & 0 & \dots \end{matrix} & \dots & \begin{matrix} - 1 & 0 & \dots \end{matrix} \\ \begin{matrix} - 1 \\ 0 \\ ⋮ \end{matrix} & N_{i_{1}} - λ I_{i_{1}} & \dots & 0_{i_{1} \times i_{ℓ}} \\ ⋮ & ⋮ & ⋮ \\ \begin{matrix} - 1 \\ 0 \\ ⋮ \end{matrix} & 0_{i_{ℓ} \times i_{1}} & \dots & N_{i_{ℓ}} - λ I_{i_{ℓ}} \end{array}] [\begin{matrix} v_{1} \\ 0 \\ v_{2} \end{matrix}] = 0

(22)

where

v_{2} \in R^{a_{ℓ}}

with

a_{ℓ} \leq i_{ℓ}

, and both

v_{1}

and

v_{2}

nonzero. Exploiting (22) one has:

\begin{matrix} L_{{\bar{S}}_{1}} v_{1} = λ v_{1}, \\ {(v_{1})}_{1} = {(v_{2})}_{1}, \\ L_{N_{a_{ℓ}}} v_{2} = λ v_{2} . \end{matrix}

(23)

where

{\bar{S}}_{1}

is the starlike graph obtained by removing the subpath of length

a_{ℓ}

from the s-th branch. Last equation

L_{N_{a_{ℓ}}} v_{2} = λ v_{2}

implies that, in such a case of eigenvector with one zero component, then

λ

must be necessarily also an eigenvalue of

N_{a_{ℓ}}

, and by property

P 2

of Proposition 2,

λ

must be also eigenvalue of

L_{P_{2 a_{ℓ} + 1}}

. Since the ordering of the branches is generic, this proof applies to any branch, and the statement follows. □

Coming back to the example depicted in Figure 1, the interested reader can verify that

Λ_{b}

can never be expressed as an eigenvalue of the constitutive paths, and the whole set of eigenvector is nowhere zero, so that the starlike graph of Figure 1-(b) is reachable and observable from any node of the graph.

4. Zero-Nonzero Pattern of Eigenvectors Associated to $λ = 1$

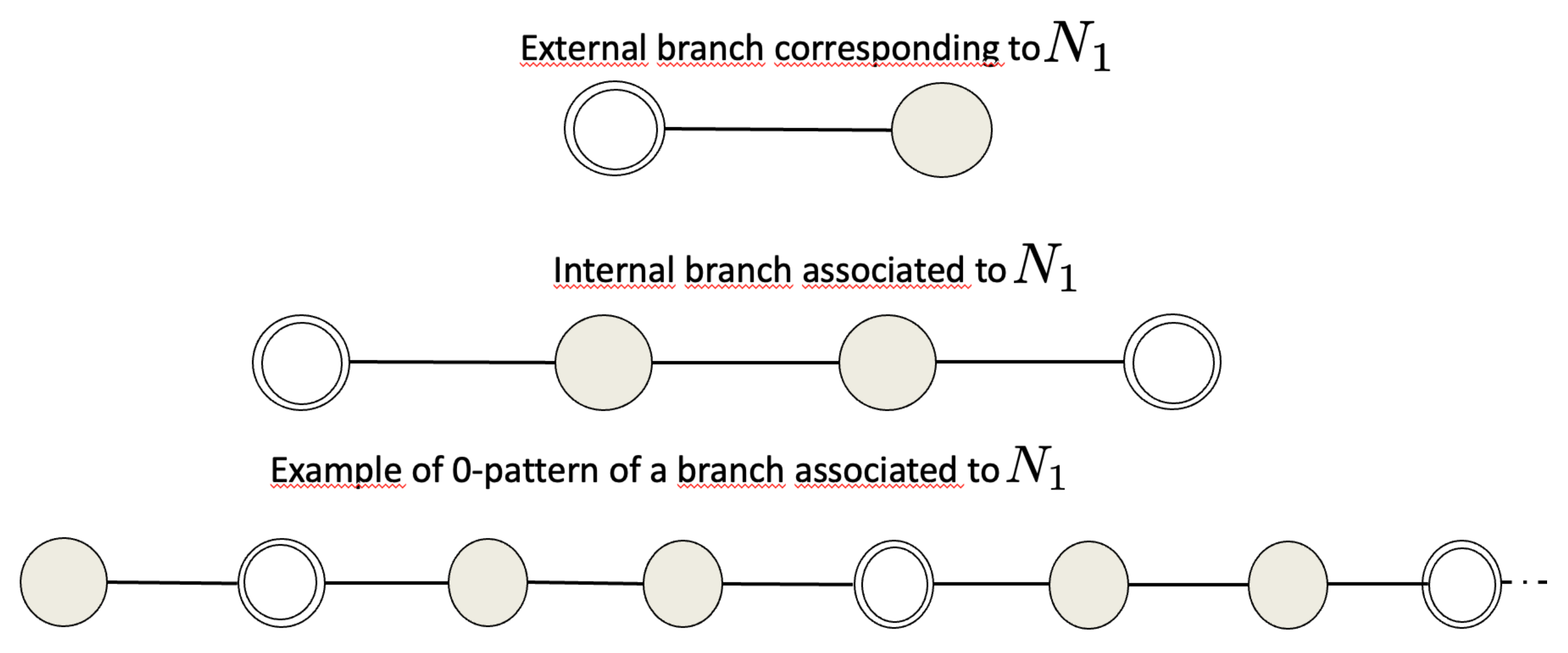
Starting from the previous result, we start the investigation by considering subpaths of incresing dimension. In this Section, we thoroughly discuss the case

λ = 1

. The corresponding matrix

N_{1}

is the scalar value

N_{1} = 1

, so that its only eigenvalue is

λ = 1

It is worth noting that the eigenstructure of

λ = 1

for tree graphs is widely considered in the literature from the seminal work of [36] to our days [38], and it is still a debated topic. In the following, we fully characterize the eigenstructure of

λ = 1

for starlike trees.

Consider the eigenvalue equation applied to each node, namely:

(d_{i} - λ) {(v)}_{i} = \sum_{j \in N_{i}} {(v)}_{j}

(24)

where

d_{i}

is the degree of node i, and

{(v)}_{i}

the i-th component of an eigenvector associated to

λ

(also called valuation of an eigenvector

v

affording

λ

[36]).

Applying Equation (24) with

λ = 1

to the first branch, starting from one pendant node and moving to the center according to the usual labeling, one has:

\begin{matrix} (1 - 1) {(v)}_{a_{1} + 1} & = {(v)}_{a_{1}}, \\ (2 - 1) {(v)}_{a_{1}} & = {(v)}_{a_{1} + 1} + {(v)}_{a_{1} - 1}, \\ (2 - 1) {(v)}_{a_{1} - 1} & = {(v)}_{a_{1}} + {(v)}_{a_{1} - 2}, \\ ⋮ \\ (2 - 1) {(v)}_{2} & = {(v)}_{3} + {(v)}_{1}, \end{matrix}

(25)

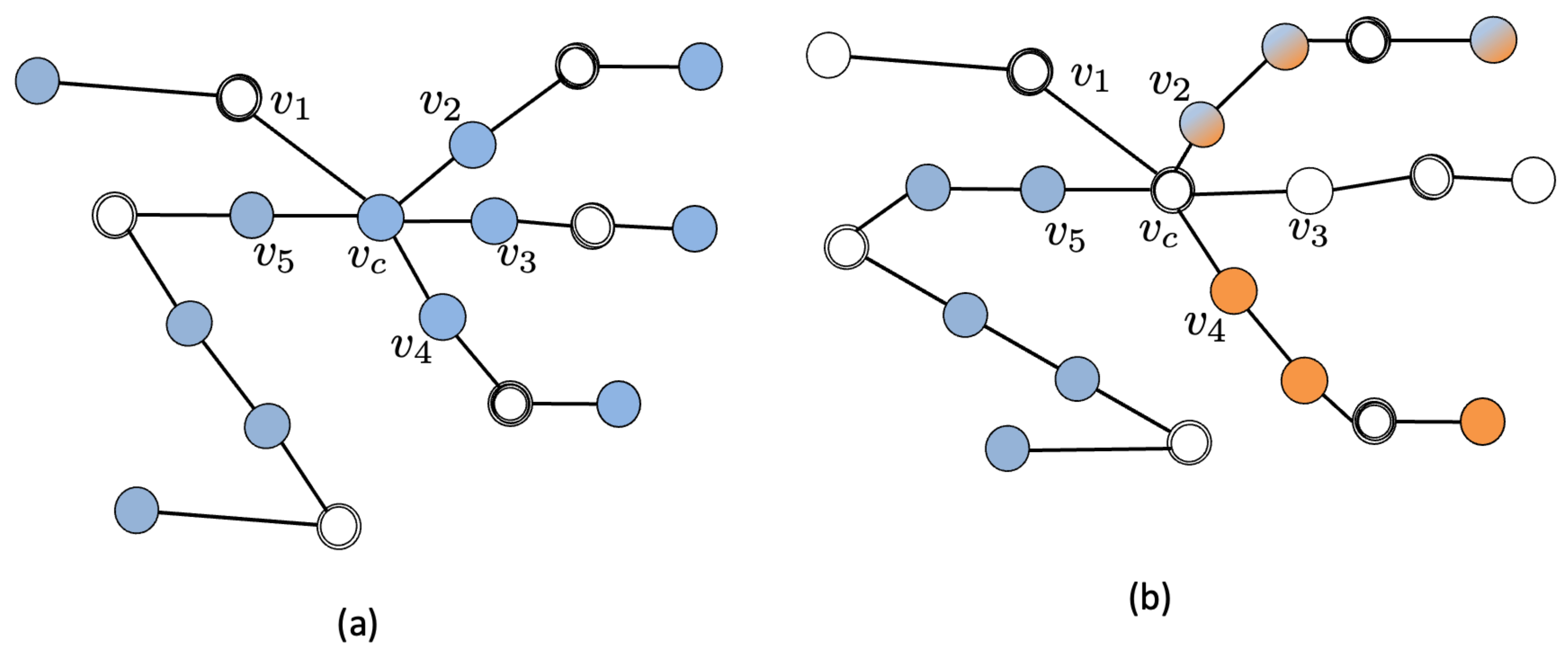
and this amounts to saying that the eigenvector associated to

λ = 1

must satisfy the evaluation

{(v)}_{p} = α, {(v)}_{p + 1} = 0, {(v)}_{p + 2} = - α, {(v)}_{p + 3} = α, {(v)}_{p + 4} = 0, . . .

, with

α

a nonzero value, thus showing the zero value in positions

p + 1 + 3 k

, as depicted in Figure 3.

This approach can be applied to any branch of a star graph, thus reducing any star to a ’core’ of few nodes. Figure 4 shows an example of reduction to a core.

We now focus on a generic core, and we apply Equation (24) to the central node evaluation, with the objective of studying when it is satisfied, and this in turn implies that the considered Laplacian admits

λ = 1

as eigenvalue, or eventually not. In the first case, the evaluation at any node gives a consistent result and

λ = 1

is ideed an eigenvalue with the zero pattern obtained as described above, otherwise

λ = 1

is not in the spectrum of the considered graph.

Consider the central node and its neighbors, with reference to the notation of Figure 4.

We consider the two different cases, namely

{(v)}_{c} = a \neq 0

and

{(v)}_{c} = 0

Writing the eigenvalue equation Equation (24) applied to the central node and its neighbors, one has:

\begin{matrix} (s - 1) {(v)}_{c} & = {(v)}_{1} + {(v)}_{2} + \dots + {(v)}_{s}, \\ {(v)}_{1} & = {(v)}_{c} + {(v)}_{1 p r e}, \\ {(v)}_{2} & = {(v)}_{c} + {(v)}_{2 p r e}, \\ ⋮ \\ {(v)}_{s} & = {(v)}_{c} + {(v)}_{s p r e}, \end{matrix}

(26)

where

{(v)}_{1 p r e}

{(v)}_{2 p r e}

,... are the values afforded by the neighbors of

{(v)}_{1}

{(v)}_{2}

,... at the opposite position with respect to

{(v)}_{c}

applying the reduction technique described above.

4.1. Necessary and Sufficient Conditions to the Existence of $λ = 1$

From the above equation, one can draw several rules, as follows:

R1: If any of the relations (24) shows ${(v)}_{i} = {(v)}_{i p r e}$ , then at least one another should show analogously ${(v)}_{j} = {(v)}_{j p r e}$ , othewise $λ = 1$ is not an eigenvalue of $S$ . This is the case when ${(v)}_{c} = 0$ .
R2: If all ${(v)}_{i} \neq {(v)}_{i p r e}$ , then first equation of (24) has solution if and only if only one ${(v)}_{i} = 0$ and all the other ${(v)}_{j} = a \neq 0$ , for any $j \neq i$ . In this case, the solution is ${(v)}_{c} = a$ .

4.2. Multiplicity of $λ = 1$ and Zero/Nonzero Eigenvector Structure

We now construct the structure of an eigenvector, separately in case (R1) and (R2). On one hand, this provides the solution of Problem 2 (relative to

λ = 1

), on the other hand, it gives the fundamental information for the solution of Problem 1.

We first consider case (R1). We still adopt the labeling described at the beginning of Section 3.1 and coherent with the Laplacian matrix in Equation (13), the central node being in first position, and the labeling goes from the center to the pendant node.

Assume that the first

2 \leq r \leq s

branches satisfy

(R 1)

, so that

λ = 1

is a Laplacian eigenvalue, thus their reduction to the core satisfies

{(v)}_{j} = {(v)}_{j p r e}

, while the remaining

s - r

show

{(v)}_{i} \neq {(v)}_{i_{p r e}}

A generic eigenvector satisfying the above relations together with (24) has the structure:

x^{⊤} = {[0 \underset{f i r s t b r a n c h}{\underset{︸}{α_{1} α_{1} 0 - α_{1} \dots}} \underset{r - t h b r a n c h}{\underset{︸}{α_{r} α_{r} 0 - α_{r} \dots}} \underset{l a s t (s - r) b r a n c h e s}{\underset{︸}{0 0 0 \dots}}]}^{⊤}

(27)

where

α_{i} \in R - {0}

, with the only condition that

\sum_{i = 1}^{r} α_{i} = 0

. Moreover, the above parametrization shows that

m_{g} (1) = r - 1

; indeed a basis for the eigenspace

V_{1}

λ = 1

is:

\begin{matrix} x_{1}^{⊤} & = {[0 \underset{f i r s t b r a n c h}{\underset{︸}{1 1 0 - 1 - 1 \dots}} \underset{s e c o n d b r a n c h}{\underset{︸}{- 1 - 1 0 1 1 \dots}} \underset{l a s t (s - 2) b r a n c h e s}{\underset{︸}{0 0 0 \dots}}]}^{⊤}, \\ x_{2}^{⊤} & = {[0 \underset{f i r s t b r a n c h}{\underset{︸}{1 1 0 - 1 - 1 \dots}} \underset{s e c o n d b r a n c h}{\underset{︸}{0 0 0 \dots}} \underset{t h i r d b r a n c h}{\underset{︸}{- 1 - 1 0 1 1 \dots}} \underset{l a s t (s - 3) b r a n c h e s}{\underset{︸}{0 0 0 \dots}}]}^{⊤}, \\ ⋮ & ⋮ ⋮ ⋮ \\ x_{r - 1}^{⊤} & = {[0 \underset{f i r s t b r a n c h}{\underset{︸}{1 1 0 - 1 - 1 \dots}} \underset{i n t e r m e d i a t e b r a n c h e s}{\underset{︸}{0 0 0 \dots}} \underset{r - t h b r a n c h}{\underset{︸}{- 1 - 1 0 1 1 \dots}} \underset{l a s t (s - r) b r a n c h e s}{\underset{︸}{0 0 0 \dots}}]}^{⊤} . \end{matrix}

(28)

Considering condition

(R 2)

, we order the node labeling such that the first branch is the only one having zero value in the first position, and then all the others:

x^{⊤} = {[α \underset{f i r s t b r a n c h}{\underset{︸}{0 - α - α 0 \dots}} \underset{o t h e r b r a n c h e s}{\underset{︸}{α 0 - α \dots}} \underset{︸}{α 0 - α \dots}]}^{⊤} .

(29)

The structure of eigenvectors compatible with condition

(R 2)

as in Equation (27) shows that the case of

λ = 1

asociated to

(R 2)

hase always

m_{g} (1) = 1

. Indeed, in this case the eigenspace

V_{1}

is spanned by only one eigenvector:

x^{⊤} = {[1 \underset{first branch}{\underset{︸}{0 - 1 - 1 0 \dots}} \underset{other branches}{\underset{︸}{1 0 - 1 \dots}} \underset{third branch}{\underset{︸}{1 0 - 1 \dots}}]}^{⊤} .

(30)

As for example, we come back to the graph depicted in Fig. (Figure 4). It is possible to see that node evaluation matches the condition

{(v)}_{i} \neq {(v)}_{i p r e}

, so we fall in

(R 2)

. However in this case two nodes have

{(v)}_{i} = 0

(namely,

{(v)}_{1} = 0

and

{(v)}_{3} = 0

), so that

(R 2)

is not satisfied, and this means that

λ = 1

is not an eigenvalue of

S (2, 3, 2, 3, 6)

. Indeed, in this case, Equation (24) does not hold.

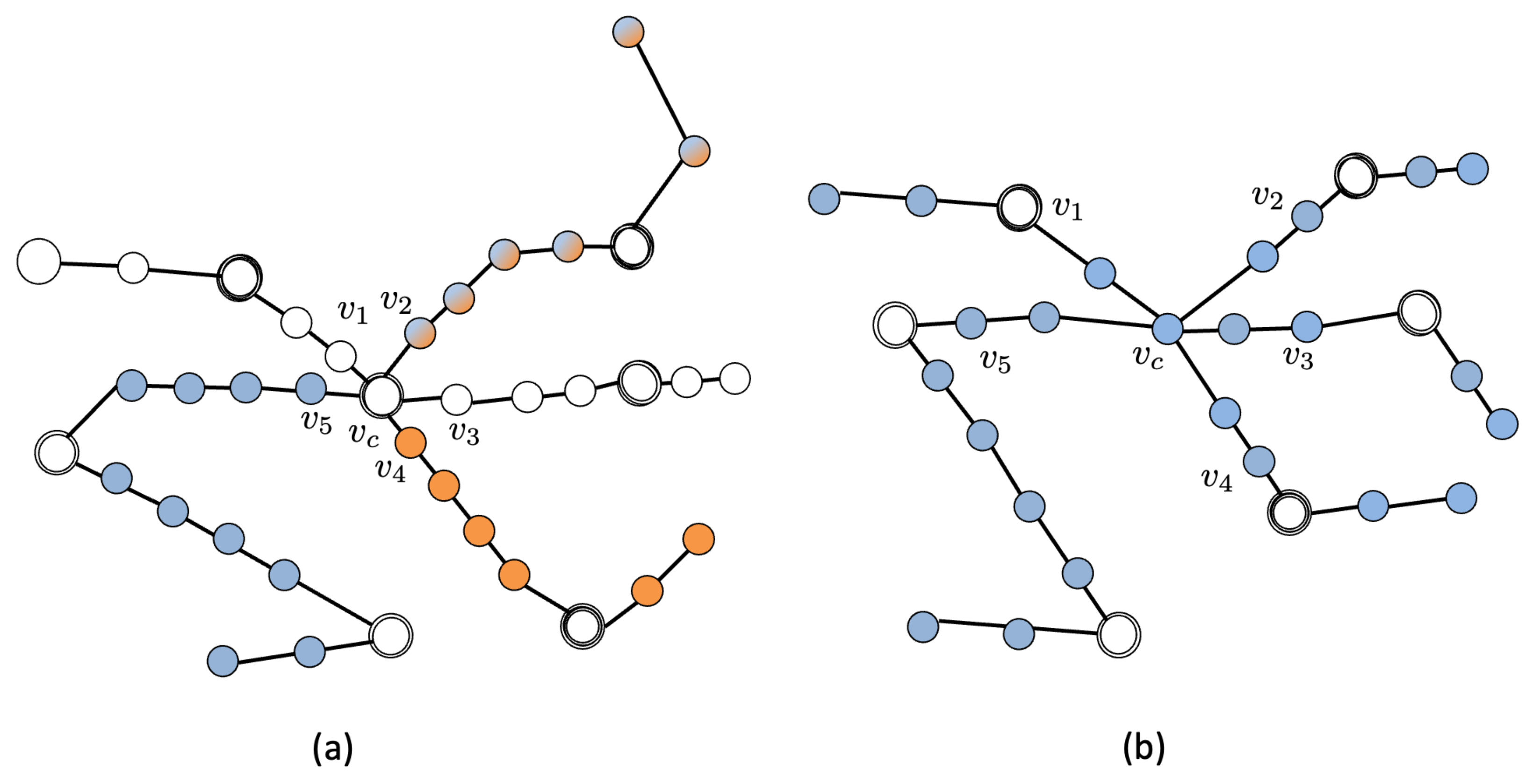
Figure 5 shows some graphs with few differences from Figure 4, namely

S (2, 3, 3, 3, 6)

and

S (2, 4, 3, 4, 7)

, but they both have

λ = 1

in their spectrum, and different multiplicity. Consider Figure 5-(a), in this case condition

(R 2)

is fully met. As for Figure 5-(b), it matches condition

(R 1)

with

r = 3

, so that

m_{g} (1) = 2

. The two branches with white nodes satisfy the eigenvalue equation for zero node values only.

4.3. Node Selection for Reachability and Observability of $λ = 1$

Considering all the above analysis and results, and specifically the eigenspace dimension and zero/nonzero structure, it is now easy to deduce the node selection rule to achieve reachability and observability in the case of

λ = 1

One main peculiarity of the node selection preocedure that here follows is that it does not require any theoretical knowledge in dynamical systems or spectral graph theory.

Moreover, a strong practical advantage of the following procedure is that it is purely graphical so that it does never incur numerical errors, as opposite computation based on matrices (6) and (7), which have the structure of Vandermonde matrices, so that numerical errors arise starting from relatively small dimensions (less than 10), and also Equation (9) and (10) that require rank evaluation and they are adequate for graphs up to 20-30 nodes.

For the above reason, the following procedure is preferable in the case of complex graphs, with hundreds or more nodes. In the following procedure, we denote the eigenvector of

λ = 1

by the symbol

v_{1}

(in general,

v_{λ}

denotes the eigenvector associated to

λ

In the next Section, stemming from the experience on

λ = 1

, we easily develop an algortihm for a general

λ

and we derive an overall Algorithm having Algorithm 1 as one of its blocks.

5. Zero-Nonzero Pattern of Eigenvectors Associated to Any $λ$ of $N_{k}$

Interestingly, the above conditions on

λ = 1

can be extended in the general case of any

λ \in Λ_{N_{k}}

We start this generalization by an example regarding

N_{2}

, then we describe the general procedure that extends conditions (R1)-(R2) to the general case of

λ

N_{k}

Consider the two graphs depicted in Figure 6. They represent the generalization to

N_{2}

of the two graphs discussed in Figure 5, and they are related respectively to the condition (R1) and (R2) for

λ \in Λ_{N_{2}}

, namely

λ_{N_{2}} = \frac{3 \pm \sqrt{5}}{2}

They have been obtained by replacing the branches characterizing

N_{1}

(see Figure 3) with those of

N_{2}

(Figure 7), and by adding one neighbor node to each branch around the central node

v_{c}

By inspection of the Laplacian eigenstructure, namely by direct computation of the Laplacian eigenvectors, it is easy to verify that their zero/nonzero structure corresponds respectively to the generalization of Equation (28) in the case of Figure 6-(a), and Equation (30) considering the case of Figure 6-(b).

Starting from the above consideration, we are now ready to generalize rules (R1)-(R2), as follows.

Let

λ \in Λ_{N_{k}}

k \leq a_{i}

R1: The reduction related to $N_{k}$ of at least two branches provides ${(v)}_{c} = 0$ . If r denotes the number of branches whose reduction satisfies ${(v)}_{c} = 0$ , ( $2 \leq r \leq s$ ), then $λ$ has multiplicity $m_{g} (λ) = r - 1$ .
R2: After reducing the graph, if the core is made of branches all of length k but only one of length $k - 1$ . In this case, $v_{c} \neq 0$ and $m_{g} (λ) = 1$ .

It is possible to verify by direct inspection, and it is here omitted for the sake of length space, that the eigenvectors relative any eigenvalue

λ \in Λ_{N_{k}}

k \leq a_{i}

have the structure of Equation (28) in case of

(R 1)

, and of Equation (30) in case of

(R 2)

However, eigenvectors as in Equation (28) can be written if and only if

k \leq min {a_{1}, a_{2}, . ., a_{s}}

, so that its search is limited to the length of the smallest branch, while vectors as in Equation (30) can be written until there are two possible branches, so that its search must be done up to the largest-but-one branch. In this latter case, ordering the branches such that

a_{i} \leq a_{i + 1}

for

i = 1, . ., s

, when

a_{i} \leq k \leq a_{i + 1}

then the eigenvectors components relative to the branches

a_{1}

,...,

a_{s}

are necessarily zero.

This allows us to state a generalization of Algorithm 1 to any k. In the following, we state the algorithm for

k \leq a_{1}

a_{1}

being the shortest branch, then we provide the algorithm adapted for the remaining branches for

a_{1} \leq k \leq a_{s - 1}

When

a_{1} \leq k \leq a_{s - 1}

, only one case is possible, and the Algorithm is simplified, as follows.

Figure 8. External and internal branches associated to

N_{k}

Figure 8. External and internal branches associated to

N_{k}

The above algorithms must exploited together, sequentially, indeed the set of control/observation nodes to achieve controllability and observability is the union of the set of control/observation nodes of each eigenvalue, so that, for

κ = 1, \dots, a_{s - 1}

V_{c} = ⋃_{k = 1}^{a_{s - 1}} V^{N_{k}} .

(31)

6. An Illustrative Example

As a final Section, we practice with the overall algorithm through an illustrative example, which puts in evidence also the effectiveness of the proposed approach when dealing with large graphs and hence in the framework of complex networks.

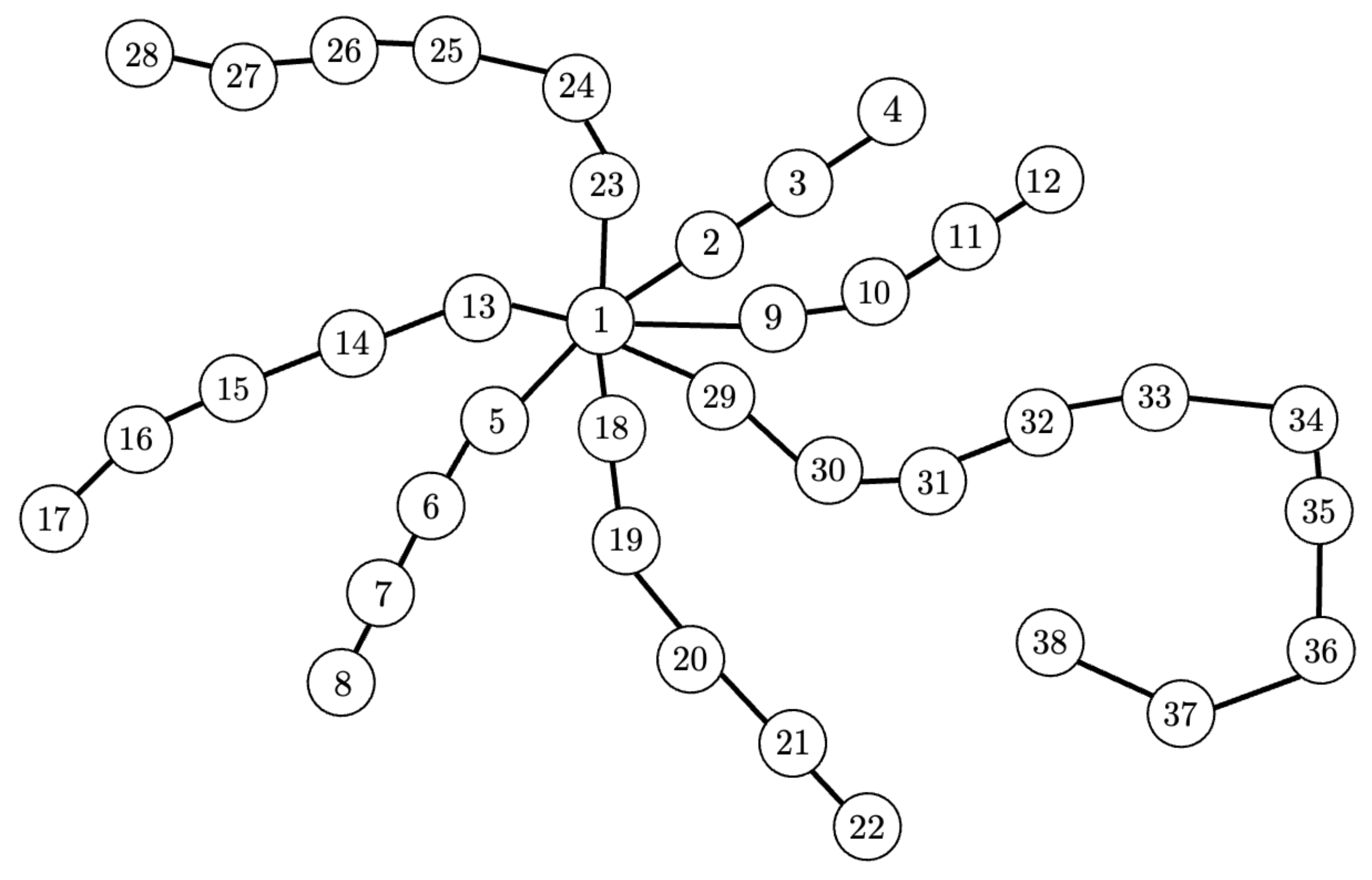
Consider the starlike tree graph depicted in Figure 9, which is made of 6 branches and 37 nodes, and it corresponds to

S (3, 4, 4, 5, 5, 6, 10)

. Nodes are labeled according to the convention adoptedalong the paper, namely the center is labeled as node 1, then the branches are numbered from the center to the leaves, and they are ordered starting from the shortest to the longest one.

In the following, we report the multiplicity of the eigenvalues of

N_{i}

i = 1, . ., 6

, together with the set of control/observation nodes that are selected according to Algorithms 2 and 3.

\begin{matrix} λ \in Λ_{N_{3}}, m_{g} (λ) = 1, & V_{c}^{N_{3}} = {2, 3, 4, 29, 30, 31, 32, 33, 34, 36, 37, 38}, \\ λ \in Λ_{N_{4}}, m_{g} (λ) = 1, & V_{c}^{N_{4}} = {5, 6, 7, 8, 9, 10, 11, 12}, \\ λ \in Λ_{N_{5}}, m_{g} (λ) = 1, & V_{c}^{N_{5}} = {13, 14, 15, 16, 17, 18, 19, 20, 21, 22}, \end{matrix}

while all the other

λ \in Λ_{N_{i}}

for

i \in {1, 2, 6}

are not eigenvalues of

L_{S (3, 4, 4, 5, 5, 6, 10)}

Considering that the above sets

V_{c}^{N_{i}}

are disjoint, a set of control/observation nodes to achieve controllability must contain one node for each of the above set, and an example of a minimal set is

V^{c} = {2, 5, 13}

7. Conclusions

In this paper, the Laplacian controllability and observability of a consensus network with a starlike tree topology is considered, and thoroughly analyzed. Some novel results are drawn based on node positions within the network only. The resulting methods are graphical, thus effective and exempt from numerical errors, and a final algorithm is provided to perform the analysis by machine computation, showing numerical robustness and the important feature of dealing with large scale networks and complex systems.

The results achieved so far and described thoroughly in this paper are promising, and the proposed apporach can be extended to other, more general, topology classes.

Funding

This research received no external funding.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Conflicts of Interest

The author declares no conflicts of interest.

References

Herrera, M.; Pérez-Hernández, M.; Kumar Parlikad, A.; Izquierdo, J. Multi-agent systems and complex networks: Review and applications in systems engineering. Processes 2020, 8, 312. [Google Scholar] [CrossRef]
Van Mieghem, P. Graph spectra for complex networks; Cambridge University Press, 2023.
Yan, G.; Tsekenis, G.; Barzel, B.; Slotine, J.J.; Liu, Y.Y.; Barabási, A.L. Spectrum of controlling and observing complex networks. Nature Physics 2015, 11, 779–786. [Google Scholar] [CrossRef]
Leitold, D.; Vathy-Fogarassy, Á.; Abonyi, J. Controllability and observability in complex networks–the effect of connection types. Sci. Rep. 2017, 7, 151. [Google Scholar] [CrossRef]
Liu, Y.Y.; Slotine, J.J.; Barabási, A.L. Controllability of complex networks. Nature 2011, 473, 167–173. [Google Scholar] [CrossRef]
Liu, Y.Y.; Slotine, J.J.; Barabási, A.L. Observability of complex systems. Proceedings of the National Academy of Sciences 2013, 110, 2460–2465. [Google Scholar] [CrossRef]
Antsaklis, P.J.; Michel, A. Linear Systems; Birkhauser, 1997.
Doostmohammadian, M.; Rabiee, H.R. On the observability and controllability of large-scale IoT networks: Reducing number of unmatched nodes via link addition. IEEE Control. Syst. Lett. 2020, 5, 1747–1752. [Google Scholar] [CrossRef]
Stigter, J.; Joubert, D.; Molenaar, J. Observability of complex systems: Finding the gap. Sci. Rep. 2017, 7, 16566. [Google Scholar] [CrossRef]
Knorn, S.; Chen, Z.; Middleton, R.H. Overview: Collective control of multiagent systems. IEEE Trans. Control. Netw. Syst. 2015, 3, 334–347. [Google Scholar] [CrossRef]
Chen, F.; Ren, W.; et al. On the control of multi-agent systems: A survey. Foundations and Trends® in Systems and Control 2019, 6, 339–499. [Google Scholar] [CrossRef]
Montanari, A.N.; Aguirre, L.A. Observability of network systems: A critical review of recent results. J. Control. Autom. Electr. Syst. 2020, 31, 1348–1374. [Google Scholar] [CrossRef]
Rahmani, A.; Ji, M.; Mesbahi, M.; Egerstedt, M. Controllability of multi-agent systems from a graph-theoretic perspective. SIAM J. Control. Optim. 2009, 48, 162–186. [Google Scholar] [CrossRef]
Martini, S.; Egerstedt, M.; Bicchi, A. Controllability analysis of multi-agent systems using relaxed equitable partitions. Int. J. Syst. Control. Commun. 2010, 2, 100–121. [Google Scholar] [CrossRef]
Aguilar, C.O.; Gharesifard, B. Almost equitable partitions and new necessary conditions for network controllability. Automatica 2017, 80, 25–31. [Google Scholar] [CrossRef]
Mousavi, S.S.; Haeri, M.; Mesbahi, M. On the structural and strong structural controllability of undirected networks. IEEE Trans. Autom. Control. 2017, 63, 2234–2241. [Google Scholar] [CrossRef]
Pasqualetti, F.; Zampieri, S.; Bullo, F. Controllability metrics, limitations and algorithms for complex networks. IEEE Trans. Control. Netw. Syst. 2014, 1, 40–52. [Google Scholar] [CrossRef]
Pasqualetti, F.; Zhao, S.; Favaretto, C.; Zampieri, S. Fragility limits performance in complex networks. Sci. Rep. 2020, 10, 1774. [Google Scholar] [CrossRef]
Parlangeli, G.; Notarstefano, G. On the reachability and observability of path and cycle graphs. IEEE Trans. Autom. Control. 2011, 57, 743–748. [Google Scholar] [CrossRef]
Liu, X.; Ji, Z. Controllability of multiagent systems based on path and cycle graphs. Int. J. Robust Nonlinear Control. 2018, 28, 296–309. [Google Scholar] [CrossRef]
Dai, L. Minimum leader selection for controllability of undirected graphs with leader–follower framework. Iet Control. Theory Appl. 2023, 17, 505–515. [Google Scholar] [CrossRef]
Chao, Y.; Ji, Z. Necessary and sufficient conditions for multi-agent controllability of path and star topologies by exploring the information of second-order neighbours. IMA J. Math. Control. Inf. 2021, 38, 1–14. [Google Scholar] [CrossRef]
Lepović, M.; Gutman, I. No starlike trees are cospectral. Discret. Math. 2002, 242, 291–296. [Google Scholar] [CrossRef]
Nakatsukasa, Y.; Saito, N.; Woei, E. Mysteries around the graph Laplacian eigenvalue 4. Linear Algebra Its Appl. 2013, 438, 3231–3246. [Google Scholar] [CrossRef]
Weisstein, E.W. Spider Graph; MathWorld–A Wolfram Web Resource, 2025.
Akbari, S.; van Dam, E.; Fakharan, M. Trees with a large Laplacian eigenvalue multiplicity. Linear Algebra Its Appl. 2020, 586, 262–273. [Google Scholar] [CrossRef]
Pei-Duo, Y.; Tan, C.W. Unraveling the Viral Spread of Misinformation: Maximum-Likelihood Estimation and Starlike Tree Approximation in Markovian Spreading Models. IEEE Trans. Signal Process. 2025. [Google Scholar]
Yu, P.D.; Zheng, L.; Tan, C.W. Contagion source detection by maximum likelihood estimation and starlike graph approximation. In Proceedings of the 2024 58th Annual Conference on Information Sciences and Systems (CISS). IEEE; 2024; pp. 1–6. [Google Scholar]
Parlangeli, G. Laplacian Eigenvalue Allocation Through Asymmetric Weights in Acyclic Leader-Follower Networks. IEEE Access 2023, 11, 126409–126419. [Google Scholar] [CrossRef]
Parlangeli, G. A Distributed Algorithm for Reaching Average Consensus in Unbalanced Tree Networks. Electronics 2024, 13, 4114. [Google Scholar] [CrossRef]
Horn, R.; Johnson, C. Matrix analysis; Cambridge University Press, 2012.
Mesbahi, M.; Egerstedt, M. Graph theoretic methods in multiagent networks; Princeton University Press, 2010.
Bullo, F.; Cortés, J.; Martínez, S. Distributed Control of Robotic Networks; Princeton University Press, 2009. Applied Mathematics Series.
Bullo, F. Lectures on Network Systems, 1.6 ed.; Kindle Direct Publishing, 2022.
Saito, N.; Woei, E. Tree simplification and the ‘plateaux’phenomenon of graph Laplacian eigenvalues. Linear Algebra Its Appl. 2015, 481, 263–279. [Google Scholar] [CrossRef]
Grone, R.; Merris, R.; Sunder, V.S. The Laplacian spectrum of a graph. SIAM J. Matrix Anal. Appl. 1990, 11, 218–238. [Google Scholar] [CrossRef]
Barik, S.; Lal, A.; Pati, S. On trees with Laplacian eigenvalue one. Linear Multilinear Algebra 2008, 56, 597–610. [Google Scholar] [CrossRef]
Wang, Z.; Chen, Q.Q.; Guo, J.M.; Li, X.M. A relation between multiplicity of 1 as a Laplacian eigenvalue and induced matching numbers in trees. Discret. Math. 2025, 348, 114401. [Google Scholar] [CrossRef]

Figure 1. Two examples showing large differences in eigenvalue multiplicities of starlike graphs.

Figure 2. Example of external branch (above) and internal branch (below).

Figure 3. Zero pattern associated to

N_{1}

Figure 3. Zero pattern associated to

N_{1}

Figure 4. Example of a graph reduction to a core related to

N_{1}

, related to

λ = 1

Figure 4. Example of a graph reduction to a core related to

N_{1}

, related to

λ = 1

Figure 5. Example of case R1 (a) and R2 (b).

Figure 6. Example of extension of cases R1 (a) and R2 (b) for eigenvalues of

N_{2}

, with

λ_{N_{2}} = \frac{3 \pm \sqrt{5}}{2}

Figure 6. Example of extension of cases R1 (a) and R2 (b) for eigenvalues of

N_{2}

, with

λ_{N_{2}} = \frac{3 \pm \sqrt{5}}{2}

Figure 7. External and internal branches associated to

N_{2}

Figure 7. External and internal branches associated to

N_{2}

Figure 9. Graph studied in the illustrative example.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

Views

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Laplacian Controllability and Observability of Multi-Agent Systems: Recent advances in Tree Graphs

Abstract

Keywords:

Subject:

1. Introduction

1.1. Literature Review And Paper Contribution

1.2. Notation

1.2.1. Preliminaries from Graph Theory

2. Problem Setting and Preliminary Results

2.1. Problem Statement

2.2. Spectral Methods for Controllability and Observability Analysis

3. Laplacian Controllability and Observability Of Starlike Graphs

3.1. Starlike Trees With Simple Eigenvalues - Preliminary Results

3.2. Starlike Eigenvalues Associated with Nowhere Zero Eigenvactors

4. Zero-Nonzero Pattern of Eigenvectors Associated to λ = 1

4.1. Necessary and Sufficient Conditions to the Existence of λ = 1

4.2. Multiplicity of λ = 1 and Zero/Nonzero Eigenvector Structure

4.3. Node Selection for Reachability and Observability of λ = 1

5. Zero-Nonzero Pattern of Eigenvectors Associated to Any λ of N k

6. An Illustrative Example

7. Conclusions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

4. Zero-Nonzero Pattern of Eigenvectors Associated to $λ = 1$

4.1. Necessary and Sufficient Conditions to the Existence of $λ = 1$

4.2. Multiplicity of $λ = 1$ and Zero/Nonzero Eigenvector Structure

4.3. Node Selection for Reachability and Observability of $λ = 1$

5. Zero-Nonzero Pattern of Eigenvectors Associated to Any $λ$ of $N_{k}$