Custom Adaptive Kernel Strategies for Gaussian Process Regression in Wafer-Level Modeling and FPGA Delay Analysis

1. Introduction

Large-scale integrated circuits and field-programmable gate arrays are receiving significant attention in modern technology. Many sectors, from automotive to healthcare, rely heavily on these technologies. While LSIs offer high-density integration and optimized performance, FPGAs provide flexibility and reconfigurability, making them complementary technologies in many applications [19,21,22,23,24,31]. Given their critical role, ensuring device reliability through comprehensive testing has become paramount, as faulty devices can significantly impact system operations and societal functionality. This necessitates extensive testing across various manufacturing stages under diverse conditions [30]. As these semiconductor devices increase in complexity and functionality, the volume of required tests has surged, resulting in higher test costs. This increasing expense is a major concern, as testing now constitutes a substantial portion of the overall manufacturing cost for both LSIs and FPGAs [2,3,4,5,12]. The challenge of maintaining thorough testing while managing costs is particularly pronounced in FPGAs, where the reconfigurable nature of the device adds an additional layer of complexity to the testing process. Various test cost reduction methods have been proposed that apply data analytics, machine learning algorithms, and statistical methods [16,22,25,26,28,32,22]. In particular, wafer-level characteristic modeling methods based on statistical algorithms are the most promising candidates that reduce test cost, that is, measurement cost, without impairing test quality. [1,15,16,17,20,35,37].

On the other hand, the state–of–the–art FPGA estimation proposed in [4] shows that the estimated measurements can be drastically reduced through a compressed sensing-based virtual probe technique [36]. However, as experimentally shown in [25], in experiments conducted using wafer measurement data from a mass industry production, the Gaussian process (GP)-based estimation method surpasses the techniques presented in [4], which are based on compressed sensing [7]. Because estimation eliminates the need for measurement, it not only reduces the cost of measurement, but can also be used to reduce the number of test items and/or change the test limits, which is expected to improve the efficiency of adaptive testing [13,18,27,34]. In [20], the expectation maximization (EM) algorithm [10] was used to predict the measurement. The Gaussian process-based method provides more accurate prediction results [25]. The use of GP modeling has another side benefit. As it calculates the confidence of a prediction, the user can confirm whether the number and location of measurement samples are sufficient, and suitable or not, being a great advantage from a practical viewpoint. In addition, since the GP can calculate the uncertainty of the estimation result, the user can confirm whether the number and location of measurement samples are sufficient and suitable or not.

Figure 1 presents an experimental analysis in the form of a heat map, showing the full measurement results for a wafer of a 28 nm analog /RF device, with estimation based on 10% of the training data. The figure includes three heat maps (a, b, c), where (a) represents the actual measured data, while (b) and (c) show the predicted data using a virtual probe and Gaussian process regression (GPR), respectively. In both cases, 10% of the samples are used to estimate the remaining 90% of the unmeasured samples. It is evident from the figure that both VP and GPR effectively address and accurately predict the unknown measured data with high accuracy and minimal error.

Figure 2 shows a similar experiment with delay information in look-up tables (LUTs) using ring oscillators (ROs). The figure includes three heat maps (a, b, c), where (a) represents the actual measured data, while (b) and (c) show the predicted data using a 10% virtual probe and 10% training data for the Gaussian process regression (GPR), respectively. The figure shows the similar trend on Figure 1 and in both cases VP and GPR effectively address as well as accurately predict the unknown measured data with high accuracy and minimal error.

The VP technique exploits the sparsity of frequency-domain components in spatial process variation for prediction. Due to the gradual nature of process variation in FPGAs and wafers, high-frequency components approach zero, allowing seamless integration with fingerprinting techniques. The method’s effectiveness is validated through silicon measurements on commercial FPGAs.

Unlike VP’s direct frequency-domain approach, GPR models spatial process variation as a probabilistic distribution using kernel-based correlation analysis. This technique effectively handles gradual variations through Gaussian process smoothing, making it ideal for probabilistic predictions. Experimental validation using commercial FPGAs and wafer analog/RF device data demonstrates the method’s effectiveness [1,8,9,29,33].

However, when applying GPR, it is most important to select the best kernel function, but the appropriate kernel function for LSI testing is not well understood. Since there is no effective method for investigating kernel function selection, this study applies GPR to mass production LSI test data, experimentally compares a large number of kernel functions, and identifies the best kernel function. Furthermore, based on this evaluation, this study also demonstrates that estimation accuracy can be further improved by using multiple kernel functions with high estimation accuracy. The hybrid or mixture kernels are proposed in [6,8,9,11,29] where different modes of mixing and combining are explained. In [11], sum of two product kernels $(k_{\mathrm{RBF}}·k_{\mathrm{Lin}}+k_{\mathrm{RBF}}·k_{\mathrm{RQ}})·k_{\mathrm{Multiplication}}$ achieves a best result among all individual kernels.

Most importantly, even when a single kernel or composite kernel function works well, it may not outperform others in different datasets with similar performance. Additionally, composite or adaptive kernels with too many parameters may suffer from overfitting issues. This study aims to determine a custom adaptation based on prediction confidence to select the top two candidates for adaptation with dynamic weight adjustment based on the estimation confidence, instead of using fixed-weight adaptive kernels. Unlike typical hybrid or mixture kernels proposed in [6,8,9,29], this approach determines the weight of each kernel based on their difference in confidence levels. After an exhaustive analysis of various kernel functions across all possible combinations, using actual industry production data and real silicon data, it was observed that the proposed custom-adaptive kernel consistently outperformed across two different datasets.

The remainder of this paper is organized as follows: Section 2 provides an overview of GP-based modeling for wafer and FPGA process variations. Section 3 details the kernel function and proposed custom-adaptive kernel strategies. Section 4 presents a quantitative evaluation of the proposed custom kernel approach compared to conventional approaches. Finally, Section 5 offers the conclusion.

2. Gaussian Process Regression for Semiconductor Reliability

To better understand the origin and structure of the data used in our Gaussian Process Regression (GPR) modeling, we first provide an overview of the physical and logical architecture of FPGAs and wafer-level layouts.

2.1. Basic Structure

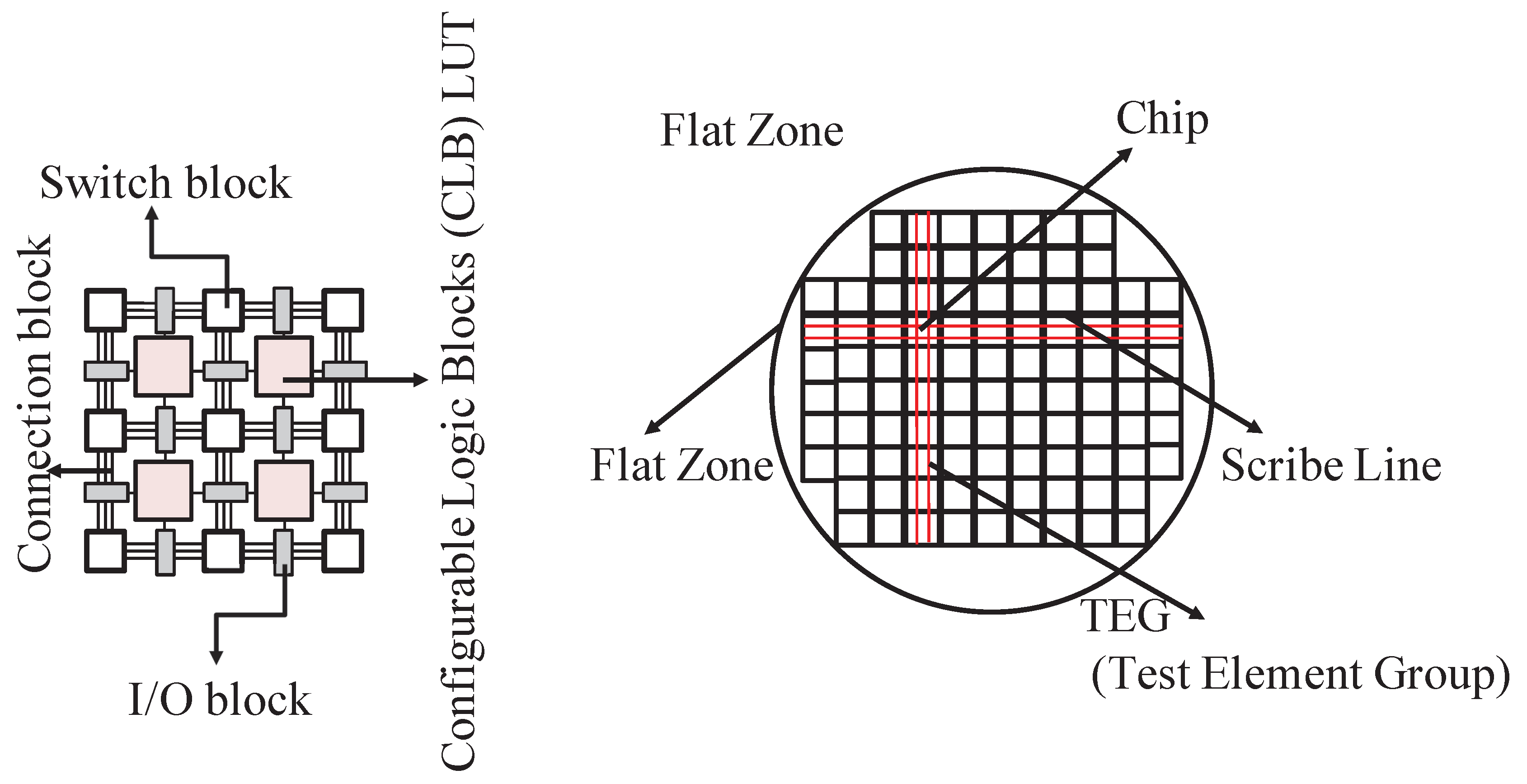
Figure 3 presents an annotated layout that bridges both the logical structure of an FPGA and the physical organization at the wafer level. Within each chip, Configurable Logic Blocks (CLBs) serve as the core computational units and are arranged in a regular grid pattern. Each CLB is composed of Look-Up Tables (LUTs), flip-flops, and carry chains, allowing the implementation of diverse digital logic through reconfigurable interconnects. These elements are connected via a combination of switch blocks and connection blocks, which form the programmable routing fabric. I/O blocks positioned around the perimeter enable external communication.

From the wafer-level perspective, each chip is bounded by scribe lines—regions without circuitry used as cutting paths during the dicing process to separate individual chips. Adjacent to the main dies, Test Element Groups (TEGs) are placed to validate process consistency and chip behavior during manufacturing. The wafer edge includes a flat zone, a small flattened segment used for alignment during lithography and testing. Together, these components contextualize how logic resources are mapped within a chip and arranged across a wafer for fabrication, validation, and testing purposes. A kernel function is a key component of Gaussian Process Regression (GPR) used to measure similarity between input data points. It defines the covariance structure of the data, enabling GPR to model complex patterns. Common examples include: the Linear kernel $K(x_i,x_j)=x_i^{\top }{x}_j$, Polynomial kernel $K(x_i,x_j)={(x_i^{\top }{x}_j+c)}^d$, and Gaussian kernel

$K(x_i,x_j)=exp\left(-{\displaystyle \frac{\parallel x_i-x_j{\parallel }^2}{2{\sigma }^2}}\right)$. The Radial Basis Function (RBF) kernel, a widely used variant, is given by $k\left(r\right)={\sigma }^{2}exp\left(-{\displaystyle \frac{1}{2}}{r}^2\right)$. Each kernel introduces different assumptions about smoothness and locality, influencing the predictive behavior of the GPR model.

2.2. Gaussian Process Regression

A Gaussian distribution is a type of probability distribution for continuous variables, also known as a normal distribution. In this distribution, the mean, mode, and median are identical, and the distribution is symmetric around the mean. Since it is continuous rather than discrete, the distribution is represented as a smooth curve rather than a histogram. The probability density function of the Gaussian distribution is given by:

$${\displaystyle \frac{1}{\sqrt{2\pi }\sigma }}·e^{-{\displaystyle \frac{{(x-\mu )}^2}{2{\sigma }^2}}},$$

(1)

where $\mu$ represents the expected value (mean) and $\sigma$ denotes the standard deviation.

The probability distribution treats the function $f\left(x\right)$ as a random variable, creating a probabilistic model that predicts y for a given input x. When $f\left(x\right)$ is defined, the outputs $f\left(x_1\right),f\left(x_2\right),\dots ,f\left(x_N\right)$ for inputs $x_1,x_2,\dots ,x_N$ follow a Gaussian process. The joint distribution of $y\left(x\right)$ at any set of points $x_1,x_2,\dots ,x_N$ is Gaussian. This property holds true even as N approaches infinity, making a Gaussian process an infinite-dimensional Gaussian distribution.

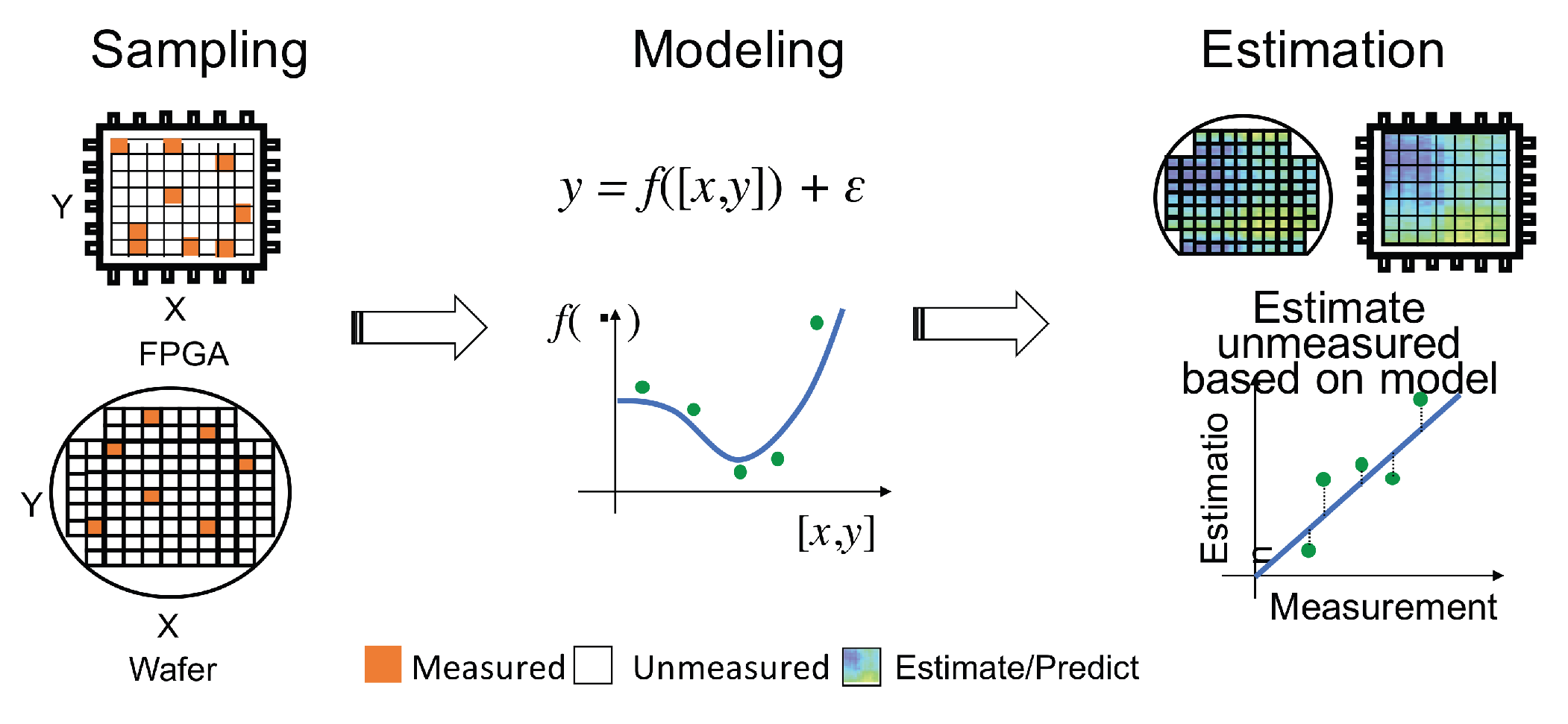
As illustrated in Figure 4, Gaussian process methods are used to model the relationship between input X and output Y. This relationship is expressed mathematically as:

$$Y=f\left(\right[X,Y\left]\right)+\epsilon ,$$

(2)

where $\epsilon$ represents the model’s noise or uncertainty. Data collected from the Wafer and FPGA are used to establish this relationship. Using this model, we can estimate the new output $Y(n+1)$ for both Wafer and FPGA is the new input data $X(n+1)$. The model is constructed as a function of the probability distribution using Bayesian inference.

As mentioned earlier, the semiconductor industry is pursuing methods to improve quality without increasing test costs, or to reduce costs while maintaining quality. Particularly for the latter, wafer-level characteristic modeling methods based on statistical algorithms yield good results. This model uses Gaussian process regression for prediction, creating a prediction model based on limited sample measurements on the wafer surface or FPGA lookup table to predict the entire wafer surface and entire lookup tables.

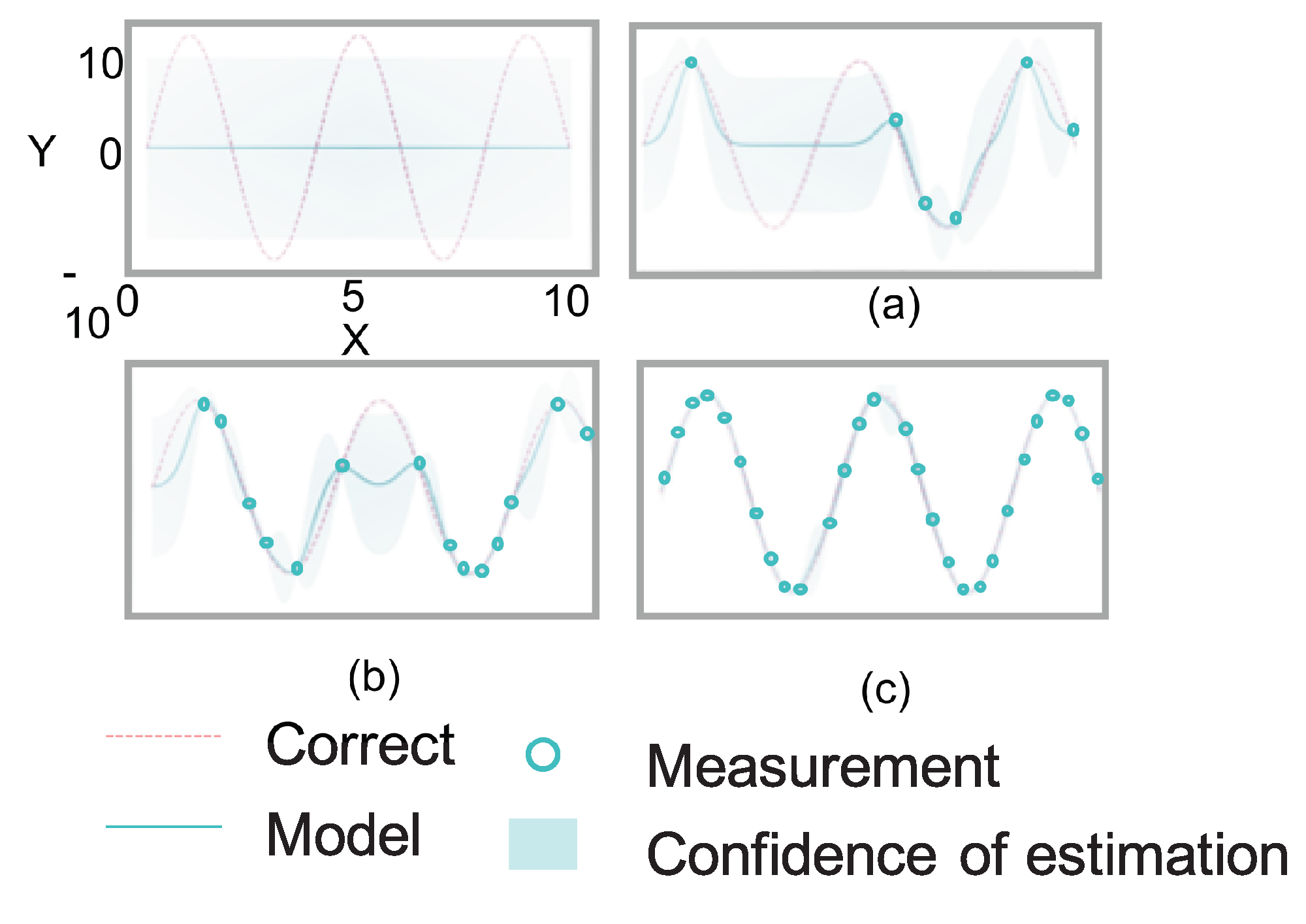
Figures [Figure 5] (a-c) illustrate how the model the relationship between input x and output y. Data D is utilized to model the relationship. The new output y(n+ 1) for the new data x (n+ 1) is estimated based on the model. The model is calculated as a function of the probability distribution with the Bayesian manner.

3. Proposed Custom-Adaptive Kernel Approach

The GP-based regression employs kernel functions from the GPy [14] framework to model and predict the characteristics of wafers and FPGAs.

This method learns from the measurement results of a small number of wafers’ characteristics and FPGA delay information. After the learning phase, it determines two functions: $f(·)$, which relates to the wafer LSI coordinates, and $g(·)$, which relates to FPGA delay information in look-up tables (LUTs) using ring oscillators (ROs). These functions estimate the characteristics of unmeasured wafers and FPGAs.

Let ${\mathbf{x}}_{\mathrm{wafer}}$ represent the wafer surface coordinates, and ${\mathbf{x}}_{\mathrm{fpga}}$ represent the FPGA LUT delay information. Similarly, define $y_{\mathrm{wafer}}$ and $y_{\mathrm{fpga}}$ as the respective measurement values to be predicted.

The training and test datasets are defined as follows:

For wafer data:

$$({\mathbf{X}}_{\mathrm{wafer},\mathrm{train}},{\mathbf{y}}_{\mathrm{wafer},\mathrm{train}})={\left\{({\mathbf{x}}_{\mathrm{wafer},\mathrm{i}},y_{\mathrm{wafer},\mathrm{i}})\right\}}_{i=1}^N,$$

$${\mathbf{X}}_{\mathrm{wafer},\mathrm{test}}=({\mathbf{x}}_{\mathrm{wafer},1}^{*},\dots ,{\mathbf{x}}_{\mathrm{wafer},\mathrm{M}}^{*}),$$

For FPGA data:

$$({\mathbf{X}}_{\mathrm{fpga},\mathrm{train}},{\mathbf{y}}_{\mathrm{fpga},\mathrm{train}})={\left\{({\mathbf{x}}_{\mathrm{fpga},\mathrm{i}},y_{\mathrm{fpga},\mathrm{i}})\right\}}_{i=1}^P,$$

$${\mathbf{X}}_{\mathrm{fpga},\mathrm{test}}=({\mathbf{x}}_{\mathrm{fpga},1}^{*},\dots ,{\mathbf{x}}_{\mathrm{fpga},\mathrm{Q}}^{*}),$$

where $M\gg N$ and $Q\gg P$.

Using the predictive models $f(·)$ and $g(·)$ obtained from GPR, the predicted values for the test datasets are:

$${\mathbf{y}}_{\mathrm{wafer}}^{*}=(y_{\mathrm{wafer},1}^{*},\dots ,y_{\mathrm{wafer},\mathrm{M}}^{*}),$$

$${\mathbf{y}}_{\mathrm{fpga}}^{*}=(y_{\mathrm{fpga},1}^{*},\dots ,y_{\mathrm{fpga},\mathrm{Q}}^{*}).$$

3.1. Hybrid or Mixture Kernel Strategy

The Hybrid or Mixture Kernel approach combines multiple kernel functions, each tailored to specific data characteristics, into a composite kernel. This strategy traditionally uses fixed weights for individual kernels, expressed as:

$$K_{\mathrm{hybrid}}=\sum _{i=1}^n{w}_i{K}_i,$$

(3)

where $K_i$ are the individual kernels, and $w_i$ are their static weights with $\sum w_i=1$. However, such static weighting lacks adaptability to varying data properties, limiting robustness and flexibility. Although there are several ways to select the number of kernels and assign their weights, a common approach is to distribute the weights equally. For example, if two kernels are used, each is assigned a weight of 0.5; similarly, if four kernels are used, each receives a weight of 0.25.

3.1.1. Adaptive Kernel Strategy

Unlike the hybrid kernel strategy, the adaptive kernel strategy dynamically adjusts weights $w_i$ based on kernel performance metrics, thereby enhancing flexibility and robustness.

This strategy aims to improve GPR’s adaptability across wafer and FPGA data by adjusting kernel influence dynamically. Let the dataset be represented as:

$${\mathit{D}}_1,{\mathit{D}}_2,\dots ,{\mathit{D}}_n,$$

where each ${\mathit{D}}_i=({\mathbf{x}}_i,y_i)$ is a measured input–output pair from a probe point. The candidate kernels are modeled as:

$$f\left(k_1\right),f\left(k_2\right),\dots ,f\left(k_n\right),$$

where $f\left(k_i\right)$ denotes the regression model trained using kernel $k_i$. Kernel performance is evaluated using validation errors:

$${\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_r,$$

These are used to determine kernel ranking and influence in the final model.

3.1.2.1 Composite Adaptive Strategy

This strategy considers performance differences and a threshold $\tau$ to determine whether reweighting is necessary. It is effective when kernel performance is close and noise robustness is desired.

Let $a_k$ denote the performance score of kernel k, and define the top three indices as:

$$i_1=arg\underset{k}{max}\left(a_k\right),i_2=arg\underset{k\ne i_1}{max}\left(a_k\right),i_3=arg\underset{k\notin \{i_1,i_2\}}{max}\left(a_k\right)$$

Let ${\delta }_{ij}=|a_i-a_j|$ represent pairwise performance differences. The composite kernel is defined as:

$$\begin{array}{c}{K}_{\mathrm{composite}}(x,x^{\prime })=w_1{K}_1(x,x^{\prime })+w_2{K}_2(x,x^{\prime })\hfill \\ \hfill +w_3{K}_3(x,x^{\prime })+w_4{K}_4(x,x^{\prime }),\end{array}$$

(4)

Where K₁, K₂, K₃, K₄ are the top four candidate kernels respectively.

Weights are assigned as:

$$w_i=\left\{\begin{array}{cc}0.6\hfill & \mathrm{if}max({\delta }_{i_1{i}_2},{\delta }_{i_2{i}_3})>\tau \mathrm{and}i=i_1\hfill \\ 0.35\hfill & \mathrm{if}max({\delta }_{i_1{i}_2},{\delta }_{i_2{i}_3})>\tau \mathrm{and}i=i_2\hfill \\ 0.4\hfill & \mathrm{if}max({\delta }_{i_1{i}_2},{\delta }_{i_2{i}_3})\le \tau \mathrm{and}i=i_1\hfill \\ 0.3\hfill & \mathrm{if}max({\delta }_{i_1{i}_2},{\delta }_{i_2{i}_3})\le \tau \mathrm{and}i=i_2\hfill \\ 0.25\hfill & \mathrm{if}max({\delta }_{i_1{i}_2},{\delta }_{i_2{i}_3})\le \tau \mathrm{and}i=i_3\hfill \\ 0.05\hfill & \mathrm{if}i=4\left(\mathrm{jitter}\right)\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(5)

The final composite kernel is:

$$K_{\mathrm{composite}}=w_1{K}_1+w_2{K}_2+w_3{K}_3+w_4{K}_4$$

(6)

$$\sum _{i=1}^4{w}_i=1,0\le w_i\le 1$$

(7)

3.1.2.2 Aggressive Adaptive Strategy

This simplified strategy omits thresholding and assigns weights directly based on kernel ranking. It is suitable when kernel performance gaps are consistently clear.

The composite kernel is defined as:

$$\begin{array}{c}{K}_{\mathrm{aggressive}}(x,x^{\prime })=w_1{K}_1(x,x^{\prime })+w_2{K}_2(x,x^{\prime })\hfill \\ \hfill +w_3{K}_{\mathrm{jitter}}(x,x^{\prime }),\end{array}$$

(8)

Weights are assigned as:

$$K_{\mathrm{aggressive}}=\sum _{i=1}^3{w}_i{K}_i$$

(9)

$$w_i=\left\{\begin{array}{cc}0.7\hfill & \mathrm{if}i=arg\underset{k}{max}\left(a_k\right)\hfill \\ 0.25\hfill & \mathrm{if}i=arg\underset{k\ne arg{max}_k\left(a_k\right)}{max}\left(a_k\right)\hfill \\ 0.05\hfill & \mathrm{if}i=3\left(\mathrm{jitter}\right)\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(10)

$$\sum _{i=1}^3{w}_i=1,0\le w_i\le 1$$

(11)

$$K_{\mathrm{aggressive}}=w_1{K}_1+w_2{K}_2+w_3{K}_{\mathrm{jitter}}$$

(12)

3.2. Proposed Custom-Adaptive Model

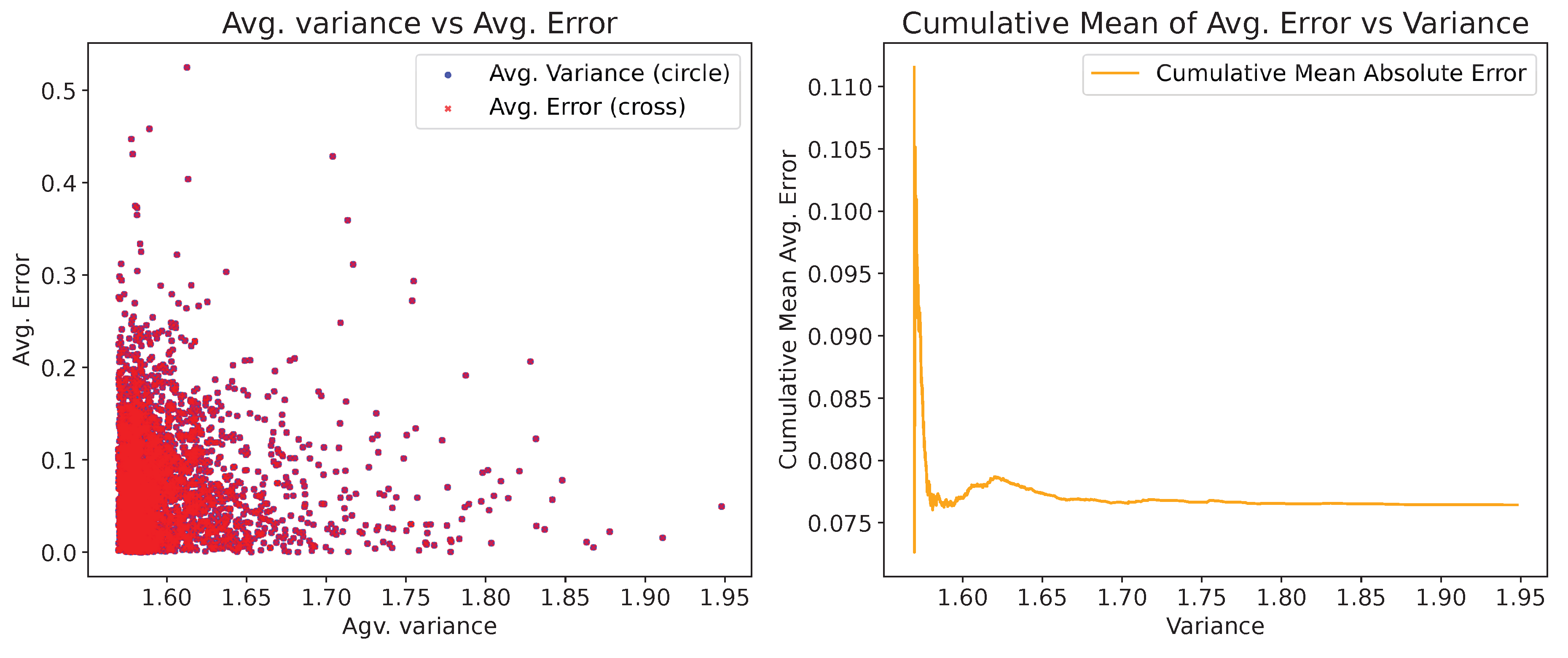
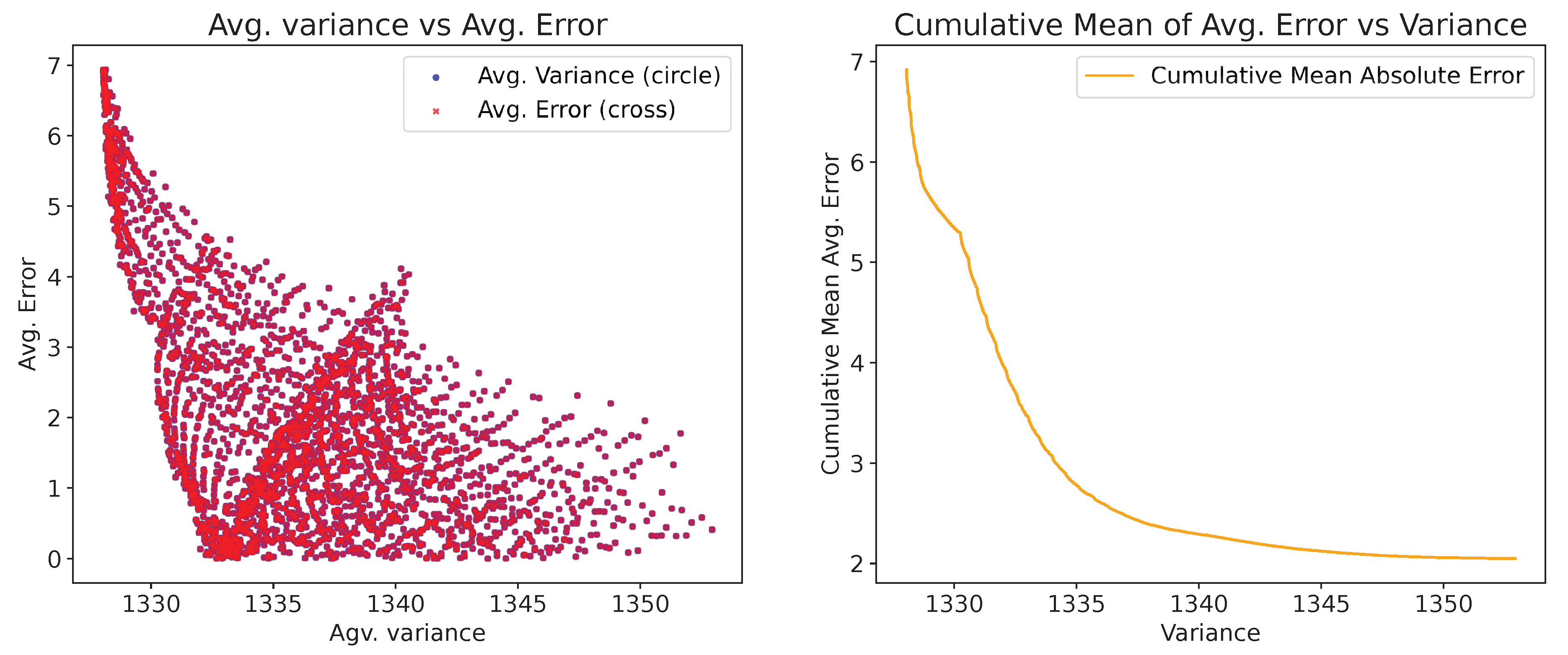
Before discussing the proposed custom adaptive strategy, we first analyze the correlation between predictive variance and average error, as illustrated in Figure 6 and Figure 7. These figures show the scatter plot of predictive variance versus average error, and the cumulative mean of average error versus predictive variance, for the Matern52 and the Linear kernel, respectively. In both figures, Gaussian Process Regression (GPR) is used to predict the input data using a randomly selected 10% of the samples for training, with error calculated as defined in Equation 17 in Section 4. The variance versus average error scatter plot and the cumulative mean of average error versus variance illustrate this relationship under different kernel behaviors.

Although lower predictive variance is often associated with reduced prediction error, certain regions exhibit deviations due to underestimation of uncertainty, particularly in sparse or non-representative test samples. In the case of the Matern-52 kernel, the error remains consistently low, with the cumulative trend exhibiting a slight increase as variance grows. The scatter plot demonstrates a weak positive trend where higher variance corresponds to slightly lower errors. For the linear kernel, where the prediction uncertainty is higher, the correlation exhibits a stronger negative trend. In both cases, regardless of the kernel choice, the negative correlation establishes that lower variance is associated with lower error. A similar trend is also examined in wafer data. We examined a negative correlation between the cumulative average error and the predictive variance. Although in some cases, such as for certain wafer and FPGA paths, we observed a positive correlation for some kernels, the overall correlation averaged across the datasets was found to be negative in both cases.

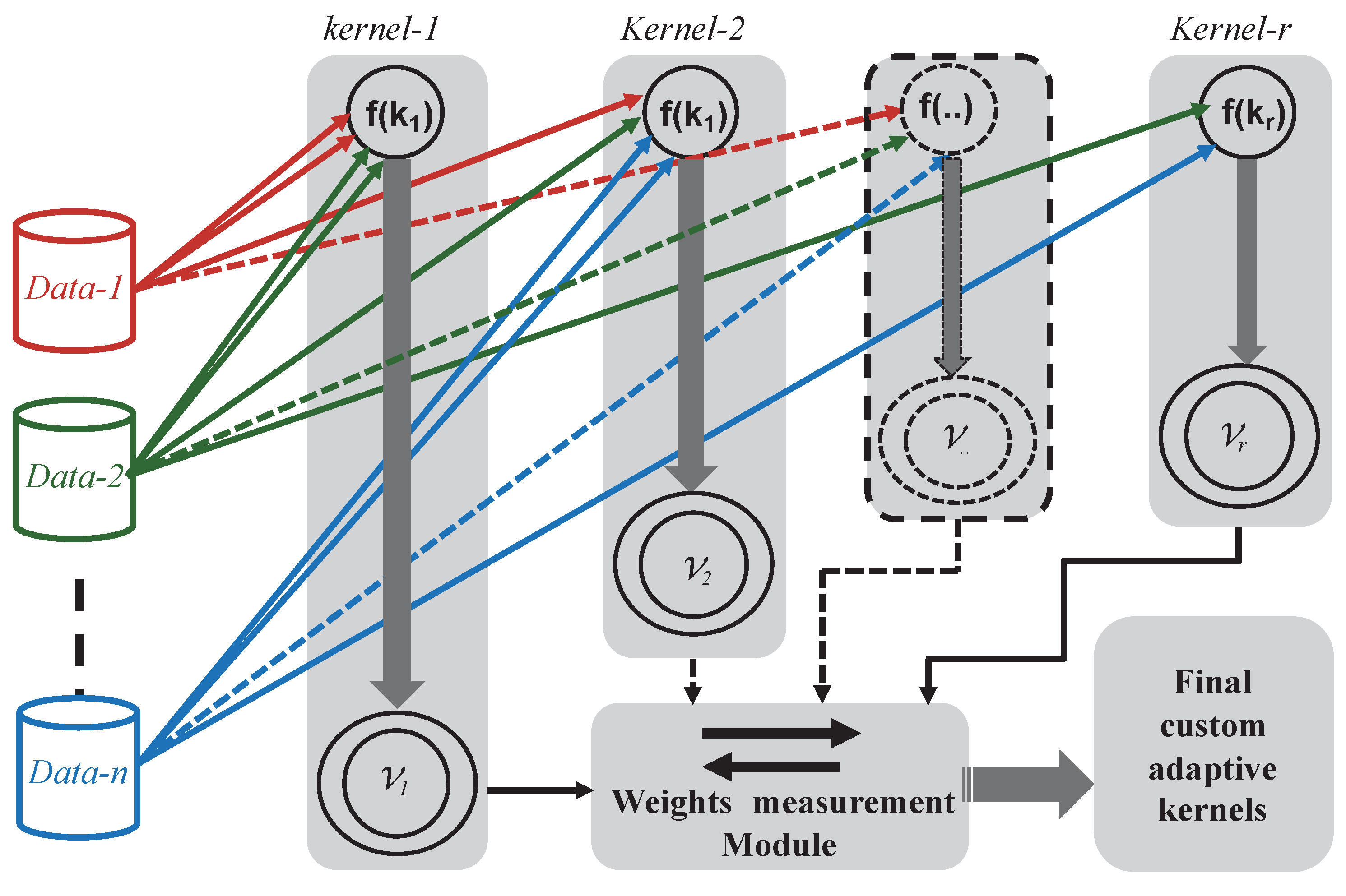
Considering this relationship, the proposed custom adaptive strategy is depicted in Figure 8. The figure illustrates how kernel weights are adapted based on confidence levels derived from the variance. In this approach, the kernel weights are calculated based on predicted variance instead of during the estimation process.

Figure 8 presents the different datasets

$Dat{a}_1,Dat{a}_2,\dots ,Dat{a}_n$ with different kernel functions $f{k}_1,f{k}_2,\dots ,f{k}_r$. Here, each $Dat{a}_i$ represents an individual wafer in the case of wafer data (i.e., wafers within a lot), and a specific path in the case of FPGA data (i.e., delay paths measured across devices). The Gaussian Process Regression (GPR) estimates the variance $V_1,V_2,\dots ,V_r$ for each kernel function. Based on these variance estimates, the top two kernel candidates $f{k}_{\mathrm{top}1}$ and $f{k}_{\mathrm{top}2}$ are selected using the criterion of lowest average predictive variance across all datasets.

The weights $w_1$ and $w_2$ are defined to satisfy the following condition:

$$w_1+w_2=1,$$

(13)

where the weights are assigned based on the difference in the variances $f{k}_{top1}$ and $f{k}_{top2}$:

$$\Delta f=|f{k}_{top1}-f{k}_{top2}|.$$

(14)

The weight $w_1$ is calculated as:

$$w_1=\left\{\begin{array}{cc}0.5,\hfill & \mathrm{if}f{k}_{top1}=f{k}_{top2}\hfill \\ 0.5+\beta ·\Delta f,\hfill & \mathrm{if}f{k}_{top1}>f{k}_{top2}\hfill \\ 0.5-\beta ·\Delta f,\hfill & \mathrm{if}{f}_{ktop1}<f{k}_{top2}\hfill \end{array}\right.$$

(15)

where $\beta$ is a scaling factor to control the impact of the variance difference on the weight.

Similarly, $w_2$ is given by:

$$w_2=1-w_1.$$

(16)

Here, if $f{k}_{top1}=f{k}_{top2}$, then $w_1=w_2=0.5$ and as the variance difference $\Delta f$ increases, $w_1$ increases if $f{k}_{top1}>f{k}_{top2}$ and decreases if $f{k}_{top1}<f{k}_{top2}$. The smaller the variance of $f{k}_{top1}$ compared to $f{k}_{top2}$, the more $w_1$ dominates.

This approach ensures that the kernel with higher confidence level receives greater weight, reflecting its importance in the combined kernel function. The proportional adjustment of $w_1$ and $w_2$ accommodates scenarios where one kernel significantly outperforms the other in terms of variance.

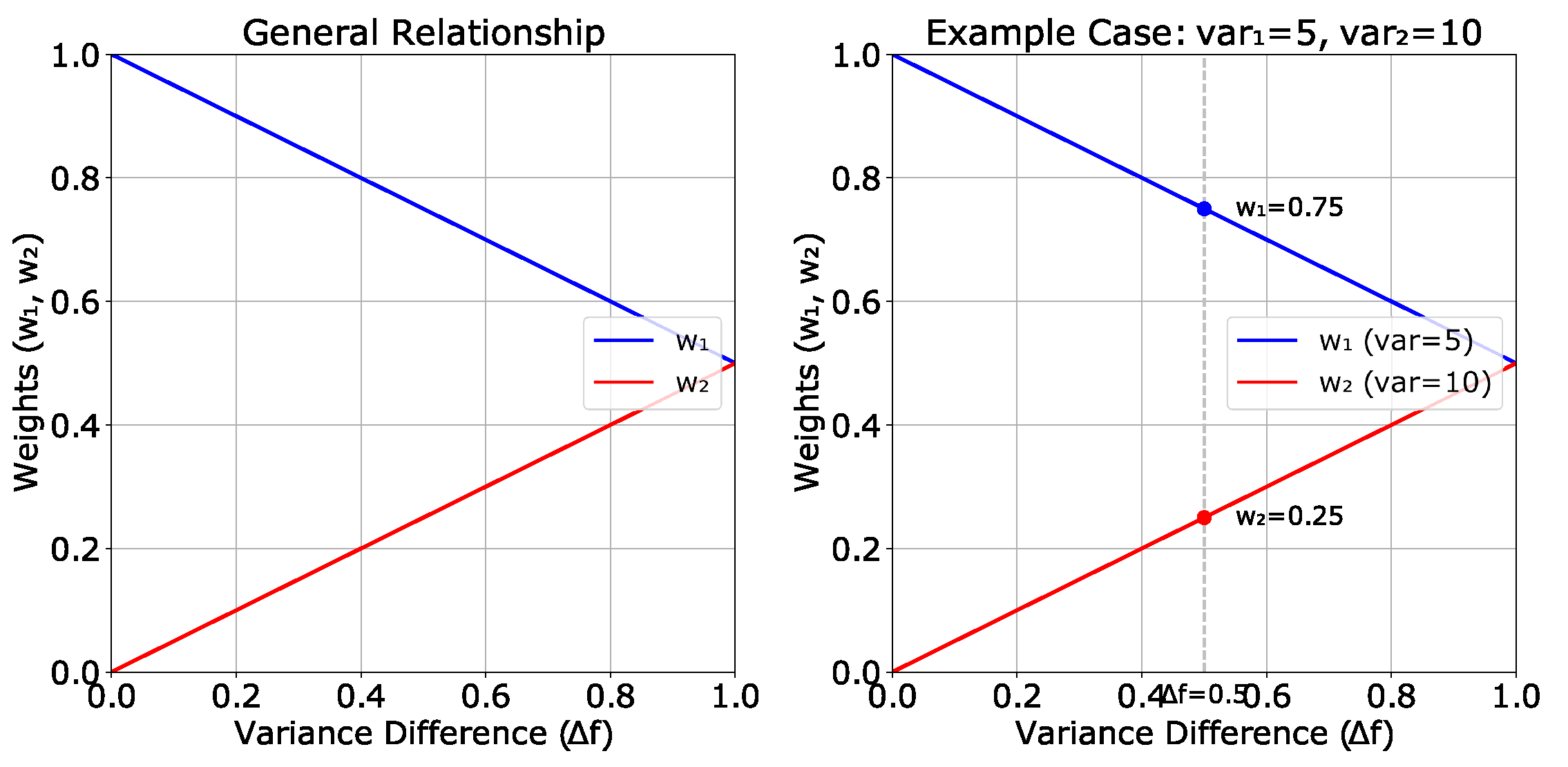
Figure 9 illustrates the relationship between the kernel weights $w_1$, $w_2$, and the variance difference $\Delta f$. It consists of a general plot showing how the weights shift as $\Delta f$ changes, and an example inset demonstrating the calculation for two specific variances: 10 and 5. For example, the calculation for kernel weights (with scaling factor $\beta =0.05$) is as follows:

Consider two kernel predictive variances, 5 and 10. The variance difference is calculated as $\Delta f=|5-10|=5$. Using the variance-based weighting strategy, the kernel with lower variance (5) is assigned a higher weight:

$$w_1=0.5+\beta ·\Delta f=0.5+0.05\times 5=0.75$$

$$w_2=1-w_1=1-0.75=0.25$$

Thus, the resulting weights are $w_1=0.75$ and $w_2=0.25$, as shown in Figure 9.

The proposed weighting mechanism adjusts $w_1$ and $w_2$ based on the variance difference between the two kernels. This hypothesis provides a robust framework for assigning weights, ensuring that kernels with lower variance contribute more to the combined kernel function.

4. Experimental Result

In this study, we conducted experiments using two different computational environments tailored to two distinct datasets. The wafer data was processed on a Linux workstation running Debian with an Intel Core i7 processor and 32 GB of memory. In contrast, the FPGA data was analyzed on a Windows 11 workstation equipped with an AMD processor and 16 GB of memory.

The kernel selection strategy, as summarized in Table 1, adopts a systematic methodology: (1) Hybrid kernels combine the top two performers (MLP and Exponential for wafer data; RatQuad and Matern52 for FPGA) based on preliminary error evaluations (see Tables 2–3); (2) Adaptive kernels incorporate four high-performing kernels—MLP, Exponential, RBF, and OU for wafer; Matern52, RatQuad, Matern32, and Exponential for FPGA; (3) Proposed Custom Adaptive kernels utilize the top two candidates (Exponential + RBF for wafer; Matern52 + Exponential for FPGA), selected dynamically via a variance-based weighting scheme, as outlined in Section 3.2 (Eqs. 13–16).

4.1. Experimental Setup

This section outlines the experimental setup used to evaluate the proposed custom-adaptive kernel method, along with a summary of existing studies on kernel functions in Gaussian Process Regression (GPR). It includes details on the FPGA and wafer datasets, kernel selection strategies, modeling framework, and estimation error calculation procedures.

4.1.1. Wafer Data

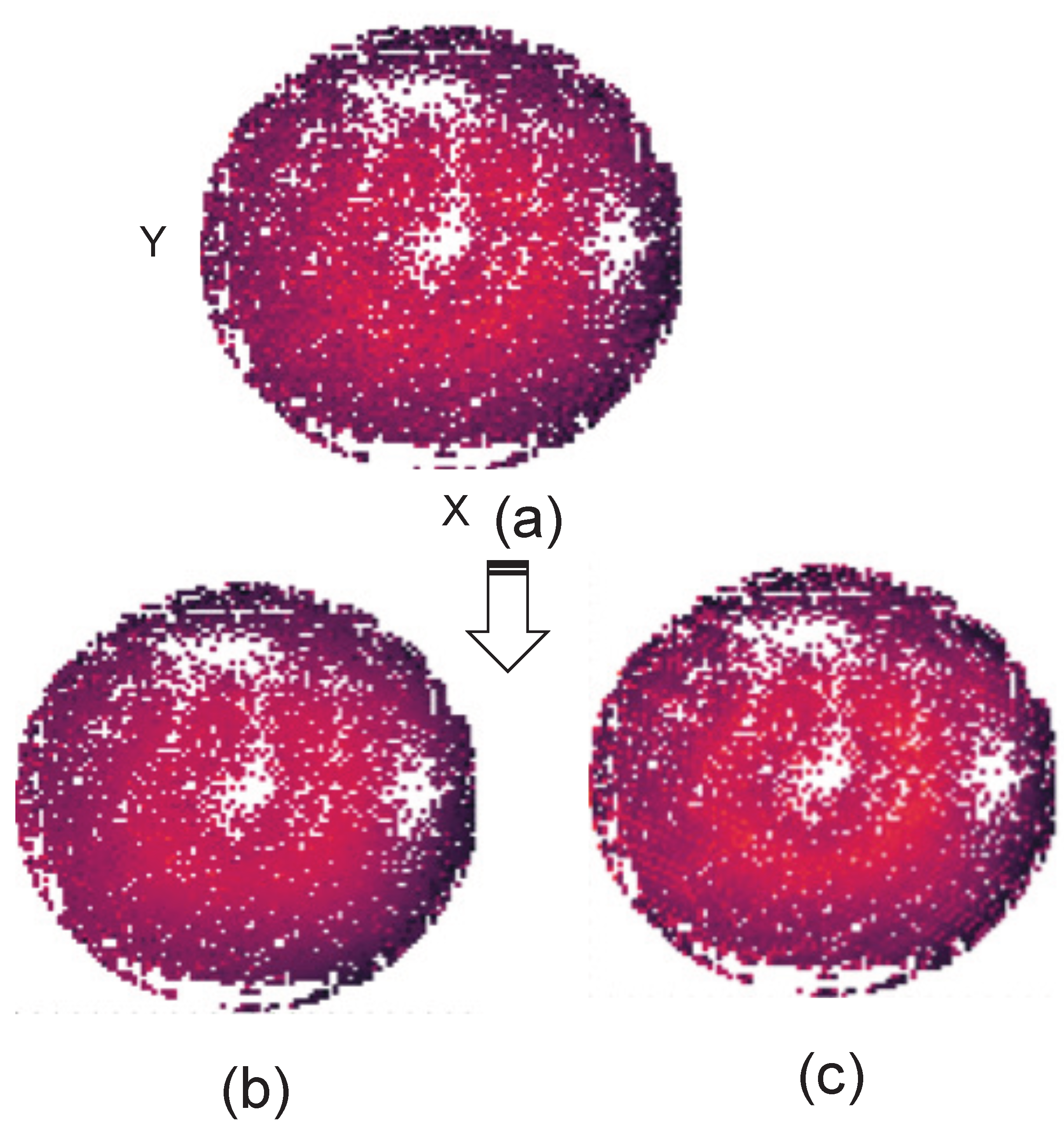
For wafer data, we conducted experiments using an industrial production test dataset of a 28 nm analog/RF device. Our dataset contains 150 wafers from six lots, each lot contains 25 wafers, and a single wafer featuring approximately 6,000 devices under test (DUTs). In this experiment, we utilized a measured characteristic for an item of the dynamic current test. A heat map of the full measurement results for the first wafer of the sixth lot is displayed in Figure 1(a) and Figure 10. For ease of experimentation, the faulty dies were removed from the dataset. In the data set, there are 16 sites in a single touchdown. However, in this experiment, the site information is not considered separately during the training phase. Although the data comes from a multi-site environment, all 16 sites are treated as a single entity because the source data does not show any discontinuous changes for each site as shown in Figure 1(a) and Figure 10

4.1.2. FPGA Data

For FPGA data, we conducted experiments using measurements using the Xilinx Artix-7 FPGA. In this experiment, 10 FPGAs (FPGA-01 to FPGA-10) were used. An on-chip measurement circuit has been implemented using 7-stages (i.e., 7 LUTs) in a Configurable Logic Block (CLB). The Ring Oscillator (RO) is based on XNOR or XOR logic gates. By keeping the same internal routing, logic resources, and structure for each RO placed in a CLB, the frequency variation caused by internal routing differences can be minimized. A total of 3,173 ROs were placed on a geometrical grid of $33\times 120$ (excluding the empty space of the layout) through hardware macro modeling using the Xilinx CAD tool, Vivado [3,4]. Figure 2(a) shows a single path’s measured frequency heat-map. This style is followed to cover the total layout of the FPGA. The Artix-7 FPGA has 6-input LUTs, which create a total of 32 ($2^6-1$) possible paths for XNOR- and XOR-based RO configurations (path-01 to path-32). In total, to complete the exhaustive fingerprint (X-FP) measurement, 32 fingerprint measurements were conducted for all the 32 paths.

4.1.3. GPR Kernel

We use all supported kernels by the GPy framework, along with the proposed custom-adaptive kernels, for both wafer-level and FPGA-based data.

4.1.4. Estimated Prediction Error

To quantitatively evaluate the modeling, we defined the error ($\mathbf{\delta }$) between the correct (${\mathbf{y}}_{\mathrm{true}}$) and the predicted mean ($\mathbf{\mu }$) normalized using the maximum and minimum values of ${\mathbf{y}}_{\mathrm{true}}$ as follows:

$$\begin{array}{c}\hfill \mathbf{\delta }={\displaystyle \frac{\mathbf{\mu }-{\mathbf{y}}_{\mathrm{true}}}{d_{\mathrm{spec}}}},\end{array}$$

(17)

where $d_{\mathrm{spec}}$ indicates the range between the minimum and maximum values of the fully measured characteristics.

4.1.5. Experimental analysis

Table 2 and Table 3 present a detailed evaluation using data from 150 wafers across six lots and 32 delay paths from 10 FPGAs, respectively. The analysis is based on actual industry production and silicon measurement data. In both tables, the bold values indicate the lowest prediction error for each individual lot or FPGA instance. The results suggest that the relatively smooth variation in wafer data is well captured by the Exponential and MLP kernels. In contrast, the higher complexity and nonlinearity of FPGA delay patterns are better handled by the Exponential kernel. The MLP kernel shows weaker performance on FPGA data, likely due to its sensitivity to hyperparameter tuning in high-dimensional spaces.

The hybrid and adaptive kernels perform well, while the proposed custom-adaptive kernel outperforms all cases in terms of average performance and in most cases in terms of individual device values and lot-wise averages across both wafer and FPGA datasets.

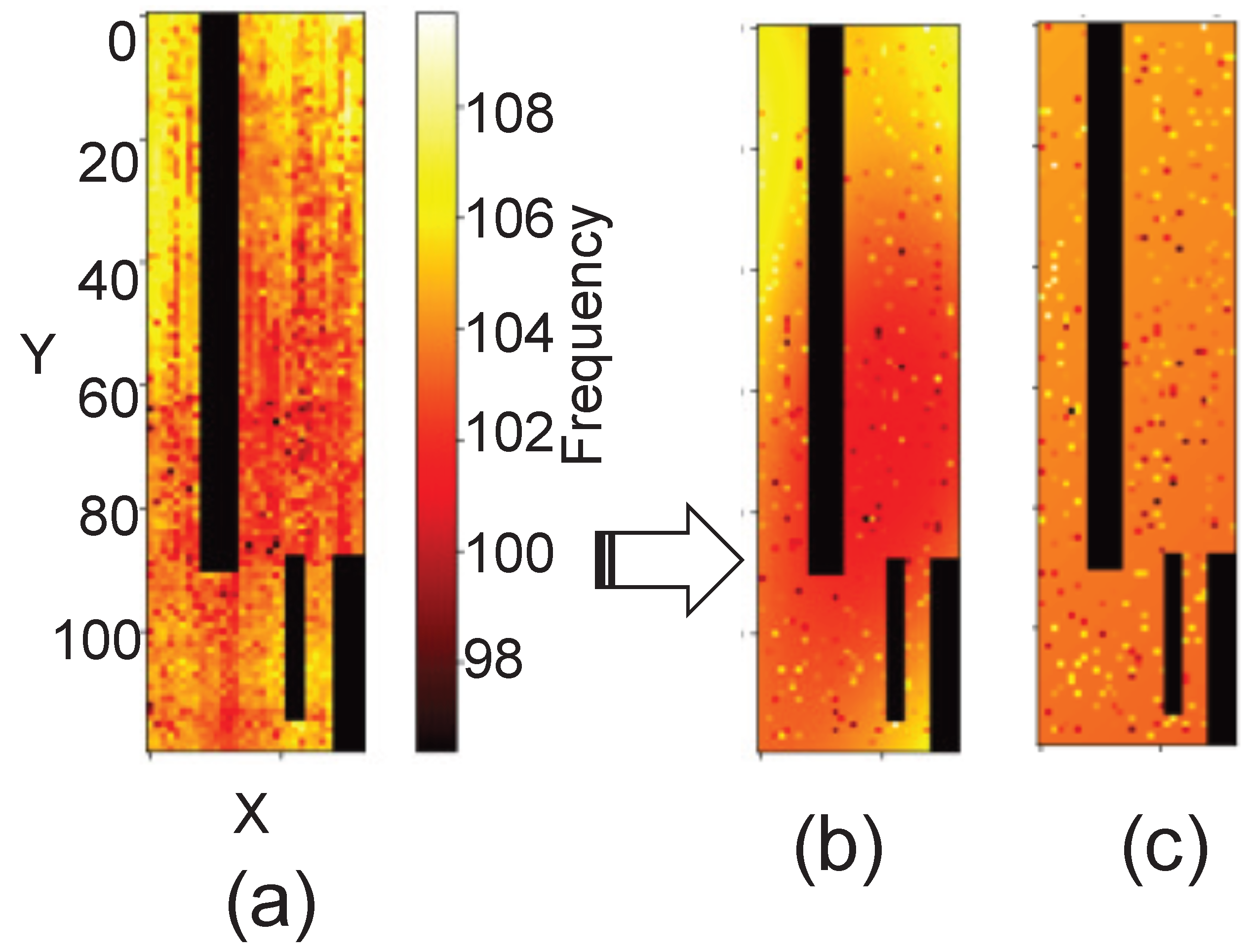
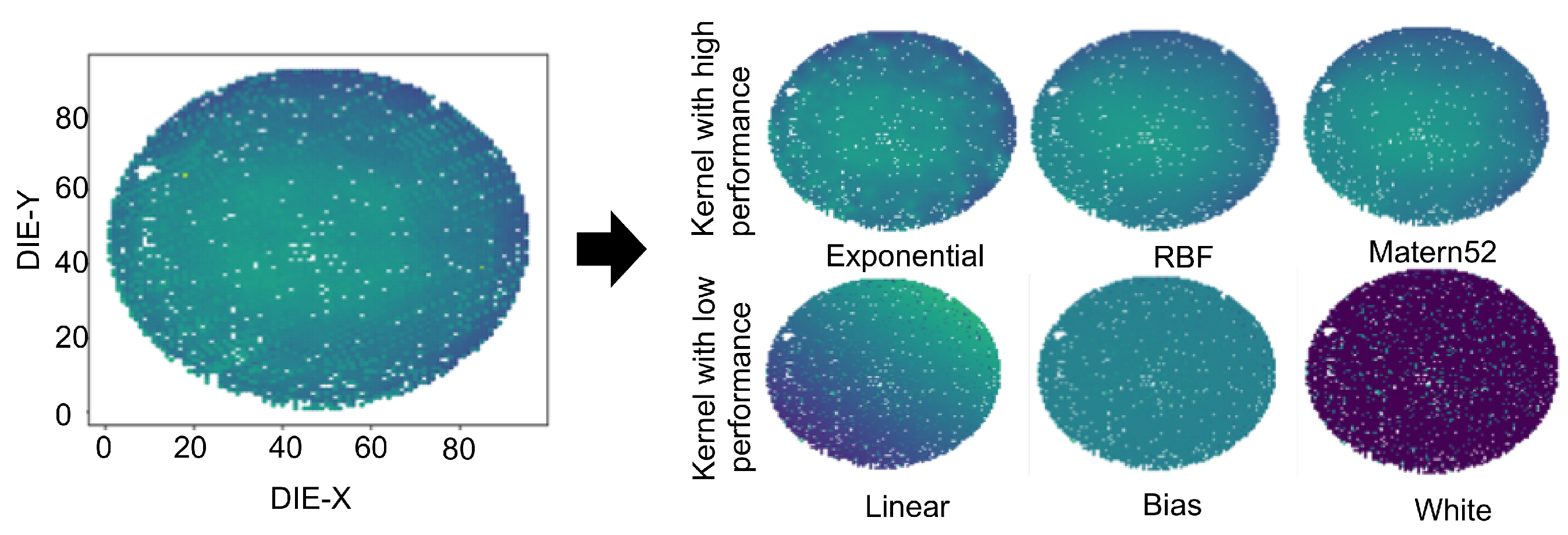
Figure 10 and Figure 13 show the heat map comparisons for the wafer and FPGA, respectively. In Figure 10, the first wafer of the third lot is examined, while in Figure 13, the first path of the first FPGA is depicted with three well-performing and three poorly performing kernels. In the wafer data, the Exponential, RBF, and Matern52 kernels closely reproduce the original die, whereas the Linear, Bias, and White kernels demonstrate poor performance, as shown in the corresponding heat maps (Figure 10). 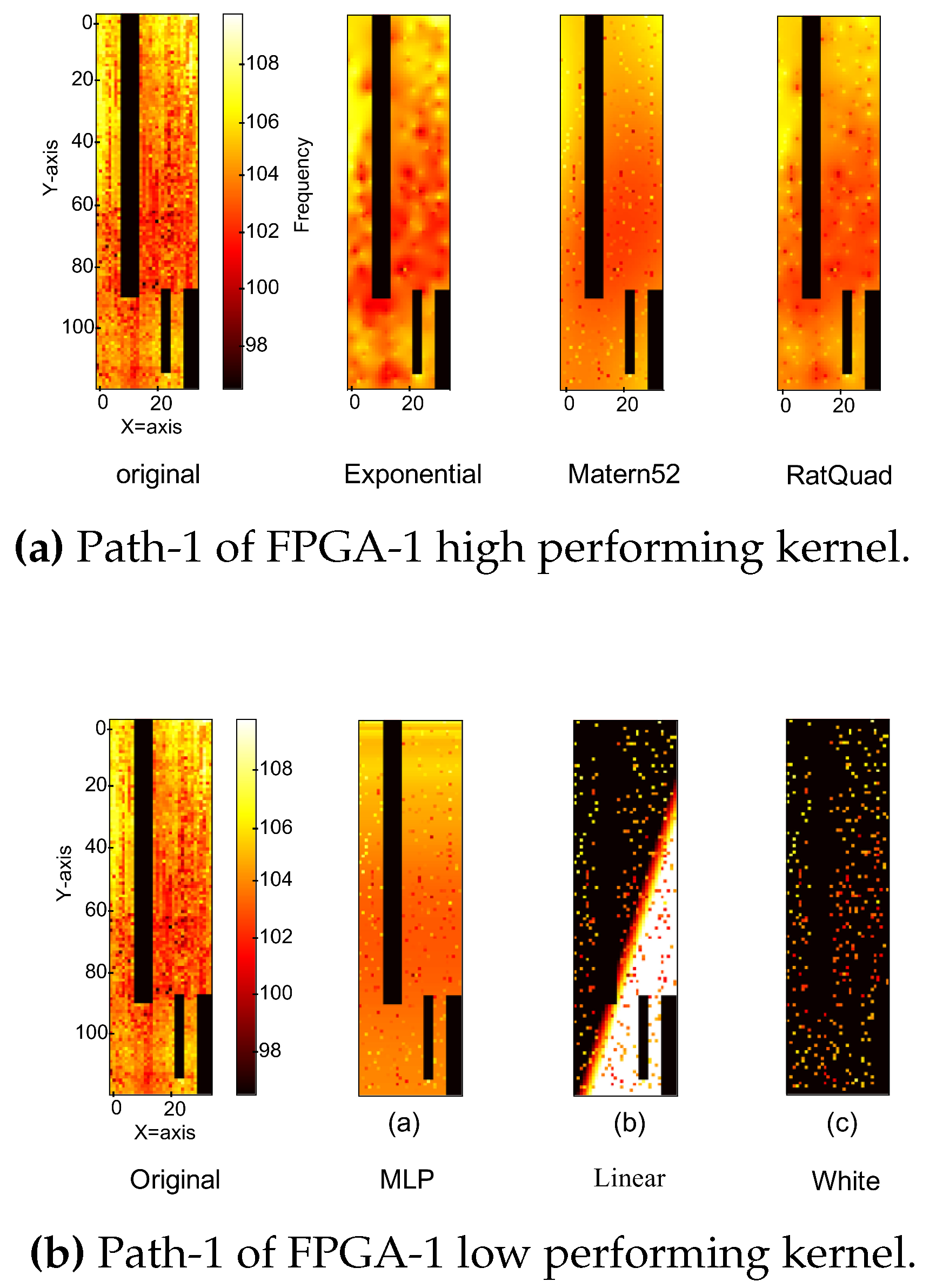On the other hand, in Figure 13, the heat map of FPGA data shows that the exponential, Matern, and TatQuad kernels are performing well, while MLP, linear, and white kernels are performing poorly. From the figure, it is also clearly shown that in both cases of FPGAs and wafer data, the well-performing kernels are reflected in their corresponding heat maps as well.

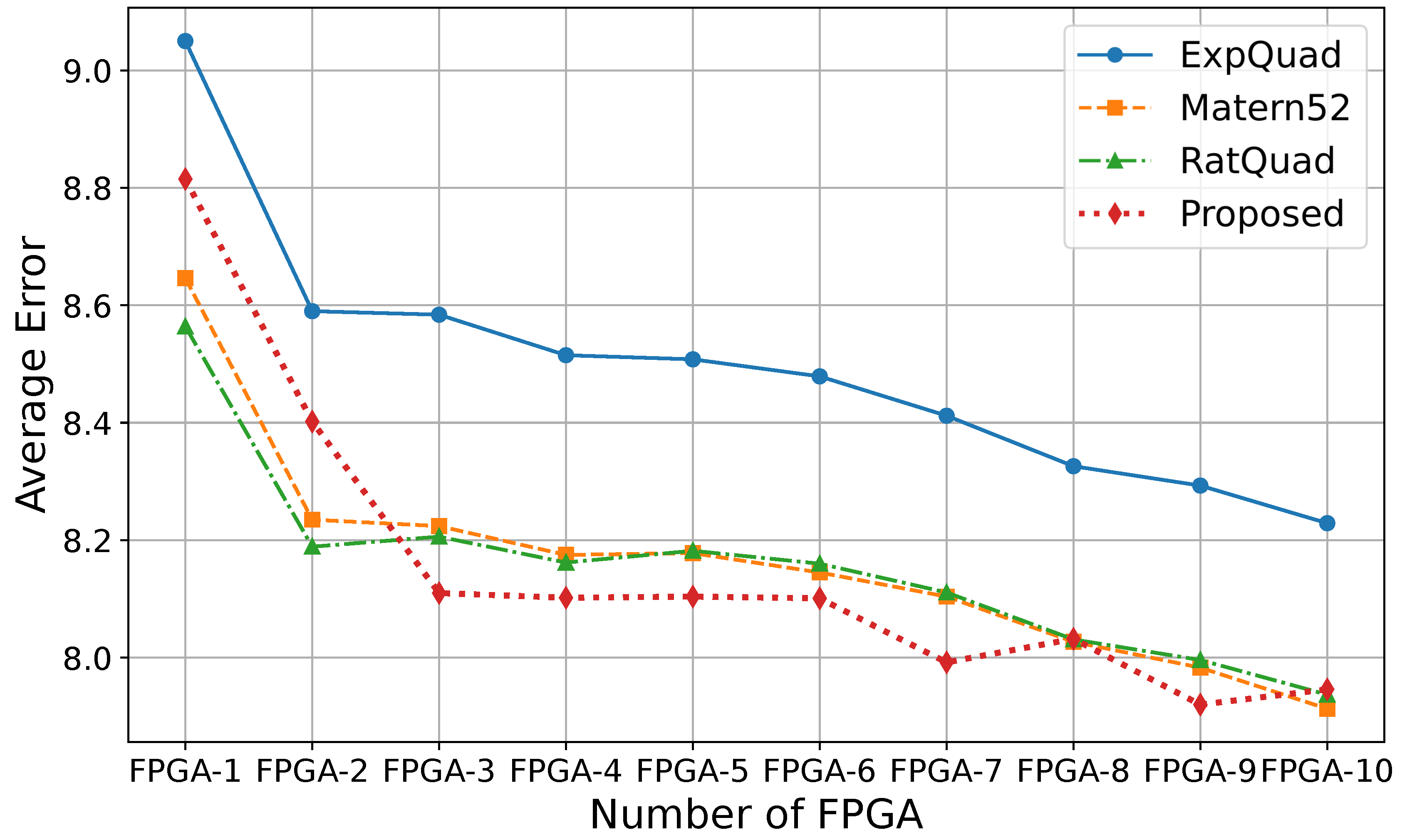
The comparison of the top four performing kernels in both cases of wafer and FPGAs is depicted with a line graph in Figure 11 and Figure 12, respectively. To find a common performer in both cases, only the proposed custom-adaptive kernel is outperforming in the two different environments.

Finally, Figure 14 illustrates the comparison of Wafer and FPGA accuracy across different kernel configurations to explore significant insights. For wafer accuracy measurements, the hybrid kernel achieves a low error rate of 0.115, which is comparable to the best kernel’s error rate of 0.116. However, the proposed custom-adaptive kernel demonstrates superior performance with the lowest Wafer error rate of 0.111.

Figure 13. Comparison of heat maps for the measured frequency between the original and other kernels.

Figure 13. Comparison of heat maps for the measured frequency between the original and other kernels.

Figure 14. Overall estimation error comparison of the best individual, hybrid, and adaptive kernels, and the proposed custom-adaptive kernel for FPGA and Wafer data.

Figure 14. Overall estimation error comparison of the best individual, hybrid, and adaptive kernels, and the proposed custom-adaptive kernel for FPGA and Wafer data.

In the FPGA dataset, the analysis is also shown in Figure 14, the single best kernel slightly outperforms both the adaptive and hybrid kernels in baseline comparisons. Nevertheless, the Proposed custom adaptive kernel again demonstrates superior performance with the lowest FPGA error rate of 8.152, followed closely by the best kernel at 8.163 and the adaptive kernel with an error rate of 8.36. The hybrid kernel, however, exhibits notably higher FPGA error rates, indicating suboptimal performance for FPGA-based applications.

In the comprehensive analysis across both datasets, the Proposed custom adaptive-kernel kernel emerges as the most effective solution, consistently achieving superior performance. While the hybrid kernel demonstrates competitive accuracy in wafer-based applications, its significantly elevated FPGA error rate renders it unsuitable for universal deployment across both platforms.

The proposed adaptive kernel strategy introduces a modest overhead, primarily due to the one-time kernel selection and weight assignment step. Training time increases by approximately 1.3× to 1.5× compared to single-kernel GPR, while inference time remains nearly unchanged.

5. Conclusion

This study investigated the application of Gaussian Process Regression (GPR), a state-of-the-art technique, for wafer-level variation modeling and FPGA delay prediction, with an emphasis on kernel function selection. Through exhaustive analysis, various kernel functions, including hybrid and adaptive kernels, were evaluated using wafer-level industry production data and silicon measurements from FPGAs. While no single kernel function consistently excelled across all datasets, our proposed custom-adaptive kernel through a dynamic weighted-kernel approach demonstrated superior versatility and reliability. This novel methodology enhances the predictive performance and adaptability of GPR, addressing limitations in current state-of-the-art applications. Although the performance improvement in terms of average error may appear marginal on a per-dataset basis, the strength of the proposed custom-adaptive kernel lies in its robust generalization across structurally diverse datasets. Unlike single or static hybrid kernels, our approach dynamically adapts to the underlying data distribution by assigning data-driven weights to the top-performing kernels. This adaptability leads to consistent performance on both wafer-level and FPGA datasets each having distinct noise characteristics and spatial variance patterns demonstrating the model’s practical utility in semiconductor testing scenarios. By offering robust accuracy across diverse scenarios, this approach presents a practical and innovative solution for optimizing semiconductor testing and production processes, with the potential to significantly reduce costs and improve efficiency. These contributions represent a meaningful advancement in leveraging GPR for semiconductor manufacturing and related domains.

Riaz-ul-haque Mian received B.E. from Islamic University Bangladesh and M.E degree from Bangladesh University of Engineering and Technology (BUET) in 2009 and 2017 respectively. He received his Ph.D. degree from Graduate School of Information Science, Nara Institute of Science and Technology (NAIST), Japan in 2021. He was with Synesis IT Ltd. and GIZ from 2009 to 2017. Currently, he is an assistant professor of the Department of Information System Design and Data Science at Shimane University, Japan. His research interests include computer architecture, VLSI testing and decimal computing. He is a member of IEEE.

Foisal Ahmed (Member, IEEE) received his Bachelor of Engineering (B.E.) degree from Prime University, Dhaka, Bangladesh, in 2008. He completed his Postgraduate Diploma (P.G.D.) at the Bangladesh University of Engineering and Technology (BUET), Dhaka, in 2014, and his Master of Engineering (M.E.) degree at the Islamic University of Technology, Dhaka, in 2016. In 2020, he earned his Doctor of Philosophy (Ph.D.) degree from the Graduate School of Information Science at the Nara Institute of Science and Technology (NAIST), Nara, Japan. Previously, he served as a faculty member in the Department of Electrical and Electronic Engineering at Prime University, Bangladesh. He later worked as a postdoctoral researcher in the Department of Computer Systems at Tallinn University of Technology, Tallinn, Estonia. Currently, he is an Embedded Software Engineer at Stonridge Electronics, Inc., based in Estonia. His research interests encompass reliable embedded system design, fault-tolerant computing systems, counterfeit FPGA detection, hardware security and reliability, very-large-scale integration (VLSI) testing, the Internet of Things (IoT), and cyber-physical systems.

Hagihara Yoshito Currently pursuing B.E. degree from the Interdisciplinary Faculty of Science and Engineering, Department of Information System Design and Data Science at Shimane University, Japan. His research interests include VLSI testing.

Souma Yamane Received B.E. degree from the Interdisciplinary Faculty of Science and Engineering, Department of Information System Design and Data Science at Shimane University, Japan. He is currently pursuing her MS degree in the Smart Computing Lab, in the same department. His research interests include VLSI testing.