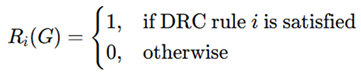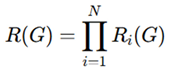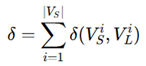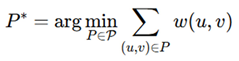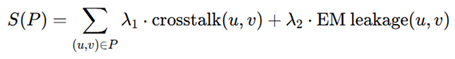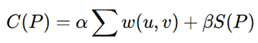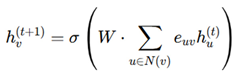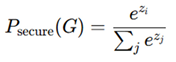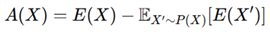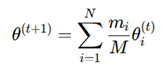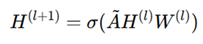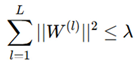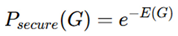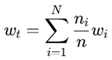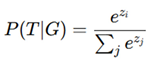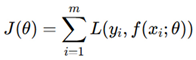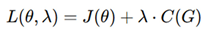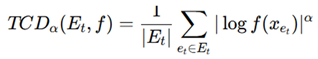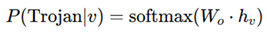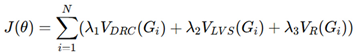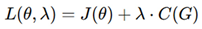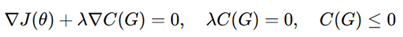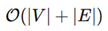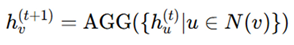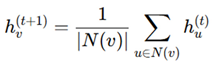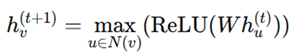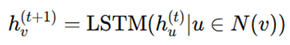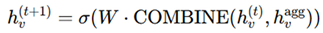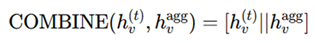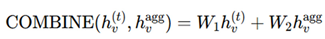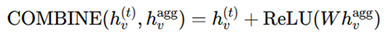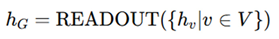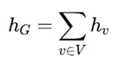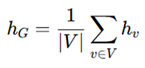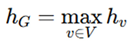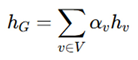Mathematical Foundations of AI-Based Secure Physical Design Verification

1. Introduction

This quickening development of semiconductor expertise particularly increases the fears about hardware security for physical design inspection. Hardware security testing practices are based on patterns. Still, as increasingly sophisticated attackers have demonstrated, they are no match for Trojan horses built into hardware, side-channel vulnerabilities, post-layout hidden mods, and so on [1].

These methods also concentrate on functional correctness and manufacturability more than dynamic security risks, which arise at every stage of the design process, from Register Transfer Level (RTL) to layout synthesis [2]. Since most design engineers are not particularly familiar with security at System-on-Chip, this situation will improve. In turn, however, it will have little effect on the fact that we can’t trust others to build our chips, and there are particular security loopholes in this Golden Reference Model-based chip.

Semiconductor Manufacturing makes the increasing integration of designs from third-party suppliers possible, bringing risks of nonstandard golden reference-based security models [3].

This paper introduces a new technique for security model validation based on a cross-layer, AI-driven, theoretical verification method that employs Graph Neural Networks (GNNs) in reinforcement learning (RL) and constrained optimization. By treating security verification like a graph-based learning problem, these methods systematically analyze structural weaknesses, unauthorized routing changes, and design modifications introduced by opponents [4]. Moreover, secure route optimization is developed as a problem for reinforcement learning to solve. In this approach to layout, the learning agent minimizes EM (electromagnetic) leakage and crosstalk-induced side hazards without sacrificing manufacturability while maintaining layout quality [5].

This theoretical model spans every abstraction layer, increasing independence from justification and golden reference models and thus yields reliable scalability and usability [6].

Key Challenges

Conventional security check methods have severe defects. They are reactive, which means they can only find known threats based on predefined confirmations. Because of this, no known attack vectors are in operation, and one never knows whether or not an HT exists. Deviating from this approach may prove dangerous for new insertion techniques and covert channels.

However, yet unseen adversarial changes mean the rule-based check engine fails to cover these. Moreover, in modern IC verification process flows, which check for design rule observation, layout vs. schematic (LVS) concurrence, and timing closure, implications of the stealthy hardware modifications occurring in every development phase are frequently ignored [9]. A further obstacle is the reliance on golden reference models, which presumes a trustworthy, HT-free starting design exists. However, in the outsourced IC manufacturing setting, it is impossible to get such security references, making traditional mechanical methods or even recent models from intelligence analysis ineffective against the new types of attacks [10].

Finally, hardware security problems go beyond HT detection. They embrace IC cloning, malicious modifications, side channel leakage attacks, supply chain risk, and a dozen other issues. For these, we need a strategy driven by self-adaptation rather than intelligence [11]. Most current work on hardware safety tries to harness lightweight PUFs for authentication and models from machine learning-resistant cryptography to prevent key extraction attacks [12]. However, these methods cannot frequently adapt to new threats. At most, they apply machine learning to search for new approaches [13]. Emerging AI-driven security approaches provide dynamic anomaly detection and reinforcement learning-based security optimization to ease these ills [13].

AI-based frameworks that model IC layouts as heterogeneous graphs can learn hidden security trends, discover unallowable routing changes, and expose adversarial changes typically left uncovered by traditional rule-based systems [14].

Scope of the Paper

The paper formalized a cross-layer AI-driven security verification framework that tackles the problems of regular hardware security models. EDAC rethinks hardware security verification of ICs along the following avenues:

1.

Graph Neural Networks (GNNs) for Security-aware Anomaly Detection:

• Facilitates circuit-level inconsistencies arising from Trojan insertions and stealthily modified routing.

2.

AI-enhanced Design Rule Checking or Rule Closing Procedure (AI-DRC):

• This design begins with hand-picking matters (probabilistic) that can lead to security violations.
• Moves beyond judgment on a static set of rules, looking ahead to whether security violations result from their application.

3.

Security-aware Routing Optimization:

• Under the framework of reinforcement learning-based dynamic path selection.
• Minimizes adjacent noise and parasitic power.
• Reduces the switching speed of crosstalk and number rays by prioritizing EM dissipation levels.

4.

This improves security vulnerability.

5.

Lagrange Multiplier-based Constrained Optimization:

• Employed to make security constraints uniformly enforced mathematically.
• Ensures scalability and achieves efficiency.

6.

Softmax Basis for Trojan Detection:

• Security scores are propagated through GNN node embeddings on an IC layout graph.
• Nodes are classified as benign or compromised.

The verification model proposed in this paper is based on AI and eliminates the reliance on padding or padding layers. Without artificially assisted judgment (golden references), future chip manufacturing processes are ensured to have fewer determinable security testing points.

Significance of Study

The significance of this study lies in its ability to embed AI-driven, probabilistic security verification methods across multiple layers, surpassing traditional rule-based verification systems [1,2]. With fast-moving hardware security risks, traditional pattern-based checking techniques cannot meet the increasing complexity of attacks from adversaries, including hardware Trojans (HTs), side-channel vulnerabilities, and victim layout retrofits that fall beyond their scope [3,4].The next generation of integrated circuits requires that the system be adaptive and that AI-style dynamically assess risks and deploy proper measures for real-time responses against such attacks [5]. In trying to improve current verification techniques, Graph Neural Networks (GNNs) have emerged as a very effective hardware verification tool for finding malfunctions. GNN-based anomaly detection differs from traditional heuristic models because it enables mathematical modeling and categorization without reliance on pre-labeled empirical data sets, which are typically narrow in scope and have dubious applicability [6,7]. This simplifies and promotes verification automation in hardware security research, which greatly reduces reliance on human annotations in safety IC processes [8,9].

Fare optimization for secure routing is essential to minimizing EM leakage and crosstalk-induced risks. Routing paths based on AI and security measures of reinforcement learning can adapt dynamically and optimally while conforming to performance demands and safety constraints [10,11]. Such methods raise the security resistance level of semiconductor designs, which has long been a thorny problem in the struggle for traditional security verification [12].

In a scalable AI-based intelligent IC verification process, introducing collaborative security through federated learning will let semiconductor foundries anonymously share any discoveries among them without fear of publicizing proprietary design. This decentralized learning mode enhances the overall security environment for semiconductors worldwide, with participants able to respond collectively and still preserve proprietary rights in their work [13,14]. It reduces security defects at multiple fabrication points—which means it is possible to enter prevention work at an early stage of risk before there is any chance that an attack vector may be developed [15,16].

This report lays out a large-scale and theoretically sound framework for creating trusted semiconductor manufacturing installations by employing AI-driven models in hardware security authentication rather than those that rely merely on rules. Plus, it raises questions regarding the future of cloud-based security infrastructures and AI-assisted verification models—not only in detecting hardware Trojans but also in creating dependable semiconductor safety solutions [17].

2. Methodology and Implementation

To formally verify the security, an integrated circuit (IC) is converted into a multi-layer heterogeneous graph. In this graph, the nodes are actual circuit components such as gates and vias—physical points where wires cross inside metal layers (this layer’s attribute)—and connections between them are represented by edges. Each DRC rule is converted to a requirement function that a subset of the IC graph must meet; in this way, the design only passes verification if all restraints are satisfied [3].

The overall DRC compliance function is given by:

where N is the total number of DRC rules, ensuring that a design passes DRC verification only when all rules hold true [3].

Design Rule Checking (DRC) Compliance Function

The DRC compliance function can be represented as:

G = (V, E, L)

• V consists of nodes such as gates, vias, and interconnections.
• E is a collection of edges corresponding to the metal layers and routing interconnections on an integrated circuit.
• L indicates layer-specific information like diffusion and polysilicon.

Incidentally, it will be conducive to simplifying the subsequent discussion if we refer to different designs by numerical indices, but hereafter, we shall use the abbreviation ’the unnumbered point’ for just such a node.

For LVS verification, we cast the problem as a graph-isomorphism test: the schematic netlist graph G_S must match the netlist layout-and-extractor graph G_L. We name a function ϕ for this mapping: a match function must check (5) at each node:

The LVS violation function measures discrepancies:

where δ (x, y) returns 1 if the two nodes do not match, otherwise 0. If δ>0, a mismatch is detected, failing LVS verification [4]. To address LVS verification challenges, we define the problem as a graph isomorphism check between the schematic netlist graph G_s= (V_s, E_s) and the layout-extracted netlist graph G_l= (V_l, E^l). A mismatch function V_diff = V_s − V_l is used, where a non-empty V_diff indicates a failure in LVS verification.

Routing security is addressed through applying AI-driven optimization to mitigate crosstalk, electromagnetic (EM) leakage, and side-channel risks. Routing should be made into a Constrained Shortest-path Problem: we aim to minimize the following expression on routing distance:

where P represents all possible paths, and w (u, v) represents the routing cost considering wirelength, congestion, and security risks. A security-aware routing function minimizes:

with the total cost function:

ensuring that the AI-based routing engine optimizes performance while maintaining security constraints [5].

The parameters α and β serve as weighting coefficients that regulate the balance between two distinct components. The coefficient α determines the contribution of this term to the overall cost function. By adjusting α and β, one can prioritize different aspects of the problem, making these parameters crucial in tuning the behavior of the objective function in applications such as machine learning, optimization, or graph-based modeling.

Graph Neural Networks (GNNs) play a crucial role in anomaly detection and layout learning. Each node feature is updated iteratively using:

where W is a trainable weight matrix, σ is an activation function, and N(v)represents the neighboring nodes of v. This enables GNNs to identify structural anomalies introduced by hardware Trojans [6]. Score functions determine whether a circuit component is secure or compromised. The probability of a secure design is modeled using an energy-based function:

Security Score (Softmax Classification) - where z_i is the logit value for secure classification.

E(X) quantifies deviation from verified designs. An anomaly score is computed as:

where a higher A(X) value indicates potential security risks [7]. Federated learning further enhances verification by training AI models across multiple fabrication sites while preserving data privacy. The federated learning update rule aggregates local models:

where θi^(t) are local model weights, and m_i are the samples per fabrication node, ensuring collaborative, privacy-preserving training [8].

For AI-driven security verification, Graph Neural Networks (GNNs) are employed to analyze circuit layouts, leveraging adjacency matrices A and node attributes X. The node feature updates follow the propagation rule:

where H^(l) is the node representation at layer l, W^(l) is the trainable weight matrix, σ is the activation function, and A is the normalized adjacency matrix.

For stable learning, we impose:

where λ is a bound ensuring weight stability. The eigen value decomposition of A~ guarantees that propagation does not lead to vanishing or exploding gradients, ensuring that the model effectively learns circuit vulnerabilities.

Anomalous circuit modifications are detected using an energy-based function:

where E(G) quantifies deviations from expected circuit layouts, and a higher energy score indicates security threats. Federated learning is incorporated to train AI models across multiple fabrication sites, ensuring privacy-preserving security updates. The global model aggregation follows:

where w_i are local model weights, n_i is the sample size at site i, and N is the total number of participating sites.

In a case study involving an AI-based hardware Trojan detection system applied to a 4-bit ALU, the methodology identifies a malicious XOR gate modification in the carry path. The extracted netlist graph G_mod is compared with the original schematic graph G_orig and a classification function:

predicts the likelihood of a node belonging to a Trojan circuit. The AI model achieves high detection accuracy by leveraging node embeddings and anomaly classification.

Mathematical optimization plays a crucial role in ensuring secure physical design. A cost function is defined as:

where L is the loss function, y_i are ground truth labels, and f (x_{i; θ}) is the security-aware predictor. Security constraints are enforced using Lagrange multipliers:

ensure optimal security-aware verification.

Additional optimization techniques include adversarial robustness strategies such as adversarial training using an attack-resilient Trojan Classification Distance (TCD):

where α determines the sensitivity to adversarial modifications. Reducing TCD_α minimizes false positives while enhancing Trojan detection reliability.

The AI-driven secure physical design verification framework integrates these mathematical models and learning techniques, ensuring scalable and adaptive security verification for modern semiconductor manufacturing.

A case study involving hardware Trojan detection in a 4-bit ALU illustrates the framework’s effectiveness. A Trojan is inserted by modifying the carry path of a full adder with an XOR gate, altering graph structure and connectivity. GNN-based anomaly detection identifies unexpected XOR insertions by comparing extracted netlist graphs:

where W_o represents final classification weights, and h_v is the GNN-learned embedding for node v [9]. The AI model successfully flags Trojan nodes with a probability of 0.97, demonstrating high detection accuracy [10].

To ensure constraint-aware verification, AI-based mathematical optimization is employed. The cost function incorporates DRC, LVS, and routing constraints:

where each term quantifies security violations in DRC, LVS, and routing. The Lagrange optimization formulation is defined as:

where λ is a Lagrange multiplier enforcing security constraints. The optimization satisfies Karush-Kuhn-Tucker (KKT) conditions:

ensuring provably secure verification while maintaining design performance [11]. By integrating AI-driven anomaly detection, secure routing optimization, and mathematical modeling, this framework provides a scalable, automated, and adaptive approach to IC security verification [12]. The AI-driven methodology continuously evolves, ensuring that security verification adapts dynamically to counter emerging threats, making it an essential part of next-generation semiconductor manufacturing [13,14].

For large-scale ICs, computational overhead is a concern. The complexity of GNN training is approximately:

where ∣V∣ and ∣E∣ are the number of nodes (gates) and edges (interconnects). Compared to traditional rule-based verification, which has an exponential complexity for large-scale circuits, the proposed model scales efficiently.

3. Evaluation based on Aggregator, Combination, and Readout Functions

The Multi-View Verification method presents a system supporting a layered layout such that evaluation criteria are discernible from the structure itself. The nodes of the graph are the components of the circuit, and the links are how they are laid out and connected.

The capabilities of the verification method can be accessed via aggregator functions, combination functions, and a readout. In this way, the model can capture a circuit’s local and global context.

Aggregator functions are employed in Graph Neural Networks (GNNs) to collect and summarize information from a user’s neighbors, thereby allowing the model to learn local characteristics in IC layouts. Where hv(t+1) is the updated feature of node v, N(v) represents neighboring nodes, and AGG is the aggregation function. Many common aggregators include:

where hv^(t+1) is the updated feature of node v, N(v) represents neighboring nodes, and AGG is the aggregation function. Common aggregators include:

Mean Aggregator (Averaging Neighbor Features)

This smoothens node features, reducing noise in circuit layouts [1].

Max Pooling Aggregator (Capturing Maximum Influence)

This highlights dominant neighbor features, useful in Trojan detection.

LSTM-Based Aggregator (Capturing Sequential Dependencies)

Useful for modeling propagation effects in circuit timing analysis [2].

Combination functions: After all the aggregation is done, the combination function ensures that the updated node representation retains its original property and can reflect neighbors’ influence. Where standard COMBINE functions include:

where common COMBINE functions include:

Concatenation: This retains distinctive self-information and neighborhood context.

Weighted Sum: Useful when balancing local vs. global importance in verification [3].

Residual Connection (Skip Connection): Helps stabilize deeper GNN layers, preventing gradient vanishing.

Readout functions: These aggregate node embeddings into a global view of all nodes on the circuit, permitting the highest-level classification or verification. Standard READOUT functions include:

Sum Readout: This method works when nothing and gates the need as trivial, such as in Trojan localization.

Mean Readout: The node layout is balanced so that this method becomes effective.

Max Pooling Readout: This identifies the dominant security issues and makes them easy to spot in local Trojan detection.

Attention-Based Readout: Here, the attention weight αv assigning values to different nodes gives adaptive verification the chance of improvement [5].

4. Comparison with Existing Models

AI-driven secure physical design verification, which is a burgeoning field, has been directly addressed by several research efforts. They resorted to rule-based methods, machine learning, and hybrid techniques for hardware security challenges. Anomaly detection and specifically constrained optimization based on GNNs proposes a new method since existing methods lack many aspects that will be key for the future: federated learning, policies learning involving security for the route itself (routing security), and AI-based design rule checking (DRC).

Methodology	Strengths	Limitations	How Our Model Improves
Golden Reference-Based Verification	High accuracy for known threats	Requires trusting chips, and outsourced design cannot be accommodated	Our model eliminates the dependency on golden reference by employing AI-based anomaly detection.
Machine Learning (ML) for Security Verification	Adaptable to emerging threats	Fields require large amounts of labeled data.	Our GNN-based framework uses graph structure learning to achieve larger generalization
SAT-Based Trojan Detection	Effective for combinational Trojans	Fails on HTs (both sequential and deep).	Our approach uses deep learning to capture structural and behavioral anomalies.
Side-Channel Analysis for Hardware Security	Detects Trojans via power/EM signatures	Minor errors in the data or disturbances caused by environmental constraints	To mitigate side-channel hazards, our framework integrates power/routing optimization based on AI.

5. Future Directions

Although the paper is theoretical, discussing how this model could be implemented in real-world EDA tools would enhance its applicability.

Integration into Existing EDA Tools

Hardware Deployment Considerations

• Computational Overhead: AI models require high-performance GPUs for training, yet one can use FPGAs to implement them in a real-time security monitoring application.

• Compatibility with Commercial Foundries: A federated learning approach ensures one can train AI models across different IC manufacturers while keeping the design confidential.

Discussing real-world feasibility ensures that the theoretical framework has practical adoption potential.

6. Conclusions

The proposed AI-driven secure physical design verification framework adopts graph-based learning, constrained optimization, and federated AI anomaly detection as a theoretical foundation for next-generation IC security verification. Modeling IC verification as an adaptive security-aware optimization problem removes any dependence on so-called golden reference models and ensures that porting-level issues are adequately addressed under pressure from implementation considerations. Future research directions should focus on:

Quantum-Resilient IC Security – Extending the AI model to verify quantum-secure cryptographic designs.

Adversarial AI Training for Hardware Security: Enhancing model robustness against adversarial attacks that try to evade anomaly detection.

Integration with Cloud-Based EDA Platforms – Making it possible for IC manufacturers to use scalable and distributed methods in constructing their security environments.

By offering a mathematically rigorous and scalable security model, this paper provides a path for semiconductor manufacturers to move to AI, the trusted assistant.