Submitted:
05 January 2025
Posted:
06 January 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Related Work
3. Methodologies
3.1. Graph Convolutional Neural Networks and Feature Aggregation
3.2. Cross-Modal Attention Mechanisms
4. Experiments
4.1. Experimental Setup
4.2. Experimental Analysis
5. Conclusion
References
- Wei, Cong, et al. "Uniir: Training and benchmarking universal multimodal information retrievers." European Conference on Computer Vision. Springer, Cham, 2025.
- Kaur, Parminder, Husanbir Singh Pannu, and Avleen Kaur Malhi. "Comparative analysis on cross-modal information retrieval: A review." Computer Science Review 39 (2021): 100336. [CrossRef]
- Lin, Weizhe, et al. "Fine-grained late-interaction multi-modal retrieval for retrieval augmented visual question answering." Advances in Neural Information Processing Systems 36 (2023): 22820-22840.
- Deldjoo, Yashar, Johanne R. Trippas, and Hamed Zamani. "Towards multi-modal conversational information seeking." Proceedings of the 44th International ACM SIGIR conference on research and development in Information Retrieval. 2021.
- Zhang, Zhengkun, et al. "Unims: A unified framework for multimodal summarization with knowledge distillation." Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 36. No. 10. 2022.
- Lance, Christopher, et al. "Multimodal single cell data integration challenge: results and lessons learned." BioRxiv (2022): 2022-04. [CrossRef]
- Zhang, Yuhao, Peng Qi, and Christopher D. Manning. "Graph convolution over pruned dependency trees improves relation extraction." arXiv preprint arXiv:1809.10185 (2018).
- Zhang, Changhe, et al. "Exploration of deep learning-driven multimodal information fusion frameworks and their application in lower limb motion recognition." Biomedical Signal Processing and Control 96 (2024): 106551. [CrossRef]
- Cai, Jie, et al. "Multimodal continual graph learning with neural architecture search." Proceedings of the ACM Web Conference 2022. 2022.
- Nguyen, Thien, and Ralph Grishman. "Graph convolutional networks with argument-aware pooling for event detection." Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 32. No. 1. 2018. [CrossRef]
- Marcheggiani, Diego, Jasmijn Bastings, and Ivan Titov. "Exploiting semantics in neural machine translation with graph convolutional networks." arXiv preprint arXiv:1804.08313 (2018).
- Cai, Jie, et al. "Multimodal continual graph learning with neural architecture search." Proceedings of the ACM Web Conference 2022. 2022.
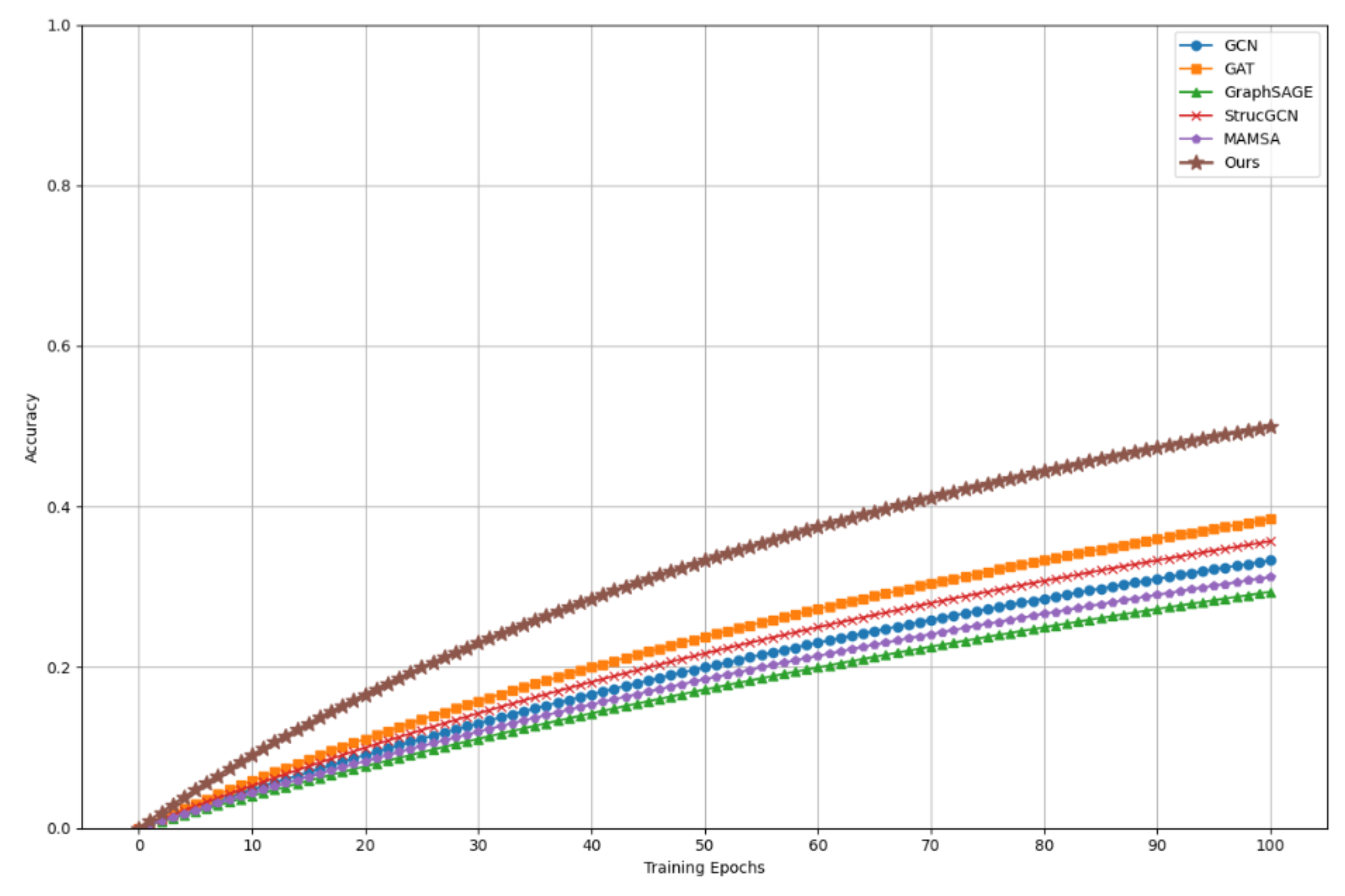
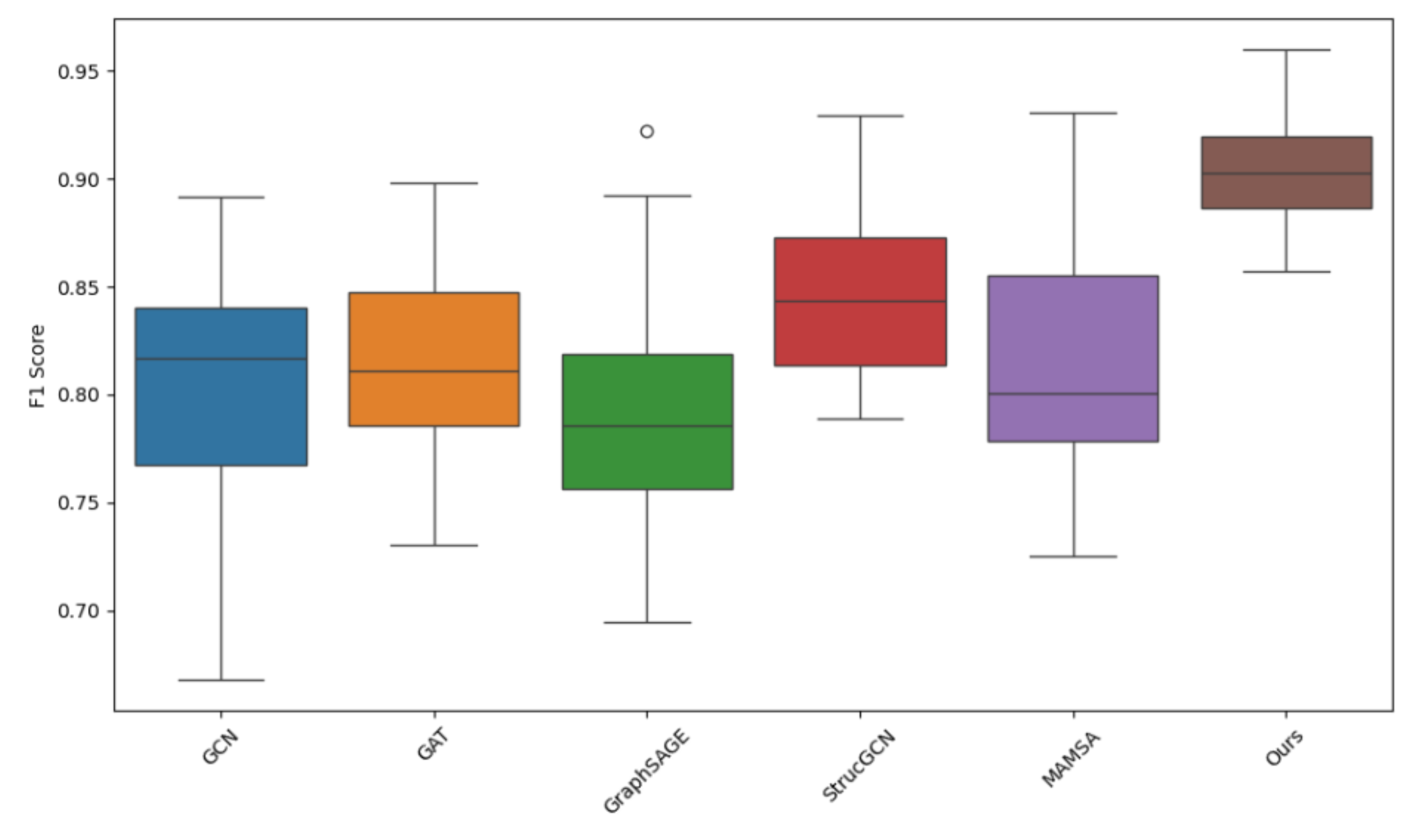
| Methods | Learning Rate 0.01 | Learning Rate 0.001 | Learning Rate 0.0001 | Learning Rate 0.00001 |
|---|---|---|---|---|
| GCN | 0.245 | 0.235 | 0.255 | 0.265 |
| GAT | 0.225 | 0.215 | 0.245 | 0.255 |
| GraphSAGE | 0.21 | 0.205 | 0.23 | 0.25 |
| StrucGCN | 0.2 | 0.19 | 0.22 | 0.24 |
| MAMSA | 0.19 | 0.18 | 0.21 | 0.23 |
| Ours | 0.17 | 0.16 | 0.19 | 0.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





