1. Introduction
Children’s Pneumonia
Pneumonia is a leading inflammatory lung disease and a major cause of morbidity and mortality among children under 5 years of age, especially in countries with limited health resources. With epidemiological data showing over 146 million cases and 4 million deaths annually, the disease represents a serious public health problem [
1]. Significant progress in the control and prevention of childhood pneumonia has been achieved through the introduction of vaccines against Haemophilus influenzae type B and pneumococcal infections, which have significantly reduced morbidity and complications [
2]. However, pneumonia remains widespread, especially among children in low-income areas and those with limited access to health services.
Pneumonia is a multifactorial disease caused by viruses, bacteria, and sometimes fungal or parasitic organisms. In children under 5 years of age, viruses are the leading causes, including respiratory syncytial virus (RSV), Streptococcus pneumoniae, and Haemophilus influenzae. Symptoms vary with age but typically include fever, cough, shortness of breath, fatigue, and anorexia [
3]. In younger children, nonspecific signs such as abdominal pain, stiff neck, and even apnea may be observed.
Radiographic examinations are essential for the diagnosis and follow-up of pneumonia in children. Radiography can visualize specific changes in the lung parenchyma that aid in the clinical diagnosis. Viral pneumonias are often characterized by bilateral interstitial infiltrates and peribronchial disruptions. On the other hand, bacterial pneumonias caused by S. pneumoniae or S. aureus, can lead to lobar involvement, pleural effusion, empyema, and even necrotizing pneumonia [
4]. In severe cases, radiographic findings may include pneumatocele or lung abscess, requiring urgent treatment.
Early and accurate diagnosis is critical for successful treatment of pneumonia and minimizing complications. According to the World Health Organization (WHO), a child with pneumonia should undergo radiography in the presence of “unexplained” fever, respiratory distress, or suspicion of bacterial infection. X-rays not only help identify the pathology, but also provide a basis for monitoring the effectiveness of treatment.
Complications of pneumonia in children include respiratory distress, apnoea, bronchial hyperresponsiveness, and, in severe cases, death. Long-term sequelae such as bronchiectasis, bronchiolitis obliterans, and pneumosclerosis may also develop in chronic or poorly treated cases [
5]. Radiography is an indispensable tool for detecting these complications, making it a key component in disease management.
Intuitionistic Fuzzy Sets
Intuitionistic fuzzy sets (IFS) are sets whose elements have degrees of belonging and not belonging. They are defined by Krassimir Atanassov [6, 7, 8] (1983) as an extension of fuzzy sets of Lotfi A. Zadeh. In the classical theory, element belongs or does not belong to the summary. Zadeh defines membership in the interval [0, l]. The theory of intuitionistic fuzzy sets extends above concepts by comparing belonging and not belonging real numbers in the interval [0, l] and the sum of these numbers must also belongs to the interval [0, l].
Let the universe is E. Let A be a subset of E. Let us construct the set
A*= {〈x, μA(x), νA(x)〉|x∈E},
where 0 ≤ μA(x) + νA(x) ≤ 1.
We will call A* an IFS.
The functions μA(x): E→[0, 1] and νA(x): E→[0, 1] set degree of membership and non-membership.
It is defined the function πA(x): E→[0, 1] through πA(x) = 1-μA(x)-νA(x), corresponding to the degree of uncertainty.
In addition to constructing a model, here we will define an assessment of the training accuracy rate
µ, degree of training inaccuracy
ν and the degree of uncertainty
π.
where
µ ∈[0; 1];
ai – current value of accuracy;
B – maximum of the accuracy;
A - validation loss maximum; non-affiliation coefficient –
ν, reflecting the degree of recognition accuracy, and
where
ν ∈[0; 1];
bi – current value of validation loss and a uncertainty degree reflecting the degree of discrepancy between these two countermeasures
At the beginning is done statistics of the values that we used for learning the neural network. Initially when still no information has been obtained, all estimations are given initial values of <0, 0>. When
k > 0, the current (
k+l)-st estimation is calculated on the basis of the previous estimations according to the recurrence relation
where 〈μk, νk〉 is the previous estimation, and 〈μ, ν〉 is the estimation of the latest measurement, for m, n ∈ [0, l] and m+ n ≤ 1.
Мodular Neural Network (MNN)
In recent years, modular neural networks (MNN) have established themselves as a powerful tool for analysis and diagnosis in medicine. Unlike traditional “monolithic” architectures, MNNs divide complex tasks into smaller and independent submodules that can be trained in parallel. This modularity provides several key advantages, especially in disease recognition. This type of neural network has the following advantages. The use of modular architectures for medical imaging allows achieving high accuracy in tasks such as tumor detection and anomaly classification. According to Dao and Ly [
9] modular systems combining convolutional networks and transformers provide better extraction of global and local features from images, making them extremely suitable for diagnosing diseases such as cancer and brain tumors [
9]. Modular networks can process different data sources – such as computed tomography (CT) and magnetic resonance imaging (MRI) – with high efficiency. [
10] emphasize that combining different modules in neural networks improves the recognition of spatiotemporal features of images, which is especially useful in neurological diseases such as Alzheimer's [
10]. An advantage of the modular architecture is the ability to train specialized modules for different subtasks. Guebsi and Chokmani [
11] demonstrate how networks can be applied in the precise recognition of heart and lung diseases by dividing the diagnostic process into separate components [
11]. MNNs allow for parallel training and optimization of submodules, which significantly reduces computational complexity. El Hajjar et al. (2024) demonstrate this in building models for cardiovascular disease recognition, where the modular approach reduces data processing time by up to 40% [
12]. Another advantage of MNN is the easier interpretation of the models. Ashraf et al. [
13] emphasize that modular structures provide clear dependencies between input data and predictions, which is crucial for clinical applications [
13].
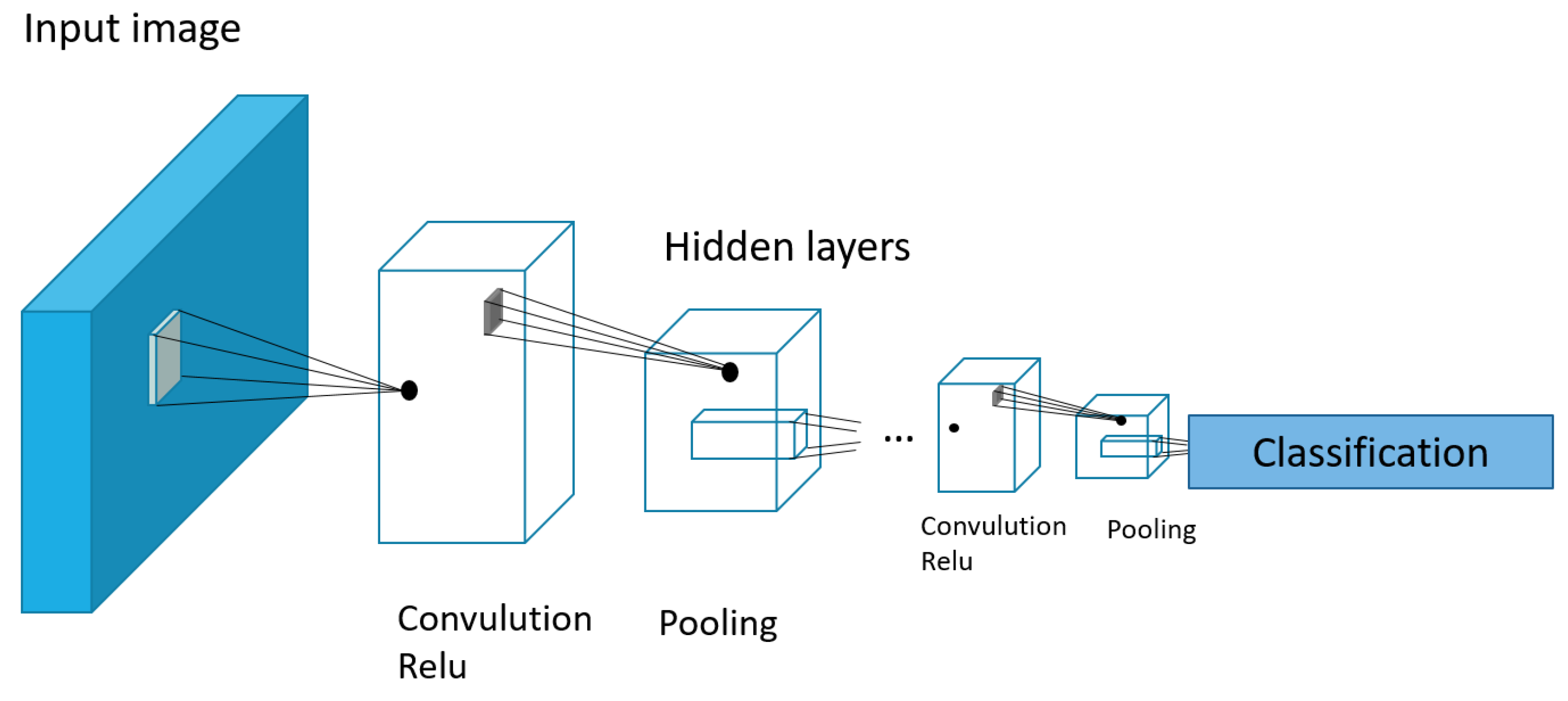
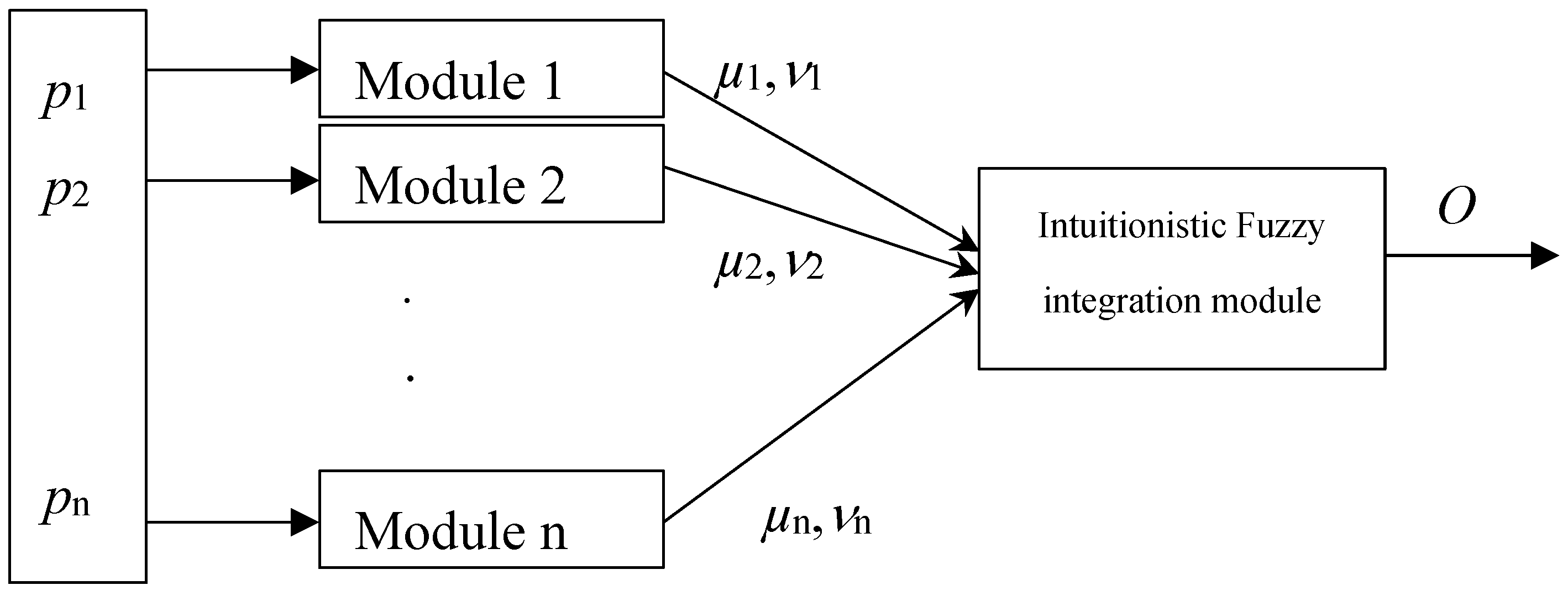
Figure 1.
Modular neural network structure.
Figure 1.
Modular neural network structure.
The output O is calculated according to the following equation [
14], which essentially performs a weighted integration of the module outputs.
where:
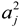
output
of the Module
j ∈ [1, 2, …,
m]
;
kj – coefficient of existence of Module j. The coefficient of existence of every module shows the presence/ absence of the respective module, with respect to the need of that module in the particular case.
In our case m = 3 (3 for the images).
This article is a continuation of three other articles [15, 16, 17].
2. Implementation
Here we have conditionally chosen three separate modules, the inputs of which are supplied with pixels with a color in the interval 0-1/3*256; 1/3*256 - 2/3*256; 2/3*256 - 256.
The main idea of the article is based on the fact that the positive results from each of the modules are taken.
In the first module, an image is located in which the black color predominates. This is the part in which the lack of bone structure or soft tissues of the person is visible on the X-ray. Here is the unimportant part of the image. The second module receives information from the middle part of the image. Here the greatest information about the lung and possible diseases is obtained.
In the third module is the brightest part of the X-ray image, which is usually in the area of the bone structure.
The method for working with X-ray images in CNN proposed by us is in the following sequence and includes the following sequence of steps:
Data preprocessing: X-ray images are collected from databases or medical sources and then converted to a standard size and format (in our case, this is 299x299 pixels). Techniques such as rotation, scaling and brightness change are applied to increase the volume of the training set. Pixels are scaled to valuesbetween 0 and 1 or standardized around the arithmetic mean value.
Core part: The X-ray image is entered into the network as a matrix of pixels. The so-called convolutional layers are used, which include: Extraction of local features by applying filters, with each filter identifying different aspects such as edges, textures and structures; The so-called ReLU activation - a nonlinear function that removes negative values, improving the modelability of the network. Then, the data size is reduced using techniques such as max pooling or average pooling, which reduces complexity and prevents overloading. Using so-called deep convolutional layers, which serve to identify more complex features, such as lobar involvement, pleural effusion or interstitial infiltrates.
In the last step, the individual images are classified: Converting the 2D data into a one-dimensional vector. Using fully connected layers (Dense Layers) and finally using the Softmax function. It determines the probabilities for different classes (e.g. “normal”, “pneumonia”, “other pathologies”).
In this article, we use Inception v3, one of the neural network architectures that is specifically designed for image processing. It was developed by Google and is part of the Inception series of models. It has 33 layers and is a reasonable compromise between accuracy and processing speed (Figure 2.).
Figure 2.
Structure of the CNN Inseption V3 neural networks.
Figure 2.
Structure of the CNN Inseption V3 neural networks.
3. Results
For image processing, a database of 3000 images of children up to 5 years of age was created, collected from various sources, mainly from Internet databases. In order to perform image processing, first the entire database of 3000 X-ray images is divided into three identical databases with three groups with the interval 0-1/3*256; 1/3*256 - 2/3*256; 2/3*256 - 256. Each group is fed to one of the three modules. For the interval 0-86 pixel values are fed to Module 1, for those in the interval 87 – 167 are fed to Module 2 and finally from values 168 – 255 to Module 3.
And each of the modules is fed 3000 x-ray images distributed in the ratio of 80% for training, 10% for testing and 10% for verification.
When the X-ray images are submitted, the distribution
shown in Figure 3 is obtained. It shows
the number of X-ray images labeled with the presence of pneumonia and the
absence of pneumonia for the three groups (training, testing, and
verification).
Figure 3.
Distribution of individual X-ray images by training, testing and verification groups.
Figure 3.
Distribution of individual X-ray images by training, testing and verification groups.
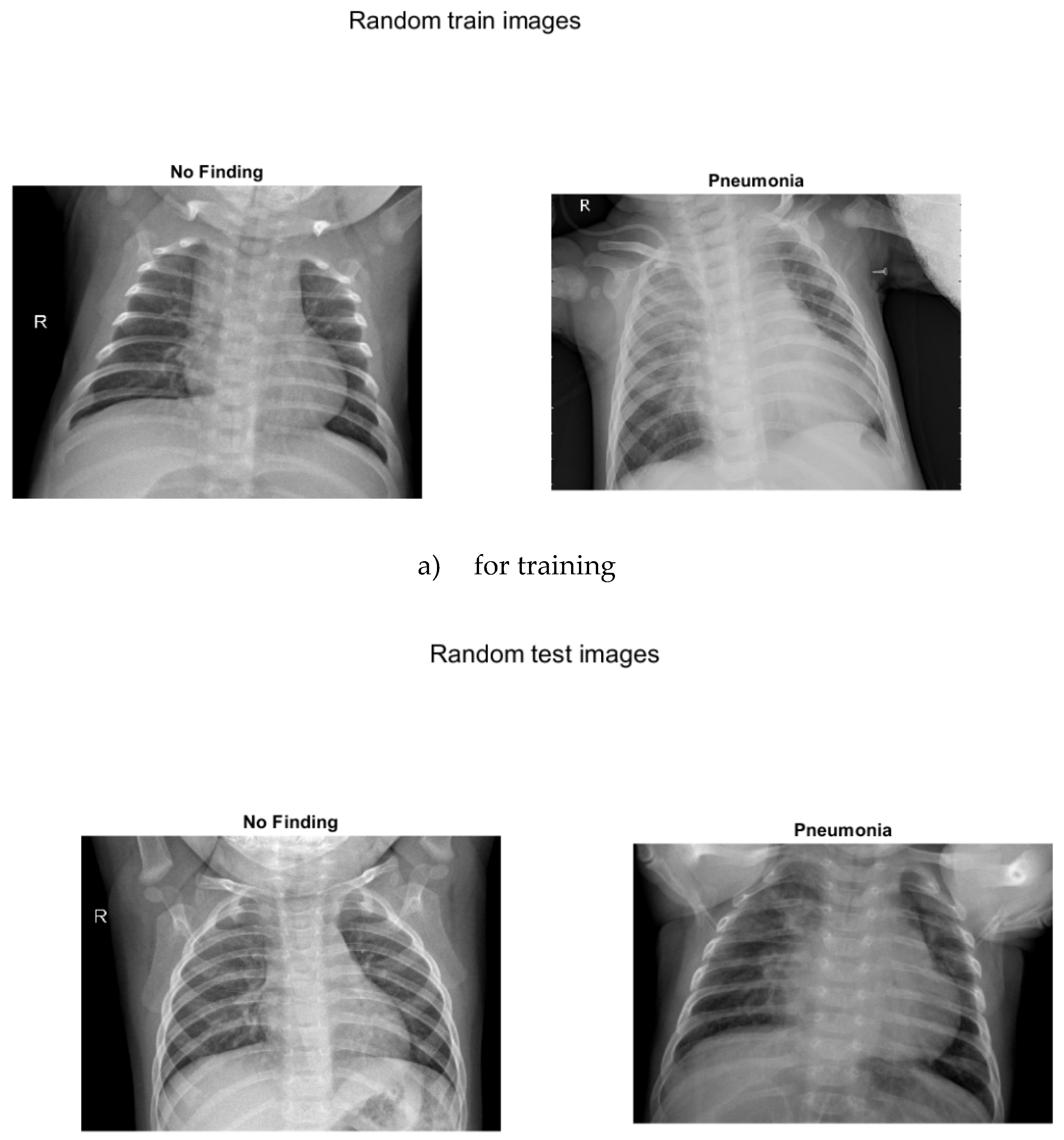
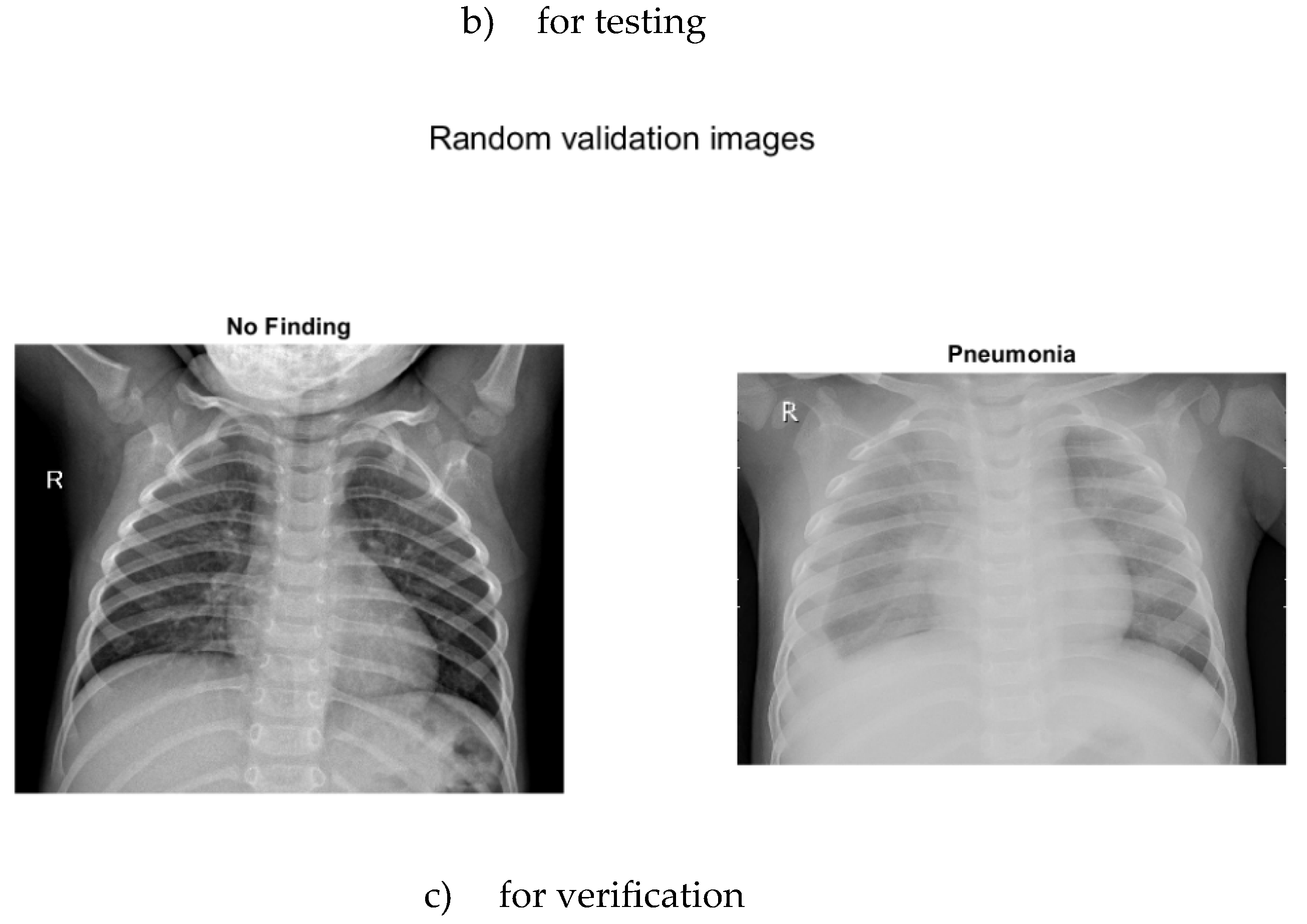
Three separate images show sample images with and without pneumonia of children up to 5 years old
Figure 4. a) for training, b) for testing, c) for verification.
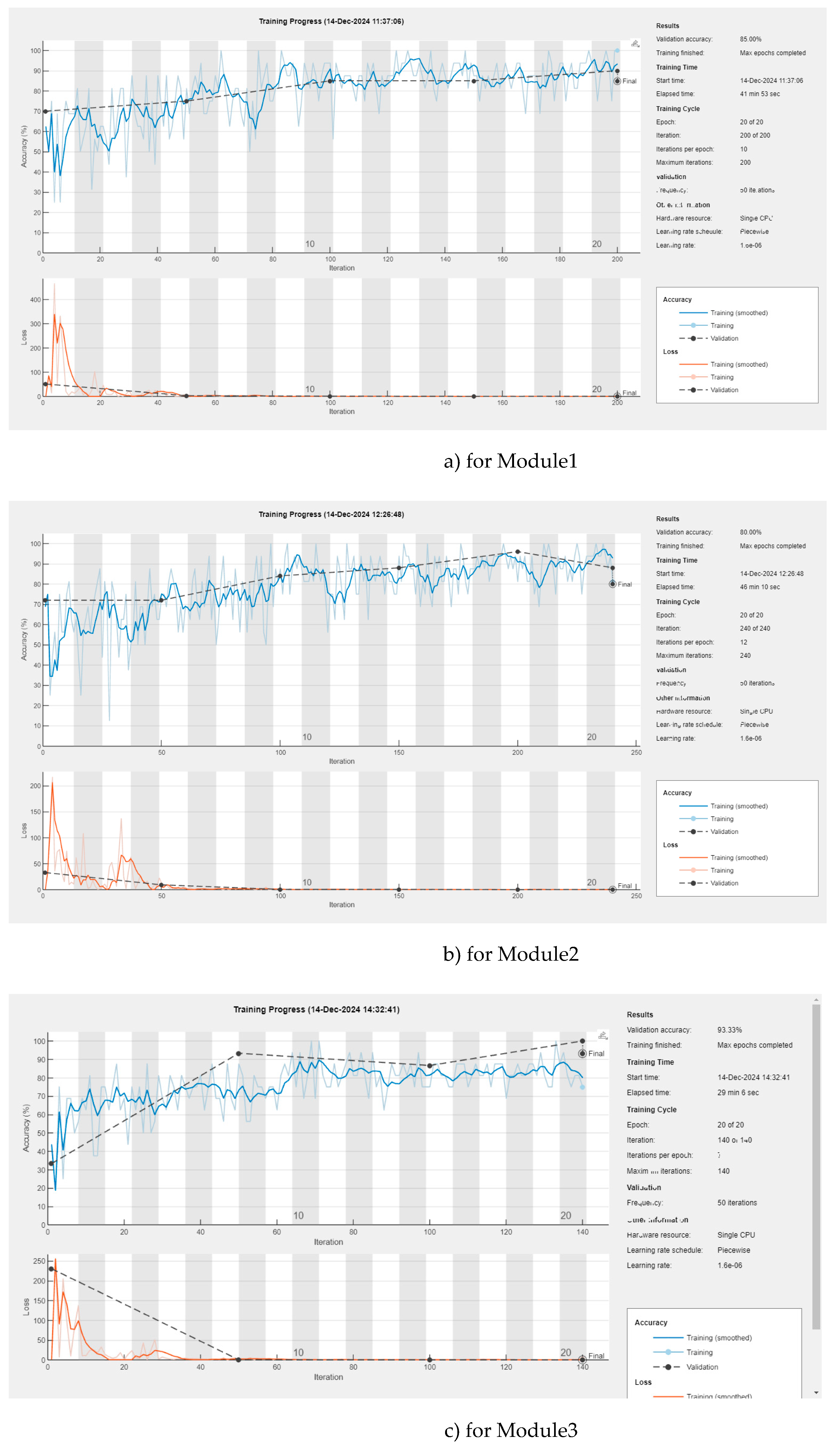
Each of the modules is taught separately with the corresponding X-rays separately. The teaching of each of the modules 1, 2 and 3 can be seen in
Figure 5 a) for Module1, b) for Module2, c) for Module3
The following table (Table 1) contains the results of the three modules 1, 2, 3 and the result after using the Intuitionistic Fuzzy integration module
| Title |
Module 1 |
Module 2 |
Module 3 |
Output O |
| Number of epoches/iteration |
20/200 |
20/240 |
20/140 |
|
| Accuracy |
85.00% |
80% |
93.33% |
94.93% |
| Validation lost |
0.0043 |
0.0053 |
0.0032 |
0.0017 |
4. Discussion
The presented hybrid convolutional neural network (CNN) combined with intuitionistic fuzzy estimators (IFE) demonstrates significant progress in the detection of pneumonia in children. The system uses three modules to process different parts of X-ray images - background, lung tissue and bone structure - ensuring maximum information extraction. The results of each module show high accuracy: Module 1 achieved 85.00%, Module 2 achieved 80.00% and Module 3 achieved 93.33%. After integrating the data using the intuitionistic fuzzy logic module, the overall accuracy of the system reached an impressive 94.93%, making it significantly more efficient compared to traditional approaches. The validation losses were also minimal, being 0.0043 for module 1, 0.0053 for module 2, 0.0032 for module 3 and only 0.0017 for the entire system, indicating excellent model optimization.
The network uses the 33-layer Inception v3 architecture, specifically tailored for image processing, which helps in identifying complex features such as interstitial infiltrates, lobar involvement and pleural effusions. The model was trained and tested on a dataset of 3000 X-ray images, split in a ratio of 80:10:10 for training, testing and validation. The data distribution and modular learning ensure the robustness of the system when working with noisy and variable data. A key strength of the approach lies in the use of intuitionistic fuzzy logic, which successfully manages uncertainty and reduces the risk of misclassification.
These results have broad clinical applicability, providing a reliable tool for early diagnosis of pneumonia in children. The developed model can be extended with additional data and adapted to detect other respiratory diseases, improving health outcomes, especially in resource-limited settings. Future steps include testing larger and more diverse datasets and comparing them with other hybrid architectures to validate the flexibility and efficiency of the approach.
5. Conclusions
The proposed hybrid convolutional neural network (CNN) enriched with intuitionistic fuzzy estimation (IFE) offers a reliable and highly accurate approach for pneumonia detection in children. By using modular analysis of X-ray images and integrating the results through phase logic, the system achieves an overall accuracy of 94.93%, outperforming traditional methods. This innovative combination of CNN and intuitionistic phase logic effectively addresses the challenges associated with uncertainties and noise in medical images, providing reliable diagnostic results. Low validation loss values in all modules highlight the optimization and robustness of the model. With its clinically applicable results, the model provides a valuable tool for early diagnosis and treatment, which can reduce mortality and complications associated with pneumonia in children. Future work should focus on expanding the dataset, exploring the applicability to other diseases, and further validating the model in real clinical settings to improve its universality and impact. This approach represents a promising step forward in the integration of artificial intelligence in pediatric medical diagnostics.
The proposed method, based on a hybrid convolutional neural network (CNN) enriched with intuitionistic fuzzy estimation (IFE), has the potential for widespread application in medical diagnostics, especially in X-ray image processing and detection of pulmonary diseases. Its main applications include:
1. Pneumonia diagnosis in clinical settings, as the model can assist medical professionals in the rapid and accurate detection of pneumonia, especially in pediatrics, where early diagnosis is critical to prevent complications and mortality.
2. Telemedicine and mobile health applications in regions with limited access to qualified radiologists, the method can be integrated into telemedicine platforms or mobile devices for remote diagnosis of patients by uploading X-ray images.
3. The method can support monitoring of therapy effectiveness through periodic analysis of patients' X-ray images, allowing for precise adjustments in treatment.
4. Research projects: The method offers a platform for testing new algorithms and hybrid approaches that combine artificial intelligence and phase logic aimed at improving medical technologies.
The potential of this approach is best deployed in environments with high requirements for accuracy and robustness, allowing the integration of artificial intelligence into everyday medical practice and healthcare.
Author Contributions
The conceptualization and methodology were developed by Sotir Sotirov and Evdokia Sotirova. Data processing was performed by Daniela Orozova. The initial draft of the manuscript was written by Sotir Sotirov, and the editing and review of the manuscript were carried out by Evdokia Sotirova. The validation of the data and conclusions related to the medical aspects were contributed by Boris Angelov and Magdalena Vylcheva.
Funding
The article is supported by two projects: Bulgarian National Recovery and Resilience Plan, Component “Innovative Bulgaria”, the Project No. BG-RRP-2.004-0006-C02 “Development of research and innovation at Trakia University in service of health and sustainable well-being ” and European Regional Development Fund through the Operational Program “Science and Education for Smart Growth” under contract UNITe No BG05M2OP001–1.001–0004.
References
- UNICEF (2021). State of the World's Children: Reimagining primary health care for every child.
- Klugman, K.P.; Black, S. Impact of conjugate pneumococcal vaccines on developing countries. Vaccine 2018, 36, 4306–4314. [Google Scholar]
- Shann, F. Pneumonia in children: Priorities for the research agenda. Bulletin of the World Health Organization 2010, 88, 340–346. [Google Scholar]
- Harris, M. , Clark, J., Coote, N., et al. British Thoracic Society guidelines for the management of community-acquired pneumonia in children. Thorax, 66(Suppl 2), ii1-ii23. [Google Scholar]
- Bradley, J.S. , Byington, C. L., Shah, S.S., et al. The management of community-acquired pneumonia in infants and children older than 3 months of age: Clinical practice guidelines by the Pediatric Infectious Diseases Society and the Infectious Diseases Society of America. Clinical Infectious Diseases 2011, 53, e25–e76. [Google Scholar]
- Atanassov, K. : Intuitionistic Fuzzy Sets. Springer, Heidelberg (1999).
- Atanassov, K. : On Intuitionistic Fuzzy Sets Theory. Springer, Berlin (2012.
- Atanassov, K. : Intuitionistic fuzzy logics as tools for evaluation of Data Mining processes. Knowledge-Based Systems 2015, 80, 122–130. [Google Scholar] [CrossRef]
- Dao, L.; Ly, N.Q. Recent Advances in Medical Image Classification. Recent Advances in Medical Image Classification 15.7 ( 2024. [CrossRef]
- Hu, Z.; Wu, H.; He, L. A Neural Network for EEG Emotion Recognition that Combines CNN and Transformer for Multi-scale Spatial-temporal Feature Extraction. IAENG International Journal of Computer Science 2024, 51. [Google Scholar]
- Gabsi, Abd El Hedi. "Integrating artificial intelligence in industry 4.0: insights, challenges, and future prospects–a literature review." Annals of Operations Research 2024, 1-28.
- Saleem, Amjad, et al. "A Comprehensive Systematic Survey of IoT Protocols: Implications for Data Quality and Performance. IEEE Access (2024).
- Shin, J. , Miah, A. S. M., Kabir, M. H., Rahim, M. A., & Al Shiam, A. (2024). A Methodological and Structural Review of Hand Gesture Recognition Across Diverse Data Modalities. IEEE Access.
- NDong, L. Zhao, C. H. Wu, J.F. Chang,Inception v3 based cervical cell classification combined with artificially extracted features, Applied Soft Computing 2020, 93, 106311. [Google Scholar]
- Kralev, K. , Sotirov, S., Sotirova, E., Petrova-Geretto, E., Petkov, D. Modular Convolutional Neural Network for Children Pneumonia Detection via X-ray Images. In: Kahraman, C., Cevik Onar, S., Cebi, S., Oztaysi, B., Tolga, A.C., Ucal Sari, I. (eds) Intelligent and Fuzzy Systems. INFUS 2024. Lecture Notes in Networks and Systems 2024, 1088.
- Kralev, K. , Mirincheva, Z., Sotirov, S. Hybrid Convolutional Neural Network with Intuitionistic Fuzzy Estimations for Detection of Kidney Damage in Patients with Diabetes Mellitus. In: Kahraman, C., Cevik Onar, S., Cebi, S., Oztaysi, B., Tolga, A.C., Ucal Sari, I. (eds) Intelligent and Fuzzy Systems. INFUS 2024. Lecture Notes in Networks and Systems 2024, 1088.
- Kralev, K. , Mirinchev, N., Sotirov, S., Sotirova, E., Cholakova, Z. A Modular Deep Convolutional Neural Network for Imroving Accuracy in Prostate Biopsies. In: Kahraman, C., Cevik Onar, S., Cebi, S., Oztaysi, B., Tolga, A.C., Ucal Sari, I. (eds) Intelligent and Fuzzy Systems. INFUS 2024. Lecture Notes in Networks and Systems, vol 1088. Springer: Cham, 2024.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
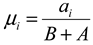
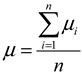
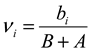
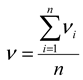
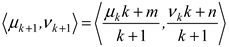
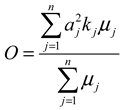
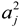 output
of the Module j ∈ [1, 2, …, m]
;
output
of the Module j ∈ [1, 2, …, m]
;