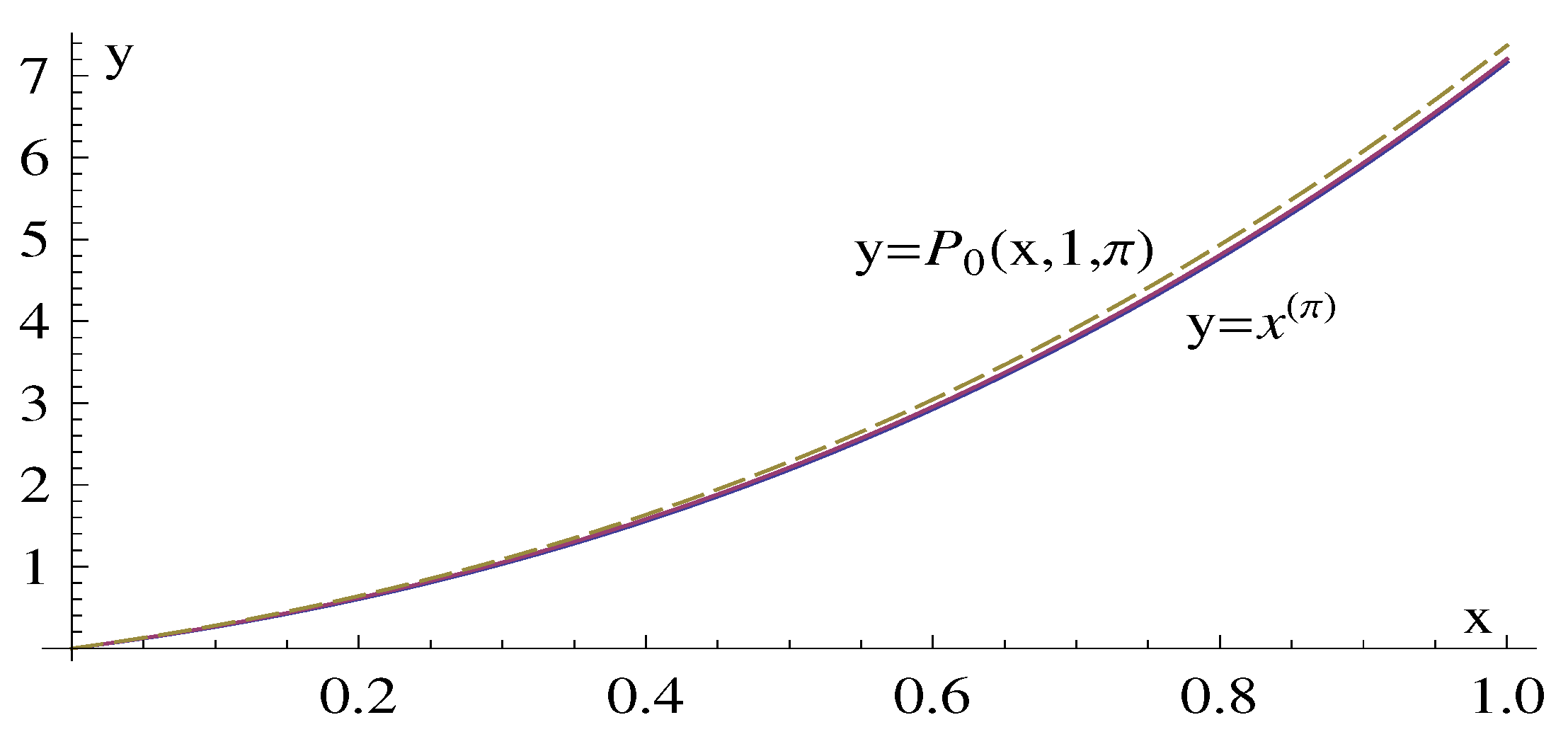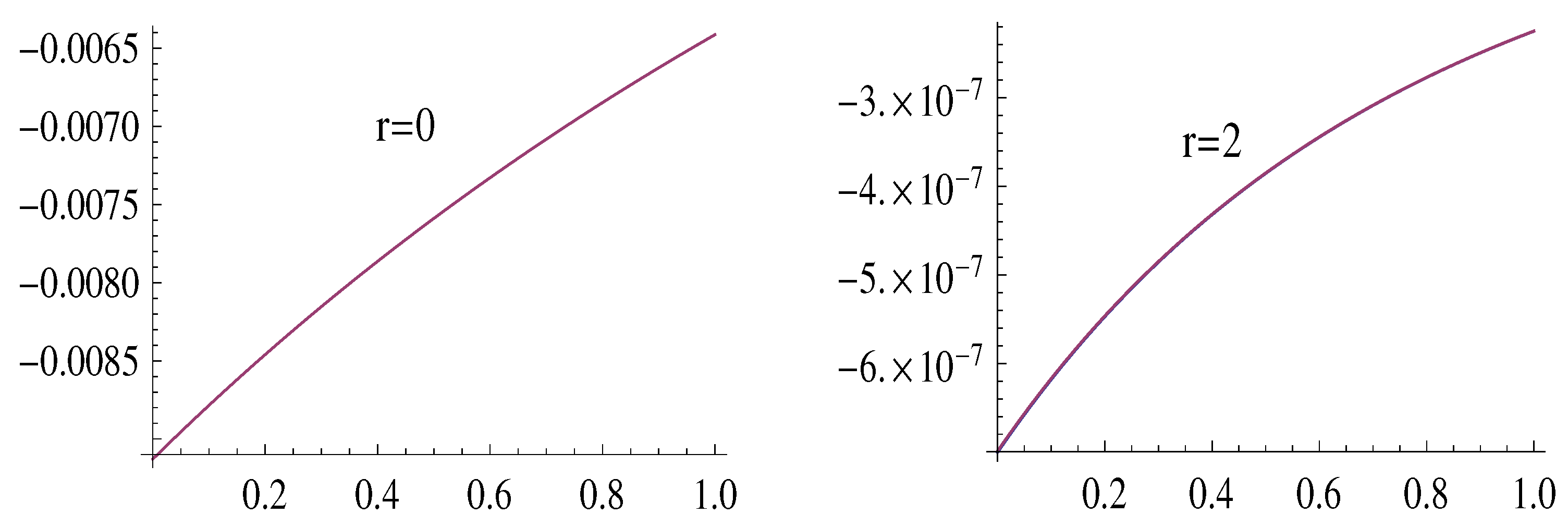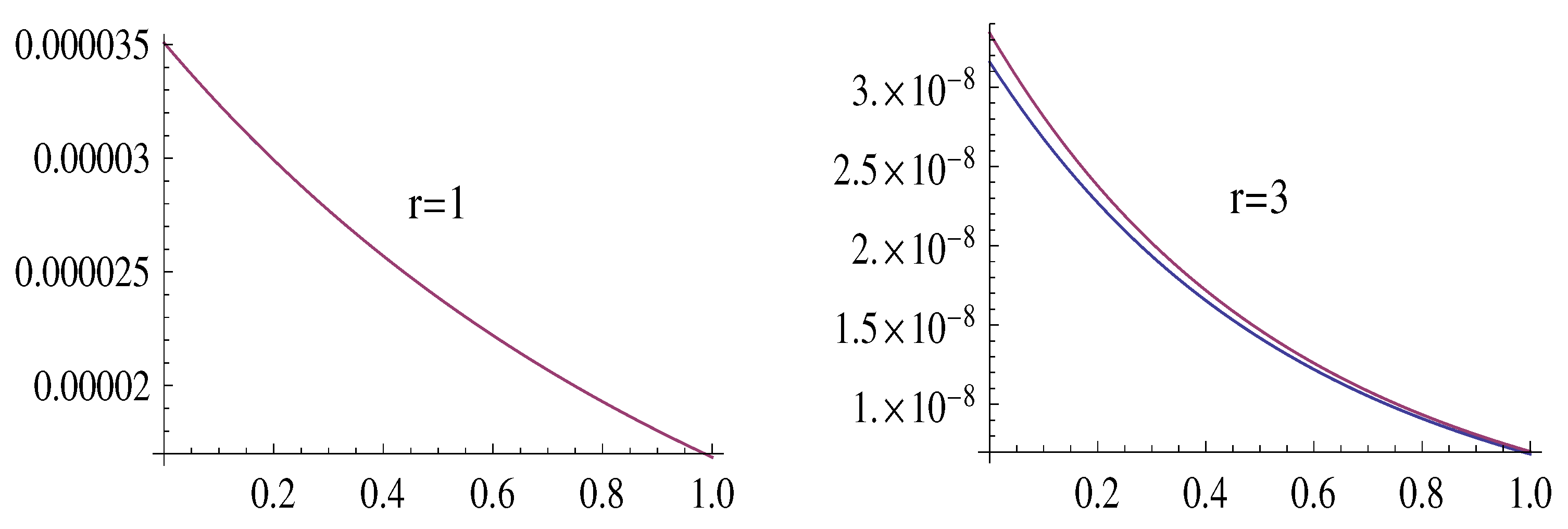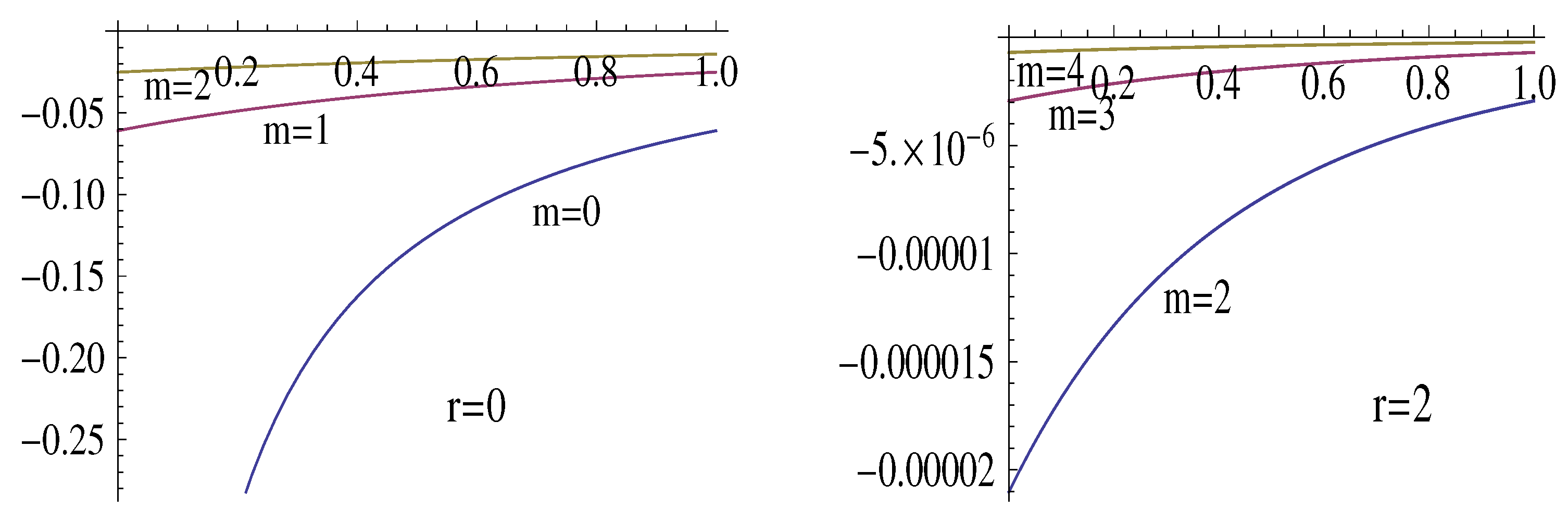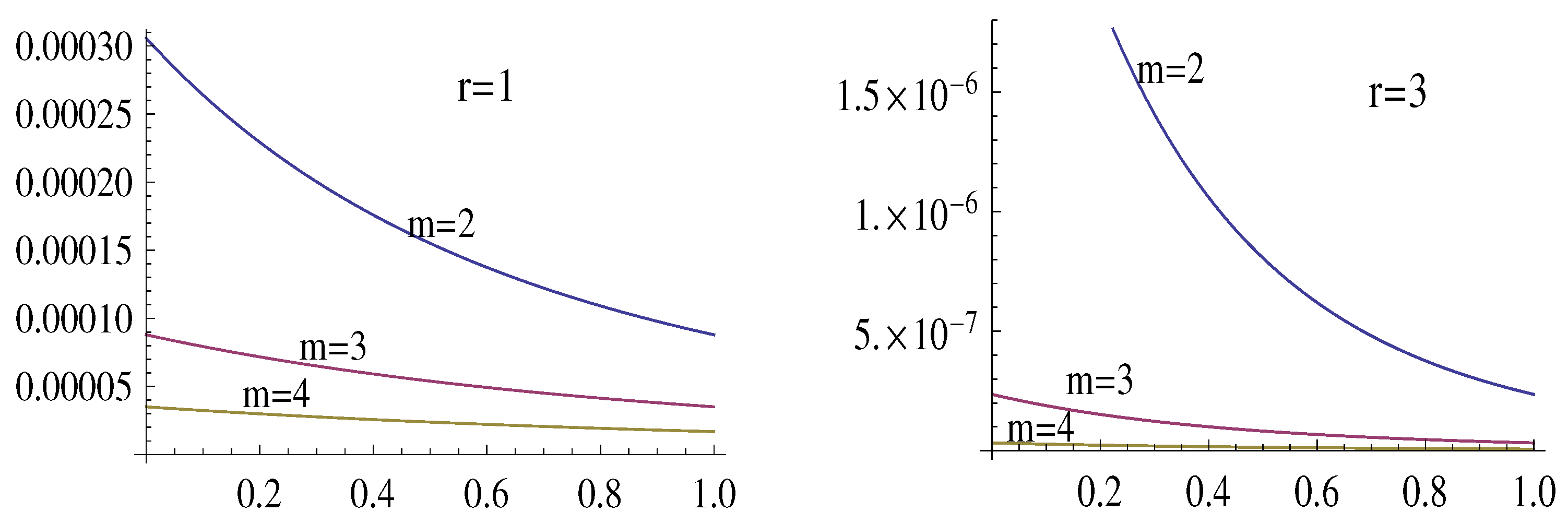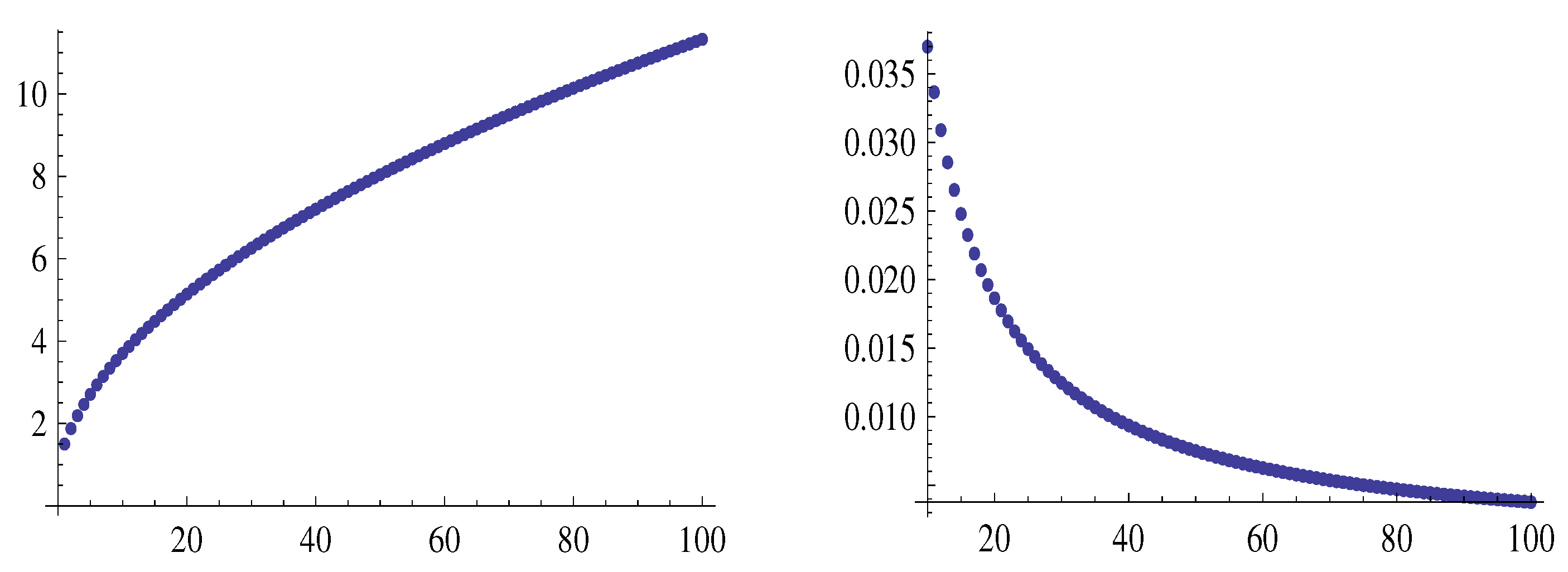Sharp Estimates of Pochhammer’s Products

1. Introduction

Pochhamer’s products or shifted factorials, falling (lower) and rising (upper), are often encountered in pure and applied mathematics and in several exact sciences too. For example, we meet them in combinatorics, number theory, probability, statistics, statistical physics, etc. These products are closely related to the famous $\mathsf{\Gamma }$ function which is well accessible also in a numerical sense.

The classical rising Pochhammer’s product1 of the order $n\in \mathbb{N}=\{1,2,3,\dots \}$ and the basis $x\in \mathbb{C}$,

$$x^{\left(n\right)}:=\prod _{j=0}^{n-1}(x+j)=x·(x+1)·\dots ·(x+n-1),$$

can be expressed, for $x\in \mathbb{N}$, in terms of $\mathsf{\Gamma }$ function as

$$x^{\left(n\right)}={\displaystyle \frac{(x+n-1)!}{(x-1)!}}={\displaystyle \frac{\mathsf{\Gamma }(x+n)}{\mathsf{\Gamma }\left(x\right)}}.$$

There are only a few articles on approximating the Pochhammer product. One of them is [3], where are given several approximations to the products in question. In our paper, we would like to present sharper and more general results than those given in [3].

The last equation above suggests the most useful extension of the classical rising discrete-order Pochhammer’s factorial to a continuous-order Pochhammer’s factorial $x^{\left(p\right)}$ by setting the following definition.

Definition 1.

The rising Pochhammer’s factorial $x^{\left(p\right)}$ is defined as

$$x^{\left(p\right)}:={\displaystyle \frac{\mathsf{\Gamma }(x+p)}{\mathsf{\Gamma }\left(x\right)}},\mathrm{for}x\in {\mathbb{R}}^{+}\mathrm{and}\mathrm{a}\mathrm{real}p>-x.$$

(1)

Obviously, $x^{\left(0\right)}=1$ and $x^{\left(1\right)}=x$, for $x\in {\mathbb{R}}^{+}$.

Lemma 1.

For $p,q,x\in {\mathbb{R}}^{+}$, we have

$$x^{\left(p\right)}={\displaystyle \frac{x^{\left(q\right)}}{{(x+p)}^{\left(q\right)}}}·{(x+q)}^{\left(p\right)}.$$

(2)

Proof. 

Considering Definition 1, we have, for $p,q,x\in {\mathbb{R}}^{+}$,

$$\begin{array}{cc}\hfill {(x+q)}^{\left(p\right)}& =\frac{\mathsf{\Gamma }(x+q+p)}{\mathsf{\Gamma }(x+q)}=\frac{\mathsf{\Gamma }(x+p+q)}{\mathsf{\Gamma }(x+q)}=\frac{{(x+p)}^{\left(q\right)}\mathsf{\Gamma }(x+p)}{x^{\left(q\right)}\mathsf{\Gamma }\left(x\right)}=\frac{{(x+p)}^{\left(q\right)}}{x^{\left(q\right)}}{x}^{\left(p\right)}.\hfill \end{array}$$

□

The classical falling Pochhammer’s product of order $n\in \mathbb{N}=\{1,2,3,\dots \}$ and basis $x\in \mathbb{C}$,

$$x_{\left(n\right)}:=\prod _{j=0}^{n-1}(x-j)=x·(x-1)·\dots ·(x-n+1),$$

(3)

can be expressed by the rising Pochhammer’s factorial as

$$x_{\left(n\right)}={\displaystyle \frac{x}{x-n}}{(x-n)}^{\left(n\right)},$$

(4)

for an integer n and a real x satisfying $x>n>0$. Therefore, we extend the domain of the falling Pochhammer’s factorial to continuous case setting

$$x_{\left(p\right)}={\displaystyle \frac{x}{x-p}}·{(x-p)}^{\left(p\right)}={\displaystyle \frac{x}{x-p}}·{\displaystyle \frac{\mathsf{\Gamma }\left(x\right)}{\mathsf{\Gamma }(x-p)}}.$$

Moreover, since $y\mathsf{\Gamma }\left(y\right)=\mathsf{\Gamma }(y+1)$, for $y>0$, we set the next definition.

Definition 2.

The falling Pochhammer’s factorial $x_{\left(p\right)}$ we define as

$$x_{\left(p\right)}:={\displaystyle \frac{\mathsf{\Gamma }(x+1)}{\mathsf{\Gamma }(x-p+1)}}={(x-p+1)}^{\left(p\right)},\mathrm{for}x,p\in {\mathbb{R}}^{+}\mathrm{such}\mathrm{that}x>p>0.$$

Obviously, $x_{\left(0\right)}=1$ and $x_{\left(1\right)}=x$, for $x\in {\mathbb{R}}^{+}$.

2. Auxiliary Result (Approximation of $\gamma$ Function)

The Stirling approximation formula of order $r\ge 0$ for $\mathsf{\Gamma }$ function says that for $x\in {\mathbb{R}}^{+}$ we have [2], [sect. 9.5]

$$\mathsf{\Gamma }\left(x\right)=\sqrt{{\displaystyle \frac{2\pi }{x}}}·{\left({\displaystyle \frac{x}{e}}\right)}^x·exp\left(s_r\left(x\right)+d_r\left(x\right)\right),$$

(5)

where

$$s_0\left(x\right)\equiv 0\mathrm{and}{s}_r\left(x\right)=\sum _{i=1}^r{\displaystyle \frac{B_{2i}}{(2i-1)\left(2i\right)x^{2i-1}}}\mathrm{for}r\ge 1,$$

(6)

and, for some ${\mathsf{\Theta }}_r\left(x\right)\in (0,1)$,

$$d_r\left(x\right)={\mathsf{\Theta }}_r\left(x\right)·{\displaystyle \frac{B_{2r+2}}{\left(2r+1\right)(2r+2)·x^{2r+1}}}.$$

(7)

The numbers $B_2$, $B_4$, $B_6$, …are known as the Bernoulli coefficients2. We have, for example,

$$\begin{array}{ccc}\hfill B_2& =& {\displaystyle \frac{1}{6}},B_4=B_8=-{\displaystyle \frac{1}{30}},B_6={\displaystyle \frac{1}{42}},B_{10}={\displaystyle \frac{5}{66}},B_{12}=-{\displaystyle \frac{691}{2730}},\hfill \\ \hfill B_{14}& =& {\displaystyle \frac{7}{6}},B_{16}=-{\displaystyle \frac{3617}{510}},B_{18}={\displaystyle \frac{43867}{798}},B_{20}=-{\displaystyle \frac{174611}{330}},\hfill \\ \hfill B_{22}& =& {\displaystyle \frac{854513}{138}},B_{24}=-{\displaystyle \frac{236364091}{2730}}\mathrm{and}{B}_{26}={\displaystyle \frac{8553103}{6}},\hfill \end{array}$$

(8)

with the estimates $-{\displaystyle \frac{1}{3}}<B_{12}<-{\displaystyle \frac{1}{4}}$, $-8<B_{16}<-7$, $54<B_{18}<55$, $-530<B_{20}<-529$, $6192<B_{22}<6193$, $-86581<B_{24}<-86580$, $1.42·{10}^6<B_{26}<1.43·{10}^6$.

As a consequence, we have for the (continuous) factorial function $x!:=\mathsf{\Gamma }(x+1)=x\mathsf{\Gamma }\left(x\right)$ the expression (the Stirling factorial formula)

$$x!=\sqrt{2\pi x}{\left({\displaystyle \frac{x}{e}}\right)}^{x}exp\left(s_r\left(x\right)+d_r\left(x\right)\right)(x\in {\mathbb{R}}^{+}).$$

(9)

3. Approximations to Pochhammer’s Products

Using (1) and (5) we calculate

$$\begin{array}{cc}\hfill x^{\left(p\right)}=& \sqrt{{\displaystyle \frac{2\pi }{x+p}}}·{\left({\displaystyle \frac{x+p}{e}}\right)}^{x+p}·exp\left(s_r(x+p)+d_r(x+p)\right)\hfill \\ \hfill & ·{\left[\sqrt{{\displaystyle \frac{2\pi }{x}}}·{\left({\displaystyle \frac{x}{e}}\right)}^x·exp\left(s_r\left(x\right)+d_r\left(x\right)\right)\right]}^{-1}\hfill \\ \hfill =& {\left({\displaystyle \frac{x+p}{x}}\right)}^{x-1/2}{\left({\displaystyle \frac{x+p}{e}}\right)}^{p}exp\left(s_r(x+p)-s_r\left(x\right)\right)\hfill \\ \hfill & ·exp\left(d_r(x+p)-d_r\left(x\right)\right),\hfill \end{array}$$

(10)

According to (7) we have, for $p,x>0$,

$$|d_r(x+p)-d_r\left(x\right)|<2·{\displaystyle \frac{|B_{2r+2}|}{(2r+1)(2r+2)·x^{2r+1}}}.$$

(11)

At small x the estimate (8) becomes useless. Therefore, in (10) we replace x with $x+m$, where m is a positive integer, not being too large. Using the formulas (10) and (8) together with (2), we find an asymptotic approximation of the generalized Pochhammer’s rising product given in the next theorem.

Theorem 1.

For $p,x\in {\mathbb{R}}^{+}$ and for integers $m,r\ge 0$, the equality

$$x^{\left(p\right)}=P_r(x,m,p)·exp\left({\delta }_r(x,m,p)\right)$$

(12)

holds, where3

$$\begin{array}{cc}\hfill P_r(x,m,p):=& P^{*}(x,m,p)·exp\left({\sigma }_r(x,m,p)\right),\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill P^{*}(x,m,p):=& {\displaystyle \frac{x^{\left(m\right)}}{{(x+p)}^{\left(m\right)}}}{\left({\displaystyle \frac{x+m+p}{x+m}}\right)}^{x+m-1/2}{\left({\displaystyle \frac{x+m+p}{e}}\right)}^p,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\sigma }_r(x,m,p):=& \sum _{i=1}^r{\displaystyle \frac{B_{2i}}{(2i-1)\left(2i\right)}}\left({\displaystyle \frac{1}{{(x+m+p)}^{2i-1}}}-{\displaystyle \frac{1}{{(x+m)}^{2i-1}}}\right),\hfill \end{array}$$

(15)

and, uniformly in p,

$$\left|{\delta }_r(x,m,p)\right|<{\tilde{\delta }}_r(x,m):={\displaystyle \frac{\left|B_{2r+2}\right|}{(r+1)(2r+1){(x+m)}^{2r+1}}}.$$

(16)

Example 1.

For $p,x>0$ we have

$$P_0(x,0,p)=P^{*}(x,0,p)={\left({\displaystyle \frac{x}{x+p}}\right)}^{1/2-x}{\left({\displaystyle \frac{x+p}{e}}\right)}^p,{\tilde{\delta }}_0(x,1)<{\displaystyle \frac{1}{6(x+1)}}$$

and

$$P_1(x,1,p)=\frac{x}{x+p}{\left(\frac{x+p+1}{x+1}\right)}^{x+1/2}{\left(\frac{x+p+1}{e}\right)}^{p}exp\left(\frac{1}{12}\left(\frac{1}{x+p+1}-\frac{1}{x+1}\right)\right)$$

with ${\tilde{\delta }}_1(x,1)<{\displaystyle \frac{1}{180{(x+1)}^3}}$.

For $x\in {\mathbb{R}}^{+}$ and any integer $p\ge 2$ we obviously have $x^p<x^{\left(p\right)}<{(x+p-1)}^p$. Moreover, setting $m=1$ and $r=0$ in Theorem 1, we get a more accurate estimate, given in the next corollary4.

Corollary 1.

For $p,x\in {\mathbb{R}}^{+}$, there hold the following inequalities:

$$\begin{array}{cc}\hfill x^{\left(p\right)}& >A(x,p):=\frac{x}{x+p}{\left(\frac{x+p+1}{x+1}\right)}^{x+1/2}{\left(\frac{x+p+1}{e}\right)}^{p}exp\left(-\frac{1}{6(x+1)}\right)\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill x^{\left(p\right)}& <B(x,p):=\frac{x}{x+p}{\left(\frac{x+p+1}{x+1}\right)}^{x+1/2}{\left(\frac{x+p+1}{e}\right)}^{p}exp\left(\frac{1}{6(x+1)}\right).\hfill \end{array}$$

(18)

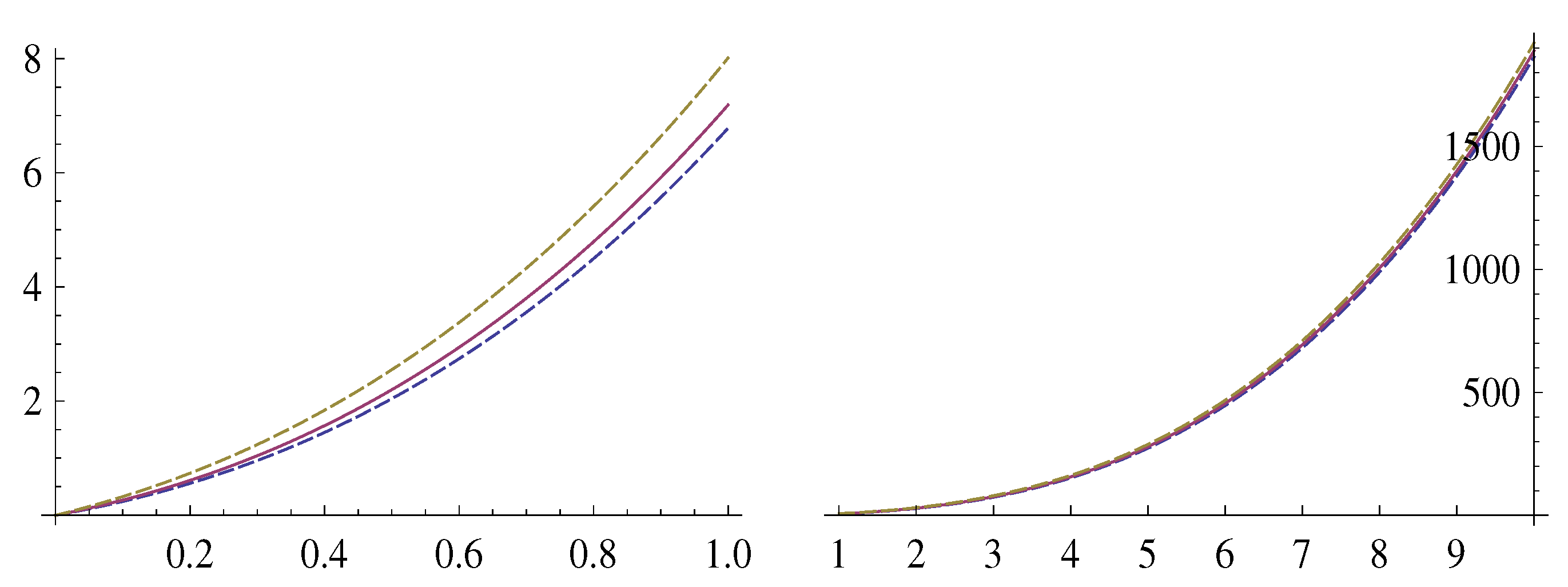
Figure 1 illustrates5 the relations (17) and (18) by plotting the graphs of the functions $x\mapsto A(x,\pi )$ and $x\mapsto B(x,\pi )$, together with the graph (continuous line) of the function $x\mapsto P_2(x,3,\pi )$, which nearly coincides with the function $x\mapsto x^{\left(\pi \right)}$.

Remark 1.

In the formula (16), m and r are the parameters that affect the error term ${\delta }_r^{*}(x,m,p)$. We stress that $|B_{2r+2}|$ becomes very large for large r. Indeed, according to [1, 23.1.15], we have

$$2{\displaystyle \frac{\left(2n\right)!}{{\left(2\pi \right)}^{2n}}}<\left|B_{2n}\right|<4{\displaystyle \frac{\left(2n\right)!}{{\left(2\pi \right)}^{2n}}},\mathrm{for}n\in \mathbb{N}.$$

(19)

In addition, referring to (5) and (7), or using [5], we have the double inequality

$$\sqrt{2\pi m}{\left({\displaystyle \frac{m}{e}}\right)}^m<m!<\sqrt{2\pi m}{\left({\displaystyle \frac{m}{e}}\right)}^{m}exp\left(\frac{1}{12m}\right),\mathrm{for}m\in \mathbb{N}.$$

(20)

Consequently,

$$4\sqrt{\pi n}{\left({\displaystyle \frac{n}{e\pi }}\right)}^{2n}<\left|B_{2n}\right|<9\sqrt{\pi n}{\left({\displaystyle \frac{n}{e\pi }}\right)}^{2n},\mathrm{for}n\in \mathbb{N}.$$

(21)

Thus, considering (16), we find6

$$\begin{array}{cc}\hfill {\tilde{\delta }}_r(x,m)<{\delta }_r^{*}(x,m)& :=\frac{9\sqrt{r+1}}{e\sqrt{\pi }(2r+1)}{\left(\frac{r+1}{e\pi (x+m)}\right)}^{2r+1}(m,r\ge 0,x>0)\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & <\frac{1}{\sqrt{r}}{\left(\frac{r+1}{e\pi (x+m)}\right)}^{2r+1}(m\ge 0,r\ge 1,x>0).\hfill \end{array}$$

(23)

Corollary 2.

For $p,x\in {\mathbb{R}}^{+}$ and for integers $m,r\ge 1$, satisfying $r\le 4m-1$, the approximation $x^{\left(p\right)}\approx P_r(x,m,p)$, given in Theorem 1, has the relative error

$${\rho }_r(x,m,p):={\displaystyle \frac{x^{\left(p\right)}-P_r(x,m,p)}{P_r(x,m,p)}},$$

(24)

estimated as

$$\left|{\rho }_r(x,m,p)\right|<\left(1+\frac{8}{100}\right)\left|{\delta }_r(x,m,p)\right|<\sqrt{{\displaystyle \frac{2}{r}}}{\left({\displaystyle \frac{r+1}{e\pi (x+m)}}\right)}^{2r+1}.$$

Proof. 

According to Theorem 1, using Taylor’s formula, we obtain, for some $\vartheta \in (0,1)$,

$$\begin{array}{cc}\hfill \left|{\rho }_r(x,m,p)\right|& =\left|{\displaystyle \frac{P_r{e}^{{\delta }_r}-P_r}{P_r}}\right|=|e^{{\delta }_r}-1|\hfill \\ \hfill & =\left|{\delta }_r+\frac{1}{2}{e}^{\vartheta ·{\delta }_r}·{\delta }_r^2\right|\hfill \\ \hfill & \le \left|{\delta }_r\right|+\frac{e^{|{\delta }_r|}}{2}\left|{\delta }_r\right|·\left|{\delta }_r\right|.\hfill \end{array}$$

(25)

Now, for integers $m,r\ge 1$, satisfying $r\le 4m-1$, and for $x>0$, we have $0<{\displaystyle \frac{r+1}{e\pi (x+m)}}<{\displaystyle \frac{r+1}{8(x+m)}}<{\displaystyle \frac{1}{2}}$. Consequently, referring to (16) and (23), we estimate $\left|{\delta }_r\right|<{\displaystyle \frac{1}{\sqrt{r}}}{\left({\displaystyle \frac{1}{2}}\right)}^{2r+1}\le {\displaystyle \frac{1}{8}}$. Hence, considering (25), we get

$$\left|{\rho }_r(x,m,p)\right|<\left|{\delta }_r\right|+\frac{e^{1/8}}{2}·\frac{1}{8}·\left|{\delta }_r\right|<\left(1+\frac{8}{100}\right)\left|{\delta }_r\right|<\sqrt{2}·\left|{\delta }_r\right|<\sqrt{2}·\left|{\delta }_r^{*}\right|.$$

□

The immediate consequence of Corollary 2 is the next corollary.

Corollary 3.

For $p,x\in {\mathbb{R}}^{+}$ and for integers $m,r\ge 1$, satisfying $r\le 4m-1$, the inequalities

$$\begin{array}{cc}\hfill x^{\left(p\right)}& >\left(1-\sqrt{{\displaystyle \frac{2}{r}}}{\left({\displaystyle \frac{r+1}{e\pi (x+m)}}\right)}^{2r+1}\right)P_r(x,m,p)\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill x^{\left(p\right)}& <\left(1+\sqrt{{\displaystyle \frac{2}{r}}}{\left({\displaystyle \frac{r+1}{e\pi (x+m)}}\right)}^{2r+1}\right)P_r(x,m,p)\hfill \end{array}$$

(27)

hold.

Example 2.

Setting $r=1$ and $r=7$ in Corollary 3 we obtain the following double inequalities:

$$\left(1-\frac{1}{50{(x+m)}^3}\right)P_1(x,m,p)<x^{\left(p\right)}<\left(1+\frac{1}{50{(x+m)}^3}\right)P_1(x,m,p),$$

(28)

true for $p,x\in {\mathbb{R}}^{+}$ and $m\ge 1$, and

$$\left(1-\frac{1}{4{(x+m)}^{15}}\right)P_7(x,m,p)<x^{\left(p\right)}<\left(1+\frac{1}{4{(x+m)}^{15}}\right)P_7(x,m,p),$$

(29)

valid for $p,x\in {\mathbb{R}}^{+}$ and $m\ge 2$.

The inequalities in (28) are illustrated in Figure 2, where the dashed line represents the graph of the function $x\mapsto P_0(x,1,\pi )$ and the continuous line, compressed between the nearly coinciding graphs of the functions $x\mapsto \left(1\mp {\displaystyle \frac{1}{50{(x+1)}^3}}\right)P_1(x,1,\pi )$, represents the graph of the function $x\mapsto x^{\left(\pi \right)}$.

We are interested in how the sequence $r\mapsto {\delta }_r(x,m,p)$ varies. Indeed, thanks to Theorem 1, for $p,x\in {\mathbb{R}}^{+}$ and integers $m,r,r^{\prime }\ge 0$, we have

$$\begin{array}{cc}\hfill & P^{*}(x,m,p)·exp\left({\sigma }_r(x,m,p)+{\delta }_r(x,m,p)\right)\hfill \\ \hfill & =x^{\left(p\right)}=P^{*}(x,m,p)·exp\left({\sigma }_{r^{\prime }}(x,m,p)+{\delta }_{r^{\prime }}(x,m,p)\right).\hfill \end{array}$$

Therefore, for integers $0\le r<r^{\prime }$ and $m\ge 0$, for real $p,x>0$, and for the difference $D_{r,r^{\prime }}(x,m,p)$,

$$\begin{array}{cc}\hfill D_{r,r^{\prime }}(x,m,p)& :={\sigma }_{r^{\prime }}(x,m,p)-{\sigma }_r(x,m,p)\hfill \\ \hfill & =\sum _{i=r+1}^{r^{\prime }}{\displaystyle \frac{B_{2i}}{(2i-1)\left(2i\right)}}\left({\displaystyle \frac{1}{{(x+m+p)}^{2i-1}}}-{\displaystyle \frac{1}{{(x+m)}^{2i-1}}}\right),\hfill \end{array}$$

(30)

using (16), we estimate

$$\begin{array}{cc}\hfill {\delta }_r(x,m,p)& >D_{r,r^{\prime }}(x,m,p)-{\tilde{\delta }}_{r^{\prime }}(x,m)\hfill \\ \hfill {\delta }_r(x,m,p)& <D_{r,r^{\prime }}(x,m,p)+{\tilde{\delta }}_{r^{\prime }}(x,m).\hfill \end{array}$$

(31)

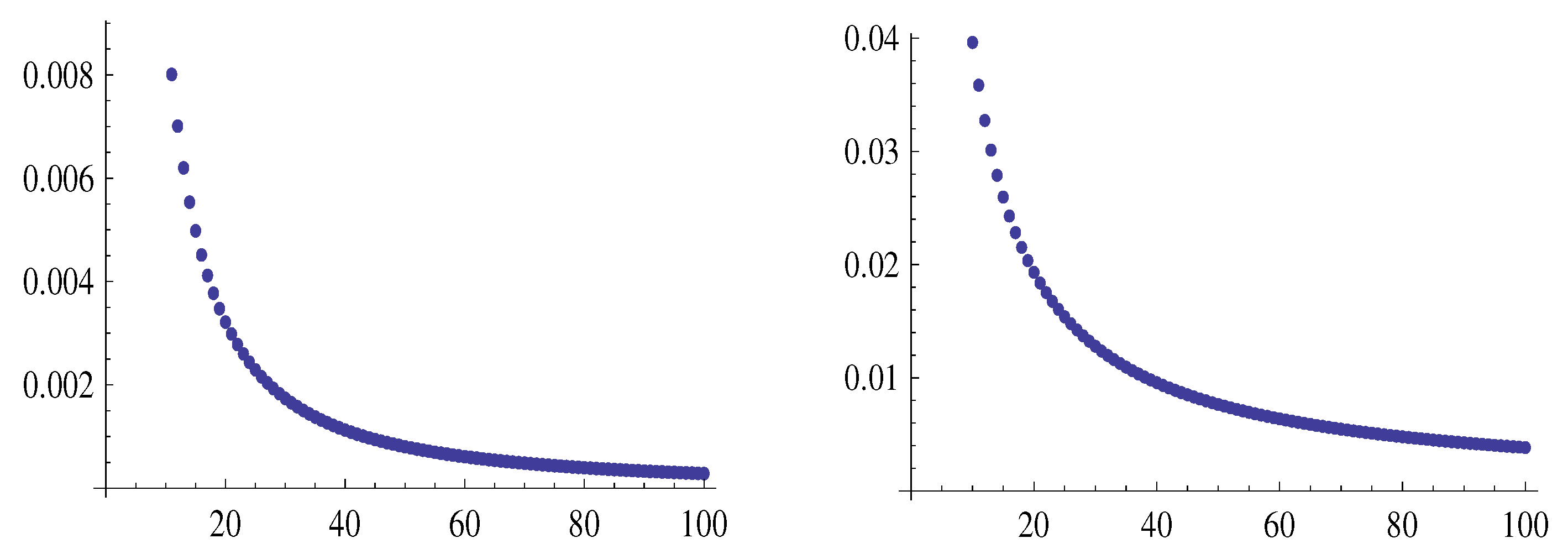
The inequalities (31) can be used to estimate the error ${\delta }_r(x,m,p)$ by using the appropriate $r^{\prime }>r$, which specifies a negligibly small ${\tilde{\delta }}_{r^{\prime }}(x,m)<{\delta }_{r^{\prime }}^{*}(x,m)$ (see (22)) and thus provides a useful estimate for ${\delta }_r(x,m,p)$. Figure 3 and Figure 4 illustrate the estimate (31), for $r\in \{0,1,2,3\}$, by showing the graphs of the functions7$x\mapsto D_{r,5}(x,4,\pi )-{\tilde{\delta }}_5(x,4)$ and $x\mapsto D_{r,5}(x,4,\pi )+{\tilde{\delta }}_5(x,4)$, cramming the graphs of the functions $x\mapsto {\delta }_r(x,4,\pi )$.

Remark 2

(open problem). Figure 3, Figure 4, Figure 5 and Figure 6 suggest the hypotheses that ${(-1)}^{r+1}{\delta }_r(x,m,p)>0$, for all allowed values of all arguments.

For $p\in \mathbb{N}$, the quantity $p!={\prod }_{k=1}^{p}k=1^{\left(p\right)}$ is called p–factorial. The discrete factorial function $p\mapsto p!$ is extended continuously, for real $p>-1$, as $p!:=1^{\left(p\right)}$. Immediately from Theorem 1 we read the next corollary, which presents a formula for $p!$ that does not contain the constant $\pi$.

Corollary 4

(approximation of continuous factorial function). For $p\in {\mathbb{R}}^{+}$ and integers $m,r\ge 0$ we have8

$$\begin{array}{cc}\hfill p!=& {\displaystyle \frac{m!}{{(p+1)}^{\left(m\right)}}}{\left({\displaystyle \frac{m+p+1}{m+1}}\right)}^{m+1/2}{\left({\displaystyle \frac{m+p+1}{e}}\right)}^p\hfill \\ \hfill & ·exp\left(\sum _{i=1}^r\frac{B_{2i}}{(2i-1)\left(2i\right)}\left(\frac{1}{{(m+p+1)}^{2i-1}}-\frac{1}{{(m+1)}^{2i-1}}\right)+\frac{\vartheta ·\left|B_{2r+2}\right|}{(r+1)(2r+1){(p+m)}^{2r+1}}\right),\hfill \end{array}$$

(32)

for some $\vartheta =\vartheta (m,p,r)$ from the interval $(-1,1)$.

Using Definition 2 and Theorem 1 we obtain the approximation of generalized Pochhammer’s falling product presented in the next theorem.

Theorem 2.

For real $x,p$, satisfying $x>p>0$ and for integers $m,r\ge 0$, we have the equality

$$x_{\left(p\right)}=Q_r(x,m,p)·exp\left({\Delta }_r(x,m,p)\right),$$

(33)

where $Q_r(x,m,p)=P_r(x-p+1,m,p)$, that is

$$\begin{array}{cc}\hfill Q_r(x,m,p):=& {\displaystyle \frac{{(x-p+1)}^{\left(m\right)}}{{(x+1)}^{\left(m\right)}}}{\left({\displaystyle \frac{x+1+m}{x-p+1+m}}\right)}^{x-p+m+1/2}\hfill \\ \hfill & ·{\left({\displaystyle \frac{x+1+m}{e}}\right)}^{p}exp\left({\sigma }_r(x-p+1,m,p)\right),\hfill \end{array}$$

(34)

with ${\sigma }_r(x,m,p)$ defined in (15), and

$$\left|{\Delta }_r(x,m,p)\right|<{\Delta }_r^{*}(x,m,p):={\displaystyle \frac{\left|B_{2r+2}\right|}{(r+1)(2r+1){(x-p+1+m)}^{2r+1}}}.$$

(35)

Remark 3.

For $x\in {\mathbb{R}}^{+}$ and any integer p, satisfying $2\le p<x$, we obviously have ${(x-p+1)}^p<x_{\left(p\right)}<x^p$. In addition, using the inequality ${\left(1+{\displaystyle \frac{p}{t}}\right)}^t<e^p$, true for $t>\left|p\right|$, from (34) we obtain

$$\begin{array}{cc}\hfill Q_r(x,m,p)<& \frac{x}{x-p}·\frac{{(x-p)}^{\left(m\right)}}{x^{\left(m\right)}}{\left(1+\frac{p}{x+m-p}\right)}^{x+m-p}{\left(x+m\right)}^p\bcancel{{\left(x+m-p\right)}^{-p}}\hfill \\ \hfill & ·{\left(\frac{x+m}{x+m-p}\right)}^{-1/2}\bcancel{{\left(x+m-p\right)}^p}·e^{-p}\hfill \\ \hfill <& \frac{x}{x-p}·\frac{{(x-p)}^{\left(m\right)}}{x^{\left(m\right)}}·e^p·{(x+m)}^p·1·e^{-p}.\hfill \end{array}$$

Thus, for all integers $m\ge 0$ and $x,p\in {\mathbb{R}}^{+}$ such that $p<x$, we have a rough estimate9

$$Q_r(x,m,p)<{\displaystyle \frac{x}{x-p}}·{\displaystyle \frac{{(x-p)}^{\left(m\right)}}{x^{\left(m\right)}}}·{(x+m)}^p.$$

Using Definition 2 and Corollary 3 we read the next result.

Corollary 5.

For real $p,x$ satisfying $x>p>0$ and for integers $m,r\ge 1$ such that $r\le 4m-1$, the inequalities

$$\begin{array}{cc}\hfill x_{\left(p\right)}& >\left(1-\sqrt{{\displaystyle \frac{2}{r}}}{\left({\displaystyle \frac{r+1}{e\pi (x-p+1+m)}}\right)}^{2r+1}\right)Q_r(x,m,p)\hfill \end{array}$$

(36)

and

$$\begin{array}{cc}\hfill 1-1x_{\left(p\right)}& <\left(1+\sqrt{{\displaystyle \frac{2}{r}}}{\left({\displaystyle \frac{r+1}{e\pi (x-p+1+m)}}\right)}^{2r+1}\right)Q_r(x,m,p)\hfill \end{array}$$

(37)

hold.

Thanks to Corollary 5, the approximation $x_{\left(p\right)}\approx Q_r(x,m,p)$ has the relative error ${\epsilon }_r(x,m,p):=\left(x_{\left(p\right)}-Q_r(x,m,p)\right)/Q_r(x,m,p)$ estimated as

$$\left|{\epsilon }_r(x,m,p)\right|<\sqrt{{\displaystyle \frac{2}{r}}}{\left({\displaystyle \frac{r+1}{e\pi (x-p+1+m)}}\right)}^{2r+1},$$

true for $x,p,m,r$ that meet all conditions given in Corollary 5.

4. Sequences of classical binomial coefficients

According to (3), the binomial coefficient “x over n”,

$$\left({\displaystyle \genfrac{}{}{0pt}{}{x}{n}}\right):={\displaystyle \frac{{\prod }_{k=0}^{n-1}(x-k)}{n!}}={\displaystyle \frac{x_{\left(n\right)}}{1^{\left(n\right)}}}(x\in \mathbb{R},n\in \mathbb{N}),$$

can be expressed using the upper Pochhammer product in the way, given in the next Proposition.

Proposition 1.

For every real x and any integer $n\ge 3$, we have10

$$\left({\displaystyle \genfrac{}{}{0pt}{}{x}{n}}\right)n!=\left\{\begin{array}{cc}{(-1)}^n{\left|x\right|}^{\left(n\right)}\hfill & (x\le 0),\hfill \\ {(-1)}^{n-1-\lfloor x\rfloor }{\left(x-\lfloor x\rfloor \right)}^{(\lfloor x+1\rfloor )}{\left(\lfloor x+1\rfloor -x\right)}^{(n-1-\lfloor x\rfloor )}\hfill & (0<x<n),\hfill \\ {\left(x-n+1\right)}^{\left(n\right)}\hfill & (x\ge n).\hfill \end{array}\right.$$

(38)

Proof. 

The first and the last cases are obvious. Relating to the second one, for $0<x<n$, we have11

$$\begin{array}{cc}\hfill \prod _{k=0}^{n-1}(x-k)& =\prod _{k=0}^{\lfloor x\rfloor }(x-k)\prod _{k=\lfloor x\rfloor +1}^{n-1}(x-k)\hfill \\ \hfill & =\prod _{j=0}^{\lfloor x\rfloor }(x-\lfloor x\rfloor +j)·{(-1)}^{n-1-\lfloor x\rfloor }\prod _{k=\lfloor x\rfloor +1}^{n-1}(k-x)\hfill \\ \hfill & ={(-1)}^{n-1-\lfloor x\rfloor }·{\left(x-\lfloor x\rfloor \right)}^{(\lfloor x\rfloor +1)}·{\left(\lfloor x\rfloor +1-x\right)}^{\left(n-1-\lfloor x\rfloor \right)}.\hfill \end{array}$$

□

Thanks to Proposition 1, Theorem 1 and (9), we present the following three examples.

Example 3.

Using $m=4$ and $r=1$ in Theorem 1 and in (9), we obtain, for some $\vartheta \in (0,1)$ and $\mathsf{\Theta }\in (-1,1)$,

$$\begin{array}{cc}\hfill & \left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{3}{2}}{n}}\right)={(-1)}^n{\displaystyle \frac{{\left(\frac{3}{2}\right)}^{\left(n\right)}}{n!}}\hfill \\ \hfill & ={(-1)}^n{\displaystyle \frac{{\left(\frac{3}{2}\right)}^{\left(4\right)}}{{\left(\frac{3}{2}+n\right)}^{\left(4\right)}}}{\left({\displaystyle \frac{\frac{3}{2}+4+n}{\frac{3}{2}+4}}\right)}^{{\displaystyle \frac{3}{2}}+4-{\displaystyle \frac{1}{2}}}{\left({\displaystyle \frac{\frac{3}{2}+4+n}{e}}\right)}^n\hfill \\ \hfill & ·exp\left({\displaystyle \frac{\frac{1}{6}}{1·2}}\left({\displaystyle \frac{1}{\frac{3}{2}+4+n}}-{\displaystyle \frac{1}{\frac{3}{2}+4}}\right)+{\displaystyle \frac{\mathsf{\Theta }·(-\frac{1}{30}}{2·3{(\frac{3}{2}+4)}^3}}\right)\hfill \\ \hfill & ·{\displaystyle \frac{1}{\sqrt{2\pi n}}}{\left({\displaystyle \frac{e}{n}}\right)}^{n}exp\left(-{\displaystyle \frac{\frac{1}{6}}{1·2·n}}-{\displaystyle \frac{\vartheta ·(-\frac{1}{30})}{3·4·n^3}}\right).\hfill \end{array}$$

Thus, for every $n\in \mathbb{N}$ and some $\vartheta \in (0,1)$ and $\mathsf{\Theta }\in (-1,1)$, we have

$$\begin{array}{cc}\hfill \left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{3}{2}}{n}}\right)& ={\displaystyle \frac{{(-1)}^n·3·5·7·9·{(11+2n)}^5}{(3+2n)(5+2n)(7+2n)(9+2n)·{11}^5·\sqrt{2\pi n}}}{\left(1+{\displaystyle \frac{11/2}{n}}\right)}^n\hfill \\ \hfill & ·exp\left({\displaystyle \frac{1}{12}}\left({\displaystyle \frac{2}{11+n}}-{\displaystyle \frac{2}{11}}-{\displaystyle \frac{1}{n}}\right)+{\displaystyle \frac{\vartheta }{360n^3}}-{\displaystyle \frac{\mathsf{\Theta }}{180{(\frac{3}{2}+4)}^3}}\right).\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill \left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{3}{2}}{n}}\right)\approx b_1\left(n\right)& :={(-1)}^n·{\displaystyle \frac{3·5·7·9\sqrt{2n}}{{11}^5\sqrt{\pi }}}·exp\left({\displaystyle \frac{11}{2}}-{\displaystyle \frac{2}{12·11}}\right)\hfill \\ \hfill & \approx {(-1)}^n{\displaystyle \frac{1128}{1000}}\sqrt{n},\mathrm{for}\mathrm{an}\mathrm{integer}n\gg 1.\hfill \end{array}$$

Figure 7 shows the graphs of the sequences $n\mapsto \left|\left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{3}{2}}{n}}\right)\right|$ and $n\mapsto {\displaystyle \frac{|\left(\genfrac{}{}{0pt}{}{-\frac{3}{2}}{n}\right)-b_1\left(n\right)|}{\left|b_1\left(n\right)\right|}}$, left and right respectively.

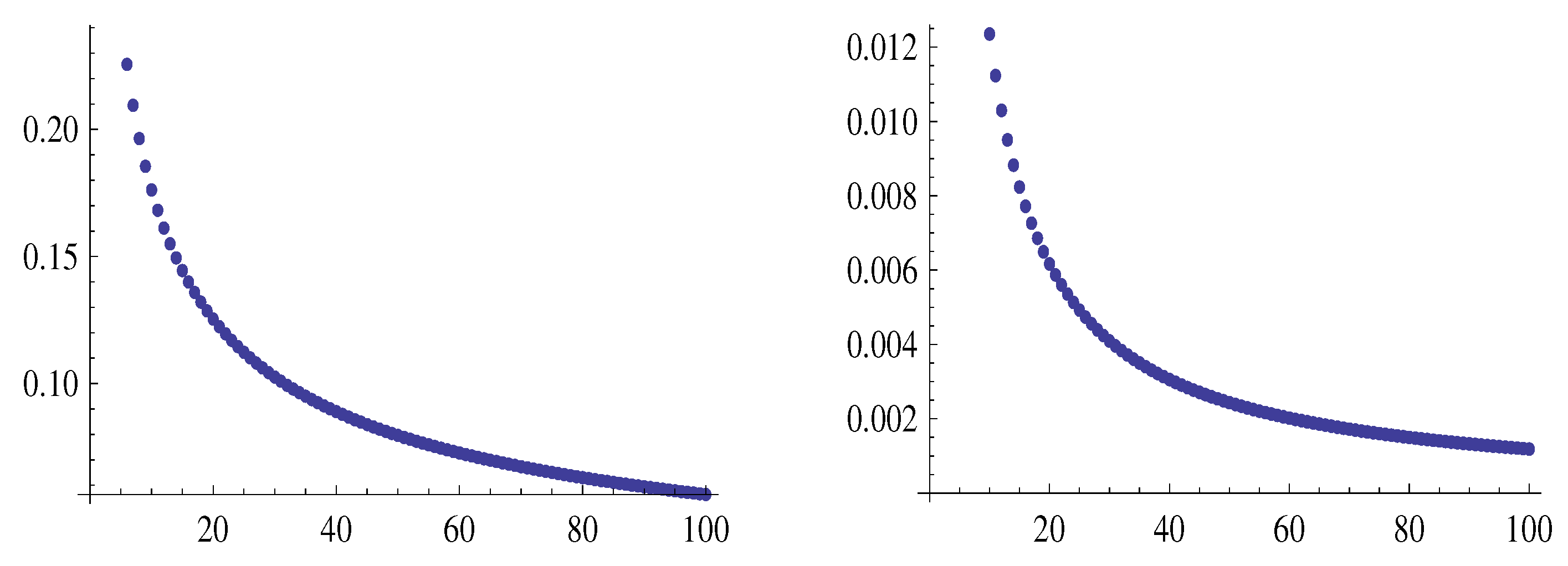
Example 4.

Setting $m=3$ and $r=2$ in Theorem 1 and in (9), we get, for some $\vartheta \in (0,1)$ and $\mathsf{\Theta }\in (-1,1)$,

$$\begin{array}{cc}\hfill & \left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{1}{2}}{n}}\right)={(-1)}^n{\displaystyle \frac{{\left(\frac{1}{2}\right)}^{\left(n\right)}}{n!}}\hfill \\ \hfill & ={(-1)}^n{\displaystyle \frac{{\left(\frac{1}{2}\right)}^{\left(3\right)}}{{\left(\frac{1}{2}+n\right)}^{\left(3\right)}}}{\left({\displaystyle \frac{\frac{1}{2}+3+n}{\frac{1}{2}+3}}\right)}^{{\displaystyle \frac{1}{2}}+3-{\displaystyle \frac{1}{2}}}{\left({\displaystyle \frac{\frac{1}{2}+3+n}{e}}\right)}^n\hfill \\ \hfill & ·exp\left({\displaystyle \frac{\frac{1}{6}}{1·2}}\left(\frac{1}{\frac{1}{2}+3+n}-\frac{1}{\frac{1}{2}+3}\right)+{\displaystyle \frac{-\frac{1}{30}}{3·4}}\left(\frac{1}{{(\frac{1}{2}+3+n)}^3}-\frac{1}{{(\frac{1}{2}+3)}^3}\right)+{\displaystyle \frac{\mathsf{\Theta }·\frac{1}{42}}{5·6{(\frac{1}{2}+3)}^5}}\right)\hfill \\ \hfill & ·{\displaystyle \frac{1}{\sqrt{2\pi n}}}{\left({\displaystyle \frac{e}{n}}\right)}^{n}exp\left(-{\displaystyle \frac{\frac{1}{6}}{1·2·n}}-{\displaystyle \frac{-\frac{1}{30}}{3·4·n^3}}-{\displaystyle \frac{\vartheta ·\frac{1}{42}}{5·6·n^5}}\right).\hfill \end{array}$$

Therefore, for any $n\in \mathbb{N}$, using some $\vartheta \in (0,1)$ and $\mathsf{\Theta }\in (-1,1)$, we find

$$\begin{array}{cc}\hfill \left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{1}{2}}{n}}\right)& ={\displaystyle \frac{{(-1)}^n·3·5·{(7+2n)}^3}{(1+2n)(3+2n)(5+2n)·7^3·\sqrt{2\pi n}}}{\left(1+{\displaystyle \frac{7/2}{n}}\right)}^n\hfill \\ \hfill & ·exp({\displaystyle \frac{1}{12}}\left(\frac{2}{7+n}-{\displaystyle \frac{2}{7}}-\frac{1}{n}\right)+{\displaystyle \frac{1}{360}}\left(\frac{1}{n^3}-\frac{1}{{(\frac{1}{2}+3+n)}^3}+\frac{1}{{(\frac{1}{2}+3)}^3}\right)\hfill \\ \hfill & +{\displaystyle \frac{\mathsf{\Theta }}{1260{(\frac{1}{2}+3)}^5}}-{\displaystyle \frac{\vartheta }{1260n^5}}).\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill \left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{1}{2}}{n}}\right)& \approx b_2\left(n\right):={(-1)}^n{\displaystyle \frac{3·5}{7^3\sqrt{2\pi }}}exp\left({\displaystyle \frac{7}{2}}-{\displaystyle \frac{1}{42}}\right)·{\displaystyle \frac{1}{\sqrt{n}}}\hfill \\ \hfill & \approx {(-1)}^n{\displaystyle \frac{564}{1000\sqrt{n}}},\mathrm{for}\mathrm{an}\mathrm{integer}n\gg 1.\hfill \end{array}$$

Figure 9 shows the graphs of the sequences $n\mapsto \left|\left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{1}{2}}{n}}\right)\right|$ and $n\mapsto {\displaystyle \frac{|\left(\genfrac{}{}{0pt}{}{-\frac{1}{2}}{n}\right)-b_2\left(n\right)|}{\left|b_2\left(n\right)\right|}}$, left and right respectively.

Example 5.

Using $m=3$ and $r=2$ in Theorem 1 and in (9), and considering Example 4, we have12

$$\begin{array}{cc}\hfill & \left({\displaystyle \genfrac{}{}{0pt}{}{\frac{1}{2}}{n}}\right)={\displaystyle \frac{1}{n!}}·{(-1)}^{n-1}{\left({\displaystyle \frac{1}{2}}\right)}^{\left(1\right)}{\left({\displaystyle \frac{1}{2}}\right)}^{(n-1)}=-{\displaystyle \frac{1}{2(n-\frac{1}{2})}}·{(-1)}^n{\displaystyle \frac{{\left(\frac{1}{2}\right)}^{\left(n\right)}}{n!}}\hfill \\ \hfill & =-{\displaystyle \frac{1}{2(n-\frac{1}{2})}}·{\displaystyle \frac{{(-1)}^n·3·5·{(7+2n)}^3}{(1+2n)(3+2n)(5+2n)·7^3·\sqrt{2\pi n}}}{\left(1+{\displaystyle \frac{7/2}{n}}\right)}^n\hfill \\ \hfill & ·exp({\displaystyle \frac{1}{12}}\left(\frac{2}{7+n}-{\displaystyle \frac{2}{7}}-\frac{1}{n}\right)+{\displaystyle \frac{1}{360}}\left(\frac{1}{n^3}-\frac{1}{{(\frac{1}{2}+3+n)}^3}+\frac{1}{{(\frac{1}{2}+3)}^3}\right)\hfill \\ \hfill & +{\displaystyle \frac{\mathsf{\Theta }}{1260{(\frac{1}{2}+3)}^5}}-{\displaystyle \frac{\vartheta }{1260n^5}}),\hfill \end{array}$$

for some $\vartheta \in (0,1)$ and $\mathsf{\Theta }\in (-1,1)$. Thus, for every $n\in \mathbb{N}$ there exists some $\vartheta \in (0,1)$ and some $\mathsf{\Theta }\in (-1,1)$ such that

$$\begin{array}{cc}\hfill \left({\displaystyle \genfrac{}{}{0pt}{}{\frac{1}{2}}{n}}\right)& ={(-1)}^{n+1}{\displaystyle \frac{15·{(7+2n)}^3}{(2n-1)·(1+2n)(3+2n)(5+2n)·7^3·\sqrt{2\pi n}}}{\left(1+{\displaystyle \frac{7/2}{n}}\right)}^n\hfill \\ \hfill & ·exp({\displaystyle \frac{1}{12}}\left(\frac{2}{7+n}-{\displaystyle \frac{2}{7}}-\frac{1}{n}\right)+{\displaystyle \frac{1}{360}}\left(\frac{1}{n^3}-\frac{1}{{(\frac{1}{2}+3+n)}^3}+\frac{1}{{(\frac{1}{2}+3)}^3}\right)\hfill \\ \hfill & +{\displaystyle \frac{\mathsf{\Theta }}{1260{(\frac{1}{2}+3)}^5}}-{\displaystyle \frac{\vartheta }{1260n^5}}).\hfill \end{array}$$

Consequently,

$$\begin{array}{cc}\hfill \left({\displaystyle \genfrac{}{}{0pt}{}{\frac{1}{2}}{n}}\right)& \approx b_3\left(n\right):={(-1)}^{n+1}{\displaystyle \frac{15}{7^3\sqrt{2\pi }}}exp\left({\displaystyle \frac{7}{2}}-{\displaystyle \frac{1}{42}}\right)·{\displaystyle \frac{1}{(2n-1)\sqrt{n}}}\hfill \\ \hfill & \approx {(-1)}^{n+1}{\displaystyle \frac{282}{1000n\sqrt{n}}},\mathrm{for}\mathrm{an}\mathrm{integer}n\gg 1.\hfill \end{array}$$

Figure 9 shows the graphs of the sequences $n\mapsto \left|\left({\displaystyle \genfrac{}{}{0pt}{}{\frac{1}{2}}{n}}\right)\right|$ and $n\mapsto {\displaystyle \frac{|\left(\genfrac{}{}{0pt}{}{\frac{1}{2}}{n}\right)-b_3\left(n\right)|}{\left|b_3\left(n\right)\right|}}$, left and right respectively.

Remark 4.

More about binomial coefficients can be find in [4].