Introduction
We are currently witnessing a fascinating development of the theory of surface and bulk acoustic waves. New extraordinary properties in the domain of acoustic waves appeared with the invention of a new class of materials, i.e., metamaterials. The use of elastic metamaterials for the construction of ultrasonic waveguides has created a fertile ground for the discovery of a series of new ultrasonic waves.
As an example of newly discovered elastic surface waves propagating on a flat interface between two elastic half-spaces, one of which is an elastic metamaterial with a negative elastic compliance, can serve the SH surface acoustic waves discovered by Kiełczyński and presented in [
1,
2].
The search for new types of ultrasonic sensors led the authors of this paper to the discovery of new torsional elastic waves propagating on the curved surface of metamaterial elastic cylinders embedded in a conventional elastic medium. These newly discovered elastic torsional waves can be applied to develop a new generation of acoustic cylindrical sensors with very high mass sensitivity. Needless to say, such a property of the sensor is of crucial importance in measurements in many applications in domains, such as medicine, biology, toxicology or environmental studies.
In this paper, the authors proved the existence of a new class of elastic torsional surface waves propagating in cylindrical waveguides with a metamaterial cylindrical rod, with a negative elastic compliance , embedded in a conventional elastic medium. The newly discovered torsional elastic surface waves have only one angular (shear) mechanical displacement component that is tangential to the cylinder circumference and depends only on the radial coordinate .
The curved cylindrical structure of the waveguide offers many advantages in practical field measurements. Simultaneously, we expect that the newly discovered torsional elastic surface waves, propagating along cylindrical rods, will exhibit very high mass sensitivity.
The main feature of the newly discovered torsional elastic surface waves is their close affinity with the Surface Plasmon Polariton (SPP) electromagnetic (optical) waves propagating along the interface between the metallic core cylinder and the dielectric outer medium [
3,
4,
5]. In fact, the newly discovered torsional elastic surface waves can be considered as an elastic counterpart of the electromagnetic SPP waves described in [
3,
4,
5].
Ultrasonic elastic waves propagating in pure elastic rectangular (flat) and circular waveguide structures have found applications in sensors of physical quantities, such as viscosity sensors, to investigate the elastic parameters of surface layers, to investigate the physicochemical parameters of liquids, etc. [
6,
7,
8,
9,
10,
11,
12,
13,
14].
Torsional waves propagating in pure elastic cylindrical rods have been mainly used in viscosity sensors since the 1950s [
15]. Classical ultrasonic cylindrical liquid viscosity sensors are made of conventional elastic materials. These sensors are usually used to determine the viscosity of liquids in biosensors and chemosensors.
However, sensors of this type are not free from disadvantages. Namely, the ultrasonic field of this classical torsional wave is distributed in a large volume of the circular waveguide, which results in a moderate mass sensitivity of the cylindrical sensor. Therefore, the need to solve this problem arose.
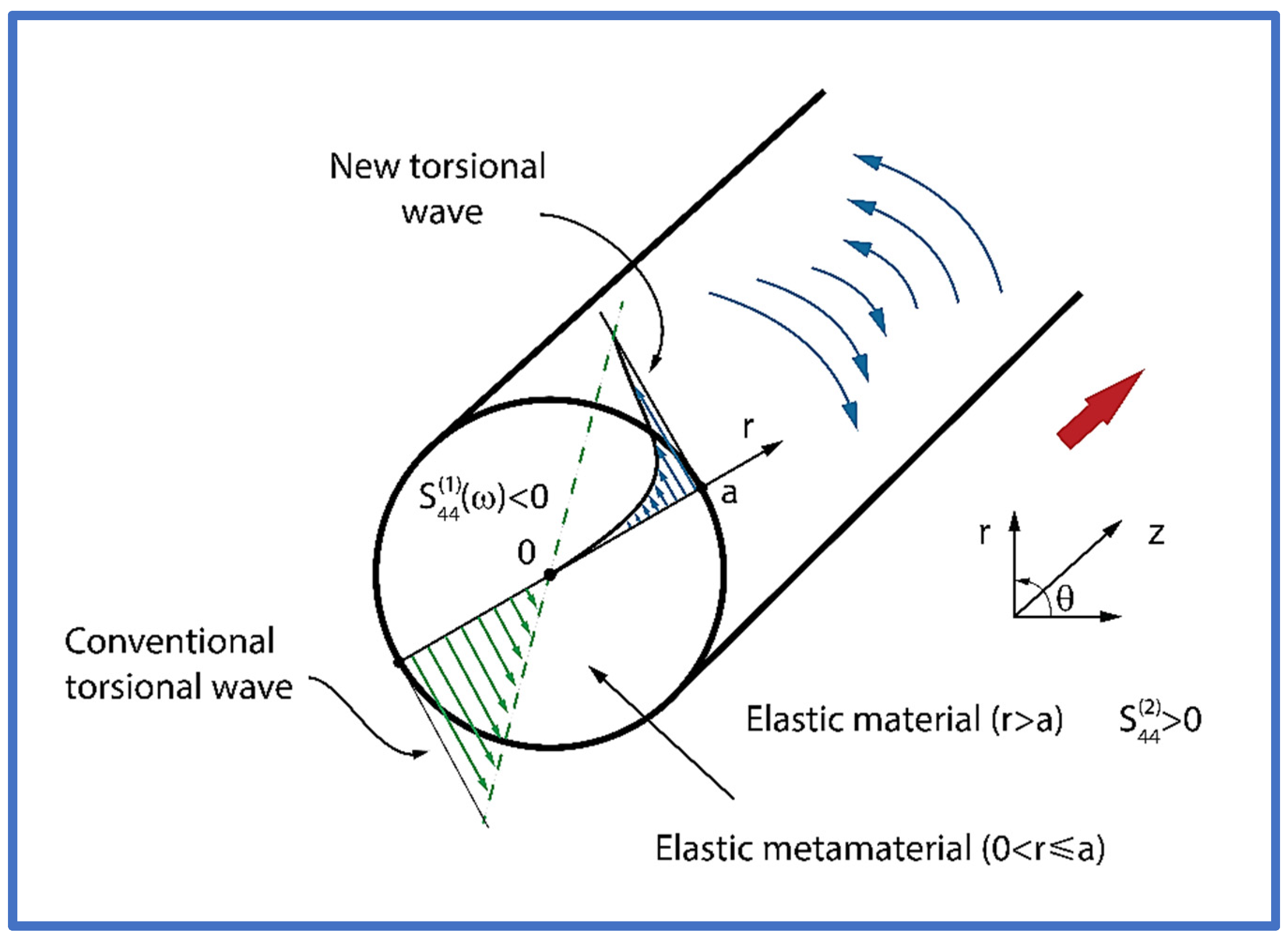
The aim of the authors’ work was to overcome these drawbacks. To solve this problem, the authors used the extraordinary properties of elastic metamaterials with a negative elastic compliance
. The waveguide proposed by the authors consists of a metamaterial cylindrical core immersed in a three-dimensional (3D) elastic external medium (see
Figure 1). The mechanical compliance
of the metamaterial cylindrical core (rod) follows the Drude model. Consequently, the mechanical compliance of the core cylinder can take negative and positive values as a function of angular frequency
.
The equations of motion written in a cylindrical coordinate system were formulated and solved. Analytical formulas of 1) the dispersion equation and 2) group velocity were developed for the elastic torsional wave propagating in layered cylindrical metamaterial structures in the z-axis direction, see
Figure 1.
The key property of the newly discovered torsional ultrasonic waves is that their mechanical displacement is concentrated close to the curved surface () of the cylinder, which greatly increases the mass sensitivity of the sensors that use the newly discovered torsional waves.
It should be finally mentioned that the proposed newly discovered torsional elastic surface waves exhibit virtually all extraordinary properties of their electromagnetic SPP counterparts, such as: 1) strong subwavelength concentration of energy in the vicinity of the curved cylindrical surface of the guiding rod, 2) very low phase and group velocities, 3) subwavelength penetration depth, 4) possibility to achieve a resolution below a wavelength (super resolution), 5) ability to amplify the evanescent waves etc.
The layout of this paper is as follows. After introduction in Section 1 we present in
Section 2 geometrical structure and material parameters of the cylindrical metamaterial waveguide supporting the new torsional elastic surface waves. In
Section 3 we develop mathematical equations for the mechanical displacement, shear stresses, dispersion relation and group velocity for the new torsional elastic surface waves.
Section 4 contains numerical results and figures resulting from the analysis performed in
Section 3.
Section 5 and 6 contains the discussion and conclusions, respectively.
2. Physical Model
2.1. Geometry and Material Parameters of the Waveguide
The geometry of the waveguide supporting the new torsional elastic surface waves is presented in
Figure 1. The waveguide consists of a metamaterial elastic cylindrical rod
embedded in a conventional elastic medium
). As it will be shown explicitly in the next
Section 2.2 the elastic compliance of the metamaterial cylindrical rod
can exhibit negative values
in the frequency range adjacent to zero frequency
. The remaining material parameters of the waveguide, i.e., the density in the metamaterial rod
and in a conventional elastic surrounding medium
as well as its elastic compliance
, are all positive.
2.2. Elastic Compliance of the Metamaterial Elastic Cylinder
It is assumed throughout this paper that the elastic compliance
of the metamaterial cylinder (rod), as a function of angular frequency
, changes analogously to the dielectric function
in Drude’s model of metals [
16], namely
where:
is the angular frequency of the local mechanical resonators in the metamaterial and
is its reference elastic compliance for
.
In the Drude’s model of metals the angular frequency
is called the angular frequency of bulk plasmon resonance [
17]. The adjacent medium (
) is a conventional elastic material with a positive compliance
and density
that are both frequency independent.
It should be stressed that the according to Equation (1) the elastic compliance
of the metamaterial rod is negative in the frequency range
. How to realize the elastic metamaterial with a negative elastic compliance
was shown in the recent paper of Kiełczyński [
2].
3. Mathematical Model
An unique feature of the new torsional elastic surface waves is the fact that they possess only one component of the mechanical displacement
that is polarized along the angular coordinate
which is tangential to the circumference of the cylinder (see
Figure 1).
The mechanical displacement of the new torsional elastic surface wave decays rapidly with the distance from the surface of the cylinder () in both directions, i.e., into the metamaterial elastic cylinder () and into the adjacent elastic medium ().
3.1. Mechanical Displacement and Shear Stress
The new torsional elastic surface wave propagates along the axis of the cylinder
, The mechanical displacement
of the new torsional elastic surface wave in the metamaterial elastic cylinder
can be expressed in the following generic form:
where: the function
depends only on the radial distance
,
stands for the imaginary unit,
is the wavenumber of the new torsional elastic surface wave,
is its angular frequency,
is an arbitrary real constant and
stands for time.
By definition, the associated shear stress
of the new torsional elastic surface wave in the metamaterial elastic cylinder
is given by:
Analogous expressions can be written for the mechanical displacement
and the associated shear stress
in the adjacent conventional elastic medium (
), namely
and
where: the function
depends only on the radial distance
and
is an arbitrary real constant.
The functions and with a radial argument describe the change in the amplitude of the new torsional elastic surface wave inside the cylindrical metamaterial rod and in the surrounding medium, respectively.
The functions
and
will be given in a closed analytical form by Equations (10) and (11) and the wavenumber
will be determined from the dispersion relation Equation (14) in
Section 3.5 of this paper.
3.2. Equations of Motion
The mechanical displacements of the new torsional elastic surface wave: in the metamaterial elastic rod
and in the adjacent conventional elastic medium
satisfy the following equations of motion, written in the cylindrical system of coordinates:
and
where: for the sake of clarity the arguments in the mechanical displacements
were omitted.
3.3. Explicit Analytical Formulas for the Mechanical Displacements and
Substituting Equation (2) for the mechanical displacement
in the metamaterial rod into the equation of motion Equation (6) we obtain an ordinary differential equation for the unknown radial function
. It can be shown that the solution for this differential equation takes the following form:
where:
is the radial wavenumber
and
stands for the modified Bessel function of the first kind of order 1.
Similarly, substituting Equation (4) for the mechanical displacement
in the adjacent medium into the equation of motion Equation (7) we obtain an ordinary differential equation for the unknown radial function
, whose solution reads
where:
is the radial wavenumber
and
stands for the modified Bessel function of the second kind of order 1.
Finally, substituting Equation (8) into Equation (2) and Equation (9) into Equation (4) one obtains
3.4. Boundary Conditions
The mechanical displacement
and shear stress
of the new torsional elastic surface wave must be continuous across the surface of the cylindrical surface
of the metamaterial rod, i.e.,
3.5. Dispersion Equation
In the first step in determination of the dispersion equation for the new torsional elastic surface waves we will substitute Equations (2)–(5) into the boundary conditions Equations (12) and (13). As a result, we will obtain a system of two linear homogeneous algebraic equations for the unknown constants
and
. Equating the determinant of this system of equations to zero we obtain the following dispersion equation of the new torsional elastic surface waves:
where:
and
are the modified Bessel functions of the first kind of order 1 and 2, and similarly,
and
are the modified Bessel functions of the second kind of order 1 and 2.
The dispersion relation Equation (14) is a transcendental nonlinear algebraic equation for the wavenumber at a fixed angular frequency which can be solved numerically using appropriate numerical procedures, such as e.g., the iterative Newton-Raphson method.
3.6. Group Velocity
Group velocity
of the new torsional elastic surface waves was evaluated analytically using the following formula:
, where the function
represents the dispersion equation (see Equation (14)) which is obviously an implicit function of the angular frequency
and wavenumber
. Thus, after lengthy but quite elementary algebra we obtain:
where:
;
;
;
and
.
At first glance Equation (15) looks lengthy and intimidating, with doubtful operational significance, however it can be easily implemented in numerical calculations using standard procedures from software packages, such as Scilab or Matlab.
4. Results of Numerical Calculations
4.1. Material Parameters of the Waveguide
Numerical calculations were performed employing an exemplary waveguide structure consisting of metamaterial cylindrical rod (
) made of ST-Quartz with embedded local oscillators and PMMA surrounding medium (
). We assume that, the frequency of the local elementary oscillators equals
. The radius of the metamaterial cylindrical rod is
. Losses in the cylindrical waveguide structure are neglected. The actual values of the material parameters used in the numerical calculations are given in
Table 1.
Numerical calculations were performed with the help of the Scilab software packed
4.2. Dispersion Curve
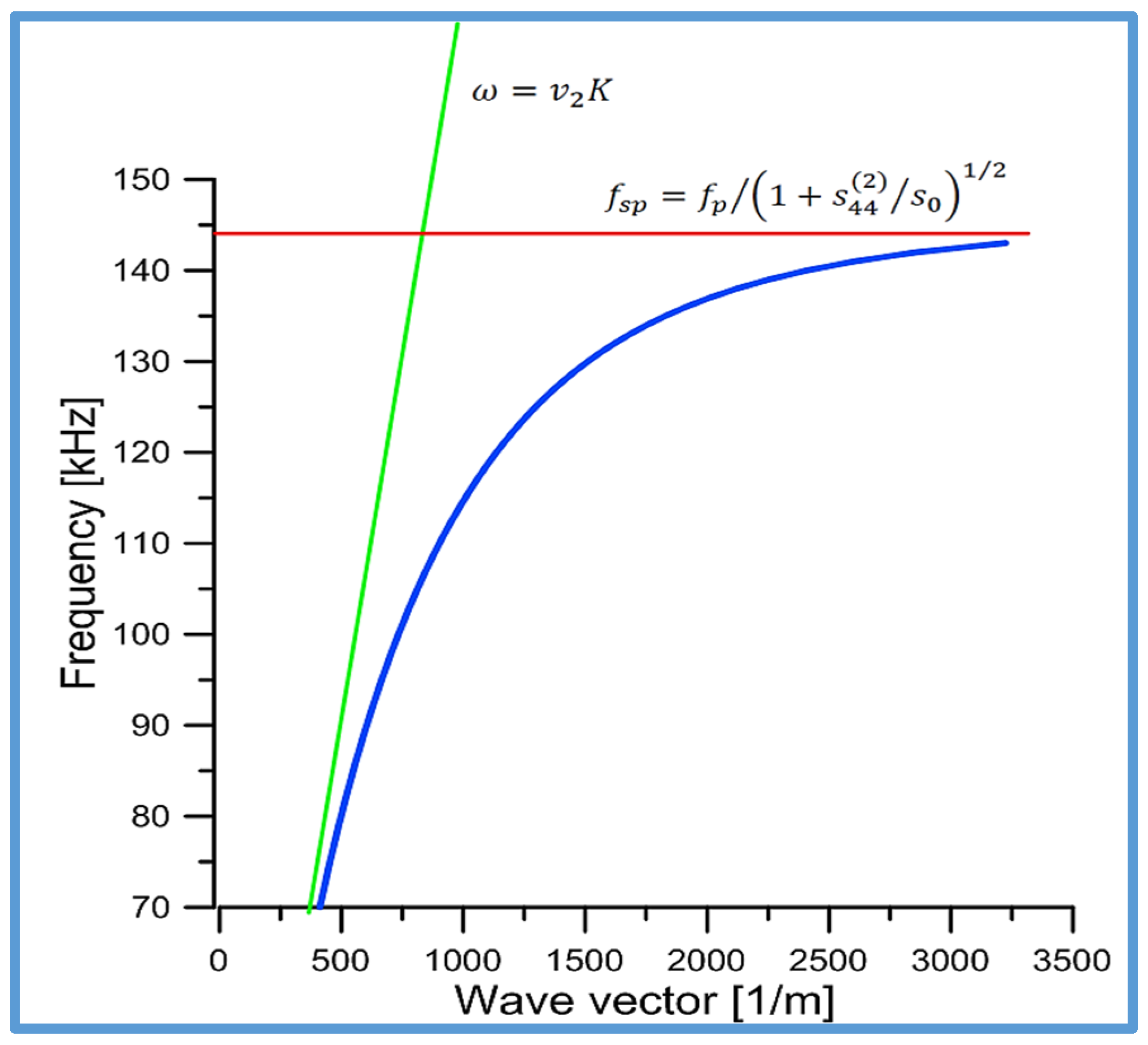
The dispersion curve of the new torsional elastic surface wave was calculated from the solution of the dispersion relation Equation (14) and plotted in
Figure 2 as the wave frequency
versus the wave number
. The phase velocity of the bulk shear elastic waves in the surrounding conventional elastic medium was denoted in
Figure 2 as
. Surface resonant frequency
is an upper cut-off frequency, since above this frequency the new torsional elastic surface wave cannot propagate.
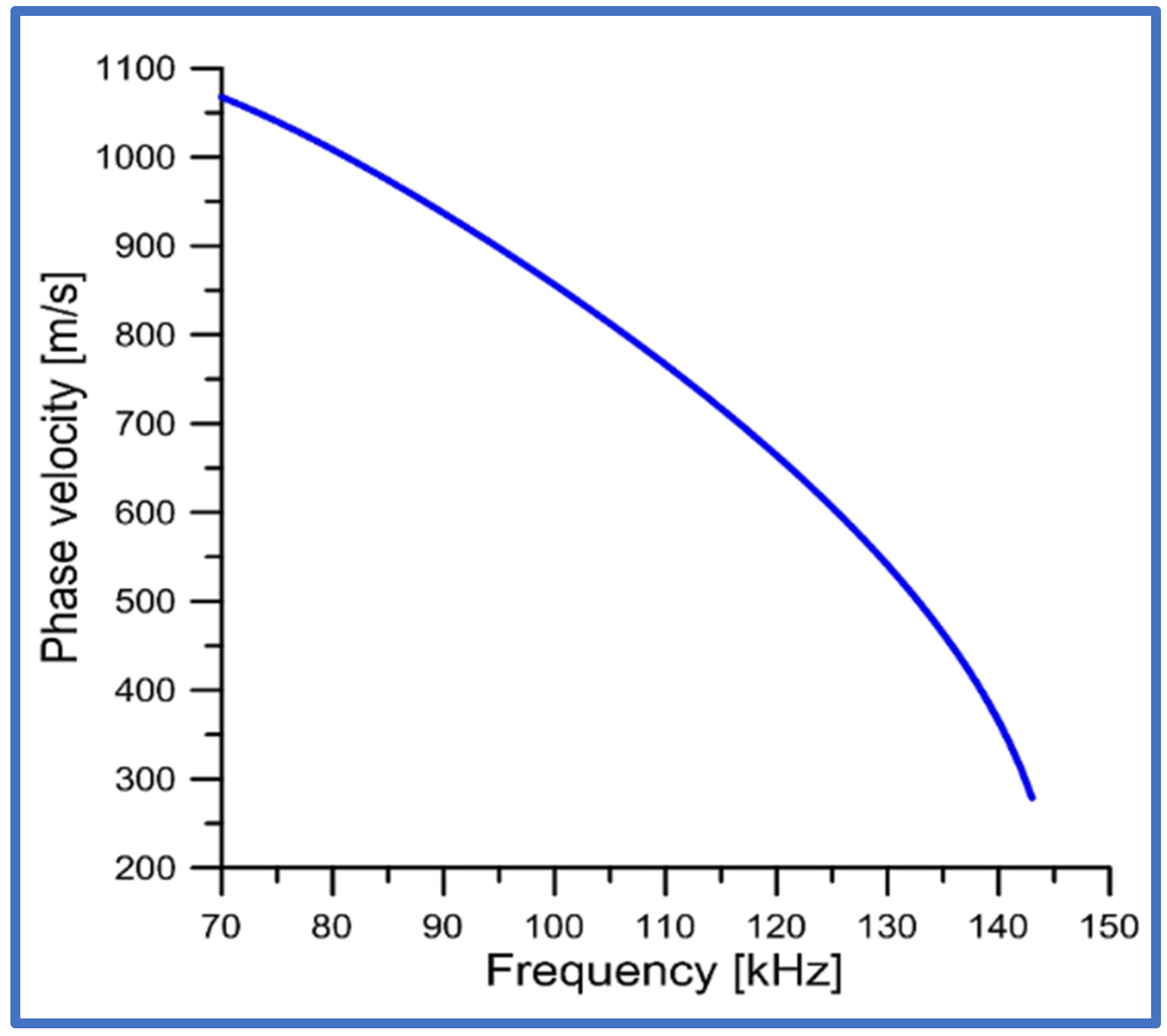
4.3. Phase Velocity
Using the solution of the dispersion Equation (14), the plot of the phase velocity
, as a function of the wave frequency
was evaluated and presented in
Figure 3. In our calculations the surface resonant frequency
is equal to
.
4.4. Group Velocity
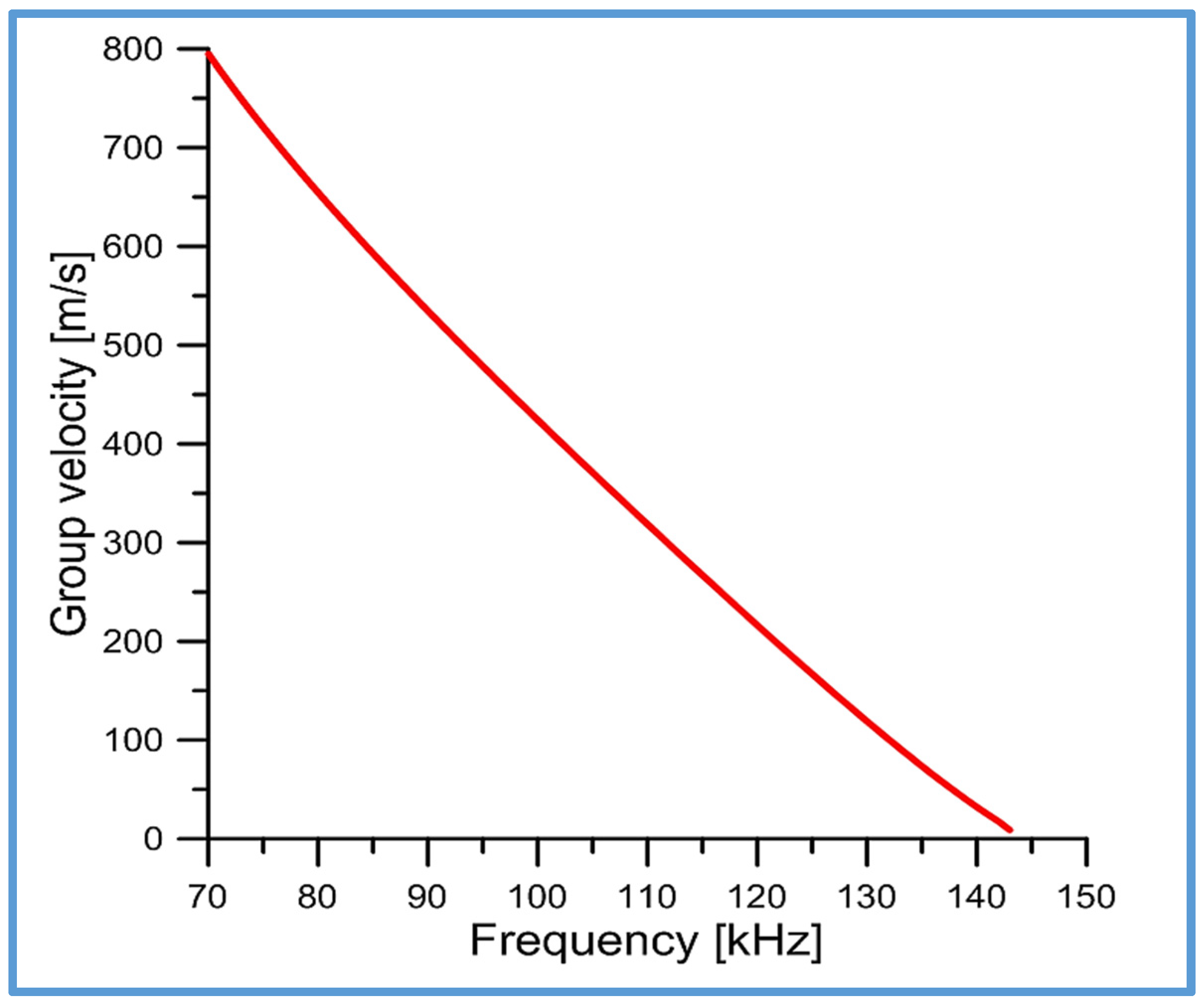
Figure 4 shows the plot of the group velocity
of the newly discovered torsional elastic surface wave as a function of the wave frequency
. The numerical calculations were performed using an analytical formula, Equation (15).
Note that group velocity
of the new torsional elastic surface wave is always lower than its phase velocity
shown in
Figure 3, but has the same cut-off frequencies.
5. Discussion
The characteristic feature of the dispersion curve (see
Figure 2) of the newly discovered torsional wave is that as the wave frequency grows and approaches the surface resonance frequency
, the wavenumber
increases significantly. Consequently, the wavelength
decreases and can reach the subwavelength region. This feature is responsible for the increase in the concentration of wave energy near the surface of the cylinder
, see
Figure 1, therefore for a substantial increase in the mass sensitivity of the new torsional wave.
The quest for sensors with enhanced parameters, such as very high sensitivity or very low detection threshold, is driven by the requirements resulting from numerous applications in medicine, biology, environmental studies, toxicology, etc.. In fact, an early detection of harmful bacteria, viruses or toxins requires development of the appropriate sensors with a very high sensitivity and very low threshold of detection.
These important goals can be achieved using in general two different ways: first, by improvement of the existing sensors and technologies and second, by employment of new concepts, new types of waves or new materials. Evidently, the second approach offers a chance to develop new revolutionary solutions with sensors of extraordinary parameters. However, it requires the navigation on uncharted waters, which may be not only very difficult but very often disappointing.
In this paper we adhere to the second approach. In fact, in order to develop sensors with a very high mass sensitivity we propose to use the new type of elastic torsional surface waves which were discovered recently by the authors. These newly discovered elastic torsional waves propagate in the vicinity of the curved surface of the metamaterial cylindrical rod in which the elastic compliance is analogous to the dielectric function in Drude’s model of metals.
Our choice of the new type of torsional elastic surface waves, propagating in metamaterial waveguides, can be justified by their extraordinary properties, which cannot be found in the existing elastic surface waves propagating in conventional pure elastic waveguides. For example, the newly discovered torsional elastic surface waves propagating along metamaterial cylinders (rods) exhibit the following unique properties:
very high concentration of the wave energy in the vicinity of the cylindrical guiding surface () of the waveguide
subwavelength penetration depth in both directions from the cylindrical guiding surface ()
As a matter of fact, all the above characteristics of the new torsional elastic surface waves can be employed in development of ultrasonic sensors with a very high mass sensitivity. In addition, the cylindrical shape of the waveguide supporting the new torsional elastic surface waves can be advantageous in operation in a liquid environment.
6. Conclusions
In this paper we discovered and present new torsional elastic surface waves that propagate along elastic metamaterial rods (cylinders) embedded in a conventional elastic medium. The new torsional elastic surface waves have the following unique properties:
they constitute an elastic analogue of the Surface Plasmon Polariton (SPP) electromagnetic (optical) waves propagating in layered dielectric-metal cylindrical waveguides,
new torsional elastic waves can inherit such fascinating properties of SPP optical waves as: a) superlensing, b) superresolution, and c) ability to amplify evanescent waves
they have only one component of the mechanical displacement polarized along the angular coordinate,
the energy of the wave is strongly confined in the vicinity of the guiding cylindrical surface () of the metamaterial rod,
penetration depth of the wave in both direction from the guiding cylindrical surface of the metamaterial rod can be subwavelength,
their phase and group velocities tend to zero as the wave frequency approaches the upper cut-off frequency.
Consequently, due to their unique properties, presented above, the newly discovered torsional elastic surface waves, analyzed in this paper, have a significant potential for development of a new generation of ultrasonic sensors, biosensors and chemosensors with a very high mass sensitivity for applications in medicine, biology, chemistry and environmental research.
This work has an interdisciplinary character and therefore can be of interest to a wide range of researchers and engineers working in different domains of science and technology, such as: acoustics, ultrasonics, optics, physics, microwaves, elastic metamaterials, ultrasonic sensors, biosensors and chemosensors.
Acknowledgment
The project was funded by the National Science Centre (Poland), granted on the basis of Decision No. 2020/39/B/ST8/03505.
Conflicts of Interest
The authors declare no conflict of interest
References
- Kiełczyński, P. New Surface-Plasmon-Polariton-Like Acoustic Surface Waves at the Interface Between Two Semi-Infinite Media. Archives of Acoustics, 2022, 47, 363-371. [CrossRef]
- Kiełczyński, P. New Shear Horizontal (SH) Surface-Plasmon-Polariton-like Elastic Surface Waves for Sensing Applications. Sensors, 2023, 23, 9879. [CrossRef]
- Devaux, E.; Dereux, A.; Bourillot, E., Weeber, J-C.; Lacroute, Y.; Goudonnet, J.-P. and Girard, C. Local detection of the optical magnetic field in the near zone of dielectric samples. Phys. Rev. B 2000, 62, 10504. [CrossRef]
- Schroter, U. and Dereux, A. Surface plasmon polaritons on metal cylinders with dielectric core. Physical Review B 2001, 64, 125420. [CrossRef]
- Devaux, E.; Dereux, A.; Bourillot, E.; Weeber, J-C.; Lacroute, Y.; Goudonnet, J.-P.; Christian G. Local detection of the optical magnetic field in the near zone of dielectric samples. Physical Review B, 2000, 62, 10504-10514. [CrossRef]
- Achenbach, J.D. Wave Propagation in Elastic Solids. North-Holland, Amsterdam, 1973.
- Auld, B.A. Acoustic Fields and Waves in Solids. Vol. I, II, Krieger Publishing Company, Florida, 1990.
- Royer, D. and Dieulesaint E. Elastic Waves in Solids. Vol. I, Springer, Berlin Heidelberg New York, 2000.
- Maerfeld C. and Tournois, P. Pure Shear Elastic Surface Wave Guided by the Interface of Two Semi-Infinite Media. Applied Physics Letters 1971, 19, 117–118. [CrossRef]
- Pajewski,W.; Kiełczyński, P. and Szalewski, M. Resonant piezoelectric ring transformer. In IEEE Ultrasonics Symposium Proceedings, Sendai, Japan, 1998, 977-980.
- Kiełczyński, P. Pajewski, W. Szalewski, M. Piezoelectric sensors for investigations of microstructures. Sensors and Actuators A-Physical 1998, 65, 13–18. [CrossRef]
- Kiełczyński, P.; Szalewski, M.; Balcerzak, A. and Wieja, K. Group and phase velocity of Love waves propagating in elastic functionally graded materials. Archives of Acoustics 2015, 40, 273–281. [CrossRef]
- Kiełczyński, P. Direct Sturm–Liouville problem for surface Love waves propagating in layered viscoelastic waveguides. Applied Mathematical Modelling 2018, 53, 419–432. [CrossRef]
- Kiełczyński, P. New Fascinating Properties and Potential Applications of Love Surface Waves. Invited Speaker presentation at the IEEE, International Ultrasonic Symposium, September 11-16, 2021, Xi’an, China. http://zbae.ippt.pan.pl/strony/publikacje.htm.
- Mason, W.P. Piezoelectric Crystals and Their Application to Ultrasonics. Van Nostrand, New York, 1950.
- Born M. and Wolf E. Principles of Optics. Cambridge University Press, Cambridge, sixth edition, p. 625, 1980.
- Nkoma, J.; Loudon, R.; Tilley, D.R. Elementary properties of surface polaritons. Journal of Physics C: Solid State Physics 2001, 7, 3547–3559. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).