Prerpints.org logo
Preprint
Article

A Computational Model of Minimal Phenomenal Experience (MPE)

Altmetrics

Downloads

166

Views

226

Comments

0

This version is not peer-reviewed

Submitted:

08 November 2024

Posted:

12 November 2024

You are already at the latest version

Alerts
Abstract
Minimal phenomenal experience (MPE), or "pure consciousness," represents a fundamental form of conscious experience characterised by reflexive meta-awareness and the absence of many features of regular phenomenology. It has been described as e.g. non-conceptual, atemporal, non-egoic and aperspectival. This paper aims to develop a computational model of MPE using the mathematics of variational free energy minimization derived from the free energy principle (FEP). I employ a computational neurophenomenology approach, formalising key phenomenological features of MPE within the active inference framework. The model incorporates parametric depth, allowing for higher-order inferences about generative model parameters. I relate specific model parameterisations to reported MPE qualities such as meta-awareness, equanimity, effortlessness, and non-conceptuality. The proposed model suggests that MPE arises when an agent achieves very low free energy through self-directed awareness and modulation of their generative model, particularly by emphasising awareness of awareness itself. The model predicts elements of MPE phenomenology including a sense of effortlessness, timelessness, and the potential for a "zero-person perspective”. The implementation details for a simulation of the proposed model are outlined, as well as directions for empirical validation.
Keywords: 
Subject: Social Sciences  -   Cognitive Science

1. Introduction

The context of this paper is the research program initiated by Thomas Metzinger on the topic of minimal model explanations of human consciousness (Ramstead, Albarracin, Kiefer, Williford, et al., 2023; Wiese, 2020). He has argued that any explanation of consciousness should endeavour to first explain the simplest version of the phenomenon we can identify. This raises the question, what is the simplest form of conscious experience we find in humans? In an effort to answer this, Metzinger embarked on an ambitious phenomenological enquiry, documenting the experience of hundreds of individuals reporting to have experienced (or be experiencing) an absolutely stripped back, “minimal phenomenal experience” (MPE) (Metzinger, 2020), also known as “pure consciousness”.
The results of the “MPE-project” have been documented in Metzinger’s recent book The Elephant and the Blind (Metzinger, 2024), which documents the emergent clusters of commonly reported qualities or features of MPE. His work has shown that there exists a phenomenological cluster of seemingly related experiences that are reported primarily by experienced meditation practitioners. The hallmark of these experiences are their simplicity, MPE seems to be devoid of many of the features we might usually expect, such as conceptual content, a sense of temporality or even a subjective perspective. An explanation of this simple, yet uncommon, experience might form a sound foundation upon which to build further scaffolding for consciousness research. Or at the very least, serve as an experiential data point that any theory of consciousness must account for.
However, the primary aim of this paper is not to generate evidence for a theory of consciousness. Instead my aim is to outline a methodology for engaging in computational phenomenology and demonstrate its potential by developing the beginnings of an explanation of MPE, which myself and others can continue to build upon. The value of this methodology resides in the computational language it provides for explaining and understanding our experience, and in particular the intriguing and often transformative phenomenology associated with MPE and contemplative practice. These modes of perception have profound intrinsic value to those who experience them, therefore a mechanistic explanation of MPE has value beyond the evidence it would lend to a candidate theory of consciousness. Computational phenomenology as presented here is best understood as a rigorous conceptual scaffolding for facilitating the first person investigation of our own lived experience (a “laser pointing at the moon”). This, I would argue, is where the true “fruit” of this work is to be found — in a direct experiential recognition of consciousness. Therefore, the claims here are pragmatic rather than metaphysical. Any evidence that this work provides for the validity of the underlying modelling framework as a theory of consciousness is a secondary effect, open to the reader’s interpretation, and not the central motivation.
The model presented here is an iteration on the model initially proposed in (Metzinger, 2024, pp. 475–477), updated to account for a broader range of phenomenological features of MPE. The modelling approach is couched within a methodology known as computational neurophenomenology (Ramstead et al., 2022; Sandved-Smith et al., 2024) that leverages the mathematics of variational free energy minimization derived from the free energy principle (FEP) (Friston, 2019). The FEP states that living systems that persist in time can be understood as engaging in a form of variational Bayesian inference about their environment (Da Costa et al., 2020; Da Costa, Friston, et al., 2021; Friston et al., 2022). The core assumption that enables an FEP based computational neurophenomenology is that the (Bayesian) beliefs resulting from this variational inference, i.e. the variational density, can be used to model first person phenomenology (Hohwy, 2013). This can be read as a modern iteration of the neurophenomenology (NPh) research program first proposed by Francisco Varela (Varela, 1996, 1997).
Given that the corpus of evidence for MPE is primarily phenomenological reports, in this paper I build the explanatory model by formalising a few select features of MPE phenomenology. For each feature I ask how it might be described computationally, which then builds up a collection of computational constraints that will inform the proposed model of MPE. A unique feature of an FEP based neurophenomenology is that this model, constructed using the phenomenology, can then in principle generate neurobiological predictions that serve to test and further refine the proposed model and our understanding of MPE.
In what follows I first provide a brief overview of the free energy principle and its relationship to the computational neurophenomenology approach taken here. Then I motivate computational interpretations of a few key phenomenological features of MPE. With these elements in place I construct a proposed model of MPE. Please refer to the Appendix for simulation implementation details and neurobiological predictions that follow from the proposal.
In doing so a hypothesis emerges that MPE represents the phenomenology of an individual in a regime of very low free energy made possible by recursive self-modelling and optimisation of their own generative model parameters.

2. From the FEP to Deep Active Inference

To build a computational model that accounts for the core features of MPE, we need a robust modelling framework. The framework employed here is known as the active inference framework (AIF) (Smith et al., 2022), which is a particular application of the free energy principle to agentic systems. In addition to engaging in variational inference about their environment, agentic systems perform autonomous actions to minimise free energy, making them capable of planning and decision-making. This entails the minimization of not only variational free energy (based on current and past sensory data) but also expected free energy (EFE), which is based on predictions about the sensory input they would receive were they to select a specific course of action (policy). Notably, acting to minimise free energy is equivalent to maximising evidence for a generative model of self and environment, a process known as self-evidencing (Hohwy, 2016).
As mentioned above, we make the assumption that phenomenology is related to the dynamics of the posterior distribution, i.e. state inference. Practically this means that we are hunting for the state inferences that might be related to specific features of MPE reported by participants, and crucially the evidence upon which these inferences are formed.
The computational model outlined here takes the form of a partially observable markov decision process (POMDP), which is a common approach to modelling the belief updating that underpins the perception and action in active inference agents.
In particular, this model exhibits a form of reflexivity or depth. In previous work we have proposed that awareness of cognitive states, and mental action, can be modelled using a hierarchical active inference model exhibiting parametric depth (Sandved-Smith et al., 2021). This depth enables the agent to make higher order inferences about the parameters of other inferential processes, i.e. form beliefs about beliefs. This formally captures a notion of metacognition or “deep inference” (Da Costa & Sandved-Smith, 2024; Sandved-Smith & Da Costa, 2024), and provides a mechanism for mental or covert action.
In this paper, I will adopt this same approach. This is important because it provides a mechanism for state inference on the basis of observing one’s own model parameters. Without this depth, the phenomenal experience (i.e. state inference) is only about external states and the agent is not capable of perceiving anything about how their perception is formed (i.e. the parameters of the generative model implicated in inference). The process of perceptual formation would be “transparent” to the agent, in the sense that the world is seen through the parameterisation of their generative model. When the agent is able to perform second order inferences by observing their internal parameters we say that they have “opacified” a previously transparent aspect of their generative model (Metzinger, 2003; Limanowski & Friston, 2018). This allows the agent to form posterior beliefs that can be used to model deeper aspects of human phenomenology, such as the awareness of cognitive states, and, as we’ll see — the awareness of awareness itself.

3. Methodology

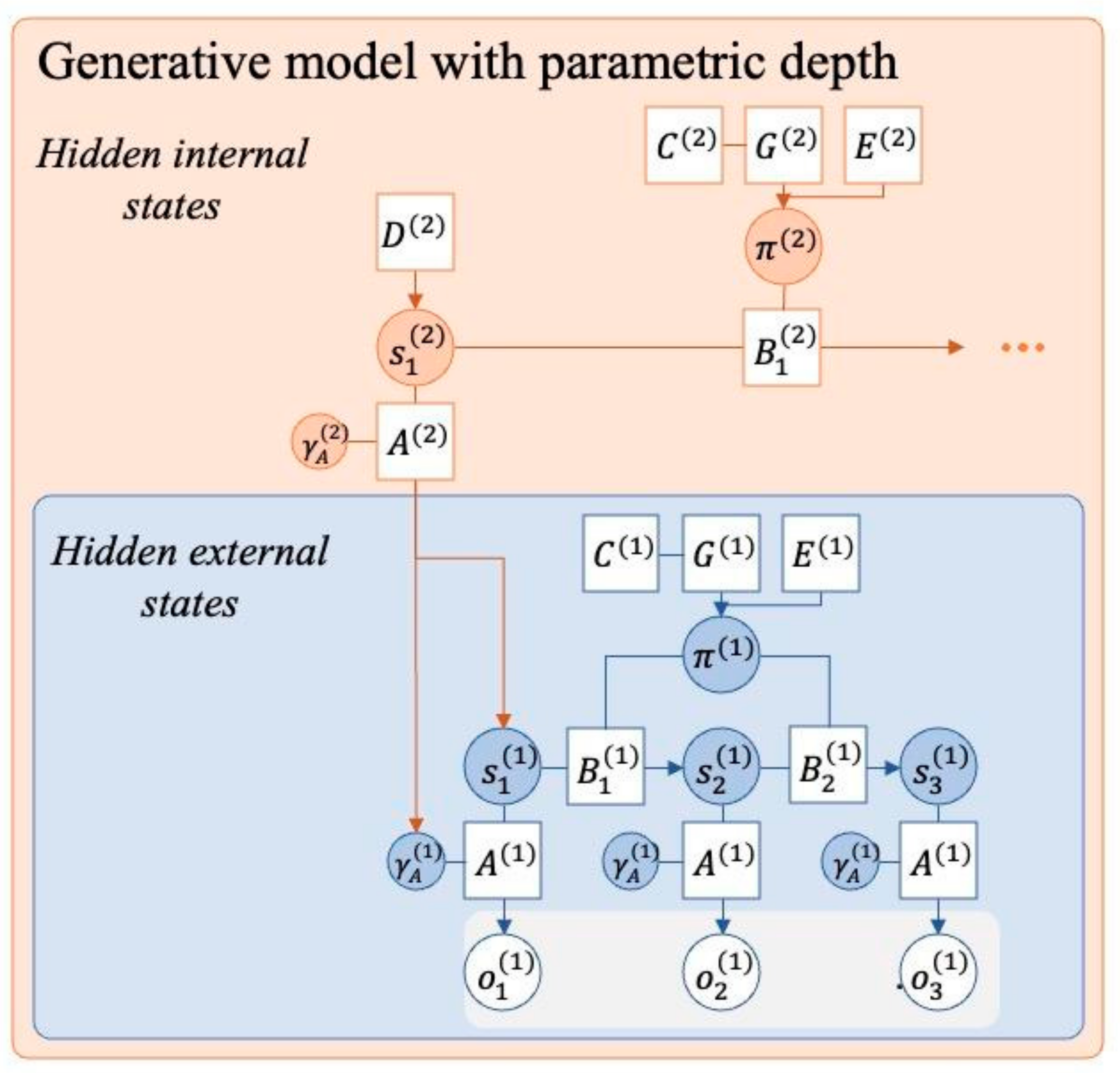
Part of the novelty in the model presented here arises from extending the mechanism of parametric depth to a wider range of the model parameters. In the previously proposed model, only the likelihood precision was subject to second order inferences. Here I endow the model with the ability to form deep inferences about other parameters, such as the preference precision and the policy precision (see Figure 2). This broadens the explanatory power of the model since the resulting state inferences can be related to various phenomenological features.
The methodology for performing this relation between phenomenology and model parameters starts by understanding the mathematical role that each parameter performs in the posterior formation. With practice, this allows us to intuit what it ‘would be like’ (from the perspective of the modelled agent) to modulate that particular parameter, in terms of how their perceptual or behavioural experience might change. From this mathematically grounded intuition we can form hypotheses about how to model different phenomenological features. This is facilitated by also having an intimate first person familiarity of the phenomenology in question, e.g. a regular meditation practice.
This methodology might initially sound like mathematical story telling — how do we (in)validate any of the hypothetical relations made between phenomenology and parameters? The first point to note is that the modelling architecture enforces a degree of internal coherence. This is because the model parameters are interdependent. Therefore, a hypothesis we make about one parameter has ramifications for other parameters and their related phenomenology. As a result, the internal consistency of the model, and its alignment with the relationship between phenomenological features, provides an initial source of construct validity.
In addition, the resulting generative model has predictive power that we can leverage to test the predictive validity of the proposal. By virtue of being a computational model we can run simulations of expected future model dynamics. This gives rise to three forms of prediction: phenomenological, behavioural and neurobiological. The phenomenological predictions arise from studying the expected dynamics of the perceptual inferences given the proposed parameterisations. We will see examples of a phenomenological prediction in Section 4.4, Section 4.5, Section 4.6 and Section 4.7. The behavioural predictions arise from the ability to simulate action selection in a given task setting. This is not treated here but is tractable in principle. For example, does access to MPE change behaviour in a go/no-go task designed to test impulsiveness?
Neurobiological predictions are enabled by the dual interpretation of the dynamics of the agent’s internal states, which can be read in terms of the belief dynamics or in terms of the thermodynamics of the states per se. This so-called “dual information geometry” is the basis for deep computational neurophenomenology (Sandved-Smith et al., 2024), which enables a flow of predictions between the phenomenology and neurobiology. This is explained further in Appendix B.

4. Formalising Phenomenological Features of MPE

In the following sections we will examine a selection of the core phenomenological characteristics associated with MPE. Each section will propose a computational account of the feature as we progressively build up a detailed model. The resulting model serves as a computational explanation of the experience of MPE, which we can then use to derive insights about the mechanisms of MPE and to generate empirical predictions in order to test the translation of the phenomenology into the mathematical model. See Table 1 in Section 5 for a summary of the formalisations.

4.1. Meta-Awareness

Meta-awareness is the first phenomenological characteristic of MPE we will formalise in the construction of the proposed MPE model. In MPE, participants frequently report 1 a high degree of meta-awareness, i.e. a wakeful awareness of the contents of consciousness.
“687 I am in a state of wakefulness. I have a strong awareness of the pre sent moment. It is as if I am a guard dog: All my perceptions seem heightened. I am in consciousness but I am not doing anything except perceiving sounds, smells, sensations in my body.”
(Metzinger, 2024, pp. 33–34)
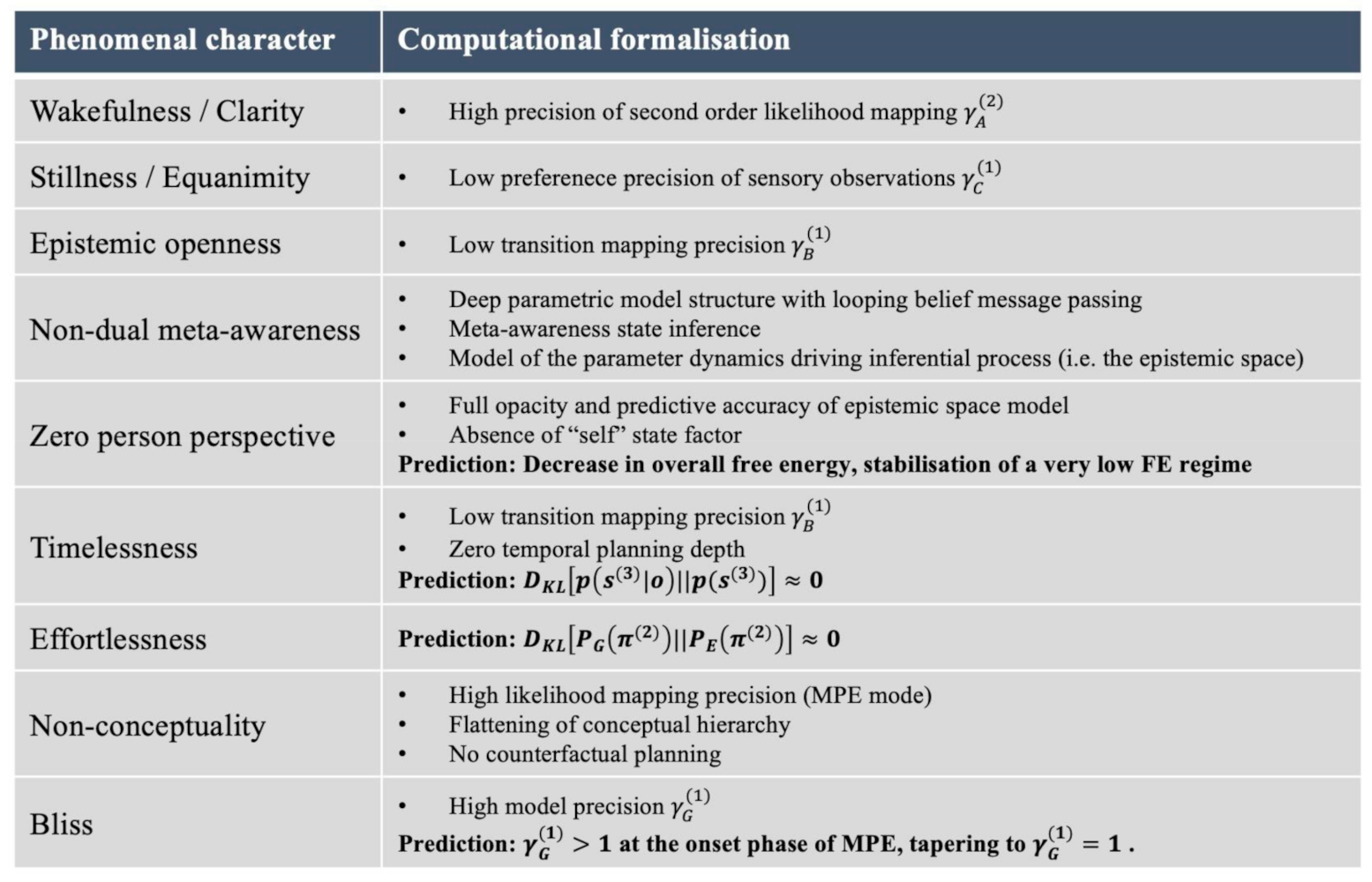
In previous work we proposed that meta-awareness can be modelled as the likelihood precision of second order observations of model parameters (Sandved-Smith et al., 2021). See the γ A 2 parameter in Figure 1. To justify the face validity of this definition, we simulated the effect of high and low meta-awareness in an attentional task, demonstrating that periods of mind-wandering (being distracted whilst unaware of the distraction) were reduced with higher meta-awareness. This recapitulates empirical results and aligns with existing definitions of meta-awareness. (Dunne et al., 2019)
This meta-awareness parameter enables the agent to become aware of their internal states, since it acts to set the precision or weighting of observations generated by the parameters of the generative model. Given that these parameters define the action-perception model of the agent, high meta-awareness amounts to an ongoing opacification of the processes driving their inferential processes. This accords with the common definition of meta-awareness as the capacity to explicitly notice the contents of consciousness.
Hence when parameterising a computational model of MPE, we can use this phenomenological data to inform the value of this higher order likelihood precision parameter, setting it to “high”. Numerically this implies a value >1. The effect, computationally, is that the agent is able to form unambiguous inferences about the state of the various generative model parameters.

4.1.1. Meta vs Reflexive Awareness

Interestingly, the experience of meta-awareness during MPE is often reported with a quality of reflexivity. In other words, meta-awareness is experienced as a bare awareness of awareness itself.
“1350 […] When the relevant state arises, it is like seeing seeing, or awareness of being aware.”
“1617 Experiencing awareness of consciousness or of cognizance as such.”
(Metzinger, 2024, pp. 396–398)
At a first glance, this reflexiveness can seem at odds with the meta-awareness mechanism proposed thus far. The term “meta” can evoke notions of a ‘higher perspective’ or separate vantage point from which to look from. Furthermore, this tension can be reinforced by a naive interpretation of the hierarchical model presented in Figure 1. It seems as if the agent is split, creating some separation between the part which is aware of the internal states, and the internal states themselves. However, upon closer investigation we can see that this reflexive phenomenology is in fact in accordance with this computational account.
The misunderstanding to address is the idea that hierarchical inference creates a separate ‘higher perspective’, or internal homunculus. By leveraging the mathematics of Bayesian mechanics, we can show that despite the hierarchical, or nested, structure of the agent — there exists an inner-most “cognitive core” or “inner screen” that contains all the information from the other levels. This topic is explored further in (Ramstead, Albarracin, Kiefer, Klein, et al., 2023; Sandved-Smith & Da Costa, 2024, §8.1) for interested readers. The key point for our purposes here is that there exists a single variational density that captures the beliefs from all levels of the inferential hierarchy. Some of these beliefs are about the processes that underpin the formation of other beliefs, and yet all are experienced simultaneously.
Let’s further unpack the computational mechanisms that give the experience of meta-awareness a reflexive quality. Or what Metzinger calls the “phenomenal signature of self-knowing”. There are three sources of reflexivity in the flow of the computational logic when parametric depth and meta-awareness are introduced into the model. These provide a mathematical grounding for the phenomenology of reflexive awareness that others have described as a “beautiful loop” (Laukkonen & Chandaria, 2024).
The first mechanism relates to the role of the meta-awareness parameter in rendering the dynamics of the agent’s own model parameters available for inference. The agent’s model parameters collectively underpin the inferential process that leads to the formation of the posterior beliefs, which we relate to the perceptual experience. Said differently, meta-awareness enables modelling the process of becoming aware of perceptual content (i.e. the formation of posterior beliefs). Therefore, high meta-awareness enables the agent to become aware of the process by which their experience arises — they are becoming aware of the process of becoming aware of perceptual content. This idea is unpacked further in Section 4.2.
A second mechanism of reflexivity emerges when we model the agent as capable of state inference on the basis of the meta-awareness parameter (see Figure 2). This higher order (third level) inference of the state of meta-awareness gives the agent an experience of being aware (i.e. meta-awareness state inference) of the degree to which they are aware (i.e. meta-awareness parameter value) of the process of awareness (i.e. the dynamics of the parameters of the generative model). Before observing this particular parameter, the agent was already awake and aware of their experience. This additional reflexivity of the meta-awareness provides a recognition of the already awakeness.
Finally, a third mechanism of reflexivity emerges from “loopy” logic of belief message passing in the hierarchical scheme. Top level inferences influence, and are influenced by, lower level inferences. The layers of hierarchical inference therefore induce a hierarchical looping of the belief message passing. However, as mentioned above, the beliefs generated by this looping are captured in the dynamics of an inner-most variational density — and therefore experienced as a single gestalt experience. We would therefore expect that phenomenological reports of meta-awareness attempt to express an impression of reflexive self-knowing, that the field of experience refers to itself. Or in Metzinger’s words:
“[…] it is as if the phenomenal signature of knowing dynamically folds back into itself, silently but continuously reembedding awareness into itself.” (Metzinger, 2024, p. 394)
Before moving on, note that Metzinger makes a distinction between dual meta-awareness and non-dual meta-awareness, distinguished by the presence or absence of a sense of “me” experiencing the meta-awareness. I do not consider this distinction a part of the meta-awareness mechanism itself, but instead a consequence of the degree to which the individual’s model contains a “self as cause” state factor. This is discussed in Section 4.6: “Zero-person perspective”.

4.2. Modelling the Epistemic Space

A key intuition proposed by Metzinger is the notion of an “epistemic space”. This is the space of possible phenomenal content that can be known by the agent. Metzinger goes on to propose that pure awareness, ie. awareness of awareness, might be related to the capacity for an agent to know, or model, the epistemic space itself.
“In my view, the epistemic-space metaphor is the best phenomenological metaphor for pure consciousness or minimal phenomenal experience (MPE). […] and experiencing pure awareness simply means having a model of this space, nonconceptually knowing that it exists.”
(Metzinger, 2024, pp. 46–47)
This phenomenologically motivated intuition finds a credible computational counterpart when we consider the ramifications of a model with parametric depth. The output of a generative model, known as the posterior distribution over states, is a belief in the form of a probability distribution. This distribution is the agent's best explanation for the causes of their sensory data and is generally understood as a computational analogue of the agent’s perceptual experience. The inferential process that gives rise to this explanation is a consequence of the observations received and a particular parameterisation of the generative model at that moment in time. If we assume a POMDP model structure, these parameters include e.g. the likelihood mapping A which encodes beliefs about state observation mappings and the transition mapping B which encodes beliefs about possible transitions of a state from one moment to the next. A different parameterisation (e.g. different learning history) would result in a different posterior distribution.
We can plot each possible posterior as a point on a statistical manifold, i.e. a high dimensional plane where each point defines a probability distribution and each dimension is a parameter of the generative model. This manifold effectively represents all the possible beliefs the agent might entertain, i.e. all the possible perceptual experiences. This has a strong semblance to Metzinger’s notion of epistemic space:
“By definition, an epistemic space is a space of possibilities: It contains every possi ble epistemic scenario and every dynamic partitioning of itself that could ever take place— every thing that could potentially be known and experienced by a given system. An epistemic space contains the repertoire of knowledge states that a given system has. Therefore, it encompasses many ways of accessing world and self, of making real ity available to itself, at this specific location in time and space.”
(Metzinger, 2024, p. 50)
A posterior distribution is intrinsically epistemic in the sense that it captures the agent’s current belief state. Hence the statistical manifold that defines all possible posteriors seems a suitable candidate for a computational model of epistemic space.
If we assume this, what would it mean for an agent to form a model of this epistemic space? This is precisely what is made possible by the second order inferences enabled by parametric depth. This endows the agent with the ability to take their own model parameters as observations for further inference. The result is a generative model of the model parameters themselves. Given that these parameters define the dimensions of the statistical manifold (epistemic space) of possible posteriors (experiences), we can argue that an agent with high meta-awareness is capable of forming a model of this space — by modelling the dynamics and interactions of the parameters themselves.
Hence we find a natural computational analogue of Metzinger’s concept of pure awareness as a model of the epistemic space. Note that this creates another interesting recursion or reflexivity in the model, the agent is essentially modelling the modelling process that underpins their perception. See Appendix C for additional insights we might draw from this computational account of the epistemic space.

4.2.1. MPE as a Consequence of Generative Model Mastery

Computationally, the model of the epistemic space is learned through experience and introspection, paying attention to the dynamics of the parameters that constitute the agent’s inferential process. This evokes a notion similar to the idea of meditative insight into the nature of mind, i.e. refining a model of the space of awareness itself.
Doing this well confers a unique advantage when we assume that some of the model parameters are sensitive to the agent’s beliefs about them, i.e. that there exists a form of mental action that modulates the parameters of the generative model (Limanowski & Friston, 2018). This opens an entirely new degree of freedom the agent can leverage in the free energy minimising process. In addition to updating its model and actively soliciting data that confirms the model (i.e. active inference), with parametric depth the agent can dynamically and intelligently adjust its model. Changing the model parameters amounts to adopting a “way of seeing” (Burbea, 2014) since the resulting posterior (perceptual experience) is changed.
This leads to a high level hypothesis for what MPE might be at an abstract computational level, as well as how it is reached and why this experience arises most reliably for individuals with extensive meditation training: With sufficient awareness and control of the parameters of the generative model an agent is able to enter a regime of minimal free energy, primarily through the self-directed modulation of the generative model itself (i.e. internal rather than external mastery).
This converges onto an MPE absorption when the agent emphasises an awareness of awareness itself. This provides the possibility of incurring very low free energy since the agent is modelling a feature of its model that is always present, namely the space in which any experience would take place. Under the right conditions this leads to a nearly perfect predictive feedback loop (“Aware? Aware. Aware? Aware. Etc.”) due to the “counterfactual invariance” caused by the impossibility of imagining what it's like to be unconscious (Metzinger, 2024, p. 51). This hypothesis makes a connection between the “minimal” in MPE and “minimal free energy”.

4.2.2. Unbounded Epistemic Openness as a Flat State Prior

Metzinger also introduces the concept of “epistemic openness”, which he defines as an “unobstructed epistemic space” and argues that this an important phenomenal character of pure awareness (Metzinger, 2024, p. 47), related to the commonly reported quality of “unboundedness” in MPE. Computationally, this feature implies an attenuation of the prior expectations encoded by the transition mapping B. Precise priors act to constrain the space of possible posterior beliefs, whereas a completely flat prior opens the possibility of any posterior moment by moment. Flattening the influence of the prior expectations is achieved via modulation of the transition precision, γ B (see Figure 2). The resulting hypothesis is that during MPE the value of the transition precision is low, such that the epistemic space of possible beliefs remains unbounded. The agent is therefore completely open to the possibility of any epistemic state, without constraining the interpretation of the next moment.

4.3. Equanimity

Another central feature of MPE phenomenology is the quality of equanimity, described as tranquillity, calm, stillness or even “existential ease”. This feature implies a state of non-reactivity or imperturbability to incoming stimuli, which can be modelled as a flat distribution over prior preferences.
“2985 […] In my opinion, the most impor tant thing was the letting go. I was able to perceive bodily sensations and thoughts, but in contrast to everyday life I did nothing with them. And this brought me step by step to a deeper level, to a state of consciousness that I had never experienced before. It was a state of infinite peace. […]”
(Metzinger, 2024, p. 10)
In active inference terms, actions are selected on the basis of the expected free energy, G. This is the free energy the action (or sequence of actions π ) might incur in the future, given beliefs about how the actions will influence state transitions and the likely observations that might be generated by those future states. The expected free energy can be decomposed into epistemic and pragmatic terms, where the pragmatic term is dependent on the agent’s prior preferences over outcomes, denoted C. These preferences drive the agent to select actions that will solicit the expected observations from the internal (interoceptive) or external environments.
A precise distribution over the prior preferences will result in high expected free energy should expected observations diverge from the preferences, driving the agent to avoid or seek out the unpreferred or preferred observations respectively. High preference precision translates to high sensitivity and reactivity, a strong driver for avoidant action.
In MPE we observe the opposite phenomenology, with participants reporting a stable calm and sense of ease. This implies a down regulation of this precision, such that the pragmatic driver of action is flattened and the reactivity to incoming observations is reduced. Computationally this is enabled by extending the parametric depth mechanism to the prior preferences C. As with the other model parameters, the information used for second order inferences is not the parameter itself, but instead the second-order beliefs about the parameter captured by the precision inference. For example, in Figure 1 the likelihood precision  γ A is fed back into the model, not the likelihood A itself. These precision parameters (denoted γ ) are inferred by the agent via free energy minimisation, and represent the confidence in the beliefs encoded by the associated parameter (Parr et al., 2022, eq. (B.20)).
Hence, the modulation of the preferences can be achieved computationally by introducing a second order precision parameter γ C that weighs the influence of C on policy selection. The expected free energy becomes:
G π = ∑ τ o π τ ⋅ ln o π τ − γ C C ⏟ Phenotypic risk (pragmatic   driver) − diag A ⋅ ln A ⋅ s ¯ π τ ⏟ Percpetual ambiguity (epistemic   driver)
By introducing this parameter into a deep generative model, the agent is able to observe its value and perform state inference based on those observations (see Figure 2). Once this is possible, the agent has opacified (i.e. modelled) an aspect of their model that was previously transparent. This confers the ability to select mental actions on the basis of expected free energy minimisation, which influence the parameter value via descending message passing.
Therefore, during MPE episodes, the hypothesis is that individuals are deliberately cultivating a deep state of equanimity. We can model as a flattening of the prior preferences via a mental action that decreases the preference precision. The description of “existential ease” is particularly apt, given that the preferences define the attracting set of states characteristic to the agent’s biological survival and continued existence (the ‘pullback attractor’) (Sajid et al., 2022).

4.4. Effortlessness

The mechanism enabling much of the phenomenological modelling, so far, has been the mental actions enabled by parametric depth. This provides a computational account of how a cognitive agent might effect changes to the parameters of their own perceptual system that would plausibly give rise to aspects of the reported MPE phenomenology.
This active mechanism seems to be in contradiction with an important phenomenological feature of MPE: the quality of effortlessness. Individuals report MPE as a state of minimal or zero sense of cognitive effort. This is an interesting report that allows us to further test this computational model explanation. We will see that effortlessness is in fact predicted by the model given the parameterisations we have already laid out above.
“79 […] The experience was one of effortlessness, and without any noticeable sense of desire. There was no longer any feeling of needing to get someplace or something.
(Metzinger, 2024, p. 331)
I will adopt the argument outlined in (Parr et al., 2023), wherein the authors propose that cognitive effort can be formalised as the divergence between context sensitive mental action selection and habitual mental action selection. This divergence represents a complexity term and can be understood as the information length of the belief update for mental actions given contextual sensory information. This argument rests in part on the thermodynamic requirement of updating the habitual prior beliefs given the contextual information, and the shift from context in-sensitive to context sensitive action selection that incurs a “cost” in information processing requirements, experienced as cognitive effort. The cognitive effort term is thus defined as:
ξ = def D K L P G π ‖ P E π P G π = Cat σ − G − E P E π = Cat σ − E
Where   D K L denotes the Kullback–Leibler divergence, π is the beliefs about covert policies (a sequence of mental actions), G is the expected free energy, E is the prior beliefs over policies (or habits).
The phenomenology of effortlessness therefore, finds its computational counterpart as this effort term tends towards zero. Mathematically, this can occur under a few specific conditions: 1) when G is uniform or similar for all policies, 2) when the amplitude of E is large compared to G or 3) when G and E are aligned.
In the case of MPE, conditions 1 and 2 are at play simultaneously. We have seen above that during MPE, the level of meta-awareness is high and the preference precision is low. This translates into a very low and uniform value of the expected free energy across mental policies. To see this, refer to the expression for G in equation (1) and notice that high meta-awareness acts to increase the precision of the likelihood mapping A(2), which decreases its entropy and therefore reduces the amplitude of the perceptual ambiguity term. The cost term is also reduced via the equanimity mechanism described in the previous section. Hence the expected free energy G will be low amplitude and uniform across policies. Furthermore, as we’ll see in the next section, the temporal planning depth is flattened during MPE, which also results in a uniform distribution over policies. Finally, given the meditative context usually associated with MPE, we can expect the magnitude of E to be high through repeated training and habituation.
Therefore, the computational model of MPE outlined thus far predicts the sense of effortlessness reported in MPE, which lends a degree of predictive validity to the model.

4.5. Non-Conceptuality

The experience of MPE is often reported to be devoid of any conceptual processing. This is sometimes described as an absence of discursive thinking or mental quietude, and other times described as the absence of any conceptuality whatsoever, including any notion of a narrative self-concept.
“1196 […] the experience itself in my opinion is best described by the term “nonconceptual.”
(Metzinger, 2024, pp. 23–24)
Previous work has argued that non-conceptual modes of cognitive processing can arise in situations that lead to a flattening of the temporal planning horizon (i.e. zero temporal depth). These situations include psychedelics (Deane, 2021), flow states (Parvizi-Wayne et al., 2024) and deep meditative absorption (Laukkonen & Slagter, 2021; Czajko et al., 2024). The commonality is an emphasis on processing present moment observations. Whether this is pharmacologically induced, situationally enforced or deliberately cultivated, in each case these experiences drive a dedication of cognitive resources to the present moment. The argument that connects this to non-conceptuality assumes a thermodynamic limit to the inferences a physical agent can perform moment by moment, hence a strong weighting of present moment inference implies a corresponding attenuation of future oriented inferences required in planning.
The simulation of the counterfactual future requires an implicit concept of the agent to be projected forward through time, as well as conceptual coarse grainings of the counterfactual consequences of future action sequences. We can relate this aspect of the computational process of policy inference to what Metzinger calls the “epistemic agent model”.
Hence by flattening the temporal depth entirely, the agent is no longer inferring the roll-out of these concepts for the purpose of action selection. And therefore they do not feature phenomenologically, resulting in a state free from self-related thinking or the higher order cognitive processing and conceptualisation associated with planning.
Non-conceptuality therefore implies that the precision of current observational data is sufficiently high to require a dedication of cognitive resources to their processing, resulting in a small or zero temporal depth. Practically for our model, this translates to high likelihood precision (already expected from the formalisation of meta-awareness) and a value near zero for the parameter controlling planning depth.
The absence of conceptualisation and counterfactual planning also aligns with the flattening of the transition beliefs discussed in Section 4.2.3. As the transition precision drops, any inferred posterior is no longer carried into the next moment. This results in a perception that is completely open to the moment without any conceptual constraint. This also has the effect of rendering counterfactual planning intractable, since the state roll outs are maximally ambiguous.

4.5.1. MPE Modes vs MPE States

The experience of MPE can be separated into two broad categories, MPE absorption states and ongoing MPE modes. An MPE mode is characterised by the experience of pure awareness with other perceptual content present, whereas an absorption episode is a state of pure awareness without perceptual content.
If both MPE modes and states share this emphasis on present moment processing, what is the mechanism that distinguishes them? In (Metzinger, 2024, pp. 475–477) we suggested that an MPE state entails the attenuation of sensory data, whilst maintaining high precision on the inference underpinning an awareness of awareness (see s(3) in Figure 2). Whereas an MPE mode can be modelled as having both this meta-awareness inference and other ongoing perceptual inference.
In an MPE mode with perceptual content, the likelihood precisions for all sensory mappings remain high. An MPE absorption on the other hand can be modelled by a full allocation of available precision to the higher order observation modality exclusively. This implies that an absorption episode can be modelled by a system whose incoming data is predominantly the internally generated observations of the parameters of their generative model.

4.6. Zero-Person Perspective

Possibly the most intriguing quality of MPE is what Metzinger describes as the “zero-person perspective” (Metzinger, 2024, p. xix). For a portion of people reporting MPE-like phenomenology, the experience is described as being free from a sense of a subject or any egoic form of self-awareness.
“1612 […] The world I was experiencing no longer existed in de pen dently, because I had become the unfolding of that experience. The previous “I” as experiencer, chooser, thinker did not exist. Instead there was experience itself. There was a visual center to the experience, but only because that’s where light met the eyes. The center was no longer meaningful in any way.”
(Metzinger, 2024, p. 397)
This is difficult to imagine or conceptualise without first hand experience since the subject-object distinction appears so self-evident. And yet, advanced meditators commonly describe the possibility of a “centreless mode of perception” (Ingram, 2018). Assuming the existence of this phenomenal character in MPE states and modes (i.e. ongoing centerlessness), how might we explain this computationally?
Above we discussed how the flattening of temporal depth attenuates the narrative self construct and conceptualisation. However, I put forward that the zero-person perspective represents a more fundamental shift in perceptual processing. We can motivate this by appealing to the fact that the zero-person perspective is a continuous mode of being, not restricted to a temporary state. This is true even when e.g. scheduling a dentist appointment, which requires deep temporal planning. Hence, this particular form of non-egoic awareness can not be reduced to the mechanism of shallow temporal depth.
Since experience is modelled as being related to the posterior beliefs, we can approach this by asking: what is the posterior distribution associated with the habitual sense of self? What is the “I” or “me” posterior? A posterior is the best guess the agent has about the cause of some subset of observations. So we can rephrase this question as, what observations exist for the agent, which might be explained as being caused by the agent itself?
Due to parametric depth, the agent is observing their own model parameters (Figure 1). The causal process that generates these observations is dependent on both the external dynamics and the agent’s internal dynamics (i.e. the interdependent dynamics of the parameters of the agent’s model). Therefore, if an agent does not have an accurate model of their own internal states, there will be factors influencing their self-observations that can not be predicted (namely their own parameter dynamics), which result in unexpected observations, i.e. free energy.
Therefore, the computational hypothesis for the source of the self concept is that the agent explains away this source of uncertainty by attributing its cause to the agent itself. In other words, the self concept is the explanation of the unperceived influence of generative model parameters on experience.
This posterior explanation is, in a sense, correct — the agent's internal states (which parameterise its beliefs) are indeed the cause of the prediction error. However, the appeal to an abstract cause, the “me” concept, does not provide the predictive capacity for avoiding the prediction errors in the first place. Instead, the posterior is applied post hoc, as a reasonable coarse grained explanation of causal processes that have not yet been modelled. As a result, the prediction error persists but is quickly swept under the rug of the ego-inference.
Why would this self-inference be absent in MPE? If we assume, as discussed in the previous section, that MPE arises when an individual has a sufficiently opacified model of the epistemic space, i.e. of their own model parameters, then it follows that MPE would be devoid of self-concept defined in this way. With such a precise model, the agent would no longer have a need for the abstract explanation to explain away the prediction errors caused by their lack of understanding of their own parameter dynamics, because these prediction errors would not arise in the first place — precisely because of the accurate predictive model that has been developed. In other words, the appeal to “self as cause” to explain away the unperceived internal causes is not required when the agent has a good model of these causes.
Hence the self state factor gets pruned away in a moment (or series of moments) of insight or Bayesian model reduction (Friston, Lin, et al., 2017), in favour of a more accurate understanding of the mechanisms underpinning the inferential construction of the perceptual content, i.e. the dynamics of the parameters being modelled via parametric depth. Said differently, by clearly seeing the workings of the mind, the agent is liberated from the abstract self concept and the predictive dissonance born of a lack of understanding.

4.7. Atemporality

Another fascinating feature of MPE is the reported sense of timelessness.
“3330 I would best describe my experiences with terms like “stopping of time”, "perception of space without time” […]
2771 It was an experience of not moving forward, not moving back, neither of staying still.”
(Metzinger, 2024, p. 248)
Two computational mechanisms might explain different aspects of this experience. In some cases, timelessness is described as “timeless change” or a “changing now”, whereas in other cases the experience is a more abstract or pure timelessness (e.g. “an eternity experience”). We’ll see that both of these are predicted by the model presented thus far.
The experience of a “changing now” is well captured by the flattening of the temporal planning horizon described in Section 4.5. Under those conditions, there is no mental time travel or projection into future or past states. Instead, perceptual inference of present moment sensory data is dominant, without a sense of what will happen next. Change is still present since the posterior distribution is being updated moment by moment, however only the current belief about present observations are entertained.
Pure timelessness, on the other hand, can be explained computationally as resulting from the small information length of belief updates during an MPE absorption. The experience of temporal duration has recently been associated with the information length of the trajectory of beliefs (Da Costa, et al., forthcoming). A lack of temporal duration would therefore imply a very small information length in the belief updates. Mathematically this relates the sense of temporal duration to KL divergence between prior and posterior beliefs about states:
D K L p s ∣ o ‖ p s
This hypothesis has yet to be tested empirically. However, phenomenologically it has a prima facie plausibility as the information length represents how much the agent's experience is changing moment by moment.
If we adopt this point of view, then the experience of pure timelessness in MPE follows from the computational model outlined thus far. Recall that parametric depth enables the agent to perceive their own model parameters. The observations at each level are generated by the precision of the parameter at the layer below. The precision can be understood as a summary statistic of the parameter; it fluctuates on a slower timescale and contains less information than the parameter itself. Therefore, as we ascend the parametric hierarchy, the amplitude of the belief updating decreases 2.
As we have seen, during an MPE absorption, only the higher level inferences are present, with lower level sensory data being attenuated. Assuming the individual has stabilised their awareness, the information length of updates to this state inference will trend towards zero. Which is experienced subjectively as a ceasing of temporal duration.

4.8. Bliss

Finally, how does this computational model explain the reports of positive affect during MPE?
“3305 […] Great happiness flowed through me. […]
2687 […] a deep feeling of joy, timelessness, happiness emerged.”
(Metzinger, 2024, p. 147)
The experience of joy, awe, bliss or gratitude is common in reports of MPE, however not a necessary feature. Many meditators report pure awareness experiences without these qualities. Furthermore, these qualities are often reported in otherwise normal daily experiences. So how does our computational model account for this variance?
Within the active inference framework, the experience of affect has been modelled as state inference on the basis of observations of the “model precision” parameter. The model precision (denoted γ or γ G ) is a global summary statistic that is dependent on all the other parameters of the generative model. It encodes the agent’s confidence in their entire action model. Inferring this parameter is answering the question “how well am I doing at minimising free energy compared to how well I expected to be doing?”. Therefore, this computational account of “affective inference” (Hesp et al., 2021) ties valence to the rate of change of the free energy (Joffily & Coricelli, 2013). Hence we can model high valence as a negative rate of change in the free energy, i.e. when the agent is doing ‘better and better’ at minimising free energy.
In the sections above we discussed how the accurate modelling of the agent’s model parameters can lead to improved free energy minimisation, as the prediction errors arising from internal causes are resolved through improved self-modelling. This decrease in free energy is also a result of high meta-awareness (low perceptual ambiguity) and high equanimity (low preference precision). If we assume that the transition into these conditions that define MPE extends over some duration of time, this creates a scenario where the free energy incurred by the agent may be decreasing faster than their model predicts.
Therefore, whilst this is the case, computationally they will be ‘pleasantly surprised’ by the decrease in free energy that accompanies the increasingly opaque and preferenceless self-model, which in turn will register as an increase in model precision and uptick of positive valence. However, once a stable optimum of free energy has been reached, the rate of change will decrease and the associated valence will taper. This may account for the variance seen in reports of MPE and forms the basis of a prediction that positive valence is most likely encountered in the onset phase of MPE.

5. Conclusion

This paper presents an updated computational model of minimal phenomenal experience (MPE) grounded in the mathematics of the free energy principle and active inference. By formalising key phenomenological features of MPE within a deep active inference framework, we have developed a mechanistic account that explains first-person experiential reports with computational descriptions.
The model suggests that MPE emerges as a consequence of entering a regime of very low free energy (or equivalently very high self-evidencing) characterised by:
  • High meta-awareness, modelled as increased precision of higher-order observations of model parameters.
  • Flattened prior preferences, resulting in a state of equanimity.
  • A precise model of the agent's own modelling process (i.e. generative model parameters), enabling a "zero-person perspective."
These conditions lead to further computational predictions related to reported phenomenological qualities of MPE, including effortlessness, timelessness, and a sense of pure awareness devoid of conceptual content.
The significance of this work extends beyond explaining MPE. It demonstrates the potential of computational neurophenomenology to formalise and help us understand subtle aspects of conscious experience, providing a rigorous framework for investigating altered states of consciousness and meditative practices. Moreover, it offers a new perspective on the nature of self-awareness and the computational underpinnings of different modes of perception.
However, several limitations must be acknowledged. The model remains theoretical and requires empirical validation. Future work will focus on deriving and testing predictions about neurobiological dynamics during MPE states and designing experiments to assess the model's accuracy.
Finally, as mentioned in the introduction, my hope with this work is to contribute to a computational language for describing phenomenology. Such a language can serve a map for guiding and inspiring the first person investigation of our own lived experience. It is my view that an experiential grokking of consciousness is far more valuable than another theory of consciousness.

Ethical Statement

This submission consists solely of theoretical analysis. No experiments were conducted involving AI, human or animal subjects. I have carefully designed our approach to focus on formal descriptions rather than implementations that could potentially give rise to sentience, however unlikely. This research aims to further scientific understanding while maintaining strict ethical boundaries against creating or risking the creation of artificial sentient beings.

Appendix A. Simulating MPE

The formalisations of MPE phenomenology explored here are detailed enough to define a generative model parameterisation apt for simulating the experience and dynamics of MPE. The simulation implementation and results are outside the scope of this paper, however Figure 2 below depicts the model structure as a Bayes graph and the table below summarises the parameterisations to be implemented, derived from the phenomenological features of MPE.
Preprints 138976 g002
Figure 2. Deep generative model structure of MPE. This figure depicts a Bayes graph representation of the proposed generative model of minimal phenomenal experience. The first (blue) layer captures the agent’s inferences about external states (i.e. their perceptual inference) and overt motor actions u(1). Perceptual inference on this level is dependent on a number of generative model parameters shown in white boxes. The agent is inferring the precision of these parameters, shown in shaded blue circles, e.g. γ A 1 . These precision parameters are observed by the agent, and the basis of second order inferences shown in the orange box. The model constructed at this level captures the dynamics of and interactions between the parameters underpinning the perceptual process, which we have related to the model of the epistemic space (awareness). Actions at this level are mental (covert) actions that modulate the various precision parameters. The ambiguity of this second level of inference is dependent on the higher order likelihood precision γ A 2 . When this is high, the agent is able to form inferences on the basis of their model parameters, i.e. they are aware of or have “opacified” an aspect of their perceptual process. Finally, at the third level the agent is able to make inferences about γ A 2 giving rise to an experience of being aware of the degree of awareness of the space of awareness.
Figure 2. Deep generative model structure of MPE. This figure depicts a Bayes graph representation of the proposed generative model of minimal phenomenal experience. The first (blue) layer captures the agent’s inferences about external states (i.e. their perceptual inference) and overt motor actions u(1). Perceptual inference on this level is dependent on a number of generative model parameters shown in white boxes. The agent is inferring the precision of these parameters, shown in shaded blue circles, e.g. γ A 1 . These precision parameters are observed by the agent, and the basis of second order inferences shown in the orange box. The model constructed at this level captures the dynamics of and interactions between the parameters underpinning the perceptual process, which we have related to the model of the epistemic space (awareness). Actions at this level are mental (covert) actions that modulate the various precision parameters. The ambiguity of this second level of inference is dependent on the higher order likelihood precision γ A 2 . When this is high, the agent is able to form inferences on the basis of their model parameters, i.e. they are aware of or have “opacified” an aspect of their perceptual process. Finally, at the third level the agent is able to make inferences about γ A 2 giving rise to an experience of being aware of the degree of awareness of the space of awareness.
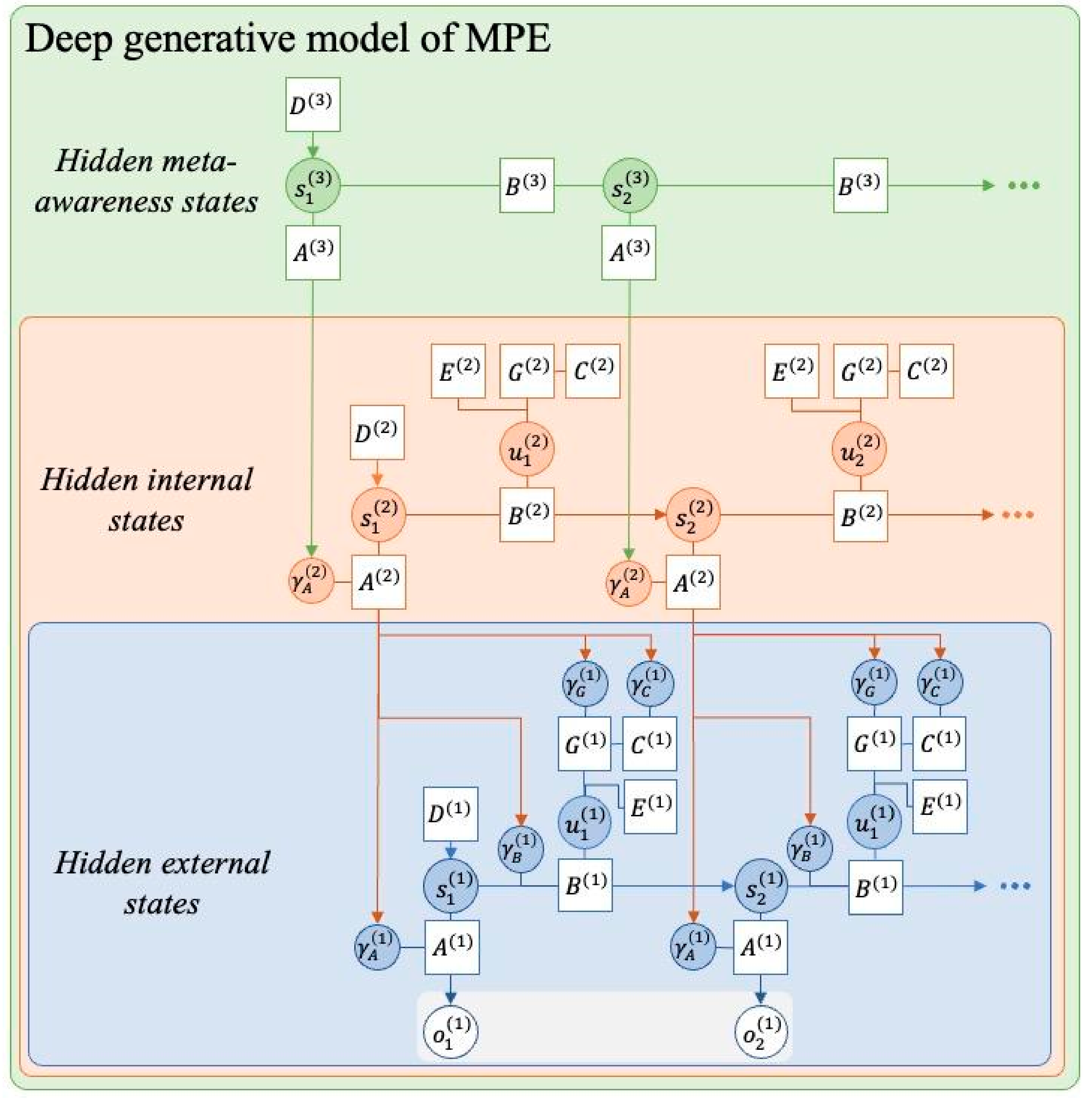
Preprints 138976 g002
Table 1. Summary of computational formalisations of core features of MPE.
Table 1. Summary of computational formalisations of core features of MPE.
Preprints 138976 i001

Appendix B. Empirical Predictions

The advantage of employing the free energy principle in the construction of a neurophenomenological model is that the formalism provides a principled route towards the empirical testing of the proposed model. Please refer to (Ramstead et al., 2022; Sandved-Smith et al., 2024) for a detailed treatment on this topic. Briefly, this is enabled by the dual interpretation of the dynamics of the internal states under the FEP. The internal states can be understood, on the one hand, as parameterising the agent’s beliefs about external states (the so-called “extrinsic dynamics”). And on the other hand, their dynamics can be described in terms of the internal states per se (the “intrinsic dynamics”). (Friston et al., 2020)
The upshot is that the assumptions we make about the belief dynamics necessarily entail predictions about the thermodynamics of the internal states that can be tested empirically. The relationship between the equations governing the intrinsic thermodynamics and empirical neurobiology is described by the neural process theory that accompanies the free energy principle (Friston, FitzGerald, et al., 2017; Parr & Friston, 2018; Da Costa, Parr, et al., 2021). A detailed treatment of the neurobiological ramifications implied by the model presented here is the subject of future work. However, to demonstrate the logic a few example directions are highlighted below.

B.1. Timelessness and Metabolic Cost

The information length of belief updating, which we related to the experience of temporal duration, has also been related to the metabolic cost incurred by the belief updating (Da Costa, et al., forthcoming). Therefore, the computational account of phenomenal timelessness as small information length in the belief trajectory entails a prediction about the metabolic load. We can therefore make the prediction that the overall energy consumption of the brain, as measured by the amplitude of a BOLD fMRI signal, will be lower during MPE.

B.2. Effortlessness and the Brain

In (Parr et al., 2023) the authors propose that their account predicts that we can associate cognitive effort with the basal ganglia and prefrontal cortices. This leads to a tractable empirical prediction — during MPE we should observe reduced activation in the prefrontal cortex and anterior cingulate regions associated with cognitive control.

B.3. Precision Parameters and Neurotransmitters

Others have argued that the functional role of the likelihood, transition and model precision parameters are mediated by the cholinergic, noradrenergic and dopaminergic neurotransmitter systems respectively. What these systems have in common is the same basic effect on synaptic transmission (i.e. neuromodulatory gain control). (Parr & Friston, 2017a; Schwartenbeck et al., 2015)
The computational model of MPE proposed here entails specific dynamics for these parameters, namely high likelihood precision, low transition precision and an initially high, then tapering model precision. This translates into empirical predictions about activity in the brain regions associated with the respective neurotransmitter systems, i.e. the nucleus basalis of Meynert (cholinergic), the locus coeruleus (noradrenergic) and the ventral tegmental area (dopaminergic). In the transition from normal waking consciousness to MPE, we should observe changes in the activation patterns in these regions.

Appendix C. Deepening Awareness, Emptiness and Cessation

By describing awareness as the model of the epistemic space of possible posteriors, we are confronted by the fact that the map is not the territory, i.e. the model of the epistemic space is not the epistemic space itself. This is only the agent's model of the statistical manifold that encompasses the full potential of possible beliefs. Two insights can be drawn from this fact. First, this provides a mechanism for the experience of “becoming more aware” or the experience of “deepening into pure awareness”.
“1354 […] The experience of pure awareness in meditation has become more and more
evident over time and with evolving meditation practice.”
(Metzinger, 2024, p. 450)
This also resonates with contemplative traditions that view awareness as an evolving, limitless process, where recognising awareness is both an initial insight and an ever-expanding journey without a fixed endpoint. The computational metaphor for this expansion is the continued mapping of the manifold of possible posterior beliefs.
Several commentators have highlighted that this process is inherently open-ended due to intrinsic limits to self-representation (Friston et al., 2012; Fields et al., 2024; Sandved-Smith & Da Costa, 2024). Heuristically we can understand why; as more of the space is mapped, the agent themself is changed, which changes the thing to be mapped. In other words, by knowing ourselves we are changing the thing to be known, in a way that keeps full self-representation alway just out of reach. At a first glance, relating MPE to a regime of minimal free energy might seem at odds with a process of continued model expansion. However note that minimising free energy is equivalent to maximising evidence for a generative model, i.e. “self-evidencing”.
A second insight that we can draw from the computational understanding of the epistemic space is the idea that “awareness itself is empty”. Emptiness refers to the notion that a feature of experience does not possess inherent qualities or existence. Pure awareness per se is often reported to be the fundamental ground of experience, something deeply ‘true’. However, if we model awareness as the agent’s model of the epistemic space — we can see that the experience of pure awareness itself is also an ongoing construction (i.e. empty of intrinsic nature separate from the agent).
This points to the possibility of a deeper non-experience beyond awareness, accessed by deconstructing even this fundamental model of the epistemic space itself.
“3323 […] However, later on there were more “experiences” in which the very last remnant of this pure consciousness in meditation was extinguished. This was like an inner death, but then also an even greater freedom than pure consciousness itself. There it was clearly experienced that pure consciousness is far from being the deepest pos si ble (or highest pos si ble) thing, but that “ behind” it there exists a much more extensive, indescribable “not- anything.” But it cannot be described in words, since it is no longer an experience; rather, it can at most be described as the absence of all experience, or as absolute freedom.”
(Metzinger, 2024, p. 189)
This beautiful quote speaks to the experience of “cessations” that are not uncommon in advanced meditation practitioners (Laukkonen et al., 2023; Agrawal & Laukkonen, 2024; van Lutterveld et al., 2024). A cessation is a discontinuity in experience, a short or extended moment of nothing at all. This is distinct from MPE, which is still an experience however minimal it might be. However, we might ask, what is the relationship (if any) between MPE and cessation?
A preliminary hypothesis is that MPE is a phenomenological cluster that exists in the vicinity of cessation, i.e. MPE is the experience of a region of state space incurring minimal free energy whereas a cessation is a limit case of zero free energy.

References

  1. Agrawal, V., & Laukkonen, R. (2024). Nothingness in meditation: Making sense of emptiness and cessation. Available online: https://osf.io/tygdf.
  2. Bāhiya Sutta: Bāhiya (Ud 1.10) (T. Bhikkhu, Trans.; Access to Insight (BCBS Edition)). (2012). Available online: https://www.accesstoinsight.org/tipitaka/kn/ud/ud.1.10.than.html#fn-2.
  3. Brasington, L. (2021). Dependent Origination and Emptiness. Leigh Brasington.
  4. Burbea, R. (2014). Seeing That Frees: Meditations on Emptiness and Dependent Arising. Hermes Amāra Publications. Available online: https://books.google.fr/books?id=kwntoQEACAAJ.
  5. Czajko, S., Zorn, J., Daumail, L., Chetelat, G., Margulies, D. S., & Lutz, A. (2024). Exploring the Embodied Mind: Functional Connectome Fingerprinting of Meditation Expertise. Biological Psychiatry Global Open Science, 4(6), 100372. [CrossRef]
  6. Da Costa, L., Friston, K., Heins, C., & Pavliotis, G. A. (2021). Bayesian mechanics for stationary processes. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 477(2256), 20210518. [CrossRef]
  7. Da Costa, L., Parr, T., Sajid, N., Veselic, S., Neacsu, V., & Friston, K. (2020). Active inference on discrete state-spaces: A synthesis. Journal of Mathematical Psychology, 99, 102447. [CrossRef]
  8. Da Costa, L., Parr, T., Sengupta, B., & Friston, K. (2021). Neural Dynamics under Active Inference: Plausibility and Efficiency of Information Processing. Entropy, 23(4), 454. [CrossRef]
  9. Da Costa, L., & Sandved-Smith, L. (2024). Towards a Bayesian mechanics of metacognitive particles: A commentary on “Path integrals, particular kinds, and strange things” by Friston, Da Costa, Sakthivadivel, Heins, Pavliotis, Ramstead, and Parr. Physics of Life Reviews, 48, 11–13. [CrossRef]
  10. Deane, G. (2021). Consciousness in active inference: Deep self-models, other minds, and the challenge of psychedelic-induced ego-dissolution. Neuroscience of Consciousness, 2021(2), niab024. [CrossRef]
  11. Dunne, J. D., Thompson, E., & Schooler, J. (2019). Mindful meta-awareness: Sustained and non-propositional. Current Opinion in Psychology, 28, 307–311. [CrossRef]
  12. Feldman, H., & Friston, K. J. (2010). Attention, uncertainty, and free-energy. Frontiers in Human Neuroscience, 4, 215. [CrossRef]
  13. Fields, C., Glazebrook, J. F., & Levin, M. (2024). Principled Limitations on Self-Representation for Generic Physical Systems. Entropy, 26(3), Article 3. [CrossRef]
  14. Friston, K.J. (2019). A free energy principle for a particular physics. arXiv:1906.10184. [CrossRef]
  15. Friston, K. J., Da Costa, L., Sajid, N., Heins, C., Ueltzhöffer, K., Pavliotis, G. A., & Parr, T. (2022). The free energy principle made simpler but not too simple. arXiv:2201.06387. [CrossRef]
  16. Friston, K. J., FitzGerald, T., Rigoli, F., Schwartenbeck, P., & Pezzulo, G. (2017). Active Inference: A Process Theory. Neural Computation, 29(1), 1–49. [CrossRef]
  17. Friston, K. J., Lin, M., Frith, C. D., Pezzulo, G., Hobson, J. A., & Ondobaka, S. (2017). Active Inference, Curiosity and Insight. Neural Computation, 29(10), 2633–2683. [CrossRef]
  18. Friston, K. J., Thornton, C., & Clark, A. (2012). Free-Energy Minimization and the Dark-Room Problem. Frontiers in Psychology, 3. [CrossRef]
  19. Friston, K. J., Wiese, W., & Hobson, J. A. (2020). Sentience and the Origins of Consciousness: From Cartesian Duality to Markovian Monism. Entropy, 22(5), 516. [CrossRef]
  20. Hesp, C., Smith, R., Parr, T., Allen, M., Friston, K. J., & Ramstead, M. J. D. (2021). Deeply Felt Affect: The Emergence of Valence in Deep Active Inference. Neural Computation, 33(2), 398–446. [CrossRef]
  21. Hohwy, J. (2013). The predictive mind. Oxford University Press. [CrossRef]
  22. Hohwy, J. (2016). The Self-Evidencing Brain. Noûs, 50(2), 259–285. [CrossRef]
  23. Ingram, D.M. (2018). Mastering the core teachings of the Buddha: An unusually hardcore Dharma book (Revised and expanded edition). Aeon.
  24. Joffily, M., & Coricelli, G. (2013). Emotional Valence and the Free-Energy Principle. PLOS Computational Biology, 9(6), e1003094. [CrossRef]
  25. Laukkonen, R. E., & Chandaria, S. (2024). A beautiful loop: An active inference theory of consciousness. OSF. [CrossRef]
  26. Laukkonen, R. E., Sacchet, M. D., Barendregt, H., Devaney, K. J., Chowdhury, A., & Slagter, H. A. (2023). Cessations of consciousness in meditation: Advancing a scientific understanding of nirodha samāpatti. Progress in Brain Research, 280, 61–87. [CrossRef]
  27. Laukkonen, R. E., & Slagter, H. A. (2021). From many to (n)one: Meditation and the plasticity of the predictive mind. Neuroscience & Biobehavioral Reviews, 128, 199–217. [CrossRef]
  28. Limanowski, J., & Friston, K. (2018). ‘Seeing the Dark’: Grounding Phenomenal Transparency and Opacity in Precision Estimation for Active Inference. Frontiers in Psychology, 9. Available online: https://www.frontiersin.org/articles/10.3389/fpsyg.2018.00643.
  29. Metzinger, T. (2003). Phenomenal Transparency and Cognitive Self-Reference. Phenomenology and the Cognitive Sciences, 2(4), 353–393. [CrossRef]
  30. Metzinger, T. (2020). Minimal phenomenal experience: Meditation, tonic alertness, and the phenomenology of “pure” consciousness. Philosophy and the Mind Sciences, 1(I), Article I. [CrossRef]
  31. Metzinger, T. (2024). The Elephant and the Blind: The Experience of Pure Consciousness: Philosophy, Science, and 500+ Experiential Reports. The MIT Press.
  32. Nanamoli, B., & Bodhi, B. (1995). The Middle Length Discourses of the Buddha: A Translation of the Majjhima Nikaya. Somerville: Wisdom Publications.
  33. Parr, T., & Friston, K. J. (2017a). Uncertainty, epistemics and active inference. Journal of The Royal Society Interface, 14(136), 20170376. [CrossRef]
  34. Parr, T., & Friston, K. J. (2017b). Working memory, attention, and salience in active inference. Scientific Reports, 7(1), Article 1. [CrossRef]
  35. Parr, T., & Friston, K. J. (2018). The Anatomy of Inference: Generative Models and Brain Structure. Frontiers in Computational Neuroscience, 12. Available online: https://www.frontiersin.org/articles/10.3389/fncom.2018.00090.
  36. Parr, T., Holmes, E., Friston, K. J., & Pezzulo, G. (2023). Cognitive effort and active inference. Neuropsychologia, 184, 108562. [CrossRef]
  37. Parr, T., Pezzulo, G., & Friston, K. J. (2022). Active inference: The free energy principle in mind, brain, and behavior. The MIT Press.
  38. Parvizi-Wayne, D., Sandved-Smith, L., Pitliya, R. J., Limanowski, J., Tufft, M. R. A., & Friston, K. J. (2024). Forgetting ourselves in flow: An active inference account of flow states and how we experience ourselves within them. Frontiers in Psychology, 15. [CrossRef]
  39. Ramstead, M. J. D., Albarracin, M., Kiefer, A., Klein, B., Fields, C., Friston, K., & Safron, A. (2023). The inner screen model of consciousness: Applying the free energy principle directly to the study of conscious experience. PsyArXiv. [CrossRef]
  40. Ramstead, M. J. D., Albarracin, M., Kiefer, A., Williford, K., Safron, A., Fields, C., Solms, M., & Friston, K. (2023). Steps towards a minimal unifying model of consciousness: An integration of models of consciousness based on the free energy principle. PsyArXiv. [CrossRef]
  41. Ramstead, M. J. D., Sakthivadivel, D. A. R., Heins, C., Koudahl, M., Millidge, B., Da Costa, L., Klein, B., & Friston, K. J. (2023). On Bayesian mechanics: A physics of and by beliefs. Interface Focus, 13(3), 20220029. [CrossRef]
  42. Ramstead, M. J. D., Seth, A. K., Hesp, C., Sandved-Smith, L., Mago, J., Lifshitz, M., Pagnoni, G., Smith, R., Dumas, G., Lutz, A., Friston, K., & Constant, A. (2022). From Generative Models to Generative Passages: A Computational Approach to (Neuro) Phenomenology. Review of Philosophy and Psychology. [CrossRef]
  43. Sajid, N., Tigas, P., & Friston, K. (2022). Active inference, preference learning and adaptive behaviour. IOP Conference Series: Materials Science and Engineering, 1261(1), 012020. [CrossRef]
  44. Sandved-Smith, L., Bogotá, J. D., Hohwy, J., Kiverstein, J., & Lutz, A. (2024). Deep computational neurophenomenology: A methodological framework for investigating the how of experience. OSF. [CrossRef]
  45. Sandved-Smith, L., & Da Costa, L. (2024). Metacognitive particles, mental action and the sense of agency. arXiv:2405.12941. [CrossRef]
  46. Sandved-Smith, L., Hesp, C., Mattout, J., Friston, K., Lutz, A., & Ramstead, M. J. D. (2021). Towards a computational phenomenology of mental action: Modelling meta-awareness and attentional control with deep parametric active inference. Neuroscience of Consciousness, 2021(1), niab018. [CrossRef]
  47. Schwartenbeck, P., FitzGerald, T. H. B., Mathys, C., Dolan, R., & Friston, K. (2015). The Dopaminergic Midbrain Encodes the Expected Certainty about Desired Outcomes. Cerebral Cortex, 25(10), 3434–3445. [CrossRef]
  48. Smith, R., Friston, K. J., & Whyte, C. J. (2022). A step-by-step tutorial on active inference and its application to empirical data. Journal of Mathematical Psychology, 107, 102632. [CrossRef]
  49. van Lutterveld, R., Chowdhury, A., Ingram, D. M., & Sacchet, M. D. (2024). Neurophenomenological Investigation of Mindfulness Meditation “Cessation” Experiences Using EEG Network Analysis in an Intensively Sampled Adept Meditator. Brain Topography, 37(5), 849–858. [CrossRef]
  50. Varela, F. J. (1996). A Methodological Remedy for the Hard Problem. Journal of Consciousness Studies, 3(4), 330–349.
  51. Varela, F.J. (1997). The Naturalization of Phenomenology as the Transcendence of Nature: Searching for Generative Mutual Constraints. Alter: Revue de Phénoménologie, 5, 355–385.
  52. Wiese, W. (2020). The science of consciousness does not need another theory, it needs a minimal unifying model. Neuroscience of Consciousness, 2020(1), niaa013. [CrossRef]
Preprints 138976 g001
Figure 1. Generative model with parametric depth. This figure depicts a Bayes graph representation of an example generative model with parametric depth. Parametric depth involves the addition of a hierarchical level that takes the parameters of the lower level as input for inference. An agent endowed with parametric depth is capable of performing second order inferences, i.e. forming beliefs about beliefs. In this example the likelihood precision γ A 1 is the basis of second order inference). Notice the precision of the higher level likelihood mapping, γ A 2 , which has previously been related to meta-awareness (Sandved-Smith et al., 2021), and is central to the model of MPE outlined in this paper.
Figure 1. Generative model with parametric depth. This figure depicts a Bayes graph representation of an example generative model with parametric depth. Parametric depth involves the addition of a hierarchical level that takes the parameters of the lower level as input for inference. An agent endowed with parametric depth is capable of performing second order inferences, i.e. forming beliefs about beliefs. In this example the likelihood precision γ A 1 is the basis of second order inference). Notice the precision of the higher level likelihood mapping, γ A 2 , which has previously been related to meta-awareness (Sandved-Smith et al., 2021), and is central to the model of MPE outlined in this paper.
Preprints 138976 g001

Notes

1
Citations preceded by numbers represent MPE reports from participants.
2
This is also the mechanism that prevents an infinite regress of the hierarchical levels. Each additional level becomes less informative as it tracks slower time scale fluctuations. Therefore the complexity cost of the additional model structure quickly outweighs the accuracy gained by tracking ever more subtle dynamics.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated