Experience Teaching Mathematics at the University of Defence in the Study Field of Cybersecurity

Radovan Potůček

doi:10.20944/preprints202407.0350.v1

Preprint

Article

Experience Teaching Mathematics at the University of Defence in the Study Field of Cybersecurity

This version is not peer-reviewed.

Radovan Potůček^*

This version is not peer-reviewed.

Downloads

Views

Comments

Submitted:

03 July 2024

Posted:

04 July 2024

You are already at the latest version

Abstract

The teaching of mathematics at the Faculty of Military Technology of the University of Defense in the first two years of the five-year Military master’s degree is divided into the teaching of students in four specializations: Military Technologies – Mechanical, Military Technologies – Electrical, Military Geography and Cartography, and Cybersecurity. The article discusses the previous five-year experience in teaching the subjects Mathematics I, Mathematics II, Mathematics III, and Graph theory for the specialization in Cybersecurity, that the author of the paper gained while teaching, as a guarantor of these four subjects. The article provides an overview of the topics that are covered, typical exam assignments, and an evaluation of the results of the semester exams in the five years since the accreditation of the Cybersecurity specialization was granted.

Keywords:

University of Defence

;

Faculty of Military Technology

;

Cybersecurity study program

;

teaching mathematics

;

teaching graph theory

;

semester exam

;

classified credit test

;

thematic units

;

exam evaluation.

Subject:

Computer Science and Mathematics - Discrete Mathematics and Combinatorics

1. Introduction

This paper deals with the problems of teaching mathematics, and especially discrete mathematics, at the Faculty of Military Technology at the University of Defence in Brno. The tradition of teaching mathematics at this high military school has its origins in 1951, when this school was established. We will deal with mathematical education and the ranges and thematic areas of mathematics teaching in the Cybersecurity study program, which has been accredited at the Faculty of Military Technology since 2019. The Cybersecurity study program from the perspective of teaching mathematics can be read in the paper [1]. Interesting information about new trends in the education of mathematics around the world can be found, for example, in the paper [2].

Mathematics teaching in the study field of Cybersecurity takes place during the first four semesters of this five-year master’s degree program. In the first, second, and third semesters, mathematics teaching consists of lectures and exercises in the subjects of Mathematics I, Mathematics II, and Mathematics III. Two mathematical subjects are taught in the fourth semester: Graph theory and Probability theory along with mathematical statistics. Since the author of the paper does not teach the subject of Probability and mathematical statistics, this paper will focus on the content, topics, semester examinations, and the success of students in the subjects of Mathematics I, II, and III, as well as the subject of Graph theory. Detailed information on degree programs accredited to the University of Defence since 2019 can be found on the Intranet [3]. Papers dealing with mathematics teaching of Cybersecurity study program at foreign universities include, for example, [5,6,7,8,9,10]. On the Internet, the relationship between mathematics and cybersecurity is engaged in, for example, articles [11,12].

Between the academic years 2019/2020 to 2022/2023, civil students were also admitted to the study of Cybersecurity, in addition to military students and students from the Socialist Republic of Vietnam. Since the academic year 2023/2024, only students of military studies have been accepted. The number of students who take part in the entrance exams for the Cybersecurity field of study is usually between 50 and 80 applicants. Information on the entrance tests at the Faculty of Military Technology can be found in the paper [4]. The number of students admitted to study and successfully completing basic military training in September, in the case of military students, ranges from 20 to 40 students. They are either in one learning group or divided into two learning groups.

2. Mathematics I

The teaching of this subject is subsidized for 90 lessons. The lecture and exercises each have a duration of two lessons, so it consists of 45 learning units. The teaching consists of 22 lectures and 23 exercises, including 2 laboratory exercises being conducted in a computer classroom. The mathematical software used in the laboratory exercises in Mathematics I, Mathematics II, Mathematics III and Graph theory is the computer algebra system Maple.

2.1. Topics of Mathematics I

Individual topics discussed within the subject Mathematics I are stated in the following Table 1, which, in addition to the topics, includes hourly subsidies (HS) for lectures (LE), exercises (EX) and laboratory exercises in a computer classroom (CC).

2.2. Semester Exam in Mathematics I

Students are always introduced to the content of the semester exam at the beginning of the semester. At the end of the semester, several sets (usually 4 to 6) of solved preparatory tasks for the exam are made available to students for the purposes of independent study. The semester exam in Mathematics I consist of a theoretical part and a practical part.

The theoretical part contains five questions about theory. 0 to 4 points can be obtained for each answered question, so a student can receive a maximum of 20 points for the theoretical part. The content of the theoretical questions are the definitions of the most important terms, their basic properties and the most important sentences of the relevant theoretical unit. Part of the theoretical question can also be made up of a simple example illustrating the given concept.

A maximum of another 20 points, which are included in the total point gain in the exam, can be gained by the student from exercises based on partial written works and homework. The practical part of the exam consists of the assignment of six tasks. These practical tasks evenly cover the topics presented at the lectures and correspond to the assignment of solved preparatory examples. For each task, the student can get 0 to 10 points, so for the practical part, the student can receive a maximum of 60 points. For the semester exam, the student can get a maximum of 100 points, while at least 50 points must be achieved to successfully pass the exam.

2.3. Example of a Semester Exam in Mathematics I

One of the assignments of the semester exam had the following theoretical and practical part. The theoretical part lasts 30 minutes, and after a short break, the practical part follows, for which 120 minutes are reserved.

▸......................................The theoretical part ......................................

A. Define the power set of the n-element set M and its cardinality.

Determine the power set of the 3-element set

M = {a, b, c}

and its cardinality. [4 points]

B. Define the

R S

composition of the binary relations

R \subset A \times B

S \subset B \times C

Write a relation for

{(R S)}^{- 1}

for binary relations

R \subset A \times B

and

S \subset B \times C

. [4 points]

C. Define the least element and the minimal element of the ordered set

(A, \leq)

What is the relationship between the least and the minimal element of an ordered set

(A, \leq)

? [4 points]

D. Write a necessary and sufficient condition for the algebraic structure

(T, +, \cdot)

to be a field.

Give an example of an infinite field and an example of a finite field. [4 points]

E. Define linearly dependent vectors

u_{1}, u_{2}, \dots, u_{n}

Define linearly independent vectors

u_{1}, u_{2}, \dots, u_{n}

. [4 points]

▸......................................The practical part ......................................

1) Verify that the propositional formula

((p \land q) \leftrightarrow r) \to p

is consistent, express it in the conjunctive normal form and simplify as much as possible by using the algebraic properties of logical connectives. [10 points]

2) Determine how many different 4-digit numbers that are divisible by 5 can be formed from the six digits

0, 1, 3, 5, 7, 9

if the digits a) cannot repeat, b) can repeat? [10 points]

3) On the set

A = {1, 4, 9, 12, 17, 20}

, the relation R is defined such that

(x, y) \in R \leftrightarrow x - y = 8 k for some k \in Z .

Determine the number of elements of the relation R (i.e., the number of ordered pairs

(x, y) \in A^{2}

that satisfy the relation R). Prove that R is an equivalence relation. Determine the partition of the set A into the equivalence classes

A / R

. [10 points]

4) Decide whether the basis of the vector space of the matrices

R^{2 \times 2}

can be formed by the matrices

A = (\begin{matrix} 0 & 1 \\ 2 & 3 \end{matrix}), B = (\begin{matrix} 1 & 2 \\ 3 & 0 \end{matrix}), C = (\begin{matrix} 2 & 3 \\ 0 & 1 \end{matrix}), D = (\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}) . [10 points]

5) Determine some basis of the subspace U of the vector space

P_{2}

generated by the vectors (polynomials)

P (x) = x^{2} - x + 2

Q (x) = x^{2} + x - 1

R (x) = x^{2} - 3 x + 5

. Fill the basis of the subspace U with suitable vectors from the canonical basis of a vector space of polynomials of degree at most 2 on the basis B of the vector space

P_{2}

. Determine the coordinates of the vector

T (x) = x

with respect to the chosen basis B. [10 points]

6) Determine the linear mapping matrix

L : R^{3} \to R^{2}

, which is given by the relation

L (x, y, z) = (x + 2 y, y - 2 z)

with respect to the bases G and H of the spaces

R^{3}

and

R^{2}

, where

G = ((1, 1, 0), (1, 0, 1), (0, 1, 1))

and

H = ((1, 1), (0, 1))

. Determine the image of the vector

x

in the linear mapping L if

G_{x} = {(1, 0, - 1)}^{T}

. [10 points]

2.4. Students’ Success in the Mathematics I Exam

The following Table 2 presents the success of students in the semester exam in Mathematics I in the winter semesters of the academic years (AY) 2019/2020, 2020/2021, 2021/2022, 2022/2023, 2023/2024, cumulatively for the academic years 2019/2020 to 2023/2024 and the total number (TN) of students who continue to study successfully and did not leave their studies or left because of failure to fulfill their study obligations.

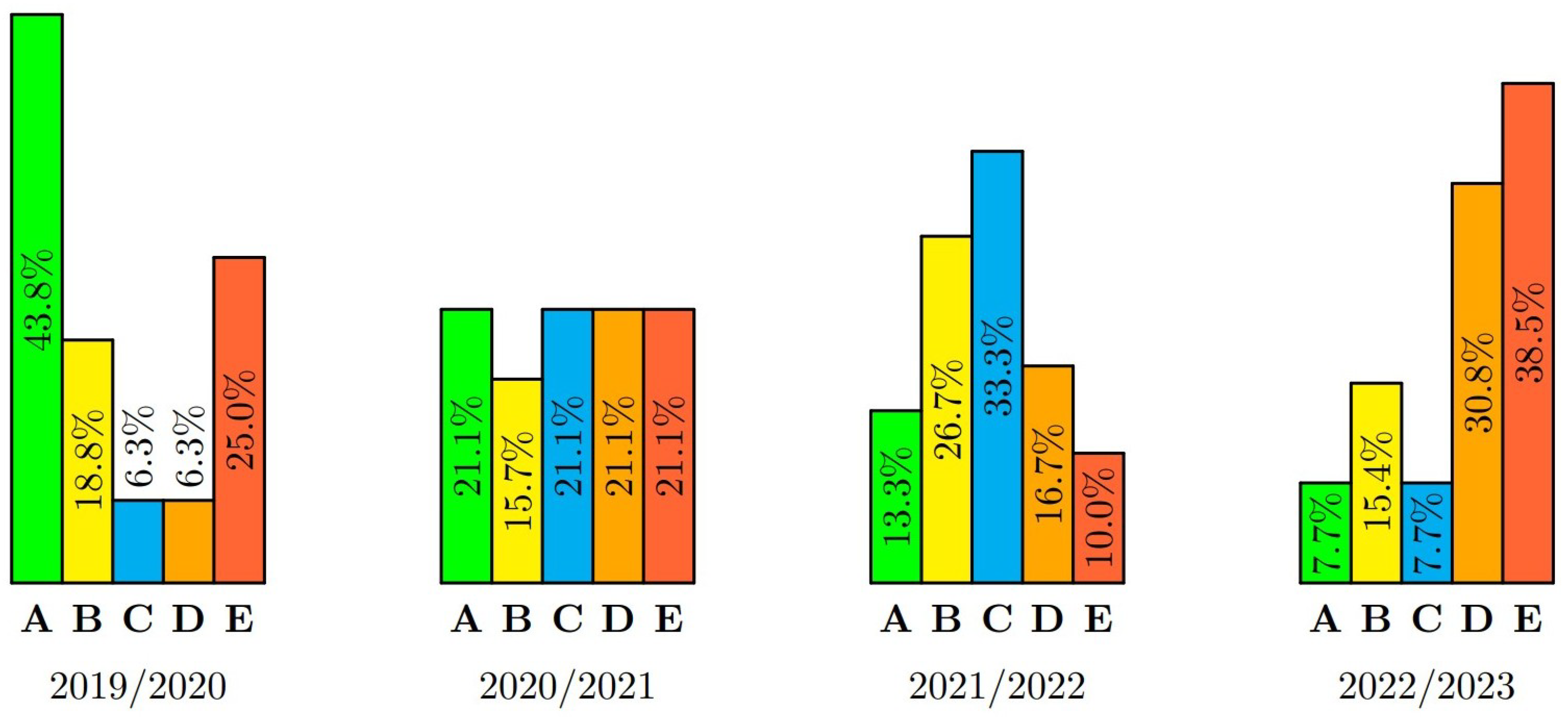
Figure 1 shows the percentage success rate of students in semester exams in Mathematics I from the academic year 2019/2020 to 2023/2024, with the fact that grade E also includes grade E in the 1st or 2nd correction period. If the student rejected grades B, C or D and wrote a repair examination, only the final grade is written in this table.

2.5. Students’ Success in Solving Single Types of Tasks in the Mathematics I Exam

Based on experience with semester exams, the author can state that the success of students in solving individual types of tasks in semester exams does not change significantly in individual years. The following Table 3, therefore, contains the evaluation of success in the exam in AY 2023/2024.

Traditionally, solving task concerning linear map and task to verify whether a given relation is an equivalence relation have the least success rate. On the contrary, students achieve the best results when solving a task from propositional logic and a task concerning matrix operations.

At the beginning of the semester, students are acquainted with the eight types of tasks that can be expected in the semester exam. These types of tasks are listed in the second column of Table 3. The third column contains the number of students (NS) who solved this type of task. The fourth column always shows the average score (AS), i.e., the number of points always out of the maximum number of 10. The average score received by students on the theoretical part of the exam on a total of 49 exams was only 4.86 out of 20 points.

3. Mathematics II

The teaching of the subject Mathematics II is subsidized for 90 lessons. 45 learning units consist of 22 lectures and 23 exercises, including 3 laboratory exercises.

3.1. Topics of Mathematics II

Individual topics of subject Mathematics II are stated in the following Table 4.

3.2. Semester Exam in Mathematics II

Students are again, just as in Mathematics I, introduced to the content of the semester exam at the beginning of the semester. At the end of the semester, several sets (usually 4 to 6) of solved preparatory tasks for the exam are made available to students. The semester exam in Mathematics II consist of a theoretical part and a practical part.

The practical part of the exam consists of the assignment of six tasks. For each task, the student can get 0 to 10 points, so for the practical part, the student can receive a maximum of 60 points. For the semester exam, the student can get a maximum of 100 points.

3.3. Example of a Semester Exam in Mathematics II

One of the assignments of the semester exam had the following theoretical and practical part. The theoretical part lasts 30 minutes, the practical part follows, for which 120 minutes are reserved. Thus, the Mathematics II exam took 150 minutes, as was the case with the Mathematics I exam.

▸......................................The theoretical part ......................................

A. Formulate Cramer’s rule, give two applications of determinants in linear algebra or in analytical geometry. [4 points]

B. Write the axiomatic definition of the scalar product of the vectors. [4 points]

C. Convert a system of equations

A \cdot x = b

to the iteration form expressing

(k + 1)

-th approximation its solution

x^{(k + 1)}

. [4 points]

D. Define a monoid, give two examples of monoids, formulate three inversion properties in the monoid. [4 points]

E. Define a cyclic group and a group generator, give two examples of the cyclic group. [4 points]

▸......................................The practical part ......................................

1) Solve the matrix equation

(\begin{matrix} 2 & 1 \\ 3 & 2 \end{matrix}) \cdot X \cdot (\begin{matrix} 1 & 1 & 0 \\ 1 & 3 & 1 \\ 0 & 1 & 1 \end{matrix}) = (\begin{matrix} 3 & 8 & 3 \\ 5 & 13 & 5 \end{matrix})

. [10 points]

2) Verify that the vectors

u_{1} = (1, 1, 1)

u_{2} = (1, 1, 0)

u_{3} = (1, 0, 0)

form the basis of the Euclidean vector space

R^{3}

with a standard scalar product, and use the Gram-Schmidt process to determine the orthonormal basis of

R^{3}

. [10 points]

3) Using matrix diagonalization (not matrix multiplication), calculate the 8th power

A^{8}

of the matrix

A = (\begin{matrix} 0 & 1 \\ - 2 & 3 \end{matrix})

. [10 points]

4) Using modular arithmetic (not just using calculator) for given numbers

a = 13^{11}

b = 9

a) determine the rest after dividing a by b, b) determine the last digit of a, c) show that the number

(a \cdot b + 17)

is divisible by 50. [10 points]

5) There are given two algebraic structures

(Z_{4}, \oplus)

, where

x \oplus y = (x + y) (mod 4)

and

(Z_{8}^{*}, ⊙) = ({1, 3, 5, 7}, ⊙)

, where

a ⊙ b = (a \cdot b) (mod 8)

a) Create Cayley tables of both algebraic structures. b) Verify, that both structures form a group. c) Determine all subgrups of both groups. d) Decide whether these groups are isomorphic, and justify your claim. [10 points]

6) In a set of all polynomials

Z_{7} [x]

write down the Bézout’s identity for polynomials

P (x) = 6 x^{3} + 5 x^{2} + 4 x + 3

and

Q (x) = 2 x + 1

. [10 points]

3.4. Students’ Success in the Mathematics II Exam

The following Table 5 presents the success of students in the semester exam in Mathematics II in the summer semesters of the academic years 2019/2020, 2020/2021, 2021/2022, 2022/2023, cumulatively for the academic years 2019/2020 to 2022/2023 and the total number of students who continue to study successfully.

Figure 2 shows the percentage success rate of students in semester exams in Mathematics II from the academic year 2019/2020 to 2022/2023, with the fact that grade E also includes grade E in the 1st or 2nd correction period. If the student rejected grades B, C or D and wrote a repair examination, only the final grade is written in this table.

3.5. Students’ Success in Solving Single Types of Tasks in the Mathematics II Exam

The following Table 6 contains the evaluation of success in the last exam in AY 2022/2023.

The task concerning polynomial factor rings and the task to determine the orthogonal basis along with the task concerning geometrical applications of different types of vector products have the least success rate. The highest scores achieve a task concerning isomorphic algebraic structures and their properties and the task to determine the greatest common divisor (GCD) and the least common multiple (LCM) of two integers along with the task of solving a system of linear congruence equations.

At the beginning of the semester, students are acquainted with the eight types of tasks that are stated in the second column of Table 6. The third column contains the number of students who solved this type of task. The fourth column always shows the average score, i.e., the number of points that students achieved from a maximum of 10 points. The average score received by students on the theoretical part of the exam on a total of 27 exams was 6.85 out of 20 points.

4. Mathematics III

The teaching of the subject Mathematics III is again, just as Mathematics I and Mathematics II, subsidized for 90 lessons. 45 learning units consist of 22 lectures and 23 exercises, including 2 laboratory exercises.

4.1. Topics of Mathematics III

The list of lecture topics on the subject Mathematics III is given by the following Table 7.

4.2. Semester Exam in Mathematics III

Students are again always introduced to the content of the semester exam at the beginning of the semester. At the end of the semester, several sets of solved preparatory tasks for the exam are made available to students. The semester exam in Mathematics III consist of a theoretical part and a practical part.

4.3. Example of a Semester Exam in Mathematics III

One of the assignments of the semester exam had the following theoretical and practical part. The theoretical part lasts 30 minutes, the practical part lasts 120 minutes. Thus, the Mathematics III exam took 150 minutes, as was the case with the Mathematics I and the Mathematics II exams.

▸......................................The theoretical part ......................................

A. Define Peirce logical NOR operator and write its truth table. [4 points]

B. Present the symbols and their names that form the alphabet of predicate logic. [4 points]

C. Define the root of the polynomial and state how to determine the integer and rational roots of the polynomial. [4 points]

D. Define a continuous function at a point, give the types of discontinuation and state relationship between continuity and derivatives at that point. [4 points]

E. Formulate the integral test of the convergence of an infinite series. [4 points]

▸......................................The practical part ......................................

1) Reformulate the sentences into the propositional formulas and decide whether the formula under the line is a logical consequence of the formula above the line:

Pavel has a ticket purchased, but urban transport does not work.

If urban transport works, Pavel will come to work on time.

Pavel has a ticket purchased and will not come to work on time.

[10 points]

2) Using an algebraic minimization for the propositional formula

f (p, q, r)

, which has a vector evaluation of

h = (0, 0, 0, 1, 0, 0, 1, 1)

for the ordered triplet of truth values

(0, 0, 0), (0, 0, 1), \dots, (1, 1, 1)

of propositional variables

(p, q, r)

, determine its minimal disjunctive form. [10 points]

3) The finite-state machine

A

with a set of states

q = {1, 2, 3}

, alphabet

Σ = {a, d, s}

and with the state diagram

is given. Write the state-transition table and decide which of the words

d a d

s a d

a s a d

d a s a

s a d a

a a d s s

the finite-state machine

A

recognizes. [10 points]

4) Function is given by the formula

f : y = \frac{π}{2} + tan (2 x + \frac{π}{3}) .

Determine the inverse function

f^{- 1} (x)

and a domain

D (f)

so that for

f (x)

the function

f^{- 1} (x)

can exist. Determine the domain

D (f^{- 1})

and a range

H (f^{- 1})

and draw the graphs of the functions f and

f^{- 1}

. [10 points]

5) Function is given by the formula

f : y = (1 - 2 x) e^{2 x - 1} .

Determine its local minima and maxima, intervals of monotony and inflexion points.

[10 points]

6) Using a definite integral, calculate the volume V of the revolution solid that is created by the rotation of the subgraph of function

y = ln x

x \in 〈 1, e 〉

, around the x-axis.

[10 points]

4.4. Students’ Success in the Mathematics III Exam

The following Table 8 presents the success of students in the semester exam in Mathematics III in the winter semesters of the academic years 2020/2021, 2021/2022, 2022/2023, 2023/2024, cumulatively for the academic years 2020/2021 to 2023/2024 and the total number of students who continue to study successfully.

Figure 3 shows the percentage success rate of students in semester exams in Mathematics III from the academic year 2020/2021 to 2023/2024, with the fact that grade E also includes grade E in the 1st or 2nd correction period. If the student rejected grades B, C or D and wrote a repair examination, only the final grade is written in this table.

4.5. Students’ Success in Solving Single Types of Tasks in the Mathematics III Exam

The following Table 9 contains the evaluation of success in the last exam in AY 2023/2024.

Students’ success in the semester exam in Mathematics III was relatively high for the tasks of the propositional and predicate logic and theory of finite-state machines, and quite low in the tasks of the theory of real variable, differential and integral calculus and of convergence criteria of series.

At the beginning of the semester, students are acquainted with the eight types of tasks that are stated in the second column of Table 9. The third column contains the number of students who solved this type of task. The fourth column always shows the average score, i.e., the number of points that students achieved from a maximum of 10 points. The average score received by students on the theoretical part of the exam on a total of 15 exams was 5.47 out of 20 points.

5. Graph Theory

Teaching Graph theory at the Faculty of Military Technology began in the mid 1990s, when the subject Graphic algorithms was taught by the author and at first also one of his colleagues, as the facultative subject of the doctoral study.

Teaching Graph theory in the master’s degree for students of the specialization in Cybersecurity, which covers the basic thematic units from this part of discrete mathematics along with the most important graph algorithms, began until academic year 2019/2020 after accreditation of this study program.

The subject Graph theory, unlike the three previous subjects, Mathematics I, II and III, does not end with a semester exam, but a classified credit. The teaching of the subject Graph theory is subsidized for 60 lessons. 30 learning units consist of 15 lectures and 15 exercises, including 3 laboratory exercises.

Laboratory exercises from Graph theory, as well as laboratory exercises in the subjects Mathematics I, II and III, take place in computer classrooms using the computer algebra system Maple, which, together with the programming language Matlab, is licensed at the Faculty of Military Technology for teaching and research work.

5.1. Topics of Graph Theory

The list of lecture topics on the subject Graph theory, including hourly subsidies for lectures, exercises and laboratory exercises in a computer classroom, is given by the following Table 10.

5.2. Classified Credit in Graph Theory

Students are again always introduced to the content of the classified credit at the beginning of the semester. At the end of the semester, several sets of solved preparatory tasks for the exam are made available to students. The classified credit in Graph theory consists of a theoretical part and a practical part.

The theoretical part contains four questions about theory. 0 to 5 points can be obtained for each answered question, so a student can receive a maximum of 20 points for the theoretical part. A maximum of another 20 points can be gained from exercises.

The practical part of the classified credit consists of the assignment of six tasks. For each task, the student can get 0 to 10 points, so for the practical part, the student can receive a maximum of 60 points. For the classified credit, the student can get a maximum of 100 points, such as with exams in the subjects Mathematics I, II and III.

5.3. Example of a Classified Credit Test in Graph Theory

One of the assignments of the classified credit test had the following theoretical and practical part. The theoretical part lasts 30 minutes, the practical part lasts 120 minutes. Thus, the Graph theory classified credit test took 150 minutes, as was the case with the Mathematics I, II and III exams.

▸......................................The theoretical part ......................................

A. Define a degree sequence, formulate Havel-Hakimi algorithm, and illustrate it in a example. [5 points]

B. Define an acyclic graph, forest, tree, formulate statements equivalent to statement that the graph with n vertices is a tree. [5 points]

C. Define an area of a planar graph, formulate Euler’s formula and its two consequences for the number of edges of the planar graph. [5 points]

D. Define a Hamiltonian cycle, a Hamiltonian graph, a Hamiltonian path, formulate Ore’s theorem. [5 points]

▸......................................The practical part ......................................

1. a) Using the Havel-Hakimi algorithm, show that the degree sequence

D (G) = (4, 4, 4, 3, 3, 2, 2)

is a graph sequence.

b) Draw an example of a graph G with a graph sequence

D (G)

c) In the graph G, mark an example of an Eulerian trail. [10 points]

2. Using the Hungarian algorithm, determine all the cheapest maximal matchings M and their cost c in a bipartite graph

G = (V, W)

that has a cost matrix

C = (\begin{matrix} 4 & 3 & 2 & 1 \\ 1 & 4 & 3 & 2 \\ 1 & 3 & 2 & 4 \\ 4 & 2 & 1 & 3 \end{matrix}) .

[10 points]

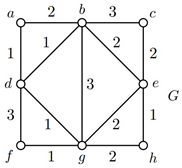
3. Solve the Chinese postman problem for the weighted graph G with vertices

a, b, c, d, e, f, g, h

shown in the figure, whose start and end vertices are vertex a:

[10 points]

4. a) Determine which two of the graphs

F, G, H

are isomorphic and describe the isomorphism using the bijection of their vertices: Preprints 111119 i003

b) Show the plane drawing of the remaining non-isomorphic graph and verify Euler’s formula for it.

c) Determine the chromatic number of a non-isomorphic graph and show an example of its minimal coloring by marking the vertices with the numbers. [10 points]

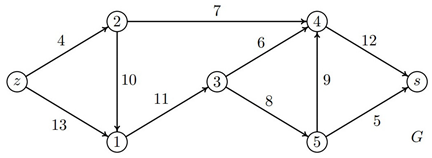
5. In the network in the figure, determine the maximum flow using the Ford-Fulkerson algorithm: Preprints 111119 i004

[10 points]

6. Using the CPM method, determine the critical path, the project completion time T and the total time reserves

R_{c}

of the individual activities of the project specified by a network graph with vertices

1, 2, 3, 4, 5, 6, 7

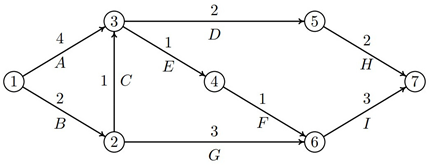
and weighted oriented edges: Preprints 111119 i005

[10 points]

5.4. Students’ Success in the Classified Credit Test in Graph Theory

The following Table 11 presents the success of students in the classified credit test in Graph theory in the summer semesters of the academic years 2020/2021, 2021/2022, 2022/2023, cumulatively for the academic years 2020/2021 to 2022/2023 and the total number of students who continue to study successfully.

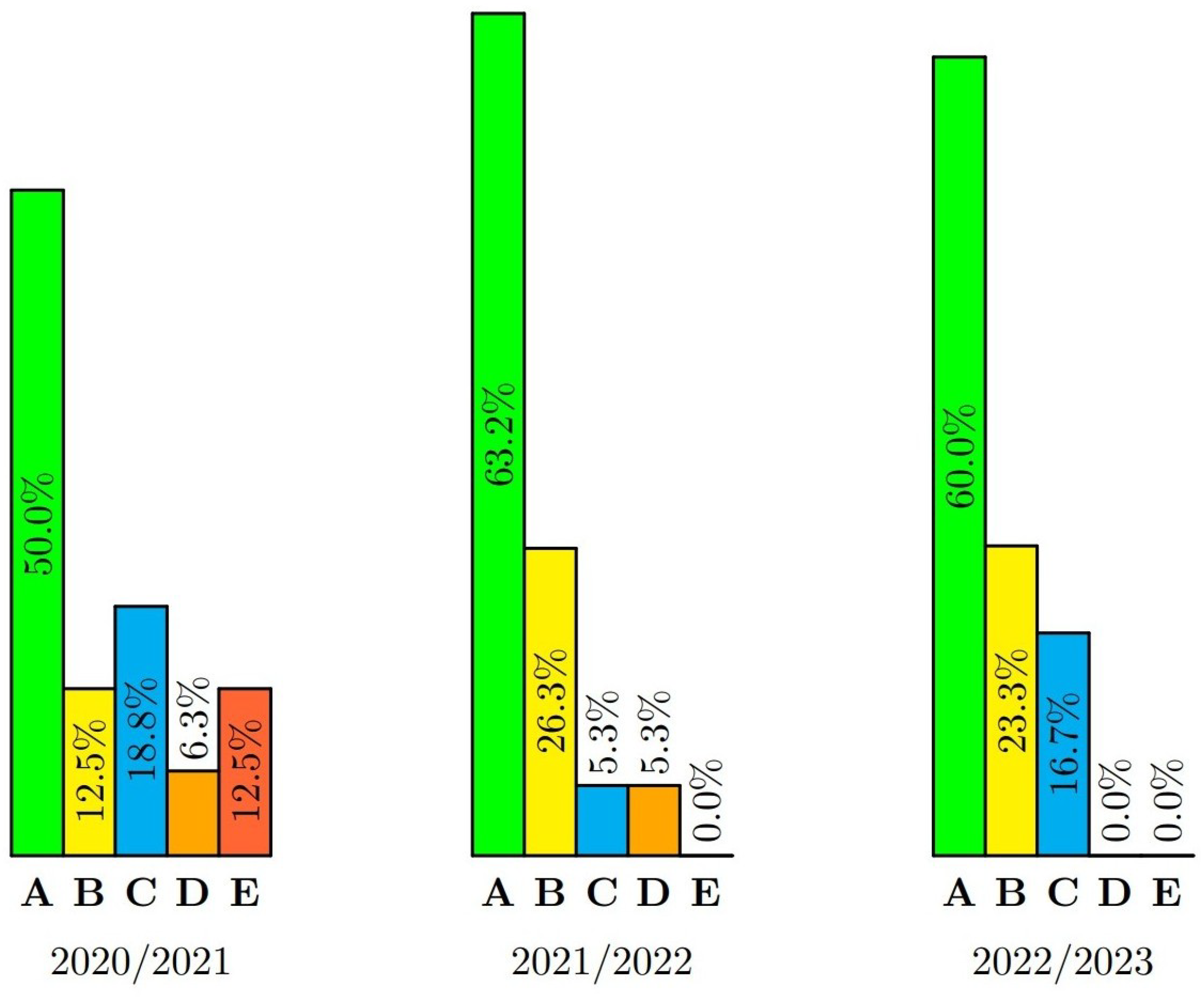
Figure 4 shows the percentage success rate of students in the classified credit test in Graph theory from the academic year 2020/2021 to 2022/2023.

5.5. Students’ Success in Solving Single Types of Tasks in the Classified Credit Test in Graph Theory

The following Table 12 contains the evaluation of success in the last exam in AY 2022/2023.

Students’ success in the classified credit test in Graph theory was very high for all the tasks. The average evaluation of all six types of tasks used in the academic year 2022/2023 was over 9 points out of 10 possible points.

At the beginning of the semester, students are again acquainted with the eight types of tasks that are stated in the second column of Table 12. The third column contains the number of students who solved this type of task. The fourth column always shows the average score, i.e., the number of points that students achieved from a maximum of 10 points. The average score received by students on the theoretical part of the classified credit test on a total of 30 classified credit tests was 14.13 out of 20 points.

6. Discussion

In the following subsections, we will present a list of tasks in the semester exams from Mathematics I, II and III and in the classified credits from Graph theory, where students achieved the worst and best results, along with the likely causes.

Let us remark that the originally weak results in answering the theoretical questions in the theoretical part of examinations were mostly improved with the progressing semesters (4.86, 6.85, 5.47 and 14.13 points out of 20 points), as students gradually got used to studying the theory and not only practical tasks, and they began to study the theory of greater importance.

In general, unfortunately, the success of students in semester exams in the subjects Mathematics I, II and III has a declining tendency. This is probably due to weaker knowledge of high school mathematics for students who had a lower proportion of direct teaching in high school and studied some parts of mathematics at home during the Covid-19 pandemic.

A certain reason is the decreasing number of Vietnamese students, whose knowledge of secondary school mathematics is traditionally at a high level and whose application and diligence exceed those qualities of an average Czech student.

On the other hand, the success of the classified credit from the subject Graph theory is high and relatively permanent, with percentage success rate of grade A around 60%.

This may be due to the relative popularity of the subject Graph theory, students’ awareness of many applications of this subject in the Cybersecurity specialization, and a more responsible attitude of students of the 4th semester to study.

6.1. the Least and Most Successful Types of Tasks in the Mathematics I Exam

Solving a task concerning a linear map has the least success rate (3.17 points out of 10 points), because a linear map is the last topic which is not quite easy and which students do not sufficiently experienced and practice. The task to verify whether a given relation is an equivalence relation, also has a very small success rate (3.67 pts), because it is difficult for students to prove the reflexivity, symmetry and transitivity of a given relation based on the property it is defined.

Students achieve the best results (6.95 pts) when solving a task from propositional logic, which they usually got to know already in secondary school, and a task concerning matrix operations (6.23 pts) because the operations with matrices represent a relatively simple practical task for students.

6.2. the Least and Most Successful Types of Tasks in the Mathematics II Exam

The least success rate has the task concerning polynomial factor rings (2.31 pts), because it is the last and most difficult topic for students and the task to determine the orthogonal basis, along with the task concerning geometrical applications of different types of vector products (4.33 pts), because some students have problem with the Gram-Schmidt process formulas and because some students have a weak plane and space power of visualization.

The students achieve the highest scores by solving the task concerning isomorphic algebraic structures and their properties (7.52 pts), because this topic has greater attention and sufficient time subsidy. Also, the task to determine the GCD and LCM of two integers, along with the task of solving a system of linear congruence equations, achieve a relatively high score (6.75 pts), because the students the notions GCD and LCM, just as the elimination method for solving linear systems of equations, know from the secondary school.

6.3. the Least and Most Successful Types of Tasks in the Mathematics III Exam

The tasks from the first part of the lectures concerning logic and finite-state machines were very successful. The highest score (9.88 pts) achieved a relatively simple task for the finite-state machine and the decision of which words the finite-state machine recognizes. High scores (9.67 pts) were achieved in solving tasks from logic, which the students had already acquired in the subject Mathematics I, and minimization of formulas.

On the contrary, the tasks of the second part of the lectures concerning the function of real variables, differential and integral calculus and infinite series managed students with fewer or greater problems. The lowest score (3.27 pts) was achieved by the students to solve the tasks on the integral calculus and its geometric application and the tasks of differential calculus concerning local extrema and function properties (3.71 pts).

6.4. the Least and Most Successful Types of Tasks in the Graph Theory Classified Credit

Based on a 5-year experience of teaching the subject Graph theory, the author may state that students are more popular with this subject than most of the classical topics from discrete mathematics and differential and integral calculus. The popularity of this subject corresponds to the very nice evaluation that students achieve in the classified credits.

Students have solved all six types of practical tasks very well, so it is not possible to talk about tasks with the smallest or greatest success. The lowest average score (9.13 pts) was received by the students for the task of the cheapest maximum matching solved by the Hungarian algorithm. The highest score (9.80 pts) students achieved in the task determining the maximum flow using the Ford-Fulkerson algorithm.

7. Conclusions

In conclusion, it can be stated that the study of the subjects Mathematics I, II and III is quite challenging for students specializing in Cybersecurity. There are several reasons. One of the most fundamental is the decreasing level of knowledge of high school mathematics with which students come to the Faculty of Military Technology, as well as a less responsible approach to studies at first. For students, their studies and preparation for semester exams are often complicated by bad study habits, little diligence and willingness to study mathematics and solve homework examples independently and with understanding, and little or almost no ability to work with recommended literature.

As a rule, with the passage of time, students’ study habits improve and their responsibility in studying and preparing for exams increases. At the same time, during the first year, students supplement their knowledge of high school mathematics, mainly thanks to mentoring, which takes place every week in the afternoon for weaker students at the Faculty of Military Technology. Mentoring, both individual and group, has been introduced to the faculty for the third year. It can be stated that this form of supplementary teaching has proven itself very well and is considered beneficial even by the students themselves.

The author wants to continue monitoring the success of Cybersecurity students while studying mathematics, because five years of teaching experience is not a very long time for any more fundamental conclusions.

Funding

This research received no external funding.

Acknowledgments

This work was supported by the Project for the Development of the Organization DZRO ”Military autonomous and robotic systems” under Ministry of Defence and Armed Forces of Czech Republic.

Conflicts of Interest

The author declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:

AS	Average score
AY	Academic year
CC	Laboratory exercises in a computer classroom
EX	Exercises
GCD	Greatest common divisor
HS	Hourly subsidy
LCM	Least common multiple
LE	Lecture
NS	Number of students

References

Jánský, J.; Potůček, R. The Tradition and New Approach to the Mathematical Education of Officers in the Czech Army. Studies in Systems, Decision and Control, Flaut, D. et al. (Eds): Decision Making in Social Sciences: Between Traditions and Innovations, Switzerland: Springer International Publishing. 2020; 247, 155–168ISBN 978-3-030-30658-8. [Google Scholar] [CrossRef]
Abdulwahed, M.; Jaworski, B.; Crawford, A.R. Innovative Approaches to Teaching Mathematics in Higher Education: A Review and Critique. Nordic Studies in Mathematics Education 2012, 17 (2), 49–68. Available online: https://dspace.lboro.ac.uk/dspace-jspui/handle/2134/11988 (accesed on 28-05-2024).
Intranet of University of Defence – Accredited Study Programs. Available online: https://apl.unob.cz/Akreditace/Programy.aspx (accesed on 28-05-2024).
Hošková-Mayerová, Š.; Potůček, R. Qualitative and quantitative evaluation of the entrance draft tests from mathematics. Studies in Systems, Decision and Control Antonio Maturo et al. (Eds): Recent Trends in Social Systems: Quantitative Theories and Quantitative Models, Switzerland: Springer International Publishing, ISBN 978-3-319-40583-4. 2017, 66, 53–46. [Google Scholar]
Arney, C.; Vanatta, N.; Nelson, T. Cyber Education via Mathematical Education. The Cyber Defence Review Fall 2016, 49-59. Connolly, J.C. (Editor in Chief), West Point, New York. ISSN 2474-2120. Available online: https://cyberdefensereview.army.mil/Portals/6/Documents/CDR-FALL2016.pdf (accesed on 28-05-2024).
Carriegos, M.V. Main challenges in teaching/learning of mathematics for cyber-security. Conference: INDRUM 2016: First conference of the International Network for Didactic Research in University Mathematics, Montpellier, France. Available online: https://hal.archives-ouvertes.fr/hal-01337917 (accesed on 28-05-2024).
Byrd, R. Cybersecurity: 1) what math is necessary and 2) developing ubiquitous cybersecurity in current computing programs. Journal of Computing Sciences in Colleges 2018, 33/4, 53–59. [Google Scholar] [CrossRef]
Knijnenburg, B.P.; Bannister, N.; Caine, K. Using Mathematically-Grounded Metaphors to Teach AI-Related Cybersecurity. IJCAI-21 Workshop on Adverse Impacts and Collateral Effects of Artificial Intelligence Technologies (AIofAI), Montréal, Canada. Available online: https://par.nsf.gov/biblio/10273277-using-mathematically-grounded-metaphors-teach-ai-related-cybersecurity (accesed on 28-05-2024).
Neri, F. Teaching Mathematics to Computer Scientists: Reflections and a Case Study. SN COMPUT. SCI. 2021, 2(75). [Google Scholar] [CrossRef]
Koziuk, Y. Application of Mathematics in Cyber security. Thesis, Vinnytsia National Technical University, Ukraine, June 2023. [CrossRef]
MOOC BLOG TEAM: How is math used in cybersecurity? 2024. Available online: https://www.edx.org/resources/how-is-math-used-in-cybersecurity (accesed on 28-05-2024).
Bowcut, S. Why math matters in cybersecurity. Cybersecurity Guide 2024. Available online: https://cybersecurityguide.org/resources/math-in-cybersecurity (accesed on 28-05-2024).

Figure 1. The percentage success rate in the Mathematics I exam from AY 2019/20 to 2023/24.

Figure 2. The percentage success rate in the Mathematics II exam from AY 2019/20 to 2022/23.

Figure 3. The percentage success rate in the Mathematics III exam from AY 2020/21 to 2023/24.

Figure 4. The percentage success rate in the classified credit test in Graph theory from AY 2020/21 to 2022/23.

Table 1. Topics of Mathematics I with their hourly subsidies (LE/EX/CC).

#	Topic	HS	LE/EX/CC
1	Mathematical logic	8	4/4/0
2	Set theory	8	4/4/0
3	Binary relations	8	4/2/2
4	Mapping	4	2/2/0
5	Partially ordered sets	4	2/2/0
6	Combinatorics	8	4/4/0
7	Fields nad vector spaces	8	4/4/0
8	Matrices and matrix operations	8	4/4/0
9	Solving systems of linear equations	10	4/4/2
10	Vector subspaces and linear span	4	2/2/0
11	Intersection and sum of vector subspaces	4	2/2/0
12	Basis and dimension of vector space	8	4/4/0
13	Linear mapping	8	4/4/0

Table 2. Final evaluations for the semester exam in Mathematics I in the academic years 2019/2020, 2020/2021, 2021/2022, 2022/2023, 2023/2024 and from the academic year 2019/2020 to 2023/2024.

AY	A	B	C	D	E	F/E	F/F/E	TN
2019/2020	3	3	2	1	4	3	1	17
2020/2021	3	1	4	4	4	1	1	18
2021/2022	4	6	6	11	3	0	0	30
2022/2023	0	1	2	4	3	3	1	14
2023/2024	1	0	4	5	6	6	4	26
2019/20–2023/24	11 (10.5%)	11 (10.5%)	18 (17.1%)	25 (23.8%)	20 (19.0%)	13 (12.4%)	7 (6.7%)	105

Table 3. Success of students in the task solving at exam in Mathematics I in AY 2023/2024.

#	Type of exam task	NS	AS
1	Checking whether a propositional formula is a tautology/contradiction/consis- tent, conversion to disjunctive
	normal form.	20	6.95
2	Proof of the equality of expressions with natural numbers
	by mathematical induction. / Proof of the statement of divisibility by mathematical induction.	29	4.59
3	Combinatorics – combinatorial principles (product, sum, inclusion and exclusion), permutation, variation, combination
	without repetition/with repetition.	49	5.14
4	Binary relations and their properties. / Verification that the given relation is an equivalence relation,
	decomposition into equivalence classes.	49	3.67
5	Basic operations with matrices. / Determination the rank of a matrix depending on a parameter.	22	6.23
6	Verification that vectors/polynomials/matrices form a basis of the vector space. / Coordinates of a vector/polynomial/matrix
	with respect to the basis.	34	4.47
7	Determination the dimension and basis of a vector subspace and its completion based on the vector space. / Determination the basis and dimension of
	the intersection and the sum of two vector subspaces of the given vector space.	49	4.16
8	Determination the kernel, image, defect, and rank of a linear map. / Verification of the linearity of the
	map and determination of its matrix.	42	3.17

Table 4. Topics of Mathematics II with their hourly subsidies.

#	Topic	HS	LE/EX/CC
1	Determinants, their calculation and application	8	4/4/0
2	Inverse matrices, their calculation and applications	4	2/2/0
3	Linear transformation, transition matrix	8	4/4/0
4	Eigenvalues and eigenvectors of a matrix and their calculation	8	4/2/2
5	Similar matrices, diagonalization of matrices, matrix functions	4	2/2/0
6	Scalar product, Euclidean space, orthogonal vectors	8	4/4/0
7	Finite and iterative methods of solving systems of linear equations	8	4/2/2
8	Divisibility criteria, Euclidean algorithm, Bézout’s identity	4	2/2/0
9	Prime numbers and composite numbers, Euclid’s theorem	4	2/2/0
10	Congruence relation, linear congruence equations and their systems	6	2/4/0
11	Euler’s totient function, Fermat’s little theorem, Euler’s theorem	4	2/0/2
12	Groupoids, semigroups, monoids, groups	8	4/4/0
13	Subgroups, cyclic groups, factor groups	8	4/4/0
14	Rings, polynomial rings, Galois fields, lattices, Boolean algebras	8	4/4/0

Table 5. Final evaluations for the semester exam in Mathematics II in the academic years 2019/2020, 2020/2021, 2021/2022, 2022/2023 and from the academic year 2019/2020 to 2022/2023.

AY	A	B	C	D	E	F/E	F/F/E	TN
2019/2020	7	3	1	1	2	2	0	16
2020/2021	4	3	4	4	1	2	1	19
2021/2022	4	8	10	5	3	0	0	30
2022/2023	1	2	1	4	3	2	0	13
2019/20–2022/23	16 (20.5%)	16 (20.5%)	16 (20.5%)	14 (17.9%)	9 (11.5%)	6 (7.7%)	1 (1.3%)	78

Table 6. Success of students in the task solving at exam in Mathematics II in AY 2022/2023.

#	Type of exam task	NS	AS
1	Solving a matrix equation of type $A X = B$ or $X A = B$ or $A X B = C$ using an inverse matrix.	23	6.35
2	Determination the transition matrix from basis to basis, determination of the coordinates of the vector on a given basis.	7	6.57
3	Determination the orthogonal and orthonormal
	bases of the subspace of Euclidean space products. / Geometric applications of scalar, vector and triple products.	27	4.33
4	Determination eigenvalues and eigenvectors of a given matrix. / Calculation of the power of the
	matrix using its diagonalization.	27	4.56
5	Determination GCD and LCM of two integers, Euclidean algorithm, Bézout’s identity. / Solving a system of linear congruence
	equations by an elimination method.	24	6.75
6	Solving the linear congruence equation using Euler’s theorem. / Determination the remainder after dividing two natural numbers, determination
	the latest digits of the natural number in the form of a power.	14	6.00
7	Creating Cayley tables of two algebraic structures, verification of the properties of the group, determination its subgroups and the justification of whether
	these groups are isomorphic or determination group generators.	27	7.52
8	Determination GCD and Bézout’s identity for polynomials in $Z_{p} [x]$ . / Solving the linear polynomial equation
	in the factor ring.	16	2.31

Table 7. Topics of Mathematics III with their hourly subsidies.

#	Topic	HS	LE/EX/CC
1	Propositonal logic, disjunctive and conjunctive normal form	8	4/4/0
2	Algebraic minimization of normal forms, the Karnaugh maps	8	4/4/0
3	Deductive system, deduction, correctness and completeness theorems	4	2/2/0
4	Predicate logic	6	2/4/0
5	Proofs in predicate logic, model theory	4	2/2/0
6	Finite-state machines, languages recognized by the finite-state machine	8	4/4/0
7	Real function of one real variable, elementary functions	8	4/4/0
8	Limit of a function, continuous functions	4	2/2/0
9	Derivative of a function, L’Hôspital’s rule	8	4/4/2
10	Applications of differential calculus, Taylor polynomials	8	4/4/0
11	Indefinite integral, integration of some special functions	8	4/4/0
12	Definite integral and its computation	4	2/2/0
13	Improper integral and its computattion	4	2/0/2
14	Sequences, infinite series	4	2/2/0
15	Power series, generating functions	4	2/2/0

Table 8. Final evaluations for the semester exam in Mathematics III in the academic years 2020/2021, 2021/2022, 2022/2023, 2023/2024, and from the academic year 2020/2021 to 2023/2024.

AY	A	B	C	D	E	F/E	F/F/E	TN
2020/2021	4	2	5	0	0	5	0	16
2021/2022	3	3	5	2	1	2	3	19
2022/2023	9	6	4	6	3	2	0	30
2023/2024	0	0	3	4	5	1	0	13
2020/21–2023/24	16 (20.5%)	11 (14.1%)	17 (21.8%)	12 (15.4%)	9 (11.5%)	10 (12.8%)	3 (3.9%)	78

Table 9. Success of students in the task solving at exam in Mathematics III in AY 2023/2024.

#	Type of exam task	NS	AS
1	Verification of logical equivalence/logical consequence by using a truth table. / Reformulating sentences
	into logical formulas and decisions whether a given logical formula is their logical consequence.	15	9.67
2	Determination of minimal disjunctive forms of 3 or 4 propositional variables using algebraic minimization/Karnaugh map.	15	7.40
3	Formal notation of the predicate formula, its negation and verbal expression of negation.	7	8.14
4	Determination the state-transition table of the finite-state machine and words that it recognizes.	8	9.88
5	Determination the inverse function, its domain and range and drawing graphs of the function and inverse function.	8	5.50
6	Determination local minima and maxima, intervals of monotony and inflexion points of a given function.	14	3.71
7	Evaluation the definite integral by a suitable integration method. / Calculation the indefinite integral using partial fraction decomposition. / Geometric
	applications of a definite integral.	15	3.27
8	Decision on convergence of two given series using a suitable convergence criterion.	8	4.00

Table 10. Topics of Graph theory with their hourly subsidies.

#	Topic	HS	LE/EX/CC
1	Basic terminology, basic types of graphs, simple graphs, degree sequence	4	2/2/0
2	Subgraphs, graph representation, operations on graphs	4	2/2/0
3	Walks, trails, paths, and cycles in graphs, connectivity in graphs	4	2/0/0
4	Trees, spanning trees, Cayley’s formula, Prüfer sequence, Laplacian matrix	4	2/2/0
5	Graph labeling, depth-first search, breadth-first search	4	2/0/2
6	Isomorphism of graphs and rooted trees, tree code	4	2/2/0
7	Vertex and edge connectivity, blocks of a graph, articulation points	4	2/2/0
8	Matchings and covers in bipartite graphs, perfect matching	4	2/2/0
9	Edge colorings, chromatic index, Vizing’s theorem	4	2/2/0
10	Vertex colorings, chromatic number, Brooks’ theorem	4	2/0/2
11	Planar graphs, Kuratowski’s theorem, Euler’s formula, dual graph	4	2/2/0
12	Eulerian and Hamiltonian graphs, Chinese postman problem	4	2/2/0
13	Digraphs, basic terminology, digraph connectivity, Eulerian digraphs	4	2/2/0
14	Flow networks, algorithm for finding a maximal flow	4	2/2/0
15	Critical Path Method, Project Evaluation and Review Technique	4	2/0/2

Table 11. Final evaluations for the classified credit test in Graph theory in the academic years 2020/2021, 2021/2022, 2022/2023, and from the academic year 2020/2021 to 2022/2023.

AY	A	B	C	D	E	F/E	F/F/E	TN
2020/2021	8	2	3	1	2	0	0	16
2021/2022	12	5	1	1	0	0	0	19
2022/2023	18	7	5	0	0	0	0	30
2020/21–2022/23	38 (58.5%)	14 (21.5%)	9 (13.8%)	2 (3.1%)	2 (3.1%)	0 (0.0%)	0 (0.0%)	65

Table 12. Success of students in the task solving at classified credit test in Graph theory in AY 2022/2023.

#	Type of exam task	NS	AS
1	Verification that the degree sequence is a graph sequence, drawing an example of such a graph, and determining the Eulerian trail
	in this graph.	30	9.67
2	Determination the distance matrix and the reachability matrix for the graph and directed graph.	0	—
3	Determination of the number of spanning trees of the graph using subdeterminants of the incidence matrix and
	using Kirchhoff’s theorems.	0	—
4	Determination all the cheapest maximum matchings in a bipartite graph with a given cost matrix using the Hungarian algorithm.	30	9.13
5	Solving the problem of the Chinese postman with a given weighted graph and determining the length of the shortest
	walk covering all the edges.	30	9.30
6	Finding isomorphic graphs, plane drawing of the graph, verifying the Euler’s formula, determining the chromatic number of the graph and
	its minimum vertex coloring.	30	9.20
7	Determination and drawing the maximum flow in the network using the Ford-Fulkerson algorithm.	30	9.80
8	Determination of the critical path, the crash duration and the total time reserves of individual project activities by the CPM method.	30	9.60

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

Views

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Experience Teaching Mathematics at the University of Defence in the Study Field of Cybersecurity

Abstract

Keywords:

Subject:

1. Introduction

2. Mathematics I

2.1. Topics of Mathematics I

2.2. Semester Exam in Mathematics I

2.3. Example of a Semester Exam in Mathematics I

2.4. Students’ Success in the Mathematics I Exam

2.5. Students’ Success in Solving Single Types of Tasks in the Mathematics I Exam

3. Mathematics II

3.1. Topics of Mathematics II

3.2. Semester Exam in Mathematics II

3.3. Example of a Semester Exam in Mathematics II

3.4. Students’ Success in the Mathematics II Exam

3.5. Students’ Success in Solving Single Types of Tasks in the Mathematics II Exam

4. Mathematics III

4.1. Topics of Mathematics III

4.2. Semester Exam in Mathematics III

4.3. Example of a Semester Exam in Mathematics III

4.4. Students’ Success in the Mathematics III Exam

4.5. Students’ Success in Solving Single Types of Tasks in the Mathematics III Exam

5. Graph Theory

5.1. Topics of Graph Theory

5.2. Classified Credit in Graph Theory

5.3. Example of a Classified Credit Test in Graph Theory

5.4. Students’ Success in the Classified Credit Test in Graph Theory

5.5. Students’ Success in Solving Single Types of Tasks in the Classified Credit Test in Graph Theory

6. Discussion

6.1. the Least and Most Successful Types of Tasks in the Mathematics I Exam

6.2. the Least and Most Successful Types of Tasks in the Mathematics II Exam

6.3. the Least and Most Successful Types of Tasks in the Mathematics III Exam

6.4. the Least and Most Successful Types of Tasks in the Graph Theory Classified Credit

7. Conclusions

Funding

Acknowledgments

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe