Prerpints.org logo
Preprint
Article

Chalcogen-Bond-Assisted Formation of the N→C Dative Bonds in the Complexes between Chalcogenadiazoles/Chalcogenatriazoles and Fullerene C60

This version is not peer-reviewed.

Submitted:

06 May 2024

Posted:

06 May 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
The existences of the N→C dative bonds in the complexes between N-containing molecules and fullerenes have been verified both theoretically and experimentally. However, finding stable N→C dative bonds is still a highly challenging task. In this work, we investigated computationally the N→C dative bonds in the complexes formed by fullerene C60 with 1,2,5-chalcogenadiazoles, 2,1,3-benzochalcogenadiazoles and 1,2,4,5-chalcogenatriazoles, respectively. It was found that the N→C dative bonds are formed along with the formation of the N–Ch···C (Ch = S, Se, Te) chalcogen bonds. In the gas phase, from S-containing complexes through Se-containing complexes to Te-containing complexes, the intrinsic interaction energies become more and more negative, which indicates that the N–Ch···C chalcogen bonds can facilitate the formation of the N→C dative bonds. The intrinsic interaction energies are compensated by the large deformation energy of fullerene C60. The total interaction energies of Te-containing complexes are negative, while both of the total interaction energies of S-containing complexes and Se-containing complexes are positive. This means that the N→C dative bonds in the Te-containing complexes are more easily observed in experiments in comparison with those in the S-containing complexes and Se-containing complexes. This study provides a new theoretical perspective on the experimental observation of the N→C dative bonds in the complexes involving fullerenes. Further, the formation of stable N→C dative bonds in the complexes involving fullerenes can significantly change the properties of fullerenes, which will greatly simulate and expand the application range of fullerenes.
Keywords: 
N→C dative bond
;  
chalcogen bond
;  
chalcogenadiazole
;  
fullerene C60
Subject: 
Chemistry and Materials Science  -   Theoretical Chemistry

1. Introduction

The “dative bond” is not a new term. In 1999, the International Union of Pure and Applied Chemistry (IUPAC) defined the dative bond as “the coordination bond formed upon interaction between molecular species one of which serves as a donor and the other as an acceptor of the electron pair to be shared in the complex formed” [1]. Unlike covalent bonds, dative bonds have more significant polarity, weaker strength, and longer bond lengths. The distinctive feature and nature of dative bonds have been reviewed extensively [2,3,4,5]. In a relatively recent review article, Nandi and Kozuch detailed the historical development of dative bonds and provided an outlook on their future advancement [5]. Currently, controversies related to dative bonds have become increasingly rare.
The well-known dative bond is the central bond in ammonia borane (H3N→BH3). Like the case in H3N→BH3, the dative bond is always represented by an arrow from the electron donor to the electron acceptor. There are many different kinds of dative bonds [2,3,4,5]. Fullerenes are of considerable interest due to their unusual structures and peculiar properties [6]. Through combined experimental and theoretical studies, Hobza and coworkers have discovered the existence of N→C dative bonds in the complexes between piperidine and fullerene molecules such as C60 and C70 [7,8,9]. The charge transfer from piperidine to fullerenes significantly changes the properties of fullerenes. Subsequently, it was found by quantum chemical calculations that the N→C dative bonds also exist in the complexes between piperidine and cyclo[n]carbons [10,11]. Further, the P→C dative bonds were computationally found in the complexes involving molecular carbon materials [12,13]. The N→C/P→C dative bonds in these complexes are unstable due to the large deformation energies of molecular carbon materials. This greatly limits the experimental observation and further applications of N→C/P→C dative bonds. It is still a highly challenging task to find stable N→C/P→C dative bonds in the complexes involving important molecular carbon materials.
The N→C dative bond in the 1:1 complex between piperidine and fullerene C60 is not very stable, whereas it is stable in the 2:1 complex between piperidine and fullerene C60 [7]. This is mainly caused by two factors. First, the strong N–H···N hydrogen bond between two piperidine molecules further stabilizes the 2:1 complex. Second, the stability of the N→C dative bond is greatly enhanced by the σ-bond cooperativity with the N–H···N hydrogen bond [14]. Note that the cooperativity is a very common phenomenon between noncovalent bonds of the same or different types [15]. As is well known, besides hydrogen bonds, there are many other types of noncovalent bonds [16,17,18,19,20]. By similar principles, other noncovalent bonds should also enhance the N→C dative bonds in the complexes involving important molecular carbon materials. In this study, we focused on the chalcogen bonds [21,22,23], and explored how and why they can enhance the N→C dative bonds. Fullerene C60 was selected as a model molecule for molecular carbon materials. The small molecules 1,2,5-chalcogenadiazoles, 2,1,3-benzochalcogenadiazoles and 1,2,4,5-chalcogenatriazoles contain both nitrogen atoms and chalcogen atoms. They are ideal model molecules for studying the chalcogen-bond-enhanced N→C dative bonds. This is also one of the reasons why we are studying the influence of chalcogen bonds on the N→C dative bonds first.

2. Materials and Methods

Unless otherwise stated, the structures and properties of all the monomers and complexes were calculated using the PBE0 density functional with Grimme's D3 dispersion correction in conjunction with the def2-TZVPP basis set [24,25,26]. The Becke–Johnson damping function and ultrafine integration grid were used in all PBE0-D3/def2-TZVPP calculations [27]. Our previous publications have shown that the PBE0-D3/def2-TZVPP calculations are reliable for the study of noncovalent systems [7,28,29]. The basis set superposition error was corrected with the conventional counterpoise method [30].
In order to avoid possible computational artifacts, the structures of the complexes without tellurium were fully optimized at the B3LYP-D3/6-31G(d), HF/6-31G(d) and MP2/6-31G(d) levels of theory, respectively, and the structures of the complexes containing tellurium were fully optimized at the B3LYP-D3/SDD, HF/SDD and MP2/SDD levels of theory, respectively. The obtained results are completely consistent with the PBE0-D3/def2-TZVPP calculations. On the other hand, the corresponding frequency calculations were also performed at these theory levels. The results show that the structures of the complexes considered in this study are true minima on their respective potential energy surfaces.
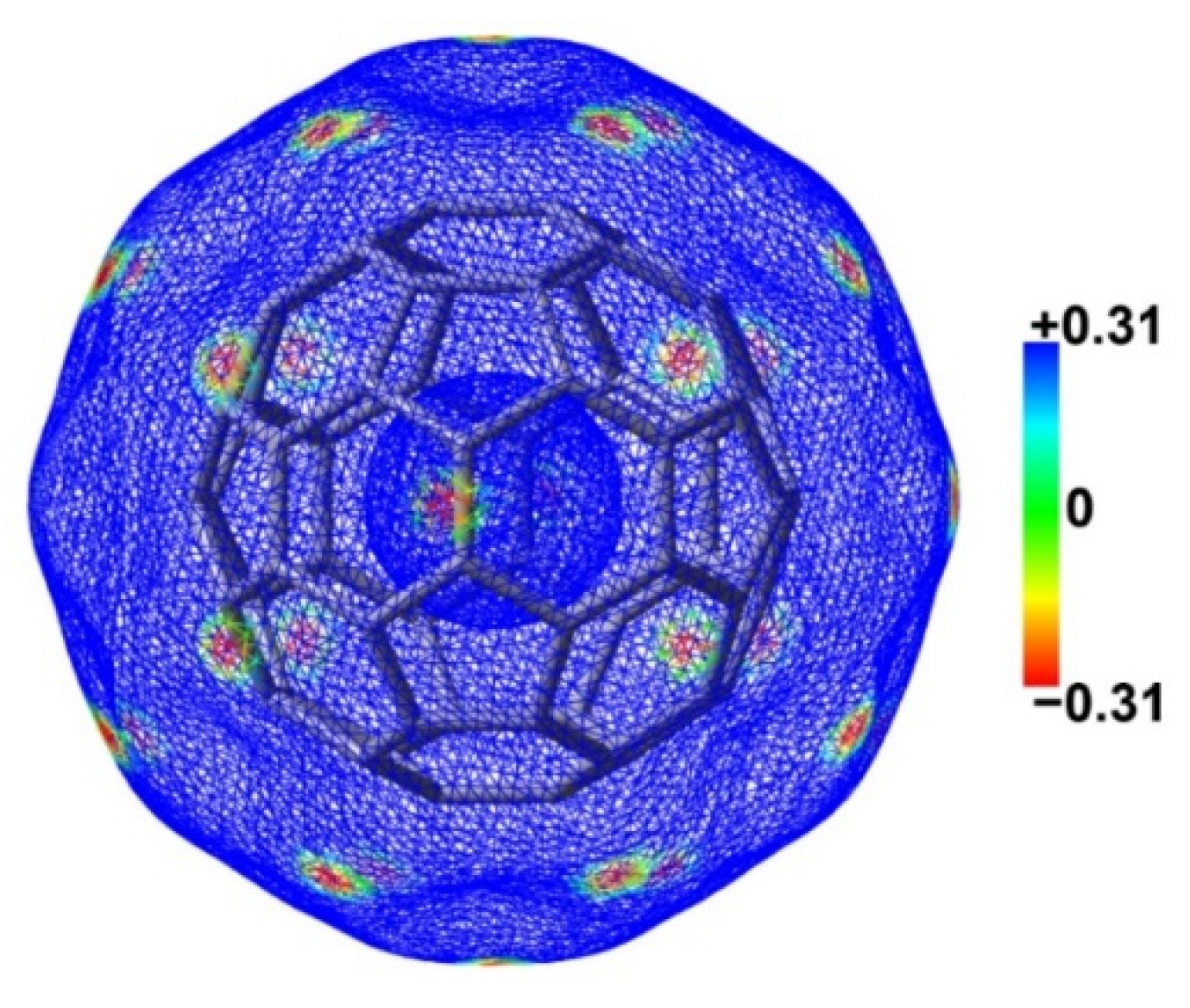
The fullerene C60 has two different types of carbon-carbon bonds: the 6:6 bonds between two hexagons [1.401(10) Å] and the 6:5 bonds between a hexagon and a pentagon [1.458(6) Å] [31]. The 6:6 bonds are shorter than the 6:5 bonds, and are more akin to the nature of double bonds. Figure 1 shows the electrostatic potential mapped electron density surface of fullerene C60. The electrostatic potentials above the 6:6 bonds are more negative than those above 6:5 bonds. The C atoms of fullerene C60 act as the electron donors upon the formation of the N–Ch···C chalcogen bonds. Therefore, only the interactions between 6:6 bonds of fullerene C60 and N–Ch bonds of chalcogenazoles were considered in this study.
The formation of the N–Ch···C chalcogen bonds was analyzed employing Bader’s “atoms in molecules” (AIM) theory [32]. Despite some controversies, the AIM theory remains a very useful tool for analyzing the noncovalent interactions. The AIM analyses were performed with the AIM2000 software [33]. The most positive electrostatic potential of each σ-hole of chalcogen atoms in 1,2,5-chalcogenadiazoles and 2,1,3-benzochalcogenadiazoles was calculated by using the Multiwfn software, version 3.7 [34,35]. Other calculations were carried out with the GAUSSIAN 09 program package [36].

3. Results and Discussion

3.1. Complexes between Chalcogenadiazoles and Fullerene C60

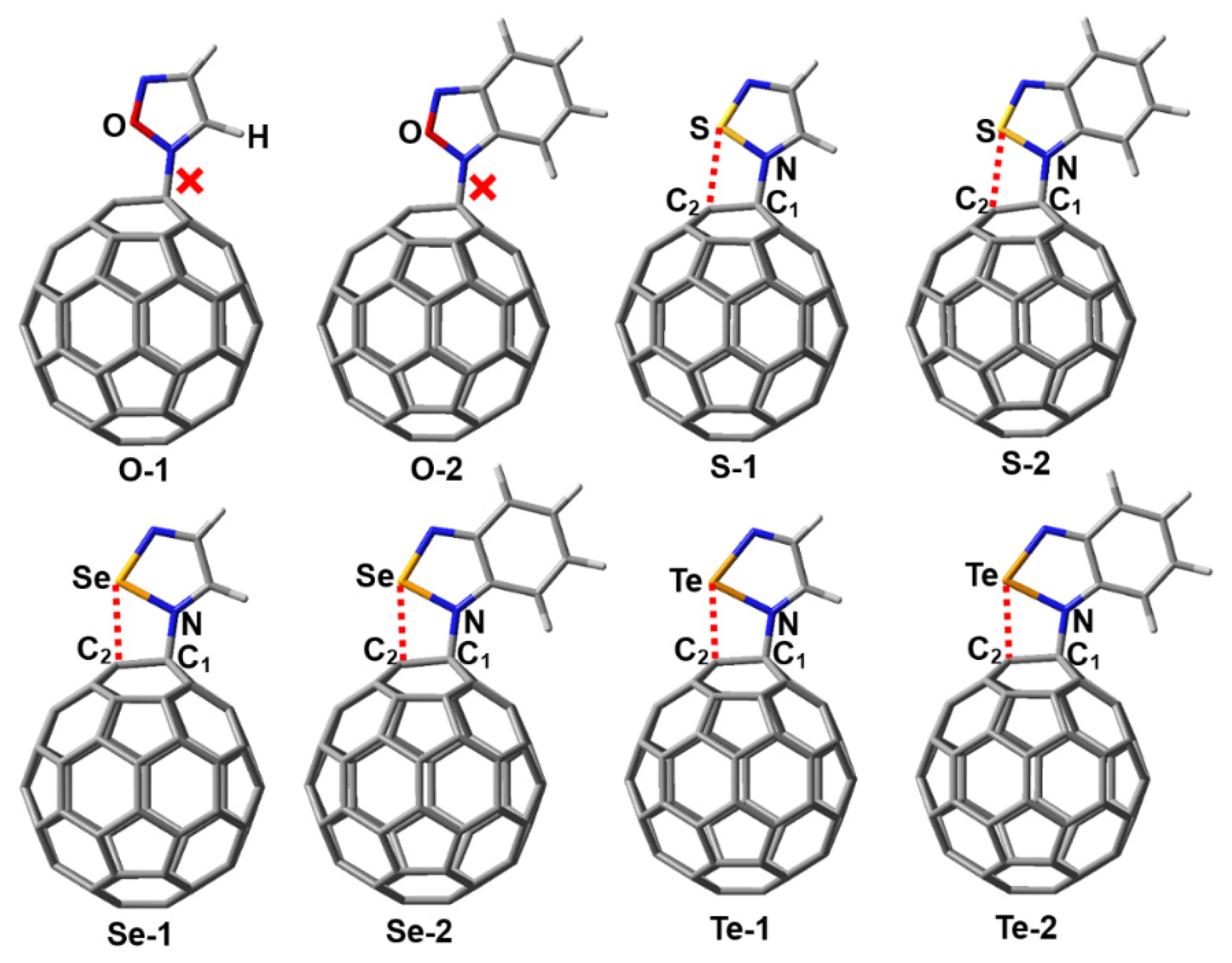
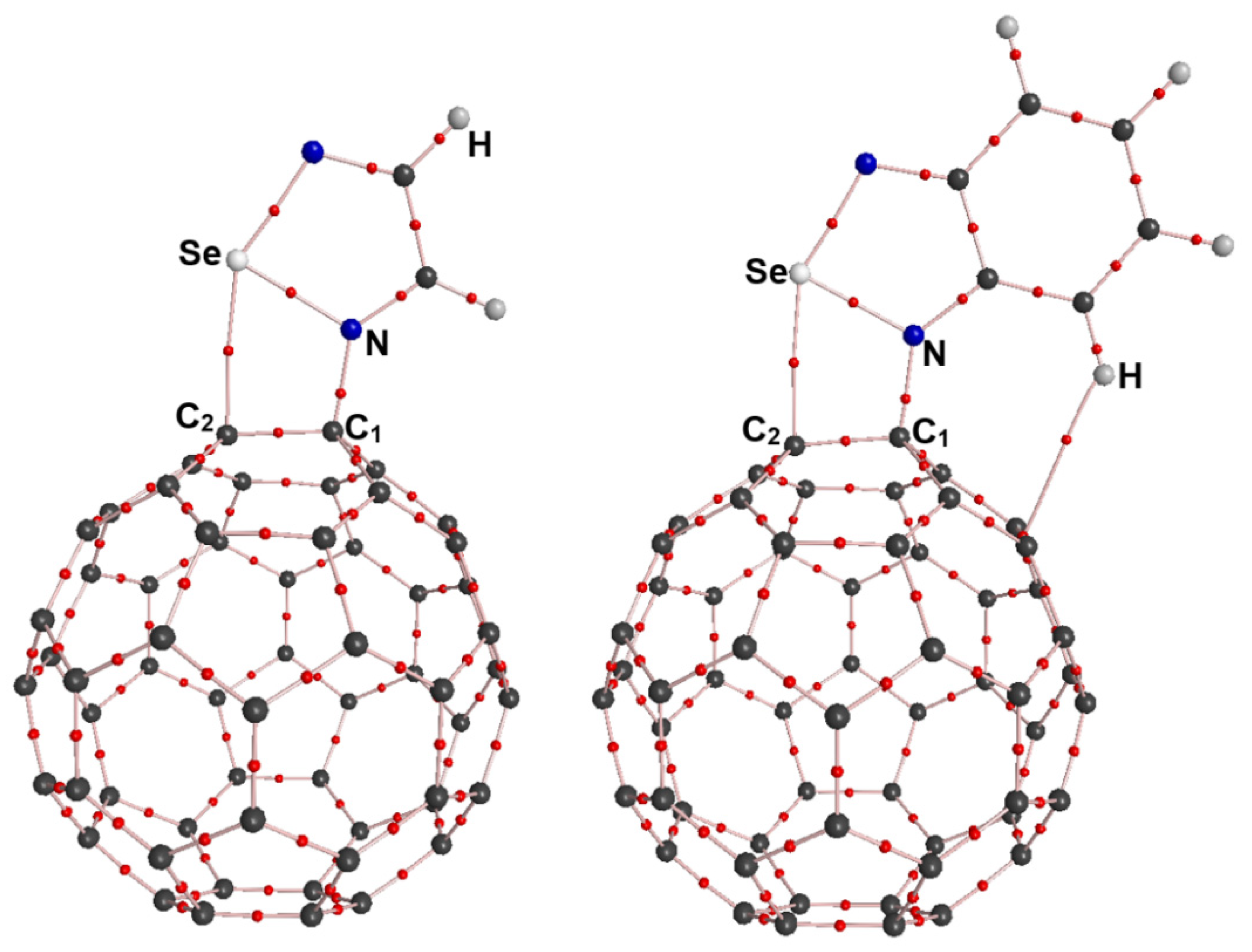
At the outset of the research, we designed a series of complexes containing the N→C dative bonds (Figure 2). After the initial structures of the complexes O-1, O-2, S-1, S-2, Se-1, Se-2, Te-1 and Te-2 were fully optimized at the PBE0-D3/def2-TZVPP level of theory, we found that only the complexes O-1 and O-2 did not exist and instead transformed into corresponding complexes bound by the π···π stacking interactions. It can be clearly seen form Figure 2 that the fullerene C60 molecules undergo significant deformation in the PBE0-D3/def2-TZVPP optimized structures of the complexes S-1, S-2, Se-1, Se-2, Te-1 and Te-2. Table 1 lists the N···C1 and Ch···C2 interatomic distances, intrinsic interaction energies, total interaction energies, total dipole moments and Mulliken charges on N, C1, Ch and C2 for the complexes S-1, S-2, Se-1, Se-2, Te-1 and Te-2.
The van der Waals radii of S, Se, Te and C are 1.80, 1.90, 2.06 and 1.70 Å, respectively [37]. The Ch···C2 interatomic distances in Table 1 are all smaller than the sum of the radii of two interacting atoms, which provides preliminary support for classifying the Ch···C2 interactions as chalcogen bonds. The N···C1 interatomic distances are in the range of 1.466-1.507 Å, which is clearly less than the interatomic distance of 1.606 Å for the N→C dative bond in the complex between piperidine and fullerene C60 [7]. This means that the covalent character of the N→C dative bonds in this study is significantly enhanced. In Table 1, the intrinsic interaction energies and total interaction energies contain the contributions of all the noncovalent interactions because it is difficult to completely separate N→C dative bonds from other noncovalent interactions. From S-containing complexes through Se-containing complexes to Te-containing complexes, the intrinsic interaction energies become more and more negative. It is well known that the strength of a chalcogen bond increases in the order of S < Se < Te. Hence, such a result indicates that the N–Ch···C chalcogen bonds facilitate the formation of the N→C dative bonds. The intrinsic interaction energies are compensated by the large deformation energies of the monomers. Unlike the intrinsic interaction energies, the total interaction energies do not neglect the deformation energies of the monomers. As shown in Table 1, the total interaction energies of Te-containing complexes are negative, while both of the total interaction energies of S-containing complexes and Se-containing complexes are positive. These results indicate that the N→C dative bonds in the Te-containing complexes are more easily observed in experiments in comparison with those in the S-containing complexes and Se-containing complexes.
∆ E I N T R ∆ At the PBE0-D3/def2-TZVPP theory level, the calculated total dipole moments of the monomers are in the range of 0-1.78 Debye. Compared to the monomers, the total dipole moments of the complexes significantly increase. This also conforms to the characteristics of dative bond formation. It is very convenient to employ the Mulliken charge for qualitative estimation of possible changes in electron distribution, although it is often criticized that Mulliken charge is arbitrary and heavily basis set dependent. Table 1 summarizes the Mulliken charges on N, C1, Ch and C2. The Mulliken charges on Ch atoms are all positive and the Mulliken charges on C2 atoms are all negative, which once again demonstrates the formation of chalcogen bonds.

3.2. Molecular Electrostatic Potential Maps of Chalcogenadiazoles

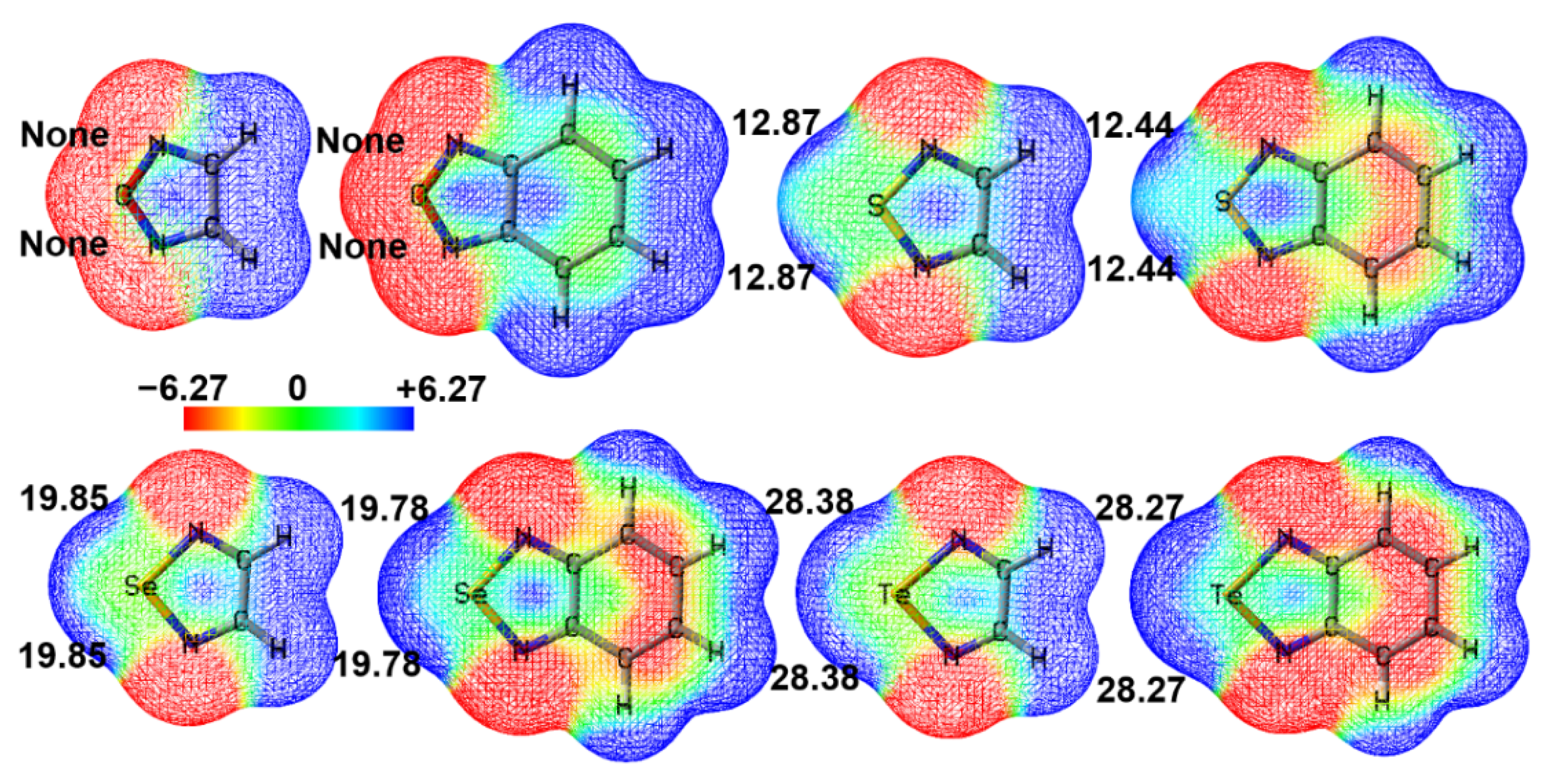
So far, there is still one question left unanswered: why do the complexes O-1 and O-2 in Figure 2 not exist? To address this question, we plotted the electrostatic potential mapped electron density surfaces for 1,2,5-chalcogenadiazoles and 2,1,3-benzochalcogenadiazoles. Figure 3 shows that, except for 1,2,5-oxadiazole and 2,1,3-benzooxadiazole, other chalcogenadiazoles all have two σ-holes on the chalcogen atoms. In 1,2,5-oxadiazole and 2,1,3-benzooxadiazole, the electrostatic potentials on the extensions of the N–O bonds are all negative, which means that the N–O···C chalcogen bonds cannot be formed in the two complexes. When N–O···C chalcogen bonds are absent, N→C dative bonds are also absent; when N–Ch···C (Ch = S, Se, Te) chalcogen bonds are present, N→C dative bonds are also present. Clearly, the formation of chalcogen bonds determines whether N→C dative bonds form or not.
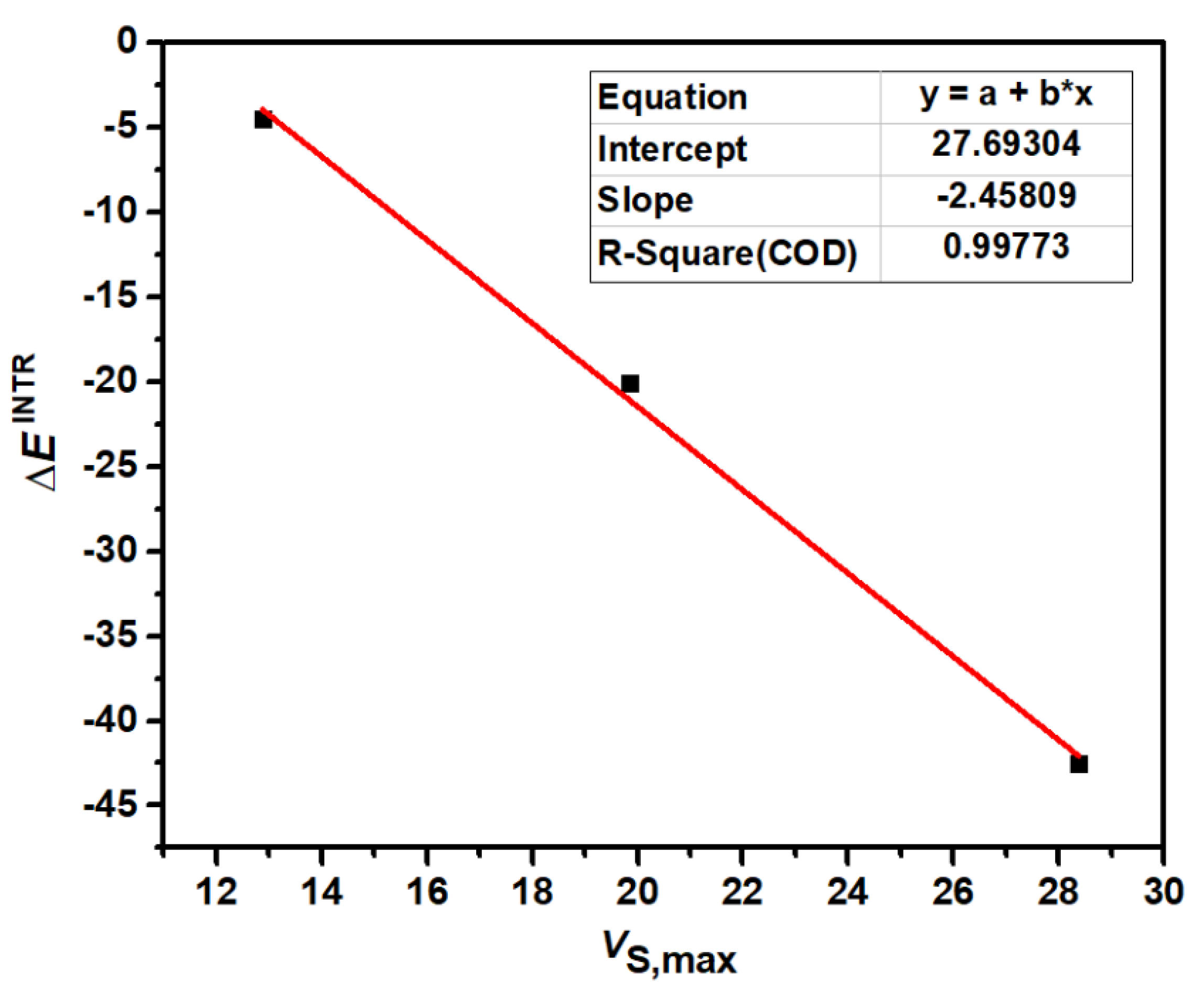
Figure 4 shows the correlation between the most positive electrostatic potentials of σ-holes and the intrinsic interaction energies of S-1, Se-1 and Te-1. We did not generate the correlation figure for S-2, Se-2 and Te-2 because it is very similar to Figure 4 for S-1, Se-1 and Te-1. The correlation coefficient (R-Square) in Figure 4 is close to 1, indicating a very strong correlation between VS,max and ∆EINTR. The value of VS,max determines the strength of a chalcogen bond. At the same time, the more stable the complex, the more stable the N→C dative bond. Once again, it proves that the formation of chalcogen bonds determines the formation of N→C dative bonds.

3.3. AIM Analyses

As can be seen in Figure 2, according to the bonding situation of the nitrogen atom, it can be determined that a N→C dative bond is formed between the nitrogen atom and the carbon atom. In previous studies, the dative bonds with significant covalent bond components were also referred to as "dative/covalent bonds", “covalent/dative bond” or "covalent dative bonds" [8,10,11,38]. Therefore, we will no longer discuss the nature of N→C dative bonds in this section and instead focus on the nature of chalcogen bonds.
The AIM theory was often used to study the nature of the noncovalent bonds [39,40,41,42,43]. Figure 5 shows the bond critical points and bond paths for the complexes Se-1 and Se-2. The molecular graphs of S-1 and Te-1 are almost the same as the one of Se-1, and the molecular graphs of S-2 and Te-2 are almost the same as the one of Se-2. For the sake of clarity, only the bond critical points and bond paths of Se-1 and Se-2 are shown in Figure 5. The electron density, Laplacian of electron density, eigenvalues of the Hessian of electron density and ellipticity at the Ch···C2 bond critical point of each complex are summarized in Table 2.
The bond paths between Ch and C2 and corresponding bond critical points can be clearly seen in the representative Figure 5. This is a necessary condition for the formation of the N–Ch···C2 chalcogen bond. The electron densities at the bond critical points of N–Ch···C2 chalcogen bonds range from 0.0393 to 0.0651 au. In contrast, the electron densities at the bond critical points of hydrogen bonds range from 0.002 to 0.035 au [39,40]. The larger electron density means much stronger noncovalent bond. Here, the N–Ch···C2 chalcogen bonds should belong to strong chalcogen bonds. The Laplacian of electron density is the sum of λ1, λ2 and λ3. According to AIM theory, the Laplacian of electron density is positive at the bond critical point of a noncovalent bond [32]. The values of ▽2ρb in Table 2 are all positive at the Ch···C2 bond critical point of each complex, which proves once again that the Ch···C2 contacts are of chalcogen bonds. The ellipticity ε can be calculated using the formula λ1/(λ2−1), and it can be used to assess the π character and structural stability of a bond. In Table 2, the values of ε are all very small, which indicates that the N–Ch···C2 chalcogen bonds are all very stability. This is consistent with the results of electron densities at the Ch···C2 bond critical points.

3.4. Complexes between Chalcogenatriazoles and Fullerene C60

It is meaningful to expand the complexes studied above to include more complexes. First, the fullerene C60 in the complexes can be replaced by other fullerene molecules or other molecular carbon materials. The results should be very similar. Second, the chalcogenadiazole can be replaced by its derivatives or other similar molecules. Here, we studied the complexes between 1,2,4,5-chalcogenatriazoles and fullerene C60.
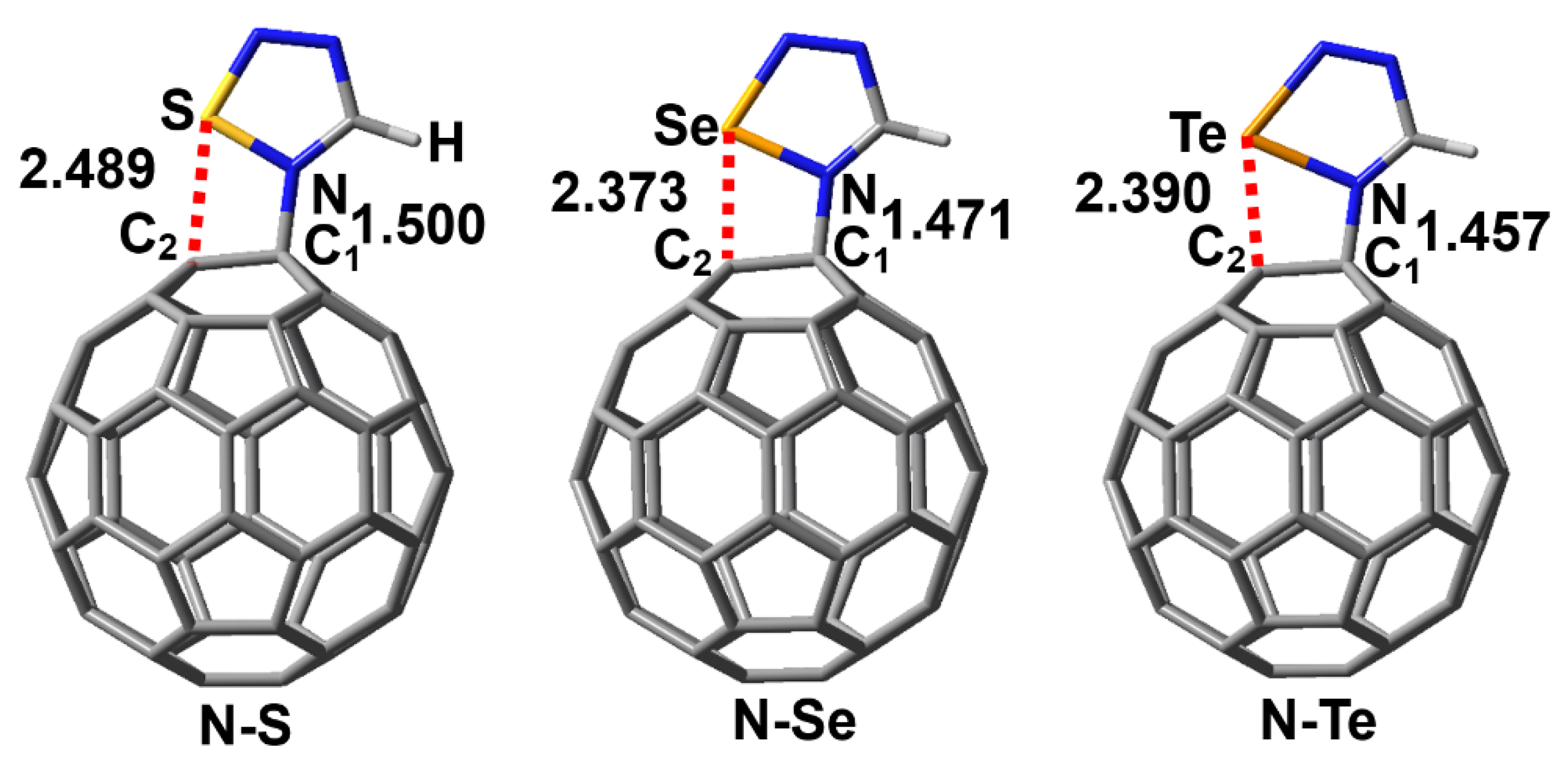
Figure 6 shows the PBE0-D3/def2-TZVPP optimized structures of the complexes N-S, N-Se and N-Te along with the N···C1 and Ch···C2 interatomic distances. Similarly, the Ch···C2 interatomic distances in Figure 6 are all smaller than the sum of the radii of two interacting atoms, which indicates the formation of the N–Ch···C2 chalcogen bonds. At the same time, the bonding situation in the three complexes clearly shows the formation of the N→C dative bonds. The intrinsic interaction energies of the complexes N-S, N-Se and N-Te are −0.11, −18.55 and −43.62 kcal/mol, respectively, whereas the total interaction energies of the complexes N-S, N-Se and N-Te are +27.22, +17.44 and +1.21 kcal/mol, respectively. The positive total interaction energies indicate that these three complexes are difficult to form in the gas phase. In fact, the calculated total interaction energy of the complex between piperidine and fullerene C60 is also positive, but it has been detected by both FTIR spectra and NMR spectroscopy [7]. As pointed out above, the influence of the chemical environment around the complexes is also very important and must be considered during the experimental process. Besides the 1,2,4,5-chalcogenatriazoles, we believe that there should be many similar nitrogen-containing organic compounds that can form stable chalcogen-bond-assisted N→C dative bonds with molecular carbon materials.

4. Conclusions

The N→C dative bonds in the complexes between chalcogenadiazoles and fullerene C60 have been investigated by employing the quantum chemical calculations. The research scope has been further expanded to the complexes between 1,2,4,5-chalcogenatriazoles and fullerene C60. The results clearly show that the N–Ch···C chalcogen bonds facilitate the formation of the N→C dative bonds in these complexes. From S-containing complexes through Se-containing complexes to Te-containing complexes, the complexes become increasingly stable as the N–Ch···C chalcogen bonds become stronger. Attractive N→C dative bonds and N–Ch···C chalcogen bonds together can overcome the significant repulsive deformation energy of fullerene C60. We therefore predict that the N→C dative bonds in the complexes between Te-containing molecules and fullerenes should be more easily observed experimentally and further applied. Indeed, following this line of thought, more stable complexes bound by the N→C dative bonds can be designed and synthesized. The formation of stable N→C dative bonds in the complexes containing fullerenes can significantly change the properties of fullerenes. Such a molecular modification strategy will greatly simulate and expand the application range of fullerenes.
In this study, we only focused on the chalcogen-bond-assisted N→C dative bonds. Naturally, the other noncovalent bonds such as halogen bonds, pnictogen bonds, tetrel bonds, etc. can also facilitate the N→C/P→C dative bonds in the complexes involving important molecular carbon materials. The relevant research is currently ongoing in our laboratory. On the other hand, all the calculations in this study were performed in the gas phase. It must be pointed out that the chalcogen-bond-assisted N→C dative bonds may be more stable in certain solvents. The solvation effect is also one of our future research focuses.

Author Contributions

Y.Z. performed all the calculations; W.W. designed and supervised this project; Y.Z. and W.W. wrote and revised the paper. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Natural Science Foundation of Henan Province of China, grant number 232300421147.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data is contained within the article.

Acknowledgments

We thank the Natural Science Foundation of Henan Province of China for the financial support. W.W. thanks the National Supercomputing Center in Shenzhen for the computational support.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Minkin, V.I. Glossary of Terms Used in Theoretical Organic Chemistry (IUPAC Recommendations 1999). Pure Appl. Chem. 1999, 71, 1919–1981. [Google Scholar] [CrossRef]
  2. Haaland, A. Covalent versus Dative Bonds to Main Group Metals, a Useful Distinction. Angew. Chem. Int. Ed. Engl. 1989, 28, 992–1007. [Google Scholar] [CrossRef]
  3. Lepetit, C.; Maraval, V.; Canac, Y.; Chauvin, R. On the Nature of the Dative Bond: Coordination to Metals and Beyond. The Carbon Case. Coord. Chem. Rev. 2016, 308, 59–75. [Google Scholar] [CrossRef]
  4. Zhao, L.; Hermann, M.; Holzmann, N.; Frenking, G. Dative Bonding in Main Group Compounds. Coord. Chem. Rev. 2017, 344, 163–204. [Google Scholar] [CrossRef]
  5. Nandi, A.; Kozuch, S. History and Future of Dative Bonds. Chem. Eur. J. 2020, 26, 759–772. [Google Scholar] [CrossRef]
  6. Hirsch, A. The Chemistry of the Fullerenes; WILEY-VCH Verlag GmbH &, Co. KGaA: Weinheim, Germany, 2008.
  7. Lamanec, M.; Lo, R.; Nachtigallová, D.; Bakandritsos, A.; Mohammadi, E.; Dračínský, M.; Zbořil, R.; Hobza, P.; Wang, W. The Existence of a N→C Dative Bond in the C60–Piperidine Complex. Angew. Chem. Int. Ed. 2021, 60, 1942–1950. [Google Scholar] [CrossRef] [PubMed]
  8. Lo, R.; Lamanec, M.; Wang, W.; Manna, D.; Bakandritsos, A.; Dračínský, M.; Zbořil, R.; Nachtigallová, D.; Hobza, P. Structure-Directed Formation of the Dative/Covalent Bonds in Complexes with C70···Piperidine. Phys. Chem. Chem. Phys. 2021, 23, 4365–4375. [Google Scholar] [CrossRef]
  9. Lo, R.; Manna, D.; Lamanec, M.; Wang, W.; Bakandritsos, A.; Dračínský, M.; Zbořil, R.; Nachtigallová, D.; Hobza, P. Addition Reaction between Piperidine and C60 to Form 1,4- Disubstituted C60 Proceeds through van der Waals and Dative Bond Complexes: Theoretical and Experimental Study. J. Am. Chem. Soc. 2021, 143, 10930–10939. [Google Scholar] [CrossRef]
  10. Lo, R.; Manna, D.; Hobza, P. Cyclo[n]carbons Form Strong N→C Dative/Covalent Bonds with Piperidine. J. Phys. Chem. A 2021, 125, 2923–2931. [Google Scholar] [CrossRef]
  11. Nandi, A.; Martin, J.M.L. Heavy-Atom Tunneling in the Covalent/Dative Bond Complexation of Cyclo[18]carbon–Piperidine. J. Phys. Chem. B 2022, 126, 1799–1804. [Google Scholar] [CrossRef]
  12. Lo, R.; Manna, D.; Hobza, P. Tuning the P–C Dative/Covalent Bond Formation in R3P–C60 Complexes by Changing the R Group. Chem. Commun. 2021, 57, 3363–3366. [Google Scholar] [CrossRef] [PubMed]
  13. Lo, R.; Manna, D.; Hobza, P. P-Doped Graphene–C60 Nanocomposite: A Donor–Acceptor Complex with a P–C Dative Bond. Chem. Commun. 2022, 58, 1045–1048. [Google Scholar] [CrossRef]
  14. Steiner, T. The Hydrogen Bond in the Solid State. Angew. Chem. Int. Ed. 2002, 41, 48–76. [Google Scholar] [CrossRef]
  15. Riel, A.M.S.; Rowe, R.K.; Ho, E.N.; Carlsson, A.-C.C.; Rappé, A.K.; Berryman, O.B.; Ho, S.P. Hydrogen Bond Enhanced Halogen Bonds: A Synergistic Interaction in Chemistry and Biochemistry. Acc. Chem. Res. 2019, 52, 2870–2880. [Google Scholar] [CrossRef] [PubMed]
  16. Scheiner, S. The Pnicogen Bond: Its Relation to Hydrogen, Halogen, and Other Noncovalent Bonds. Acc. Chem. Res. 2013, 46, 280–288. [Google Scholar] [CrossRef] [PubMed]
  17. Fanfrlík, J.; Holub, J.; Růžičková, Z.; Řezáč, J.; Lane, P.D.; Wann, D.A.; Hnyk, D.; Růžička, A.; Hobza, P. Competition between Halogen, Hydrogen and Dihydrogen Bonding in Brominated Carboranes. ChemPhysChem 2016, 17, 3373–3376. [Google Scholar] [CrossRef] [PubMed]
  18. Brammer, L. Halogen Bonding, Chalcogen Bonding, Pnictogen Bonding, Tetrel Bonding: Origins, Current Status and Discussion. Faraday Discuss. 2017, 203, 485–507. [Google Scholar] [CrossRef] [PubMed]
  19. Alkorta, I.; Elguero, J.; Frontera, A. Not Only Hydrogen Bonds: Other Noncovalent Interactions. Crystals 2020, 10, 180. [Google Scholar] [CrossRef]
  20. Zierkiewicz, W.; Michalczyk, M.; Scheiner, S. Noncovalent Bonds through Sigma and Pi-Hole Located on the Same Molecule. Guiding Principles and Comparisons. Molecules 2021, 26, 1740. [Google Scholar] [CrossRef]
  21. Wang, W.; Ji, B.; Zhang, Y. Chalcogen Bond: A Sister Noncovalent Bond to Halogen Bond. J. Phys. Chem. A 2009, 113, 8132–8135. [Google Scholar] [CrossRef]
  22. Aakeroy, C.B.; Bryce, D.L.; Desiraju, G.R.; Frontera, A.; Legon, A.C.; Nicotra, F.; Rissanen, K.; Scheiner, S.; Terraneo, G.; Metrangolo, P.; et al. Definition of the Chalcogen Bond. Pure Appl. Chem. 2019, 91, 1889–1892. [Google Scholar] [CrossRef]
  23. Kolb, S.; Oliver, G.A.; Werz, D.B. Chemistry Evolves, Terms Evolve, but Phenomena Do Not Evolve: From Chalcogen–Chalcogen Interactions to Chalcogen Bonding. Angew. Chem. Int. Ed. 2020, 59, 22306–22310. [Google Scholar] [CrossRef] [PubMed]
  24. Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6169. [Google Scholar] [CrossRef]
  25. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
  26. Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
  27. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  28. Wang, W.; Sun, T.; Zhang, Y.; Wang, Y.B. The Benzene···Naphthalene Complex: A more Challenging System than the Benzene Dimer for newly Developed Computational Methods. J. Chem. Phys. 2015, 143, 114312. [Google Scholar] [CrossRef] [PubMed]
  29. Wang, W.; Zhang, Y.; Wang, Y.B. Highly Accurate Benchmark Calculations of the Interaction Energies in the Complexes C6H6···C6X6 (X = F, Cl, Br, and I). Int. J. Quantum Chem. 2017, 117, e25345. [Google Scholar] [CrossRef]
  30. Boys, S.F.; Bernardi, F. The Calculation of Small Molecular Interactions by the Difference of Separate Total Energies. Some Procedures with Reduced Errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
  31. Hedberg, K.; Hedberg, L.; Bethune, D.S.; Brown, C.A.; Dorn, H.C.; Johnson, R.D.; De Vries, M. Bond Lengths in Free Molecules of Buckminsterfullerene, C60, from Gas-Phase Electron Diffraction. Science 1991, 254, 410–412. [Google Scholar] [CrossRef]
  32. Bader, R.F.W. Atoms in Molecules−A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
  33. Biegler-König, F.; Schönbohm, J.; Bayles, D. AIM2000-A Program to Analyze and Visualize Atoms in Molecules. J. Comput. Chem. 2001, 22, 545–559. [Google Scholar]
  34. Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
  35. Lu, T.; Chen, F. Quantitative Analysis of Molecular Surface Based on Improved Marching Tetrahedra Algorithm. J. Mol. Graph. Model. 2012, 38, 314–323. [Google Scholar] [CrossRef]
  36. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
  37. Bondi, A. van der Waals Volumes and Radii. J. Phys. Chem. A 1964, 68, 441–451. [Google Scholar] [CrossRef]
  38. Lo, R.; Manna, D.; Miriyala, V.M.; Nachtigallová, D.; Hobza, P. Trends in the Stability of Covalent Dative Bonds with Variable Solvent Polarity Depend on the Charge Transfer in the Lewis Electron-Pair System. Phys. Chem. Chem. Phys. 2023, 25, 25961–25964. [Google Scholar] [CrossRef] [PubMed]
  39. Koch, U.; Popelier, P.L.A. Characterization of C–H–O Hydrogen Bonds on the Basis of the Charge Density. J. Phys. Chem. 1995, 99, 9747–9754. [Google Scholar] [CrossRef]
  40. Popelier, P.L.A. Characterization of a Dihydrogen Bond on the Basis of the Electron Density. J. Phys. Chem. A 1998, 102, 1873–1878. [Google Scholar] [CrossRef]
  41. Wang, W.; Wong, N.-B.; Zheng, W.; Tian, A. Theoretical Study on the Blueshifting Halogen Bond. J. Phys. Chem. A 2004, 108, 1799–1805. [Google Scholar] [CrossRef]
  42. Zeng, Y.; Zhang, X.; Li, X.; Zheng, S.; Meng, L. Ab Initio and AIM Studies on Typical π-Type and Pseudo-π-Type Halogen Bonds: Comparison with Hydrogen Bonds. Int. J. Quantum Chem. 2011, 111, 3725–3740. [Google Scholar] [CrossRef]
  43. Grabowski, S.J. QTAIM Characteristics of Halogen Bond and Related Interactions. J. Phys. Chem. A 2012, 116, 1838–1845. [Google Scholar] [CrossRef]
Preprints 105681 g001
Figure 1. The electrostatic potential mapped electron density surface (isoval = 0.001 au) of fullerene C60. The colour bar is in kcal/mol.
Figure 1. The electrostatic potential mapped electron density surface (isoval = 0.001 au) of fullerene C60. The colour bar is in kcal/mol.
Preprints 105681 g001
Preprints 105681 g002
Figure 2. PBE0-D3/def2-TZVPP optimized structures of the complexes S-1, S-2, Se-1, Se-2, Te-1 and Te-2. The red dashed line indicates the possibility of a chalcogen bond.
Figure 2. PBE0-D3/def2-TZVPP optimized structures of the complexes S-1, S-2, Se-1, Se-2, Te-1 and Te-2. The red dashed line indicates the possibility of a chalcogen bond.
Preprints 105681 g002
Preprints 105681 g003
Figure 3. The electrostatic potential mapped electron density surfaces (isoval = 0.001 au) of 1,2,5-chalcogenadiazoles and 2,1,3-benzochalcogenadiazoles. The most positive electrostatic potential of each σ-hole (VS,max) is also shown. The electrostatic potentials are given in kcal/mol.
Figure 3. The electrostatic potential mapped electron density surfaces (isoval = 0.001 au) of 1,2,5-chalcogenadiazoles and 2,1,3-benzochalcogenadiazoles. The most positive electrostatic potential of each σ-hole (VS,max) is also shown. The electrostatic potentials are given in kcal/mol.
Preprints 105681 g003
Preprints 105681 g004
Figure 4. The correlation between VS,max (kcal/mol) of 1,2,5-chalcogenadiazoles and ∆EINTR (kcal/mol) of S-1, Se-1 and Te-1.
Figure 4. The correlation between VS,max (kcal/mol) of 1,2,5-chalcogenadiazoles and ∆EINTR (kcal/mol) of S-1, Se-1 and Te-1.
Preprints 105681 g004
Preprints 105681 g005
Figure 5. The bond critical points (small red dots) and bond paths of the complexes Se-1 and Se-2.
Figure 5. The bond critical points (small red dots) and bond paths of the complexes Se-1 and Se-2.
Preprints 105681 g005
Preprints 105681 g006
Figure 6. PBE0-D3/def2-TZVPP optimized structures of the complexes N-S, N-Se and N-Te. The red dashed lines represent the chalcogen bonds. The numbers shown are the interatomic distances (Å).
Figure 6. PBE0-D3/def2-TZVPP optimized structures of the complexes N-S, N-Se and N-Te. The red dashed lines represent the chalcogen bonds. The numbers shown are the interatomic distances (Å).
Preprints 105681 g006
Table 1. The N···C1 and Ch···C2 interatomic distances (d, Å), intrinsic interaction energies (∆EINTR, kcal/mol), total interaction energies (∆E, kcal/mol), total dipole moments (µ, Debye) and Mulliken charges (q, e) on N, C1, Ch and C2 of the complexes studied.
Table 1. The N···C1 and Ch···C2 interatomic distances (d, Å), intrinsic interaction energies (∆EINTR, kcal/mol), total interaction energies (∆E, kcal/mol), total dipole moments (µ, Debye) and Mulliken charges (q, e) on N, C1, Ch and C2 of the complexes studied.
Complex d(N···C1) d(Ch···C2) ∆ E I N T R ∆ E µ q(N) q(C1) q(Ch) q(C2)
S-1 1.504 2.569 −4.52 20.85 8.14 0.081 1.121 0.351 −0.507
S-2 1.500 2.557 −8.75 18.13 10.18 0.090 1.153 0.381 −0.545
Se-1 1.480 2.467 −20.05 11.40 5.60 0.007 0.923 0.341 −0.221
Se-2 1.478 2.468 −24.04 8.35 7.59 −0.004 0.952 0.383 −0.241
Te-1 1.467 2.471 −42.54 −4.11 3.39 −0.142 1.019 0.443 −0.245
Te-2 1.466 2.464 −46.88 −7.32 4.92 −0.150 1.043 0.497 −0.245
Table 2. The electron density (ρb), Laplacian of electron density (▽2ρb), eigenvalues of the Hessian of electron density (λ1, λ2, λ3) and ellipticity (ε) at the Ch···C2 bond critical point of each complex. All the values are given in atomic units.
Table 2. The electron density (ρb), Laplacian of electron density (▽2ρb), eigenvalues of the Hessian of electron density (λ1, λ2, λ3) and ellipticity (ε) at the Ch···C2 bond critical point of each complex. All the values are given in atomic units.
Complex ρb ▽2ρb λ1 λ2 λ3 ε
S-1 0.0393 0.0659 −0.0336 −0.0257 0.1253 0.3091
S-2 0.0398 0.0683 −0.0345 −0.0259 0.1287 0.3305
Se-1 0.0550 0.0493 −0.0509 −0.0491 0.1493 0.0370
Se-2 0.0544 0.0517 −0.0495 −0.0489 0.1502 0.0136
Te-1 0.0645 0.0302 −0.0618 −0.0544 0.1464 0.1355
Te-2 0.0651 0.0313 −0.0623 −0.0559 0.1496 0.1138
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

71

Views

39

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated