Partition Entropy as a Measure of Regularity of Music Scales

Preprint

Article

Partition Entropy as a Measure of Regularity of Music Scales

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Rafael Cubarsi^*

This version is not peer-reviewed

Submitted:

17 April 2024

Posted:

18 April 2024

You are already at the latest version

Alerts

Abstract

The entropy of the partition generated by an n-tone music scale is proposed to quantify its regularity. The normalized entropy relative to a regular partition, and its complementary, here referred to as the bias, allow to analyze various conditions of similarity between an arbitrary scale and a regular scale. Interesting particular cases are scales having limited bias because their tones are distributed along interval fractions of a regular partition. The most typical case in music concerns partitions associated with well-formed scales generated by a single tone h. These scales are maximal even sets that combine two elementary intervals. Then, the normalized entropy depends on the number of tones as well as the relative size of both elementary intervals. When well-formed scales are refined, several nested families stand out with increasing regularity. It is proven that a scale of minimal bias, i.e. with less bias than those with fewer tones, is always a best rational approximation of log2h.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

An n-tone music scale determines a partition of the octave in n intervals. Regarding their regularity, scales can be of equal divisions of the octave, i.e., with n tones of equal temperament (n-TET scale), where discretization precision increases as the number of tones grows, or of different divisions, where precision increases in two ways, on the one hand, as the size of the intervals decreases and, on the other hand, as its regularity increases. In particular, well-formed scales of one generator, hereinafter referred to as cyclic scales, if they are non-degenerate (of equal temperament) are formed from two elementary intervals [1,2], one longer than the interval of an n-TET scale and the other of shorter width. These scales also fulfill the condition of maximum evenness [3,4], that is, they present the most even distribution, which does not depend on the relative size of the intervals. In many cases, as increasing the number of tones of a cyclic scale, the regularity of the intervals decreases, still satisfying the condition of maximal even set. Therefore, for cyclic scales it is not obvious how to quantify precision and regularity of the partition as increasing the number of tones. The present work has the purpose of analyzing it, as well as studying the bias from regular temperament in more general cases.

The regularity of the intervals of an n-tone scale

E_{n}

can be quantified in several ways. A fairly common way is from their standard deviation. In the octave, the intervals

A_{i}

i \in I = {1, \dots, n}

, between consecutive tones, considered as a discrete random variable of equal probability such that

\sum_{i \in I} A_{i} = 1

, have expected value

t = \frac{1}{n}

, which is the size of the elementary interval of the n-TET scale. A measure of dispersion of these values about the mean is the standard deviation

σ

, defined from its square, the variance, as

σ^{2} = \frac{1}{n} \sum_{i \in I} {(A_{i} - t)}^{2}

. In this way it is possible to compare different n-tone scales in terms of the average dispersion of their intervals relatively to the n-TET scale. However, this procedure does not present interesting properties to deal, for instance, with successive refinements of cyclic scales.

Another way to measure the regularity of

E_{n}

may be based on the quadratic sum of its intervals. We consider it in a more general way. Let us assume that

(M, μ)

is a Lebesgue-measurable space such that

μ (M) = 1

, and

α = {A_{i}}_{i \in I}

is a finite measurable partition of

M

, that is1,

μ (\cup_{i \in I} A_{i}) = 1

and

μ (A_{i} \cap A_{j}) = 0

i \neq j

. Then, the sum of squares for the partition

α

relative to the measure

μ

S (α) = \sum_{i \in I} μ {(A_{i})}^{2}

. The function

S (α)

is a convex function of

μ (A_{i})

, which constrained to

\sum_{i \in I} μ (A_{i}) = 1

has an absolute minimum for

μ (A_{i}) = \frac{1}{n}

\forall i

. In this case,

S (α) = \frac{1}{n}

is a decreasing function of n. When the partition is refined, that is, if

β = {B_{j}}_{j \in J}

is another partition of the octave, then its sum

α \lor β = {A_{i} \cap B_{j}}_{i \in I, j \in J}

is a refinement of them, in order to make successive refinements it would be desirable to be able to express

S (α \lor β) = S (α) + F (α, β)

, with a function F that is a linear combination of squares of

μ (A_{i} \cap B_{j})

, i.e., also a sum of squares of the refinement. But this is not so, because in F it will necessarily appear cross products.

Fortunately, the notions of regularity and fineness of a partition have in several fields a well-known way of being quantified, which is the partition entropy. The concept of entropy was introduced by Clasius in thermodynamics (in 1850), Boltzmann applied it to statistical mechanics (1877), Planck related it to probability theory (1906), Shannon applied it to information theory (1948), Jaynes used it as a measure of uncertainty (1957), and Kolmogorov extended it to deterministic systems (1958).

Certainly, entropy has been used in music almost from the beginning of information theory [5,6,7] by considering the musical language as a source that produces a sequence of symbols representing musical tones and by associating them with certain probabilities according to their frequency of appearance. In particular, a wide range of works have used entropy to identify music styles, e.g., [8,9,10,11] although results may vary depending on the preanalytical assumptions made in order to treat the data (scale degrees, pitch class, octave equivalence, weighting by duration, key-signature dependency, modal bias, etc.). With the same purpose, cross-entropy, e.g., [12] has been used to quantify stylistic similarity between two sequences [13]. An up-to-date review on entropy and other physical parameters applied to music is provided by Gündüz [14].

Nevertheless, it seems that entropy as a measure of regularity of music scales has been neglected. Therefore, in the current paper it is proposed to use the normalized entropy as a measure of their regularity. Its application is illustrated in two cases. On one hand to study the similarity between an arbitrary scale and an n-TET scale. On the other hand, to study the regularity of cyclic scales generated by a tone h and the relationship between their bias and the rational approximation of

{log}_{2} h

they provide.

2. Partition Entropy

Following the notation and terminology of Arnold and Avez [15], the entropy of the partition2

α

is defined from a concave function

z (t)

as follows,

H (α) = \sum_{i \in I} z (μ (A_{i})); z (t) = \{\begin{matrix} - t {log}_{2} t, 0 < t \leq 1 \\ 0, t = 0 \end{matrix}

(1)

It is fulfilled3,

H (α) = n \frac{1}{n} \sum_{i} z (μ (A_{i})) \leq n z (\frac{1}{n} \sum_{i} μ (A_{i})) = n z (\frac{1}{n}) = {log}_{2} n

Therefore, for a partition of n elements, the value

{log}_{2} n

is the maximum value that the entropy can reach, and it is reached when the elements of the partition are of equal measure.

Thus,

\sum_{i} z (μ (A_{i})) = \sum_{i} μ (A_{i}) {log}_{2} \frac{1}{μ (A_{i})}

is the weighted average of the values

{log}_{2} \frac{1}{μ (A_{i})}

(what in probabilities would be the information associated with the value of the random variable

A_{i}

, i.e., the expected value of the information content or self-information of the variable

A_{i}

). The smaller

μ (A_{i})

, the greater is the above logarithm, so this average gives an idea of how much refined the partition is.

Shannon (1948) showed that the entropy defined in this way is the only function that, except for a multiplicative constant, satisfies the following postulates:

1.: $H (α)$ is a continuous function of $μ (A_{i})$ .
2.: If $μ (A_{1}) = \dots = μ (A_{n}) = \frac{1}{n}$ , then $H (α)$ is an increasing function of n.
3.: Let’s consider partitions $α = {A_{i}}_{i \in I}$ , $β = {B_{j}}_{j \in J}$ and a refinement of both $α \lor β = {A_{i} \cap B_{j}}_{i \in I, j \in J}$ . The conditional entropy of $α$ relative to $β$ is defined as

$H (α / β) = \sum_{j} μ (B_{j}) \sum_{i} z (μ (A_{i} / B_{j})) \equiv \sum_{j} μ (B_{j}) \sum_{i} z (\frac{μ (A_{i} \cap B_{j})}{μ (B_{j})})$

(2)

where $μ (A_{i} / B_{j})$ is the conditional measure of $A_{i}$ relative to $B_{j}$ . Then, the following specific property of entropy (sub-additivity)4 holds,

$H (α \lor β) = H (α) + H (β / α) \leq H (α) + H (β)$

(3)
4.: If $φ$ is an automorfism of $(M, μ)$ and $α = {A_{i}}_{i \in I}$ , $φ α = {φ A_{i}}_{i \in I}$ are both partitions, then $φ (α \lor β) = φ α \lor φ β$ and $H (α / β) = H (φ α / φ β)$ .

Therefore, the partition entropy seems an appropriate parameter to measure how much a scale of n arbitrary tones differs from an n-TET scale. It is also the parameter that provides us with an estimate of how refined a scale is, because the entropy of a scale of n tones will always be greater than that of a subscale of

n - 1

tones, and less than or equal to that of an n-TET scale. This will be useful when dealing with cyclic scales. In addition, as the intervals of a partition are subdivided, the entropy is additive with regard to the intervals being refined, which saves calculations.

3. Cyclic Scales

Computation of entropy for cyclic scales requires a brief review of their properties, which hereinafter are summarized by following Cubarsi [16], Cubarsi [17].

For any frequency ratio

ν \in Ω \equiv (0, \infty)

, the values

2^{k} ν

k \in Z

, define one equivalence class. A ratio of 2 between values corresponds to the frequency range of one octave. The set

Ω

is a commutative group for multiplication. The set of all the octaves of the fundamental frequency ratio (

ν_{0} = 1

) is a monogenous subgroup of

Ω

of infinite cardinal,

Ω^{2} = {2^{k}, k \in Z}

. The frequency classes are the elements of the quotient group

Ω_{0} = Ω / Ω^{2}

, also commutative for multiplication. For each equivalence class, we choose a representative in

[1, 2)

, the reference octave, which we identify with

Ω_{0}

. A finite set of these representatives will be referred to as scale tones.

An n-tone cyclic scale

E_{n}^{h}

is a scale of one generator, a real positive value h, which satisfy the symmetry condition, consisting of displaying several degrees of rotational symmetry that are equivalent to the closure condition [18,19,20], although such an equivalence does not hold for scales with more than two generators [21,22]. The partition of the octave induced by the scale notes has exactly two sizes of scale steps, and each number of generic intervals occurs in two different sizes, which is known as Myhill’s property [1,2]. For

h = 3

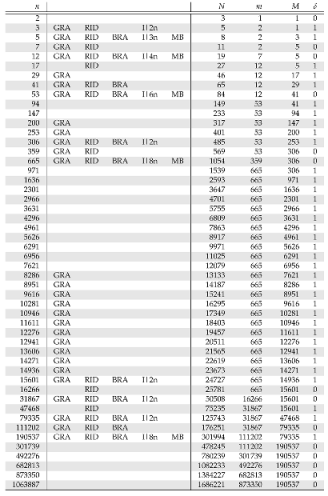
we meet the particular case of the 12-tone Pythagorean scale, generated by fifths, as well as those listed in Table 1, and for h other than a rational power of 2 (which would lead to degenerate cases of equal temperament scales) we get generalized Pythagorean scales.

The scale tones are

ν_{k} = \frac{h^{k}}{2^{〚 k 〛}}

;

k = 0, \dots, n - 1

; with

〚 k 〛 = ⌊ k {log}_{2} h ⌋

(floor function). When the scale tones are ordered clockwise direction from lowest to highest pitch in

[1, 2)

(say, in cyclic order) we find two extreme tones, the minimum tone

ν_{m}

and the maximum tone

ν_{M}

, which determine the two elementary factors

U = ν_{m} = \frac{h^{m}}{2^{〚 m 〛}}

(up the fundamental) and

D = \frac{2}{ν_{M}} = \frac{2^{〚 M 〛 + 1}}{h^{M}}

(down the fundamental) associated with the generic widths of the step interval, so that

U^{M} D^{m} = 2

. The indices satisfy

n = m + M

, all of them coprime.

The tone

ν_{n} = \frac{h^{n}}{2^{〚 n 〛}}

, which does not belong to the scale

E_{n}^{h}

, provides the closure condition (either

ν_{n} \to 1^{+}

ν_{n} \to 2^{-}

) determining the n-order comma

κ_{n} = min (ν_{n}, \frac{2}{ν_{n}})

(in the frequency space), i.e., the error in closing the scale near the fundamental, with no other scale notes between them. The comma itself does not provide information about whether

ν_{n}

closes above or below the fundamental. By using the index

N = 〚 m 〛 + 〚 M 〛 + 1 = ⌊ n {log}_{2} h + \frac{1}{2} ⌋

, two parameters provide this information. On the one hand, the scale closure,

γ_{n} = \frac{h^{n}}{2^{N}}

, which is a value close to 1 satisfying

\frac{U}{D} = γ_{n}

. On the other hand, the scale digit

δ = N - 〚 n 〛

, taking values 0 or 1. Then,

δ = 0 \Leftrightarrow γ_{n} > 1

(

ν_{n} \to 1^{+}, γ_{n} = κ_{n}

) or

δ = 1 \Leftrightarrow γ_{n} < 1

(

ν_{n} \to 2^{-}, γ_{n} = κ_{n}^{- 1}

). The value

| {log}_{2} γ_{n} | = {log}_{2} κ_{n}

multiplied by 1200 measures the distance from

ν_{n}

to 1 in cents ( Preprints 104176 i002

Alternatively, each tone

ν_{k}

in the frequency space is associated with a note or pitch class

{log}_{2} ν_{k}

in the octave

S_{0} = R / Z

, so that the above quantities have the corresponding one in

S_{0}

. Thus, the elementary intervals

u = {log}_{2} U, d = {log}_{2} D

generate the partition of the octave in n intervals,

M u + m d = 1

, satisfying

u - d = ϕ_{n}

, with interval closure

ϕ_{n} = {log}_{2} γ_{n}

and interval comma

| ϕ_{n} | = {log}_{2} κ_{n}

. Sometimes is more useful to work in the multiplicative space of tones and sometimes in the additive space of notes.

The fractions

\frac{N}{n}

are associated with convergent or semi-convergent continued fraction expansions of

{log}_{2} h

[23,24]. Among cyclic scales, two categories may be pointed out. On the one hand, optimal scales, associated with the best closure

γ_{n} \approx 1

, corresponding to the best rational approximations5

\frac{N}{n}

{log}_{2} h

, i.e., the convergents of its canonical continued fraction expansions from both sides. On the other hand, what we shall name accurate scales, which are associated with the best estimations of the generator tone

\frac{2^{\frac{N}{n}}}{h} \approx 1

, corresponding to the good rational approximations

\frac{N}{n}

{log}_{2} h

. Apart from accurate scales, which include optimal scales, there are cyclic scales not associated with good or best rational approximations, still corresponding to semiconvergents. For all these scales, the values

U, D

and

γ_{n}

have bounds according to Appendix A. In particular,

| {log}_{2} γ_{n} |

quantifies the error of the rational approximation of

{log}_{2} h

. These bounds determine the interval between a note of the cyclic scale

E_{n}^{h}

and the one with the same ordinal in the n-TET scale, which is analyzed in Appendix B.

Finally, the family of cyclic scales follow a chain,

E_{n}^{h} \subset E_{n^{+}}^{h}

, so that starting from the indices

(m, M)

E_{n}^{h}

, the same values for the next scale

E_{n^{+}}^{h}

are (i)

m^{+} = m + M, M^{+} = M \Leftrightarrow δ = 0

, and (ii)

m^{+} = m, M^{+} = m + M \Leftrightarrow δ = 1

(see Table 1).

4. Entropy of a Cyclic Scale

For a cyclic scale

E_{n}^{h}

, with the measure defined for tone intervals as

μ ([x_{0}, x_{1}]) = {log}_{2} \frac{x_{1}}{x_{0}}

for

0 < x_{0} \leq x_{1}

, consider the partition of the octave

α \equiv (u^{M}, d^{m})

composed of M intervals of width u and m intervals of width d, regardless of the order in which the intervals follow each other. The partition entropy is

H (u^{M}, d^{m}) = M z (u) + m z (d)

(4)

We will explicitly write it in terms of the indices of the minimum and maximum tones m and M. In order to do so, we define the values

| x 〉 = {{log}_{2} h^{x}}, 〈 x | = 1 - {{log}_{2} h^{x}}; x \in R

where

{{log}_{2} x}

is the mantissa of

{log}_{2} x

, that is,

{log}_{2} h^{x} - ⌊ {log}_{2} h^{x} ⌋

, so that the elemental intervals

u, d

can be expressed in terms of the indices of the minimum and maximum tones as

u = | m 〉, d = 〈 M |

(5)

In this way, Eq. 4 becomes

H {(| m 〉}^{M}, 〈 M |^{m}) = M z (| m 〉) + m z (〈 M |)

(6)

Let’s see how to express the entropy of the cyclic scale

E_{n^{+}}^{h}

, the one following

E_{n}^{h}

in the chain of cyclic scales. The scale refinement process is as follows. The partition

(u^{M}, d^{m})

breaks, so that the major interval splits into two, one of the same size as the minor one plus a remainder. This residual is only smaller than the size of the smaller interval when the scale is optimal. This process is iterated.

As explained in §Section 3, we must distinguish two cases, depending on whether

γ_{n}

is greater or less than 1, or equivalently, if

δ

equals 0 or 1: (i)

δ = 0

γ_{n} > 1

U > D

u > d

. In this case,

N = 〚 n 〛, m^{+} = n, M^{+} = M

The refinement is done in the M intervals of size u and the m intervals of size d are maintained,

\begin{matrix} u^{'} = u - d = ϕ_{n} \Leftrightarrow u^{'} \equiv | m^{+} 〉 = | m 〉 - 〈 M | \\ d^{'} = d \Leftrightarrow d^{'} \equiv 〈 M^{+} | = 〈 M | \end{matrix}

We express6 the entropy according to Eq. 3, being the new partition

α \lor β = (u^{'}^{M^{+}}, d^{'} (m^{+})

\begin{matrix} H (u^{'}^{M^{+}}, d^{'} (m^{+}) = H (u^{M}, d^{m}) + M u H (\frac{d}{u}, 1 - \frac{d}{u}) = \\ = H (u^{M}, d^{m}) + M [z (d) - z (u) + z (κ_{n})] \end{matrix}

In terms of the indices of the extreme tones, by noting

H_{n} = H (E_{n}^{h})

, it can be written as

H_{n^{+}} = H_{n} + Δ_{M}; Δ_{M} = M [z (〈 M |) - z (| m 〉) + z (κ_{n})]

(7)

(ii)

δ = 1

γ_{n} < 1

U < D

u < d

. In this case,

N = 〚 n 〛 + 1, m^{+} = m, M^{+} = n

The refinement is done in the m intervals of size d and the M intervals of size u are maintained,

\begin{matrix} d^{'} = d - u = - ϕ_{n} \Leftrightarrow d^{'} \equiv 〈 M^{+} | = 〈 M | - | m 〉 \\ u^{'} = u \Leftrightarrow u^{'} \equiv | m^{+} 〉 = | m 〉 \end{matrix}

The entropy of the new partition

α \lor β = (u^{'}^{M^{+}}, d^{'} (m^{+})

\begin{matrix} H (u^{'}^{M^{+}}, d^{'} (m^{+}) = H (u^{M}, d^{m}) + m d H (\frac{u}{d}, 1 - \frac{u}{d}) = \\ = H (u^{M}, d^{m}) + m [z (u) - z (d) + z (κ_{n})]) \end{matrix}

In terms of the indices of the extreme tones it is equivalent to

H_{n^{+}} = H_{n} + Δ_{m}; Δ_{m} = m [z (| m 〉) - z (〈 M |) + z (κ_{n})]

(8)

5. Partition Modulation

According to Eq. A2, we write the elementary intervals of a cyclic scale as

u = \frac{1 + m ϕ_{n}}{n}, d = \frac{1 - M ϕ_{n}}{n}

(9)

We have referred to one degenerate case of cyclic scale, the limiting case when the two intervals are one,

u \to d

. In this case

u = d = \frac{1}{n}

and

E_{n}^{h} = E_{n}^{⊤}

, the n-TET scale. This is equivalent to

ϕ_{n} \to 0

in the expressions of Eq. 9. However, we should consider two more degenerate cases. The larger is one interval, the smaller is the other, always filling a full octave,

M u + m d = 1

. Therefore, if

d \to 0

, then the cyclic scale becomes an equal temperament scale of M tones and, if

u \to 0

, the scale becomes an equal temperament scale of m tones. In other words,

(i): According to Appendix A, for $ϕ_{n} > 0$ , by Eq. A5, $ϕ_{n} < \frac{1}{M}$ . If $ϕ_{n} \to \frac{1}{M}$ then $d \to 0$ . In this case, the intervals of the cyclic scale satisfy $0 < d < ϕ_{n} < u$ . Since $u - d = ϕ_{n}$ , then, when $u \to ϕ_{n}$ the scale in no more non-degenerate and becomes an M-TET scale, with entropy

$H_{n} = H (u^{M}, d^{m}) \underset{d \to 0}{\to} H (u^{M}) = H_{M} = {log}_{2} (M)$

Obviously, an optimal cyclic scale is far from this situation, because it satisfies $0 < ϕ_{n} < d < u$ .
(ii): Also, according to Appendix A, for $ϕ_{n} < 0$ , owing to Eq. A8, $ϕ_{n} > - \frac{1}{m}$ . If $ϕ_{n} \to - \frac{1}{m}$ then, $u \to 0$ . In this case, the intervals of the cyclic scale satisfy $0 < u < | ϕ_{n} | < d$ . Then $d \to | ϕ_{n} |$ , so that the scale becomes a degenerate m-TET scale, with entropy

$H_{n} = H (u^{M}, d^{m}) \underset{u \to 0}{\to} H (d^{m}) = H_{m} = {log}_{2} (m)$

An optimal cyclic scale case is also far from this situation, since it satisfies $0 < | ϕ_{n} | < u < d$ .

Lemma 1.

The scales formed from the two elementary intervals

u^{'} = \frac{1 + m ξ}{n}

and

d^{'} = \frac{1 - M ξ}{n}

with values

- \frac{1}{m} < ξ < \frac{1}{M}

generate an infinite and continuous family of n-tone cyclic scales

C_{n}^{h} (ξ)

, which are neighbors of

E_{n}^{h}

, such that

C_{n}^{h} (ϕ_{n}) = E_{n}^{h}

and

C_{n}^{h} (0) = E_{n}^{⊤}

. In addition, if

- \frac{1}{n + m} < ξ < \frac{1}{n + M}

, the scales

C_{n}^{h} (ξ)

are optimal.

These results are immediate consequence of the bounds obtained in Appendix A.

5.1. Modulating Temperament Scales

The most usual case of cyclic scale

E_{n}^{h}

is the one associated with a generator corresponding to a harmonic

h \in Z^{+}

of the fundamental tone. Then, the tonal class of the generator is

g = \frac{h}{⌊ {log}_{2} h ⌋} \in (1, 2)

, which can be written as

g = 2^{\frac{μ + ϕ_{n}}{n}}

, where

μ = N - 〚 1 〛 n

is the ordinal of the scale tone that better approximates g [17], known as chromatic length of the pitch class of the generator. The value

μ = ⌊ n {log}_{2} g + \frac{1}{2} ⌋

also determines the indices m and M of the extreme tones, corresponding to the ordinals 1 and

n - 1

of the scale notes. Since, as

μ m - n 〚 m 〛 = 1

, m is the positive integer,

0 < m < n

, so that

μ m = 1 mod n

For fixed n (and also m and M), the family of cyclic scales

C_{n}^{h} (ξ)

has generators that, in general, are not the tonal class of any harmonic, that is, they are real scales. In this case we write them as

g^{'} = 2^{\frac{μ + ξ}{n}}

, so that, for

ξ \in (- \frac{1}{m}, \frac{1}{M})

, we get a partition modulation, which is a continuum of irregular temperaments [27,28] close to

E_{n}^{h}

and

E_{n}^{⊤}

, also corresponding to cyclic scales. Hence, the n-tone cyclic scales

C_{n}^{h} (ξ)

is a family of modulating temperament scales around the generator

2^{\frac{μ}{n}}

, namely

T_{n}^{μ} = {C_{n}^{h} (ξ); ξ \in (- \frac{1}{m}, \frac{1}{M})}

For example, for

n = 12

, and

g^{'} = \sqrt[4]{5}

, the value

ξ = \frac{12}{4} {log}_{2} 5 - ⌊ \frac{12}{4} {log}_{2} 5 + \frac{1}{2} ⌋ = - 0.03422

gives rise to the quarter-comma meantone temperament, which fits well the class of the fifth harmonic, in exchange for decreasing in 5 the accuracy of the third one. Since the value of

| ξ |

is lower than

\frac{1}{n + m} = \frac{1}{19} = 0.05263

, it results in an optimal scale.

5.2. Entropy in Terms of the Closure

Let us consider an n-tone modulating the temperament scale

C_{n}^{h} (ξ) \in T_{n}^{μ}

. According to equations 4 and 9, we write the entropy of

C_{n}^{h} (ξ)

H_{n} = H (m, M, ξ) = M z (\frac{1 + m ξ}{n}) + m z (\frac{1 - M ξ}{n})

Using the relationship

z (\frac{a}{b}) = \frac{1}{b} z (a) + a z (\frac{1}{b})

, it is immediate to see that

H (m, M, ξ) = {log}_{2} n + \frac{M}{n} z (1 + m ξ) + \frac{m}{n} z (1 - M ξ)

that is,

H (m, M, ξ) = {log}_{2} n - \frac{M}{n} (1 + m ξ) {log}_{2} (1 + m ξ) - \frac{m}{n} (1 - M ξ) {log}_{2} (1 - M ξ)

(10)

By deriving Eq. 10 respect of

ξ

, we get,

\frac{\partial H}{\partial ξ} = - \frac{M m}{n} [{log}_{2} (1 + m ξ) - {log}_{2} (1 - M ξ)]

(11)

0 < ξ < \frac{1}{M}

, the two terms of the previous equation are positive and the derivative is negative, therefore, in this interval the entropy is a decreasing function. If

- \frac{1}{m} < ξ < 0

, both terms in the above equation are negative and the derivative is positive, so in this interval the entropy is an increasing function. At

ξ = 0

there is a local maximum, since

{log}_{2} (1 + m ξ) - {log}_{2} (1 - M ξ) = 0

if and only if

ξ = 0

. Thus,

H

in terms of

ξ

is a concave function, since

\frac{\partial^{2} H}{\partial ξ^{2}} = - \frac{M m}{n ln 2} (\frac{m}{1 + m ξ} + \frac{M}{1 - M ξ}) < 0

. Therefore,

(a): If $0 < ξ < \frac{1}{M}$ , then $H (m, M, 0) = {log}_{2} n > H (m, M, ξ) > {log}_{2} M = H (m, M, \frac{1}{M})$ .
(b): If $- \frac{1}{m} < ξ < 0$ , then $H (m, M, - \frac{1}{m}) = {log}_{2} m < H (m, M, ξ) < {log}_{2} n = H (m, M, 0)$ .

In addition, it is straightforward to see the following properties,

(c): If $m < M$ , $H (m, M, ξ) < H (m, M, - ξ)$ for $ξ > 0$ and $H (m, M, ξ) > H (m, M, - ξ)$ for $ξ < 0$ .
(d): If $m > M$ , $H (m, M, ξ) > H (m, M, - ξ)$ for $ξ > 0$ and $H (m, M, ξ) < H (m, M, - ξ)$ for $ξ < 0$ .
(e): $H (m, M, ξ) > H (M, m, - ξ)$ for $- \frac{1}{m} < ξ < \frac{1}{M}$

Properties (c) and (d) refer to the slight asymmetry of the entropy far from

ξ = 0

, which, as we shall see in the last section, is negligible around

ξ = 0

. Property (e) means that a cyclic scale generated by h and its inverse scale, generated counter-clockwise with swapped indices of the extreme tones, although they have different notes that differ in one comma, have the same entropy.

Therefore, the entropy of any n-tone modulating temperament scale in the family

T_{n}^{μ}

only depends on the closure.

6. Normalized Entropy

Since the entropy increases as the partition is refined, to be able to compare qualities of different scales, whether they are cyclic or not, we will consider the normalized entropy, i.e., relatively to the maximum value it can reach, that of the equally tempered scale. For an n-tone scale

E_{n}

it is defined as7

η (E_{n}) = \frac{1}{{log}_{2} (n)} H (E_{n}); 0 \leq η \leq 1

so that

η

tends to 1 as

E_{n}

approaches to an n-TET scale. For a cyclic scale

E_{n}^{h}

, we will write

η_{n} = η (E_{n}^{h})

Let us see in which case the normalized entropy increases when a scale is being refined. Let us assume two scales, not necessarily cyclic,

E_{n} \subset E_{n^{+}}

with

n < n^{+}

(i.e.,

E_{n^{+}}

is a refinement of

E_{n}

Lemma 2.

The normalized entropy increases if and only if the relative increment of entropy in refining the partition is greater than the relative increment of entropy of the corresponding equal temperament scales.

Proof.

By the sub-additivity property,

H (E_{n^{+}}) = H (E_{n}) + Δ

. It will be

η (E_{n}) < η (E_{n^{+}})

if and only if

\frac{H (E_{n})}{{log}_{2} n} < \frac{H (E_{n^{+}})}{{log}_{2} n^{+}}

, so

\frac{H (E_{n^{+}})}{{log}_{2} n} < \frac{H (E_{n^{+}}) + Δ}{{log}_{2} n^{+}}

. Hence

\frac{{log}_{2} n^{+} - {log}_{2} n}{{log}_{2} n} < \frac{Δ}{H (E_{n})}

(12)

□

The deviation of an n-tone scale

E_{n}

, not necessarily cyclic, relatively to the regular n-TET scale will be measured from the complementary of the normalized entropy, which we will call bias,

θ (E_{n}) = 1 - η (E_{n}); 0 \leq θ \leq 1

(13)

7. Bias of a Cyclic Scale

For a non-degenerate n-tone cyclic scale

C_{n}^{h} (ξ) \in T_{n}^{μ}

the bias

θ (C_{n}^{h} (ξ)) = θ_{n} (ξ)

depends on the divergence of its elementary intervals u and d with regard to the elementary interval of the n-TET scale. Thus, bearing in mind Eq. 10,

\begin{matrix} θ_{n} (ξ) = \frac{1}{n ln n} [M (1 + m ξ) ln (1 + m ξ) + m (1 - M ξ) ln (1 - M ξ)] \end{matrix}

(14)

The graph of the function

θ_{n}

is the mirror image up-to-down of

H_{n}

, scaled by the factor

\frac{1}{{log}_{2} n}

, hence it is convex (Figure 1); the value

θ_{n} (0) = 0

is its minimum in the interval

ξ \in (- \frac{1}{m}, \frac{1}{M})

, and at the extremes (corresponding to degenerate scales) it takes the values

θ_{n} (- \frac{1}{m}) = 1 - \frac{ln m}{ln n}

and

θ_{n} (\frac{1}{M}) = 1 - \frac{ln M}{ln n}

. Therefore, in the interval

(- \frac{1}{m}, 0)

θ_{n} (ξ)

is a decreasing function and in

(0, \frac{1}{M})

it is an increasing function of

ξ

Remark that this behavior of

θ_{n}

in terms of

ξ

holds when n is fixed. In other words,

θ_{n} = θ (ξ; m, M)

. Then, although for another

n^{'}

-tone cyclic scale,

n^{'} \neq n

, the bias

θ_{n^{'}}

has a similar behavior with respect to

ξ^{'}

, we cannot assure that if

ξ < ξ^{'}

then

θ (ξ; m, M) < θ (ξ^{'}; m^{'}, M^{'})

, since this also depends on the values of

m^{'}

and

M^{'}

, such that

m^{'} + M^{'} = n^{'}

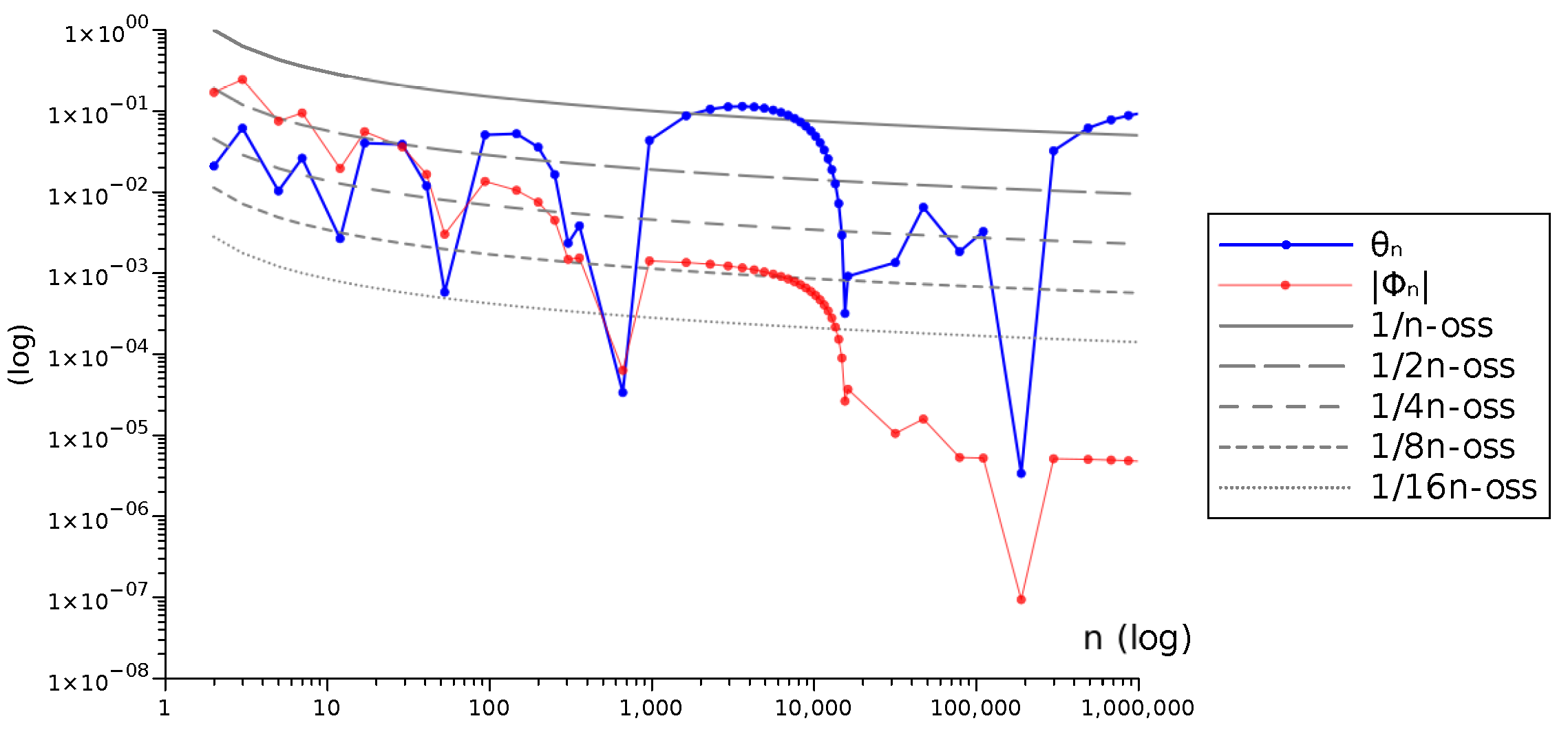
Figure 2 shows the trends of the bias

θ_{n}

and the interval comma

| ϕ_{n} |

for Pythagorean scales (generated by

h = 3

) in terms of n. In general, optimal scales have low bias, but not always a scale is refined the bias decreases. For example, the first optimal scales are those of

n = 5; 12; 41; 53; 306; 665 \dots

and the bias decreases for

n = 5; 12; 53; 665

but the scale of

n = 41

has greater bias than that of

n = 5; 12

; and the one of

n = 306

has greater bias than those of

n = 12; 53

. Also notice that there are intervals where

| ϕ_{n} |

decreases but

θ_{n}

increases.

We will say that a cyclic scale

E_{n}^{h}

is of minimal bias (MB) if for any cyclic scale

E_{n^{'}}^{h}

with

n^{'} < n

, then

θ_{n} < θ_{n^{'}}

. Obviously, this is tantamount to say that

η_{n} > η_{n^{'}}

, hence, the scale has greater normalized entropy than the previous ones. Not all optimal cyclic scales are MB.

Before a deeper analysis, in an approximate way we may estimate how close an MB scale and an equal temperament scale of the same number of tones are. We may use the criterion for which a cyclic scale (not necessarily optimal) unambiguously approximates an n-TET scale if every note of the former is at a distance equal or less than half an elementary interval from the latter. According to Eq. A12 with

λ = 2

, this leads to the condition

(κ_{n}) \leq \frac{600}{n - 1}

(say condition I|2n).

This condition can be satisfied by optimal and non-optimal cyclic scales. For example, for

n = 3

condition I|2n is hold although the scale is not optimal. On the contrary,

n = 41; 306; 111 202

are optimal scales but the condition I|2n is not met.

Let’s see what happens with the MB condition. In this case, up to

n = 2 \cdot 10^{5}

, all scales that satisfy MB also satisfy I|2n, but there are scales that are I|2n and not MB scales, for example for

n = 3; 306; 15 601; 31 867; 79 335

. Hence, the condition that a note of the cyclic scale is closer than half an interval of a note of a tempered scale is weaker than the MB condition. On the contrary, if we further restrict the above condition, let’s say, that the respective notes are at most at a third interval, i.e.,

(κ_{n}) \leq \frac{400}{n - 1}

(say condition I|3n), then, up to

n = 2 \cdot 10^{5}

all I|3n scales are MB scales. In Table 1 these and other properties are displayed.

8. Scales with Limited Bias

8.1. Scale Distributed within Regular Intervals

We study several families of scales for which it is possible to estimate a priori the lower limit of the entropy.

We say that two n-tone scales

E_{n}

and

E_{n}^{'}

sharing the fundamental tone alternate if their notes in cyclic order,

s_{j} = {log}_{2} σ_{j} \in E_{n}

s_{j}^{'} = {log}_{2} σ_{j}^{'} \in E_{n}^{'}

0 < j < n

, fulfill one of the following conditions:

\begin{matrix} (a) s_{j - 1} < s_{j}^{'} \leq s_{j}; 0 < j < n (E_{n} alternate by the right of E_{n}^{'}) \\ (b) s_{j - 1}^{'} < s_{j} \leq s_{j}^{'}; 0 < j < n (E_{n} alternate by the left of E_{n}^{'}) \end{matrix}

(15)

E_{n}^{'}

is the equal temperament scale

E_{n}^{⊤}

, then we write

σ_{j}^{'} = ϑ_{j}^{'}

and say that

E_{n}

is regular interval distributed (RID). In this case, the alternance can also be defined from the following relations involving intervals between tones8,

(a) 0 \leq I (σ_{j}, ϑ_{j}^{'}) < \frac{1}{n} (b) 0 \leq I (ϑ_{j}^{'}, σ_{j}) < \frac{1}{n}; 0 < j < n

(16)

Note that these conditions are generally more restrictive than the condition

d (σ_{j}, ϑ_{j}^{'}) < \frac{1}{n} \Leftrightarrow - \frac{1}{n} < I (σ_{j}, ϑ_{j}^{'}) < \frac{1}{n}

(17)

Obviously, Eq. 16 implies the condition of Eq. 17, although, as seen in Appendix B, for cyclic scales they are equivalent.

For example, suppose case (a). If

0 \leq I (σ_{j}, ϑ_{j}^{'}) < \frac{1}{n}

, then the interval between two consecutive notes of

E_{n}

satisfies

I (σ_{j}, σ_{j + 1}) = I (σ_{j}, ϑ_{j + 1}^{'}) + I (ϑ_{j + 1}^{'}, σ_{j + 1}) = \frac{1}{n} - I (σ_{j}, ϑ_{j}^{'}) + I (ϑ_{j + 1}^{'}, σ_{j + 1}) < \frac{2}{n}

, so that

d (σ_{j}, σ_{j + 1}) < \frac{2}{n}

. Instead, if

d (σ_{j}, ϑ_{j}^{'}) < \frac{1}{n}

, then

d (σ_{j}, σ_{j + 1}) \leq d (σ_{j}, ϑ_{j}^{'}) + d (ϑ_{j}^{'}, ϑ_{j + 1}^{'}) + d (σ_{j + 1}, ϑ_{j + 1}^{'}) < \frac{3}{n}

. In a similar way would be reasoned case (b).

Lemma 3.

The interval between two consecutive notes of an n-tone RID-scale is lower than

\frac{2}{n}

8.2. Scale r-Similar to n-TET

A criterion for measuring the proximity between scales is similarity [30]. Two n-tone scales T and

T^{'}

are similar at level

r > 0

(r-similar) if for each tone

τ_{i} \in T

\exists τ_{j}^{'} \in S

, such that

d (τ_{i}, τ_{j}^{'}) \leq r

and

d (τ_{i}, τ_{k}^{'}) > r, \forall k \neq j

For example, a cyclic scale

E_{n}^{h}

and the n-TET scale have level of similarity

\frac{1}{2 n}

if and only if any pair of notes with ordinal j, i.e.,

ϑ_{j} \in E_{n}^{h}

ϑ_{j}^{'} \in E_{n}^{⊤}

, satisfy

d (ϑ_{j}, ϑ_{j}^{'}) \leq \frac{1}{2 n}

. This condition is equivalent to the condition of Eq. A12 with

λ = 2

(κ_{n}) \leq \frac{600}{n - 1}

However, for the current purpose of evaluating and comparing entropy partitions, we will slightly modify such a concept by assuming that the fundamental is shared by both scales. Then, we say a scale

E_{n}

is similar to the n-TET scale at level r, with

0 < r \leq \frac{1}{2 n}

, if their tones satisfy

d (σ_{j}, ϑ_{j}^{'}) \leq r; 0 < j < n

(18)

8.3. Scale One-Side r-Similar to n-TET

We introduce a concept that will mix the one of similarity with the one of distribution within regular intervals, which will be appropriate to study the bounds of the entropy for cyclic scales.

Let

ϑ_{j}^{'}

be the tones of the n-TET scale. We say that a scale

E_{n}

is one-side r-similar at level r (r-OSS) to the n-TET scale, with

0 < r \leq \frac{1}{n}

, if

(a) 0 \leq I (σ_{j}, ϑ_{j}^{'}) < r (b) 0 \leq I (ϑ_{j}^{'}, σ_{j}) < r; 0 < j < n

(19)

It is OSS by the right (a) or by the left (b), respectively. Therefore, when

r = \frac{1}{n}

it matches the definition of a RID-scale.

9. Entropy of a Scale $\frac{1}{λ n}$ -OSS to $n$ -TET

Consider an n-tone scale

E_{n}

, not necessarily cyclic, which is

\frac{1}{λ n}

-OSS to n-TET for

λ \geq 1

. We already know that the maximum entropy is

{log}_{2} n

. Let’s see the minimum entropy it can reach. We assume case (a) of Eq. 19 and consider the n notes (

n \geq 2

) of

E_{n}

in cyclic order in

[0, 1) \cup {1}

, since the entropy does not change if we add a null set. We also extend the range of possible variation of the intervals between notes at the extremes to include the limiting, degenerate cases. The points determining the division of the octave are

s_{0} = 0; s_{i} = \frac{i}{n} + t_{i}, 0 \leq t_{i} \leq \frac{1}{λ n}, 1 \leq i \leq n - 1; s_{n} = 1

By writing

T = \frac{1}{n}

, the respective intervals are, by assuming

t_{0} = t_{n} = 0

T_{i} = s_{i} - s_{i - 1} = T + t_{i} - t_{i - 1}, 1 \leq i \leq n

Then, scale

E_{n}

generates the partition

α = {T_{i}}

i \in {1, \dots, n}

, with entropy

H (α) = \sum_{i = 1}^{n} z (T_{i}) = - \sum_{i = 1}^{n} (T + t_{i} - t_{i - 1}) {log}_{2} (T + t_{i} - t_{i - 1})

The entropy

H (α)

is a concave and differentiable function

f (t_{1}, \dots, t_{n - 1})

f : V \to R

, with

V = {[0, \frac{1}{λ n}]}^{n - 1}

, a hypercube, which is a convex and compact space. Then, f has a local and global maximum at

(t_{1}, \dots, t_{n - 1}) = (0, \dots, 0)

, corresponding to an n-TET scale with

T_{i} = T

and

H = {log}_{2} n

, and the global minimum is reached at one or some of the vertices of V. These vertices are determined by the possible values

t_{j} \in {0, \frac{1}{λ n}}

1 \leq j \leq n - 1

, and the resulting intervals

T_{i}

can only take the following values: interval

T_{1}

, values

\frac{1}{n}

and

\frac{λ + 1}{λ n}

; interval

T_{n}

, values

\frac{1}{n}

and

\frac{λ - 1}{λ n}

; and the intermediate intervals, values

\frac{λ - 1}{λ n}

\frac{1}{n}

and

\frac{λ + 1}{λ n}

The octave is covered by a number of different intervals satisfying

A + B + C = n

(20)

of which A in number have width

\frac{λ - 1}{λ n}

, B width

\frac{1}{n}

, and C width

\frac{λ + 1}{λ n}

, so that9

A \frac{λ - 1}{λ n} + B \frac{λ}{λ n} + C \frac{λ + 1}{λ n} = 1

. Therefore,

A (λ - 1) + B λ + C (λ + 1) = λ n

(21)

The entropy at one of these vertices can be written in terms of the respective number of intervals as

\begin{matrix} f = A z (\frac{λ - 1}{λ n}) + B z (\frac{λ}{λ n}) + C z (\frac{λ + 1}{λ n}) = \\ = {log}_{2} n + \frac{1}{n} g (A, C); g (A, C) = A z (\frac{λ - 1}{λ}) + C z (\frac{λ + 1}{λ}) \end{matrix}

(22)

where z is the concave function defined in Eq. 1, also extended for values

t > 1

, where

z (t) < 0

. Among possible configurations, we look for the minimum value that f can take, which will correspond to the minimum value of g. Notice that this quantity is added to the entropy of an n-TET scale, being it consistent with the fact that the B intervals of width

\frac{1}{n}

are not involved in the expression. However, the intervals in number C, of greater width than

\frac{1}{n}

, contribute to decreasing the entropy, while those in number A, of width lower than

\frac{1}{n}

, contribute to increasing it, since the corresponding function z evaluated in values less than 1 is positive.

In the current case, by combining equations 20 and 21, we get

A = C

and

B + 2 C = n

. Therefore,

g (C) = C Z (λ, 1); Z (λ, a) = z (\frac{λ - a}{λ}) + z (\frac{λ + a}{λ}), λ \geq a

(23)

If n is even, the maximum value for C, by assuming

B = 0

, is

C = \frac{n}{2}

. Hence, the number of intervals of null-size is also

A = \frac{n}{2}

. Then10,

g (\frac{n}{2}) = \frac{n}{2} Z (λ, 1)

, corresponding to a degenerate scale of

\frac{n}{2}

non-null intervals. Therefore, if

n = \dot{2}

the entropy satisfies

{log}_{2} n + \frac{1}{2} Z (λ, 1) \leq H (α)

If n is odd, the maximum value for C and A is

\frac{n - 1}{2}

, with

B = 1

. Then,

g = \frac{n - 1}{2} Z (λ, 1)

, corresponding to a degenerate scale of

\frac{n + 1}{2}

non-null intervals. Therefore, if

n \neq \dot{2}

the entropy satisfies

{log}_{2} n + \frac{1}{2} Z (λ, 1) (1 - \frac{1}{n}) \leq H (α)

Case (b) is similar. It would be reasoned by considering that

f (t_{1}, \dots, t_{n - 1}) = f (- t_{n - 1}, \dots, - t_{1})

, i.e., it is equivalent to case (a), but following the intervals from right to left starting at 1. Therefore,

Theorem 1.

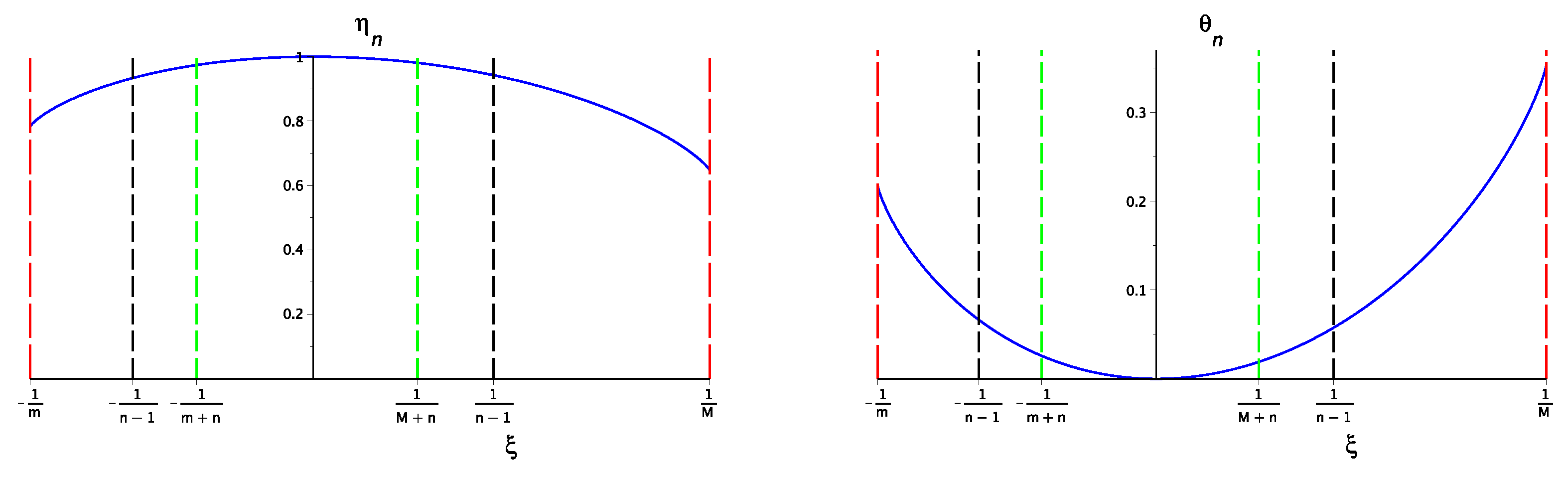
The entropy and bias of a scale

\frac{1}{λ n}

-OSS to n-TET satisfy

\begin{matrix} n = \dot{2}, & {log}_{2} n + \frac{1}{2} Z (λ, 1) \leq H (α) \leq {log}_{2} n; & 0 \leq θ (α) \leq - \frac{1}{2 {log}_{2} n} Z (λ, 1) \\ n \neq \dot{2}, & {log}_{2} n + \frac{1}{2} Z (λ, 1) (1 - \frac{1}{n}) \leq H (α) \leq {log}_{2} n; & 0 \leq θ (α) \leq - \frac{1}{2 {log}_{2} n} Z (λ, 1) (1 - \frac{1}{n}) \end{matrix}

(24)

We explicitly write two cases. For

λ = 1

, since

Z (1, 1) = - 2

, the entropy of a RID-scale satisfies, if

n = \dot{2}

{log}_{2} \frac{n}{2} \leq H (α) \leq {log}_{2} n

and, if

n \neq \dot{2}

{log}_{2} \frac{n}{2} + \frac{1}{n} \leq H (α) \leq {log}_{2} n

For

λ = 2

, since

Z (2, 1) = - 0.189

, the entropy of a scale

\frac{1}{2 n}

-OSS to n-TET satisfies, if

n = \dot{2}

{log}_{2} n - 0.189 \leq H (α) \leq {log}_{2} n

and, if

n \neq \dot{2}

{log}_{2} n - 0.189 (1 - \frac{1}{n}) \leq H (α) \leq {log}_{2} n

Levels for

λ = 1, 2, 4, 8, 16

are displayed in Figure 2.

10. Entropy of a Scale $\frac{1}{λ n}$ -Similar to $n$ -TET

Let us calculate the minimum entropy that can reach an n-tone scale

E_{n}

, not necessarily cyclic, having a similarity level

\frac{1}{λ n}

with the n-TET scale for

λ \geq 2

. According to the previous notation and considerations, the points that determine the division of the octave are

s_{0} = 0; s_{i} = \frac{i}{n} + t_{i}, - \frac{1}{λ n} \leq t_{i} \leq \frac{1}{λ n}, 1 \leq i \leq n - 1; s_{n} = 1

The respective intervals are,

T_{i} = s_{i} - s_{i - 1} = \frac{1}{n} + t_{i} - t_{i - 1}, 1 \leq i \leq n

, by assuming

t_{0} = t_{n} = 0

. As before, we write the entropy of the partition

α = {T_{i}}

i \in {1, \dots, n}

, as

H (α) = \sum_{i = 1}^{n} z (T_{i}) = f (t_{1}, \dots, t_{n - 1})

, where

f : V \to R

, with

V = {[- \frac{1}{λ n}, \frac{1}{λ n}]}^{n - 1}

, a convex and compact space. The local and global maximum of f takes place at

(t_{1}, \dots, t_{n - 1}) = (0, \dots, 0)

, corresponding to the scale of n-TET, with

T_{i} = T

and

H = {log}_{2} n

. The global minimum is reached at one or some of the vertices of V. These vertices are determined by the possible values

t_{j} \in {- \frac{1}{λ n}, \frac{1}{λ n}}

1 \leq j \leq n - 1

, and the resulting intervals

T_{i}

can only take the following values: the extreme intervals

T_{1}

and

T_{n}

values

\frac{λ - 1}{λ n}

and

\frac{λ + 1}{λ n}

, while the intermediate intervals can have values

\frac{λ - 2}{λ n}

\frac{1}{n}

, and

\frac{λ + 2}{λ n}

. The octave is covered by a number of different intervals satisfying

A + B + C + D + E = n

(25)

of which A in number have width

\frac{λ - 2}{λ n}

, B width

\frac{λ - 1}{λ n}

, C width

\frac{1}{n}

, D width

\frac{λ + 1}{λ n}

and E width

\frac{λ + 2}{λ n}

, so that

A \frac{λ - 2}{λ n} + B \frac{λ - 1}{λ n} + C \frac{λ}{λ n} + D \frac{λ + 1}{λ n} + E \frac{λ + 2}{λ n} = 1

. Therefore,

A (λ - 2) + B (λ - 1) + C λ + D (λ + 1) + E (λ + 2) = λ n

(26)

The entropy at one of these vertices can be written in terms of the respective number of intervals as

\begin{matrix} f = A z (\frac{λ - 2}{λ n}) + B z (\frac{λ - 1}{λ n}) + C z (\frac{λ}{λ n}) + D z (\frac{λ + 1}{λ n}) + E z (\frac{λ + 2}{λ n}) = \\ = {log}_{2} n + \frac{1}{n} g (A, B, D, E), g (A, B, D, E) = A z (\frac{λ - 2}{λ}) + B z (\frac{λ - 1}{λ}) + D z (\frac{λ + 1}{λ}) + E z (\frac{λ + 2}{λ}) \end{matrix}

(27)

Once again, the intervals of width

\frac{1}{n}

are not involved in this expression. The intervals in number D and E, of greater width than

\frac{1}{n}

, contribute to decreasing the entropy, while those who are there in number A and B, of width lower than

\frac{1}{n}

, contribute to increasing it.

The minimum value of g is obtained by the highest possible values of E and D (in that order) and minimum of A and B.

In the current case, by combining equations 25 and 26, we get

A = E + \frac{1}{2} D - \frac{1}{2} B

and

B + 2 C + 3 D + 4 E = 2 n

(28)

If n is even, at most there can be

E = \frac{n}{2}

intermediate intervals of width

\frac{λ + 2}{λ n}

. By substitution of this value into Eq. 28, we get

B + 2 C + 3 D = 0

, so that

B = C = D = 0

and

A = \frac{n}{2}

. Hence, the minimum g is

g (\frac{n}{2}, 0, 0, \frac{n}{2}) = \frac{n}{2} Z (λ, 2)

, corresponding to a degenerate scale of

\frac{n}{2}

non-null intervals. Therefore, if

n = \dot{2}

the entropy satisfies

{log}_{2} n + \frac{1}{2} Z (λ, 2) \leq H (α)

If n is odd, we should examine two alternatives. On the one hand, if we assume there are

E = \frac{n - 1}{2}

intermediate intervals of width

\frac{λ + 2}{λ n}

, by substitution into Eq. 28 we get

B + 2 C + 3 D - 2 = 0

. Possible interval values are

(B, C, D) = (0, 1, 0); (2, 0, 0)

. In this case, the minimum value of g is provided by the first triad, i.e.,

B = D = 0

C = 1

A = \frac{n - 1}{2}

, which yields

g (\frac{n - 1}{2}, 0, 0, \frac{n - 1}{2}) = \frac{n - 1}{2} Z (λ, 2)

, corresponding to a degenerate scale of

\frac{n + 1}{2}

non-null intervals. In this case,

{log}_{2} n + \frac{1}{2} Z (λ, 2) (1 - \frac{1}{n}) \leq H (α)

(29)

On the other hand, as second alternative, if there are

E = \frac{n - 3}{2}

intermediate intervals of width

\frac{λ + 2}{λ n}

, it is hold

B + 2 C + 3 D - 6 = 0

. Possible interval values are

(B, C, D) = (0, 0, 2); (1, 1, 1); (3, 0, 1); (0, 3, 0); (4, 1, 0)

. The minimum of g is provided by the first triad, so that

B = C = 0

D = 2

A = \frac{n - 1}{2}

, and

g (\frac{n - 1}{2}, 0, 2, \frac{n - 3}{2}) = \frac{n - 1}{2} z (\frac{λ - 2}{λ}) + 2 z (\frac{λ + 1}{λ}) + \frac{n - 3}{2} z (\frac{λ + 2}{λ})

corresponding to a degenerate scale of

\frac{n + 1}{2}

non-null intervals. Hence,

{log}_{2} n + \frac{1}{2} Z (λ, 2) [1 - \frac{1}{n} \frac{z (\frac{λ - 2}{λ}) - 4 z (\frac{λ + 1}{λ}) + 3 z (\frac{λ + 2}{λ})}{Z (λ, 2)}] \leq H (α)

(30)

The factor multiplying

\frac{1}{n}

is a positive value between

3 (2 - {log}_{2} 3) = 1.245

and

\frac{3}{2}

for

λ \geq 2

. Since the value

Z (λ, 2)

is negative, the above factor increases it. Hence, the entropy of Eq. 29 is lower than the entropy of Eq. 30. Therefore,

Theorem 2.

The entropy and bias of a scale

\frac{1}{λ n}

-similar to n-TET satisfy

\begin{matrix} n = \dot{2}, & {log}_{2} n + \frac{1}{2} Z (λ, 2) \leq H (α) \leq {log}_{2} n; & 0 \leq θ (α) \leq - \frac{1}{2 {log}_{2} n} Z (λ, 2) \\ n \neq \dot{2}, & {log}_{2} n + \frac{1}{2} Z (λ, 2) (1 - \frac{1}{n}) \leq H (α) \leq {log}_{2} n; & 0 \leq θ (α) \leq - \frac{1}{2 {log}_{2} n} Z (λ, 2) (1 - \frac{1}{n}) \end{matrix}

(31)

We explicitly evaluate the case for

λ = 2

. Since

Z (2, 2) = - 2

, if

n = \dot{2}

, then

{log}_{2} \frac{n}{2} \leq H (α) \leq {log}_{2} n

and, if

n \neq \dot{2}

, then

{log}_{2} \frac{n}{2} + \frac{1}{n} \leq H (α) \leq {log}_{2} n

, which are the same bounds as for a RID-scale.

11. Cyclic RID-Scales

We may reformulate Theorem A1 according to the above definitions.

Theorem 3.

Optimal cyclic scales are RID-scales.

Nevertheless, there are many non-optimal cyclic scales that are also RID-scales. Cyclic RID-scales correspond to partial convergents of continued fractions where the comma is not as low as for optimal scales, i.e., their closure is not a best approximation, although they belong to a family of relatively good partial convergents. However, although in most cases a convergent that gives a good approximation (i.e., an accurate scale) generates a RID-scale, there are exceptions, such as for

n = 200

11. Therefore, there exist accurate scales that are not RID, and RID-scales that are not accurate.

11.1. Comma and Elementary Intervals of a RID-Scale

It is immediate to identify a RID-scale from its interval comma

| ϕ_{n} | = | {log}_{2} γ_{n} | = | n {log}_{2} h - N |

. As seen in Appendix B, the distance between the tones

ϑ_{j}^{'} \in E_{n}^{⊤}

and

ϑ_{j} = ν_{k} \in E_{n}^{h}

for

0 \leq j < n

\frac{k}{n} | ϕ_{n} |

. So,

\frac{k}{n} | ϕ_{n} | < \frac{1}{n}

for all

0 \leq k < n

if and only if

\frac{n - 1}{n} | ϕ_{n} | < \frac{1}{n}

, that is, the interval comma is limited as

| ϕ_{n} | < \frac{1}{n - 1}

Lemma 4.

A cyclic scale is RID if and only if

| ϕ_{n} | < \frac{1}{n - 1}

This condition, which is satisfied by all optimal scales, assures us that the value of

| ϕ_{n} |

is small enough to be far from the previously seen degenerate cases of less than n notes, since for every RID-scale it is fulfilled

| ϕ_{n} | < \frac{1}{n - 1} \leq min (\frac{1}{m}, \frac{1}{M})

From another point of view, while considering RID-scales we are excluding “bad approximations” of

{log}_{2} h

that satisfy, if

ϕ_{n} > 0

\frac{1}{n - 1} \leq n {log}_{2} h - N < \frac{1}{M}

and, if

ϕ_{n} < 0

- \frac{1}{m} < N - n {log}_{2} h \leq - \frac{1}{n - 1}

. This fact also has implications on the bounds of the two elementary intervals of cyclic RID-scales, We distinguish the following cases.

(i): If $0 < ϕ_{n} < \frac{1}{n - 1}$ , according to Eq. 9, $u < \frac{1}{n} (1 + \frac{m}{n - 1}) < \frac{1}{n} (1 + \frac{n - 1}{n - 1}) = \frac{2}{n}$ . Hence12,

$\frac{1}{n} < u < min (\frac{1}{M}, \frac{2}{n})$

(32)
(ii): If $- \frac{1}{n - 1} < ϕ_{n} < 0$ , according to Eq. 9, $d < \frac{1}{n} (1 + \frac{M}{n - 1}) < \frac{1}{n} (1 + \frac{n - 1}{n - 1}) = \frac{2}{n}$ . Hence13,

$\frac{1}{n} < d < min (\frac{1}{m}, \frac{2}{n})$

(33)

In both cases, the size of the greatest elementary interval of a cyclic RID-scale is lower than

\frac{2}{n}

, as stated in Lemma 3.

11.2. Bias of RID-Scales

For large values of

| ϕ_{n} |

, that is,

| ϕ_{n} | > \frac{1}{m}

| ϕ_{n} | > \frac{1}{M}

, Eq. 14 can have a quite arbitrary and non-symmetrical behavior, but for values

| ϕ_{n} | < \frac{1}{n - 1}

, and in particular for optimal scales with

| ϕ_{n} | < \frac{1}{n + M}

| ϕ_{n} | < \frac{1}{n + m}

, depending on the value

δ

, the bias

θ_{n}

behaves as proportional to

ϕ_{n}^{2}

Being

| m ϕ_{n} | < 1

and

| M ϕ_{n} | < 1

, we can approximate the logarithms in the following expressions as

(1 + m ϕ_{n}) ln (1 + m ϕ_{n}) = m ϕ_{n} + \frac{1}{2} m^{2} ϕ_{n}^{2} - \frac{1}{6} m^{3} ϕ_{n}^{3} + O_{4} (m ϕ_{n})

(1 - M ϕ_{n}) ln (1 - M ϕ_{n}) = - M ϕ_{n} + \frac{1}{2} M^{2} ϕ_{n}^{2} + \frac{1}{6} M^{3} ϕ_{n}^{3} + O_{4} (M ϕ_{n})

and by substitution into Eq. 14 we get

θ_{n} = \frac{1}{ln n} [\frac{M m^{2} + m M^{2}}{2 n} ϕ_{n}^{2} - \frac{M m^{3} - m M^{3}}{6 n} ϕ_{n}^{3} + \frac{M m^{4} + m M^{4}}{12 n} O_{4} (ϕ_{n})] =

= \frac{m M}{2 ln n} [ϕ_{n}^{2} - \frac{m - M}{3} ϕ_{n}^{3} + \frac{m^{2} - m M + M^{2}}{6} O_{4} (ϕ_{n})]

Notice that

m | ϕ_{n} |^{3} = \frac{1}{m^{2}} | m ϕ_{n} |^{3} = O_{3} (| ϕ_{n} |) < O_{3} (| m ϕ_{n} |)

with

| m ϕ_{n} | < 1

and

M | ϕ_{n} |^{3} = \frac{1}{M^{2}} | M ϕ_{n} |^{3} = O_{3} (| ϕ_{n} |) < O_{3} (| M ϕ_{n} |)

with

| M ϕ_{n} | < 1

. The same happens with the higher order terms. Therefore, for enough small

| ϕ_{n} |

we can use the approximation derived from the following result,

Lemma 5.

The bias of a cyclic RID-scale satisfies

θ_{n} = \frac{m M}{2 ln (m + M)} ϕ_{n}^{2} + O_{3} (| ϕ_{n} |)

(34)

11.3. Cyclic Scales of Minimal Bias

As explained in §Section 4, while refining a cyclic scale, in each iteration one of the indices of the extreme tones remains fixed, while the other increases by a value equal to the one that remains fixed. Let’s see that in each refinement, the following function appearing in Eq. 34 always increases,

ψ (m, M) = \frac{m M}{ln (m + M)}

(35)

Lemma 6.

For

n = m + M \geq 2

ψ (m^{+}, M) > ψ (m, M)

with

m^{+} = m + M

, and

ψ (m, M^{+}) > ψ (m, M)

with

M^{+} = m + M

Proof.

Indeed, it suffices to check that the function

ψ (m, M) = \frac{m M}{ln (m + M)}

satisfies

\frac{\partial ψ}{\partial m} > 0

\frac{\partial ψ}{\partial M} > 0

\frac{\partial}{\partial m} \frac{m M}{ln (m + M)} = \frac{M ln (m + M) - \frac{m M}{m + M}}{{ln}^{2} (m + M)} = \frac{M^{2} ln (m + M) + m M (ln (m + M) - 1)}{{ln}^{2} (m + M)} > 0 \Leftrightarrow m + M \geq 2

\frac{\partial}{\partial M} \frac{m M}{ln (m + M)} = \frac{m ln (m + M) - \frac{m M}{m + M}}{{ln}^{2} (m + M)} = \frac{m^{2} ln (m + M) + m M (ln (m + M) - 1)}{{ln}^{2} (m + M)} > 0 \Leftrightarrow m + M \geq 2

Note that, for

m + M > 2

, the above inequalities hold and, if

m + M = 2

, then

M = m = 1

, so that the above results are also valid. □

Corollary 1.

Let us write

ψ_{n} = ψ (m, M)

. If

n > n^{'}

then

ψ_{n} > ψ_{n^{'}}

With this notation, the bias of a cyclic RID-scale can be estimated from

θ_{n} = \frac{1}{2} ψ_{n} ϕ_{n}^{2}

(36)

Theorem 4.

Every cyclic RID-scale of minimal bias is optimal.

Proof.

We prove it by denying the consequent. Assume two cyclic RID-scales

E_{n}^{h}

E_{n^{'}}^{h}

such that

n > n^{'}

with interval commas satisfying

| ϕ_{n} | > | ϕ_{n^{'}} |

, i.e.,

E_{n}^{h}

is not optimal. Then, applying the previous corollary to Eq. 36, we have

ψ_{n} ϕ_{n}^{2} > ψ_{n^{'}} ϕ_{n^{'}}^{2} \Rightarrow θ_{n} > θ_{n^{'}}

Therefore, if a cyclic RID-scale is not optimal, it cannot be MB. □

The first cyclic MB-scales for

h = 3

, i.e., Pythagorean scales, are for

n = 5; 12; 53; 665 \dots

as shown in Fig. Figure 2, as well as in Table 1.

12. Conclusions

In the current paper it is proposed to measure the regularity of the intervals of a music scale from its partition entropy. Among other properties, the fact of being a continuous increasing function of n for an n-TET scale, which is always the maximum value that the entropy of any n-tone scale can reach, together with the sub-additivity property, which guarantees that as refining the partition, the entropy always increases, make this parameter very suitable for our purpose. In order to compare scales with different number of tones, the entropy relative to the corresponding regular scale is used, which is the normalized entropy, so that their complementary to 1 quantifies the bias relative to the n-TET scale.

The main application of these concepts is to cyclic scales, whose properties are reviewed and further investigated in the Appendices. Two situations have been analyzed. First, cyclic scales with a fixed number of tones, which is a family of modulating temperament scales around one generator. In this case, the bias only depends on the closure, i.e., the relative size of both elementary intervals. Second, as cyclic scales are refined, the bias also depends on how many intervals of each size there are.

In order to study such a dependency, it has been necessary to restrict the scales in two ways. On the one hand, to those having a lower limit of the entropy determined by the condition that their notes are distributed along each of the intervals of a regular scale (RID-scales). Such a study has been made in a general way, by determining the maximum bias of several scales, not necessarily cyclic, having different levels of similarity with a n-TET scale, either from one side or from both sides. Figure 2 displays the similarity levels for cyclic scales. On the other hand, to scales with the comma not exceeding that of a RID-scale, since in this case the dependency bias-closure is well defined.

We prove that any cyclic scale of minimal bias (MB-scale), i.e., whose bias is lower than that of the cyclic scales of fewer tones, is necessarily optimal, i.e., corresponds to a best rational aproximation of

{log}_{2} h

. Therefore, in relation to the closure, scales can be ordered in nested families, from worst to best, as cyclic, accurate, and optimal scales, whilst in relation to their regularity, they can be ordered in nested families as cyclic, RID, optimal, and MB-scales.

Funding

This research received no external funding.

Conflicts of Interest

The author declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:

BRA	Best rational approximation (optimal scale)
GRA	Good rational approximation (accurate scale)
I\|Xn	maximum distance $\frac{1}{x n}$ to n-TET
MB	Minimal bias
n-TET	n-tones of equal temperament
OSS	One-side similar
RID	Regular interval distributed

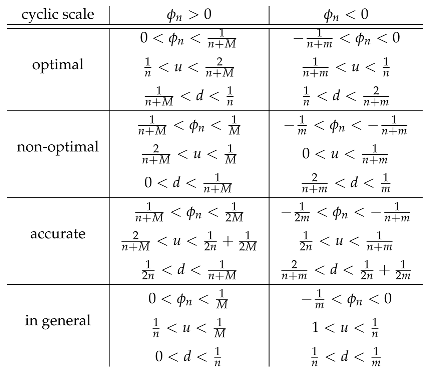
Appendix A. Bounds for the Elementary Intervals and Closure of Cyclic Scales

The notes of a cyclic scale

E_{n}^{h}

divide the circle of the octave into n intervals of width

{log}_{2} U

{log}_{2} D

, beginning and ending in the pitch class of the fundamental, so that

M {log}_{2} U + m {log}_{2} D = 1

(A1)

According to the definitions of U, D, and

γ_{n}

, these intervals can be referred to the elementary interval of the equal temperament scale as

{log}_{2} U = \frac{1}{n} + \frac{m}{n} {log}_{2} γ_{n}; {log}_{2} D = \frac{1}{n} - \frac{M}{n} {log}_{2} γ_{n}

(A2)

We may determine their bounds by distinguishing between the cases

γ_{n}

greater or less than 1.

(i)

γ_{n} > 1

, then

U > D

. Depending on the scale, we have:

(a): The closure of an optimal cyclic scale satisfies $1 < γ_{n} < \frac{2}{ν_{M}} < ν_{m}$ , hence $1 < γ_{n} < D < U$ . By taking logarithms and taking into account Eq. A2 we get

$0 < {log}_{2} γ_{n} < {log}_{2} D = \frac{1}{n} - \frac{M}{n} {log}_{2} γ_{n} ⟹ 0 < {log}_{2} γ_{n} < \frac{1}{n + M}$

(A3)

The elementary intervals satisfy

$\frac{1}{n + M} < {log}_{2} D < \frac{1}{n}; \frac{1}{n} < {log}_{2} U < \frac{2}{n + M}$
(b): The closure of a non-optimal cyclic scale satisfies $1 < \frac{2}{ν_{M}} < γ_{n} < ν_{m}$ , hence $1 < D < γ_{n} < U$ . Then, by taking logarithms,

$\begin{matrix} {log}_{2} D = \frac{1}{n} - \frac{M}{n} {log}_{2} γ_{n} < {log}_{2} γ_{n} ⟹ \frac{1}{n + M} < {log}_{2} γ_{n} \\ {log}_{2} γ_{n} < {log}_{2} U = \frac{1}{n} + \frac{m}{n} {log}_{2} γ_{n} ⟹ {log}_{2} γ_{n} < \frac{1}{M} \end{matrix}$

(A4)

Therefore,

$0 < {log}_{2} D < \frac{1}{n + M}; \frac{2}{n + M} < {log}_{2} U < \frac{1}{M}$
(c): For an accurate cyclic scale, to the above condition $0 < {log}_{2} D < {log}_{2} γ_{n} < {log}_{2} U$ we must add that of a good rational approximation, that can be written as

$0 < \frac{1}{n} {log}_{2} γ_{n} < \frac{1}{M} {log}_{2} D < \frac{1}{m} {log}_{2} U$

Then, $\frac{1}{n} {log}_{2} γ_{n} < \frac{1 - M {log}_{2} γ_{n}}{M n}$ , hence ${log}_{2} γ_{n} < \frac{1}{2 M}$ , and, since Eq. A4 is still valid, we get the following bounds,

$\frac{1}{n + M} < {log}_{2} γ_{n} < \frac{1}{2 M}; \frac{1}{2 n} < {log}_{2} D < \frac{1}{n + M}; \frac{2}{n + M} < {log}_{2} U < \frac{1}{2 n} + \frac{1}{2 M}$

Thus, in case (i), either for optimal or non-optimal scales, it is satisfied,

γ_{n} > 1 ⟹ 0 < {log}_{2} γ_{n} < \frac{1}{M}; 0 < {log}_{2} D < \frac{1}{n}; \frac{1}{n} < {log}_{2} U < \frac{1}{M}

(A5)

(ii)

γ_{n} < 1

, then

D > U

. Depending on the scale, we have:

(a): The closure of an optimal cyclic scale satisfies $\frac{ν_{M}}{2} < \frac{1}{ν_{m}} < γ_{n} < 1$ , hence $\frac{1}{D} < \frac{1}{U} < γ_{n} < 1$ . Then, by taking logarithms,

$- {log}_{2} U = - \frac{1}{n} - \frac{m}{n} {log}_{2} γ_{n} < {log}_{2} γ_{n} < 0 ⟹ - \frac{1}{n + m} < {log}_{2} γ_{n} < 0$

(A6)

The elementary intervals satisfy

$\frac{1}{n + m} < {log}_{2} U < \frac{1}{n}; \frac{1}{n} < {log}_{2} D < \frac{2}{n + m}$
(b): The closure of a non-optimal cyclic scale satisfies $\frac{ν_{M}}{2} < γ_{n} < \frac{1}{ν_{m}} < 1$ , hence $\frac{1}{D} < γ_{n} < \frac{1}{U} < 1$ . Then, by taking logarithms,

$\begin{matrix} - {log}_{2} D = - \frac{1}{n} + \frac{M}{n} {log}_{2} γ_{n} < {log}_{2} γ_{n} ⟹ - \frac{1}{m} < {log}_{2} γ_{n} < 0 \\ {log}_{2} γ_{n} < - {log}_{2} U = - \frac{1}{n} - \frac{m}{n} {log}_{2} γ_{n} ⟹ {log}_{2} γ_{n} < - \frac{1}{n + m} \end{matrix}$

(A7)

Then, the elementary intervals satisfy

$0 < {log}_{2} U < \frac{1}{n + m}; \frac{2}{n + m} < {log}_{2} D < \frac{1}{m}$
(c): For an accurate cyclic scale, to the above condition $- {log}_{2} D < {log}_{2} γ_{n} < - {log}_{2} U < 0$ we must add that of a good rational approximation, that can be written as

$- \frac{1}{M} {log}_{2} D < - \frac{1}{m} {log}_{2} U < \frac{1}{n} {log}_{2} γ_{n} < 0$

Then, $\frac{1}{n} {log}_{2} γ_{n} > - \frac{1 + m {log}_{2} γ_{n}}{m n}$ , hence $- \frac{1}{2 m} < {log}_{2} γ_{n}$ , and, since Eq. A7 is still valid, we get the following bounds,

$- \frac{1}{2 m} < {log}_{2} γ_{n} < - \frac{1}{n + m}; \frac{2}{n + m} < {log}_{2} D < \frac{1}{2 n} + \frac{1}{2 m}; \frac{1}{2 n} < {log}_{2} U < \frac{1}{n + m}$

Thus, in case (ii), either for optimal or non-optimal scales, it is satisfied,

γ_{n} < 1 ⟹ - \frac{1}{m} < {log}_{2} γ_{n} < 0; 0 < {log}_{2} U < \frac{1}{n}; \frac{1}{n} < {log}_{2} D < \frac{1}{m}

(A8)

Table A1 summarizes the above results over the octave

S_{0}

. Notice that, for optimal scales, equations A3 and A6 give the following bounds, similarly to the theory of continued fractions,

(i) |{log}_{2} h - \frac{N}{n}| < \frac{1}{n (n + M)}; (ii) |{log}_{2} h - \frac{N}{n}| < \frac{1}{n (n + m)}

Table A1. Bounds for

ϕ_{n} = {log}_{2} γ_{n}

u = {log}_{2} U

and

d = {log}_{2} D

, depending on the type of cyclic scale.

Table A1. Bounds for

ϕ_{n} = {log}_{2} γ_{n}

u = {log}_{2} U

and

d = {log}_{2} D

, depending on the type of cyclic scale.

Appendix B. Deviation of a Cyclic Scale from n-TET

We calculate the interval between the notes with ordinal j of the respective scales

E_{n}^{h}

and

E_{n}^{⊤}

, corresponding to the tones

ϑ_{j} \in E_{n}^{h}

and

ϑ_{j}^{'} = 2^{\frac{j}{n}} \in E_{n}^{⊤}

. According to equations A2 and A1, the deviations of each note of

E_{n}^{h}

with regard to

E_{n}^{⊤}

compensate each other and, in the end, they close exactly the octave. If the tone

ϑ_{j}

corresponds to the iteration

ν_{k}

, then

j = N k - n 〚 k 〛

[17], Eq. 28]. Therefore,

〚 k 〛 = \frac{N k - j}{n}

. Bearing in mind that

{log}_{2} γ_{n} = n {log}_{2} h - N

, the scale note

{log}_{2} ϑ_{j} = {log}_{2} ν_{k}

{log}_{2} ϑ_{j} = k {log}_{2} h - 〚 k 〛 = \frac{k}{n} {log}_{2} γ_{n} + \frac{j}{n}

(A9)

Lemma A1.

The interval that separates the two notes is

I (ϑ_{j}, ϑ_{j}^{'}) = {log}_{2} ϑ_{j} - {log}_{2} ϑ_{j}^{'} = \frac{k}{n} {log}_{2} γ_{n}; j = 0, \dots, n - 1

(A10)

Therefore, all of these intervals have the same sign, which is positive if

γ_{n} > 1

and negative if

γ_{n} < 1

. By taking absolute value, the interval between these close notes becomes a distance,

d (ϑ_{j}, ϑ_{j}^{'}) = \frac{k}{n} | {log}_{2} γ_{n} | = \frac{k}{n} κ_{n}; j = 0, \dots, n - 1

(A11)

As expected, these distances increase with the iterations, so that the maximum is reached by last iterate,

k = n - 1

, i.e.,

d_{\max} = {max}_{j} d (ϑ_{j}, ϑ_{j}^{'}) = \frac{n - 1}{n} κ_{n}

. Then, a condition such as

d_{\max} \leq \frac{1}{λ n}

, for

λ > 0

, becomes

κ_{n} \leq \frac{1}{λ (n - 1)}

, which, in cents is

(κ_{n}) \leq \frac{1200}{λ (n - 1)}

(A12)

For an optimal cyclic scale, according to equations A3 and A6,

- \frac{1}{n + m} < {log}_{2} γ_{n} < \frac{1}{n + M}

, so that

| {log}_{2} γ_{n} | < \frac{1}{n}

and

k | {log}_{2} γ_{n} | < 1

in Eq. A11. Therefore, we conclude

d (ϑ_{j}, ϑ_{j}^{'}) < \frac{1}{n}

Theorem A1.

The notes

ϑ_{i}

i \neq 0

, of anoptimalcyclic scale

E_{n}^{h}

and the ones of the corresponding n-TET scale

E_{n}^{⊤}

alternate, i.e., for

0 < i < n

either(i)

ϑ_{i}^{'} < ϑ_{i} < ϑ_{i + 1}^{'}

or(ii)

ϑ_{i - 1}^{'} < ϑ_{i} < ϑ_{i}^{'}

Such a situation is also possible for non-optimal scales, although there are exceptions where the tones do not alternate. For instance, in a non-optimal scale with

γ_{n} < 1

, Eq. A7 implies

m | {log}_{2} γ_{n} | < 1

. But, in a cyclic scale where

M > m

, the condition

k | {log}_{2} γ_{n} | < 1

\forall k

, stated in case (ii) is not fulfilled. An example of such a situation is the 29-tone scale, with

m = 12

and

M = 17

, where

| {log}_{2} γ_{n} |^{- 1} = 27.7

. The 28-th tone

ν_{28} = ϑ_{12}

(454.74 cents) is below

ϑ_{12}^{'}

(496.55 cents) more than a factor

2^{\frac{1}{29}}

(41.38 cents), and between

ϑ_{12}

and

ϑ_{13} = ν_{11}

there are two consecutive tones

ϑ_{11}^{'}

and

ϑ_{12}^{'}

of the 29-TET scale.

References

Clough, J.; Myerson, G. Variety and multiplicity in diatonic systems. Journal of Music Theory 1985, 29, 249–270. [Google Scholar] [CrossRef]
Clough, J.; Myerson, G. Musical scales and the generalized circle of fifths. Am. Math. Monthly 1986, 93, 695–701. [Google Scholar] [CrossRef]
Clough, J.; Douthett, J. Maximally even sets. Journal of Music Theory 1991, 35, 93–173. [Google Scholar] [CrossRef]
Douthett, J.; Krantz, R. Maximally even sets and configurations: common threads in mathematics, physics, and music. Journal of Combinatorial Optimization 2007, 14, 385–410. [Google Scholar] [CrossRef]
Pinkerton, R. Information theory and melody. Scientific American 1956, 194, 77–87. [Google Scholar] [CrossRef]
Youngblood, J. Style as information. Journal of Music Theory 1958, 2, 24–35. [Google Scholar] [CrossRef]
Lewin, D. Some applications of communication theory to the study of twelve-tone music. Journal of Music Theory 1968, 12, 50–84. [Google Scholar] [CrossRef]
Cohen, J. Information Theory and Music. Behavioral Science 1962, 7, 137–163. [Google Scholar] [CrossRef]
Knopoff, L.; Hutchinson, W. Information theory for musical continua. Journal of Music Theory 1981, 25, 17–44. [Google Scholar] [CrossRef]
Knopoff, L.; Hutchinson, W. Entropy as a measure of style: The influence of sample length. Journal of Music Theory 1983, 27, 75–79. [Google Scholar] [CrossRef]
Snyder, J. Entropy as a Measure of Musical Style: The Influence of a Priori Assumptions. Music Theory Spectrum 1990, 12, 121–160. [Google Scholar] [CrossRef]
Temperley, D. Music and Probability; The MIT Press, 2006. [CrossRef]
Sakellariou, J.; Tria, F.; Loreto, V.; Pachet, F. Maximum entropy models capture melodic styles. Scientific Reports 2017, 7, 9172. [Google Scholar] [CrossRef] [PubMed]
Gündüz, G. Entropy, energy, and instability in music. Physica A: Statistical Mechanics and its Applications 2023, 609, 128365. [Google Scholar] [CrossRef]
Arnold, V.; Avez, A. Ergodic Problems of Classical Mechanics; Mathematical physics monograph series, Benjamin, 1968.
Cubarsi, R. An alternative approach to generalized Pythagorean scales. Generation and properties derived in the frequency domain. Journal of Mathematics and Music 2020, 14, 266–291. [Google Scholar] [CrossRef]
Cubarsi, R. On the divisions of the octave in generalized Pythagorean scales and their bidimensional representation. Journal of Mathematics and Music 2024, 18, 1–19. [Google Scholar] [CrossRef]
Carey, N.; Clampitt, D. Aspects of Well-Formed Scales. Music Theory Spectrum 1989, 11, 187–206. [Google Scholar] [CrossRef]
Carey, N.; Clampitt, D. Two Theorems Concerning Rational Approximations. Journal of Mathematics and Music 2012, 6, 61–66. [Google Scholar] [CrossRef]
Carey, N.; Clampitt, D. Addendum to ”Two Theorems Concerning Rational Approximations”. Journal of Mathematics and Music 2017, 11, 61–63. [Google Scholar] [CrossRef]
Žabka, M. Generalized Tonnetz and well-formed GTS: A scale theory inspired by the Neo-Riemannians. In Mathematics and Computation in Music; Springer: Berlin, 2009; pp. 286–298. [Google Scholar]
Žabka, M. Well-Formedness in Two Dimensions: A Generalization of Carey and Clampitt’s Theorem. Journal of Mathematics and Music 2010, 4, 1–30. [Google Scholar] [CrossRef]
Hellegouarch, Y. Gammes naturelles. Gazette des Matematiciens, 1999; 82, 13–26. [Google Scholar]
Kassel, A.; Kassel, C. On Hellegouarch’s definition of musical scales. Journal of Mathematics and Music 2010, 4, 31–43. [Google Scholar] [CrossRef]
Loya, P. Amazing and Aesthetic Aspects of Analysis; Springer: New York, 2017. [Google Scholar]
Khinchin, A. Continued Fractions; University of Chicago: Chicago, 1964. [Google Scholar]
Milne, A.; Sethares, W.; Plamondon, J. Tuning continua and keyboard layouts. Journal of Mathematics and Music 2008, 2, 1–19. [Google Scholar] [CrossRef]
Sethares, W.; Milne, A.; Tiedje, S.; Prechtl, A.; Plamondon, J. Spectral Tools for Dynamic Tonality and Audio Morphing. Computer Music Journal 2009, 33, 71–84. [Google Scholar] [CrossRef]
Wilcox, A. Indices of Qualitative Variation; Oak Ridge National Lab.: Tennessee, 1967; No.ORNL-TM-1919. [Google Scholar]
Liern, V. On the construction, comparison, and exchangeability of tuning systems. Journal of Mathematics and Music 2015, 9, 197–213. [Google Scholar] [CrossRef]

1	Equalities that involve measures are understood to be true except in a null set, that is, strictly we should write $μ (M ∖ \cup_{i \in I} A_{i}) = 0$ , but we will not do it to simplify the notation.
2	It is also called metric entropy, and it consists in changing the metric of the theory of probabilities, i.e., the probability, by a generic metric, where the concepts relative to the partitions remain.
3	If the function of a random variable $f (x)$ is concave, the expected value satisfies $E (f (x)) \leq f (E (x))$ (Jensen’s inequality).
4	In general, for three measurable partitions $α, β, γ$ , $H (α \lor β / γ) = H (α / γ) + H (β / α \lor γ) \leq H (α / γ) + H (β / γ)$ .
5	The terms “good” and “best” rational approximation [25] are equivalent to best approximation “of the first kind” and “of the second kind”, respectively [26]. For the current case, the conditions mean: One-sided best approximation of ${{log}_{2} h}^{+}$ satisfies, if $γ_{n} < 1$ , $(〚 k 〛 + 1) - k {log}_{2} h > N - n {log}_{2} h > 0; 0 < k \leq n$ . One-sided best approximation of ${{log}_{2} h}^{-}$ satisfies, if $γ_{n} > 1$ , $0 < n {log}_{2} h - N < k {log}_{2} h - 〚 k 〛; 0 < k \leq n$ . Best rational approximation satisfies $0 < \| n {log}_{2} h - N \| < \| k {log}_{2} h - (〚 k 〛 + 1) \|$ and $0 < \| n {log}_{2} h - N \| < \| k {log}_{2} h - 〚 k 〛 \|; 0 < k \leq n$ . One-sided good approximation of ${{log}_{2} h}^{+}$ satisfies, if $γ_{n} < 1$ , $\frac{〚 k 〛 + 1}{k} - {log}_{2} h > \frac{N}{n} - {log}_{2} h > 0; 0 < k \leq n$ . One-sided good approximation of ${{log}_{2} h}^{-}$ satisfies, if $γ_{n} > 1$ , $0 < {log}_{2} h - \frac{N}{n} < {log}_{2} h - \frac{〚 k 〛}{k}; 0 < k \leq n$ . Good rational approximation satisfies $0 < \| {log}_{2} h - \frac{N}{n} \| < \| {log}_{2} h - \frac{〚 k 〛 + 1}{k} \|$ and $0 < \| {log}_{2} h - \frac{N}{n} \| < \| {log}_{2} h - \frac{〚 k 〛}{k} \|; 0 < k \leq n$ .
6	Since $b [z (\frac{a}{b}) + z (1 - \frac{a}{b})] = z (a) - z (b) + z (b - a)$ and $u - d = κ_{n}$ , it holds $u H (\frac{d}{u}, 1 - \frac{d}{u}) = z (d) - z (u) + z (κ_{n})$ .
7	This ratio has also been called efficiency and relative entropy [29].
8	The interval between two tones $ν_{1} < ν_{2}$ in $(0, \infty)$ is $I (ν_{2}, ν_{1}) = {log}_{2} ν_{2} - {log}_{2} ν_{1}$ .
9	Some of these intervals may have width zero, giving rise to a degenerate scale with less than n non-null intervals.
10	The function $Z (λ, a) = z (\frac{λ - a}{λ}) + z (\frac{λ + a}{λ})$ with $a > 0$ is defined for $λ \geq a$ , where satisfies $Z (λ, a) < 0$ , always increasing from $Z (a, a) = - 2$ until $Z (λ, a) \to 0$ when $λ \to \infty$ .
11	Between the notes $j = 83$ of the respective scales $E_{200}^{3}$ and $E_{200}^{⊤}$ there is a distance of nearly 1.5 elementary intervals of the equal temperament scale and between two consecutive notes of the cyclic scale there may be a distance equivalent to 2.1 regular intervals, what means that within some regular intervals there are two notes of the cyclic scale.
12	We must distinguish two cases: (a) $M > m$ , therefore $\frac{1}{n} < \frac{1}{M} < \frac{2}{n}$ and $\frac{2}{n} < \frac{1}{m}$ ; since $M u + m d = 1$ , we have $\frac{1}{n} < u < \frac{1}{M}$ and $0 < d < \frac{1}{n}$ , which does not add any new limitation. (b) $M < m$ , therefore $\frac{1}{n} < u < \frac{2}{n}$ and $\frac{1}{n} (1 - \frac{M}{m}) < d < \frac{1}{n}$ . Therefore, the extremes still correspond to n-tone scales by avoiding degenerate cases.
13	We must distinguish two cases: (a) $M > m$ , therefore $\frac{1}{n} < \frac{1}{M} < \frac{2}{n}$ and $\frac{2}{n} < \frac{1}{m}$ ; hence, $\frac{1}{n} < d < \frac{2}{n}$ and $\frac{1}{n} (1 - \frac{m}{M}) < u < \frac{1}{n}$ . Once again, the extremes correspond to n-tone scales, not degenerating toward scales of fewer tones. (b) $M < m$ , therefore $\frac{2}{n} < \frac{1}{M}$ and $\frac{1}{n} < \frac{1}{m} < \frac{2}{n}$ ; hence, $\frac{1}{n} < d < \frac{1}{m}$ and $0 < u < \frac{1}{n}$ , which does not add any new limitation.

Figure 1. Graphs of normalized entropy and bias.

Figure 2. Behavior of

| ϕ_{n} | = {log}_{2} κ_{n}

(red) and

θ_{n} = 1 - η_{n}

(blue) in terms of the number of tones n (bilogarithmic scales). In gray, maximum bias for several similarity levels to n-TET scales.

Figure 2. Behavior of

| ϕ_{n} | = {log}_{2} κ_{n}

(red) and

θ_{n} = 1 - η_{n}

(blue) in terms of the number of tones n (bilogarithmic scales). In gray, maximum bias for several similarity levels to n-TET scales.

Table 1. Properties of cyclic scales: GRA=Good rational approximation (accurate scale); RID=Regular interval distributed; BRA=Best rational approximation (optimal scale); MB=Minimal bias; I|Xn=maximum distance

\frac{1}{x n}

to a note of the n-TET scale.

\frac{1}{x n}

to a note of the n-TET scale.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Partition Entropy as a Measure of Regularity of Music Scales

Abstract

1. Introduction

2. Partition Entropy

3. Cyclic Scales

4. Entropy of a Cyclic Scale

5. Partition Modulation

5.1. Modulating Temperament Scales

5.2. Entropy in Terms of the Closure

6. Normalized Entropy

7. Bias of a Cyclic Scale

8. Scales with Limited Bias

8.1. Scale Distributed within Regular Intervals

8.2. Scale r-Similar to n-TET

8.3. Scale One-Side r-Similar to n-TET

9. Entropy of a Scale 1 λ n -OSS to n -TET

10. Entropy of a Scale 1 λ n -Similar to n -TET

11. Cyclic RID-Scales

11.1. Comma and Elementary Intervals of a RID-Scale

11.2. Bias of RID-Scales

11.3. Cyclic Scales of Minimal Bias

12. Conclusions

Funding

Conflicts of Interest

Abbreviations

Appendix A. Bounds for the Elementary Intervals and Closure of Cyclic Scales

Appendix B. Deviation of a Cyclic Scale from n-TET

References

MDPI Initiatives

Important Links

Subscribe

9. Entropy of a Scale $\frac{1}{λ n}$ -OSS to $n$ -TET

10. Entropy of a Scale $\frac{1}{λ n}$ -Similar to $n$ -TET