Cracking Factorization- Cryptography Challenges

Asset Durmagambetov; Aslan Durmagambetov

doi:10.20944/preprints202404.0125.v5

Preprint

Article

Cracking Factorization- Cryptography Challenges

This version is not peer-reviewed.

Asset Durmagambetov^*

,Aslan Durmagambetov

Asset Durmagambetov^*

,Aslan Durmagambetov

This version is not peer-reviewed.

Downloads

257

Views

Comments

Submitted:

08 April 2024

Posted:

10 April 2024

You are already at the latest version

Abstract

This article presents a description of a new method for solving the factorization problem, based on the gradient descent algorithm. This approach demonstrates significant improvements in efficiency compared to traditional methods proposed in previous research. This article describes a new method for solving the factorization problem, based on the gradient descent algorithm, and demonstrates the transition from algebraic methods to approaches based on functional analysis. The proposed approach not only improves the efficiency of solving the problem but also allows the application of computational algorithms of functional analysis, opening new possibilities for research and optimization.

Keywords:

Decryption

;

factorization problem

;

gradient descent algorithm

;

new method for solving

;

transition from algebraic methods to approaches based on functional analysis

Subject:

Computer Science and Mathematics - Security Systems

This preprints belongs to the Topic

Cyber Security and Critical Infrastructures, 2nd Edition

1. Introduction

The factorization problem, involving finding the prime factors of a composite number, is one of the fundamental challenges in the field of cryptography and number theory. This problem has gained widespread attention due to its application in the RSA encryption algorithm, proposed by Rivest, Shamir, and Adleman [1]. The complexity of the factorization task underlies the security of many cryptographic systems.

In recent years, several methods have been proposed to solve the factorization problem. For instance, the quadratic sieve algorithm and the number field sieve method [2] demonstrate high efficiency when dealing with numbers of a specific size. However, despite their success, they face significant computational limitations as the size of the input data increases.

With the development of quantum technologies, new interest has arisen in factorization algorithms specifically designed for quantum computers. Shor’s algorithm [3], proposed in 1994, is one such example, demonstrating the theoretical possibility of solving the factorization task in polynomial time on a quantum computer.

In this work, we propose an innovative approach to the factorization problem, utilizing the gradient descent method, which, we hope, will open new horizons in the research of this area [4,5].

2. Problem Formulation

Our research results show that applying gradient descent—a method widely used in functional analysis—to the factorization problem is not only feasible but also leads to significant improvements in efficiency compared to traditional algebraic approaches. This discovery underscores the importance of transitioning to functional methods in studying and solving the factorization problem. The task of factorization involves finding the prime factors of a given composite number. This task remains computationally challenging, especially for large numbers, making it one of the main problems in contemporary cryptography. Traditionally, the problem of number factorization was considered purely an algebraic task. In this work, we propose a new formulation for it using the following function:

f (x) = \frac{M}{x} - ⌊\frac{M}{x}⌋

where M is a composite number, and then the task of finding factors turns into a task of searching for the minima of this function.

3. Results

Here, we consider the gradient descent method, which allows for effectively finding the prime factors of a number. Consider the function:

f (x) = \frac{M}{x} - ⌊\frac{M}{x}⌋

(1)

Theorem 1.

Let M be a composite integer,

then the zeros of

f (x)

determine the factors of the number M

f (x)

is infinitely differentiable in the intervals between local minima.

Proof.

The proof follows from the fact that when

f (x)

is nullified, the number

\frac{M}{x} = ⌊\frac{M}{x}⌋

from which it follows that

y = \frac{M}{x}

is an integer. And since

y \cdot x = M

we obtain the integer factors of the number M. Infinite differentiability follows from the infinite differentiability of the function

{x}

. □

4. Data Analysis and Visualization

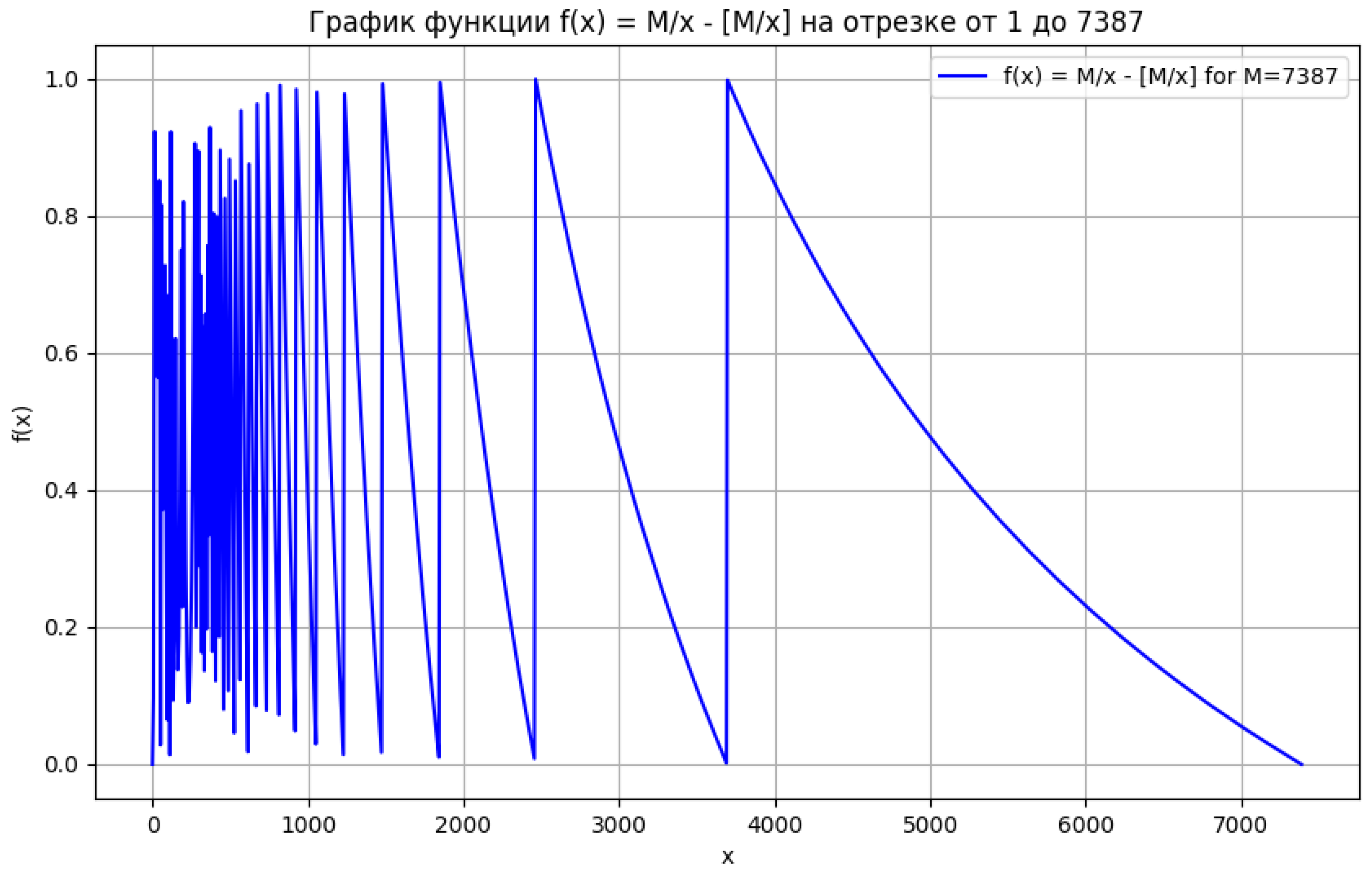
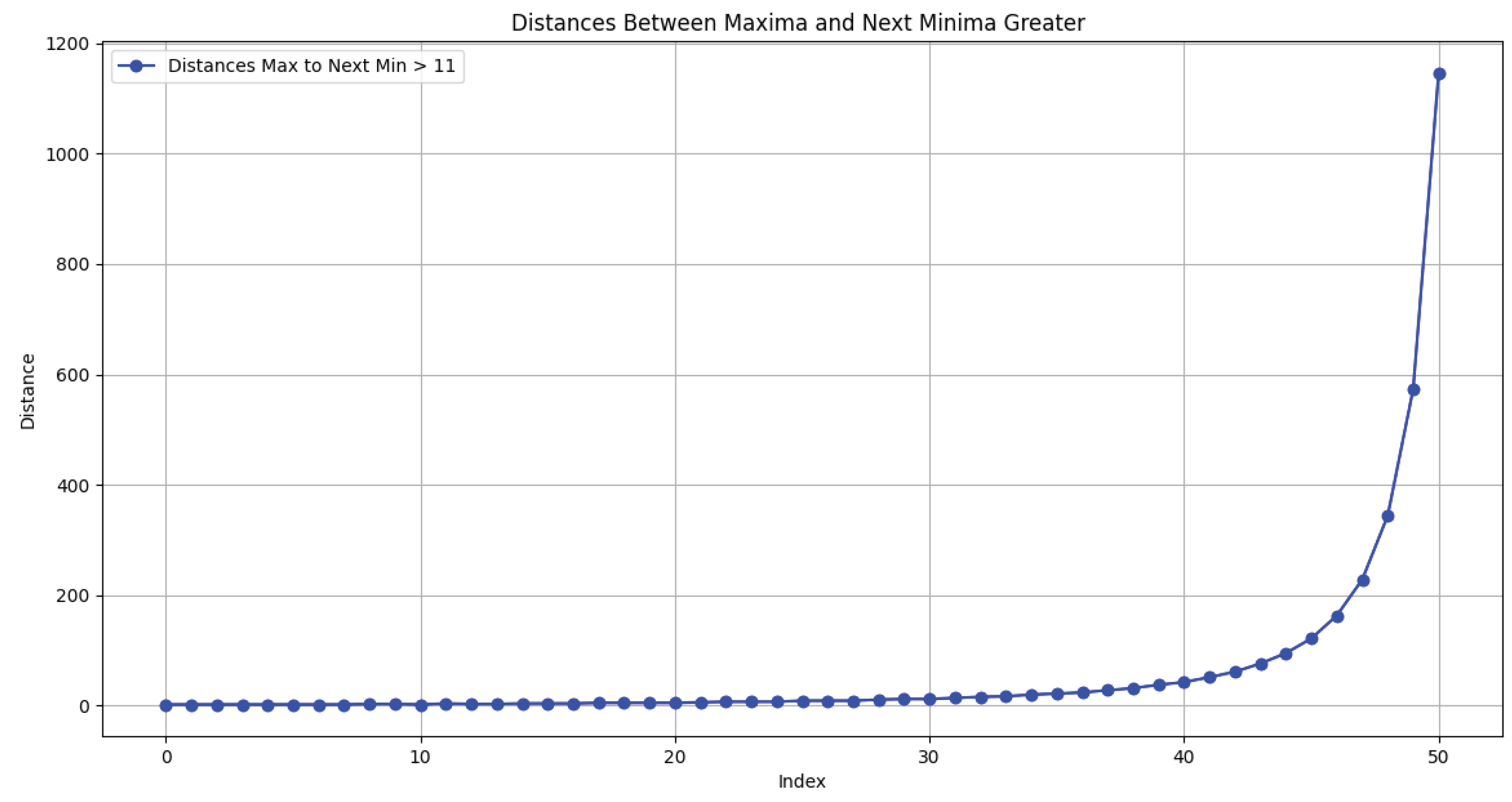
In this section, we present the main numerical methods used for analyzing the factorization task, as well as the visualization of the obtained results. An important part of the research is the application of the gradient descent method to find local minima of the function

f (x) = \frac{M}{x} - ⌊\frac{M}{x}⌋

, which allows us to visually demonstrate the effectiveness of the proposed approach to factorization.

Theorem 2.

If M is a composite number, then for the derivative within the smoothness intervals, it is valid that:

\frac{d f (x)}{d x} = - \frac{M}{x^{2}}

(2)

\frac{{x_{0}}^{2}}{M} < (x_{1} - x_{0}) < \frac{{x_{1}}^{2}}{M}

(3)

(x_{1} - x_{0}) = \frac{{x_{0}}^{2}}{M} + O (\frac{{x_{0}}^{3}}{M})

(4)

Proof.

The proof follows direct verification within the smoothness interval. The graphs show that the distance between adjacent zeros changes slightly at small x. Let’s estimate more precisely, calculate the difference in function values at the point of local maximum

x_{0}

and at the point of local minimum

x_{1}

, and use Lagrange’s Theorem, which asserts that there exists a point

x_{0} < θ < x_{1}

such that:

1 - 0 = f (x_{0}) - f (x_{1}) = \frac{d f (x)}{d x} |_{θ} (x_{1} - x_{0}) = - \frac{M}{θ^{2}} (x_{1} - x_{0})

\frac{θ^{2}}{M} = (x_{1} - x_{0})

\frac{{x_{0}}^{2}}{M} < (x_{1} - x_{0}) < \frac{{x_{1}}^{2}}{M}

The second equation follows upon examining the decomposition into higher order components. □

Theorem 3.

If M is a composite number, then the number of intervals is estimated by:

N < M^{5 / 8} + \sqrt{M}

(5)

Proof.

Consider the segments

[\sqrt{M}, M^{5 / 8}], [M^{5 / 8}, M^{3 / 4}], [M^{3 / 4}, M]

Count the number of intervals between local extrema for each separate segment,

within the first segment, we can take the actual number of points on this segment, which significantly exceeds the number of intervals. On the second segment, consider that according to Theorem 3, the length of an interval is determined by the formula

\frac{{x_{0}}^{2}}{M} < (x_{1} - x_{0}) < \frac{{x_{1}}^{2}}{M}

(6)

therefore, the number of intervals is estimated by the formula

M^{3 / 4 - 2 / 8}

since the distance between adjacent extrema is greater than

M^{2 / 8}

and correspondingly, on the last segment, the distance between extrema is greater than

\sqrt{M}

, therefore the number of intervals between adjacent extrema is less than

\frac{M}{\sqrt{M}} = \sqrt{M}

N < M^{5 / 8} - \sqrt{M} + M^{3 / 4 - 2 / 8} + M^{1 - 1 / 2}

N < M^{5 / 8} - \sqrt{M} + M^{1 / 2} + M^{1 - 1 / 2} < M^{5 / 8} + \sqrt{M}

from which we derive the theorem’s statement. □

The obtained result shows that such an approach is feasible, but at this stage, it only demonstrates the idea. Let’s move on to more substantial applications of this idea.

Theorem 4.

M = p q

, where

p, q

are prime numbers and

0 < δ < 1

, and

x_{i} = \{\frac{M}{i}\}

for

i + k < δ * p

, and

i + m < δ * p

. then

x_{i + k} - x_{i + m} = - \frac{q}{p} (k - m) + O ({(\frac{q (i + k - p)}{p})}^{2}) + O ({(\frac{q (i + m - p)}{p})}^{2})

Proof.

Let

x_{i} = \{\frac{M}{i}\}

(7)

x_{i} = \{\frac{p q}{p + i - p}\} = \{\frac{p q}{p (1 + \frac{i - p}{p})}\} =

x_{i} = \{\frac{p q}{p (1 + \frac{i - p}{p})}\} = \{\frac{q}{(1 + \frac{i - p}{p})}\} =

\{- \frac{q}{(1 + \frac{i - p}{p})}\}

= \{- \frac{q (i - p)}{p} + O ({(\frac{q (i - p)}{p})}^{2})\}

x_{i + k} = \{- \frac{q (i + k - p)}{p} + O ({(\frac{q (i + k - p)}{p})}^{2})\}

x_{i + k} = \{1 - \frac{q}{p} (i + k - p) + O ({(\frac{q (i + k - p)}{p})}^{2}) + O ({(\frac{q (i - p)}{p})}^{2})\}

Taking the difference of values for

k, m

, we get

x_{i + k} - x_{i + m} = - \frac{q}{p} (k - m) + O ({(\frac{q (i + k - p)}{p})}^{2}) + O ({(\frac{q (i + m - p)}{p})}^{2})

from which we have a monotonically decreasing sequence. By calculating the slope

\frac{q}{p}

, we obtain a value, resulting in a system of equations

p q = M, \frac{p}{q} = C + O ({(\frac{q (i + k - p)}{p})}^{2})

(8)

from which we obtain the theorem’s statement. □

The obtained results show that such an approach has the potential for further development. Below are Figure 1 and 2 demonstrating the analyzed function and the distribution of distances between its local maxima and minima. These graphs are important for visualizing the behavior of the function and confirming the effectiveness of the proposed method. According to Theorem 2 and Theorem 3, we have the ability to control intervals and construct fast algorithms for calculating local minima.

5. Conclusion

The course of this research marked an important transition in understanding the factorization task: from a traditional algebraic approach to one based on principles of functional analysis. This paradigm shift allows us to consider the factorization task not just as a search for numerical solutions, but as an optimization problem in a multidimensional functional space. Such an approach opens doors for the use of powerful functional analysis methods and accompanying computational algorithms, which was successfully demonstrated using the gradient descent method. In conclusion, the approach to factorization through gradient descent and its interpretation within the framework of functional analysis open new horizons for research and development in the fields of mathematics, cryptography, and computational technology. We expect that our research will make a significant contribution to the scientific community and stimulate further work in this direction. Data analysis and visualization are key aspects of this research, allowing not only to confirm theoretical assumptions but also to visually demonstrate the advantages of the proposed method.

References

Rivest, R. L., Shamir, A., & Adleman, L. "A method for obtaining digital signatures and public-key cryptosystems." Communications of the ACM, vol. 21, no. 2, 1978, pp. 120-126.
Lenstra, A. K., Lenstra, H. W., Manasse, M. S., & Pollard, J. M. "The number field sieve." Proceedings of the twenty-second annual ACM symposium on Theory of computing, 1990, pp. 564-572.
Shor, P. W. "Algorithms for quantum computation: Discrete logarithms and factoring." Proceedings 35th annual symposium on foundations of computer science, 1994, pp. 124-134.
Overmars, Anthony and Venkatraman, Sitalakshmi. "Mathematical Attack of RSA by Extending the Sum of Squares of Primes to Factorize a Semi-Prime." Math. Comput. Appl., vol. 25, no. 4, 2020, p. 63. [CrossRef]
Overmars, Anthony and Venkatraman, Sitalakshmi. "New Semi-Prime Factorization and Application in Large RSA Key Attacks." J. Cybersecur. Priv., vol. 1, no. 4, 2021, pp. 660–674. [CrossRef]

Figure 1. Graph of the function

f (x)

highlighting local maxima and minima.

Figure 1. Graph of the function

f (x)

highlighting local maxima and minima.

Figure 2. Distances between maxima and the following minima, greater than a given threshold.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

257

Views

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Cracking Factorization- Cryptography Challenges

Abstract

Keywords:

Subject:

1. Introduction

2. Problem Formulation

3. Results

4. Data Analysis and Visualization

5. Conclusion

References

MDPI Initiatives

Important Links

Subscribe