Prerpints.org logo
Preprint
Article

A Non-isothermal Curing Kinetic Studies of Novolac Type Phenol-Formaldehyde Resin for 3D Printing of Sustainable Building Design

Altmetrics

Downloads

115

Views

94

Comments

0

supplementary.docx (565.31KB )

Submitted:

26 March 2024

Posted:

27 March 2024

You are already at the latest version

Alerts
Abstract
Novolac phenol-formaldehyde resins have gained extensive commercial utilization across diverse applications due to their exceptional mechanical, thermal, and chemical resistance properties. In this investigation, we successfully synthesized a traditional novolac, and a biobased novolac phenol-formaldehyde resin by partially substituting phenol with a bio-oil obtained from the organic phase resulting from the fast pyrolysis of pinewood biomass. Despite extensive investigations into the curing behavior of novolac resins crosslinked with hexamethylenetetramine (HMTA) through numerous model-fitting cure kinetic studies, a comprehensive model for predicting the crosslinking of bio-based phenol-formaldehyde resins in the presence of HMTA has not yet been studied. The primary objective of this research was to compare and apply several commonly used kinetic models to predict the degree of curing and cure rate of the synthesized resins, using DSC dynamic measurements. Our results demonstrated that the autocatalytic model exhibited excellent fitting for the traditional novolac resin and HMTA mixture, while the Kamal model showed better fitting with the experimental data obtained for the bio-based phenol-formaldehyde resin and HMTA system. In addition, the results evidenced a significant drop in the curing temperature by partially replacing phenol with bio-oil. Additionally, the results revealed a notable reduction in curing temperature when phenol was partially substituted with bio-oil. This substitution not only offers environmental benefits but also promotes energy efficiency and enhances production safety. The data collected in this study is pivotal for our subsequent research endeavors, which aim to develop environmentally sustainable materials optimized for use in 3D printing manufacturing processes.
Keywords: 
Subject: Chemistry and Materials Science  -   Polymers and Plastics

1. Introduction

The rapid increase in the world's population has led to extensive utilization of building materials and construction-related energy and resources, resulting in direct and indirect environmental and human impacts [1]. Several approaches have been employed to reduce energy consumption in building construction including the sustainable framework, which remarkably alleviates adverse environmental and human impacts through efficient and sustainable material and thoughtful design [2].
In the material design approach, the use of novolac-type phenol-formaldehyde (NPF) resins is considered advantageous because of the reduced formaldehyde emission and their excellent functional properties, such as processability, strength, adhesion, and thermal and chemical stability [3]. These resins are produced from acid-catalyzed condensation polymerization reaction between phenol and formaldehyde, using an excess of phenol reactant (P/F molar ratio 1:0.8). NPF resins are linear or partially cross-linked polymers characterized by phenol moieties connected by methylene bridges. The curing reaction occurs at elevated temperatures in the presence of hardener (typically hexamethylenetetramine, HMTA), during which three-dimensional network polymer structures are formed [4]. The cross-linking reaction between NPF resin and HMTA occurs in two stages [5]. In the first stage, intermediates such as benzoxazines and benzylamines are formed. In the second stage, these intermediates decompose and react to form methylene linkages between phenolic rings for chain extension and further cross-linking [6]. However, synthesizing NPF resins still relies on nonrenewable resources, which are associated with the rapid depletion of fossil fuels and increasing concerns for the environment and individual’s health [7]. Thus, significant research is being conducted to explore renewable biomass materials as alternative feedstock to the petroleum-derived compounds. Thermochemically derived materials are considered advantageous sources for bio-based monomers, including phenolic compounds, as they can be obtained during the thermochemical conversion of biomass. These derivatives can serve as an alternative reagent during polymer resin synthesis [8,9,10].
In addition to material development, thoughtful structural design plays a significant role in creating sustainable building components. Three-dimensional printing (3DP), also known as additive manufacturing (AM), has proven to be one of the key sustainable technologies for constructing buildings as it reduces material waste and facilitates efficient, customized design at a lower cost [11]. 3DP techniques create composite materials and structures layer by layer through cross-linking or curing of thermosets polymeric resins or other materials [12].
Among all the 3DP techniques, direct ink writing (DIW) has been proven effective in the fabrication of thermoset composites. This extrusion-based additive manufacturing method deposits layer-by-layer and cures them simultaneously or post-printing via photocuring or thermal curing [13,14,15]. Thermal curing is especially suitable for thermo-reactive polymeric resins like NPF that cannot be cross-linked by photocuring, which uses ultraviolet light irradiation (UV). The thermal curing approach involves mixing two separate streams of resin and hardener, extruding the mixture on a heating bed, and then curing the material rapidly. However, this curing process is limited to geometries with a few layers of material, and is not suitable for printing of freeform structures [16]. One promising curing strategy to overcome these limitations is thermal frontal polymerization (FP), whereby curing polymerization of thermoset polymeric resins occurs rapidly via localized exothermic reaction zone through the coupling of thermal diffusion and Arrhenius reaction kinetics [16,17,18,19].
Understanding the curing kinetics of a polymeric resin is fundamental to 3D printing polymeric materials and transforming them into a solid polymeric structure, as the curing reaction mechanism strongly influences the resulting polymer properties [20]. The most popular and accurate technique used to study the curing reactions of various thermosetting resins is differential scanning calorimetry (DSC) [21,22]. DSC measures the heat flow of the sample as a function of temperature and time, and after that, the generated data is extensively used to estimate the kinetic parameters through two primary thermal kinetic analysis methods: isothermal and non-isothermal [23,24]. The isothermal method studies the reaction mechanism at a specific temperature; while the non-isothermal method includes a single or multi-heating rate [25]. The non-isothermal process has significant advantages compared to the isothermal method [26]. Two approaches, the model-free (isoconversional) method and the model-fitting method, are primarily used to fit the experimental data acquired from isothermal or non-isothermal DSC curves to estimate the activation energy and kinetic parameters [27].
Zhang et al. [28] explored the curing behavior of novolac phenol-formaldehyde resin, employing both model-fitting and model-free (isoconversion) kinetic methods. The study utilized a piecewise model, which has demonstrated effectiveness in describing the curing behavior of novolac resin. Despite the thorough investigations carried out on the curing process of the phenol-formaldehyde resin, no prior scientific inquiry has been conducted specifically on the curing kinetics of biobased phenol-formaldehyde resin synthesized by partially substituting phenol with bio-oil (derived from fast pyrolysis of pinewood) wherein preparation procedure of biobased resin closely follows the methodology outlined in a previously published article.
The primary objective of the present study was to thoroughly investigate the curing behavior of the biobased novolac phenol-formaldehyde (BNPF) resin. The Differential Scanning Calorimetry (DSC) technique was used to thoroughly examine the curing process of the resin from initiation to completion. DSC data were analyzed to determine a comprehensive set of curing kinetic parameters, using non-isothermal experimental runs at various heating rates. Both model-free (isoconversional) and model-fitting approaches were employed in our investigation. The insights derived from this study are pivotal for understanding the curing kinetics of the BNPF resin, and this knowledge can guide the optimization of the resin manufacturing processes, leading to the production of high-performance materials from sustainable resources. Ultimately, our findings seek to promote the utilization of BNPF resins in 3D printing technologies, fostering a greener manufacturing paradigm.

2. Experimental Section

2.1. Materials

Phenol crystals (99%), formalin solution (37% formaldehyde in water), hexamethylenetetramine (HMTA, >99%), and acetone (99.5%) were obtained from VWR International. Oxalic acid (anhydrous crystal, 98.0%) was purchased from Spectrum Chemical Mfg. Corp. Bio-oil, prepared by the procedure described previously [29], was received from the Center for Renewable Carbon Laboratory, University of Tennessee. All compounds purity information can be found in the supporting information section in Table S1.

2.2. Synthesis of Novolac PF Resin and Bio-Based Novolac PF Resin

Novolac phenol-formaldehyde (NPF) and bio-based novolac phenol-formaldehyde (BNPF) resins were synthesized by phenol reaction with formaldehyde, according to the previously published article [9]. Briefly, to a four-necked round 500 mL bottom flask equipped with a condenser, a dropping funnel, and a mechanical stirrer were charged phenol (94 g, 1 mol) and oxalic acid (4.70 g, 0.05 mol). The mixture was heated to 90 °C, and 37% formalin solution (64.87 g, 0.8 mol of formaldehyde) was dropped into it slowly. The reaction was allowed to continue at 90 °C for a total time of 3 hours. The reaction product was washed with distilled water and dried in a vacuum oven. The biobased novolac PF was prepared with the same procedure by partially replacing (50% w/w) phenol with bio-oil. The reaction mechanism of bio-based novolac resin is presented in Figure S1. The characterization of the synthesized resin was reported in our previous journal [9] and the corresponding FTIR and [1]H-NMR results added in the supporting information as Figure S2 and Figure S3, respectively.

2.3. Thermal Analysis

The curing reaction of NPF/HMTA and BNPF/HEXA was studied using a differential scanning calorimeter, DSC TA-Q2000 (Thermal Analysis Instruments, DE, USA), under a nitrogen atmosphere with a gas flux rate of 50 mL/min. Before any sample measurement, the DSC instrument was calibrated with pure indium standard. The samples, NPF/HMTA and BNPF/HMTA were prepared with HMTA to resin weight ratio of 15% and ground manually with mortar and pestle. For each measurement, the sample (3.0 – 5.0 mg) was weighed into the aluminum standard pan and sealed with an aluminum lid.
The DSC non-isothermal technique investigated the curing behavior of both NPF/HMTA and BNPF/HMTA resins. First, the thermal data was obtained by increasing heating samples from 25 °C to 25 °C at various heating rates (5, 10, 15, and 25 °C/min). When the curing reaction ended, the samples were cooled to 25 °C with a cooling rate of 5, 10, 15, and 25 °C/min, respectively. In the next step, a non-isothermal curing experiment was performed with the respective heating rates to determine the reaction's residual heat. The curing reactions of NPF/HMTA and BNPF/HMTA resins are presented in Figure 1a and Figure 1b, respectively.
Origin Pro 2019 software (Origin Lab Corporation, USA) and MATLAB R2022a (version 9.0) were used to analyze thermal curing data.
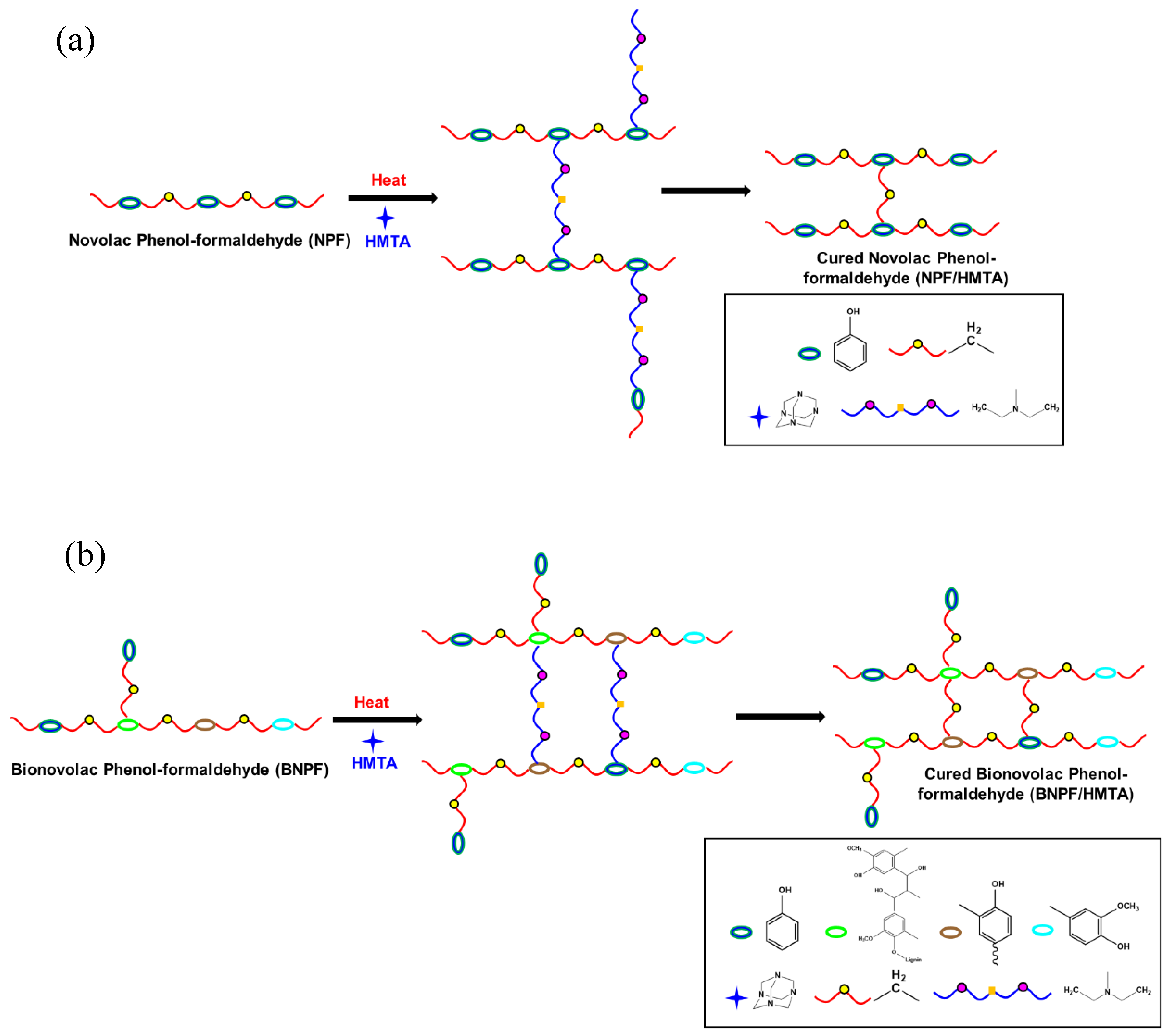
Preprints 102280 g001
Figure 1. The curing process of (a) novolac phenol-formaldehyde resin and HMTA (NPF/HMTA) and (b) bionovolac phenol-formaldehyde resin and HMTA (BNPF/HMTA).
Figure 1. The curing process of (a) novolac phenol-formaldehyde resin and HMTA (NPF/HMTA) and (b) bionovolac phenol-formaldehyde resin and HMTA (BNPF/HMTA).
Preprints 102280 g001

2.4. Fundamental Theory of Curing Kinetics

Curing reaction kinetics are performed to present the relationship between the process rates and different experimental parameters. The thermal data obtained from non-isothermal DSC technique of NPF/HMTA and BNPF/HMTA resins at different heating rates were used to calculate kinetic parameters.
The conversion of curing reaction or degree of curing (α) is directly proportional to the exothermic heat evolved during the curing process [30,31]. The degree of curing (α) can be expressed from Eq (1)
α T = Δ H T Δ H t o t a l
where, Δ H T is the heat of reaction at a specific temperature, T, and Δ H t o t a l is the total heat of reaction, which is determined by calculation the area under the exothermic curve. The curing reaction was assumed to be complete when the non-isothermal exothermic peak of resins leveled off to the baseline.
The rate of the kinetic process is considered to be directly proportional to the measured heat flow and can be determined by Eq (2)
d α d t = d H d t Δ H t o t a l
where, d α / d t is the curing kinetic reaction rate, d H / d t is heat flow measured during the kinetic process. For constant heating rate scans, d α / d t can be expressed as d α / d t = β   d α / d T at constant where β is the heating rate (K min-[1]).
The phenomenological curing kinetic model analysis is parametrized into two main functions [27] according to the following Eq (3) [32]
d α d t = k T f α
where, k T temperature-dependent kinetic rate constant and f α is the function of curing conversion [33]. The function k T can be expressed through Arrhenius relationship as shown by Eq (4) [32]
k T = A exp ⁡ − E R T
where, A is the Arrhenius frequency factor or pre-exponential factor (s-1), E is the activation energy (J mol-1), R is the universal gas constant (8.314 J mol-1 K-1), and T is the absolute temperature (K) of the sample. Combining Eq (3) and Eq (4) yields kinetic Eq (5)
d α d t = A exp ⁡ − E R T f α
Curing kinetic reactions are often analyzed by two primary methodologies, i.e., model-fitting kinetic and model-free Isoconversional kinetic methods. In the former process kinetic model is used to fit the experimental data to estimate the kinetic parameters [34]. On the other hand, the model-free isoconversional kinetic method obeys isoconversional principle [34,35].

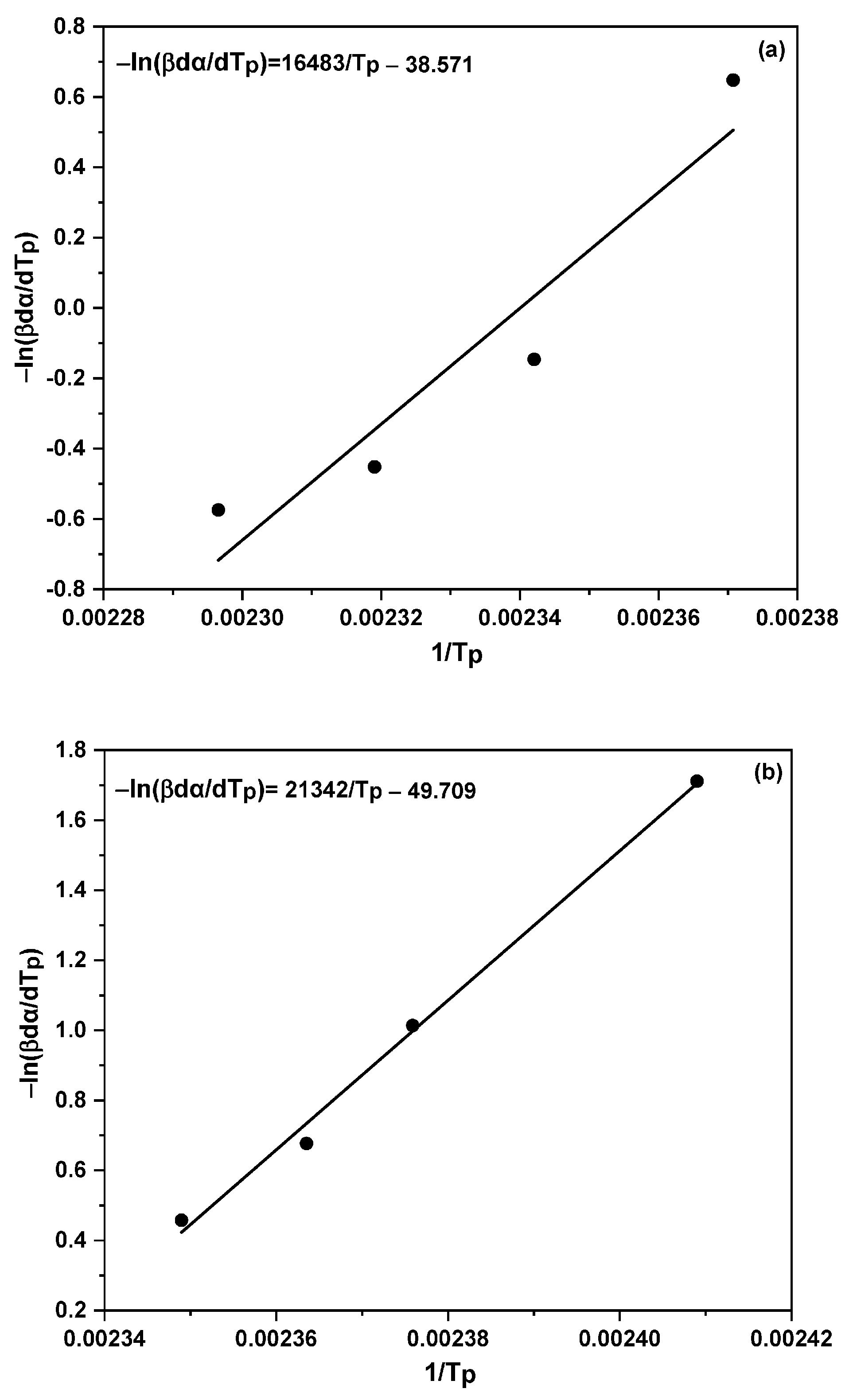
2.5. Model-Free Isoconversional Method

The model-free (isoconversional) is a useful method to determine the mechanism of curing, and the basic assumption of this method is that the reaction rate is merely a function of temperature at a constant extent of curing degree, whose analytical expression can be written by Eq (6) [34,35,36].
∂ ln ⁡ d α / d t ∂ T − 1 = − E R
The most commonly used methods include Friedman [37], Flynn-Wall-Ozawa (FWO) [38,39], Kissinger-Akahira-Sunnose (KAS) [40], and Vyazovkin [34,41,42]. These model-free isoconversional methods are used to calculate the re-activation energy (E) without assuming any specific expression of the reaction model.

2.6. Model-Fitting Method

The mechanism of curing reaction of resin that is related to the curing kinetic reaction model f α , can be divided into three kinetic models: nth-order model, autocatalytic model, and Kamal-Sourour model [33,43,44]. These models can be expressed by Eq (7), Eq (8), and Eq (9), respectively.
nth-order kinetics model can be expressed as
d α d t = A exp ⁡ − E R T 1 − α n
The autocatalytic kinetic model can be expressed as
d α d t = A exp ⁡ − E R T 1 − α n α m
The Kamal kinetic model can be expressed as
d α d t = k 1 1 − α n + k 2 1 − α n α m
where m and n are the reaction orders, k 1 = A 1 e x p ⁡ ( − E 1 / R T ) and k 2 = A 2 e x p ⁡ ( − E 2 / R T ) are the kinetic constants. A1 and A2 are the corresponding pre-exponential parameters, and E1 and E2 are the activation energies.

3. Results and Discussion

3.1. Non-Isothermal DSC Analysis of NPF/HMTA and BNPF/HMTA Resins

Isothermal and non-isothermal DSC measurements were performed to measure the heat of the reaction and investigate the curing process of NPF/HMTA and BNPF/HMTA resins and understand the curing behavior of developed NPF/HMTA and BNPF/HMTA resins. The isothermal approach yielded higher testing errors, similar to those previously reported for other systems [45]. Therefore, the non-isothermal DSC technique was adopted.
The non-isothermal DSC thermograms of the NPF/HMTA and BNPF/HMTA resins with different heating rates of 5, 10, 15, and 25 °C/min are shown in Figure 2a and Figure 2b, respectively. Each of these thermograms displays the exothermic peaks associated with the cross-linking reactions of the NPF/HMTA and BNPF/HMTA resins, and the peak temperature (Tp) inferred from these exothermic peaks is summarized in Table 1. All the curing exothermic peaks and characteristic peak temperatures shifted to higher temperatures with the increasing heating rates (ꞵ = 5-20 °C/min). The increments mentioned before can be attributed to the following: as more heat is released with an increased heating rate, the temperature gradient between the reaction center and the external environment due to thermal inertia increases [35,45,46]. The exothermic peak temperature is believed to shift to a higher temperature zone for compensation [47]. The DSC curves of BNPF/HMTA resin show two distinct exothermic peaks. The first broad exotherm is ascribed to the curing reaction, and the small exotherm at higher temperatures can be attributed to side reactions occurring during the heating process. One possible explanation for the side reactions is that other chemical groups may interact with the HMTA intermediates. Still, the exotherm is very small and was neglected in the present study. Hence, only the exotherm's first curing peak was considered for kinetic analysis.

3.2. Model-Fitting Method

The goal in the model-fitting kinetic analysis of NPF/HMTA and BNPF/HMTA resins was to find the four kinetic parameters (A, E, n, m), described in equations 7, 8, and 9 associated with the curing system according to a suitable reaction model. To examine the kinetic model, activation energy (E) is calculated by inserting (β = dT/dt) in Eq (6) and taking the logarithmic form of it (as reported in Eq. (10)), through the relation of the peak temperature (Tp) dependency on the heating rate (ꞵ). Assuming an isofractional peak temperature (Tp = Constant), activation energy E is determined by a linear regression analysis of ln(βdα/dTp) against 1/Tp across various heating rates (5, 10, 15 and 25 K/min) as reported in Eq (10) and shown in Figure 3.
E = R d − l n β d α / d T p d 1 / T p
Using the activation energy and according to the choice of the appropriate kinetic model, the reaction order (n or m) and the frequency factor (A) are calculated.
For nth-order model, by taking the logarithmic form of Eq (7), which is reported in the theory section, and expressing it in Eq (11)
ln ⁡ d α d t + E R T = n ln ⁡ 1 − α + ln ⁡ A
By applying the linear regression method to Eq (11), the values of n and A are obtained through the slope and intercept (ln A), respectively.
For the autocatalytic model, by taking the logarithmic form of Eq (8), which is reported in the theory section, and expressing it in Eq (12)
ln ⁡ d α d t + E R T = n ln ⁡ 1 − α + m ln ⁡ α + ln ⁡ A
A multilinear regression method is applied to Eq (12) for determining the values of A, n, and m. Here, for autocatalytic model, the overall order of reactions (m + n) is determined either with constraint (m + n = 2) or without constraint (m + n = 2).
Whereas, in the case of the Kamal model, a nonlinear regression method is used to estimate the kinetic parameters and reaction orders (n and m). In addition, for Kamal model, different condition were applied to investigate the kinetic constants k1 and k2 (E1 = E2 & m + n = 2, E1 = E2 & m + n ≠ 2, E1 ≠ E2 & m + n = 2 and E1 ≠ E2 & m + n ≠ 2). MATLAB R2022a software (version 9.0) is used to evaluate these parameters.
Once the kinetic parameters are determined at each heating rate for the nth-order model (E, A, and n), autocatalytic model (E, A, m and n), and Kamal model (E1, E2, A1, A2, m, and n), respectively, the next step is to fit the experimental data using the model and kinetic parameters to obtain the degree of curing (α) and reaction rate (dα/dt) at each temperature. Curing kinetic model results by fitting models are shown in Table 2.
It can be observed that the extent of conversion (α) plots for both NPF/HMTA and BNPF/HMTA depicted in Figure 4 and Figure 6 shows the sigmoid profile, i.e., the slow increase in α at the beginning and end of the curing process, while the quick increment at the intermediate stage. Whereas increasing heating rates leads to shifting these conversions (α) curves to higher temperature zones, this behavior shows good agreement with other studies [45].
According to the model fitting results for NPF/HMTA resin, the autocatalytic model shows a suitable fit for the experimental results, as shown in Figure 4 and Figure 5. This is because the autocatalytic curing mechanism controls the entire curing reaction of NPF/HMTA resin, as the intermediate products generated during the curing process catalyze the reaction with the higher order of reaction (n), and the reaction rate reaches the maximum at the middle of the reaction stage. Smaller reaction order is observed (m), where the reaction's curing rate decreases. Our results are in accordance with the published works [43,48,49].
As depicted in Figure 6 and Figure 7, the Kamal model shows superior predictability for monitoring the curing mechanism of the BNPF/HMTA resin, as the kinetic model shows good agreement with the experimental data. The Kamal model is a combination of the nth-order and autocatalytic models. The initial stage of the curing process, where the curing agent decomposes to produce intermediated that reacts with the novolac resin, is controlled by the autocatalytic reactions in later stages. The nth-order reaction mechanism controls it because the reaction rate decreases due to less availability of the free phenol and phenolic hydroxyl groups.
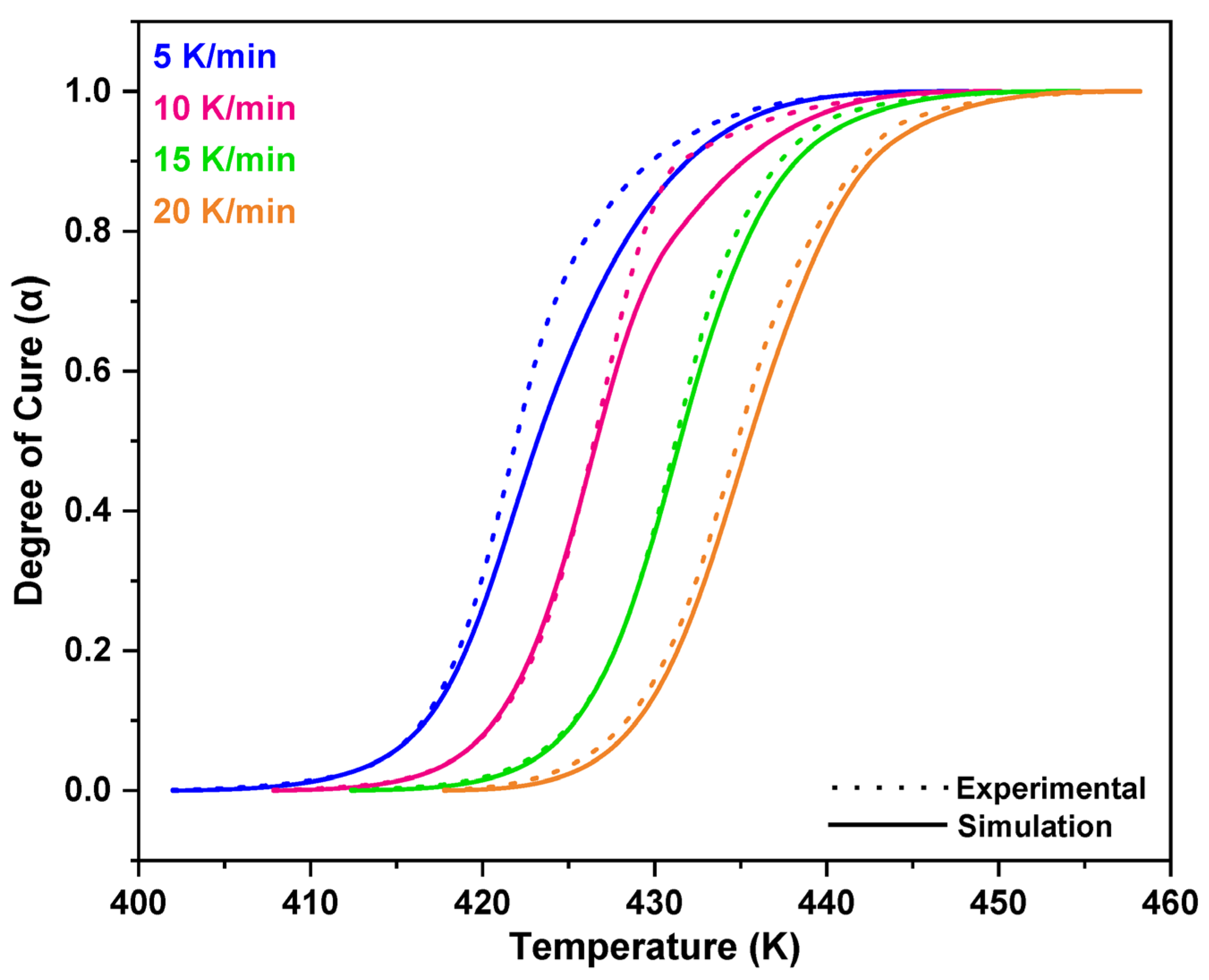
Preprints 102280 g004
Figure 4. Plot for conversion (α) as a function of temperature for the experimental and simulation results for NPF/HMTA resin at different heating rates.
Figure 4. Plot for conversion (α) as a function of temperature for the experimental and simulation results for NPF/HMTA resin at different heating rates.
Preprints 102280 g004
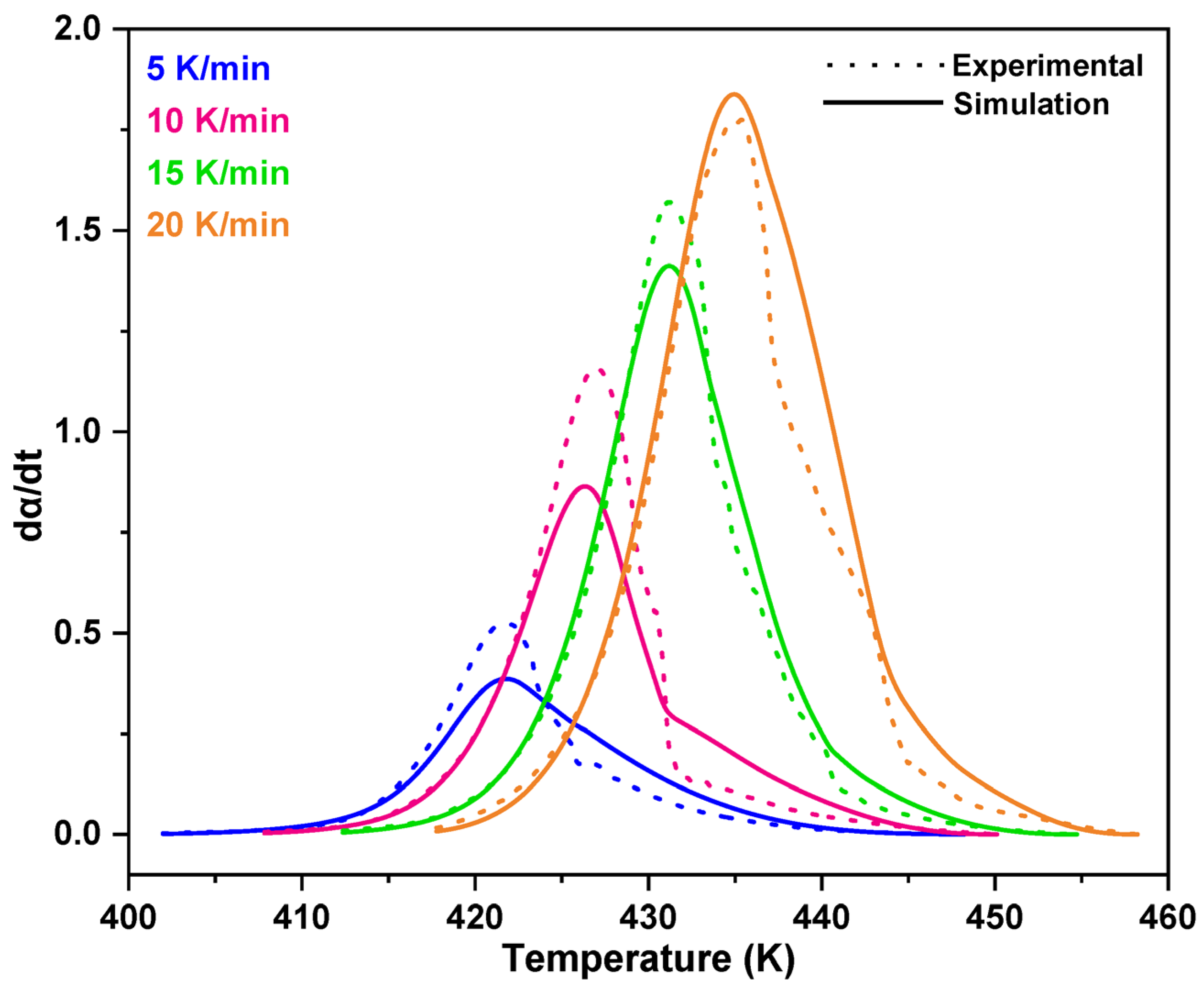
Preprints 102280 g005
Figure 5. Plot for reaction rate ( d α / d t ) as a function of temperature for the experimental and simulation results for NPF/HMTA resin at different heating rates.
Figure 5. Plot for reaction rate ( d α / d t ) as a function of temperature for the experimental and simulation results for NPF/HMTA resin at different heating rates.
Preprints 102280 g005
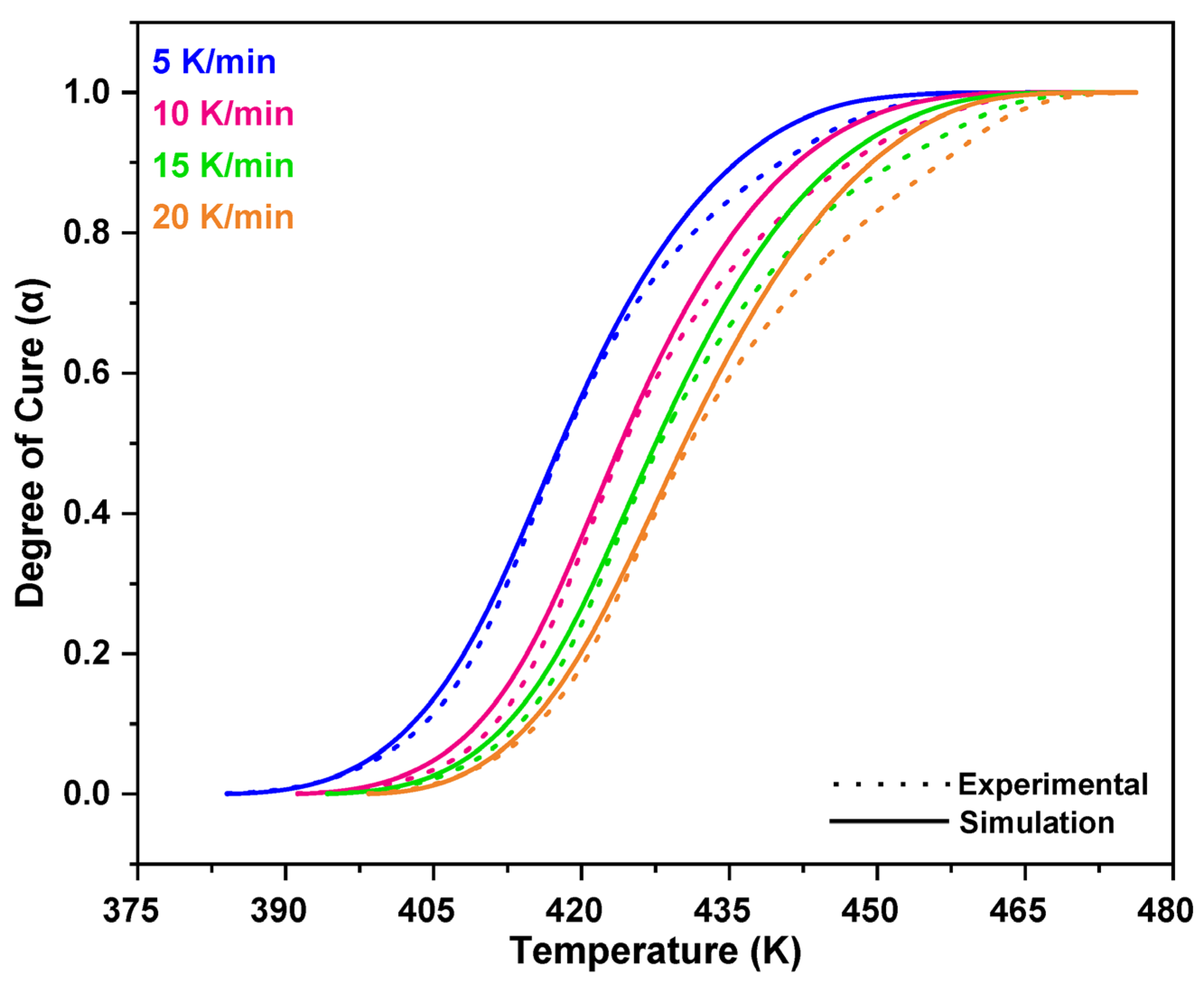
Preprints 102280 g006
Figure 6. Plot for conversion (α) as a function of temperature for the experimental and simulation results for BNPF/HMTA resin at different heating rates.
Figure 6. Plot for conversion (α) as a function of temperature for the experimental and simulation results for BNPF/HMTA resin at different heating rates.
Preprints 102280 g006
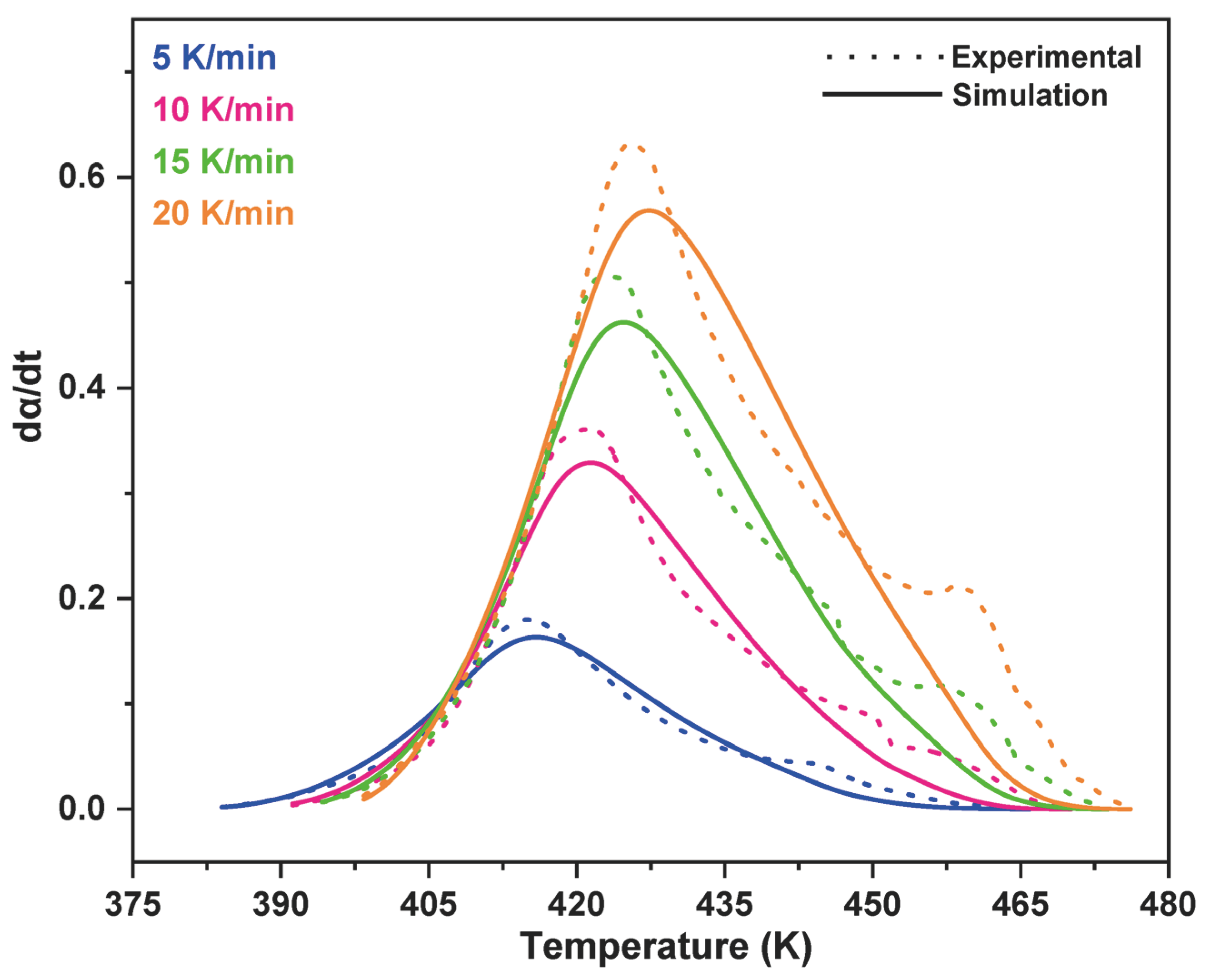
Preprints 102280 g007
Figure 7. Plot for reaction rate ( d α / d t ) as a function of temperature for the experimental and simulation results for BNPF/HMTA resin at different heating rates.
Figure 7. Plot for reaction rate ( d α / d t ) as a function of temperature for the experimental and simulation results for BNPF/HMTA resin at different heating rates.
Preprints 102280 g007

4. Conclusions

The kinetics of the curing reaction of novolac type PF resin system, i.e., NPF/HMTA and BNPF/HMTA resins, was investigated in this study with non-isothermal DSC measurements. The simulation data are verified against the experimental data for both NPF and BNPF resins. The results showed that an autocatalytic simulation model for curing NPF/HMTA resin was adapted to fit the experimental data and showed good agreement with the simulation model. At the same time, a Kamal model is employed and proved a best-fitting model in describing the curing behavior of the BNPF/HMTA resin. The curing process of BNPF/HMTA resin follows the autocatalytic mechanism at the earlier curing stage, while the nth-order kinetic mechanism controls the later part of curing. Insights of this research provide valuable and significant kinetic information for BNPF resin application in 3D printing.

Supplementary Materials

This section is not mandatory, but may be added if there are patents resulting from the work reported in this manuscript.

Acknowledgments

This research was supported by NSF-CREST Center for Sustainable Lightweight Materials (C-SLAM), grant number #1735971 and PrinTimber NSF EPSCoR RII Track-2 FEC # 2119809.

TOC

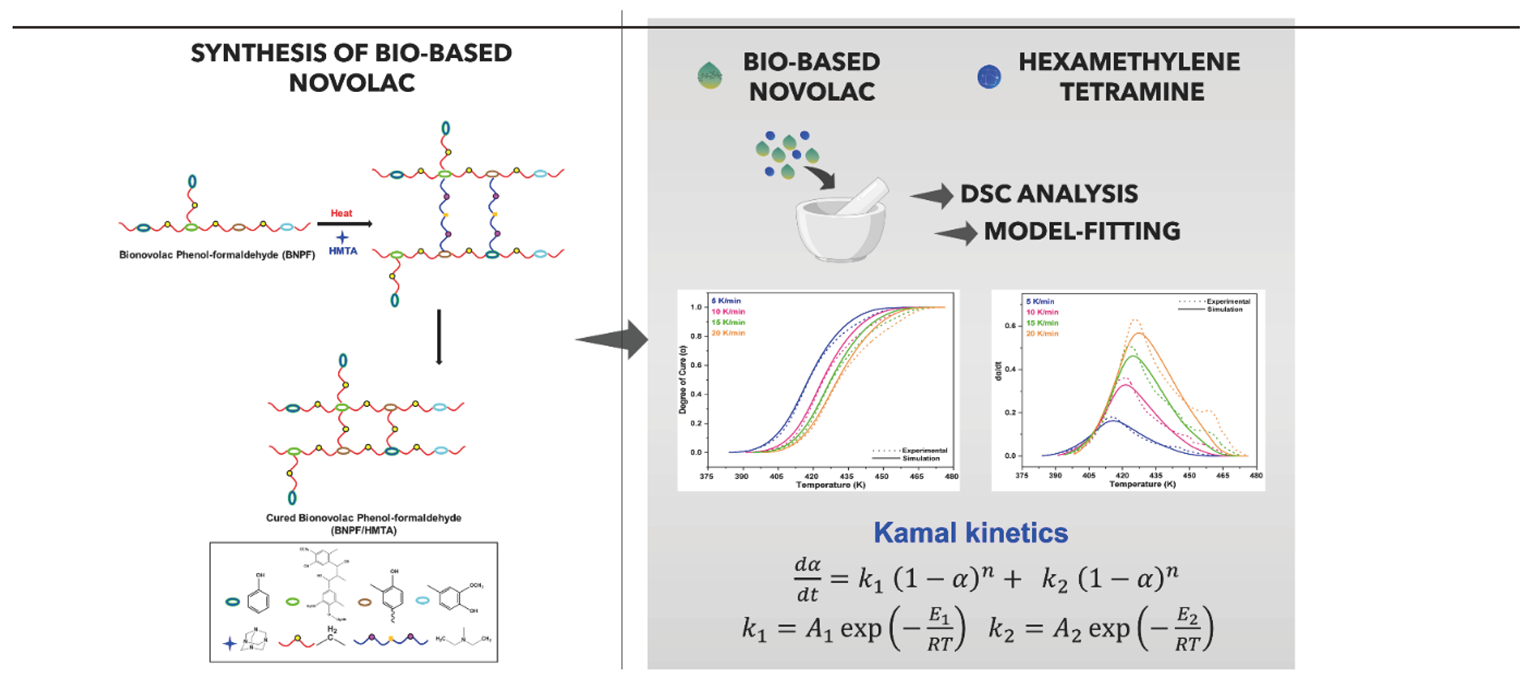Preprints 102280 i001

References

  1. Zhang, Y.; Wang, F.; Duvigneau, J.; Wang, Y.; Wang, B.; Feng, X.; Mao, Z.; Vancso, G.J.; Sui, X. Highly Stable and Nonflammable Hydrated Salt-Paraffin Shape-Memory Gels for Sustainable Building Technology. ACS Sustain. Chem. Eng. 2021, 9, 15442–15450. [Google Scholar] [CrossRef]
  2. Ertelt, M.J.; Hilbig, H.; Grosse, C.U.; Lieleg, O. Small Pores, Big Impact—Controlling the Porosity Allows for Developing More Sustainable Construction Materials. ACS Sustain. Chem. Eng. 2021. [Google Scholar] [CrossRef]
  3. Yan, N.; Zhang, B.; Zhao, Y.; Farnood, R.R.; Shi, J. Application of Biobased Phenol Formaldehyde Novolac Resin Derived from Beetle Infested Lodgepole Pine Barks for Thermal Molding of Wood Composites. Ind. Eng. Chem. Res. 2017, 56, 6369–6377. [Google Scholar] [CrossRef]
  4. Milazzo, M.; Amoresano, A.; Pasquino, R.; Grizzuti, N.; Auriemma, F.; De Stefano, F.; Sin Xicola, A.; Iodice, V.; De Rosa, C. Curing Efficiency of Novolac-Type Phenol–Formaldehyde Resins from Viscoelastic Properties. Macromolecules 2021, 54, 11372–11383. [Google Scholar] [CrossRef]
  5. Zhang, X.; Solomon, D.H. Chemistry of Novolac/Furfuryl Alcohol Resins Cured with Hexamethylenetetramine: A Solid-State NMR Study. Chem. Mater. 1998, 10, 1833–1840. [Google Scholar] [CrossRef]
  6. De Medeiros, E.S.; Agnelli, J.A.M.; Joseph, K.; De Carvalho, L.H.; Mattoso, L.H.C. Curing Behavior of a Novolac-Type Phenolic Resin Analyzed by Differential Scanning Calorimetry. J. Appl. Polym. Sci. 2003, 90, 1678–1682. [Google Scholar] [CrossRef]
  7. Mahajan, J.S.; O’Dea, R.M.; Norris, J.B.; Korley, L.S.T.J.; Epps, T.H. Aromatics from Lignocellulosic Biomass: A Platform for High-Performance Thermosets. ACS Sustain. Chem. Eng. 2020, 8, 15072–15096. [Google Scholar] [CrossRef]
  8. Nolan Wilson, A.; Price, M.J.; Mukarakate, C.; Katahira, R.; Griffin, M.B.; Dorgan, J.R.; Olstad, J.; Magrini, K.A.; Nimlos, M.R. Integrated Biorefining: Coproduction of Renewable Resol Biopolymer for Aqueous Stream Valorization. ACS Sustain. Chem. Eng. 2017, 5, 6615–6625. [Google Scholar] [CrossRef]
  9. Bansode, A.; Barde, M.; Asafu-adjaye, O.; Patil, V.; Hinkle, J.; Via, B.K.; Adhikari, S.; Adamczyk, A.J.; Farag, R.; Elder, T.; Labb, N.; Auad, M.L. Synthesis of Biobased Novolac Phenol − Formaldehyde Wood Adhesives from Biore Fi Nery-Derived Lignocellulosic Biomass. ACS Sustain. Chem. Eng. 2021. [Google Scholar] [CrossRef]
  10. Asafu-Adjaye, O.A.; Street, J.; Bansode, A.; Auad, M.L.; Peresin, M.S.; Adhikari, S.; Liles, T.; Via, B.K. Fast Pyrolysis Bio-Oil-Based Epoxy as an Adhesive in Oriented Strand Board Production. Polymers 2022, 14, 1244. [Google Scholar] [CrossRef]
  11. Hager, I.; Golonka, A.; Putanowicz, R. 3D Printing of Buildings and Building Components as the Future of Sustainable Construction? Procedia Eng. 2016, 151, 292–299. [Google Scholar] [CrossRef]
  12. Trifol, J.; Jayaprakash, S.; Baniasadi, H.; Ajdary, R.; Kretzschmar, N.; Rojas, O.J.; Partanen, J.; Seppälä, J.V. 3D-Printed Thermoset Biocomposites Based on Forest Residues by Delayed Extrusion of Cold Masterbatch (DECMA). ACS Sustain. Chem. Eng. 2021, 9, 13979–13987. [Google Scholar] [CrossRef]
  13. Shahzad, A.; Lazoglu, I. Direct Ink Writing (DIW) of Structural and Functional Ceramics: Recent Achievements and Future Challenges. Compos. Part B Eng. 2021, 225. [Google Scholar] [CrossRef]
  14. Shen, L.; Wang, T.P.; Lee, T.H.; Forrester, M.; Becker, A.; Torres, S.; Pearson, C.; Cochran, E.W. 3D Printable All-Polymer Epoxy Composites. ACS Appl. Polym. Mater. 2021, 3, 5559–5567. [Google Scholar] [CrossRef]
  15. Wang, B.; Arias, K.F.; Zhang, Z.; Liu, Y.; Jiang, Z.; Sue, H.J.; Currie-Gregg, N.; Bouslog, S.; Pei, Z.; Wang, S. 3D Printing of In-Situ Curing Thermally Insulated Thermosets. Manuf. Lett. 2019, 21, 1–6. [Google Scholar] [CrossRef]
  16. Ziaee, M.; Johnson, J.W.; Yourdkhani, M. 3D Printing of Short-Carbon-Fiber-Reinforced Thermoset Polymer Composites via Frontal Polymerization. ACS Appl. Mater. Interfaces 2022. [Google Scholar] [CrossRef]
  17. Mariani, A.; Fiori, S.; Chekanov, Y.; Pojman, J.A. Frontal Ring-Opening Metathesis Polymerization of Dicyclopentadiene [5]. Macromolecules 2001, 34, 6539–6541. [Google Scholar] [CrossRef]
  18. Pojman, J.A. Frontal Polymerization; Elsevier B.V., 2012; Volume 4. [Google Scholar] [CrossRef]
  19. Goli, E.; Parikh, N.A.; Yourdkhani, M.; Hibbard, N.G.; Moore, J.S.; Sottos, N.R.; Geubelle, P.H. Frontal Polymerization of Unidirectional Carbon-Fiber-Reinforced Composites. Compos. Part A Appl. Sci. Manuf. 2020, 130, 105689. [Google Scholar] [CrossRef]
  20. Zheng, T.; Xi, H.; Wang, Z.; Zhang, X.; Wang, Y.; Qiao, Y.; Wang, P.; Li, Q.; Li, Z.; Ji, C.; Wang, X. The Curing Kinetics and Mechanical Properties of Epoxy Resin Composites Reinforced by PEEK Microparticles. Polym. Test. 2020, 91, 106781. [Google Scholar] [CrossRef]
  21. El-Thaher, N.; Mekonnen, T.; Mussone, P.; Bressler, D.; Choi, P. Nonisothermal DSC Study of Epoxy Resins Cured with Hydrolyzed Specified Risk Material. Ind. Eng. Chem. Res. 2013, 52, 8189–8199. [Google Scholar] [CrossRef]
  22. Chaiwan, P.; Kaewkittinarong, A.; Pumchusak, J. Nonisothermal Curing Kinetics of Solid Resole by Differential Scanning Calorimetry. Thermochim. Acta 2019, 675, 119–126. [Google Scholar] [CrossRef]
  23. Um, M.K.; Daniel, I.M.; Hwang, B.S. A Study of Cure Kinetics by the Use of Dynamic Differential Scanning Calorimetry. Compos. Sci. Technol. 2002, 62, 29–40. [Google Scholar] [CrossRef]
  24. Heinze, S.; Echtermeyer, A.T. A Practical Approach for Data Gathering for Polymer Cure Simulations. Appl. Sci. 2018, 8, 2227. [Google Scholar] [CrossRef]
  25. Chandran, M.S.; Krishna, M.; Rai, S.; Krupashankara, M.S.; Salini, K. Cure Kinetics and Activation Energy Studies of Modified Bismaleimide Resins. ISRN Polym. Sci. 2012, 2012, 1–8. [Google Scholar] [CrossRef]
  26. Ma, H.; Zhang, X.; Ju, F.; Tsai, S.B. A Study on Curing Kinetics of Nano-Phase Modified Epoxy Resin. Sci. Rep. 2018, 8, 1–15. [Google Scholar] [CrossRef]
  27. Yang, G.; Lee, J.K. Curing Kinetics and Mechanical Properties of Endo -Dicyclopentadiene Synthesized Using Different Grubbs’ Catalysts. Ind. Eng. Chem. Res. 2014, 53, 3001–3011. [Google Scholar] [CrossRef]
  28. Zhang, C.; Binienda, W.K.; Zeng, L.; Ye, X.; Chen, S. Kinetic Study of the Novolac Resin Curing Process Using Model Fitting and Model-Free Methods. Thermochim. Acta 2011, 523, 63–69. [Google Scholar] [CrossRef]
  29. Kim, P.; Weaver, S.; Noh, K.; Labbé, N. Characteristics of Bio-Oils Produced by an Intermediate Semipilot Scale Pyrolysis Auger Reactor Equipped with Multistage Condensers. Energy and Fuels 2014, 28, 6966–6973. [Google Scholar] [CrossRef]
  30. Thomas, R.; Sinturel, C.; Pionteck, J.; Puliyalil, H.; Thomas, S. In-Situ Cure and Cure Kinetic Analysis of a Liquid Rubber Modified Epoxy Resin. Ind. Eng. Chem. Res. 2012, 51, 12178–12191. [Google Scholar] [CrossRef]
  31. Patel, A.; Maiorana, A.; Yue, L.; Gross, R.A.; Manas-Zloczower, I. Curing Kinetics of Biobased Epoxies for Tailored Applications. Macromolecules 2016, 49, 5315–5324. [Google Scholar] [CrossRef]
  32. Perejón, A.; Sánchez-Jiménez, P.E.; Criado, J.M.; Pérez-Maqueda, L.A. Kinetic Analysis of Complex Solid-State Reactions. A New Deconvolution Procedure. J. Phys. Chem. B 2011, 115, 1780–1791. [Google Scholar] [CrossRef]
  33. Yang, G.; Yuan, Z.; Yang, Z.; Zhang, M. Nonisothermal Curing Kinetics of a Novel Polymer Containing Phenylsilylene and Propargyl-Hexafluorobisphenol a Units. J. Appl. Polym. Sci. 2013, 127, 3178–3185. [Google Scholar] [CrossRef]
  34. Wan, J.; Li, C.; Fan, H.; Li, B.G. Branched 1,6-Diaminohexane-Derived Aliphatic Polyamine as Curing Agent for Epoxy: Isothermal Cure, Network Structure, and Mechanical Properties. Ind. Eng. Chem. Res. 2017, 56, 4938–4948. [Google Scholar] [CrossRef]
  35. Mashouf Roudsari, G.; Mohanty, A.K.; Misra, M. Study of the Curing Kinetics of Epoxy Resins with Biobased Hardener and Epoxidized Soybean Oil. ACS Sustain. Chem. Eng. 2014, 2, 2111–2116. [Google Scholar] [CrossRef]
  36. Li, J.; Qiao, Y.; Zong, P.; Wang, C.; Tian, Y.; Qin, S. Thermogravimetric Analysis and Isoconversional Kinetic Study of Biomass Pyrolysis Derived from Land, Coastal Zone, and Marine. Energy and Fuels 2019, 33, 3299–3310. [Google Scholar] [CrossRef]
  37. Friedman, H.L. Kinetics of Thermal Degradation of Char-Forming Plastics from Thermogravimetry. Application to a Phenolic Plastic. J. Polym. Sci. Part C Polym. Symp. 2007, 6, 183–195. [Google Scholar] [CrossRef]
  38. Hao, H.; Chang, T.; Cui, L.; Sun, R.; Gao, R. Theoretical Study on the Mechanism of Hydrogen Donation and Transfer for Hydrogen-Donor Solvents during Direct Coal Liquefaction. Catalysts 2018, 8, 648. [Google Scholar] [CrossRef]
  39. Langtry, B.N. Identity And Spatio-Temporal Continuity. Australas. J. Philos. 1972, 50, 184–189. [Google Scholar] [CrossRef]
  40. Blaine, R.L.; Kissinger, H.E. Homer Kissinger and the Kissinger Equation. Thermochim. Acta 2012, 540, 1–6. [Google Scholar] [CrossRef]
  41. Vyazovkin, S. Evaluation of Activation Energy of Thermally Stimulated Solid-State Reactions under Arbitrary Variation of Temperature. J. Comput. Chem. 1997, 18, 393–402. [Google Scholar] [CrossRef]
  42. Hosseinpour, A.; Nazockdast, H.; Behzad, T.; Salimijazi, H.R. Investigation of the Cure Kinetics of an Epoxy Resin by Advanced Isoconversional and Model-Fitting Methods. AIP Conference Proceedings 2016. [Google Scholar] [CrossRef]
  43. Zhang, C.; Binienda, W.K.; Zeng, L.; Ye, X.; Chen, S. Kinetic Study of the Novolac Resin Curing Process Using Model Fitting and Model-Free Methods. Thermochim. Acta 2011, 523, 63–69. [Google Scholar] [CrossRef]
  44. Li, S.; Järvelä, P. Application of a Model-Free Isoconversional Method to the Cure of Phenolic Systems. J. Polym. Sci. Part B Polym. Phys. 2001, 39, 1525–1528. [Google Scholar] [CrossRef]
  45. Ma, S.; Fan, H.; Zhang, N.; Li, W.; Li, Y.; Li, Y.; Huang, D.; Zeng, L.; Shi, X.; Ran, X.; Xu, H. Investigation of a Low-Toxicity Energetic Binder for a Solid Propellant: Curing, Microstructures, and Performance. ACS Omega. 2020, 30538–30548. [Google Scholar] [CrossRef] [PubMed]
  46. Zhan, X.; Liu, H.; Zhang, J. Two Branched Silicone Resins with Different Reactive Groups: A Comparative Evaluation. Ind. Eng. Chem. Res. 2018, 57, 5606–5615. [Google Scholar] [CrossRef]
  47. Zhou, Z.; Si, Q.; Wan, L.; Kuo, S.W.; Zhou, C.; Xin, Z. Curing Kinetics of Main-Chain Benzoxazine Polymers Synthesized in Continuous Flow. Ind. Eng. Chem. Res. 2022, 61, 2947–2954. [Google Scholar] [CrossRef]
  48. Horadam, W.; Venkat, N.; Tran, T.; Bai, L.; Josyula, K.; Mehta, V. Leaching Studies on Novolac Resin-Coated Proppants-Performance, Stability, Product Safety, and Environmental Health Considerations. J. Appl. Polym. Sci. 2018, 135. [Google Scholar] [CrossRef]
  49. Domínguez, J.C.; Alonso, M.V.; Oliet, M.; Rojo, E.; Rodríguez, F. Kinetic Study of a Phenolic-Novolac Resin Curing Process by Rheological and DSC Analysis. Thermochim. Acta 2010, 498, 39–44. [Google Scholar] [CrossRef]
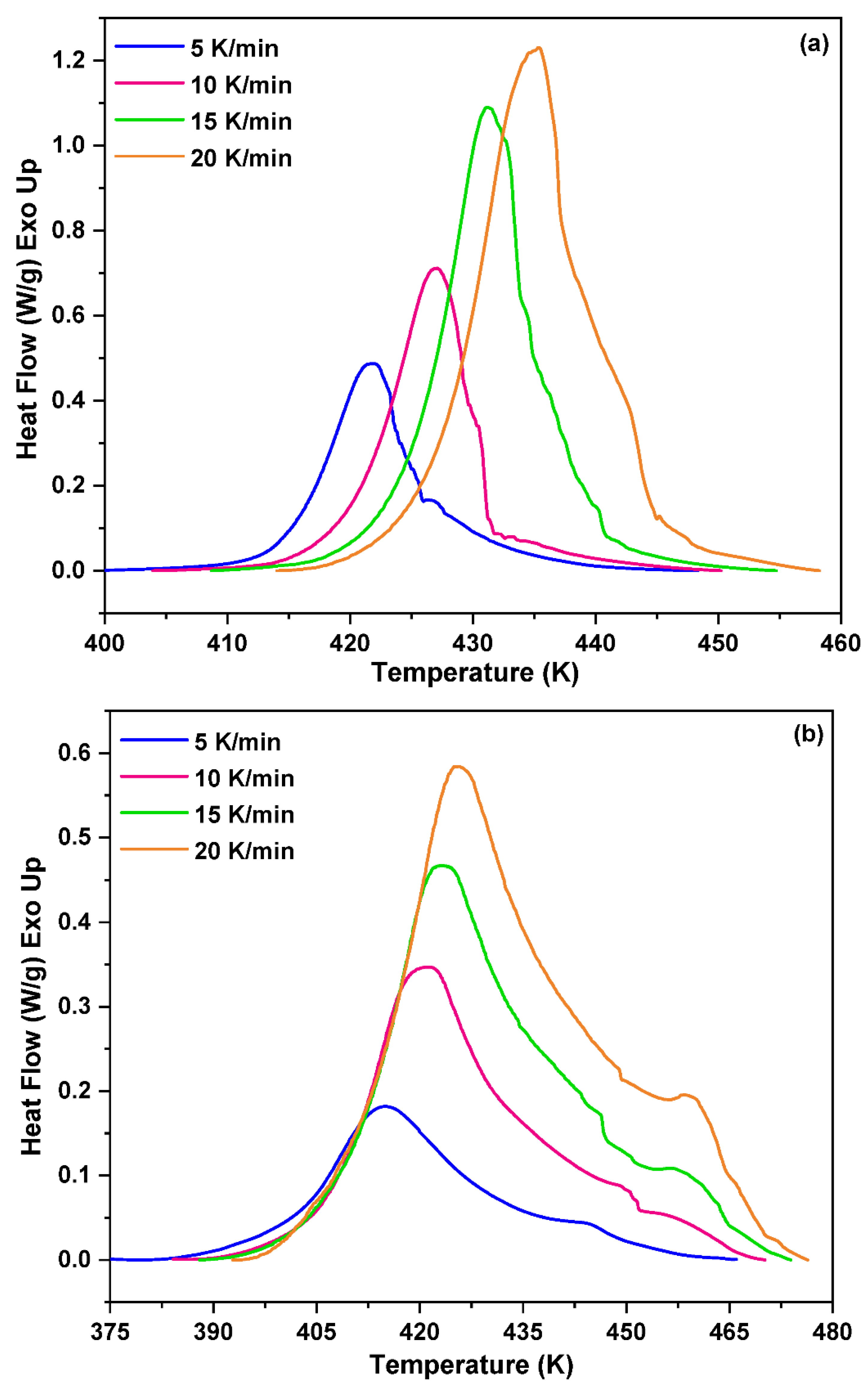
Preprints 102280 g002
Figure 2. Nonisothermal DSC scanning thermograms of the thermal curing reactions of (a) NPF/HMTA resin and (b) BNPF/HMTA resin at different heating rates (5, 10, 15, and 20 K/min).
Figure 2. Nonisothermal DSC scanning thermograms of the thermal curing reactions of (a) NPF/HMTA resin and (b) BNPF/HMTA resin at different heating rates (5, 10, 15, and 20 K/min).
Preprints 102280 g002
Preprints 102280 g003
Figure 3. Activation energy determination of the (a) NPF/HMTA resin and (b) BNPF/HMTA resin systems.
Figure 3. Activation energy determination of the (a) NPF/HMTA resin and (b) BNPF/HMTA resin systems.
Preprints 102280 g003
Table 1. Characteristic Parameters of the curing reactions of NPF/HMTA and BNPF/HMTA.
Table 1. Characteristic Parameters of the curing reactions of NPF/HMTA and BNPF/HMTA.
Heating rate (ꞵ)
(K/min)		 NPF/HMTA resin BNPF/HMTA resin
TP (K) TP (K)
5 421.81 415.11
10 426.97 420.90
15 431.21 423.10
20 435.44 425.72
NPF, novolac phenol-formaldehyde resin. BNPF, bio-based novolac phenol-formaldehyde resin. HMTA, hexamethyl tetraamine (hardener). Tp, Curing peak temperature.
Table 2. Curing kinetic results by the autocatalytic model and Kamal model.
Table 2. Curing kinetic results by the autocatalytic model and Kamal model.
Resins Ea (KJ/mol) A (min-[1]) n m
NPF/HMTA 137.00 1.982 × 10[17] 1.2342 0.7658
BNPF/HMTA 1.195
E1=E2		 A1=1.734 ×10-[8]
A2=3.038		 1.1948 0.8051
NPF, novolac phenol-formaldehyde resin. BNPF, bio-based novolac phenol-formaldehyde resin. HMTA, hexamethyl tetraamine (hardener). Ea, activation energy. A, pre-exponential parameters.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated