1. Introduction
One of the most important electronic devices for scientists is solar cells. This comes from that energy is the spirit of modern technology. One of the most preferable energy sources is the solar energy. This is because it is almost available everywhere and is pollution-free. The most popular solar energy technology is the one that converts solar energy to electricity(Wasisto et al., 2019). This comes from the fact that electric energy can be converted easily to other useful energy form. Petr. The widely used and commercially available cells are silicon solar cells (Meneghini et al.,2021). Unfortunately, silicon cells are expensive and have complex fabrication processes (石黒浩三, 1964). This encourages researchers to try to search for new generations (Raymond & Serway, 2013). The so-called Nano solar cells are now thought to be the best candidate (Li et al., 2022; Nazeeruddin, 2001). Different types of Nano cells were suggested. These include polymer cells, zinc, and copper oxide cells (Srivastava et al., 2020). The development of such cells is based on the so-called Nanoscience (Vall et al., 2021). Nanoscience is a new branch of physics that describes the behavior of Nanomaterials. Nanomaterials are in the form of isolated particles having dimensions ranging from 1 up to 300 Nanometers. The behavior of such materials obeys the laws of quantum mechanics (Schricker et al., 2014; Tantra). Unlike bulk matter, the physical properties of nanomaterials can be easily controlled and changed by changing the nanocrystal size, geometry, orientation, and chemical composition. Among these cells, the most promising are perovskite cells.
All materials with the crystal structure as ABX3 structure are considered perovskite, where A and B are cations. A is usually an alkaline or rare earth element, B is a transition metal, and X is, an anion that may be an oxide or halogen. One has two perovskite types, inorganic perovskite, and organic-inorganic hybrid perovskite.
The perovskite cell consists in general of a perovskite active layer sandwiched between two layers. One of them is the electron transport layer (ETL) which acts as an n-type semiconductor allowing electrons transport from the active layer. The other layer is the hole transport layer (HTL) which resembles a p-type semiconductor allowing holes to transport from the active layer. The electrode of the ETL should have a lower work function to match with the lower unoccupied molecular orbital (LUMO). However, the electrode of the HTL should have a high work function to match with the higher occupied molecular orbital (HOMO). The electrons in the HOMO level tend to transfer to the LUMO level leaving holes in the HOMO level and electrons in the LUMO level. This means that HOMO levels are associated with the HTL while LUMO levels are associated with the ETL.
Different attempts were made to fabricate and study the performance of perovskite solar cells. One of them was done by Yanking Zhu [
14]. Recently, metal halide perovskite materials have attracted interest due to their ease of fabrication processes and higher efficiency. Nowadays perovskite solar cells (PSCs) have high efficiency up to 25.7% and 31.3% for the perovskite-silicon tandem solar cells. Bilayer perovskite film composed of a thin low dimensional perovskite layer and a three-dimensional perovskite layer shows high efficiency and good stability conditions.
Anup Bist [
15] in his work exhibits innovative methods such as surface passivation by precursor solutions, doping, and composites to increase stability. It is shown that only a few materials that are used in the fabrication of perovskite can make it commercially available.
In the paper published by Sonali Mehra et al [
16] he studied the behavior of halide perovskites, this work mainly focuses on synthesizing and evaluating the efficiency of methyl ammonium lead halide-based perovskite (MAPbX3; X=Cl, Br, I) solar cells. The preparation technique is based on the colloidal Hot-injection method (HIM) to synthesize MAPbX3 (X=Cl, Br, I) perovskites using the specific precursors and organic solvents under ambient conditions. The results obtained indicate that the particle size and morphology of perovskites vary with halide variation. The MAPbI3 perovskite has a low band gap and low carrier lifetime but has the highest efficiency among other halide perovskite samples. The conversion efficiency of the MAPbX3 perovskites has been evaluated through extensive device simulations. Here, the optical constants, band gap energy, and carrier lifetime of MAPbX3 were used for simulating three different perovskite solar cells, namely I, Cl, or Br halide-based perovskite solar cells. MAPbI3, MAPbBr3 and MAPbCl3 absorber layer-based devices showed efficiencies ~13.7 %, 6.9 % and 5.0 %.
The work done by Asma O.et al [
17] is concerned with the performance of conventional perovskite cells. They focused on cubic single crystals. Experimental observations using x-ray photoelectron spectroscopy results indicated that Valence band maximum values consist of states contributed by Br and Pb which agrees with simulation results based on the density functional theory. In the work done by George G. Njema [
18], the deposition techniques, evaporation rate, type of solvents, and temperature were shown to have significant effects on the degree of crystallization. This in turn affects the efficiency, which increases upon increasing the crystallization degree. The inorganic perovskite cells are found to be more efficient, with a long stability lifetime and ease of fabrication processes.
The research done by Saemi Takahashi [
19] studied the effects of TiO2 interfacial morphology on perovskite solar cells by modifying micro and Nano surface roughness on the crystallinity of the perovskite layer. He found significant improvement in the crystal morphology. This increases the efficiency and reduces V-I hysterias.
Another useful work was done by Ningyu Ren et al, [
20] the performance of polycrystalline perovskite was improved when adding small amounts of Cadmium Acetate (CdAc2) in the Pbl2 precursor solution. This results in Nano-hole array films and promotes crystal orientation. This suppresses the non-radiative recombination and results in a long carrier lifetime and efficiency of 22.78%. It was also found that the tandem solar cells which are encapsulated maintain 109.78% of the initial efficiency after 300 hr. at 45 C in a nitrogen atmosphere.
The research of Sekai Tombe, et al [
21] is concerned with the behavior of methylammonium (MA) lead halide derivatives MSPb3-xYx (Cl, Br, I). The energy bandwidth is dependent on the halide type (Cl, Br, I) and its concentration. work done by Masha Moradbeigi [
22] aims to make perovskite cells commercially available. This is done by using simulation. In this work, polyethylene terephthalate (PET) is used as a substrate. Plasma polymer fluorocarbon (PPFC) coating is suggested as an anti-reflecting layer (ARL). The self-cleaning property was provided by PPFC. The results obtained indicated that the four-terminal tandem solar cell has a high efficiency of 30.14%.
The work done by Nisar Ali, et al [
23] is concerned with the attempts made by different researchers to improve the performance of perovskite materials in addition to also improving the stability, validity, consistency, and reproducibility. These attempts studied the effects of solvent, interface, and structure engineering leading toward increasing efficiency to exceed 25.4%. The paper also investigates the device instability and its role in limiting the practical applications of the hybrid perovskite solar cell. This review provides a summary of the developments to resolve these issues with the use of different synthesis routes and materials to obtain a stable ABX3-type structure of the perovskite materials. This review also includes the effects of the electron transport layer on the hysteresis phenomenon and long-term stability. A comprehensive discussion on the crystal structure, energy level, absorption coefficient, degradation, and chemical bonding in perovskite solar cell materials is also investigated. This importance of perovskite cells encourages us to do this work, where sections 1&2 are concerned with the introduction and theoretical model. Sections 3,4,5 and 6 are devoted to materials, results, discussion, and conclusion respectively.
2. Theoretical Model Based on the String Theory:
The Nano system intensity I of waves can be found using quantum laws. Where it can be found in terms of the wave function and the imaginary part of the wave number to be
To find the imaginary part of the wave number let us consider the motion small particle of mass m moving with velocity v, and with force constant k moving in a resistive medium having coefficient of friction
. Its equation of motion is given by.
One can solve this equation by suggesting the electrons as strings. Thus, the velocity v is given to be.
According to the relation of velocity with the acceleration a and displacement
, one gets.
Using equations (5) and (6) in equation (3) yields,
Multiplying both sides by
gives,
Rearranging and using the fact that.
Therefore, the velocity can be written in a complex form.
The current density J is found to be related to the velocity and the conductivity according to the relationship.
The momentum p is also related to the velocity and the wave number according to the relationship.
The wave number and the conductivity can be written in a complex form.
Thus, according to equations (12,14,15) the imaginary part of the wave number is given to be.
Equations (12,13,15) give the real conductivity to be.
For very small mass m and the high applied frequency compared to the natural frequency
Thus, the imaginary wave number in equation (16) reduces to be.
While the conductivity in equation (17) becomes
Taking the nanocrystal size to be equal to the atomic radius and assuming the proportionality constant to be equal to one for simplicity, one gets
But the velocity is related to the frequency the atomic radius and the crystal size according to the relationship.
Hence one gets the absorption coefficient and the transmission coefficient T to be.
where the absorption coefficient takes the form
The coefficient of friction is related to the mass m and the relaxation time to be in the form.
The relaxation time can also be expressed in terms of the distance d and the velocity to be.
Thus, the conductivity is given to be.
One can relate the electrical force of the nucleus of the atom to the centrifugal force according to the relationship.
Thus, the velocity is given to be.
Thus, the refractive index takes the form.
The magnetic permeability is also given by,
The relations concerning the crystal spacing d can be obtained assuming that the atoms in the crystal are very close to each other in such a way that the crystal spacing which is equal to the distance between two successive planes d is equal to the distance between the centers between two successive atoms. Thus
Thus, the imaginary part of the wave number is given by
The absorption coefficient and the transmission coefficient are given by
The conductivity can be given in terms of the displacement D and the crystal spacing d to be
The refractive index and the magnetic permeability are also given in terms of d to be
3. Materials and Methods:
The sol-gel deposition technique is used in the preparation of (BaxFe 1-xTiO4) (x=1, 0.1, 0.2, 0.3, 0.5, 0.6, 0.7,08, 0.9 and 0). Barium nitrate [Ba (NO3)2]], Iron (III) nitrate [Fe (NO3)3.9H2O]. Titanium oxide was dissolved in distilled water whereas the PH was adjusted using nitric acid to less than 5 pH meters. After that Barium nitrate and iron nitrate were weighted separately, where each one followed by the addition of a suitable quantity of distilled water to prepare the solution, which was stirred and heated after pH was adjusted to 5.0 at 70 degrees centigrade for one hour. The two solutions were mixed and added to 3.0g of titanium oxide. The resulting mixture was heated and stirred at 70 degrees centigrade continuously for about one hour, then deposited for one day and filtered. The solution was slowly evaporated to form sol-gel by continuous heat treatment to convert it to gel at 150 degrees centigrade after two hours. The gel was then dried and ground to powder. Using XRD the nanostructure was determined. The UV-vis spectrometer was used to determine the optical and electrical properties of the thin films.
Picture 1.
Relation between Magnetic Permeability μ and Crystal Spacing.
Picture 1.
Relation between Magnetic Permeability μ and Crystal Spacing.
4. Results:
The following tables and figures exhibit the change of some electrical and optical properties of the perovskite with the crystal spacing. It also exhibits the change of the energy gap with some nanostructures and some optical and electrical properties.
Table 1.
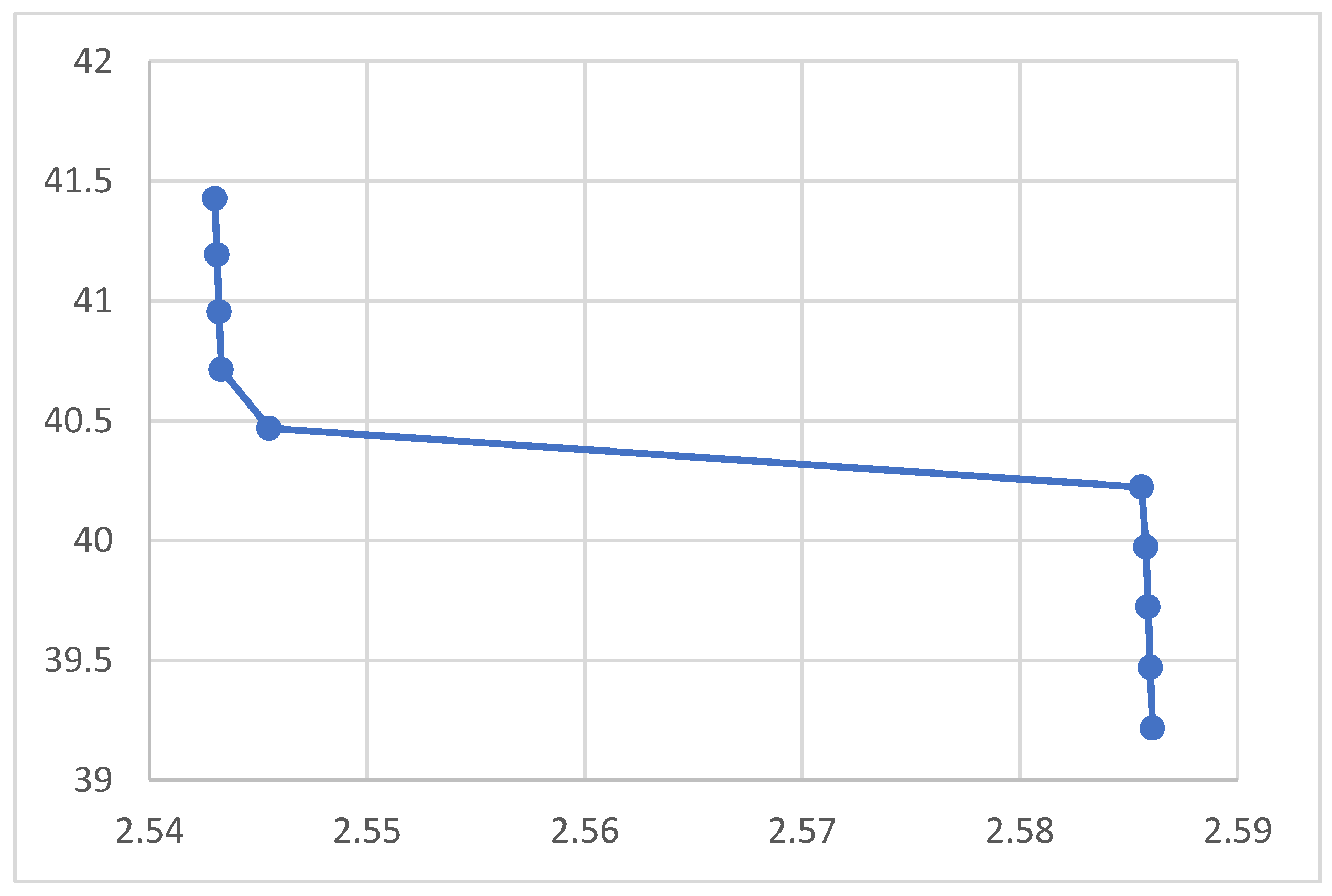
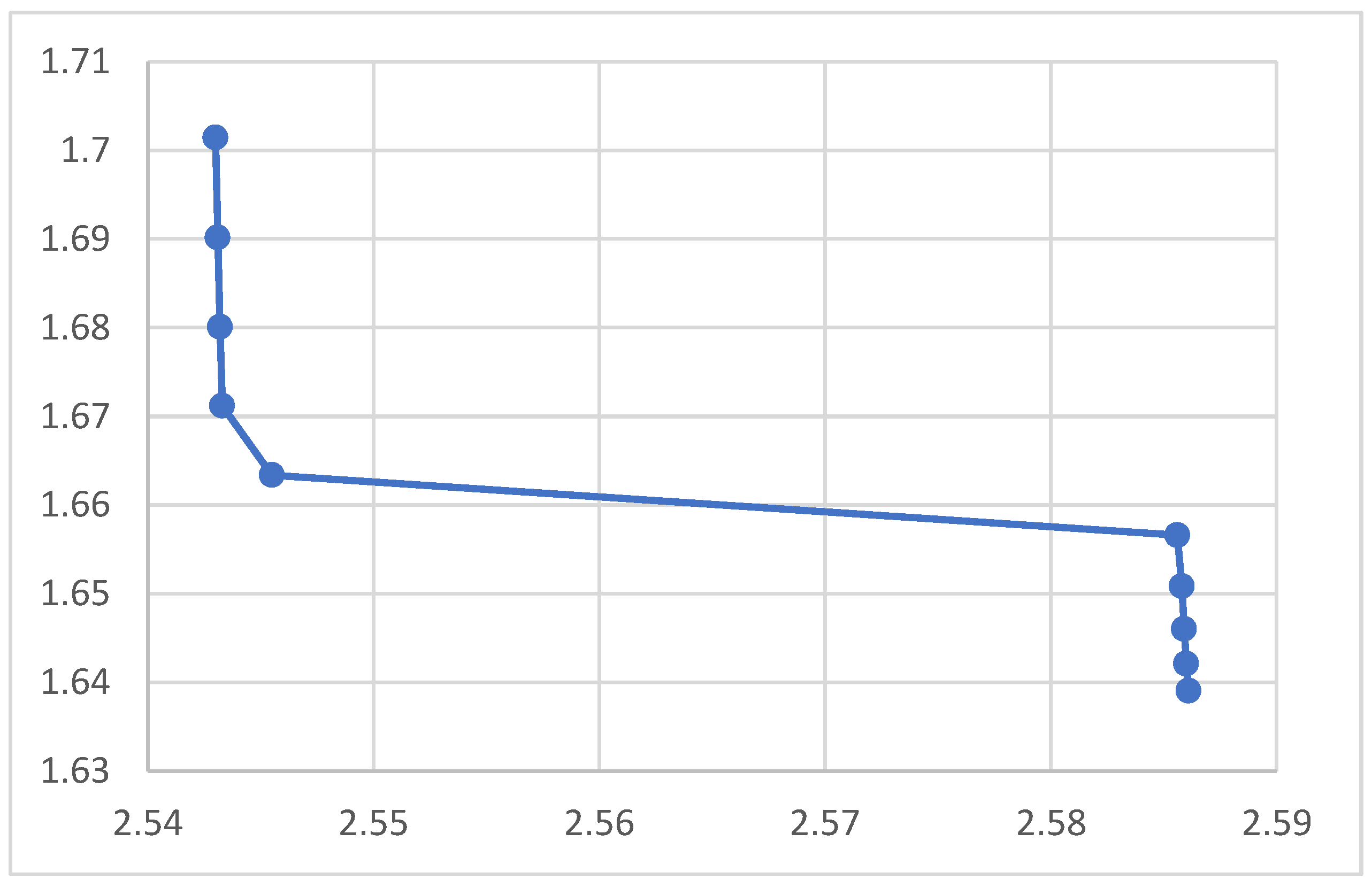
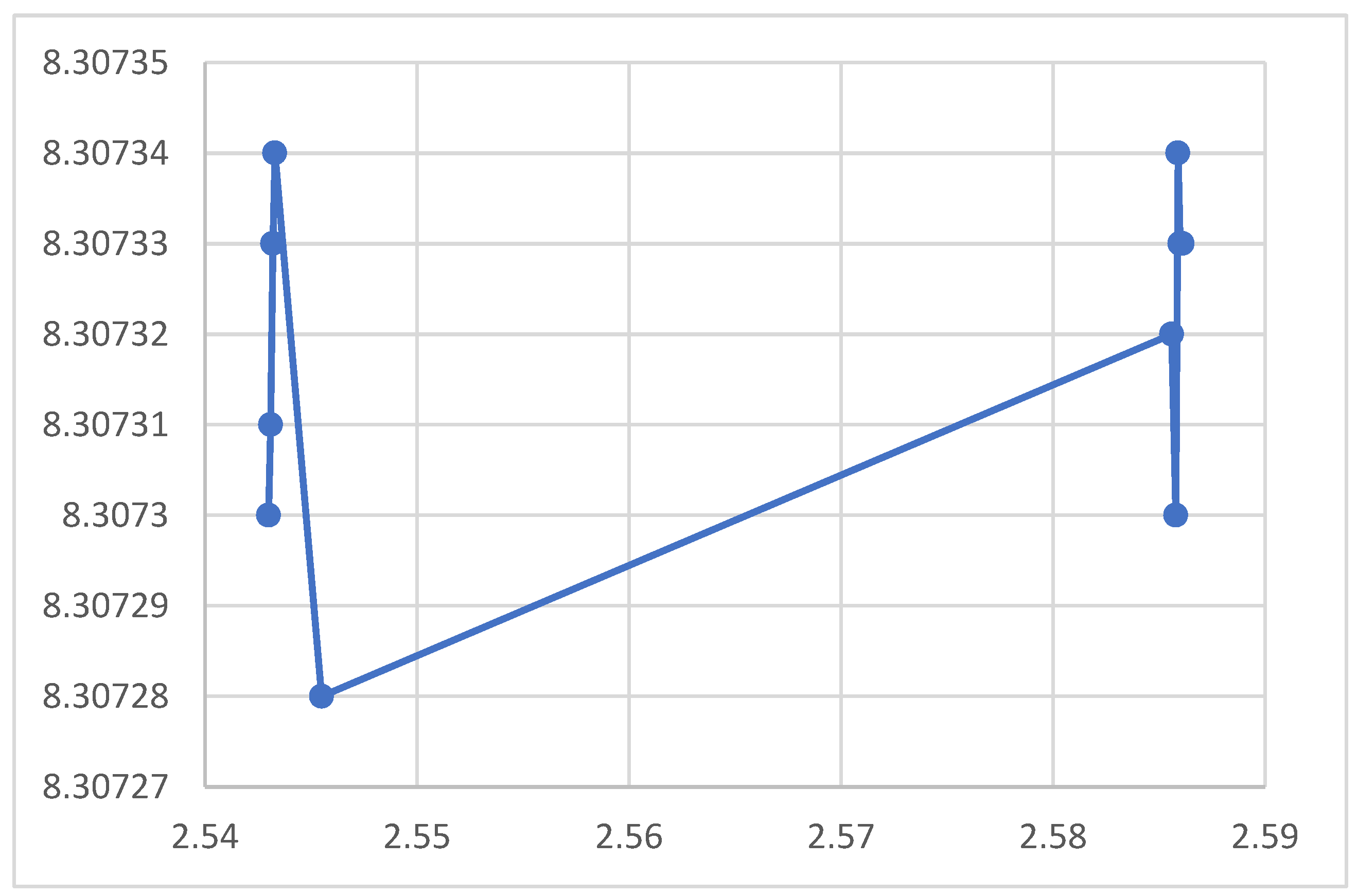
Changes of electrical conductivity, optical conductivity, magnetic permeability, and Transmittivity with d spacing.
Table 1.
Changes of electrical conductivity, optical conductivity, magnetic permeability, and Transmittivity with d spacing.
|
|
Magnetic permeability μ |
Transmissivity
T |
d-spacing |
| 39.21728 |
8.30733 |
1.63904 |
0.99378 |
2.5861 |
| 39.47080 |
8.30733 |
1.64209 |
0.99365 |
2.5860 |
| 39.72292 |
8.30734 |
1.64600 |
0.99352 |
2.5859 |
| 39.97391 |
8.30730 |
1.65083 |
0.99340 |
2.5858 |
| 40.22262 |
8.30732 |
1.65660 |
0.99326 |
2.5856 |
| 40.46889 |
8.30728 |
1.66337 |
0.99313 |
2.5455 |
| 40.71322 |
8.30734 |
1.67118 |
0.99299 |
2.5433 |
| 40.95416 |
8.30733 |
1.68009 |
0.99285 |
2.5432 |
| 41.19251 |
8.30731 |
1.69015 |
0.99271 |
2.5431 |
| 41.42708 |
8.30730 |
1.70143 |
0.99257 |
2.5430 |
Figure 1.
Relation between Electrical Conductivity and Crystal Spacing
Figure 1.
Relation between Electrical Conductivity and Crystal Spacing
Figure 2.
Relation between Magnetic Permeability μ and Crystal Spacing.
Figure 2.
Relation between Magnetic Permeability μ and Crystal Spacing.
Figure 3.
Relation between Optical Conductivity and Crystal Spacing
Figure 3.
Relation between Optical Conductivity and Crystal Spacing
Figure 4.
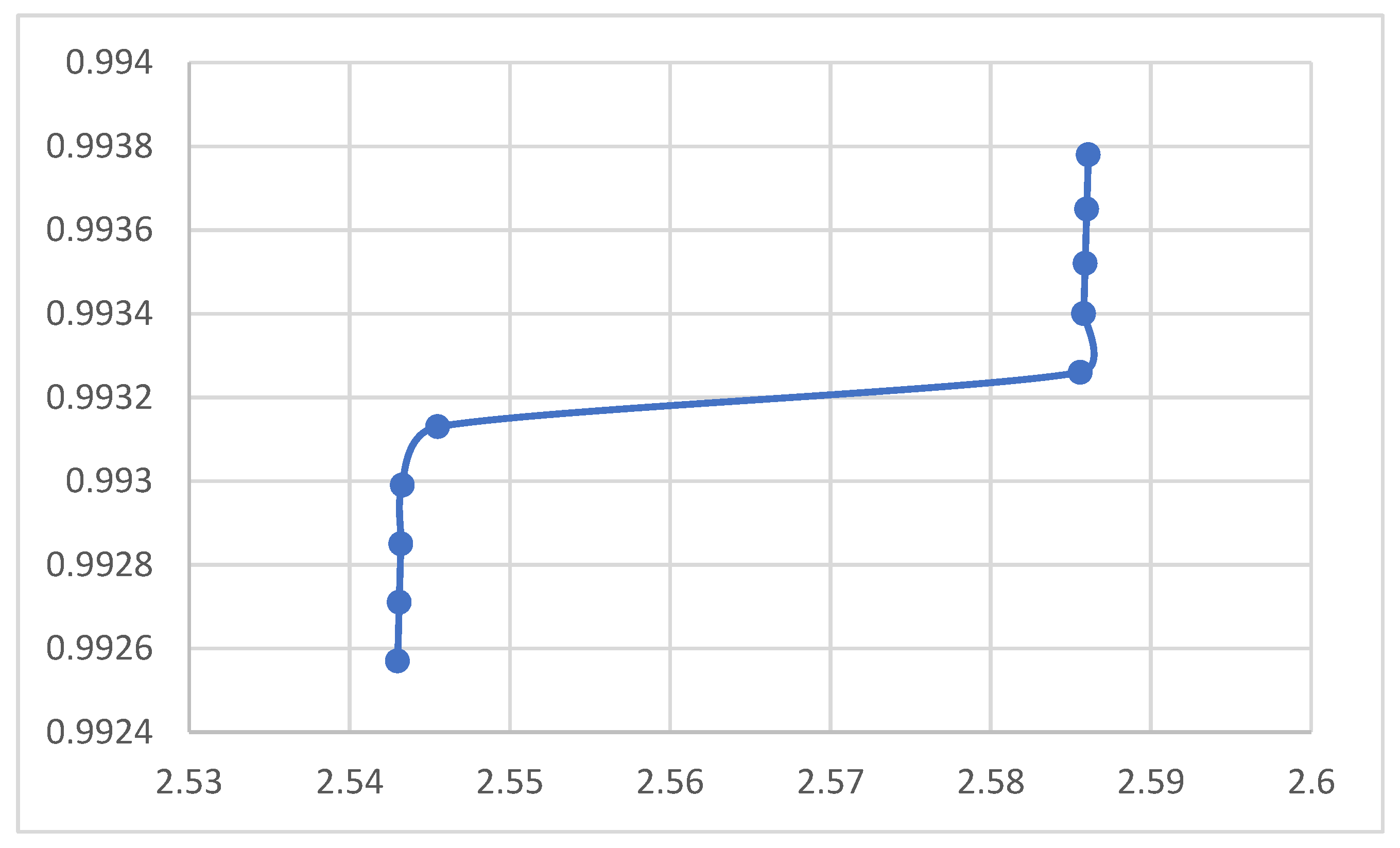
Relation between Transmissivity and Crystal Spacing
Figure 4.
Relation between Transmissivity and Crystal Spacing
Table 2.
The changes in the energy gap with crystal size, crystal spacing, absorption coefficient, and concentration.
Table 2.
The changes in the energy gap with crystal size, crystal spacing, absorption coefficient, and concentration.
| 1/x |
Energy gap Eg |
Crystal size (nm) |
Crystal spacing d |
Absorption Coefficient α |
Concentration
X |
| 0 |
806.7 |
2.5861 |
12.6 |
2.074 |
0 |
| 0.1 |
2461.4 |
2.586 |
12.4 |
2.069 |
0.1 |
| 0.2 |
2.067 |
12.4 |
2.5859 |
24510.6 |
0.2 |
| 0.3 |
2.064 |
12.3 |
2.5858 |
2560.8 |
0.3 |
| 0.4 |
2.061 |
11.9 |
2.5856 |
2612 |
0.4 |
| 0.5 |
2.058 |
11.8 |
2.5455 |
2664.3 |
0.5 |
| 0.6 |
2.055 |
11.7 |
2.5433 |
2717.6 |
0.6 |
| 0.7 |
2.052 |
110.8 |
2.5432 |
2771.9 |
0.7 |
| 0.8 |
2.049 |
10.6 |
2.5431 |
2827.4 |
0.8 |
| 0.9 |
2.046 |
9.9 |
2.543 |
2993.9 |
0.9 |
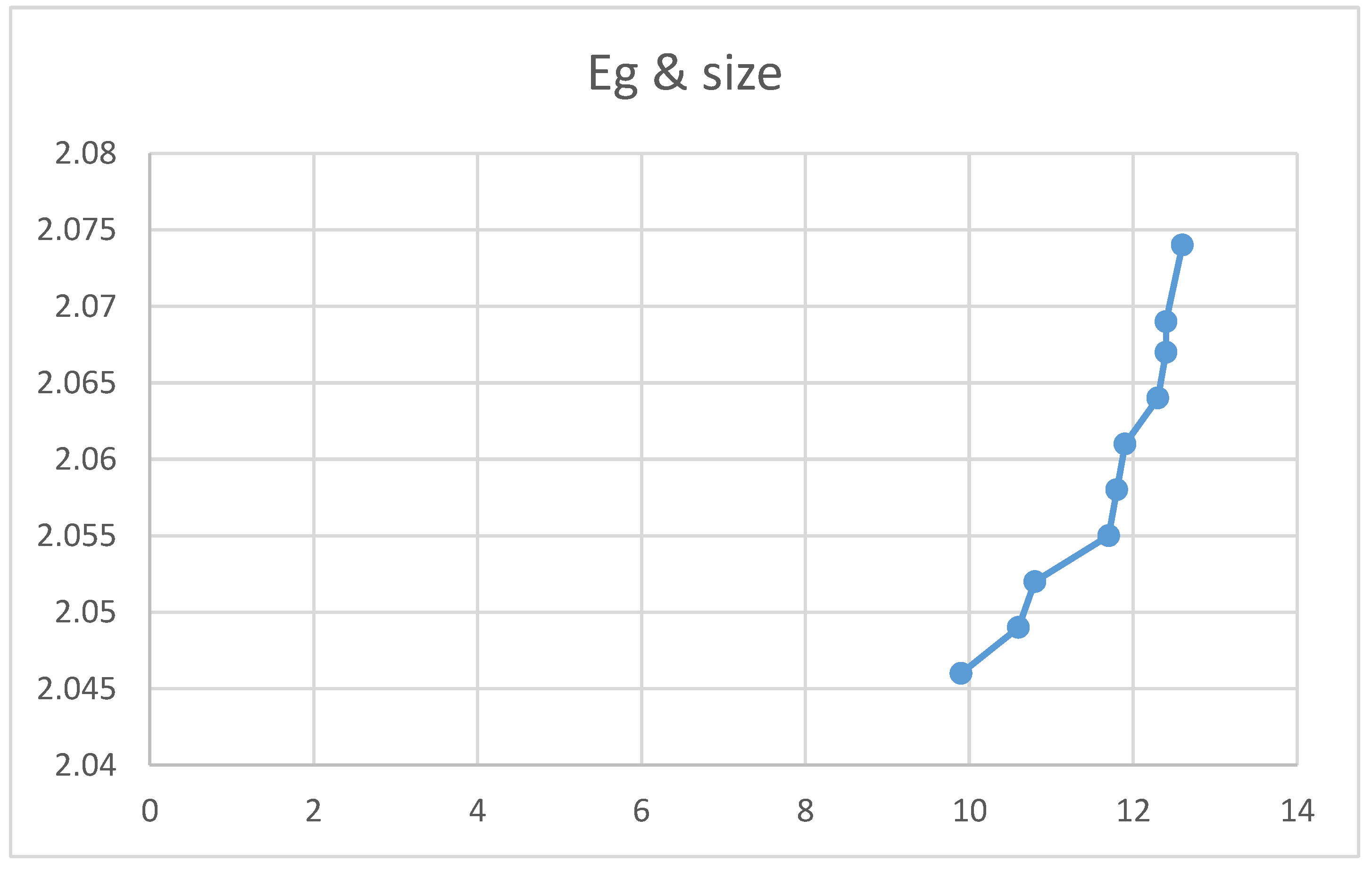
Figure 5.
Relation between Energy gap Eg and Crystal size (nm).
Figure 5.
Relation between Energy gap Eg and Crystal size (nm).
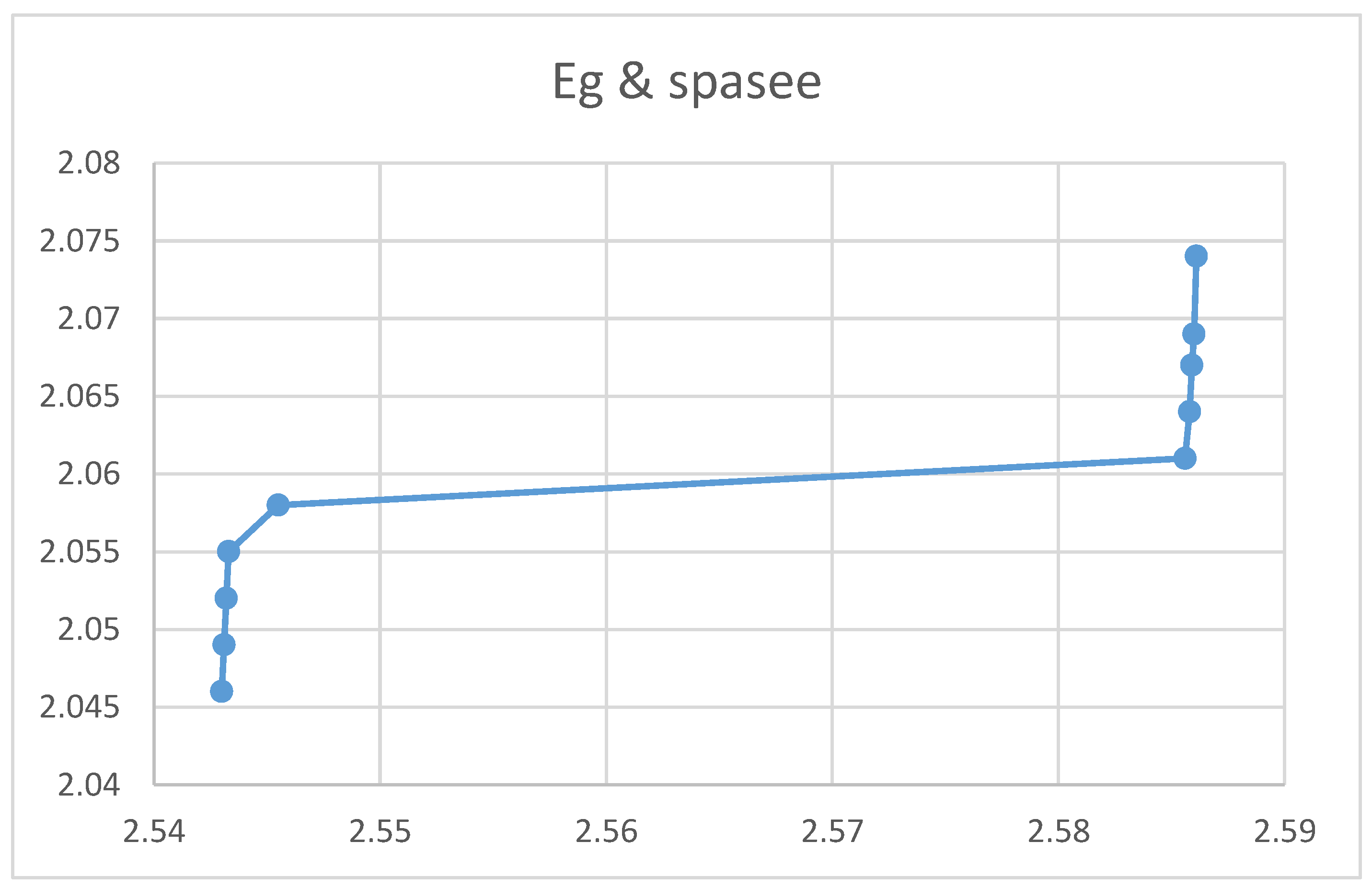
Figure 6.
Relation between Energy gap and Crystal spacing
Figure 6.
Relation between Energy gap and Crystal spacing
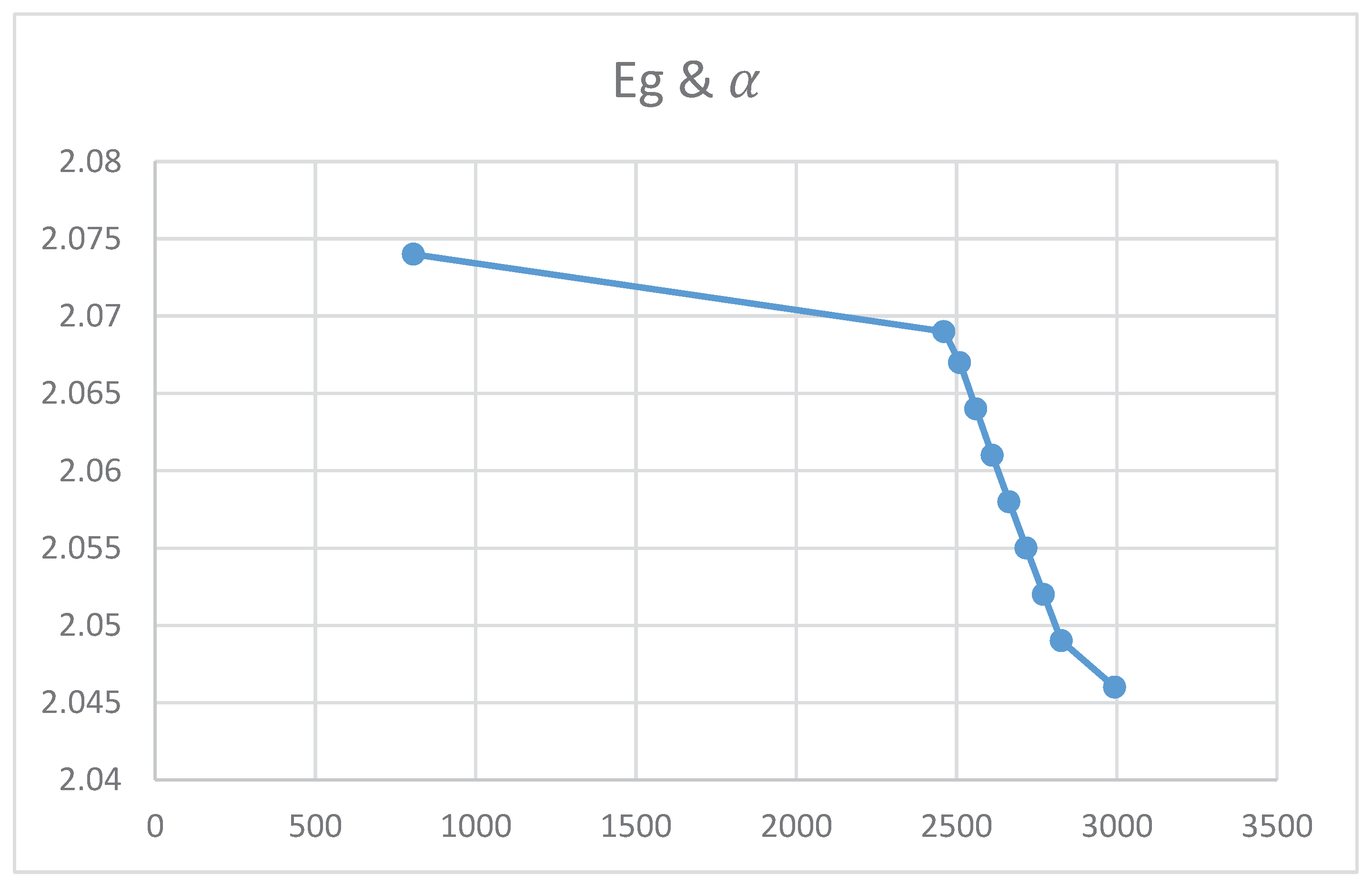
Figure 7.
Relation between Energy gap and Absorption Coefficient
Figure 7.
Relation between Energy gap and Absorption Coefficient
Figure 8.
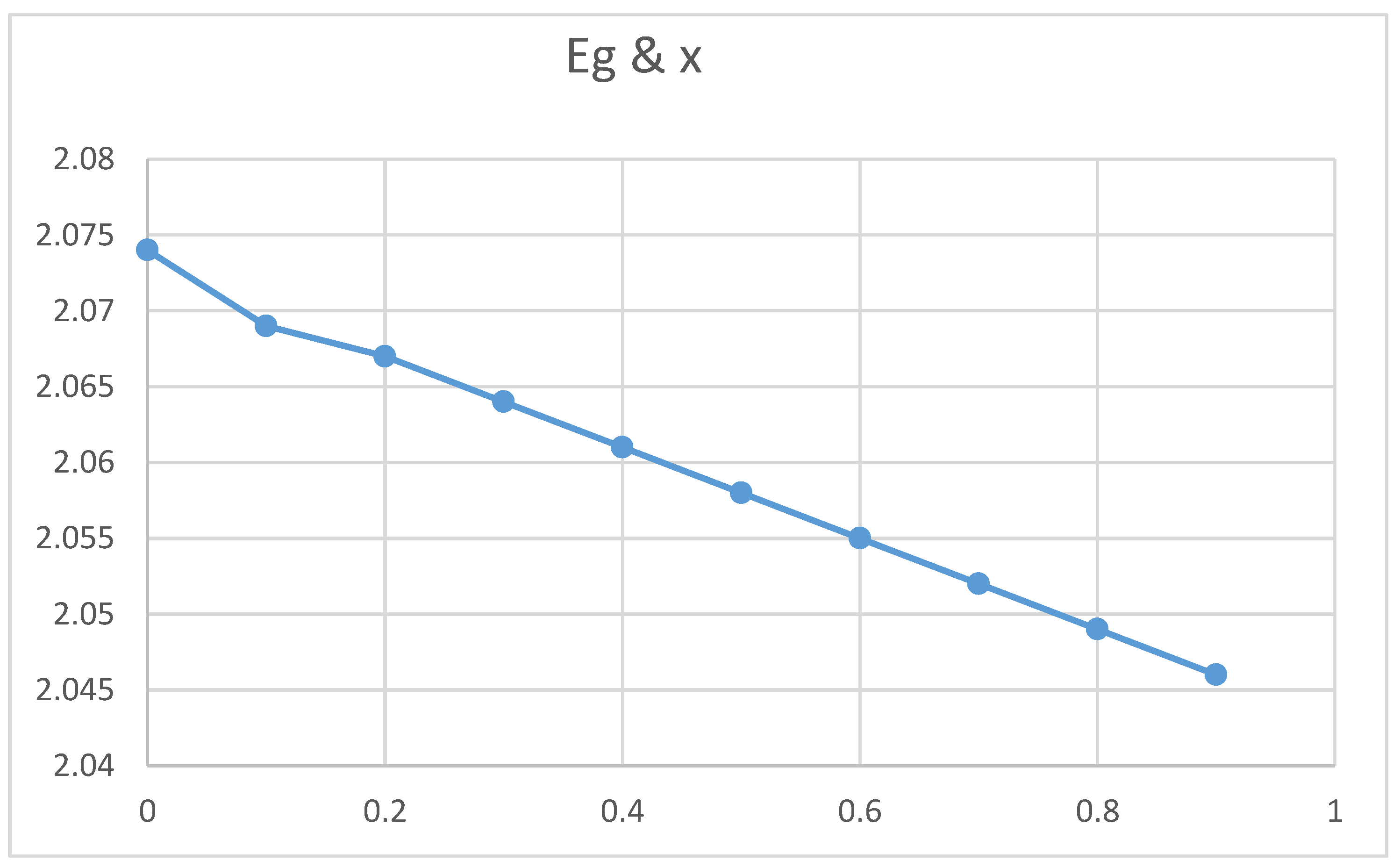
Relation between Energy gap and Concentration x.
Figure 8.
Relation between Energy gap and Concentration x.
5. Discussion
The performance of the perovskite cells prepared by Amira [
24] was investigated in this work to see how some optical and electrical properties of the thin of absorption coefficient, transmissivity, conductivity, and refractive index upon changing the nano-size Bax Fe(1-x)TiO are related to each other and the nanocrystal spacing. The explanation of these relations was theoretically explained using a string semi-quantum model.
Figures (10) and (11) show an increase in the energy gap with nanocrystal size and spacing. The theoretical equations confirmed these empirical results. However, figures indicated that the energy gap decreases upon increasing the absorption coefficient and the Ba concentration. Again, the two experimental curves can be explained theoretically according to equations.
The rest of the figures relate the crystal spacing to some optical and electrical properties. The absorption coefficient in the figure decreases upon increasing the nanocrystal spacing as shown in the figure, which agrees with the equation. According to the figures the reflection coefficient and the refractive index, however, showed no response to the variation of the nanocrystal spacing. The figure indicated that the electrical conductivity decreases when the nanocrystal spacing increases. The lower figure shows no response for the optical conductivity f to the nanocrystal spacing. According to the figure the magnetic permeability decreases upon increasing the nanocrystal spacing. The transmission according to the figure increases upon increasing the nanocrystal spacing.
The work indicated the change of the energy gap, absorption coefficient, transmissivity, conductivity, and refractive index upon changing the nanostructure like crystal size and concentration besides dopant or matrix changes. This conforms with the work of Anup Bist [
15] which shows that changing nanostructures like surface passivation increases stability. Mehra's paper [
16] agrees with our work which indicates that halide variation changes the band gap. The change of halide doping material (Cl, Br, I) Changes the band gap which becomes lower for I. George G. Njema [
18] also found that the change of nanostructure changes the physical properties of the nano cells since it indicated that increasing crystallization degree increases efficiency which is related to the absorption coefficient and conductivity. The same foundations were obtained by Saemi Takahashi [
19] where improving the crystallization degree increases the efficiency. Similarly, Ningya Ren [
20] indicated that an increase in crystal orientation increases the efficiency. The work done by Sekai Tombe [
21] also indicated that changing the nanostructure by changing the halide doping element changes the band gap. The contribution of Nisar Ali [
23], which exhibits the researcher's attempts to improve the perovskite performance, indicated that the nano-size is one of the factors that affect cell efficiency.
6. Conclusion:
The study of perovskite optical and electrical properties indicated that to increase the efficiency of the nano solar cell the energy gap should become narrower. This requires a decrease in the nanocrystal size and spacing. It also requires increasing the absorption coefficient and decreasing the transmission. It also requires increasing the conductivity and the magnetic permeability.
A useful relation between the nanocrystal size and some optical and electrical properties was found empirically. the results obtained indicated that the absorption coefficient, electrical conductivity, and magnetic permeability increase when the nanocrystal size decreases. In contrast the transmission and the refractive index increase when the nanocrystal size increases. These empirical relations can be explained using the string classical theory.
Funding
This research was funded by Research Group, Saudi Arabia under grant number (RGP. 2/201/44).
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Data availability
Data will be made available on request.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through a small group project under grant number (RGP. 2/ 201/ 44).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wasisto, Hutomo Suryo, Joan Daniel Prades, Jan Gülink, and Andreas Waag. "Beyond solid-state lighting: Miniaturization, hybrid integration, and applications of GaN nano-and micro-LEDs." Applied Physics Reviews 6, no. 4 (2019). [CrossRef]
- Meneghini, Matteo, Carlo De Santi, Idriss Abid, Matteo Buffolo, Marcello Cioni, Riyaz Abdul Khadar, Luca Nela, et al. "GaN-based power devices: Physics, reliability, and perspectives." Journal of Applied Physics 130, no. 18 (2021). [CrossRef]
- 石黒浩三. "A. Beiser: Concepts of Modern Physics, Mc-Graw-Hill 1963, 357 頁, 15× 23cm, 3,180 円." 日本物理学会誌 19, no. 6 (1964): 394. [CrossRef]
- Raymond A. Serway, physics for scientists and engineers with modern physics, Sounders College Publishing, USA (2004).
- Li, Kaiwen, Dong Lin, Jinhua Ren, and Qun Zhang. "Silicon doping and N2 annealing effects on Zn3N2 thin film transistors." Vacuum 197 (2022): 110864. [CrossRef]
- Nazeeruddin, Mohammad K., Peter Pechy, Thierry Renouard, Shaik M. Zakeeruddin, Robin Humphry-Baker, Pascal Comte, Paul Liska, et al. "Engineering of efficient panchromatic sensitizers for nanocrystalline TiO2-based solar cells." Journal of the American Chemical Society 123, no. 8 (2001): 1613-1624. [CrossRef]
- Kamat, P.V., et al., Nanoparticles, in Handbook of Nanostructured Materials and Nanotechnology., Academic Press: New York.2010.
- Neha Srivastava, Manish Srivastava, P. K. Mishra and Vijai Kumar Gupta. Green Synthesis of Nanomaterials for Bioenergy Applications, First Edition. 2021 John Wiley & Sons Lt8, New York, ISBN: 978-1-119-57679-2.
- Vall, CM Samba, M. Chaik, A. Tchenka, S. Hnawi, A. Mellalou, M. Aggour, and A. Outzourhit. "Effect of chromium percentage doping on the optical, structural, morphological and electrical properties of ZnS: Cr thin films." Physica E: Low-dimensional Systems and Nanostructures 130 (2021): 114694. [CrossRef]
- Ratna Tantra, Nanomaterial characterization, first published April 2016 Wiley & sons, Inc9, New York ISBN978111875354York, ISBN: 978-1-118-75346-0.
- Bhushan, Bharat, Dan Luo, Scott R. Schricker, Wolfgang Sigmund, and Stefan Zauscher, eds. Handbook of nanomaterials properties. Springer Science & Business Media, 2014. ISBN: 978-3-642-31106-2.
- V. Selvaraj et al., "Enhanced photodegradation of methylene blue from aqueous solution using Al-doped ZnS nanoparticles," Environmental Science and Pollution Research, pp. 1-14, 2022. [CrossRef]
- B. Yuan et al., "Optical Humidity Sensor Based on CdSe/ZnS Quantum Dots Modified by Porous Silica," Advanced Materials Interfaces, vol. 9, no. 29, p. 2201366, 2022. [CrossRef]
- N. Liu, L. Ding, H. Xue, Y. Ji, and Y. Ye, "Effect of shell thickness on optical properties of ZnSe/ZnS quantum dots under solar and laser excitation," Journal of Nanoparticle Research, vol. 24, no. 7, pp. 1-10, 2022. [CrossRef]
- Masha Moradbeigi and Mohammed Razage Investigation of optical and electrical properties of novel 4T all perovskite solar cell, Scientific reports,(2022) 12:6733. [CrossRef]
- H. A. Afify et al., "Shape-Controlled Solution-Epitaxial Perovskite Micro-Crystal Lasers Rivaling Vapor Deposited Ones," Advanced Functional Materials, vol. 32, no. 45, p. 2206790, 2022. [CrossRef]
- Zhu, Y., Hu, M., Xu, M., Zhang, B., Huang, F., Cheng, Y., & Lu, J. (2022). Bilayer metal halide perovskite for efficient and stable solar cells and modules. Materials Futures. [CrossRef]
- Bist, Anup, Bishweshwar Pant, Gunendra Prasad Ojha, Jiwan Acharya, Mira Park, and Prem Singh Saud. 2023. "Novel Materials in Perovskite Solar Cells: Efficiency, Stability, and Future Perspectives" Nanomaterials 13, no. 11: 1724. [CrossRef]
- Mehra, S., Pandey, R., Madan, J., Sharma, R., Goswami, L., Gupta, G.,.Sharma, S. N. (2023). Experimental and theoretical investigations of MAPbX3-Based perovskites (X= cl, br, I) for photovoltaic applications. Chemistry Open. [CrossRef]
- Asma O. Algaithi, S.Assa Aravind, Mohamed N. Hedhili, Tien Khee Ng ,Boon S.Oai, Optical Properties of First -Principles Study of CH3NH3pbBr3 Perovskite Structures, AC S Omega,2020,5,12313-12319. [CrossRef]
- Njema, G. G., & Kibet, J. K. (2023). A review of the technological advances in the design of highly efficient perovskite solar cells. International Journal of Photoenergy, 2023. [CrossRef]
- Takahashi, S., Uchida, S., Jayaweera, P.V.V. et al. Impact of compact TiO2 interface modification on the crystallinity of perovskite solar cells. Sci Rep 13, 16068 (2023). [CrossRef]
- Ren, N., Wang, P., Jiang, J., Li, R., Han, W., Liu, J., . . . Li, T. (2023). Multifunctional additive CdAc2 for efficient perovskite-based solar cells. Advanced Materials,, 2211806. [CrossRef]
- Ali, N., Shehzad, N., Uddin, S., Ahmed, R. R., Jabeen, M., Kalam, A., . . . Goumri-said, S. (2021). A review on perovskite materials with solar cell prospective Hindawi Limited. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).