Synchronization in a Three Level Network of All-to-All Quasi-Periodically Forced Hodgkin-Huxley Reaction-Diffusion Equations

1. Introduction

The main objective of this article is to provide some insights about the qualitative analysis of a non-autonomous neuronal network of Hodgkin-Huxley (HH) Reaction-Diffusion (RD) equations. The model under consideration writes as follows

$$\left\{\begin{array}{cc}\hfill V_{it}& ={\overline{g}}_{Na}{m}_i^3{h}_i\left(E_{Na}-V_i\right)+{\overline{g}}_K{n}_i^4\left(E_K-V_i\right)+{\overline{g}}_L\left(E_L-V_i\right)+V_{ixx}\hfill \\ \hfill & +H_i(V_1,....,V_N)+I_i(x,t),i\in \{1,...,N\}\hfill \\ \hfill n_{it}& ={\alpha }_n\left(V_i\right)(1-n_i)-{\beta }_n\left(V_i\right)n_i\hfill \\ \hfill m_{it}& ={\alpha }_m\left(V_i\right)(1-m_i)-{\beta }_m\left(V_i\right)m_i\hfill \\ \hfill h_{it}& ={\alpha }_h\left(V_i\right)(1-h_i)-{\beta }_h\left(V_i\right)h_i\hfill \end{array}\right.$$

(1)

The dynamics of each individual neuron is described by a standard HH equation containing ionic (sodium, potassium, leakage) fluxes and a spatial diffusion term. We refer for example to [1,2,3] and references therein for details about the HH RD systems. Functions and parameters on the above equation are as follows

$$\begin{array}{cccc}\hfill {\alpha }_n\left(V\right)& =0.01\frac{-V-55}{exp(-5.5-0.1V)-1}\hfill & \hfill {\beta }_n\left(V\right)& =0.125\frac{exp(-(V+65\left)\right)}{80}\hfill \\ \hfill {\alpha }_m\left(V\right)& =0.1\frac{-V-40}{exp(-4-0.1V)-1}\hfill & \hfill {\beta }_m\left(V\right)& =4\frac{exp(-(V+65\left)\right)}{18}\hfill \\ \hfill {\alpha }_h\left(V\right)& =0.07\frac{exp(-(V+65\left)\right)}{20}\hfill & \hfill {\beta }_h\left(V\right)& =\frac{1}{1+exp(-0.1V-3.5)}\hfill \end{array}$$

These values correspond to the ones found in [3]. As for the space domain, we consider a one dimensional interval $\Omega =(a,b)$. We assume Neumann boundary conditions. Each neuron is embedded in a network and receives inputs from its presynaptic neurons trough the coupling term

$$H_i(V_1,....,V_N)=\sum _{j=0}^N{c}_{ji}\left(x\right)(S-V_i)\Gamma \left(V_j(b-x)\right),$$

(2)

with,

$$\Gamma \left(V\right)=\frac{1}{1+e^{-\lambda (V-\theta )}},\lambda =20,\theta =10.$$

Since $\Gamma \left(V\right)$ is a sigmoid function, the presynaptic neurons $V_j$ of $V_i$ will have an effect only when they spike. The parameter S is set to

$$S=100,$$

which means that when there is enough presynaptic activity, the neuron $V_i$ will tend to S; this corresponds to depolarization and eventually a spike. This means that in our network all neurons have an excitatory effect. As we deal with spatial extended neurons, we need to specify where the connectivity arises with respect to the spatial position. We assume that the neurons are connected from the right-end side of the presynaptic neuron j to the left-end side of the post-synaptic neuron i. This is to model the fact that action potential travel trough the axon in one direction and kick the post-synaptic neuron through synaptic connections. As a consequence, the function c is generally set to zero everywhere but in the left-end part of size l, $(a,a+l)$ of the neuron. We assume that c has the following expression

$$c_{ij}\left(x\right)=\left\{\begin{array}{cc}c& \forall x\in (a,a+l)\\ 0& \forall xotherwise,\end{array}\right.$$

and we use the term $V_j(b-x)$ to express that only the right-end side of the presynaptic neuron j connects to the left-end side of the neuron i. Finally, the network topology is set as follows. We assume that there is three levels in the network which separate the network into three sets of neurons. At level one, the set one contains three neurons which receive periodic input $I_1\left(t\right),I_2\left(t\right),I_3\left(t\right)$. Each of this three neurons possesses only one unidirectional connection to a unique neuron in level two. Therefore, the second set of neurons contains also three neurons, each of which receives an input for a single neuron of level 1. The neurons in this second set connect to all neurons of level 2 and 3. Finally the last set of neurons, which correspond to level 3 are connected to all of the neurons of level 2 and 3, but do not receive any inputs from neurons of level 1. The network topology is represented in Figure 1.

Finally the functions $I(x,t)$ are set to 0 for all but the 3 neurons in the set 1. For these 3 neurons, indexed by $\{i_0,i_1,i_2\}$ a periodic signal is injected at neuron’s left-end as follows,

$$I_{i_0}(x,t)=Acos\left(at\right),I_{i_1}(x,t)=Acos(at+b),I_{i_2}=-I_{i_0}-I_{i_1}$$

for $x<a+l$ for some small l and 0 elsewhere. The dynamics of the $HH$ ODE have been widely studied. For the parameters’ values considered here, it is known from numerical studies that the HH system undergoes a subcritical Hopf Bifurcation around $I=...$. For a certain region of $I\simeq 7$, one can observe the coexistence of stable limit-cycle and a stable stationary point. In the next section we will consider a non-autonomous HH ODE system.

The present article is a theoretical and numerical investigation of Equation (1), a mathematical model which arises in neuroscience context. Aside from the standard HH framewoek, several specificities of the model, namely periodic stimulation at different locations with specific frequencies, are indeed inspired by recent studies which are worth to mention here. The topic of brain dynamics modeling has attracted an increasing interest in particular for the therapeutical potential of Non-Invasive Brain Stimulation (NIBS), see for example [4] for a summary about the Transcranial alternating current stimulation (tACS) method, its mechanisms, use for cognitive applications, and novel developments for personalized stimulation. A software, SimNIBS has been developed to simulate NIBS on realistic domains representing brain geometries, see [5]. SimNIBS is based on finite element methods to solve time dependent Poisson equations. In the context of EEG data driven modeling, recent studies have shown the importance of periodic current sources to retrieve real spatiotemporal signals, see [6,7]. HH neural networks have also been used recently to model the effect of specific frequency stimulation to help patients suffering from Post-Traumatic Stress Disorder (PTSD), see [8].

2. Forced ODE HH Equations

The aim of this section is to provide some insights about the response of a single HH ODE when the frequency of a periodic stimulus $I\left(t\right)$ is varied. We consider a single HH non-autonomous equation as follows

$$\left\{\begin{array}{cc}\hfill V_t& ={\overline{g}}_{Na}{m}^{3}h\left(E_{Na}-V_t\right)+{\overline{g}}_K{n}^4\left(E_K-V_t\right)+{\overline{g}}_L\left(E_L-V_t\right)+I\left(t\right)\hfill \\ \hfill n_t& ={\alpha }_n\left(V_t\right)(1-n)-{\beta }_n\left(V_t\right)n\hfill \\ \hfill m_t& ={\alpha }_m\left(V_t\right)(1-m)-{\beta }_m\left(V_t\right)m\hfill \\ \hfill h_t& ={\alpha }_h\left(V_t\right)(1-h)-{\beta }_h\left(V_t\right)h\hfill \end{array}\right.$$

(3)

with $I\left(t\right)$ set to:

$$I\left(t\right)=Acos\left(at\right)$$

and $a\in (0,2)$. The outputs of simulations are reported in Figure 2, Figure 3 and Figure 4. A careful analysis of the numerical simulations lead to the following obervations :

• When the frequency of the input is very slow (a=0.0001), then the behavior is akin to a autonomous HH with $I=7$. For the initial conditions considered here, the system evolves toward a limit-cycle and the frequency observed is intrinsic to the autonomous HH.
• When the frequency increases, for a range of $a\in (0.01,0.4)$, there are two frequencies that play a role. There is a recurrent pattern with a frequency of $\frac{a}{2\pi }$ which is imposed by $I\left(t\right)$, $i.e$ the time-periodicity of the global recurrent pattern is given by the periodicity of $I\left(t\right)$. Concurrently, within this period, the dynamics of HH appear. For example, for $a=0.03$, the system stays at an equilibrium which varies with $I\left(t\right)$, but there is no spike. For other values, such as $a\in (0.04465,0.3)$ some spike arise. For some values, one can observe the appearance of the so called Mixed Mode Oscillations (MMOs), see for example [9,10,11,12,13,14,15] and references therein cited.
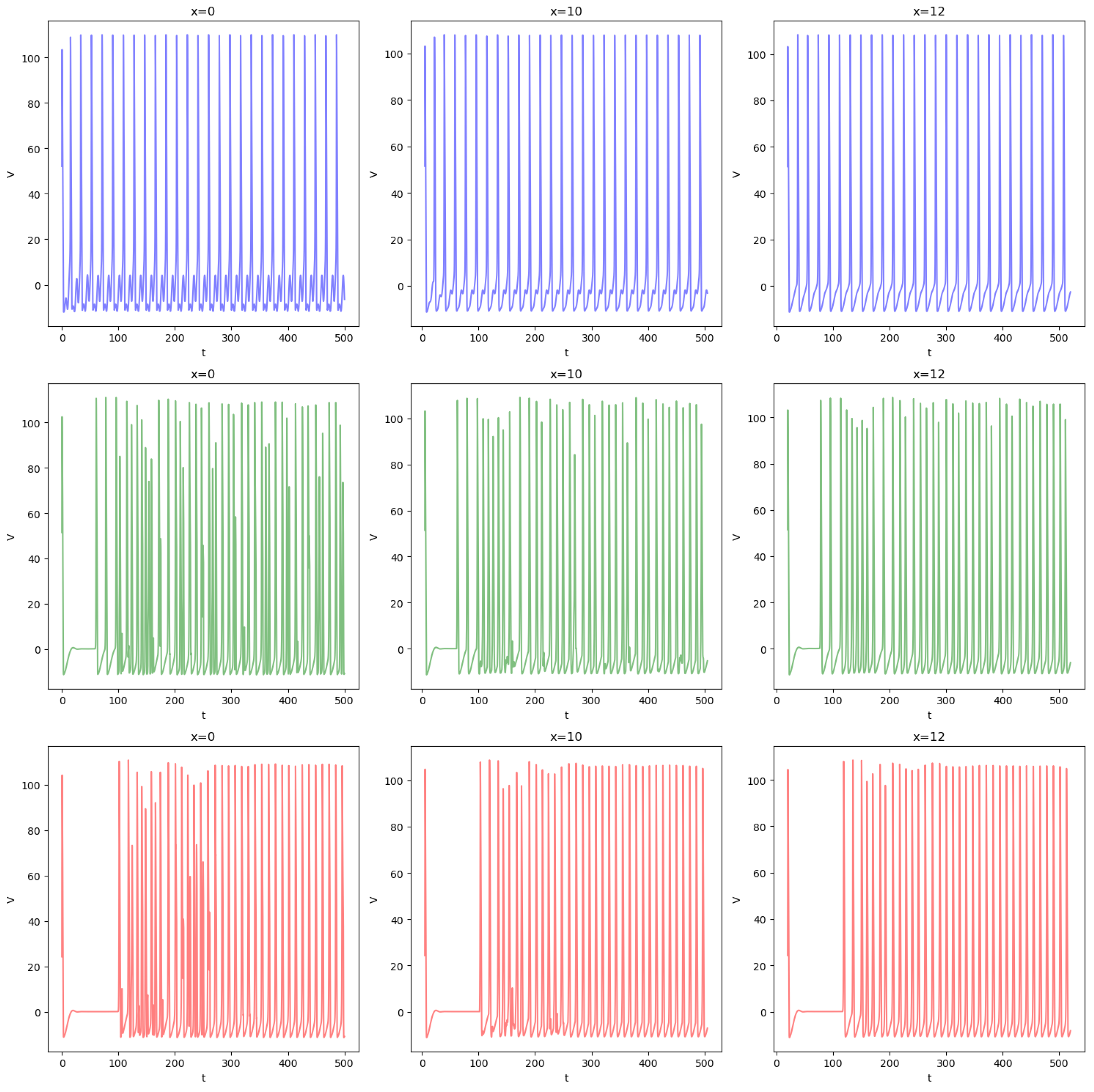
• It is worth to emphasize the qualitative difference between the output for a=0.0001 and a=0.4. Although the oscillatory frequency is the same, for a=0.0001, the oscillations correspond to the intrinsic frequency of the nonautonomous HH. In this case one can clearly observe the characteristic difference of the trajectories in a slow manifold and a jump, see [16] and references therein cited. For a=0.4, however the frequency is imposed by $I\left(t\right)$.

  

  Figure 2. Simulations of Equation (3). This figure illustrates the potential V as a function of time as the parameter a is increased from 0 to 2 with a current injection $I\left(t\right)=7cos\left(at\right)$

  Figure 2. Simulations of Equation (3). This figure illustrates the potential V as a function of time as the parameter a is increased from 0 to 2 with a current injection $I\left(t\right)=7cos\left(at\right)$

  
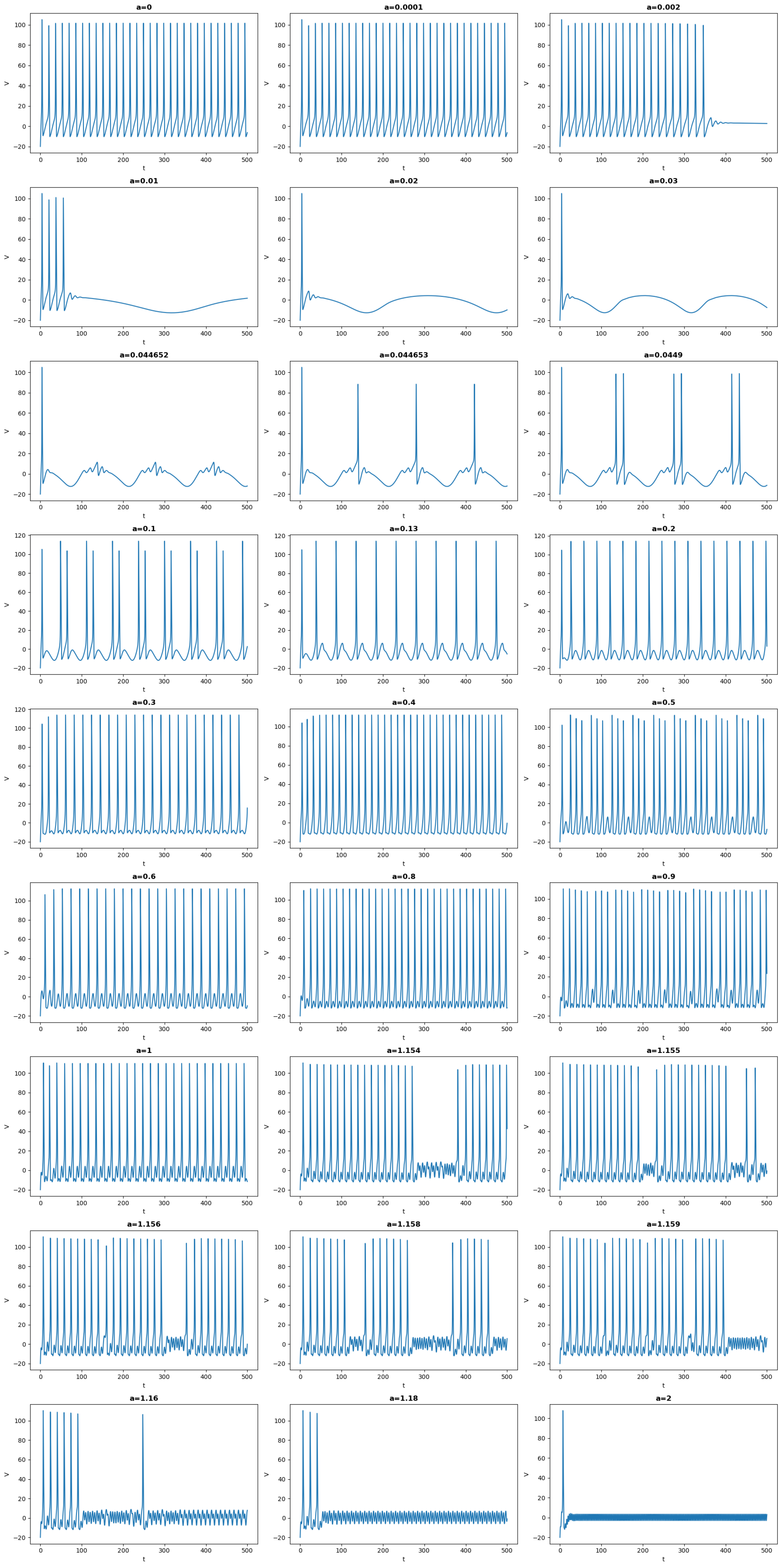
• After $a=0.5$, the situation change and the period of $I\left(t\right)$ becomes smaller than the one of the output, i.e.: there is a periodic pattern but its period results from a not straightforward interplay between the drive $I\left(t\right)$ and the dynamics of HH. An analysis of such an interplay was carried out in [17] in the simpler case of a FitzHugh-Nagumo system kicked periodically. For some values of the frequency, the behavior is more complicated and difficult to predict. The neuron can in this case spike or not in an erratic way. This is the case for example for a=1.156. see also Figure 4 in which the solution is represented in the $(V,m,h)$ phase space. In this case, the behavior is difficult to predict: the trajectories can switch between small and large oscillations in an unpredictable manner. This picture illustrates a geometry appearing in some slow-fast systems in which the switching between small and large oscillations occur as canard solutions and in a tiny space region. We refer to [11,13] for such systems derivated from the FitzHugh-Nagumo system and with three time scale. Although there is no small parameter in the HH equation, its hidden slow-fast nature has been studied for a long time, see [18,19,20].
• when the frequency is to high, for example for $a=2$, only small oscillations persist.

  

  Figure 3. Simulations of Equation (3). This figure illustrates the potential V as a function of time as the parameter a is increased from $0.02$ to $0.3$ along with the injected current $I\left(t\right)=7cos\left(at\right)$. It emphasizes how the injected current imposes its frequency.

  Figure 3. Simulations of Equation (3). This figure illustrates the potential V as a function of time as the parameter a is increased from $0.02$ to $0.3$ along with the injected current $I\left(t\right)=7cos\left(at\right)$. It emphasizes how the injected current imposes its frequency.

  

  

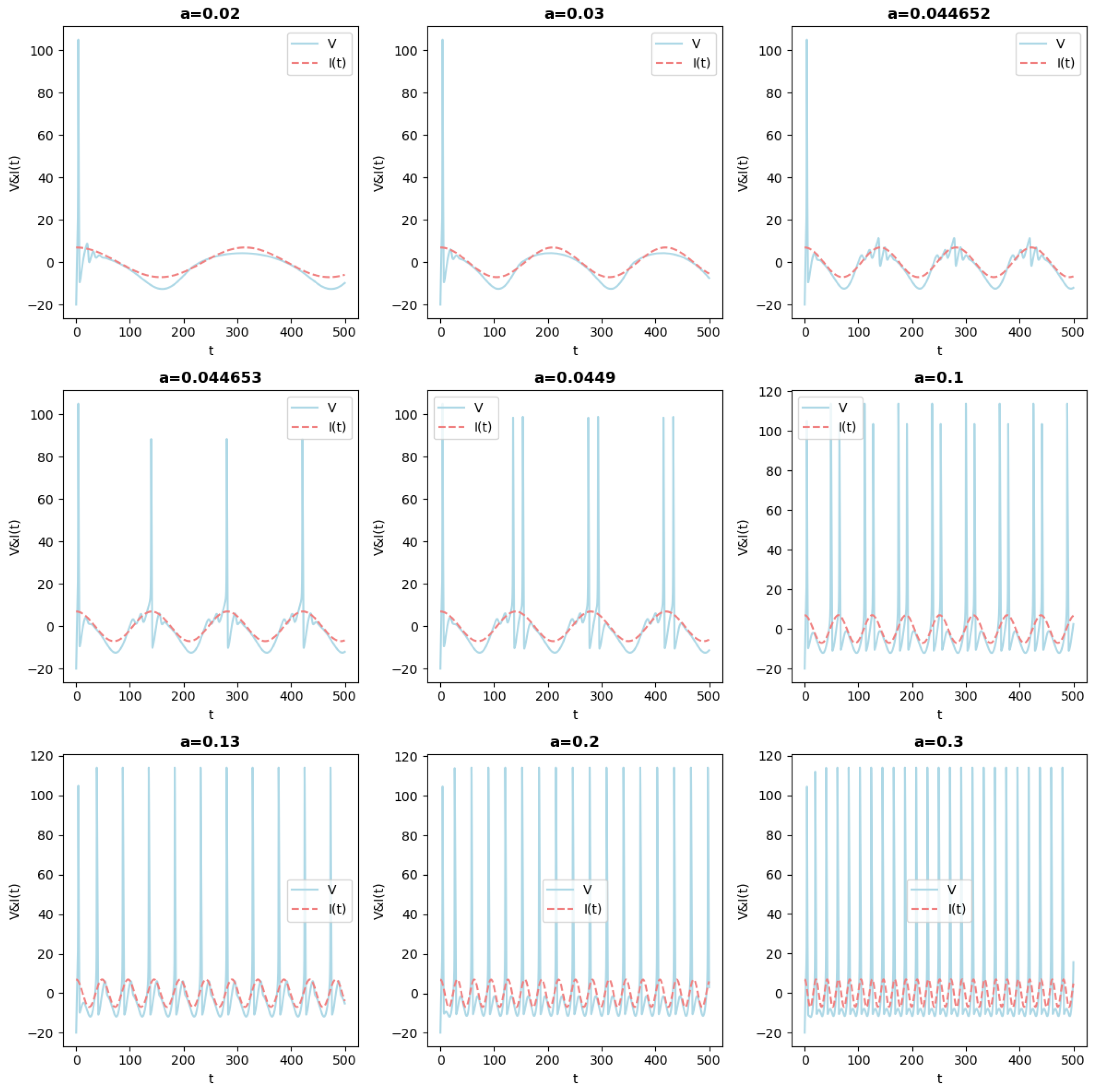  Figure 4. Solution of Equation (3) in the $(V,m,h)$ phase space for $a=1.159$. For this value of a, the behavior is difficult to predict: the trajectories can switch between small and large oscillations in an unpredictable manner. Of note, this picture illustrates a geometry appearing in some slow-fast systems in which the switching between small and large oscillations occur as canard solutions and in a tiny space region. We refer to [11,13] for such systems derivated from the FitzHugh-Nagumo system and with three time scale system. Although there is no small parameter in the HH equation, its hidden slow-fast nature has been studied for a long time, see [18,19,20].

  Figure 4. Solution of Equation (3) in the $(V,m,h)$ phase space for $a=1.159$. For this value of a, the behavior is difficult to predict: the trajectories can switch between small and large oscillations in an unpredictable manner. Of note, this picture illustrates a geometry appearing in some slow-fast systems in which the switching between small and large oscillations occur as canard solutions and in a tiny space region. We refer to [11,13] for such systems derivated from the FitzHugh-Nagumo system and with three time scale system. Although there is no small parameter in the HH equation, its hidden slow-fast nature has been studied for a long time, see [18,19,20].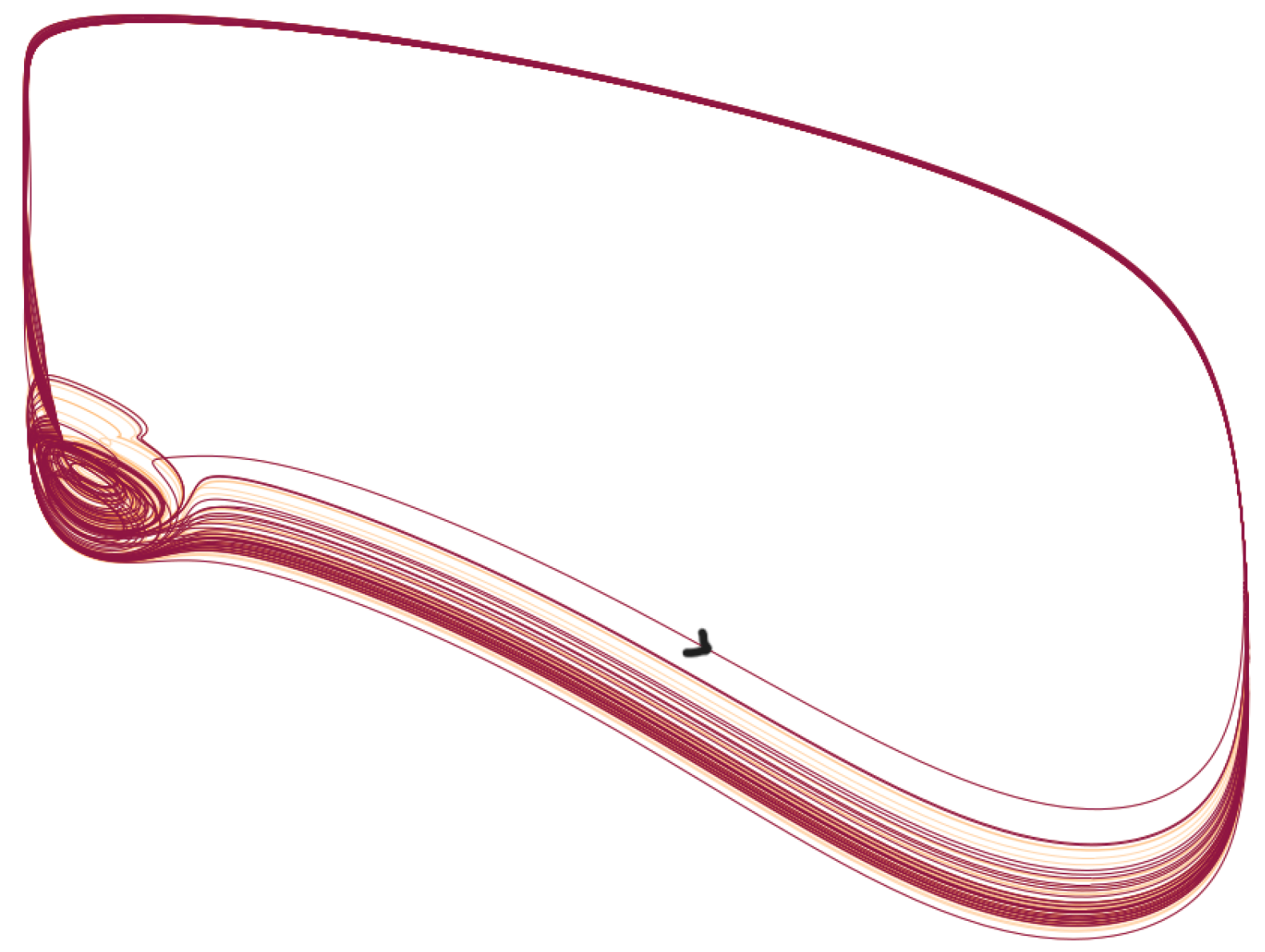

  

3. Theoretical Framework and Analysis

In this section, we provide some theoretical results. We start we the existence of solutions in an appropriate functional space. Let $X=C\left(\right[a,b\left]\right)$ the space of continuous functions defined on the real interval $[a,b]$. The following result holds.

Theorem 1.

Assume that $(V_i\left(0\right),n_i\left(0\right),m_i\left(0\right),h_i\left(0\right))\in X^{4N}$, and that for all $x\in [a,b],n_i(0,x),m_i(0,x)$ and $h_i(0,x)\in (0,1)$. Then,

1. 

There exists a unique solution of Equation (1) in $C([0,\infty ,X^{4N})$.

2. 

For all $x\in [a,b]$, for all $t\in [0,+\infty )$$n_i(t,x),m_i(t,x)$ and $h_i(t,x)\in [0,1]$,

3. 

$\underset{t\in [0,+\infty ),x\in [a,b]}{sup}\left|V_i(t,x)\right|<+\infty$.

Proof. 

The proof is based on the semigroup generated by the operator $u\to u^{″}$ with NBC and the fact that $HH$ ODE has a an invariant region. We refer to [3] in which the details have been provided for a similar system. □

Let $(U_i=(V_i,n_i,m_i,h_i)$, and let $L_3$ denotes the set of indices of level 3 in the network. The next proposition emphasizes that $U_i=U_j\forall i,j\in L_3$ is a solution of Equation (1)

Proposition 1.

We assume that at $t=0$, $U_i(x,0)=U_j(x,0)\forall i,j\in L_3$, then

$$\forall i,j\in L_3,\forall t\ge 0,U_i(x,t)=U_j(x,t).$$

Proof. 

Since for neurons in level 3 the network topology is of all to all type, each single neuron receives the same inputs. □

What is more striking for this non-autonomous network, is that the synchronizes solution attracts other solutions. The next result provides mathematical insights about this fact. It indicates that the coupling practically implies an "energy" decrease. Let

$${\mathcal{H}}_{ij}={\int }_{\Omega }{(V_i-V_j)}^2+{\int }_{\Omega }{(n_i-n_j)}^2+{\int }_{\Omega }{(m_i-m_j)}^2+{\int }_{\Omega }{(h_i-h_j)}^2$$

Theorem 2.

The following inequality holds:

$$\begin{array}{cc}\hfill \frac{d}{dt}{\mathcal{H}}_{ij}\le & -(N-3)c{\Gamma }_m{\int }_{[a,a+l]}{|V_i-V_j|}^{2}dx\hfill \\ \hfill & +{\int }_{[a,a+l]}cS(\Gamma \left(V_j(b-x)\right)-\Gamma \left(V_i(b-x)\right)(V_i\left(x\right)-V_j\left(x\right))dx\hfill \\ \hfill & +c{\int }_{[a,a+l]}\left|\begin{array}{cc}\Gamma \left(V_i(b-x)\right)& V_i\left(x\right)\\ \Gamma \left(V_j(b-x)\right)& V_j\left(x\right)\end{array}\right|(V_i-V_j)dx\hfill \\ \hfill & -A{\int }_{\Omega }{(n_i-n_j)}^2-B{\int }_{\Omega }{(m_i-m_j)}^2-C{\int }_{\Omega }{(h_i-h_j)}^2\hfill \\ \hfill & +D{\int }_{\Omega }(n_i-n_j)(V_i-V_j)dx+E{\int }_{\Omega }(m_i-m_j)(V_i-V_j)dx\hfill \\ \hfill & +F{\int }_{\Omega }(h_i-h_j)(V_i-V_j)dx\hfill \end{array}$$

where $A,B,C,D,E,F$ are positive constants.

Proof. 

Let $i,j\in l_2$. We compute

$$\frac{d}{dt}\left({\int }_{\Omega }{(V_i-V_j)}^2+{\int }_{\Omega }{(n_i-n_j)}^2+{\int }_{\Omega }{(m_i-m_j)}^2+{\int }_{\Omega }{(h_i-h_j)}^2\right).$$

We have

$$\begin{array}{}\mathrm{(4)}& \hfill \frac{d}{dt}(V_i-V_j)=& F_i(V_i,n_i,m_i,h_i)-F_j(V_j,n_j,m_j,h_j)+V_{ixx}-V_{jxx}\hfill \mathrm{(5)}& \hfill & +\sum _{k\ne i}{\alpha }_{ki}\left(x\right)(S-V_i)\Gamma \left(V_k(b-x)\right)-\sum _{k\ne j}{\alpha }_{kj}\left(x\right)(S-V_j)\Gamma \left(V_k(b-x)\right)\hfill \end{array}$$

where $F_i$ denotes the classical reaction term in the first equation of HH. Note that $k\notin L_0$, we ommit that part for simplicity. We consider different terms successively.

$$\begin{array}{cc}\hfill & \sum _{k\ne i}{\alpha }_{ki}\left(x\right)(S-V_i)\Gamma \left(V_k(b-x)\right)-\sum _{k\ne j}{\alpha }_{kj}\left(x\right)(S-V_j)\Gamma \left(V_k(b-x)\right)\hfill \\ \hfill & =\sum _{k\ne i,k\ne j}{c}_{ki}\left(x\right)(-V_i+V_j)\Gamma \left(V_k(b-x)\right)\hfill \\ \hfill & +c_{ji}\left(x\right)(S-V_i)\Gamma \left(V_j(b-x)\right)-c_{ij}\left(x\right)(S-V_j)\Gamma \left(V_i(b-x)\right)\hfill \end{array}$$

Next, note that

$$\begin{array}{cc}\hfill \sum _{k\ne i,k\ne j}{\int }_{[a,a+l]}& c_{ki}\left(x\right)(-V_i+V_j)\Gamma \left(V_k(b-x)\right)(V_i-V_j)\hfill \\ \hfill & \le -(N-3)c{\Gamma }_m{\int }_{[a,a+l]}{|V_i-V_j|}^{2}dx\hfill \end{array}$$

Also, we have,

$$\begin{array}{cc}\hfill {\int }_{[a,a+l]}& cS(\Gamma \left(V_j(b-x)\right)-\Gamma \left(V_i(b-x)\right)(V_i\left(x\right)-V_j\left(x\right))dx\hfill \\ \hfill & \le 2\sqrt{l}cS\left|\right|V_i-V_j{\left|\right|}_{L^2(a,a+l)}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\int }_{[a,a+l]}& c(-V_i)\Gamma \left(V_j(b-x)\right)+c{V}_j\Gamma \left(V_i(b-x)\right)(V_i-V_j)\hfill \\ \hfill & =c{\int }_{[a,a+l]}\left|\begin{array}{cc}\Gamma \left(V_i(b-x)\right)& V_i\left(x\right)\\ \Gamma \left(V_j(b-x)\right)& V_j\left(x\right)\end{array}\right|(V_i-V_j)dx\hfill \\ \hfill & \le 2\sqrt{2l}c\left|\right|V_i-V_j{\left|\right|}_{L^2(a,a+l)}\hfill \end{array}$$

□

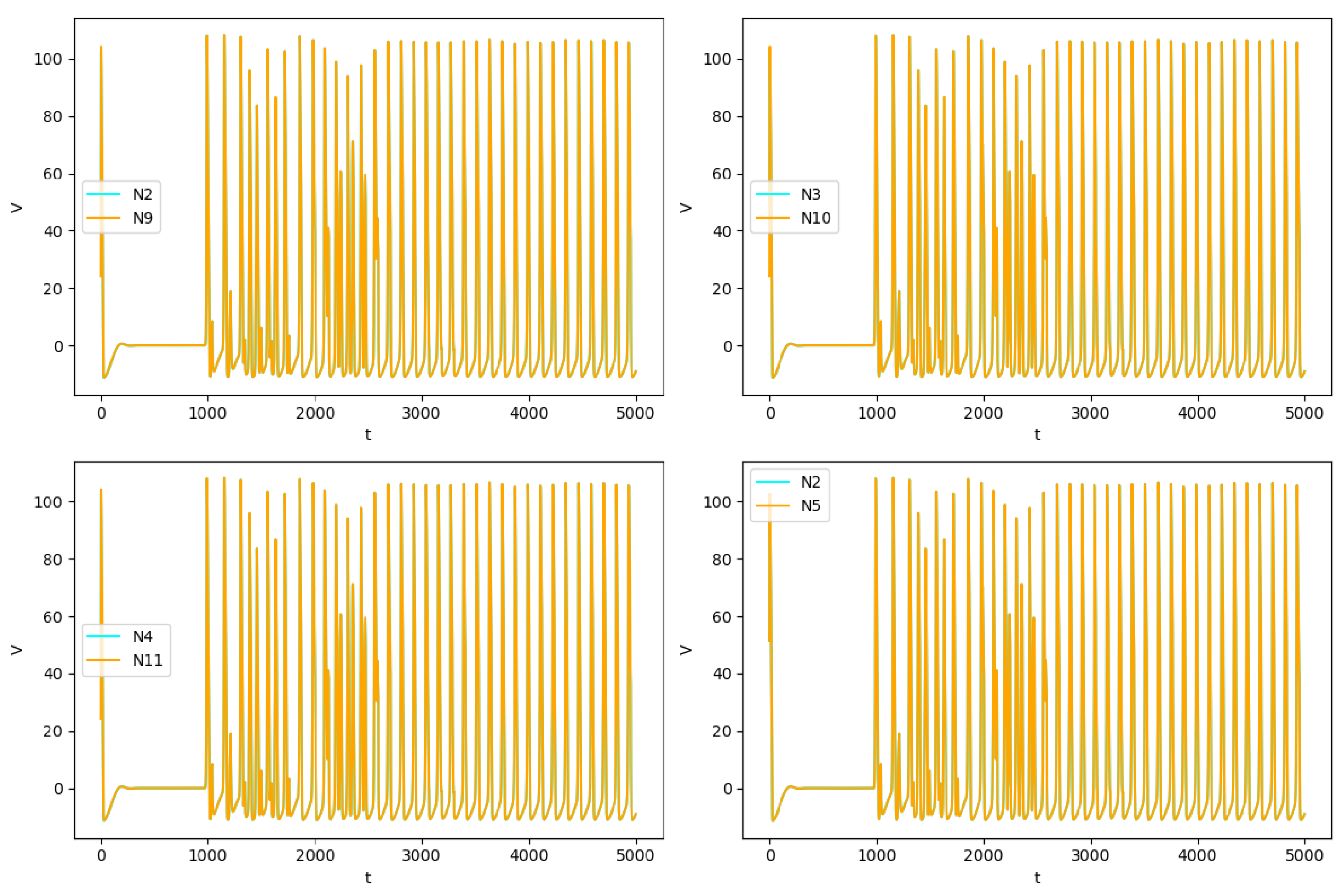
4. Synchronization in the Forced Network of PDE HH Equations

This section focuses on the illustration of numerical results obtained from simulation of Equation (1). Simulations were carried out using our own C++ program, with a finite difference scheme in space and a Runge-Kutta 4 method in time. The time step was $0.01$ and the space step was 1. The space domain was $\Omega =(0,100)$, and $l=10$. Figure 5 illustrates the time evolution of the potential for three neurons at three distinct location. The first row, in blue, corresponds to a neuron of level 1. It receives a periodic input $I\left(t\right)$. The second row, in green corresponds to the unique neuron connected to the first one. Finally, the third row, in red, corresponds to a neuron in level 3. The first column corresponds to $x=0$, the second column corresponds to $x=10$, the last column corresponds to $x=12$. This illustrates how the signal is propagated from left to right and how small oscillations in the left of the neuron are filtered. The colors as those in Figure 1.

Figure 6 and Figure 7 illustrate the synchronization phenomenon for neurons in level 3. Although, initial conditions were different, asymptotically they are the same: the synchronized manifold attracts some solutions. Figure 6 illustrates the time evolution of the potential for different neurons at fixed spaces. In each panel, two neurons are represented. The curves are almost indistinguishable to the naked eye emphasizing the synchronization phenomenon.

In our neural network, when we exclude from the network the neurons we have stimulated(blue) and the neurons that are unidirectionally connected to the stimulated neurons(green), we observe that the rest of the network synchronizes(red). In Figure 7, even if we perturb the initial conditions, we observe identical synchronization.