1. Introduction
In [
10] Kaneko and Tsumura proposed to study the
multiple T-values (MTVs)
as level two variations of
multiple zeta values which in turn were first studied by Zagier [
26] and Hoffman [
3] independently:
where
is the set of positive integers. These series converge if and only if
in which case we say
s is
admissible. As usual, we call
the weight and
d the depth. The main motivation to consider MTVs is that they have the following iterated integral expressions
which equips the MTVs with a
-algebra structure because of the shuffle product property satisfied by the iterated integral multiplication (see, e.g., [
25, Lemma 2.1.2(iv)]).
Besides MTVs, many other variants of multiple zeta values have been studied due to their important connections to a varieties of objects in both mathematics and theoretical physics (see, e.g., [
2,
6,
10,
22]). On the other hand, the congruence properties of the partial sums of MZVs were first considered by Hoffman [
5] and the author [
24] independently. Contrary to the classical cases, only a few variants of these sums exist (see, e.g., [
9,
16,
23]). In this paper, we will concentrate on the finite analog of MTVs defined by (
1).
Let
be the set of primes and put
Then we can define the
finite multiple zeta values (FMZVs) by the following:
Nowadays, the main motivation to study FMZVs is to understand a deep conjecture proposed by Kaneko and Zagier around 2014 (see Conjecture 1.1 below for a generalization). Although this conjecture is far from being proved many parallel results have been shown to hold for both MZVs and FMZVs simultaneously (see, e.g., [
12,
13,
14]). In particular, for each positive integer
, the element
is the finite analog of
, where
’s are the Bernoulli numbers defined by
And the connection goes even further to their alternating versions—the Euler sums and finite Euler sums. For
and
, we define the
Euler sumsTo save space, if
then
will be used and if a substring
S repeats
n times in the list then
will be used. For example, the finite analog of
is the Fermat quotient
Put
and
if
. For
we can define the finite
Euler sums by
In [
25, Conjecture 8.6.9] we extended Kakeko–Zagier conjecture to the setting of the Euler sums. For
, define the symmetric version of the alternating Euler sums
where
(
or ⧢) are regularized values (see [
25, Proposition 13.3.8]). They are called ♯-regularized
symmetric Euler sums. If
then they are called ♯-regularized
symmetric multiple zeta values (SMZVs).
Conjecture 1.1. (cf. [
25, Conjecture 8.6.9])
For any , let (resp. ) be the -vector space generated by all finite Euler sums (resp. Euler sums) of weight w. Then there is an isomorphism
where or ⧢.
We remark that
always lies in
, see [
25, Exercise 8.7]. Thus it does not matter which version of symmetric Euler sums is used in the conjecture.
Problem 1.2. What is the correct generalization of [
25, Theorem 6.3.5] for symmetric Euler sums? Or extension of [
25, Theorem 8.5.10] to finite Euler sums?
Our primary motivation to study finite (alternating) MTVs is to better understand this mysterious relation
. We now briefly describe the content of this paper. We will start the next section by defining finite MTVs and symmetric MTVs, which can be shown to appear on the two sides of Conjecture 1.1, respectively. The most useful property of MTVs is that they have the iterated integral expressions (
3) satisfying the shuffle multiplication. This leads us to the discovery of the linear shuffle relations for the finite MTVs (and their alternating version) in section 3 and some interesting applications of these relations. In the last section, we will consider both the finite MTVs and their alternating version by computing the dimension of the weight
w piece for
and then compare these data to their Archimedean counterparts obtained by Xu and the author [
19,
20].
2. Symmetric and finite multiple T-values
It turns out that the finite MTVs are closely related to another variant called finite MSVs. For all admissible
, we define the
finite multiple T-values (FMTVs) and the
finite multiple S-values (FMSVs) by
It is clear that
Motivated by Conjecture 1.1, we provide the following definition.
Definition 2.1. Let
and
. Let
or
T. We define the
♯-regularized MTVs (
or ⧢) and
MSVs by
We define the
♯-symmetric multiple T-values (SMTVs) and
♯-symmetric multiple S-values (SMSVs) by
where
and we set as usual
.
Proposition 2.1. Suppose is defined as in Conjecture 1.1. Let or ⧢. Then for all we have and modulo .
Proof. Suppose
d is even and
. Then modulo
The MSVs and the odd
d cases can all be computed similarly and are left to the interested reader. □
Hence, we expect that whenever certain relation hold on the finite side then the same relations should hold for the symmetric version, at least modulo
, and vice versa. Sometimes, they are valid for the symmetric version even without modulo
. For example, the following reversal relations hold for both types of sums (see [
23, Proposition 2.8 and 2.9]). For
we put
.
Proposition 2.2.(Reversal Relations
) For all , if d is even then
and if d is odd then
3. Linear shuffle relations for finite multiple T-values (FMTVs)
One of the most important tools to study MZVs and Euler sums is to consider the double shuffle relations which are produced by two ways to express these sums: one as series by definition, the other by iterated integrals. This idea will play the key role in the following discovery of the linear shuffle relations for FMTVs and their alternating version.
The linear shuffle relations for Euler sums are given by [
25, Theorem 8.4.3]. First, we extend MTVs and FMTVs to their alternating version. For all admissible
(i.e.
), we define the alternating multiple
T-values by
This is basically the same definition we used in [
20,
21] except for a possible sign difference. If we denote by
the version in loc. cit., then
We changed to our new convention in this paper because of the significant simplification in this special case. However, the old convention is still superior to treat the general alternating multiple mixed values. Similar to the convention for Euler sums, we will save space by putting a bar on top of
if
. For example,
In order to study the alternating MTVs, it is to our advantage to consider the
alternating multiple T-functions of one variable as follows. For any real number
x, define
In the non-alternating case, this function is the A-function (up to a power of 2) used by Kaneko and Tsumura in [
10]. For all
, it is then easy to evaluate the iterated integral
Let
By the change of indices
we immediately get
where
for all
and
represent the conversions between the series and the integral expressions of alternating MTVs:
Namely,
pushes a word used in the series definition to a word used in the integral expression while
goes backwards. See [
21] for more details.
To state the linear shuffle relations among FMTVs and their alternating version, we first quickly review the algebra setup and the corresponding results for Euler sums. Let
(resp.
) be the
-algebra of words on
(resp.
) with concatenation as the product. Let
(
) be the subalgebra generated by the words not ending with
. Then for each word
, we define
where
and
for all
. Set
and
Theorem 3.1. ([
25, Theorem 8.4.3])
For all words , , and , we have
- (i)
⧢,
- (ii)
⧢⧢,
- (iii)
⧢⧢
For alternating MTVs, we can similarly let
(resp.
) be the
-algebra of words on
(resp.
) with concatenation as the product. Let
(
) be the subalgebra generated by the words not ending with
. Then for each word
, let
be the two maps defined by (
18) and (
19). Then we can extend the definition of alternating MTVs and their corresponding one-variable functions to the word level:
where
can be either
, or
, or
or ⧢ even their partial sums such as
For all words
we set
Further, set
and
Theorem 3.2. For all words , and , we have
- (i)
if is even,
- (ii)
if is even,
- (iii)
if is odd.
Proof. Taking and then setting we see that (ii) implies (i). Decomposing into strings of the type we see that (iii) implies (ii). So we only need to prove (iii).
For simplicity, write
and
for the rest of this proof. Observe that for any odd prime
p, the coefficient of
of
is nontrivial if and only if
is odd. Therefore, if the depth
d of the word
is even the coefficient of
in
is given by
since
. Observe that
Hence, if
is odd, then by first applying
to the above and then extracting the coefficients of
from both sides we get
by the shuffle product property of iterated integrals. Now the last sum is
p-integral since
and
and therefore we get
which completes the proof of (iii). □
Remark 3.3. In [
8], Jarossay showed that the corresponding results of Theorem 3.1 hold for SMZVs. Theorem 3.2, Conjecture 1.1 and Proposition 2.1 clearly imply that similar statements also hold true for SMTVs when the depth conditions are satisfied as in Theorem 3.2. However, it is possible to prove this unconditionally using the generalized Drinfeld associator
and consider the words of the form
in [
25, Theorem 13.4.1]. The details of this work will appear in a future paper.
We can now derive a sum formula for FMTVs.
Theorem 3.4.
Suppose is odd. For all we have
by taking and in Theorem 3.2(iii).
Proof. This follows immediately from the linear shuffle relation
□
The following conjecture is supported by all numerically.
Proposition 3.6.
If k is odd then for all we have
If in addition we assume Conjecture 3.5 holds then
Proof. For all
, by linear shuffle relations
Thus, setting
we get
Hence
which yields (
20). Then (
21) follows immediately if we assume Conjecture 3.5. □
3.1. Values at small depths/weights
First we observe that since
for all
, by [
25, Theorem 8.2.7],
where
is the Fermat quotient (
8) and
is given by (
6). Further, in depth two, by [
23, Proposition 2.6] we see that for all
, if
is odd then
The depth three case is already complicated and we do not have a general formula. This is expected since such formula does not exist for FMZVs. In the rest of this section we will deal with some special cases.
Next, we prove a proposition which improves a result Tauraso and the author obtained more than a decade ago, by applying the newly discovered linear shuffle relations above.
Proof. It follows immediately from [
18, Proposition 7.3 and Proposition 7.6] that
By the linear shuffle relations for finite Euler sums we have
which readily yields the identity
This quickly implies all the evaluations in the proposition. □
Proof. The corollary is an immediate consequence by the definitions using Proposition 3.7. Or we can prove it directly as follows. Since
by reversal and
we get
by [
25, Theorem 8.6.4]. □
Proof. The weight three Euler sums are all expressible in terms of
and
by [
25, Proposition 14.2.7]. Hence one easily deduces that
By [
25, Proposition 14.2.7]
Thus, we get
as desired. □
Turning to the finite Euler sums in general, we can use linear shuffles to derive many relations. For examples,
We can also use reversal and stuffle relations to express all finite Euler sums of weight up to 6 by explicitly given basis in each weight. Aided by Maple computation we arrive at the following main theorem on the structure of finite Euler sums of lower weight.
Theorem 3.10.
Let be the -vector space generated by finite Euler sums of weight w. Then we have the following generating sets for :
Let be the Fibonnacci sequence defined by and for all . Then Theorem 3.10 provides strong support for the next conjecture.
Conjecture 3.11.
For every positive integer w the -space has the following basis:
Consequently, for all .
One may compare to this to the conjecture on the ordinary Euler sums proposed by Zlobin [
25, Conjecture 14.2.3]
Conjecture 3.12.
For every positive integer w the -space has the following basis:
Consequently, for all .
Theorem 3.10 implies that the set in Conjecture 3.11 is a generating set for all
since
where
and
.
Using the evaluations of finite Euler sums, we can find all FMTVs of weight less than 7. For example, we have
We then have the following structural theorem for these FMTVs.
Theorem 3.13.
Let be the -vector space generated by FMTVs of weight w. Then we have the following generating sets for :
Moreover, by using numerical computation aided by Maple (see [
25, Appendix D] for the pseudo codes) we can find a generating set of
for every
We will list the corresponding dimensions at the end of this paper.
3.2. Homogeneous cases
In this subsection, we will compute finite Euler sums when s is homogeneous, i.e., for some . Then we will consider the corresponding results for FMTVs.
Proposition 3.14.
Let be the set of odd positive integers. For any , we have
where is the Kronecker symbol. In particular, for all even s.
Proof. Let
denote any partition of
into odd parts, i.e., all of
’s are odd numbers, where
is the cardinality of the set
. Put
Observe that
if
n is even. Then it follows easily from [
4, (18)] that
The proposition follows from (
22) immediately. □
Example 3.15. There are following ways to partition 6 elements, say
into odd parts: one way to get
,
ways to get
(e.g.
),
ways to get
, and
ways to get
. Hence,
by using the formula in (
22). We would like to point out that the term
(corresponding to the second term
on the right-hand side above) was accidentally dropped from the right-hand side of [
18, (36)].
One may compare the next corollary to the well-known result that
for all
(see, e.g., [
25, Theorem 8.5.1]).
Proof. Taking in Theorem 3.4 yields the proposition at once. □
We now derive the symmetric MTV version of Proposition 3.16.
Proof. For any
we have the relation for the regularized value (see, e.g., [
7])
This implies that
By the definition,
as desired. □
By extensive numerical experiments, we found the following relations must be valid.
Conjecture 3.18.
For all odd we have
The conjecture holds when
by Corollary 3.8 and Proposition 3.9. Aided by Maple, we can also rigorously prove the conjecture for
and
by using tables of values of finite Euler sums produced by reversal, stuffle and linear shuffle relations, and the table of values for Euler sums available online [
1].
Moreover, Conjecture 3.18 still holds true for when w is even because of Propositions 3.16 and 3.17. But for S-values, we have another conjecture.
Conjecture 3.19.
For all even , there are rational numbers , , such that
Moreover, , , are -linearly independent, and , , are -linearly independent.
Note that while are all real numbers.
4. Alternating multiple T-values
We now turn to the alternating version of MTVs and derive some relations among them. These values are intimately related to the colored MZVs of level 4 (i.e., multiple polylogarithms evaluated at 4th roots of unity). We refer the interested reader to [
19,
20] for the fundamental results concerning these values.
Recall that for any
, we have defined the finite alternating multiple
T-values by
We have seen from Theorem 3.2 in
Section 3 that these values satisfy the linear shuffle relations. It is also not hard to get the reversal relations when the depth is even, as shown below.
Proposition 4.1.(Reversal Relations of finite alternating MTVs
) Let for some even . Then
where the element .
Proof. Let
p be an odd prime. Then by change of indices
we get
Let
,
, and
. Then we get by the change of indices
(since
d is even)
as desired. □
It should be clear to the attentive reader that T-values are always intimately related to the S-values when the depth is odd because of the reversal relations. Even though we did not consider this in the above, it plays the key role in the proof of the next result.
Proposition 4.2.
Let for all . Then we have
Proof. Recall that
By [
17, Theorem 3.2] we see that
Since
we see immediately that
. Taking reversal, we get
as desired. □
As we analyzed on [
25, p. 239], there is an overwhelming evidence that
in
. In [
15, Theorem 1], Silverman even showed that, if abc-conjecture holds then
In fact we are sure the following conjecture is true.
Conjecture 4.3. For every pair of positive integers , , there are infinitely many primes such that q2 (p) 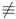 0 (mod p).
0 (mod p).
Theorem 4.4. If Conjecture 4.3 holds for , then and are -linearly independent.
Proof. If in for some , then by Proposition 4.2 we see that for infinitely many primes . If Conjecture 4.3 holds form then for infinitely many primes . This would force . Similar consideration for primes implies that . Hence, we must have which shows that and are -linearly independent. □
Define the
finite Catalan’s constant by
Proposition 4.5.
Let be the vector space generated by finite alternating MTVs over . We have the following generating sets of for :
Proof. The
case is trivial. For
, we already know
by Theorem 3.13. Let
,
and
in the rest of the proof. For alternating values, we first have the linear shuffle relation
By complicated computation (see [
23, Proposition 4.4] and notice (
16)) we have the additional relation
Then by the reversal relation (
26) we see easily that
This completes the proof of the proposition. □
5. Dimensions of and
We first need to point out that it is possible to study the alternating MTVs by converting them to colored MZVs of level 4 and then applying the setup in [
16]. For example,
The caveat is that we need to extend our scalars to
in general. At the end of [
16] we observed that
for all
, where
is the space spanned by all colored MVZ of level 4 and weight
w over
. By the following, we expect that the
where
is the space spanned by all the finite multiple mixed values. Here, according to [
19], the multiple mixed values means we allow all possible even/odd combinations in the definition of such series instead of a fixed pattern such as that has appeared in MTVs and MSVs).
Conjecture-Principle-Philosophy 5.1. Let S be a set of colored MZVs (including MZVs and Euler sums) or (alternating) multiple mixed valuess (or their variations/analogs such as finite, symmetric, interpolated versions etc.) Then the following statements should hold.
- (1)
Suppose all elements in S have the same weight. If they are linearly independent over , then they are algebraically independent over .
- (2)
If the weights of the values in S are all different then the values are linearly independent over (but of course may not be algebraically independent over ).
- (3)
If there is only one nonzero element in S, then it is transcendental over .
For example, we expect that ’s are not only irrational but also transcendental for all . We also expect that and are transcendental for all odd , and are all algebraically independent over
Recall that (resp. ) is the -vector space generated by MTVs (resp. finite MTVs) of weight w. Similarly, we denote by (resp. ) the space generated by alternating MTVs (resp. finite alternating MTVs) of weight w. From numerical computation, we conjecture the following upper bounds for the dimensions of and . To compare to the classical case, we tabulate the results together.
Table 1.
Conjectural Dimensions of , , , , and .
Table 1.
Conjectural Dimensions of , , , , and .
| w |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
0 |
1 |
0 |
1 |
2 |
3 |
3 |
6 |
9 |
15 |
17 |
32 |
44 |
76 |
|
1 |
0 |
1 |
1 |
2 |
2 |
4 |
5 |
9 |
10 |
19 |
23 |
42 |
49 |
|
0 |
2 |
2 |
6 |
12 |
20 |
40 |
76 |
|
|
|
|
|
|
|
0 |
1 |
2 |
4 |
7 |
13 |
24 |
44 |
81 |
|
|
|
|
|
|
0 |
1 |
2 |
4 |
8 |
16 |
|
|
|
|
|
|
|
|
With strong numerical support, Xu and the author conjecture that
form the tribonacci sequence (see [
20]). For MTVs, Kaneko and Tsumura conjecture that, for all
See [
10, p. 216]. From numerical computation we can formulate its finite analog as follows.
Acknowledgments
The author is supported by the Jacobs Prize from The Bishop’s School.
References
- J. Blümlein, D.J. Broadhurst and J.A.M. Vermaseren, The multiple zeta value data mine. Comput. Phys. Commun. 2010, 181, 582–625. [CrossRef]
- F. Brown, S. Carr, and L. Schneps, Algebra of cell-zeta values. Compositio Math. 2010, 146, 731–771, arXiv:0910.0122.. [CrossRef]
- M.E. Hoffman, Multiple harmonic series. Pacific J. Math. 1992, 152, 275–290. [CrossRef]
- M.E. Hoffman, The Hopf algebra structure of multiple harmonic sums. Nuclear Phys. B (Proc. Suppl.) 2004, 135, 214–219.
- M.E. Hoffman, Quasi-symmetric functions and mod p multiple harmonic sums. Kyushu J. Math. 2015, 69, 345–366. [CrossRef]
- M.E. Hoffman, An odd variant of multiple zeta values. Commun. Number Theory Phys. 2019, 13, 529–567. [CrossRef]
- K. Ihara, M. Kaneko and D. Zagier, Derivation and double shuffle relations for multiple zeta values. Compos. Math. 2006, 142, 307–338. [CrossRef]
- D. Jarossay, Double mélange des multizêtas finis et multizêtas symétrisés (in French). C. R. Acad. Sci. Paris, Ser. I 2014, 352, 767–771. [CrossRef]
- M. Kaneko, T. Murakami, and A. Yoshihara, On finite multiple zeta values of level two. Pure Appl. Math Quarterly 2023, 19, 267–280. [CrossRef]
- M. Kaneko and H. Tsumura, On multiple zeta values of level two. Tsukuba J. Math. 2020, 44, 213–234.
- M. Kaneko and D. Zagier, Finite multiple zeta values, in preparation.
- H. Murahara and S. Saito, Restricted sum formula for finite and symmetric multiple zeta values. Pacific J. Math. 2019, 303, 325–335. [CrossRef]
- S. Saito and N. Wakabayashi, Sum formula for finite multiple zeta values. J. Math. Soc. Japan 2015, 67, 1069–1076.
- K. Sakurada, Duality for finite/symmetric multiple zeta values of fixed weight, depth, and height. Int. J. Number Theory 2023, 19, 2299–2307. [CrossRef]
- J. H. Silverman, Wieferich’s criterion and the abc-conjecture. J. Number Theory 1988, 30, 226–237. [CrossRef]
- J. Singer and J. Zhao, Finite and symmetrized colored multiple zeta values. Finite Fields and Their Applications 2020, 65. [CrossRef]
- Z.-W. Sun, Congruences involving Bernoulli and Euler numbers. J. Number Thy. 2008, 128, 280–312. [CrossRef]
- R. Tauraso and J. Zhao, Congruences of alternating multiple harmonic sums. J. Comb. Number Theory 2010, 2, 129–159.
- C. Xu and J. Zhao, Variants of multiple zeta values with even and odd summation indices. Math. Zeit. 2022, 300, 3109–3142. [CrossRef]
- C. Xu and J. Zhao, Alternating multiple T-values: weighted sums, duality, and dimension conjecture. Ramanujan J. Math. 2024, 63, 13–54. [CrossRef]
- C. Xu, L. Yan and J. Zhao, Alternating multiple mixed values, regularization, parity and dimension conjecture. arXiv:2208.09593.
- S. Yamamoto, Interpolation of multiple zeta and zeta-star values. J. Algebra 2013, 385, 102–114. [CrossRef]
- J. Zhao, Finite multiple mixed values (with an Appendix by. Jeremy Feng, Angelina Kim, Sienna Li, Ryan Qin, Logan Wang and J. Zhao). arXiv:2402.08160.
- J. Zhao, Wolstenholme type Theorem for multiple harmonic sums. Intl. J. of Number Theory 2008, 4, 73–106. [CrossRef]
- J. Zhao, Multiple Zeta Functions. In Multiple Polylogarithms and Their Special Values; 620 pp.; Series on Number Theory and Its Applications; Volume 12, World Scientific Publishing, 2016.
- D. Zagier, Values of zeta functions and their applications. In First European Congress of Mathematics; (Paris, 1992), Vol. II, A. Joseph et al. Eds.; Birkhäuser: Basel, 1994; pp. 497–512.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
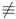 0 (mod p).
0 (mod p).




