Generalized Pareto-Type Distribution and Income Inequality: An Extension of Gibrat’s Law

Preprint

Article

Generalized Pareto-Type Distribution and Income Inequality: An Extension of Gibrat’s Law

Altmetrics

Downloads

119

Views

Comments

A peer-reviewed article of this preprint also exists.

Yong Tao^*

This version is not peer-reviewed

Submitted:

19 February 2024

Posted:

19 February 2024

You are already at the latest version

Alerts

Abstract

Motivated by empirical observations, we propose a possible extension of Gibrat's law. By applying it into the random growth theory of income distribution (Gabaix, 2009), we find that the income distribution is described by a generalized Pareto-type distribution (GPD) with three parameters. We observe that there is a parameter /elta in the GPD that plays a key role in determining the shape of income distribution. By using the Kolmogorov-Smirnov test, we empirically show that, for typical market-economy countries, /elta is close to 0 significantly, such that the income distribution is characterized by a two-class pattern in which the bottom 90% of the population is approximated by an exponential distribution and the richest 1%~3% is approximated by an asymptotic power law. However, we empirically find that, for China both in planned economy period and in early stages of market reformation (from 1978 to 1990), /elta is significantly deviated from 0, such that the bottom of the population no longer conforms to an exponential distribution.

Keywords:

Subject: Business, Economics and Management - Economics

1. Introduction

Global income inequality in the 21st century is growing, and top earners are taking hold of a larger and larger fraction of total income [1,2]. Concerning the upper tail of the income distribution, which is referred to as the richest 1%~3% of the population, it has been long known that it is approximated by the Pareto distribution [3,4]. Based on the random growth theory of income distribution (RGTID) [5,6,7,8,9], it has been acknowledged that the Pareto distribution arises because the dynamics of income obey Gibrat’s law in the stochastic process. This law was first observed by Gibrat [10] in investigating the growth of firm size. It states that firm growth is a purely random effect, independent of firm size. When this law is applied into the RGTID, the resulting distribution of income is governed by the Pareto law [5,9,11,12]. For this reason, Gibrat’s law is widely used to understand the rise in top income inequality. However, the singular focus on the top income class of households overlooks the component of earnings’ inequality that is arguably most consequential for the low- and middle-income class of households [13]. The existing empirical observation has shown that [14,15,16,17,18], for market-economy countries, the income structure of the bottom 90% of the population is approximated by an exponential distribution. Therefore, it has been proposed that [14,15] the income distribution is characterized by a two-class pattern, in which the bottom 90% of the population is approximated by an exponential distribution and the richest 1%~3% is approximated by the Pareto distribution. In this paper, we attempt to reproduce such a two-class pattern of income distribution within the framework of the RGTID by using a possible extension of Gibrat’s law.

Although Gibrat’s law accounts for the emergence of the Pareto distribution, it does not hold exactly. In fact, in the literature of firm size, it has been observed that small firms grow faster than large firms [19,20], and the independence between size and growth becomes clearer as time passes [21]. This suggests that Gibrat’s law holds asymptotically for firms above a certain size threshold. Likewise, in the literature of income distribution, Blanchet et al. [22] propose to identify the Pareto distribution of income as an asymptotic law above some high level, while Gabaix et al. [23] consider possible deviations from Gibrat’s law so as to explore the extension of the Pareto distribution. By combining these two strands of literature, in this paper we use a possible extension of Gibrat’s law to study the income distribution. As with empirical observations in the literature of firm size [19,20,21], the extension of Gibrat’s law is required to satisfy that the growth rate of a person’s income is asymptotically independent of her income above some high level. By applying this extension of Gibrat’s law into the RGTID, we find that the resulting distribution of income is denoted by a generalized Pareto-type distribution (GPD) with three parameters. In particular, we observe that there is a key parameter

η

in the GPD to determine the shape of income distribution. As

η = 0

, the GPD becomes an exponential distribution. However, as long as

η > 0

, the GPD always has an asymptotic power-law tail (or the Pareto tail) above some high level. This implies that, when

η

is close to 0, the GPD may produce a two-class pattern of income distribution, in which the bottom of the distribution is approximated by an exponential law and the upper tail of the distribution is approximated by the Pareto law.

The rest of the paper is organized as follows. Section 2 introduces a possible extension of Gibrat’s law motivated by empirical observations. Section 3 applies this extension of Gibrat’s law into the RGTID to derive the income distribution, where we find that the resulting distribution of income is denoted by the GPD with three parameters. Section 4 shows that there is a key parameter

η

in the GPD to determine the shape of income distribution. In particular, we show that, as

η \approx 0

, the GPD reproduces the two-class pattern of income distribution, in which the bottom of the distribution is approximated by an exponential law and the upper tail of the distribution is approximated by the Pareto law. Section 5 employs the Kolmogorov-Smirnov test to examine if the parameter

η

is close to 0 significantly by using the data from the United States, the United Kingdom, China, and Canada. Section 6 concludes.

2. The extension of Gibrat’s law

Gibrat’s law is a rule of proportionate growth. If one denotes the size of a firm at the time

t

X_{t}

, this law states that the increment of firm size is a linear function of firm size [19,20,21]

X_{t + Δ t} - X_{t} = Δ ε_{t} X_{t},

(1)

where,

Δ t

denotes the increment of time, and the proportional coefficient

Δ ε_{t}

is assumed to be independent of

X_{t}

. In the simplest form,

Δ ε_{t}

can be considered as a constant, but a more realistic model allows for randomness.

To extend Gibrat’s law (1), we write the increment of firm size as a general function of firm size

X_{t + Δ t} - X_{t} = Δ ε_{t} f (X_{t}),

(2)

where

f (X_{t})

is assumed to be a smooth function of

X_{t}

When

f (X_{t}) = X_{t}

, equation (2) returns to Gibrat’s law (1). Mathematically, the smooth function

f (X_{t})

can be always expanded as a Taylor series:

f (X_{t}) = a_{0} + a_{1} X_{t} + a_{2} X_{t}^{2} + a_{3} X_{t}^{3} + \dots

(3)

By using equation (3), equation (2) can be written as

X_{t + Δ t} - X_{t} = Δ ε_{t} (a_{0} + a_{1} X_{t} + a_{2} X_{t}^{2} + a_{3} X_{t}^{3} + \dots) .

(4)

Using equation (4), the growth rate of firm size,

r_{t + Δ t}

, is equal to

r_{t + Δ t} = \frac{X_{t + Δ t} - X_{t}}{X_{t}} = Δ ε_{t} (\frac{a_{0}}{X_{t}} + a_{1} + a_{2} X_{t} + a_{3} X_{t}^{2} + \dots) .

(5)

Empirical observations show that small firms grow faster than large firms [19,20], and the independence between size and growth becomes clearer as time passes [21]. This can be summarized as a stylized fact as below:

Stylized fact 1: The growth rate of firm size is asymptotically independent of the size above a certain size threshold.

By observing equation (5), we find that

a_{2} = a_{3} = a_{4} = \dots = 0

is the unique choice to satisfy the stylized fact 1. In this way, equation (5) reads

r_{t + Δ t} = \frac{X_{t + Δ t} - X_{t}}{X_{t}} = Δ ε_{t} (\frac{a_{0}}{X_{t}} + a_{1}),

(6)

which is independent of

X_{t}

X_{t} \to \infty

Therefore, we assume

a_{2} = a_{3} = a_{4} = \dots = 0

, by which equation (4) can be written as

X_{t + Δ t} - X_{t} = Δ ε_{t} (a_{0} + a_{1} X_{t}) .

(7)

In particular, by equation (6), if

Δ ε_{t} a_{0} > 0

and

Δ ε_{t} a_{1} > 0

, then

r_{t + Δ t}

is a decreasing function of

X_{t}

. This means that, for those firms whose sizes increase with time, small firms grow faster than large firms, as with empirical observations [19,20].

Let us order

{Δ W}_{t} = Δ ε_{t} a_{0}

and

η = a_{1} / a_{0}

. Thus, equation (7) can be rewritten as

X_{t + Δ t} - X_{t} = (1 + η X_{t}) {Δ W}_{t} .

(8)

Equation (8) is a possible extension of Gibrat’s law (1). It asymptotically returns to Gibrat’s law (1) as1

X_{t} \to \infty

To obtain the continuous-time form of equation (8), we assume that

{Δ W}_{t}

denotes the Brownian motion with drift, i.e.,

{Δ W}_{t} ~ N (μ Δ t, σ^{2} Δ t)

; therefore, as

Δ t \to d t

, equation (8) yields

d X_{t} = (1 + η X_{t}) (μ d t + σ d Z_{t}),

(9)

where

μ

and

σ

are two constants, and

d Z_{t} ~ N (0, d t)

denotes the standard Brownian motion.

Equation (9) can be rewritten in the form

d X_{t} = μ (1 + η X_{t}) d t + σ (1 + η X_{t}) d Z_{t} .

(10)

Equation (10) is the starting point of this paper. It is easy to check that equation (10) satisfies the asymptotical scale invariance as

X_{t} \to \infty

. To see this, we order

X_{t} \to \infty

so that equation (10) asymptotically yields

d X_{t} = μ η X_{t} d t + σ η X_{t} d Z_{t},

(11)

which is invariant under the scaling change

{X_{t}}^{'} \to λ X_{t}

. The scale invariance implies a certain kind of fractal property. Based on the RGTID, it has been known that [5,6,7,8,9,11,12], if the dynamics of income obey the random process (11), the resulting distribution of income is denoted by a power law (or the Pareto law). Jones and Kim [9] have pointed out that top income inequality is well characterized by this fractal property. However, equation (10) indicates that the scale invariance does not hold exactly but only asymptotically, such that the income distribution of top earners should be approximated by an asymptotic power law. Next, we apply equation (10) into the RGTID.

3. The basic model

By using the well-established result in the RGTID literature for generating the income distribution [5,9,11,12], if the dynamics of income

x

obey the random process (10), the density of the income distribution,

f (x, t)

, satisfies a Kolmogorov forward equation:

\frac{\partial f (x, t)}{\partial t} = - \frac{\partial [μ (1 + η x) f (x, t)]}{\partial x} + \frac{1}{2} \frac{\partial^{2} [σ^{2} {(1 + η x)}^{2} f (x, t)]}{\partial x^{2}} .

(12)

The derivation of equation (12) can be found in Appendix A.

To obtain the steady-state solution of equation (12), we consider a lower bound on income so that a person cannot go below a given level

x_{m i n}

. In real economies, the unemployment compensation plays the role of the lower bound

x_{m i n}

. Thus, equation (12) describes a random growth with a reflecting barrier

x_{m i n}

[5]. For the steady-state distribution of income,

f (x, t) = f (x)

, we should have

\partial f (x, t) / \partial t = 0

, such that equation (12) yields

- \frac{\partial [μ (1 + η x) f (x)]}{\partial x} + \frac{1}{2} \frac{\partial^{2} [σ^{2} {(1 + η x)}^{2} f (x)]}{\partial x^{2}} = 0,

(13)

It is easy to get a solution of equation (13) as below:

\{\begin{matrix} f (x) = \frac{c_{0}}{σ^{2}} {(1 + η x)}^{\frac{2 μ}{σ^{2} η} - 2} \\ x \geq x_{m i n} \end{matrix},

(14)

where

c_{0}

denotes an integral constant.

The existence of the lower bound

x_{m i n}

requires the normalization equation:

\int_{x_{m i n}}^{\infty} f (x) d x = 1,

(15)

which is used to determine the integral constant

c_{0}

By substituting equation (14) into equation (15) we get the density distribution of income

\{\begin{matrix} f (x) = (\frac{η + \frac{1}{θ}}{1 + η x_{m i n}}) {(\frac{1 + η x}{1 + η x_{m i n}})}^{- \frac{1}{θ η} - 2} \\ x \geq x_{m i n} \end{matrix},

(16)

with

θ = - \frac{σ^{2}}{2 μ},

(17)

where

μ < 0

and

η \geq 0

are used to satisfy the normalization equation (15).

Here, we denote the cumulative distribution of income by

F_{η} (X \geq x) = \int_{x}^{\infty} f (z) d z,

(18)

where

F_{η} (X \geq x)

denotes the fraction of population with the income higher than

x

Substituting equation (16) into equation (18) yields

F_{η} (X \geq x) = {(\frac{1 + η x}{1 + η x_{m i n}})}^{- \frac{1}{θ η} - 1},

(19)

where

x \geq x_{m i n}

Equation (19) is the main result of this paper. It has three parameters to determine the shape of income distribution. Remarkably, equation (19) can be written in the form of the generalized Pareto distribution:

F_{η} (X \geq x) = {[1 + A (\frac{x - x_{m i n}}{B})]}^{- \frac{1}{A}},

(20)

where

A = \frac{θ η}{1 + θ η}

and

B = \frac{θ (1 + η x_{m i n})}{1 + θ η}

Therefore, we call equation (19) the generalized Pareto-type distribution (GPD).

In particular, if

η > 0

, equation (19) always has an asymptotical power-law tail (i.e., the Pareto distribution); that is, as

x \to \infty

, one has2

F_{η > 0} (X \geq x) ~ {(\frac{x}{x_{0}})}^{- \frac{1}{θ η} - 1},

(21)

where

x_{0} = (1 + η x_{m i n}) / η

4. The parameter $η$

Here, we show that the parameter

η

in the GPD (19) plays a key role in determining the shape of income distribution. To this end, we observe that, when

η = 0

, the GPD (19) becomes an exponential distribution

F_{η = 0} (X \geq x) = \lim_{η \to 0} F_{η} (X \geq x) = e x p (- \frac{x - x_{m i n}}{θ}),

(22)

where

x_{m i n} > 0

The existing empirical observation has shown that [14,15,16,17,18], for market-economy countries, the income distribution is characterized by a two-class pattern, in which the bottom 90% of the population is approximated by the exponential law (22) and the richest 1%~3% is approximated by the power law (21). Next, we show that this empirical observation can be explained by the GPD (19) as long as

η

is close to zero. To this end, we investigate the conditions that the GPD (19) can be replaced by equations (21) and (22), respectively.

First, we consider

η \approx 0

so that

η x ≪ 1

. Thus, one has

{(1 + η x)}^{- \frac{1}{θ η} - 1} \approx e x p (- x / θ)

. Since

x \geq x_{m i n}

, one has

η x_{m i n} ≪ 1

to obtain

{(1 + η x_{m i n})}^{- \frac{1}{θ η} - 1} \approx e x p (- x_{m i n} / θ)

as well. This means that the GPD (19) for

x_{m i n} \leq x ≪ 1 / η

can be replaced by the exponential distribution (22); that is,

F_{η \approx 0} (X \geq x) = {(\frac{1 + η x}{1 + η x_{m i n}})}^{- \frac{1}{θ η} - 1} \approx e x p (- \frac{x - x_{m i n}}{θ}),

(23)

Therefore, we expect that, as long as

η

is sufficiently close to zero, the exponential law (22) is roughly valid for the majority of the population, in which each person’s income is lower than

1 / η

Second, we consider that

x

is sufficiently large so that

η x ≫ 1

. In this way, one has

F_{η \approx 0} (X \geq x) = {(\frac{1 + η x}{1 + η x_{m i n}})}^{- \frac{1}{θ η} - 1} \approx {(\frac{η x}{1 + η x_{m i n}})}^{- \frac{1}{θ η} - 1} = {(\frac{x}{x_{0}})}^{- \frac{1}{θ η} - 1},

(24)

where

x_{0} = (1 + η x_{m i n}) / η

as denoted by equation (21).

Equation (24) means that the GPD (19) for

x ≫ 1 / η

can be replaced by the Pareto distribution (21). Thus, we expect that, as long as

η

is sufficiently close to zero, the Pareto distribution (21) is roughly valid for top earners, in which each person’s income is higher than

1 / η

Based on the discussion above, we conclude that, when

η

is close to zero, the GPD (19) can be approximated by the following two-class pattern

F_{η \approx 0} (X \geq x) \approx \{\begin{matrix} e x p (- \frac{x - x_{m i n}}{θ}) & x_{m i n} \leq x < x_{0} \approx \frac{1}{η} \\ {(\frac{x}{x_{0}})}^{- \frac{1}{θ η} - 1} & x > x_{0} \approx \frac{1}{η} \end{matrix},

(25)

where

x_{0} = (1 + η x_{m i n}) / η \approx 1 / η

arises because

η x_{m i n} ≪ 1

However, if

η

is sufficiently larger than 0, then equation (22) may hold no longer for any

x \geq x_{m i n}

. For example, if

η x_{m i n} \approx 1

, one has neither

{(1 + η x_{m i n})}^{- \frac{1}{θ η} - 1} \approx e x p (- x_{m i n} / θ)

nor

{(1 + η x)}^{- \frac{1}{θ η} - 1} \approx e x p (- x / θ)

. This implies that, when

η

is significantly deviated from 0, the bottom of the population cannot be approximated by the exponential distribution (22).

In practice, the statement “the parameter

η

is close to 0” may be highly subjective. To address this problem, we use the Kolmogorov-Smirnov test to identify if the parameter

η

is close to 0 significantly.

5. Tests using the data from the US, the UK, China, and Canada

From a statistical perspective, the collection of household income data can be regarded as a sample observed from the income distribution,

F_{η} (X \geq x)

. Therefore, we selected household income data3 from the latest years available for four representative market-economy countries to test if the parameter

η

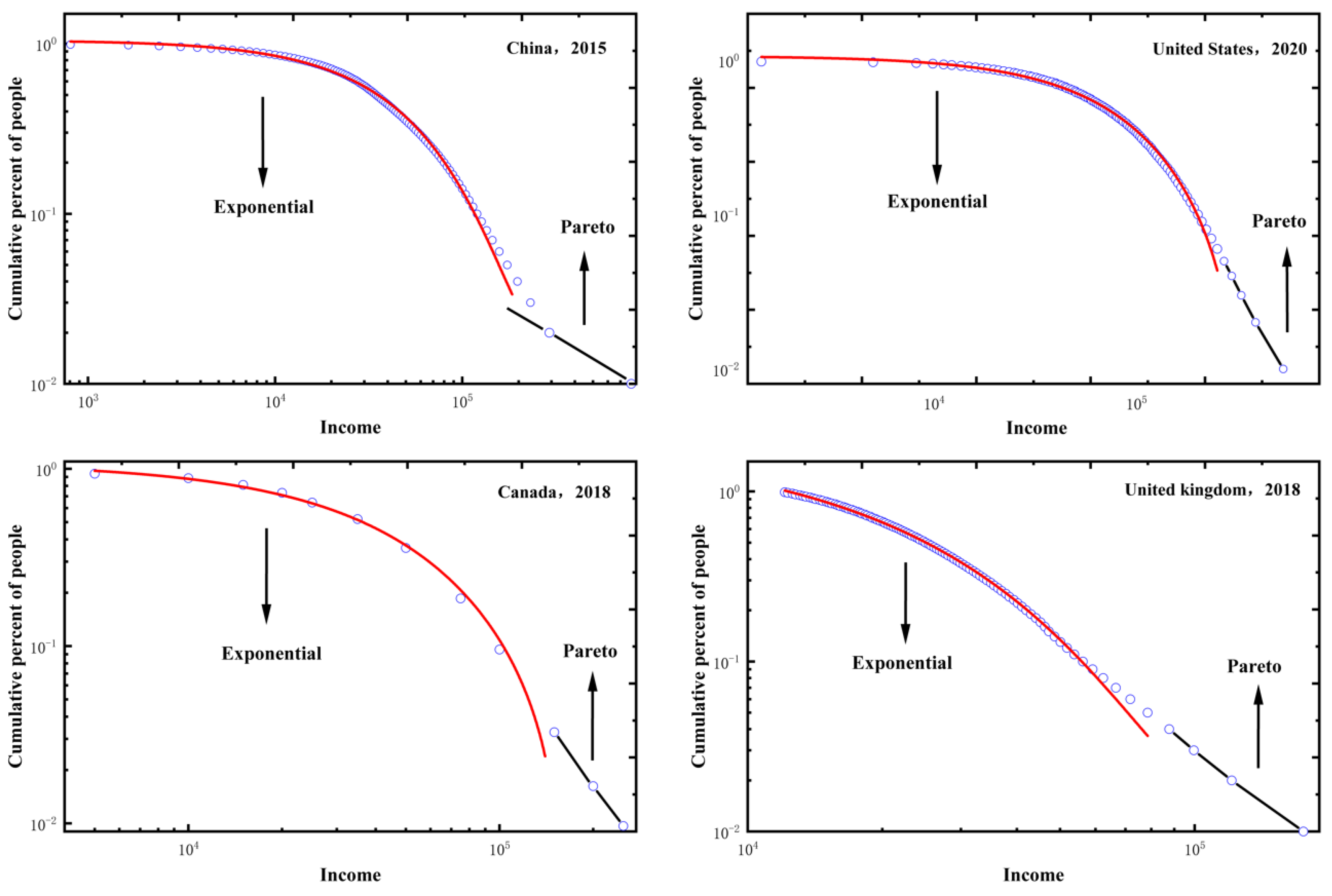
is close to 0 significantly. The four countries include three developed economy (the United States in 2020, the United Kingdom in 2018, and Canada in 2018) and one developing economy (China in 2015) that is at present the world’s second largest economy. Figure 1 shows that, for each country, the income distribution of the bottom 90% of the sample (circle) is well approximated by the exponential law (22) (red curve), while the upper tail of the sample is approximated by the power law (21) [i.e., the Pareto distribution] (black curve). By equation (25), this implies that

η

is close to 0 for four countries.

To strictly identify if the parameter

η

is close to 0 significantly for four countries, we use the Kolmogorov-Smirnov (KS) test. The hypothesis-testing is written as:

H_{0} : η = 0

H_{1} : η > 0,

where, by equation (22), the null hypothesis

η = 0

indicates that the income distribution is described by the exponential law, in which

x_{m i n}

is chosen to be the first quantile of the sample. In our database, the data from United States, the United Kingdom, and China are large samples, each of which includes 99 quantiles. This implies that the KS test is feasible for these three countries. Although the data from Canada only includes 12 quantiles, we still use the KS test to perform a rough examination.

The testing result is listed in Table 1. For the United States in 2020, the United Kingdom in 2018, Canada in 2018, and China in 2015,

η = 0

cannot be rejected at the significance level of 0.1. This means that

η

is close to 0 significantly. However,

η

is not equal to zero exactly, because Figure 1 has shown that the income distribution of each country has a power-law tail as described by equation (21).

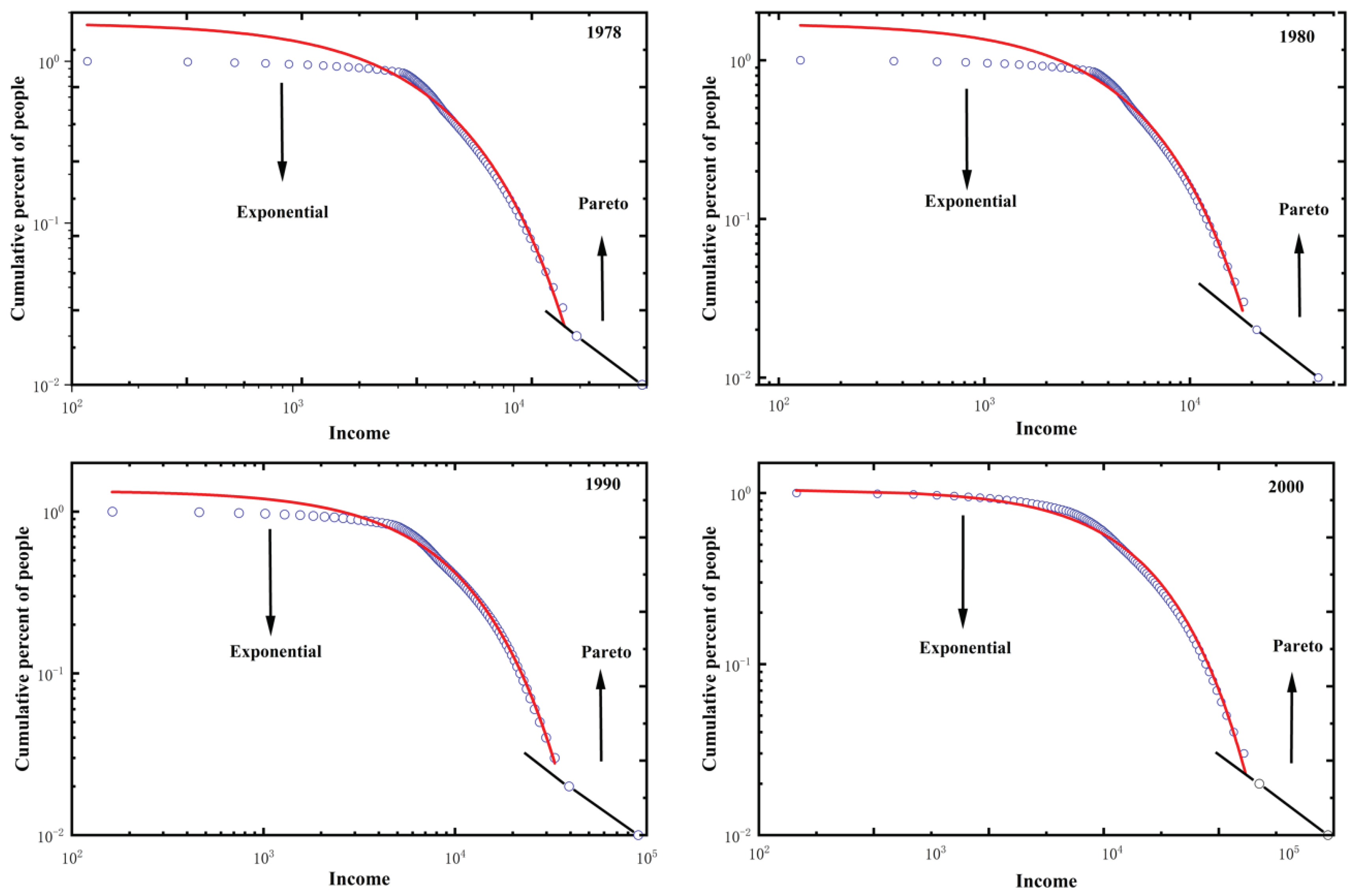
China is a special sample that has undergone the transition from a centrally planned economy to a market economy. Here, we selected the data4 from China in 1978, 1980, 1990, and 2000 to check if the parameter

η

is close to 0 significantly in the early stages of market-oriented economic reformation. As shown in Table 2,

η = 0

is rejected at the significance level of 0.01 in 1978, 1980, and 1990, while it cannot be rejected in 2000. This suggests that, for China both in planned economy period and in early stages of market reformation (from 1978 to 1990),

η

is significantly deviated from 0, such that the bottom of the population no longer conforms to an exponential distribution. The KS test results are supported by the data fitting in Figure 2, which has shown how the bottom 90% of the population in China deviates from an exponential distribution of income (red curve) during from 1978 to 1990. In Appendix B, we further discuss the economic implication of the parameter

η

. Within the framework of the random growth theory of income distribution (RGTID), we find that the parameter

η

may have the significance of characterizing the inequality of earning opportunity. Ideally,

η = 0

corresponds to the equality of earning opportunity. From this sense, the test result that

η = 0

is rejected for China in 1978, 1980, and 1990 implies that the equality of earning opportunity is broken significantly both in planned economy period and in early stages of market reformation.

However, for all the years, the income distribution always has a power-law tail (black line) as shown in Figure 2. This empirical observation agrees with equation (21).

6. Concluding remarks

Motivated by empirical observations, we propose a possible extension of Gibrat’s law, which requires that the growth rate of firm size is asymptotically independent of the size above a certain size threshold. By applying this extension of Gibrat’s law into the RGTID, we find that the income distribution is described by a generalized Pareto-type distribution (GPD) with three parameters. In particular, we observe that there is a key parameter

η

in the GPD to determine the shape of income distribution. As

η = 0

, the GPD becomes an exponential distribution. However, as long as

η > 0

, the GPD always has an asymptotic power-law tail (or the Pareto tail) above some high level. This implies that, when

η

By using the Kolmogorov-Smirnov test, we empirically show that

η = 0

cannot be rejected at the significance level of 0.1 for typical market-economy countries such as the United States, the United Kingdom, Canada, and China (after 2000), while income distributions of these countries have a power-law tail without exception. This suggests that

η

is close to 0 significantly for these market-economy countries, such that the income distribution is characterized by a two-class pattern, in which the bottom 90% of the population is approximated by an exponential distribution and the richest 1%~3% of the population is approximated by the Pareto distribution. However, we empirically find that

η = 0

is rejected at the significance level of 0.01 for China during from 1978 to 1990. This suggests that, for China both in planned economy period and in early stages of market reformation,

η

is significantly deviated from 0, such that the bottom of the population no longer conforms to an exponential distribution.

Author Contributions

The author performed the research in this paper independently.

Data Availability Statement

This study analyzed publicly available datasets. These datasets can be accessed here: Data resource for China: http://wid.world/data/; Data resource for the United States: https://ipums.org/; Data resource for Canada: https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1110000801; Data resource for the United Kingdom: https://www.gov.uk/government/statistics/percentile-points-from-1-to-99-for-total-income-before-and-after-tax.

Acknowledgements

This work was supported by the Social Science Planning Project of Chongqing (Grant No. 2019PY40) and the Research project on education and teaching reform in Southwest University (Grant No. 2021JY045)

Conflicts of Interest

The author declares no conflict of interest.

Appendixes

Appendix A: Derivation of equation (12)

Let us consider the Ito process

d X_{t} = A (t, X_{t}) d t + B (t, X_{t}) d Z_{t},

(A.1)

where

A (t, X_{t})

and

B (t, X_{t})

are two functions of

X_{t}

and

t

, and

d Z_{t}

denotes the standard Brownian motion.

By using the theory of stochastic differential equations, it has been known that, when the variable

x

evolves according to the random process (A.1), the density distribution of

x

satisfies the Kolmogorov forward equation:

\frac{\partial f (x, t)}{\partial t} = - \frac{\partial [A (t, x) f (x, t)]}{\partial x} + \frac{1}{2} \frac{\partial^{2} [{B (t, x)}^{2} f (x, t)]}{\partial x^{2}}

(A.2)

The derivation of equation (A.2) can be found in any book on stochastic calculus, e.g., see page 282 in [24] or page 50 in [25].

Comparing equations (10) and (A.1), one has

A (t, X_{t}) = μ (1 + η X_{t}),

(A.3)

and

B (t, X_{t}) = σ (1 + η X_{t}) .

(A.4)

Substituting equations (A.3) and (A.4) into equation (A.2) yields equation (12).

Appendix B: Economic implication of the parameter $η$

Here, we provide a possible economic implication for the parameter

η

within the framework of the random growth theory of income distribution (RGTID). In the setting of random growth process (10), the resulting distribution of income is characterized by the random variable

X

with cumulative distribution function,

F_{η} (X \geq x)

. This setting means that the distribution of income,

F_{η} (X \geq x)

, can be understood as a probability distribution5; that is, the probability of acquiring the income

x

for a person. Given this understanding, we propose a special definition for identifying the equality of earning opportunity. To this end, let us calculate the following conditional probability:

F_{η} (X \geq x + y| X \geq y) = \frac{F_{η} (\{X \geq x + y\} \cap \{X \geq y\})}{F_{η} (X \geq y)} = \frac{F_{η} (X \geq x + y)}{F_{η} (X \geq y)},

(B.1)

which denotes the probability of acquiring the earnings

x

for a person given that she has earned the income

y

Definition B.1 (Equality of earning opportunity):

If the probability of acquiring the earnings

x

for a person is denoted by

F_{η} (X \geq x)

, the earning opportunity is equal to everyone as long as

F_{η} (X \geq x + y| X \geq y)

is independent of

y

for any

x

and

y

To understand the implication of the Definition B.1, we substitute equation (19) into equation (B.1) to obtain

F_{η} (X \geq x + y| X \geq y) = {[\frac{1 + η (x + y)}{1 + η y}]}^{- \frac{1}{θ η} - 1} .

(B.2)

When

η = 0

, equation (B.2) becomes

F_{η = 0} (X \geq x + y| X \geq y) = \lim_{η \to 0} F_{η} (X \geq x + y| X \geq y) = e x p (- \frac{x}{θ}),

(B.3)

which means that a person’s probability of acquiring the future earnings

x

is irrelevant with her past earnings

y

. In other words, the probability of acquiring the earnings

x

is equal to everyone.

However, when

η > 0

, equation (B.2) can be written as

F_{η > 0} (X \geq x + y| X \geq y) = {[1 + \frac{η x}{1 + η y}]}^{- \frac{1}{θ η} - 1},

(B.4)

which is a monotonically increasing function of

y

. This means that, when

η > 0

, a person’s probability of acquiring the future earnings

x

is positively proportional to her past earnings

y

. This is the embodiment of the Matthew effect [26] in income accumulation.

Based on equations (B.3) and (B.4), by the Definition B.1 we identify the parameter

η

as an index of characterizing the inequality of earning opportunity. That is,

η = 0

indicates the equality of earning opportunity, while

η > 0

indicates equal opportunity breaking. It should, however, be clarified that the Definition B.1 is only applied to the RGTID, where the income distribution is ideally equivalent to a probability distribution of income. It does not mean “equality of earning opportunity” in general sense. In fact, identifying the equality of earning opportunity in general sense is a complicated issue. For example, earnings mobility should be considered [27]. From this sense, identifying

η = 0

as the equality of earning opportunity in strict sense is naive. It holds strictly if and only if the income distribution is ideally equivalent to a probability distribution of income.

By using the Definition B.1, it is possible to provide an explanation of why the richest 1%~3% of the population is taking hold of a larger and larger fraction of total income (in sharp contrast to the bottom 90% of the population) to aggravate global income inequality as reported by the literature [28]. First, we show that, if

η \neq 0

, the earning opportunity of top earners may be improved radically. To do so, by equation (B.4) we observe that

F_{η} (X \geq x + y| X \geq y)

is a monotonically increasing function of

y

as long as

η > 0

. In particular, as

y \to \infty

, by equation (B.4) one has

\lim_{y \to \infty} F_{η > 0} (X \geq x + y| X \geq y) = 1,

(B.5)

which means that, if an earner’s past income

y

is sufficiently large, then she would has the potential to win any earnings

x

in future.

Second, our empirical observation in the section 5 has implied that

η \approx 0

for typical market-economy countries. In this case, by equation (B.4),

F_{η} (X \geq x + y| X \geq y)

is approximately independent of

y

as long as

η y ≪ 1

. This means that, when

η \approx 0

, the earners6 in the bottom of the population have roughly equal probabilities denoted by equation (B.3) to win the earnings

x

. However, when

y

is sufficiently large, by equation (B.5) the earning probabilities of top earners may be improved radically even if

η \approx 0

. This in turn sharply enlarges the gap of earning opportunity between top earners and the bottom of the population.

References

Atkinson, A.B.; Piketty, T.; Saez, E. Top Incomes in the Long Run of History. Journal of Economic Literature 2011, 49, 3–71. [Google Scholar] [CrossRef]
Jones, C.I. Pareto and Piketty: The macroeconomics of top income and wealth inequality. Journal of Economic Perspectives 2015, 29, 29–46. [Google Scholar] [CrossRef]
Pareto, V. Cours d’ Economie Politique; L’ Universite de Lausanne, 1897. [Google Scholar]
Champernowne, D.G. A Model of Income Distribution. Economic Journal 1953, 63, 318–351. [Google Scholar] [CrossRef]
Gabaix, X. Zipf’s Law for Cities: An Explanation. Quarterly Journal of Economics 1999, 114, 739–767. [Google Scholar] [CrossRef]
Gabaix, X. Power Laws in Economics and Finance. Annual Review of Economics 2009, 1, 255–294. [Google Scholar] [CrossRef]
Gabaix, X. Power Laws in Economics: An Introduction. Journal of Economic Perspective 2016, 30, 185–206. [Google Scholar] [CrossRef]
Benhabib, J.; Bisin, A.; Zhu, S. The Distribution of Wealth and Fiscal Policy in Economies With Finitely Lived Agents. Econometrica 2011, 79, 123–157. [Google Scholar]
Jones, C.I.; Kim, J. A Schumpeterian Model of Top Income Inequality. Journal of Political Economy 2018, 126, 1785–1826. [Google Scholar] [CrossRef]
Gibrat, R. Les inegalites economiques; Librairie du Receuil Sirey: Paris, 1931. [Google Scholar]
Malevergne, Y.; Saichev, A.; Sornette, D. Zipf’s law and maximum sustainable growth. Journal of Economic Dynamics and Control 2013, 37, 1195–1212. [Google Scholar] [CrossRef]
Aoki, S.; Nirei, M. Zipf’s Law, Pareto’s Law, and the Evolution of Top Incomes in the United States. American Economic Journal: Macroeconomics 2017, 9, 36–71. [Google Scholar] [CrossRef]
Autor, D.H. Skills, education, and the rise of earnings inequality among the other 99 percent. Science 2014, 344, 843–851. [Google Scholar] [CrossRef]
Dragulescu, A.; Yakovenko, V.M. Exponential and power-law probability distributions of wealth and income in the United Kingdom and the United States. Physica A 2001, 299, 213–221. [Google Scholar] [CrossRef]
Nirei, M.; Souma, W. A Two Factor Model of Income Distribution Dynamics. Review of Income and Wealth 2007, 53, 440–459. [Google Scholar] [CrossRef]
Tao, Y. Spontaneous economic order. Journal of Evolutionary Economics 2016, 26, 467–500. [Google Scholar] [CrossRef]
Tao, Y.; et al. Exponential structure of income inequality: evidence from 67 countries. Journal of Economic Interaction and Coordination 2019, 14, 345–376. [Google Scholar] [CrossRef]
Tao, Y.; et al. Superlinear growth and the fossil fuel energy sustainability dilemma: Evidence from six continents. Structural Change and Economic Dynamics 2023, 66, 39–51. [Google Scholar] [CrossRef]
Almus, M. Testing “Gibrat’s Law” for Young Firms – Empirical Results for West Germany. Small Business Economics 2000, 15, 1–12. [Google Scholar] [CrossRef]
Becchetti, L.; Trovato, G. The Determinants of Growth for Small and Medium Sized Firms. The Role of the Availability of External Finance. Small Business Economics 2002, 19, 291–306. [Google Scholar] [CrossRef]
Daunfeldt, S.; Elert, N. When is Gibrat’s law a law? Small Business Economics 2013, 41, 133–147. [Google Scholar] [CrossRef]
Blanchet, T.; Fournier, J.; Piketty, T. Generalized Pareto Curves: Theory and Applications. Review of Income and Wealth 2022, 68, 263–288. [Google Scholar] [CrossRef]
Gabaix, X.; et al. The Dynamics of Inequality. Econometrica 2016, 84, 2071–2111. [Google Scholar] [CrossRef]
Karatzas, I.; Shreve, S. Brownian Motion and Stochastic Calculus, 2nd ed.; Springer-Verlag: Berlin, Germany, 1991. [Google Scholar]
Stokey, N. The Economics of Inaction: Stochastic Control Models with Fixed Costs; Princeton University Press, 2009. [Google Scholar]
Perc, M. The Matthew effect in empirical data. Journal of the Royal Society Interface 2014, 11, 20140378. [Google Scholar] [CrossRef] [PubMed]
Bowlus, A.J.; Robin, J.M. An International Comparison of Lifetime Inequality: How Continental Europe Resembles North America. Journal of the European Economic Association 2012, 10, 1236–1262. [Google Scholar] [CrossRef]
Oxfam. Survival of the Richest: How we must tax the super-rich now to fight inequality. 2023. Available online: https://www.oxfamamerica.org/explore/research-publications/survival-of-the-richest/.

Figure 1. Income distributions of the US, the UK, China, and Canada.

Figure 2. Income distribution of China during from 1978 to 2000.

Table 1. Kolmogorov-Smirnov (KS) test for the US, the UK, China, and Canada in the latest years available.

Year		2015	2018	2020
China	P-value (KS)	0.633	——	——
US		——	——	0.741
UK		——	0.970	——
Canada		——	0.593	——

Table 2. Kolmogorov-Smirnov (KS) test for China in the early stages of market-oriented economic reformation.

Year		1978	1980	1990	2000
China	P-value (KS)	0.000	0.000	0.008	0.658

Notes

1	It is easy to check that, as $X_{t} \to \infty$ , $1 + η X_{t}$ yields $η X_{t}$ asymptotically. Then, equation (8) can be asymptotically written as $X_{t + ∆ t} - X_{t} = η ∆ W_{t} X_{t}$ , which is same as equation (1).
2	As $x \to \infty$ , one has $1 + η x ~ η x$ , such that $F_{η > 0} (X \geq x) ~ {(\frac{η x}{1 + η x_{\min}})}^{\frac{1}{θ η} - 1} = {(\frac{x}{x_{0}})}^{\frac{1}{θ η} - 1} .$
3	The data resource can be found in Data Availability Statement.
4	The data resource can be found in Data Availability Statement.
5	This understanding was widely used in the literature of income distribution [9,22].
6	The statement “earners in the bottom of the population” means that their incomes in the past are much less than $1 / η$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Generalized Pareto-Type Distribution and Income Inequality: An Extension of Gibrat’s Law

Abstract

1. Introduction

2. The extension of Gibrat’s law

3. The basic model

4. The parameter η

5. Tests using the data from the US, the UK, China, and Canada

6. Concluding remarks

Author Contributions

Data Availability Statement

Acknowledgements

Conflicts of Interest

Appendixes

Appendix A: Derivation of equation (12)

Appendix B: Economic implication of the parameter η

References

Notes

MDPI Initiatives

Important Links

Subscribe

4. The parameter $η$

Appendix B: Economic implication of the parameter $η$