Anti-windup Pitch Angle Control for Wind Turbines Based on Bounded UDE

In the full load operating range, wind turbines typically use pitch control to maintain rotor speed and output power at their rated values to guarantee the whole system’s safety. Blade pitch actuators are subject to physical limitations and safety requirements, which imposes strict constraints on pitch angle’s amplitude and rate of change. These constraints will bring windup problem to the integral part of the pitch controller. It leads to deterioration of the pitch control system’s performance or even the instability problem, especially for large-scale turbines operating in extreme uncertain wind conditions or suffering from cyber attacks. This paper designs an anti-windup robust pitch angle control strategy to deal with pitch rate constraint issue to enhance the security of control system. First, to facilitate controller design, a filtered tracking error technique is employed to transform the nonaffine form into an affine one. Subsequently, a feedback robust controller based on UDE is developed to handle the model’s uncertainty and external disturbances. To address the issue of integral saturation in the pitch system and guarantee its safety, an elliptical bounded constraint is integrated into the designed UDE strategy. This bounded UDE controller can improve the stability of power generation quality, reduces the mechanical loads on components and enhance the whole system’s safety. Finally, the effectiveness of the proposed scheme is verified on the Wind Turbine Blockset platform in Matlab/Simulink. It can achieve better performance than the traditional method.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

In recent years, environmental pollution has garnered widespread attention from an increasing number of countries worldwide [1]. As using the traditional fossil energy seriously pollutes the environment, the global power grid is transforming from traditional fossil energy to clean energy. Since wind energy is one of clean energy with huge reserves as a renewable energy, wind power is developing rapidly around the world [2]. According to the forecast published by the International Renewable Energy Agency (IRENA), wind power will play a main role in power generation by 2050 [3]. Variable speed wind turbines (VSWTs) are widely in modern wind farms, thanks to their higher power capture efficiency and lower mechanical loads compared with fixed-speed turbines [1]. In order to improve the quality and quantity of the captured wind power, the height and size of VSWT are becoming larger and larger, which will increase structural loads, bring safety issue and make the system be more fragile to cyber attacks [4]. Therefore, how to develop intelligent control technologies to achieve safe operation and loads optimization of wind turbines is still a challenging and promising issue in the field of wind power.

Uneven turbulent winds easily generate fluctuations in power generation, increasing the difficulty of grid integration. Thus, VSWTs are generally designed to withstand extreme wind conditions but cannot tolerate high rotor speeds and torques [5], which will avoid damage to VSWT blades and important turbine components. When the wind speed is at high wind speed stage and its value is higher than the rated one, the pitch angle is regulated to achieve constant power output control. The aerodynamic torque can fluctuate a lot when a minor angle variation occurs, and thus pitch angle is closely related to power output, even minor angle changes can have a significant impact on power output. Due to the high sensitivity with aerodynamic torque, the randomness and uncertainty of wind speed bring great challenge for advanced pitch angle control design.

Many control strategies for pitch angle have been proposed by scholars in order to achieve a good control performance. Proportional-integral-derivative (PID) controllers play an important role in VSWT pitch angle control. However, due to the great sensitivity of nonlinear aerodynamics to pitch angle, a constant PI gain cannot achieve an effective control effect. Jason et al. [6] proposes a gain-scheduled PI blade-pitch controller which measures the sensitive degree between aerodynamic power and different pitch angles and performs linear regression processing on it. In this way, the gain coefficient is adjusted according to the real-time pitch angle to achieve a better control effect. However, different types of turbines need to re-measure the aerodynamic power-pitch angle sensitive relationship, which greatly narrows its applications in practice. To deal with this, Billel et al. [7] proposes a direct power control based on PI control using space vector modulation technology, and optimizes the gain of PI control using a root optimization algorithm, improving the stability of wind turbine power generation. What’s more, Ibrahim et al. [8] have developed a fractional order PID (FOPID) variable pitch controller based on oppositional brain storm optimization (OBSO). The parameters of the FOPID controller are effectively selected by the OBSO algorithm, improving control performance in various aspects.

The above methods do not consider the problem of integral saturation of PI-based pitch controllers, which can lead to system instability and increase mechanical loads during the actual operation of wind turbines, especially when they suffer from cyber attacks [9,10,11]. In wind turbines, the pitch angle actuator has physical limitations and safety requirements, which restrict the extent and the pitch angle variable rate. When the controller output exceeds the actuator’s limit, there is a discrepancy between the actuator input and the controller output. This discrepancy causes the integral effect in the controller to continually accumulate, leading to integral saturation [12]. This saturation results in a decline in control function and it may even cause the system to lose the original control [13,14].

In order to address integral saturation, an integral saturation judgment module is typically added. When integral saturation occurs, applying a reverse gain can obviate the cumulative values of the corresponding parameters [15]. Nevertheless, the robustness of the system cannot be ensured by this method. Another approach is to use a more complex anti-integration and saturation design [16], but this requires additional calculations of system architecture. Leith and Leithead [17] highlight the problem of blade pitch integral saturation during turbines operation, and several anti-integral saturation designs were compared. Garelli et al. [18] addresses the issue of pitch rate integral saturation by adding a module to counteract saturation and adjusting the reference signal. Validation of this approach is conducted on a small-scale wind turbine. Kanev and van Engelen [19] propose a solution to integral saturation in controllers by introducing an auxiliary loop to adjust the input signal. However, these methods involve additional auxiliary anti-integral saturation components, and their effectiveness in ensuring overall system stability remains uncertain.

Recently, the uncertainty and disturbance estimator (UDE) control theory has achieved great development in control communities [20]. It shows good performance in dealing with robust control for nonlinear uncertain systems [21]. Therefore, under the excitation of UDE control strategy, this paper develops an anti-windup pitch control scheme for VSWT based on bounded UDE. The specific contributions of this article are as follows:

By modeling the wind turbine and using filtered regulation error technique, the control signal is converted into an affine form that is suitable for controller design. A robust pitch angle controller based on UDE is utilized to handle uncertainties and disturbances in the system, which improves the robustness of the overall system and feasibility of the proposed controller for different types of turbines;
A constraint coefficient is designed to address the issue of integral saturation in traditional UDE. Integrating the elliptical bounded constraint with UDE control framework, a bounded UDE approach is developed. This strategy can improve the stability of power generation quality, reduces the mechanical loads on components and enhance the whole system’s safety. Moreover, this controller maintains the traditional UDE method’s robustness and clear system structure without requiring additional calculations;
Simulation analysis are carried out by using a professional wind turbine platform to verify the effectiveness of the proposed control scheme, and it can achieve better control performance compared with traditional UDE control.

The arrangement of this study is shown as follows. Section 2 establishes the model of VSWT. Section 3 determines the control objectives and uses filtered regulation error technique to convert non-affine system into an affine one. Section 4 presents the controller design and stability proof. Simulation result analysis are carried out in Section 5. Finally, Section 6 offers the conclusion of this study.

2. VSWT Modelling

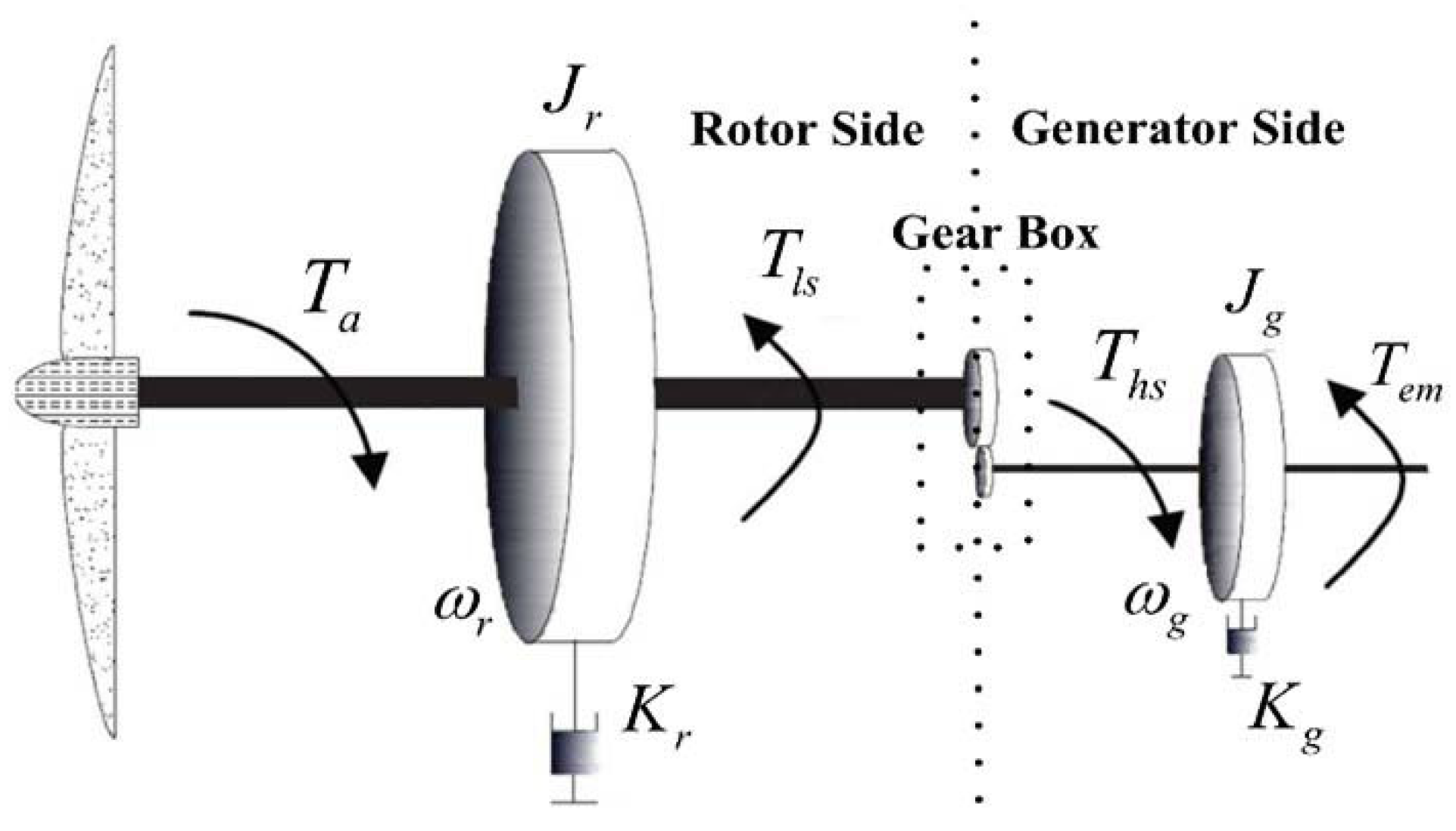
The physical model of the VSWT studied in this article is shown in Figure 1. According to Betz Law [22], the aerodynamic power

P_{a}

captured by a wind turbine from flowing air can be expressed as

P_{a} = \frac{1}{2} ρ_{1} π R^{2} C_{p} (λ, β) v^{3},

(1)

where

ρ_{1}

represents the air density, R is the is the radius of the swept area of the wind turbine rotor, v represents the effective wind speed,

λ

represents tip speed ratio and

β

is the pitch angle. The power coefficient

C_{p}

describes the wind power capture efficiency of wind turbines. It is a non-linear function determined by

λ

and

β

λ

can be described as

λ = \frac{R ω_{r}}{v},

(2)

with

ω_{r}

being the rotor speed. In general, the value of

C_{p} (λ, β)

can be determined through a large number of experiments implemented by manufacturers [23]. Moreover, the aerodynamic torque can be represented as

T_{a} = \frac{1}{2} ρ π R^{3} C_{q} (λ, β) v^{2},

(3)

with

C_{q} (λ, β)

being the torque coefficient, whose expression is

C_{q} (λ, β) = \frac{C_{p} (λ, β)}{λ}

(4)

In this research, the dual-mass structure of the VSWT is considered, assuming that the rotor-side and the generator-side drive shafts are rigid [24]. Furthermore, based on fundamental laws of physics, the dynamic characteristics of the system can be represented as

\{\begin{matrix} J_{r} {\dot{ω}}_{r} = T_{a} - K_{r} ω_{r} - T_{l s} \\ J_{g} {\dot{ω}}_{g} = T_{h s} - K_{g} ω_{g} - T_{e m} \\ n_{g} = \frac{ω_{g}}{ω_{r}} = \frac{T_{l s}}{T_{h s}} \end{matrix},

(5)

where

J_{r}

and

J_{g}

are respectively the inertial constants of rotor and generator,

ω_{g}

denotes the generator speed,

T_{l s}

and

T_{h s}

are torques of high-speed and low-speed shafts respectively,

K_{r}

and

K_{g}

are respectively external damping coefficients of wind rotor and generator and

n_{g}

is the ratio of gearbox.

Further, considering that the nonlinear turbine system always operate in an uncertain operating environment [25],

d (t)

is introduced to represent the unmodeled dynamics and unknown disturbance. Therefore, the mathematical model of wind turbines can be simplified as

{\dot{ω}}_{r} = \frac{1}{J_{t}} T_{a} - \frac{1}{J_{t}} K_{t} ω_{r} - \frac{1}{J_{t}} T_{g} + d (t),

(6)

where

J_{t}

K_{t}

and

T_{g}

are the lumped terms whose specific expressions are

\{\begin{matrix} J_{t} = n_{g}^{2} J_{g} + J_{r} \\ K_{t} = n_{g}^{2} K_{g} + K_{r} \\ T_{g} = n_{g} T_{e m} \end{matrix}

(7)

Finally, the output power of the generator in a VSWT can be represented as

P_{g} = T_{g} ω_{r}

(8)

3. Control Objectives

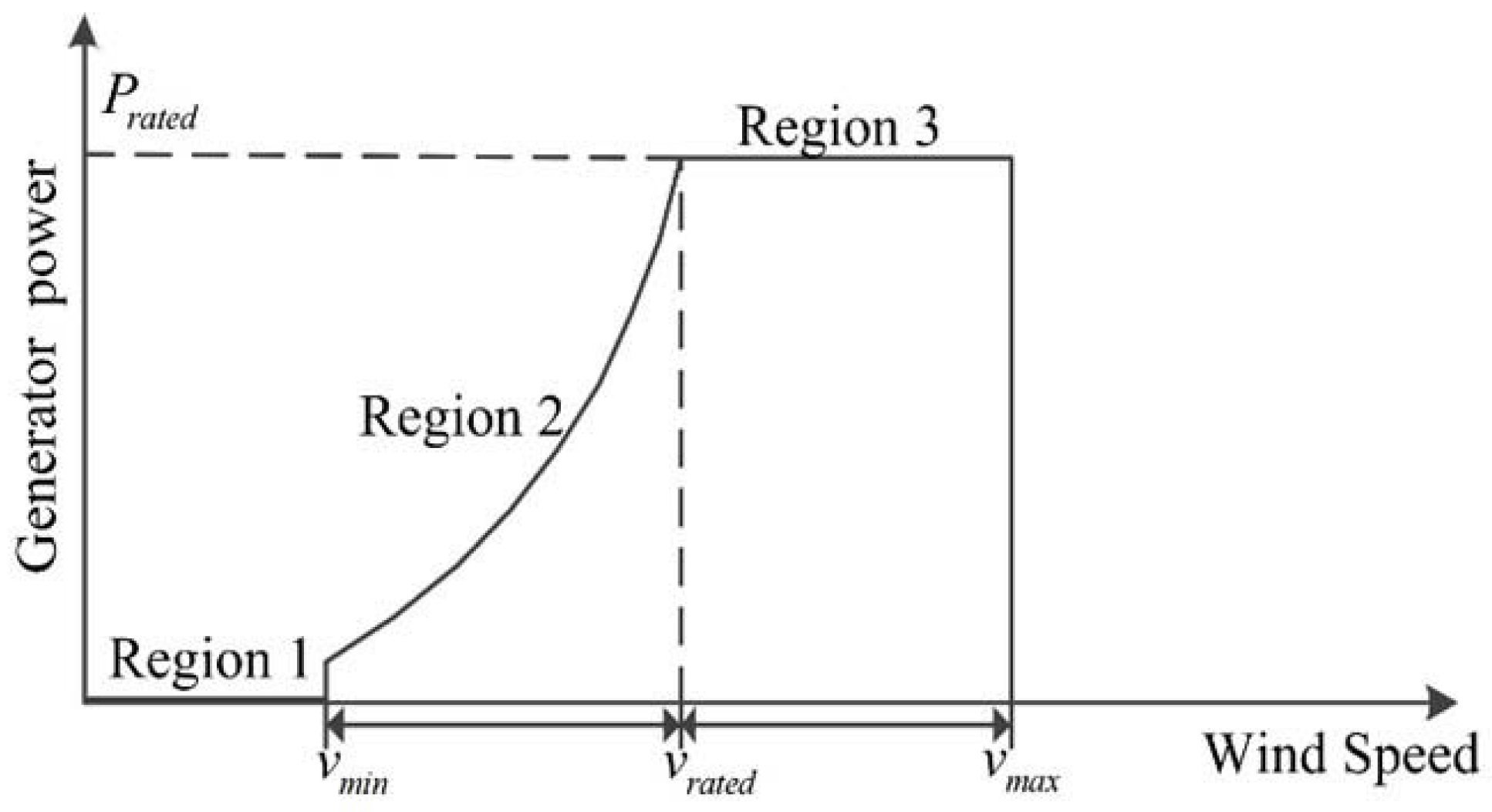
It can be observed from Figure 2 that three regions can be segmented for the operating stage of VSWT based on different wind speed values (Regions 1-3) [26]. In Region 2, the main control goal is to capture more energy from the flowing air. The rotor speed is adjusted by controlling the generator torque to achieve this control goal [27]. In region 3, there are two main control objectives. Firstly, in this stage, wind energy is relatively large, and the windup issue in the pitch controller will reduce the stability of the system operation, which is extremely likely to cause safety accidents of the wind turbine generator. In order to ensure the safe operation of the turbines, the rotor speed and power generation should be stabilized near their rated values. Secondly, in order to reduce the failure rates of the wind turbine system, the mechanical loads of its key components should be minimized as much as possible to extend turbines’ service life.

In the high wind speed range, the usual practice is to set the approach generator torque

T_{g}

to a fixed value. By controlling the change of the pitch angle

β

, the rotor speed

ω_{r}

is stable near the rated speed

ω_{d}

to realize the constant power output. The regulation error of rotor speed can be described as

e = ω_{r} - ω_{d}

(9)

From (3) and (6), it can be concluded that the control signal

β

affects the system dynamics in a non-affine form. This greatly increases the difficulties of designing the corresponding controller. In order to avoid this problem, the filtered regulation error technology is used to convert the control signal into an affine form. Thence, the regulation error r is defined as

r = k \dot{e} + e,

(10)

where

k > 0

. It can be seen that when

r \to 0

, e will also approach 0. The purpose of the controller designed for this study is to eliminate the adjustment error r and reduce the mechanical impacts of important parts.

4. Controller Design

4.1. The UDE-Based Controller

According to Equations (4) and (7), the derivative of the adjustment error is derived as follows

\begin{matrix} \dot{r} = \frac{c}{J_{t}} ({\dot{T}}_{a} - {\dot{T}}_{g} - K_{t} {\dot{ω}}_{r} + \dot{d} (t)) + (\frac{1}{J_{t}} T_{a} - \frac{K_{t}}{J_{t}} ω_{r} - \frac{1}{J_{t}} T_{g} + d (t)) \\ = f (ω_{r}, v, β) + g (ω_{r}, v, β) \dot{β} + φ (t) \end{matrix}

(11)

where

f (ω_{r}, v, β) = \frac{c}{J_{t}} [\frac{\partial T_{a}}{\partial ω_{r}} (\frac{T_{a}}{J_{t}} - \frac{K_{t}}{J_{t}} ω_{r} - \frac{T_{g}}{J_{t}}) - \frac{K_{t}}{J_{t}} (T_{a} - K_{t} ω_{r} - T_{g})] + (\frac{1}{J_{t}} T_{a} - \frac{K_{t}}{J_{t}} ω_{r} - \frac{1}{J_{t}} T_{g}),

(12)

g (ω_{r}, v, β) = \frac{c}{J_{t}} \frac{\partial T_{a}}{\partial β} < 0,

(13)

φ (t) = (\frac{c}{J_{t}^{2}} \frac{\partial T_{a}}{\partial ω_{r}} - \frac{c K_{t}}{J_{t}^{2}} + \frac{1}{J_{t}}) d (t) + \frac{c}{J_{t}} \dot{d} (t) + \frac{c}{J_{t}} \frac{\partial T_{a}}{\partial v} \dot{v},

(14)

to compensate for system uncertainties and disturbances, Equations (11) can be rewritten as

\dot{r} = f_{d} (ω_{r}, v_{d}, β) + g_{d} (ω_{r}, v_{d}, β) \dot{β} + D (t),

(15)

where

D (t) = (f - f_{d}) + (g - g_{d}) + φ (t)

, Since the wind speed is known,

f_{d}

and

g_{d}

can be calculated by the wind turbine dynamic model as

f_{d} = \frac{c}{J_{t d}} [\frac{\partial T_{a d}}{\partial ω_{r}} (\frac{T_{a d}}{J_{t d}} - \frac{K_{t d}}{J_{t d}} ω_{r} - \frac{T_{g}}{J_{t d}}) - \frac{K_{t d}}{J_{t d}} (T_{a d} - K_{t d} ω_{r} - T_{g})] + \frac{1}{J_{t d}} (T_{a d} - K_{t d} - T_{g}),

(16)

g_{d} = \frac{c}{J_{t d}} \frac{1}{2 λ_{d}} ρ π R^{3} v_{d}^{2} c_{1 d} ((- \frac{1}{λ_{i d}^{2}} \frac{\partial λ_{i d}}{\partial β} - c_{3 d}) e^{- \frac{c_{5 d}}{λ_{i d}}} + (\frac{c_{2 d}}{λ_{i d}} - c_{3 d} β - c_{4 d}) e^{- \frac{c_{5 d}}{λ_{i d}}} \frac{c_{5 d}}{λ_{i d}^{2}} \frac{\partial λ_{i d}}{\partial β}),

(17)

where

\frac{\partial T_{a d}}{\partial ω_{r}} = \frac{1}{2} ρ π R^{3} v_{d}^{2} [(c_{1 d} (- \frac{1}{λ_{i d}^{2}}) (\frac{\partial λ_{i d}}{\partial ω_{r}}) e^{- \frac{c_{5 d}}{λ_{i d}}} (c_{2 d} - c_{5 d} (\frac{c_{2 d}}{λ_{i d}} - c_{3 d} β - c_{4 d})) + c_{6 d} \frac{R}{v_{d}}) λ_{d} - C_{p d} (λ_{d}, β) \frac{R}{v_{d}}] / λ_{d}^{2}

(18)

In order for r to approach 0, the filtering error should satisfy the following relationship

\dot{r} (t) = - k r (t),

(19)

where

k > 0

, the control rate of the control signal is designed to

\dot{β} = - \frac{1}{g_{d}} (f_{d} + k r + D (t)),

(20)

The system uncertainty and disturbance

D (t)

are unknown, according to the UDE control theory, it is approximated as

\begin{matrix} \hat{D} (t) = D (t) * g_{f} (t) \\ = (\dot{r} - f_{0} - g_{0} \dot{β}) * g_{f} (t) \end{matrix}

(21)

In this formula,

g_{f} (t)

is a filter with appropriate bandwidth, and "*" is the symbol for convolution. Combined with Equation (20), it can be obtained that

\dot{β} = - \frac{1}{g_{d}} (f_{d} + (\dot{r} - f_{d} - g_{d} \dot{β}) * g_{f} (t) + k r),

(22)

arranging Equation (22) gives

- g_{d} \dot{β} = f_{d} + \dot{r} * g_{f} (t) - f_{d} * g_{f} (t) - g_{d} \dot{β} * g_{f} (t) + k r

(23)

Laplace transform is performed on both sides of the equation in Equation (23), simplify and perform inverse Laplace transform. The pitch angle control rate based on UDE is represented as

\dot{β} = - \frac{1}{g_{d}} (f_{d} + L^{- 1} (\frac{1}{1 - G_{f} (s)}) * k r + L^{- 1} (\frac{s G_{f} (s)}{1 - G_{f} (s)}) * r),

(24)

where

L^{- 1}

is the operator for Laplace inverse transformation, and

G_{f} (s)

usually uses a first-order low-pass filter, which can be expressed as

G_{f} (s) = \frac{1}{τ s + 1}

(25)

According to Equation (25), Equation (24) can be further deduced as

\dot{β} = - \frac{1}{g_{d}} (f_{d} + \frac{k}{τ} \int_{0}^{t} r (ζ) d ζ + (\frac{1}{τ} + k) r (t))

(26)

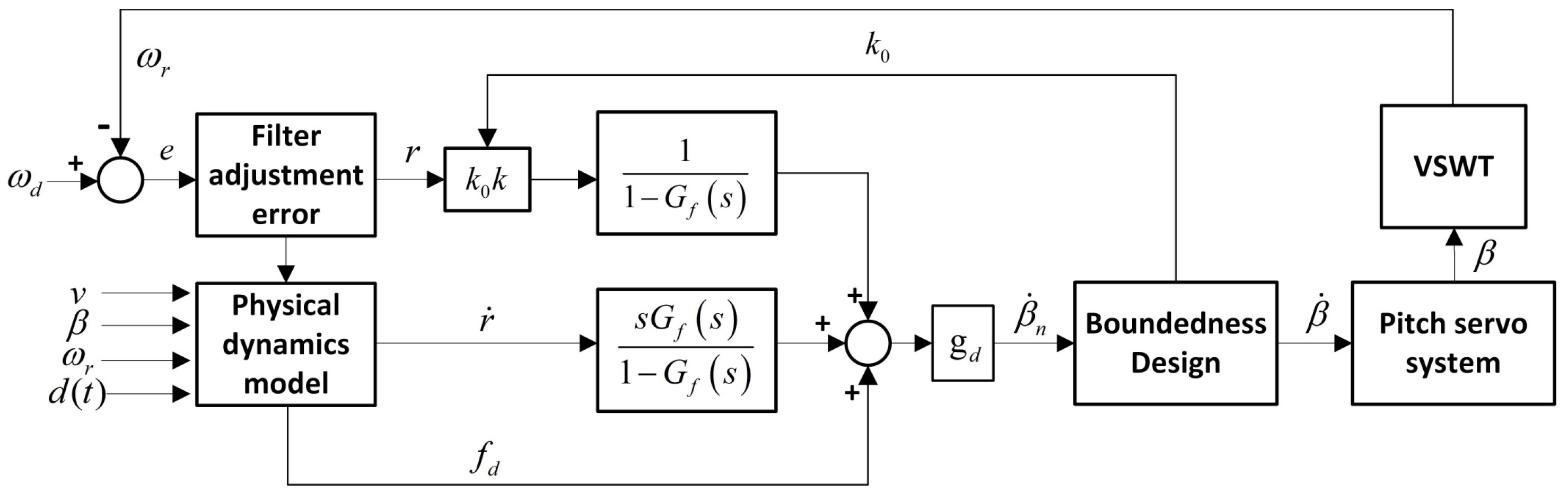
4.2. Design with Bounded Constraints

In the UDE control signal (26), the integral term generated by the characteristics of the filter exists in the

(\frac{1}{1 - G_{f} (s)})

term. The integral term continuously corrects tracking error to achieve good steady-state tracking performance. In fact, due to the non-ideal physical structure of VSWTs, the rate of change in pitch is bounded. When the controller output exceeds the input boundaries of the actuator, the traditional UDE controller would erroneously update the state, causing the accumulation of the integral term during the error adjustment process. It will then lead to integral saturation. This phenomenon will result in a deterioration in control performance, and even a system crash under cyber attacks. To alleviate the continuous impact of the integral action, a time-varying variable is designed for Equation (19) as

\dot{r} (t) = - k_{0} k r (t),

(27)

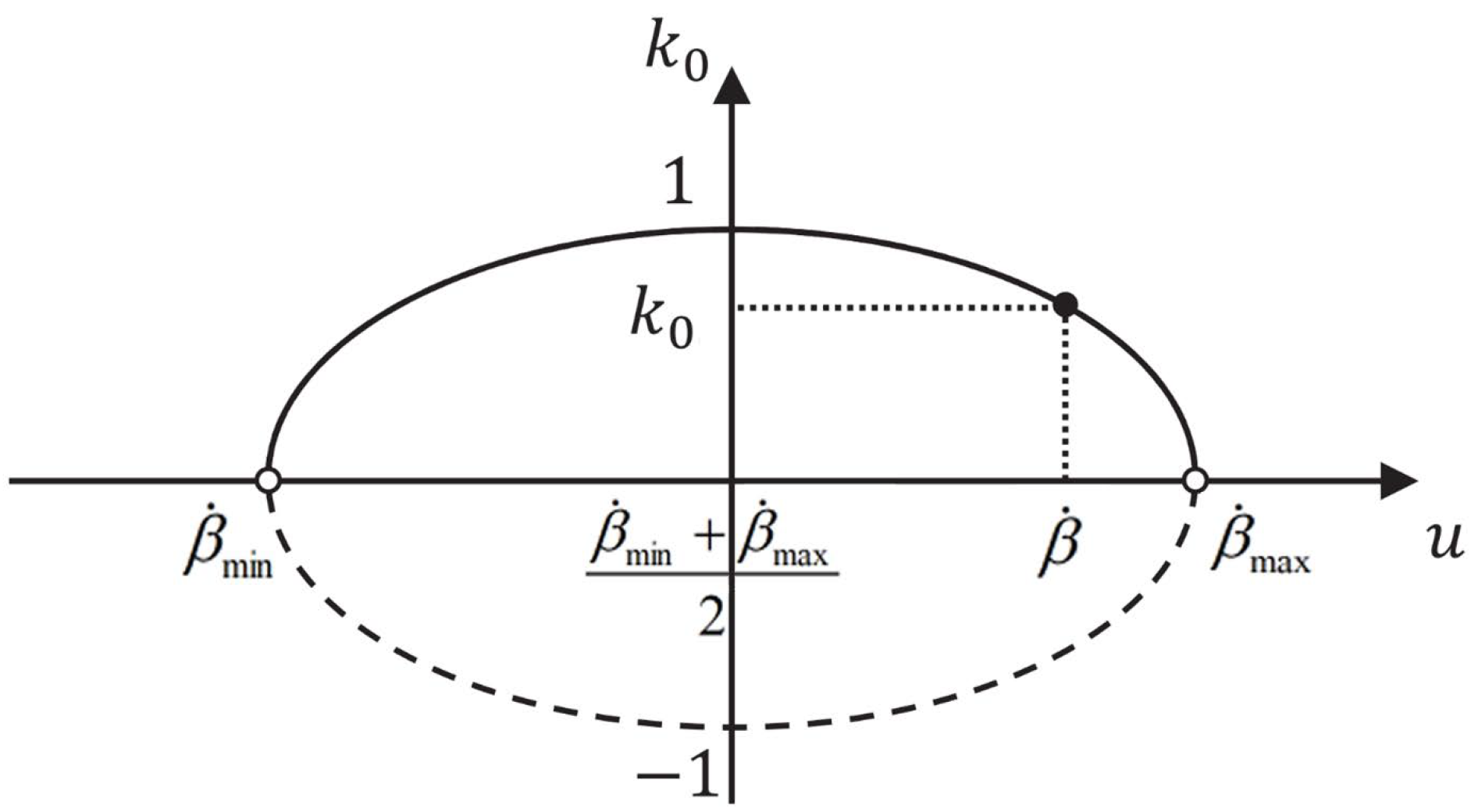
with

0 < k_{0} < 1

. If the controller output is close to the boundary of the pitch angle change rate,

k_{0}

should be close to 0 to avoid integral saturation. The pitch angle change rate range can be expressed as

\dot{β} \in ({\dot{β}}_{min}, {\dot{β}}_{max})

(28)

The boundary values of the pitch angle change rates,

{\dot{β}}_{min}

and

{\dot{β}}_{max}

, are both constants, and the values are determined by the physical limitations and safety requirements of the actuator. In order to constrain the process, an elliptic relationship can be established between the pitch angle change rate

\dot{β}

and the constraint coefficient

k_{0}

\frac{4 {(\dot{β} - \frac{{\dot{β}}_{max} + {\dot{β}}_{min}}{2})}^{2}}{{({\dot{β}}_{max} - {\dot{β}}_{min})}^{2}} + k_{0}^{2} = 1

(29)

According to the new filter error dynamics, the pitch angle control rate is modified as

{\dot{β}}_{n} = - \frac{1}{g_{0}} (f_{0} + (\frac{1}{τ} + k) r (t) + \frac{k_{0} k}{τ} \int_{0}^{t} r (ζ) d ζ)

(30)

Further, in order to realize the desired constraint model, a pitch controller with bounded constraints is developed for the time-varying constraint coefficients and final controller output as

{\dot{k}}_{0} = - k_{1} k_{0} (\frac{4 {(\dot{β} - \frac{{\dot{β}}_{max} + {\dot{β}}_{min}}{2})}^{2}}{{({\dot{β}}_{max} - {\dot{β}}_{min})}^{2}} + {k_{0}}^{2} - 1) + \frac{4 k_{2} (\dot{β} - \frac{{\dot{β}}_{max} + {\dot{β}}_{min}}{2})}{{({\dot{β}}_{max} - {\dot{β}}_{min})}^{2}} k_{0} (\dot{β} - {\dot{β}}_{n})

(31)

\ddot{β} = - k_{1} (\dot{β} - \frac{{\dot{β}}_{max} + {\dot{β}}_{min}}{2}) \cdot (\frac{4 {(\dot{β} - \frac{{\dot{β}}_{max} + {\dot{β}}_{min}}{2})}^{2}}{{({\dot{β}}_{max} - {\dot{β}}_{min})}^{2}} + {k_{0}}^{2} - 1) - k_{2} {k_{0}}^{2} (\dot{β} - {\dot{β}}_{n}),

(32)

where

\dot{β}

is the input of the pitch actuator,

k_{0}

is the constraint coefficient of the introduction of the integral term,

k_{1}

and

k_{2}

are positive constants. It should be noted that the bounded controller design only needs to occupy very little computing resources in the achievement of the bounded constraints.

4.3. Proof of Stability

The proof of stability considers the following Lyapunov function candidates

V (t) = \frac{4 {(\dot{β} - \frac{{\dot{β}}_{max} + {\dot{β}}_{min}}{2})}^{2}}{{({\dot{β}}_{max} - {\dot{β}}_{min})}^{2}} + k_{0}^{2}

(33)

According to Equations (31) and (32), the derivative of Equation (33) is taken as

\dot{V} (t) = - 2 k_{1} V^{2} (t) + 2 k_{1} V (t)

(34)

Further solving Equation (34) gives

V (t) = \frac{1}{1 - (1 - \frac{1}{V (0)}) e^{- 2 k_{1} t}},

(35)

where

V (0)

is the initial state of

V (t)

, through the initial design of

V (0) = 1

k_{0} (0) = 1

and

\dot{β} (0) = \frac{{\dot{β}}_{max} + {\dot{β}}_{min}}{2}

can be obtained, and then

\begin{matrix} V (t) = 1 & \forall t \geq 0 \end{matrix}

(36)

In Equation (33), as long as

\forall t \geq 0

, the controller output and constraint coefficients will always remain within the ellipse defined by Equation (29), ensuring system stability. With the proposed bounded design, both

\dot{β}

and

k_{0}

will always remain on the ellipse set, regardless of their changes in Equation (30). In the steady state, the derivatives of the control signal change rate and the constraint coefficient will be adjusted to 0, and the tracking error e is zero. At this point, both the pitch angle and the constraint coefficient will approach a stable point

(β_{e}, k_{0 e})

. The bounded design scheme of the controller based on UDE is illustrated in Figure 3.

5. Simulation Verification

The regulation function of the designed pitch controller is verified on the Wind Turbine Blockset platform in Matlab/Simulink [28]. The platform focuses on wind power study and provides a very good help for related technology research. It receives funding from the Danish Energy Agency in the study program "A Simulation Platform to Model, Optimize and Design Wind Turbines" and has been extensively utilized in related literature [29,30,31]. The model used on this platform is 1.5MW VSWT. Table 1 introduces the primary data used in the study. When the pitch system is subjected to excessive pitch acceleration, the contact stress of the bearings will increase, resulting in increased friction, wear and fatigue [32]. When the run time is long, this may lead to damage and failure of the bearing, which will affect the normal and safe operation of the entire VSWT and seriously affect the economic benefits of the wind farm. In an effort to make a reasonable analysis of the influence extent of the controller on the pitch mechanical shock (PMS), the average pitch angle absolute acceleration of the entire running time of the fan can be measured. The smaller it is, the smaller the mechanical shock of the pitch control system. Furthermore, to evaluate blade pitch fatigue (PF) during operation, the following indicators need to be considered [33]

P F = \frac{\sum_{k = 1}^{T_{e t}} |β (k + 1) - β (k)|}{T_{e t}}

(37)

PF measures the average blade pitch variation rate during operation. Clearly, a smaller PF value indicates less fatigue in the pitch control system [34]. In order to analyze integral saturation states more intuitively, scheduling parameters are introduced in this study as [35]

r = \frac{s a t_{r} (u)}{u}, r = 1 i f u = 0,

(38)

where the numerator is the implemented pitch rate by the actuator, and the denominator is the pitch rate signal output by the controller. When integral saturation is not present, the value of r is equal to 1. The parameters for the designed controller are chose as:

k = 3

τ = 2.5

c = 4.5

k_{1} = 18.6

and

k_{2} = 15.5

. In an effort to simulate extreme conditions, the pitch rate suffers from a limitation and the limited range is set as

\pm 3

deg/s in simulations.

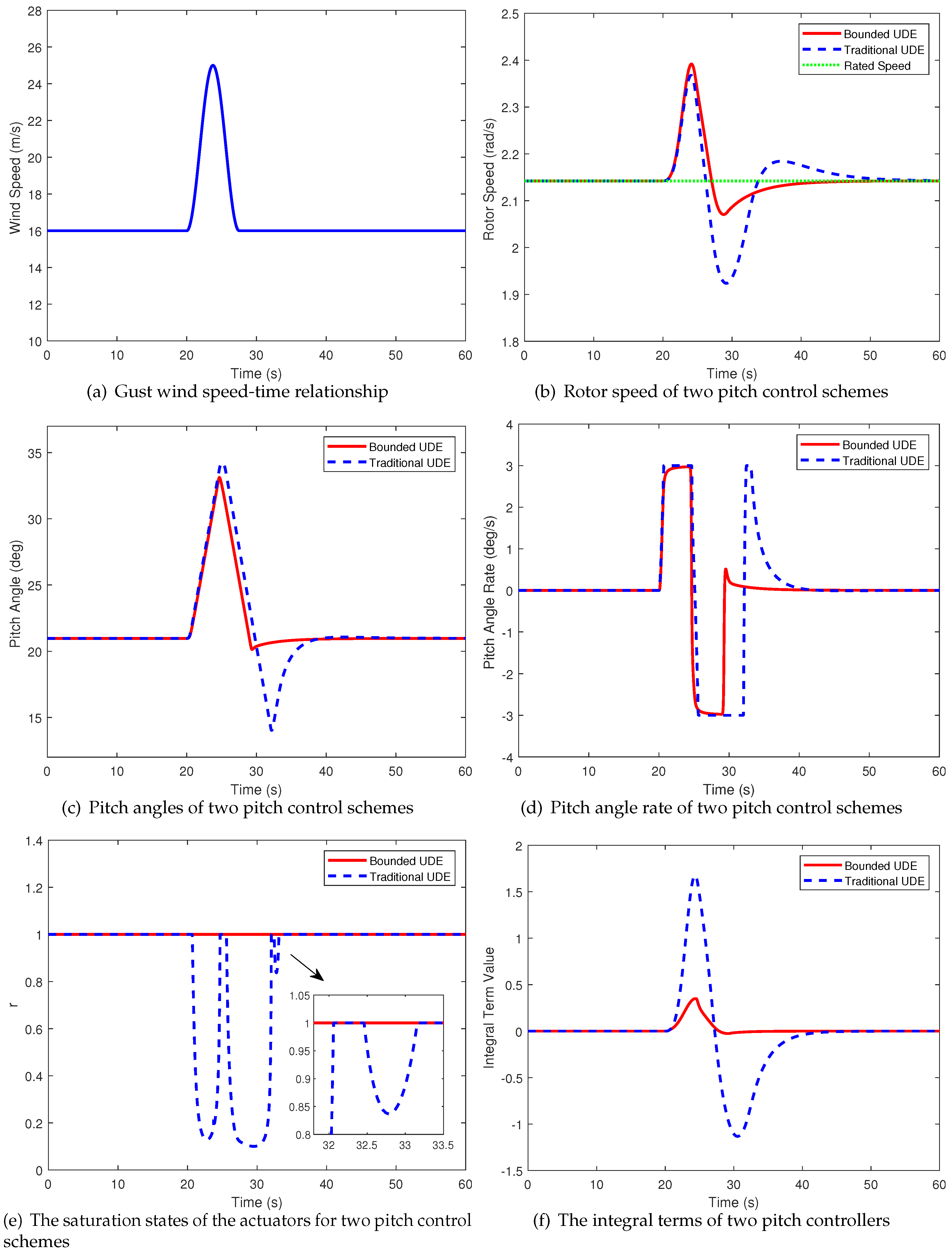
5.1. Wind Gust

In an effort to demonstrate the validity of the bounded UDE control method in extreme wind scenarios, the gust model is built as follow [15,36]

v = \{\begin{matrix} 16, t < T_{i n} \\ 16 + A_{g} [1 - cos (\frac{2 π (t - T_{i n})}{D_{g}})], T_{i n} \leq t \leq T_{o u t} \\ 16, T_{o u t} < t \end{matrix},

(39)

where

T_{i n} = 10 s

T_{o u t} = 17.5 s

A_{g} = 4.5 m / s

and

D_{g} = 7.5 s

are the entry time, exit time, amplitude value and duration of the gust. Figure Figure 5a shows the generated gust wind speed. The comparison of the experimental conclusions of the two controllers when gust is shown in Figure 5b–f. In order to compare the speed regulation performance and the pitch loads, the performance index is shown in Table 2. These include the mean absolute error (MAE), standard deviation (ST), mean absolute percentage error (MAPE), pitch mechanical shock (PMS) and pitch fatigue (PF) from the rated value. It should be noted that, although the rotor speed’s overshoot is a little bit larger than that of the UDE control, the speed regulation performance of the bounded UDE is superior to the conventional UDE in terms of MAE and MAPE, with a reduction of 41.59% and 0.73%, respectively. Figure 5e,f depict the actuator saturation states and the accumulation of integrators under two control strategies. Evidently, the bounded UDE eliminates the infinite accumulation of integral terms caused by integral saturation, and no integral saturation phenomenon occurs. The integrator in traditional UDE methods experiences significant accumulation, leading the system into an uncontrollable state during this period. The system remains in this state until the integral term is eliminated. The significant impact of bounded constraints can be observed in Figure Figure 5d, where better control performance is achieved with fewer blade pitch adjustments. PMS and PF are indicators directly affecting the turbine’s lifespan, and the bounded UDE reduces them by 40.29% and 36.15%, respectively, compared with the traditional UDE method. This improvement enhances the safety and extends service life of turbines, which is very beneficial for wind farm’s economic benefits.

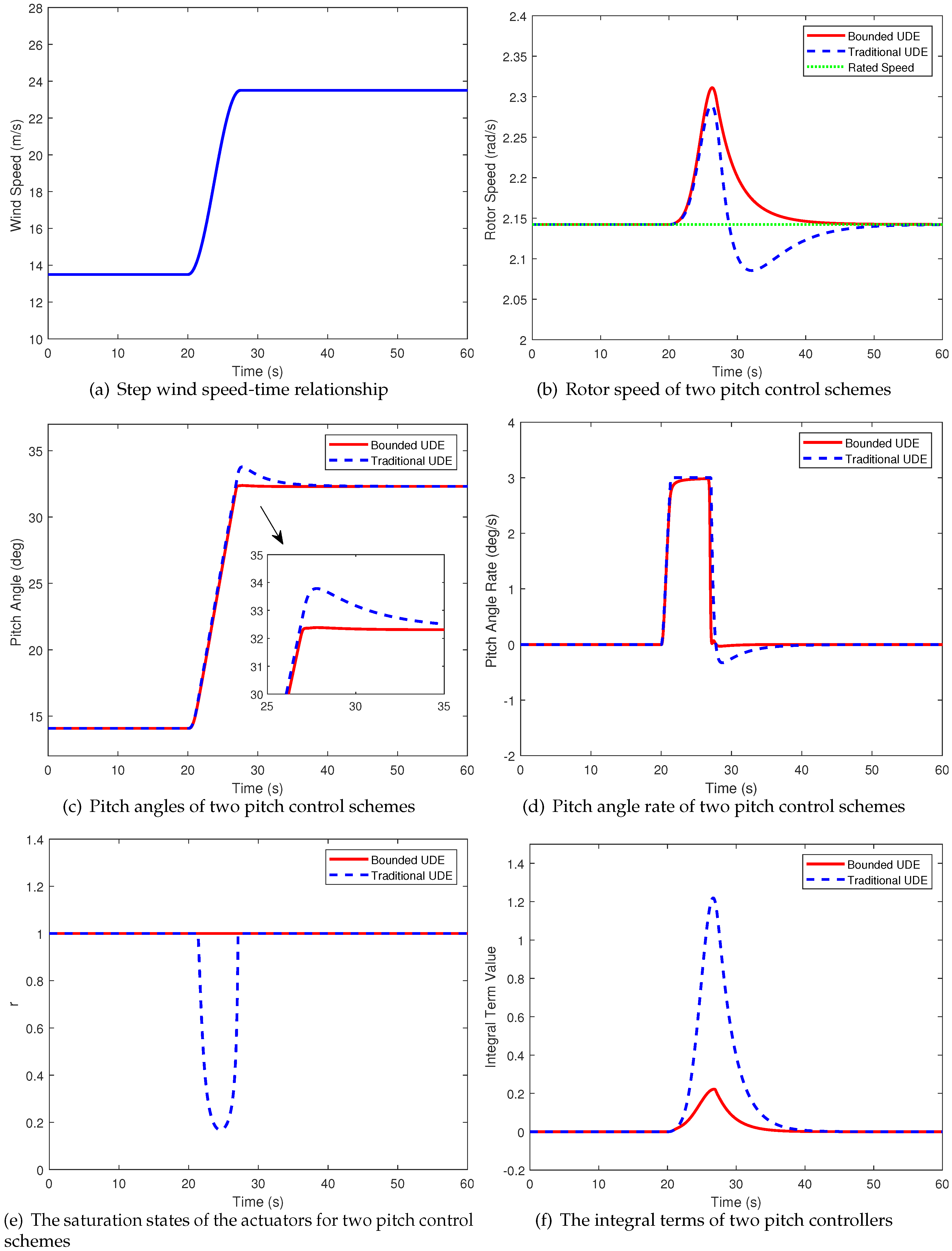
5.2. Step Wind

The designed method’s effectiveness can be testified by the step wind scene [37]. Under the airflow velocity shown in Figure Figure 6a, The simulation results of important parameters of the controller are shown in Figure 6b–d. By analyzing the obtained experiment results, the control performance indicators are shown in Table 3. It is known that the pitch rate adjustment of the traditional UDE is rapid. Between 20s and 35s, the pitch rate surpasses the boundary value of the actuator, leading to integral saturation and consequently causing an increase in the time to reach steady-state. The bounded UDE eliminates integral saturation, the signals of the controller and the actuator remain synchronized throughout the operation. During a stable wind speed, the pitch angle under the bounded UDE control strategy approaches the stable value in a shorter time. Based on the experimental results, the bounded UDE method, compared to the traditional approach, exhibits a reduction of 6.74% and 0.078% in MAE and MAPE, respectively. This suggests that the bounded UDE method provides more stable speed control performance. Similarly, the bounded design demonstrates excellent performance in integral saturation. In Figure Figure 6c, the blades of the bounded UDE exhibit no unnecessary pitch adjustments. Through calculations on mechanical impact and blade pitch fatigue, the proposed strategy in this study optimizes these aspects by 29.74% and 8.68%, respectively.

5.3. Turbulent Wind

The function of the designed controller is tested using long-time turbulent wind in this part [15,37]. Figure Figure 7a displays the wind speed. In the turbulent wind scenario, Figure 7b–d respectively display the performance of speed regulation and pitch adjustment under different controllers. It can be observed that, within a short time, the rotor speeds of both control methods stabilize near the rated values. However, the actual wind conditions in the environment exhibit randomness and intermittency, as shown between 120s and 140s in Figure Figure 7a. During this period, the saturation state indicator r of the conventional UDE proves that the controller’s output signal has exceeded the actuator’s boundaries. The controller’s state is continuously updated erroneously, and the integral term keeps accumulating. When the wind speed undergoes a significant abrupt change, the larger integral term hinders the correct adjustment of the controller’s output signal. As seen in Figure 7c,d, conventional UDE regains the controller’s tracking capability after the elimination of the integral term. During the operation of the wind turbine, controller instability can subject the system to substantial shocks, potentially leading to wind turbine safety accidents. Bounded UDE constrains the unlimited accumulation of the integral term, ensuring that the actuator saturation state remains within normal bounds. This approach achieves superior speed tracking with fewer pitch actions. To evaluate the controller’s performance more clearly, Table 4 provides a detailed analysis of the experiment results. Compared with traditional UDE, bounded UDE demonstrates a reduction of 1.37% in the MAE and a decrease of 0.03% in the MAPE. Additionally, fatigue indicators, including a 11.42% decrease in the PMS and a 5.88% decrease in the PF, clearly indicate that bounded UDE not only ensures enhanced tracking performance but also reduces the loads on pitch systems.

6. Conclusions

This paper proposes a robust bounded UDE pitch control strategy, which is intended to optimize the power generation quality of wind turbines at high wind speeds, reduce mechanical fatigues and enhance turbine’s safety. First, a UDE based pitch control is presented to deal with the uncertainties of the system. In order to eliminate the integral saturation that occurs in the designed UDE control, an elliptic bounded constraint coefficient is investigated. As a result, when integral saturation occurs, the integral action is weakened and the integral saturation is eliminated. Based on the bounded constrained design, a bounded UDE pitch angle controller is developed. It is worth noting that the design with bounded constraints will not increase the computational complexity of the system. Simulation results can prove that the bounded UDE control method has better performance in reducing the mechanical fatigue of pitch systems with good rotor speed regulation results than conventional UDE. It will reduce maintenance costs, extend the life of the turbines and enhance the overall system’s safety.

Author Contributions

Methodology, X.J., Z.Z. and X.W.; Software, G.W.; Validation, X.J. and X.W.; Investigation, X.J. and X.W.; Resources, Z.Z., Y.T. and X.F.; Data curation, G.W.; Writing-review & editing, X.J. and G.W.; Project administration, Z.Z., Y.T. and X.F. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported in part by the National Natural Science Foundation of China under Grant 62203249, Grant 62303126, and Grant 62362008, in part by the Shandong Provincial Nature Science Foundation of China under Grant ZR2021QF115, in part by the Lixian Scholar Project of Qingdao University of Technology, in part by the Open Research Project of the State Key Laboratory of Industrial Control Technology, Zhejiang University, China under Grant ICT2023B08, in part by the Taishan Scholars Program under Grant tsqn202211203, and in part by the “20 New Universities” Project of Jinan City under Grant 202228077.

Data Availability Statement

The data is unavailable due to privacy security.

Conflicts of Interest

The authors declare that they have no conflicts of interest to report regarding the present study.

References

Jiao, X.; Yang, Q.; Xu, B. Hybrid intelligent feedforward-feedback pitch control for VSWT with predicted wind speed. IEEE Transactions on Energy Conversion 2021, 36, 2770–2781. [Google Scholar] [CrossRef]
Ismaeel, A.; Houssein, E.H.; Hassan, A.Y.; Said, M. Performance of gradient-based optimizer for optimumwind cube design. Comput., Mater. Contin 2022, 71, 339–353. [Google Scholar]
IRENA, R.E.S. International renewable energy agency. Abu Dhabi 2020, 2020. [Google Scholar]
Liu, W.; Su, X.; An, Y.; Huang, K. Local buckling prediction for large wind turbine blades. Computers Materials and Continua 2011, 25, 177. [Google Scholar]
Marouani, H.; Almehmadi, F.A.; Farkh, R.; Dhahri, H. Wind Turbine Efficiency Under Altitude Consideration Using an Improved Particle Swarm Framework. Computers, Materials & Continua 2022, 73. [Google Scholar]
Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW reference wind turbine for offshore system development. Technical report, National Renewable Energy Lab.(NREL), Golden, CO (United States), 2009.
Meghni, B.; Benamor, A.; Hachana, O.; Azar, A.T.; Boulmaiz, A.; Saad, S.; El-kenawy, E.S.M.; Kamal, N.A.; Fati, S.M.; Bahgaat, N.K. Rooted Tree Optimization for Wind Turbine Optimum Control Based on Energy Storage System. Computers, Materials & Continua 2023, 74. [Google Scholar]
Mehedi, I.M.; Al-Saggaf, U.M.; Vellingiri, M.T.; Milyani, A.H.; Bin Saad, N.; Bin Yahaya, N.Z. OBSO Based Fractional PID for MPPT-Pitch Control of Wind Turbine Systems. Computers, Materials & Continua 2022, 71. [Google Scholar]
Zhao, S.; Yang, Q.; Cheng, P.; Deng, R.; Xia, J. Adaptive resilient control for variable-speed wind turbines against false data injection attacks. IEEE Transactions on Sustainable Energy 2022, 13, 971–985. [Google Scholar] [CrossRef]
Wang, Z.; Zhang, H.; Cao, X.; Liu, E.; Li, H.; Zhang, J. Modeling and Detection Scheme for Zero-Dynamics Attack on Wind Power System. IEEE Transactions on Smart Grid 2023. [Google Scholar] [CrossRef]
Zhang, Z.; Zuo, K.; Deng, R.; Teng, F.; Sun, M. Cybersecurity Analysis of Data-Driven Power System Stability Assessment. IEEE Internet of Things Journal 2023. [Google Scholar] [CrossRef]
Bohn, C.; Atherton, D. An analysis package comparing PID anti-windup strategies. IEEE Control Systems Magazine 1995, 15, 34–40. [Google Scholar]
Konstantopoulos, G.C.; Zhong, Q.C.; Ren, B.; Krstic, M. Bounded integral control of input-to-state practically stable nonlinear systems to guarantee closed-loop stability. IEEE Transactions on Automatic Control 2016, 61, 4196–4202. [Google Scholar] [CrossRef]
Tarbouriech, S.; Turner, M. Anti-windup design: an overview of some recent advances and open problems. IET control theory & applications 2009, 3, 1–19. [Google Scholar]
Inthamoussou, F.A.; Bianchi, F.D.; De Battista, H.; Mantz, R.J. LPV wind turbine control with anti-windup features covering the complete wind speed range. IEEE Transactions on Energy Conversion 2014, 29, 259–266. [Google Scholar] [CrossRef]
Beltran, B.; Ahmed-Ali, T.; Benbouzid, M.E.H. Sliding mode power control of variable-speed wind energy conversion systems. IEEE Transactions on energy conversion 2008, 23, 551–558. [Google Scholar] [CrossRef]
Leith, D.J.; Leithead, W. Implementation of wind turbine controllers. International Journal of Control 1997, 66, 349–380. [Google Scholar] [CrossRef]
Garelli, F.; Camocardi, P.; Mantz, R.J. Variable structure strategy to avoid amplitude and rate saturation in pitch control of a wind turbine. International Journal of Hydrogen Energy 2010, 35, 5869–5875. [Google Scholar] [CrossRef]
Kanev, S.; van Engelen, T. Exploring the limits in individual pitch control. Proceedings of the European Wind Energy Conference, Marseille, France, 2009, pp. 16–19.
Ren, B.; Zhong, Q.C. UDE-based robust control of variable-speed wind turbines. IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society. IEEE, 2013, pp. 3818–3823.
Wang, Y.; Ren, B.; Zhong, Q.C. Bounded UDE-based controller for input constrained systems with uncertainties and disturbances. IEEE Transactions on Industrial Electronics 2020, 68, 1560–1570. [Google Scholar] [CrossRef]
Rauh, A.; Seelert, W. The Betz optimum efficiency for windmills. Applied Energy 1984, 17, 15–23. [Google Scholar] [CrossRef]
Yang, Q.; Jiao, X.; Luo, Q.; Chen, Q.; Sun, Y. L1 adaptive pitch angle controller of wind energy conversion systems. ISA transactions 2020, 103, 28–36. [Google Scholar] [CrossRef]
Bianchi, F.D.; De Battista, H.; Mantz, R.J. Wind turbine control systems: principles, modelling and gain scheduling design; Vol. 19, Springer, 2007.
Jiao, X.; Sun, Y.; Ying, Y.; Yang, Q. Effective wind speed estimation based maximum power point tracking control for variable-speed wind turbine. 2017 Chinese Automation Congress (CAC). IEEE, 2017, pp. 6685–6690.
Shaltout, M.L.; Ma, Z.; Chen, D. An adaptive economic model predictive control approach for wind turbines. Journal of Dynamic Systems, Measurement, and Control 2018, 140, 051007. [Google Scholar] [CrossRef]
Zhao, L.; Chen, B.; Lu, J. Minimum Variance Control of Constant Power Output For Wind Energy Conversion System Above Rated Wind. 2010 Asia-Pacific Power and Energy Engineering Conference. IEEE, 2010, pp. 1–4.
Jiao, X.; Meng, W.; Yang, Q.; Fu, L.; Chen, Q. Adaptive continuous neural pitch angle control for variable-speed wind turbines. Asian Journal of Control 2019, 21, 1966–1979. [Google Scholar] [CrossRef]
Abbas, F.A.R.; Abdulsada, M.A. Simulation of wind-turbine speed control by MATLAB. International Journal of Computer and Electrical Engineering 2010, 2, 1793–8163. [Google Scholar] [CrossRef]
Zaragoza, J.; Pou, J.; Arias, A.; Spiteri, C.; Robles, E.; Ceballos, S. Study and experimental verification of control tuning strategies in a variable speed wind energy conversion system. Renewable energy 2011, 36, 1421–1430. [Google Scholar] [CrossRef]
Hansen, M.H.; Zahle, F. Aeroelastic optimization of MW wind turbines; Danmarks Tekniske Universitet, Risø Nationallaboratoriet for Bæredygtig Energi, 2011.
Plumley, C.; Leithead, W.; Jamieson, P.; Bossanyi, E.; Graham, M. Comparison of individual pitch and smart rotor control strategies for load reduction. Journal of Physics: Conference Series. IOP Publishing, 2014, Vol. 524, p. 012054.
Jain, A.; Schildbach, G.; Fagiano, L.; Morari, M. On the design and tuning of linear model predictive control for wind turbines. Renewable Energy 2015, 80, 664–673. [Google Scholar] [CrossRef]
Hatami, A.; Moetakef-Imani, B. Innovative adaptive pitch control for small wind turbine fatigue load reduction. Mechatronics 2016, 40, 137–145. [Google Scholar] [CrossRef]
Meisami-Azad, M.; Grigoriadis, K.M. Anti-windup linear parameter-varying control of pitch actuators in wind turbines. Wind Energy 2015, 18, 187–200. [Google Scholar] [CrossRef]
Jiao, X.; Yang, Q.; Fan, B.; Chen, Q.; Sun, Y.; Wang, L. EWSE and uncertainty and disturbance estimator based pitch angle control for wind turbine systems operating in above-rated wind speed region. Journal of Dynamic Systems, Measurement, and Control 2020, 142, 031006. [Google Scholar] [CrossRef]
Song, D.; Yang, J.; Cai, Z.; Dong, M.; Su, M.; Wang, Y. Wind estimation with a non-standard extended Kalman filter and its application on maximum power extraction for variable speed wind turbines. Applied energy 2017, 190, 670–685. [Google Scholar] [CrossRef]

Figure 1. Physical model of VSWT.

Figure 2. Operating regions of VSWT.

Figure 3. The framework of the bounded UDE pitch angle control method.

Figure 4. The elliptical relationship between the rate of the pitch angle and the constraint coefficients.

Figure 5. Simulation results of VSWT under gust conditions.

Figure 6. Simulation results of VSWT under step conditions.

Figure 7. Simulation results of VSWT under under turbulent wind conditions.

Table 1. Main parameters of the simulation model.

Parameters	Value	Parameters	Value
Air density	$1.25 k g / m^{3}$	Rated power	$1.5 M W$
Gearbox ratio	$83.531$	Generator rated torque	$8376 N \cdot m$
Wind rotor’s external damping coefficient	$45.52 N \cdot m / (r a d \cdot s)$	Generator’s external damping coefficient	$0.4 N \cdot m / (r a d \cdot s)$
Cut-out wind speed	$25 m / s$	Cut-in wind speed	$3 m / s$
Inertial constant of generator	$90 k g \cdot m^{2}$	Rotor radius	$40 m$
Inertial constant of rotor	$4950000 k g \cdot m^{2}$	Rated speed	$2.1423 r a d / s$

Table 2. Performance metrics of two controllers under gust conditions.

	$M A E (r a d / s)$	$S T (r a d / s)$	$M A P E (%)$	$P M S (r a d / s^{2})$	$P F (r a d / s)$
Traditional UDE	0.0339	0.0693	1.6133	1.0000	1.0000
Bounded UDE	0.0198	0.0512	0.8842	0.5971	0.6385

Table 3. Performance metrics of two controllers under step conditions.

	$M A E (r a d / s)$	$S T (r a d / s)$	$M A P E (%)$	$P M S (r a d / s^{2})$	$P F (r a d / s)$
Traditional UDE	0.0178	0.0359	0.8195	1.0000	1.0000
Bounded UDE	0.0166	0.0408	0.7415	0.7026	0.9132

Table 4. Performance metrics of two controllers under turbulent conditions.

	$M A E (r a d / s)$	$S T (r a d / s)$	$M A P E (%)$	$P M S (r a d / s^{2})$	$P F (r a d / s)$
Traditional UDE	0.0511	0.1372	2.9191	1.0000	1.0000
Bounded UDE	0.0504	0.1376	2.8890	0.8858	0.9412

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Anti-windup Pitch Angle Control for Wind Turbines Based on Bounded UDE

Abstract

1. Introduction

2. VSWT Modelling

3. Control Objectives

4. Controller Design

4.1. The UDE-Based Controller

4.2. Design with Bounded Constraints

4.3. Proof of Stability

5. Simulation Verification

5.1. Wind Gust

5.2. Step Wind

5.3. Turbulent Wind

6. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe