Prerpints.org logo
Preprint
Review

Entropy has a Great Potential to Steer Education above and Beyond

This version is not peer-reviewed.

Submitted:

04 February 2024

Posted:

05 February 2024

You are already at the latest version

Abstract
Numerous scientific fields employ entropy, the Shannonian measure of disorder and inaccessible information. Current paper examines educational uses of entropy. The major objectives of this survey are to create a coherent perspective of the applicability of classical entropies and to provide a concise detailed explanation that blends technical pertinence with conceptual extraction from the most recent literature. What's more intriguing are the closing thoughts mixed with a few unsolved issues and the creation of a future work schedule in these areas.
Keywords: 
Entropy
;  
education
Subject: 
Computer Science and Mathematics  -   Applied Mathematics

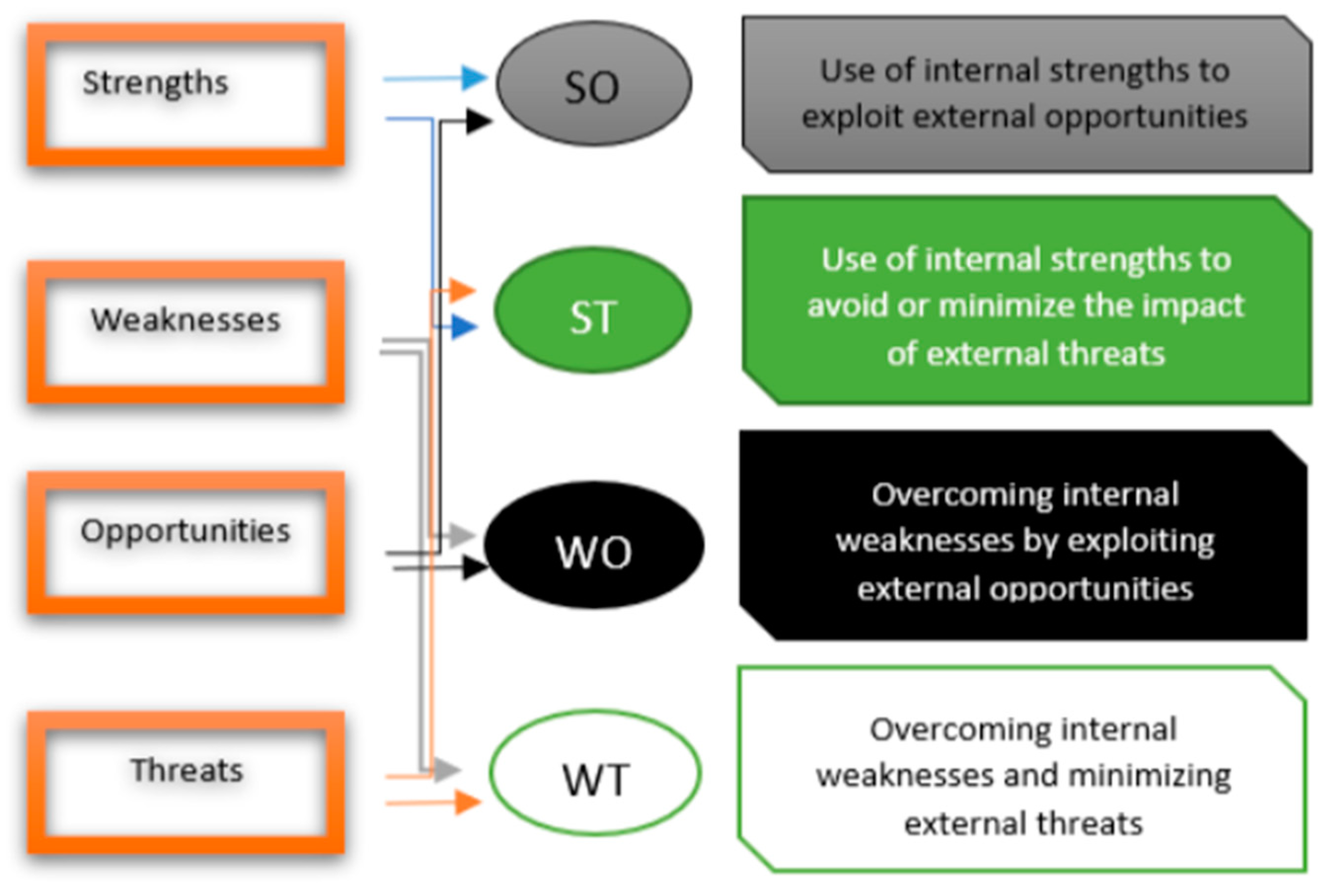
1. Introduction

As a thermodynamic and information-theoretic concept, the idea of entropy has influenced new innovations in a wide range of fields, including artificial intelligence. To provide a comprehensive review of entropy applications can sometimes prove to be impossible. Furthermore, the motivations behind incorporating entropy into knowledge areas such as information theory, queueing theory, engineering, and computation were examined (Cunha, 2020).
In the past decades newer versions of entropy have come to Approximate entropy and Ergodic theory (Arbabi et al., 2017; Montesinos et al., 2018), directional entropy (Burget, 2018), detecting nonlinearity in short and noisy time series, polynomial entropy (Zunino   & Kulp, 2017), entropy as an arrow of time (Gomes & Carneiro,2021), transfer entropy(Donglai et al., 2018; Zhang & Shang, 2020), they’re all entropy-like quantities proposed by researchers to tackle new challenges in time series analysis, cellular automata, chaos, synchronization, multiscale analysis, etc. For an in-depth account, including historical information, please consult the excellent review (Manish, 2020) and its references.
In information theory(Akundi et al., 2023), Shannon entropy quantifies the uncertainty or randomness of a set of symbols or data, and reads as:
H = − ∑ i = 1 n p i l n p i
Here p i denotes the probability of symbol i .
Entropy is a concept (Akundi et al., 2023), that has different interpretations in various fields. It is widely used in different research areas, such as assessing system robustness, vulnerability, and complexity.
The current paper is organized as follows: Section two is concerned with some entropy applications to education. Some challenging open problems are proposed in section three. Section four is concerned with conclusion combined with the next phase of research.

2. Entropy Applications to Education

(Akundi et al., 2023 ) highlighted the potential for developing assessment tools in the field of education using the concept of entropy. Several studies have explored the application of entropy in classroom assessment, such as evaluating essay content, building classification models, adaptive student assessment techniques, and assessing learner understanding based on free text answers. These approaches leverage entropy to measure the importance of words, compute information content, and determine the level of student understanding.
In the given context, (Akundi et al., 2023 ), knowledge refers to the skills and information acquired through experience and education. The model introduces the concept of entropy, which measures the average information produced based on the probability distribution of keywords in student text recordings. This helps quantify the familiarity and understanding of knowledge gained by students through activities and interactions in a classroom.
Thus, the text introduces the concept of text entropy ( T E (Akundi et al., 2023), calculated based on keyword occurrences in a text.
This introduces:
T E 1 = − ∑ p i l n p i  
T E S n = − ∑ p i l n p i    
Where, i is a specific keyword descriptor.
T E 1 defines the entropy calculated based on keyword occurrences in the instructor’s knowledge base; and T E S n refers to the entropy calculated based on keyword occurrences from text recording of a student n .
(2) and (3) represent the calculation of T E , where the summation is taken over the probability distribution of specific keywords. The text also mentions the importance of inter-individual interactions in complex systems like classrooms and presents a conceptual view of factors considered in formulating assessment models for different classroom settings.
In the context of classroom structures(Akundi et al., 2023), inter-individual interactions are crucial for creating meaningful structures, as stated by Vetromille-Castro. These interactions serve as the driving force behind the existence of complex systems, with classrooms being an example of such systems. Figure 1 (Akundi et al., 2023), provides a conceptual overview of the factors considered in formulating assessment models for different classroom settings, including the Traditional Classroom Setting, Peer-Based Classroom Setting, and Self-Organized Flipped Classroom Setting.
On another separate note, (Akundi et al., 2023), the assessment model for a traditional classroom setting is designed based on the following assumptions: the classroom is divided into two hierarchical levels, with instructors at a higher level and students at a lower level. The entropy, which measures the uncertainty of keyword occurrences, is expected to be lower for instructors compared to students due to their higher knowledge in the subject. The interactions considered in this model are limited to interactions between instructors and students. This can be portrayed by Figure 2 (c.f., Akundi et al., 2023 ).
The assessment model for a peer-based learning structure(Akundi et al., 2023), assumes a hierarchical organization with instructors at the highest level, followed by peers, and then students. Entropy, which measures the uncertainty in knowledge, is lower for instructors compared to peers, and lower for peers compared to students. This is because keywords with higher occurrence in their knowledge have lower entropy. The model is based on the understanding that instructors possess more knowledge than peers, who in turn possess more knowledge than students in each subject. This can be visualized by Figure 3(c.f., (Akundi et al., 2023 ))
In a wider view, the entropy-based classroom structural assessment framework(Akundi et al., 2023, is a method used to analyze and evaluate the observed structure of a classroom. It considers factors such as interaction patterns among students, their knowledge, the number of students, and the types of classroom interfaces. By gathering data on student communication and interaction patterns, this framework provides a conceptual framework for assessing the overall structure and dynamics of a classroom environment. The reader is encouraged to consult Figure 4(Akundi et al., 2023).
The development of private universities has provided opportunities for individuals to enhance their qualifications and skills. However, educational managers face challenges in determining the appropriate strategies for university development in a competitive environment. To address this, the study utilizes the Entropy method to assign weights to criteria (Wang et al. 2022) followed by the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) to rank private universities based on their performance. Additionally, statistical techniques like Spearman’s rank correlation coefficient and ANOVA are employed to evaluate correlations and compare criteria between groups of universities (Wang et al. 2022), respectively, creating an objective assessment environment for universities to establish development strategies.
In principles, the research problem addressed in(Wang et al. 2022) was to assess the effectiveness of resources and training in private universities in today’s competitive environment.
Multi-Criteria Decision Making (MCDM) (Wang et al. 2022), is a field that involves considering both quantitative and qualitative factors to make refined decisions. MCDM is based on fuzzy set (Wang et al. 2022), and aims to quantify standards, calculate total scores based on criteria weights, and provide decision-makers with a solid and accurate basis for making choices. TOPSIS evaluates options by measuring their distance from both the positive optimal solution (PIS) and the negative optimal solution (NIS), with the selected alternative being the one closest to the PIS and farthest from the NIS. For a more visualized illustration, the reader can consult Figure 5(Wang et al. 2022).
In their study (Wang et al. 2022), the main focus was primarily on evaluating the operational model of private universities based on two criteria:
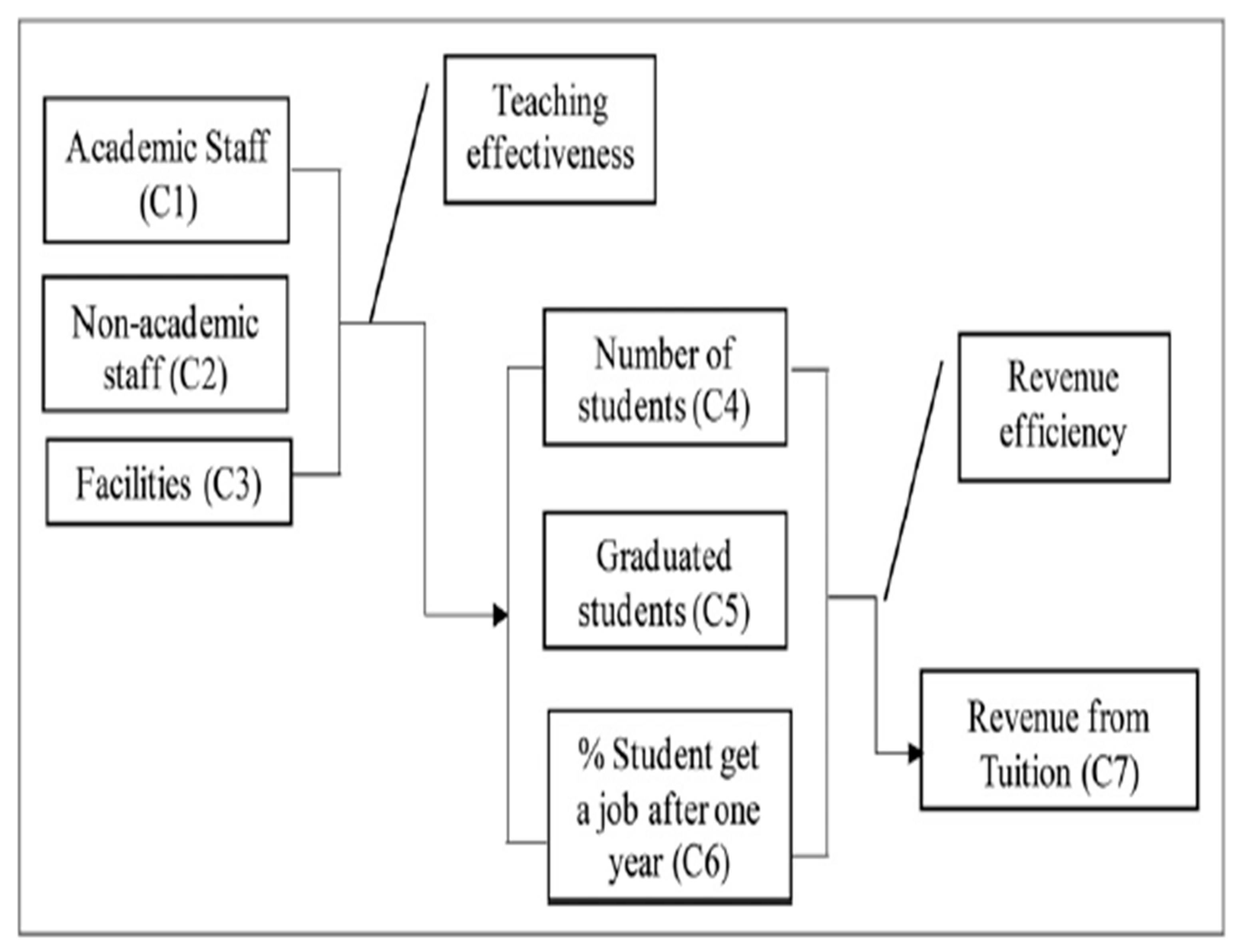
  • Teaching effectiveness, which refers to the measure of how well educational instruction is delivered and how effectively students learn and acquire knowledge.
  • Revenue efficiency, on the other hand, pertains to the effectiveness of financial resources and expenditures in generating income for the educational institution, particularly through tuition fees.
In Figure 2, the formulas presented represent mathematical calculations used to assess teaching effectiveness and revenue efficiency, although the specific details and interpretations of the formulas are not provided in the given context. See Figure 6
Sustainable development goals encompass environmental, economic, social, and cultural aspects. Higher education plays a crucial role in promoting sustainable development and empowering individuals to strive for a sustainable future. This study focuses on the quality of the higher education system in Morocco (Fahim et al., 2021), aiming to implement sustainable higher education reform.
The research utilizes a structured approach involving SWOT(strengths, weaknesses, opportunities, and threats) analysis, the analytic hierarchy process (AHP), and the entropy method to assess key factors, rank variables, and establish a SWOT matrix for decision-making and monitoring the quality of the education system. The findings highlight the need for various changes in higher education reform, such as effective budget planning, skilled experts, internationalization, improved infrastructure, curriculum reform, and up-to-date training.
Preprints 98190 g007
Figure 7. The SWOT framework considers both the organization’s internal capabilities and the external environment to guide decision-making and planning for organizational development(Fahim et al., 2021).
Figure 7. The SWOT framework considers both the organization’s internal capabilities and the external environment to guide decision-making and planning for organizational development(Fahim et al., 2021).
Preprints 98190 g007
The main objective of the undertaken study (Fahim et al., 2021), was to create a framework for measuring the quality of higher education institutions (HEIs) and providing recommendations for sustainability. The researchers used a combination of SWOT analysis, Analytic Hierarchy Process (AHP), and Entropy to develop a hybrid approach. This approach helped identify key factors influencing the quality of higher education reform and determine their priority through a stepwise strategic planning process. See Figure 8, Figure 9 and Figure 10 ((Fahim et al., 2021).
To this end, The study presented in (Fahim et al., 2021),has yielded significant results and suggests the potential for further exploration using various MCDM approaches. Future research could benefit from incorporating fuzzy multicriteria models and expert input through questionnaire development, as well as considering advanced MCDM models like COMET(Characteristic objects method) or SPOTIS.

3. Open Problems

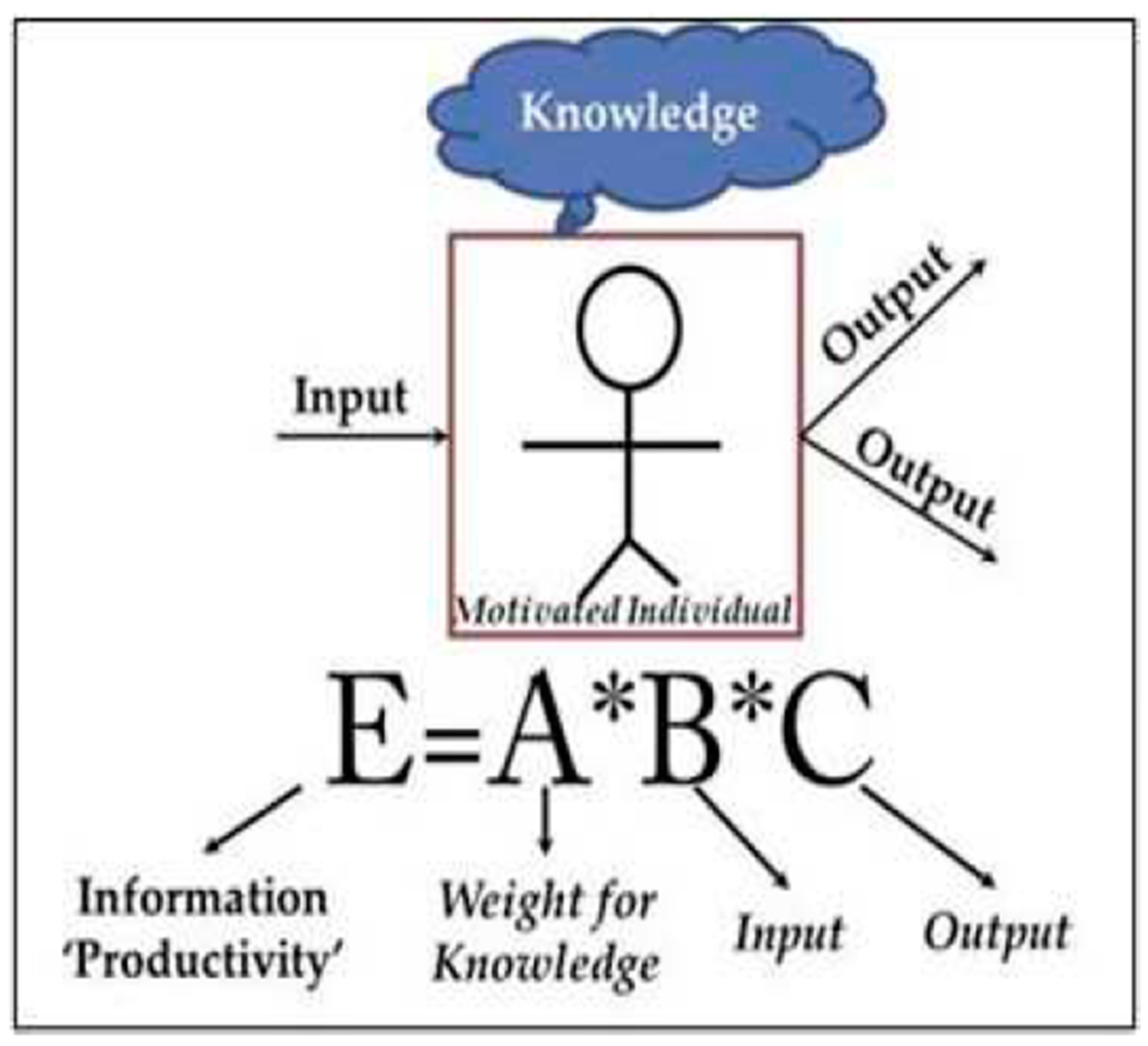
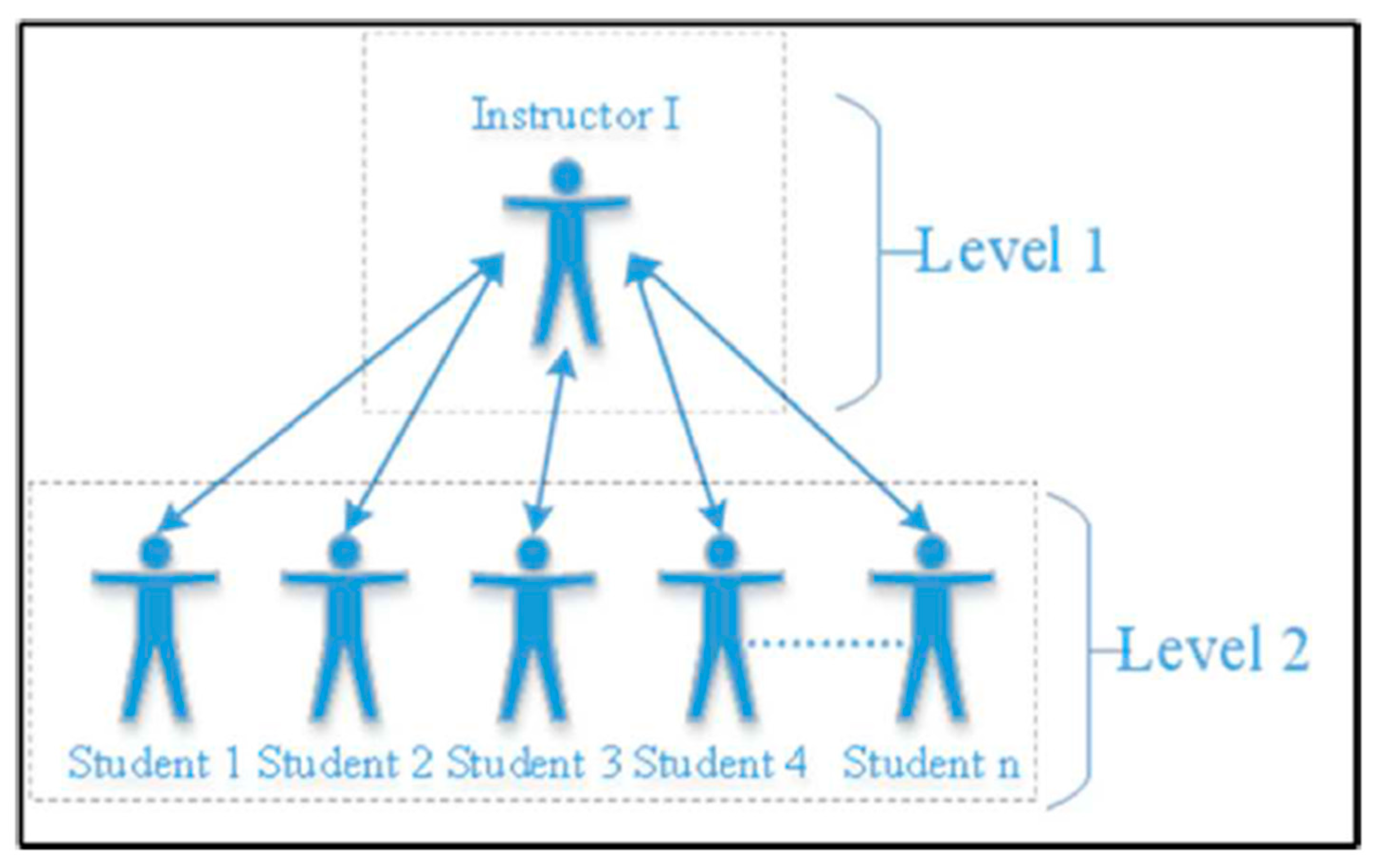
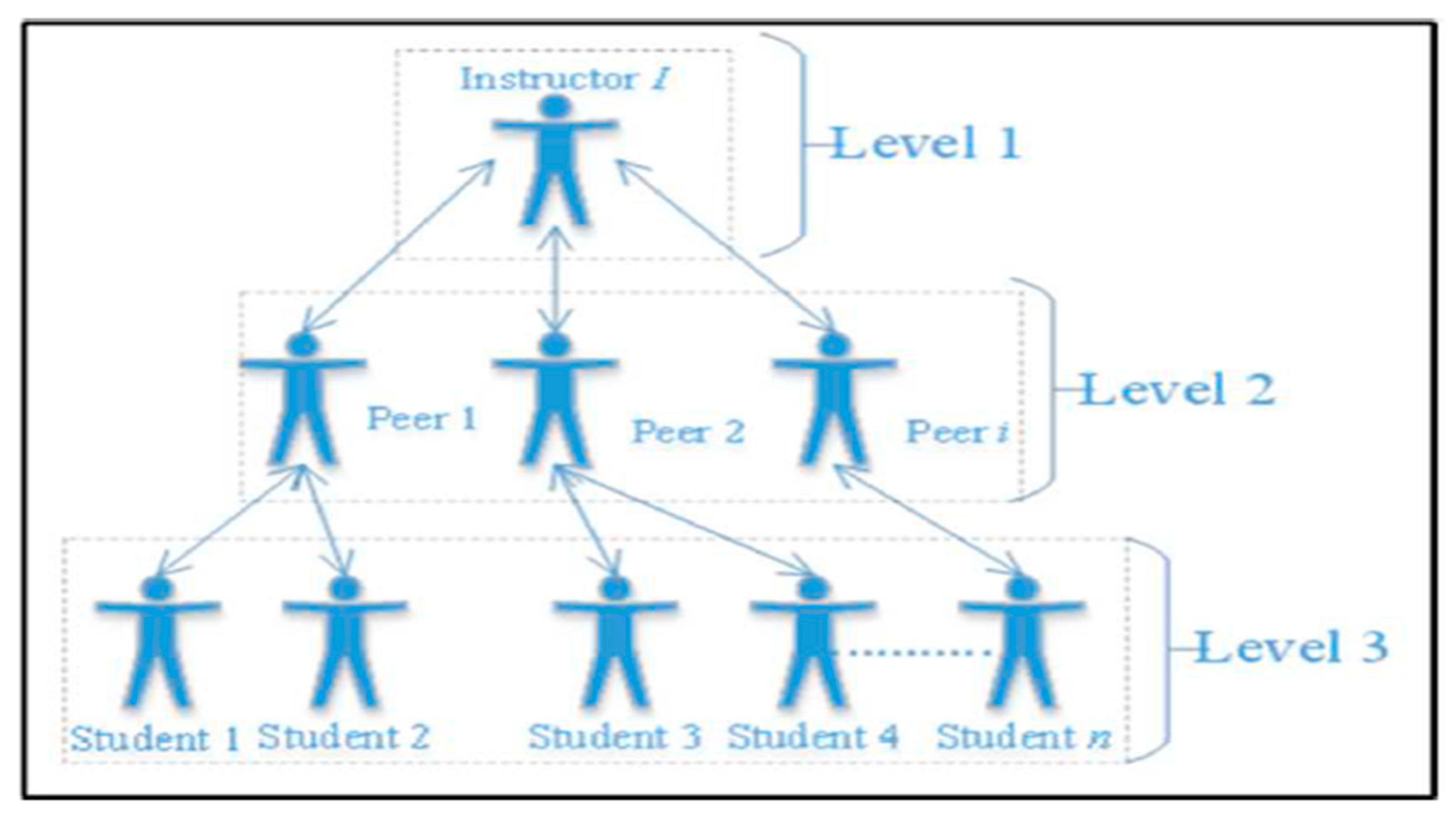
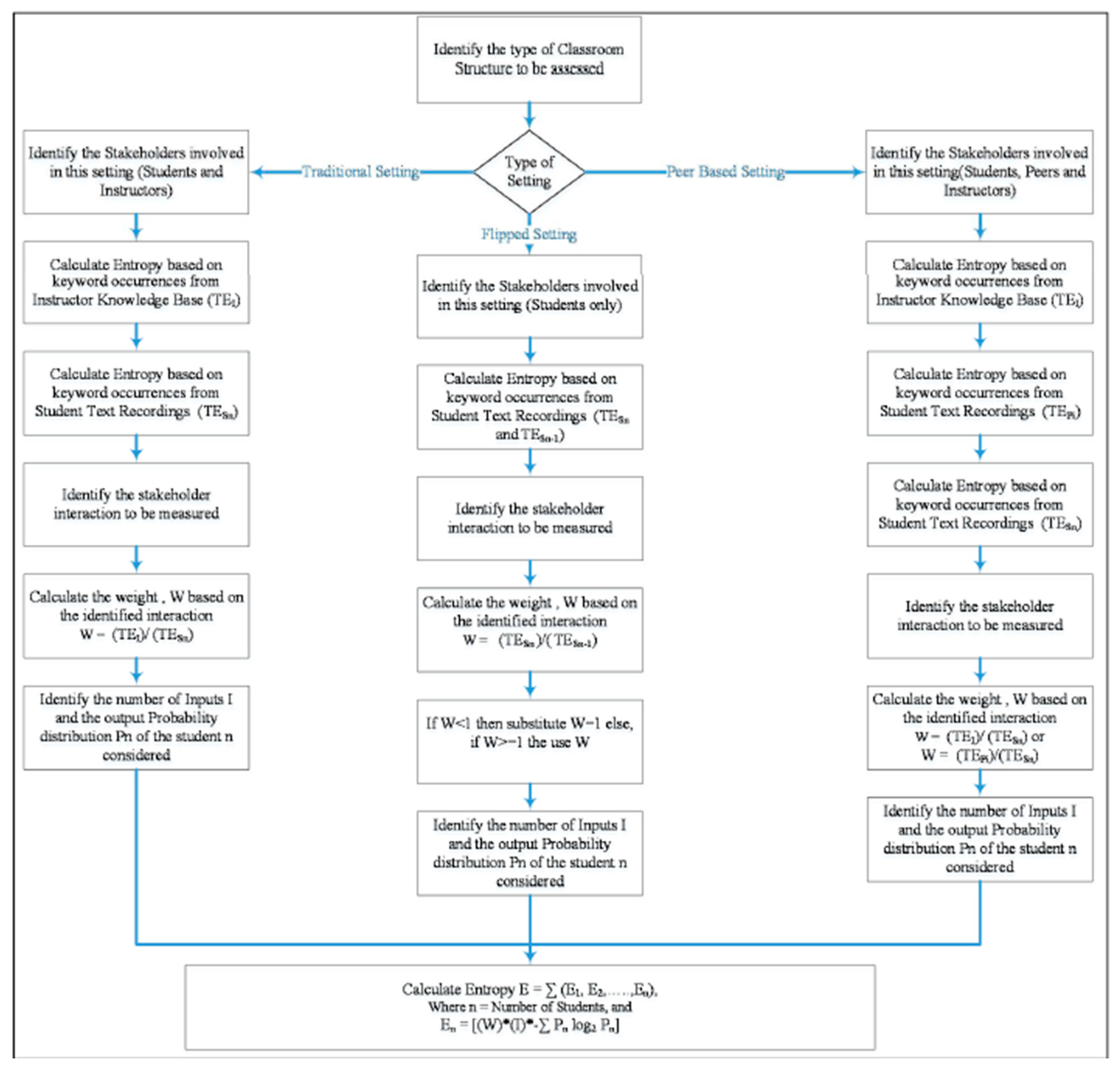
  • Following (Akundi et al., 2023), is it possible to propose an entropy-based assessment framework for a classroom the structural setting’s analysis and assessment, considering factors like interaction patterns, knowledge of the actors, number of actors, and types of classroom interfaces. The question is still open.
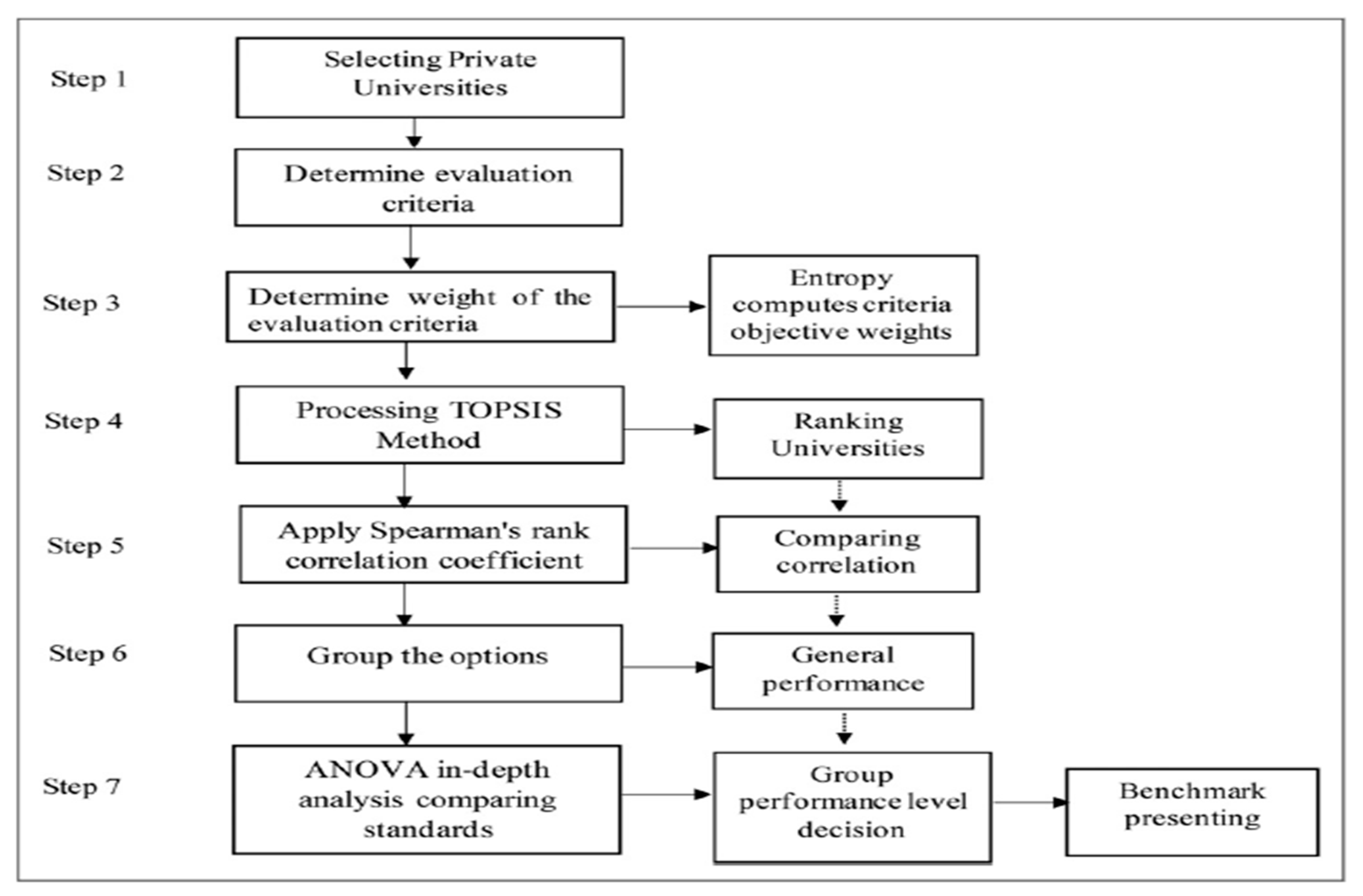
  • The proposed model (Wang et al., 2022), does not consider operational efficiency comprehensively or evaluate the impact of scientific research activities, which vary among universities. Additionally, the analysis does not cover all private universities and does not consider factors like reputation, establishment time, or location that can influence rankings. This proposes an open problem that needs to be addressed and applied to various international educational settings.
  • Having Shannon’s entropy (c.f., Equation(1)) would be the very basic entropy to employ. On another strong note, the use of Ismail’s innovative entropy forms (Mageed, 2022, 2023(a), 2023(b), 2023(c)) would add more to the stellar fusion of the educational profile on all settings. This is based on the variety of the involved parameters, especially, the information-theoretic parameter   q ( q ∈ 0.5 ,   1 ) that fine tunes LRIs(long-range interactions), while q ( q ∉ 0.5 ,   1 ) is a unique descriptor of SRIs(short-range interactions). Both LRIs and SRIs will have a significant impact on all educational setting and performance.

4. Closing Moments

This report provides updates on the state of education. There remain numerous obstacles to overcome to expand and unearth fresh findings and broaden the scope of entropy’s application in this field. There are several advancements that can be made to broaden the field in which entropy is applicable. The reader will be able to obtain knowledge from an overview thanks to the survey’s report on the most recent developments in entropy applications. Subsequent scholars can think about examining the significance of other ideas like chaos and complexity. More intriguingly, it’s possible that the entropic applicability’s range is constrained and cannot be expanded to encompass additional domains of knowledge. Entropy ideas will surely find more applications in the field of education. Apart from maximizing the applications, greater emphasis must be placed on resolving the proposed open problems and exploring entropic applications related to emotional intelligence.

References

  1. Cunha, M.d.Vale,Ribeiro Santos, C.C,Moret, M.A, de Barros Pereira, H.B. 2020. Shannon entropy in time-varying semantic networks of titles of scientific Paper. Appl Net Sci 5, 53. [CrossRef]
  2. Arbabi, H, Mezic,I. 2017. Ergodic theory, dynamic mode decomposition, and computation of spectral properties of the Koopman operator. SIAM Journal on Applied Dynamical Systems, 16(4):2096-126. [CrossRef]
  3. Montesinos, Castaldo, R,Pecchia, L. 2018.On the use of approximate entropy and sample entropy with center of pressure time-series. J Neuro Engineering Rehabil 15, 116. [CrossRef]
  4. Burget, D. 2018. Rescaled entropy and cellular Automata. Available online at: https://arxiv.org/pdf/2005.08585.pdf.
  5. Zunino,L, Kulp, CW. 2017. Detecting nonlinearity in short and noisy time series using the permutation entropy. Physics Letters A, 13;381(42):3627-35. [CrossRef]
  6. Gomes, JB, Carneiro, MJ. 2021.Polynomial Entropy for Interval Maps and Lap Number. Qualitative Theory of Dynamical Systems, 20(1):1-6. [CrossRef]
  7. Donglai, W, Joseph, Zisserman, L, Freeman, A.2018. Learning and Using The Arrow of Time. CVF version and available on IEEE Xplore. Online at: https://openaccess.thecvf.com/content_cvpr_2018/papers/Wei_L earning_ and Using CVPR_2018_paper.pdf.
  8. Zhang, B, Shang, P. 2020. Measuring information transfer by dispersion transfer Entropy. Communications in Nonlinear Science and Numerical Simulation, Vol 89. [CrossRef]
  9. Manish, KH. 2020.A Brief History of Entropy, Towards Data Science. Online at: https://towardsdatascience.com/a-brief-history-of -entropy- chapter-1-9a2f1bc0d6de.
  10. Akundi, A., Lopez, V., & Luna, S.2023. Information entropy as a basis for classroom structural assessment. In 2023 IEEE International Systems Conference (SysCon) (pp. 1-7). IEEE. [CrossRef]
  11. Wang, T. C., Thu Nguyen, T. T., & Phan, B. N. 2022. Analyzing higher education performance by entropy-TOPSIS method: A case study in Viet Nam private universities. Measurement and Control, 55(5-6), 385-410. [CrossRef]
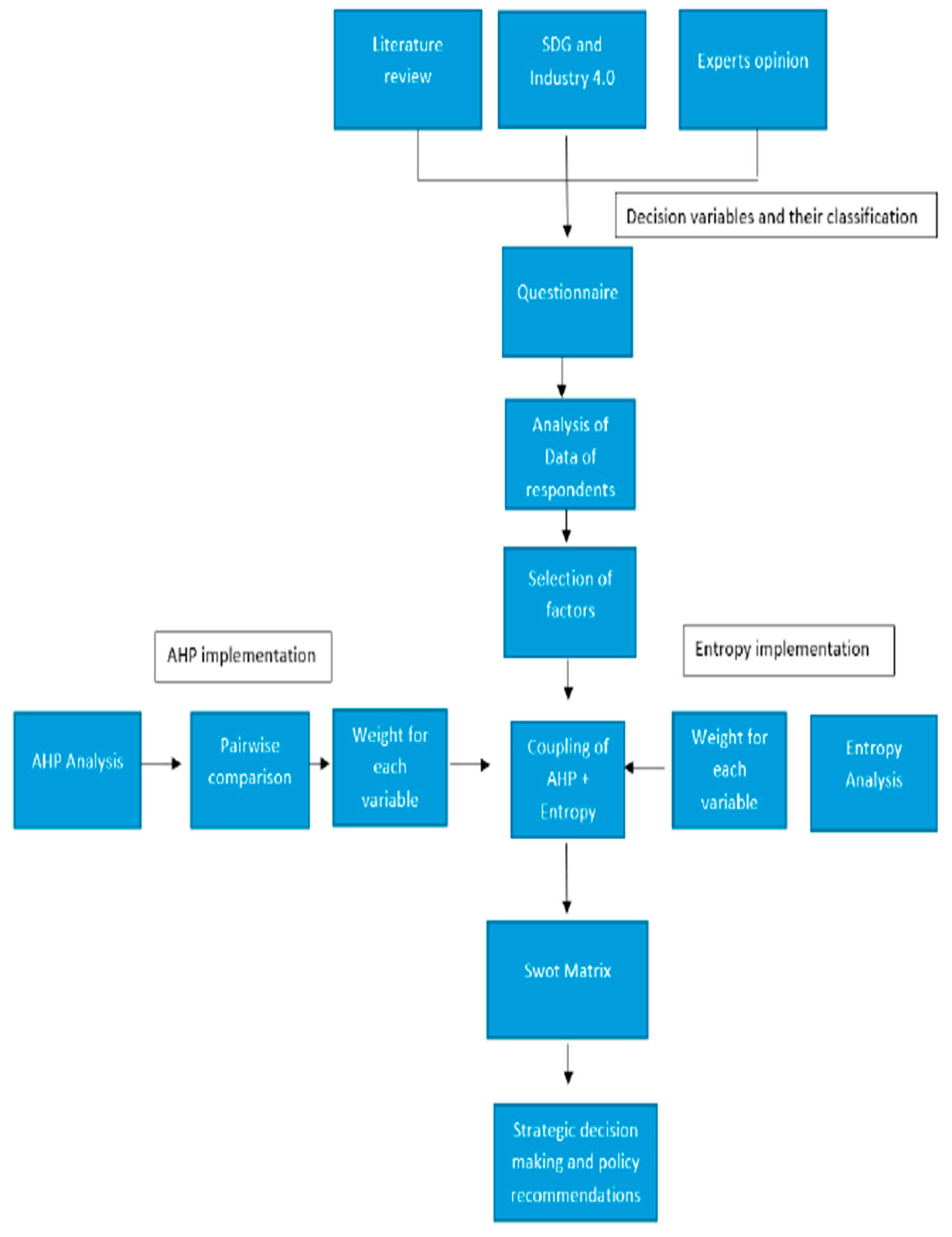
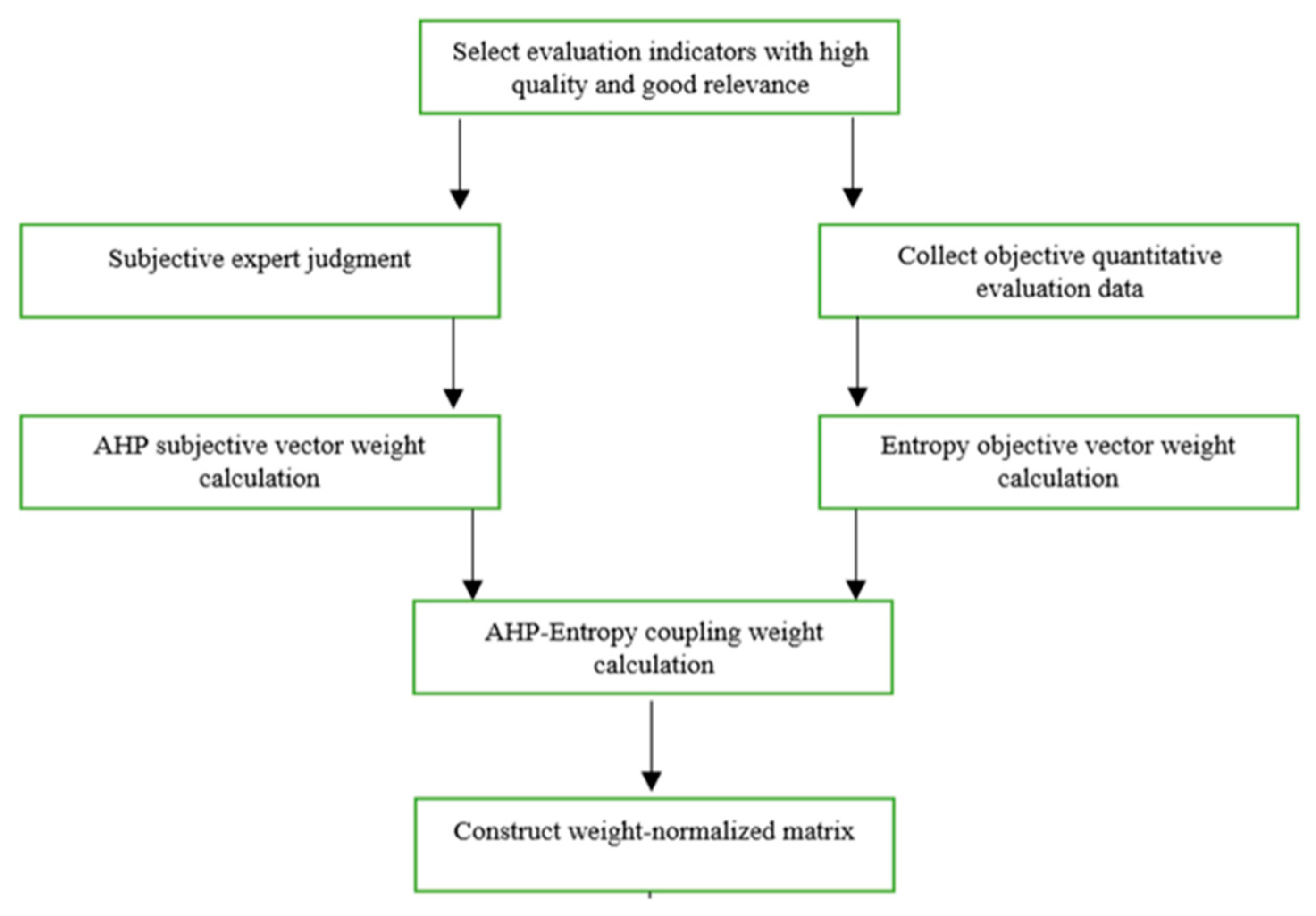
  12. Fahim, A., Tan, Q., Naz, B., Ain, Q. U., & Bazai, S. U. 2021. Sustainable higher education reform quality assessment using SWOT analysis with integration of AHP and entropy models: A case study of Morocco. Sustainability, 13(8), 4312. [CrossRef]
  13. Mageed, I.A., and Zhang,Q.2022. An Information Theoretic Unified Global Theory For a Stable M/G/1 Queue With Potential Maximum Entropy Applications to Energy Works. 2022 Global Energy Conference (GEC). Batman, Turkey, 2022, pp. 300-305. [CrossRef]
  14. Mageed, I.A. 2023(a). Fractal Dimension of Ismail’s Third Entropy with Fractal Applications to CubeSat Technologies and Education. The 2nd International Conference on Applied Mathematics, Informatics, and Computing Sciences (AMICS 2023). Ghent University, Belgium. [CrossRef]
  15. Mageed, I.A. 2023(b)."Fractal Dimension(Df) Theory of Ismail’s Second Entropy ( H I q ) with Potential Fractal Applications to ChatGPT, Distributed Ledger Technologies(DLTs) and Image Processing(IP). 2023 International Conference on Computer and Applications (ICCA), Cairo, Egypt, 2023, pp. 1-6. [CrossRef]
  16. Mageed, I.A. 2023(c).Fractal Dimension (Df) of Ismail’s Fourth Entropy H I V ( q , a 1 , a 2 , . . , a k ) with Fractal Applications to Algorithms, Haptics, and Transportation. 2023 International Conference on Computer and Applications (ICCA).Cairo, Egypt, pp. 1-6. [CrossRef]
Preprints 98190 g001
Figure 1. The conceptual view underlying the development of assessment models based on entropy for different classroom settings.
Figure 1. The conceptual view underlying the development of assessment models based on entropy for different classroom settings.
Preprints 98190 g001
Preprints 98190 g002
Figure 2. In a traditional classroom setting, the hierarchical representation consists of two levels: instructors at a higher level and students at a lower level. The assessment model for this structure assumes that the entropy, which represents the uncertainty of keyword occurrences, is higher for students’ text recordings compared to instructors’ knowledge base.
Figure 2. In a traditional classroom setting, the hierarchical representation consists of two levels: instructors at a higher level and students at a lower level. The assessment model for this structure assumes that the entropy, which represents the uncertainty of keyword occurrences, is higher for students’ text recordings compared to instructors’ knowledge base.
Preprints 98190 g002
Preprints 98190 g003
Figure 3. In an ideal peer-based learning environment, a hierarchical representation is used to illustrate the structure of interactions among students. This representation shows a clear hierarchy where students are organized into different levels based on their roles and relationships within the learning process. This hierarchical structure facilitates effective peer-to-peer interactions and promotes collaborative learning.
Figure 3. In an ideal peer-based learning environment, a hierarchical representation is used to illustrate the structure of interactions among students. This representation shows a clear hierarchy where students are organized into different levels based on their roles and relationships within the learning process. This hierarchical structure facilitates effective peer-to-peer interactions and promotes collaborative learning.
Preprints 98190 g003
Preprints 98190 g004
Figure 4. Entropy based classroom structural assessment framework.
Figure 4. Entropy based classroom structural assessment framework.
Preprints 98190 g004
Preprints 98190 g005
Figure 5. An outline of the steps involved in the TOPSIS method. The model involves selecting objects, determining evaluation criteria, assigning weights to the criteria, and normalizing the research data.
Figure 5. An outline of the steps involved in the TOPSIS method. The model involves selecting objects, determining evaluation criteria, assigning weights to the criteria, and normalizing the research data.
Preprints 98190 g005
Preprints 98190 g006
Figure 6. Teaching effectiveness and Revenue efficiency.
Figure 6. Teaching effectiveness and Revenue efficiency.
Preprints 98190 g006
Preprints 98190 g008
Figure 8. The complete model incorporates the stepwise implementation of SWOT analysis with the AHP and entropy. This model is used to assess and analyze various factors related to the adoption of Sustainable Development Goals (SDGs) and Industry 4.0 in Higher Education Institutions (HEIs).
Figure 8. The complete model incorporates the stepwise implementation of SWOT analysis with the AHP and entropy. This model is used to assess and analyze various factors related to the adoption of Sustainable Development Goals (SDGs) and Industry 4.0 in Higher Education Institutions (HEIs).
Preprints 98190 g008
Preprints 98190 g009
Figure 9. The construction of a method that combines the AHP- entropy approach. This coupling method aims to calculate comprehensive weight values by using a geometric mean. The process involves utilizing the SWOT matrix for decision-making, where important factors within each SWOT group are obtained and a quadrilateral model is built based on their priorities.
Figure 9. The construction of a method that combines the AHP- entropy approach. This coupling method aims to calculate comprehensive weight values by using a geometric mean. The process involves utilizing the SWOT matrix for decision-making, where important factors within each SWOT group are obtained and a quadrilateral model is built based on their priorities.
Preprints 98190 g009
Preprints 98190 g010
Figure 10. The AHP- entropy approach.
Figure 10. The AHP- entropy approach.
Preprints 98190 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

78

Views

20

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated