A Three-Phase Multilevel Inverter Synthesized with 31-Levels and Op-Timal Gating Angles to Supply Static and Dynamic Loads

A three-phase multilevel inverter (MLI) synthesized with 31-levels in the output voltage is used to provide ac supply to a three-phase, squirrel-cage induction motor. The gating angles required for thirty power switches in MLI are optimized by both Genetic Algorithm (GA) and Gray Wolf Op-timization (GWO). In the optimization technique, the optimal angles are determined by solving the trigonometric equations from the Fourier analysis for targeting minimum total harmonic distortion (THD) at the MLI output. Simulation model and experimental prototype are developed for performance analysis and validation. The results obtained demonstrate that the MLI is effec-tively able to produce 31-levels of three-phase ac output voltages with THD not exceeding 5% when loaded with a resistive load and a three-phase induction motor. The voltages and currents are measured and recorded for different loads and operating conditions, including the amount of energy consumed by the loads, as well as frequency analysis, which shows the absence of most of the triple harmonics that have a negative impact on the efficiency of the inverter.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Three-phase multi-level inverters (MLI) are used in applications that require a medium or high level of electrical power [1,2]. The control circuits in these inverters aim to change the amount of output voltage by changing the number of levels used, as well as changing the frequency of the output voltage, which makes them important power sources in many electrical systems. One main task of MLI application is driving three-phase motors, which are widely employed in numerous applications [3,4]. Recently, these inverters have found important applications in the field of renewable energy [5,6,7] and are also an essential part of the modern vehicle industry [8]. Researchers are working hard to develop efficient controllers for the inverters by enhancing the gating signals for the inverter switches and also by reducing the number of these switches required for minimum losses resulting from the on and off states [9,10,11,12,13,14]. In this research, a three-phase MLI with 31- levels is designed, simulated, and implemented using Spartan 3E FPGA controller with an optocoupler to drive the switches in the three-phase inverter. Genetic algorithm [15,16] and gray wolf optimization algorithm [17,18] algorithms, are employed as artificial intelligent techniques to solve and optimize for the switching angles in this three phase MLI. The paper is organized as follows: The proposed topology of the three-phase MLI is shown in section II. The details of the employed methods are presented in section III. MATLAB simulation analysis and results are discussed section IV. A prototype and experimental results are presented in section V and finally, the conclusion of the work is described in section VI.

2. Proposed Topology

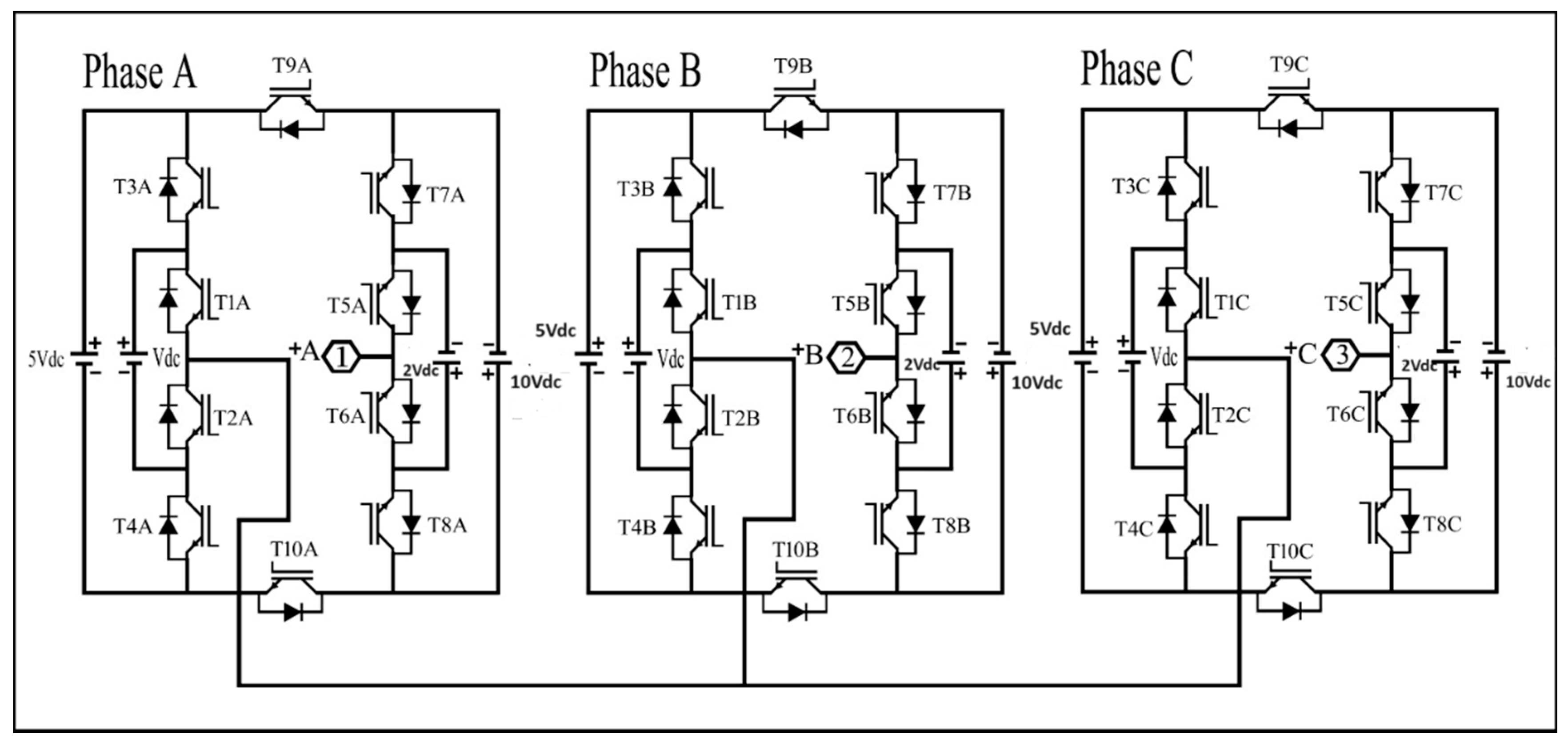
The proposed topology for the three-phase MLI with reduced number of switches consists of 10 switches (MOSFET’s or IGBT’s) and 4 DC sources for each single- phase, resulting in a total of 30 switches and 12 DC sources for a three-phase implementation, as shown in Figure 1.

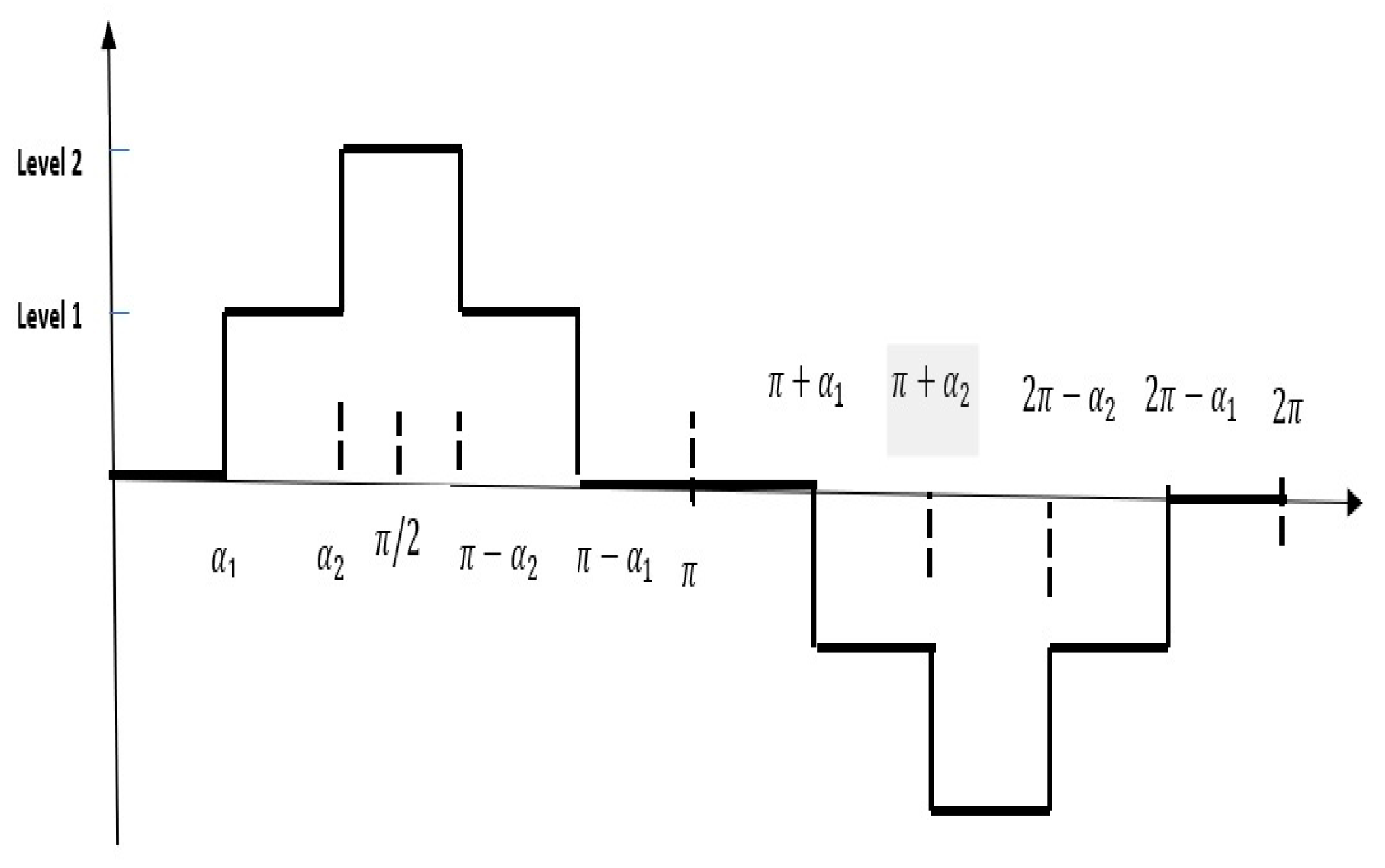
To illustrate the principle of fabricating multi-levels inverter output, Figure 2 represents the output voltage of a 5-level inverter, with two angles (

α_{1} a n d α_{2})

. These angles are determined by solving the trigonometric equations resulting from Fourier analysis of the output voltage of the inverter. The Fourier series for a stair periodic function can be expressed [19] as

v_{0} (t) = \frac{a_{o}}{2} + \sum_{k = 0}^{n} a_{n} \cos (n w t) + b_{n} \sin (n w t)

(1)

Where

a_{o},

is the average value of the output voltage,

a_{n}

and

b_{n}

, are even and odd components of the staircase periodic signal respectively. The stair waveform possesses a quarter wave symmetry which sets

a_{o}, a_{n}

and the odd

b_{n}

values to zero and simplifies equation (1) to:

v_{0} (t) = \sum_{i = 1,3, 5,7, 9,11 \dots \dots}^{n} b_{n} s i n (n w t)

(2)

where b_{n} = \frac{{4 V}_{d c}}{n π} \sum_{k = 1,3, 5,7, 9,11 \dots \dots}^{m} c o s (n α_{k})

(3)

These equations can be solved for any number of levels of the MLI. In three phase system the triple harmonics (3^rd,9^th , 15^th ….) are eliminated implicitly. To eliminate other harmonics (5^th harmonic), for example, the following equations are to be solved for optimum values of the gating angles.

b_{1} = \frac{{4 V}_{d c}}{π} \{\cos (α_{1}) + \cos (α_{2})\} = V_{f u n d}

(4)

b_{5} = \frac{{4 V}_{d c}}{5 π} \{\cos (5 α_{1}) + \cos (5 α_{2})\} = 0

(5)

where

V_{f u n d}

is the fundamental output voltage. Intelligent algorithms are employed to find the optimal solution for the values of these angles by relying on the selective harmonics elimination (SHE) technique with the restriction

α_{1} < α_{2} < \frac{π}{2}

. The other timing instants for one complete cycle of the output voltage are derived from these two angles.

3. Artificial intelligence Algorithms

Artificial intelligence (AI) algorithms work efficiently in solving mathematical problems resulting in an improved performance of the engineering systems [20]. In this research, Genetic Algorithm (GA) and Gray Wolf Optimization (GWO) algorithm are used to find the optimum gating angles of the inverter switches. A curve fitting principle is employed to determine the optimum solution between these two algorithms. For a three-phase inverter system with 31- levels, 15 angles are required for Phase A, and then a phase shift of

120 ° a n d 240 °

are set for Phase B and Phase C respectively. The inverter is operated at modulation index M=0.7. Other values of modulation index can be implemented following the same principle. This is summarized in Table 1.

4. Results

4.1. Simulation results

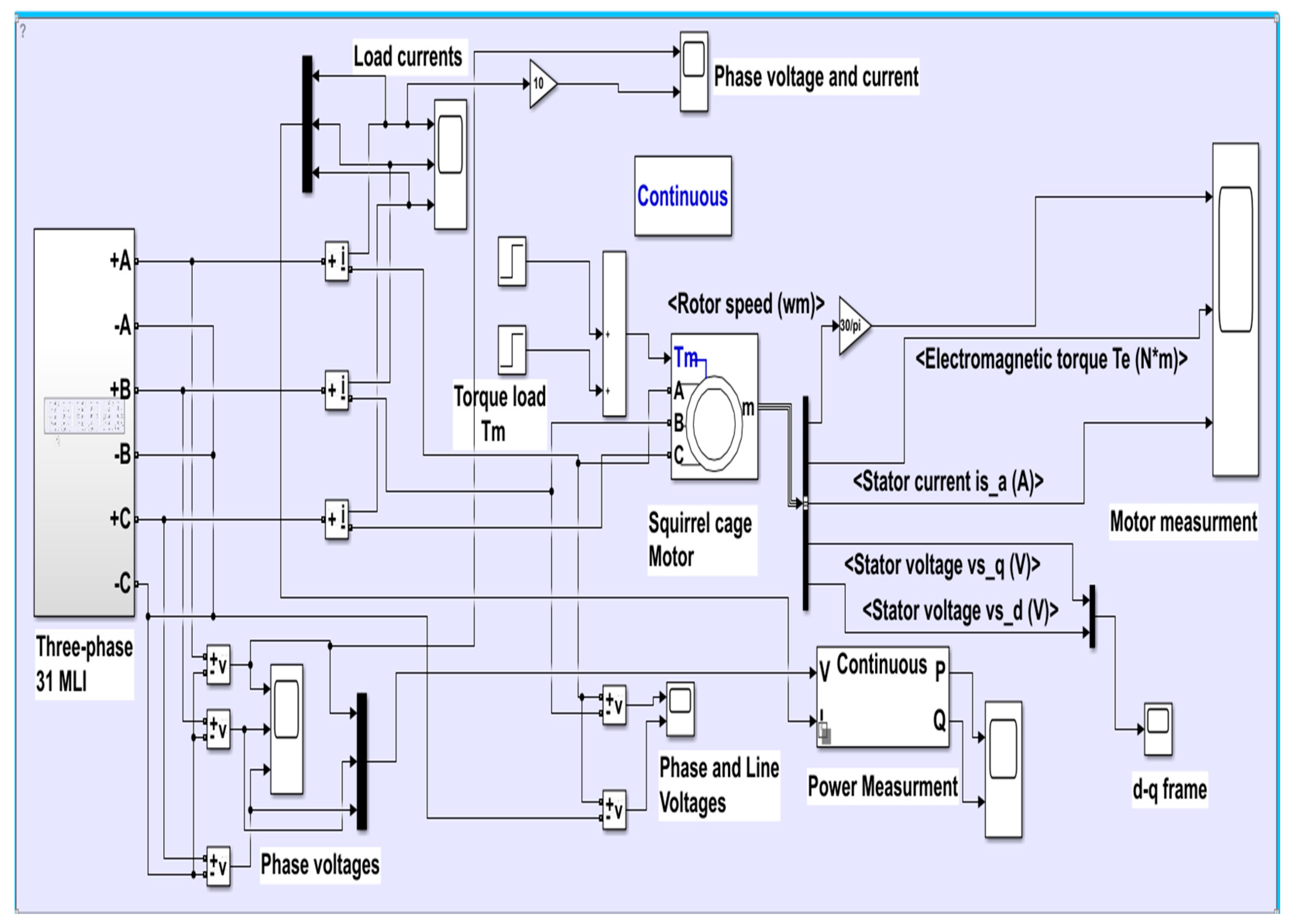
The proposed three-phase 31- levels MLI is built and simulated in MATLAB Simulink software using the optimized angles in Table 1. The three single- phase inverters are Ү-connected to form the three phase 50Hz ac supply source as shown in Figure 3. Each phase has 10 power switches (IGBT’s) and 4 DC sources. The (IGBTs) are working in complementary mode. Switches T2, T4, T6, T8, and T10 are the complements of T1, T3, T5, T7, and T9 respectively. A voltage of V_DC=24V is used for each stair level. The other three DC sources are 2V_DC=48V, 5V_DC=120V and 10V_DC=240V. To generate 31- levels at the inverter output voltage, multiple paths are chosen for the electrical current to pass through the power switches. Here, several DC sources are used, either adding them together, subtracting them from each other, or using individual sources. The peak output phase voltage =15(level)*24V (one stair voltage) =360V. The peak line voltage = 580V and V_L(RMS) = 410V. The three-phase induction motor specifications used for simulation are: Squirrel cage (5.4 HP 4 KW 50Hz 1430RPM). The Simulink model for 31- levels, three-phase MLI connected with a three-phase squirrel cage induction motor load is shown in Figure 3.

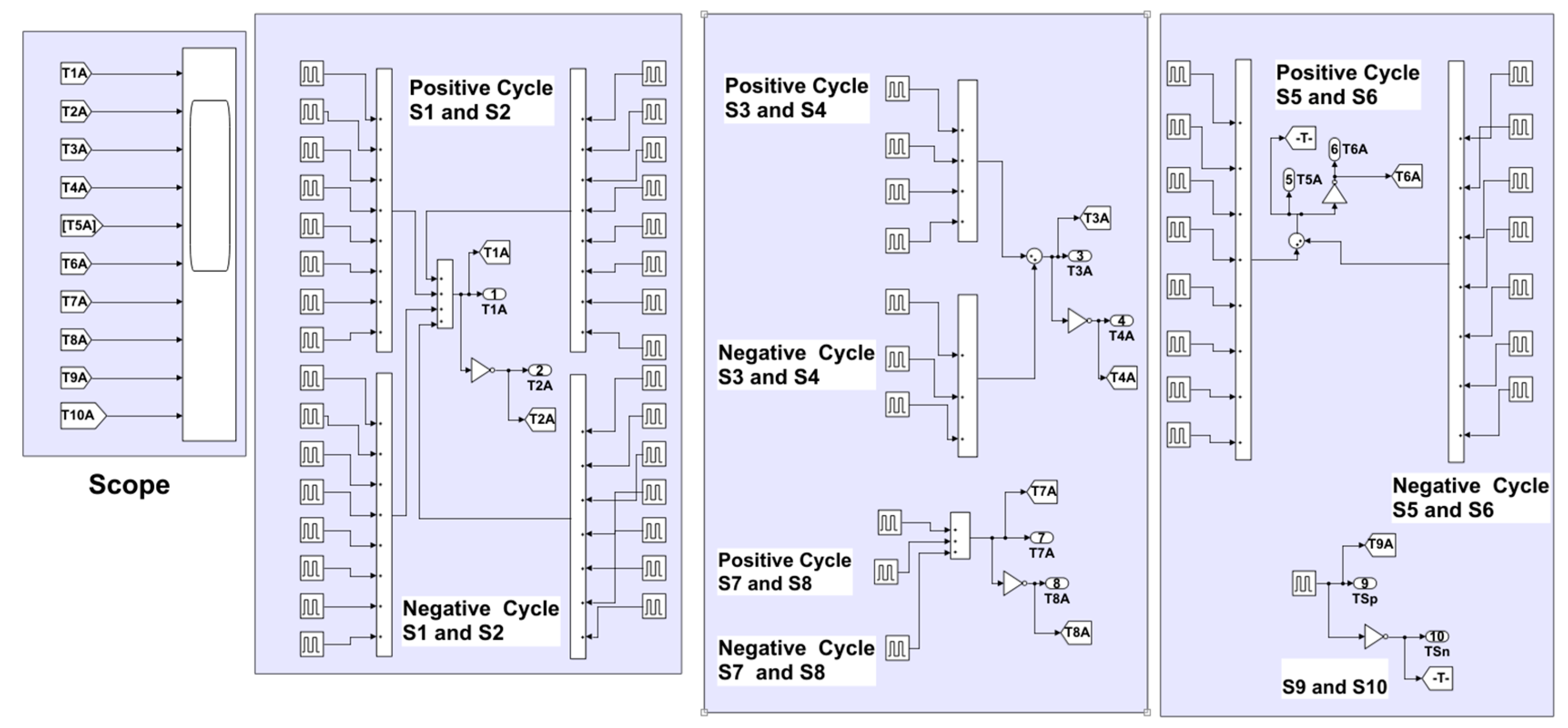
The detailed fabrication of gating periods for phase A is shown in Table 2, the asterisk * stands for complementary mode.

The detailed Simulink model of the switching controls is shown in Figure 4. The gating signals for phases B and C are derived from Phase A by adding a phase shift of

120 °

and

240 °

respectively.

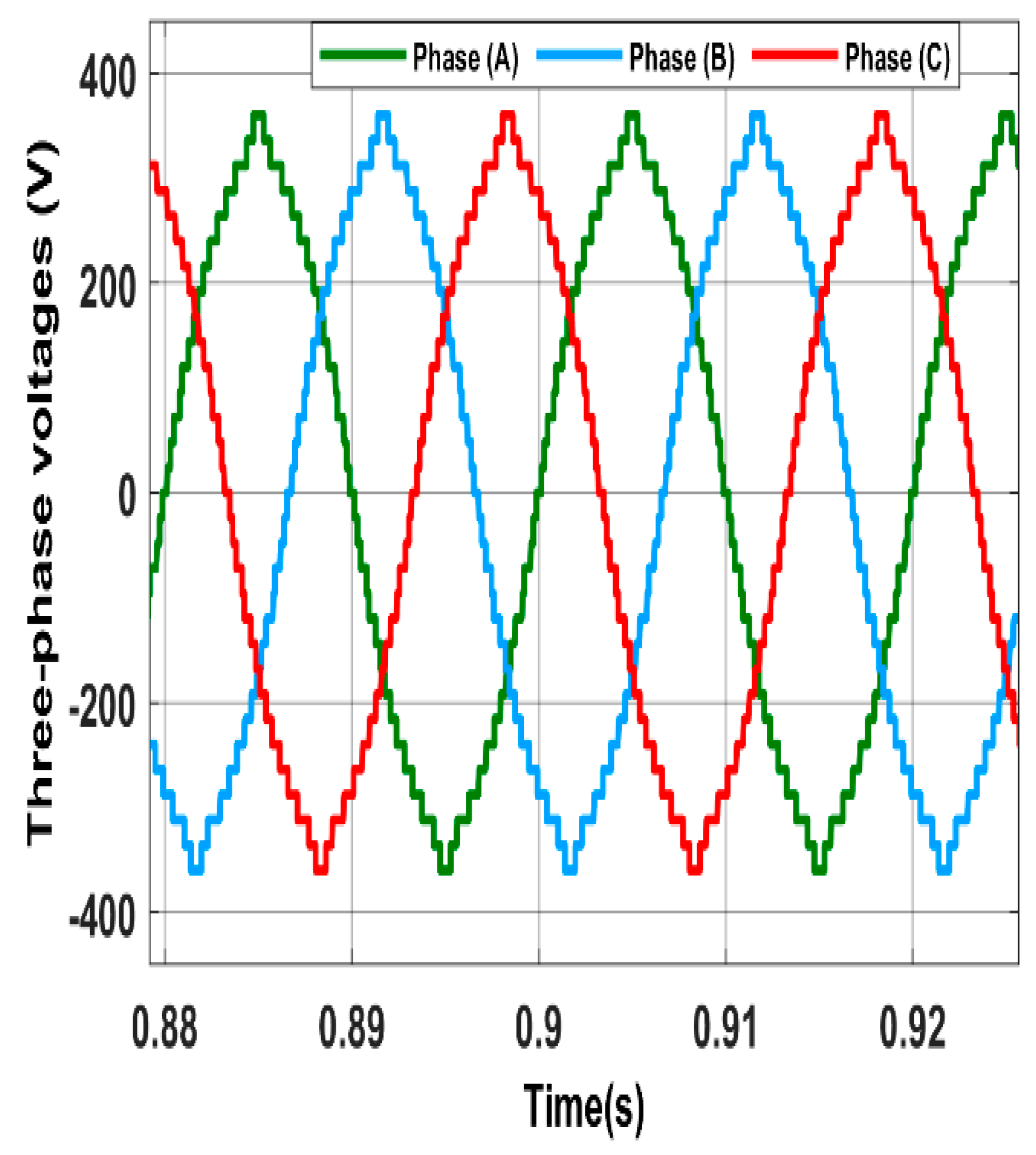
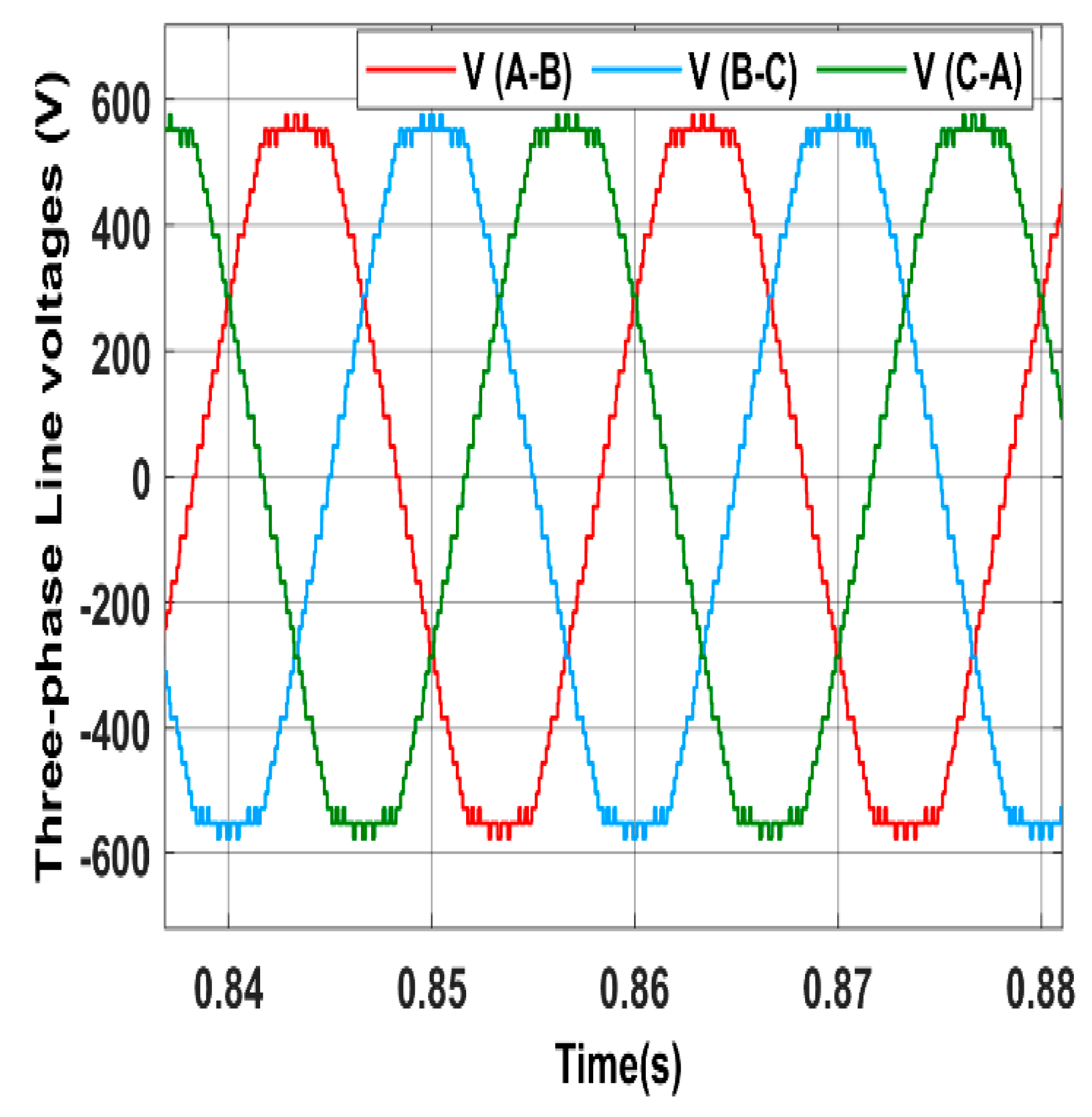
The output three-phase and line voltages for the 31-level MLI are shown in Figure 5 and Figure 6 respectively.

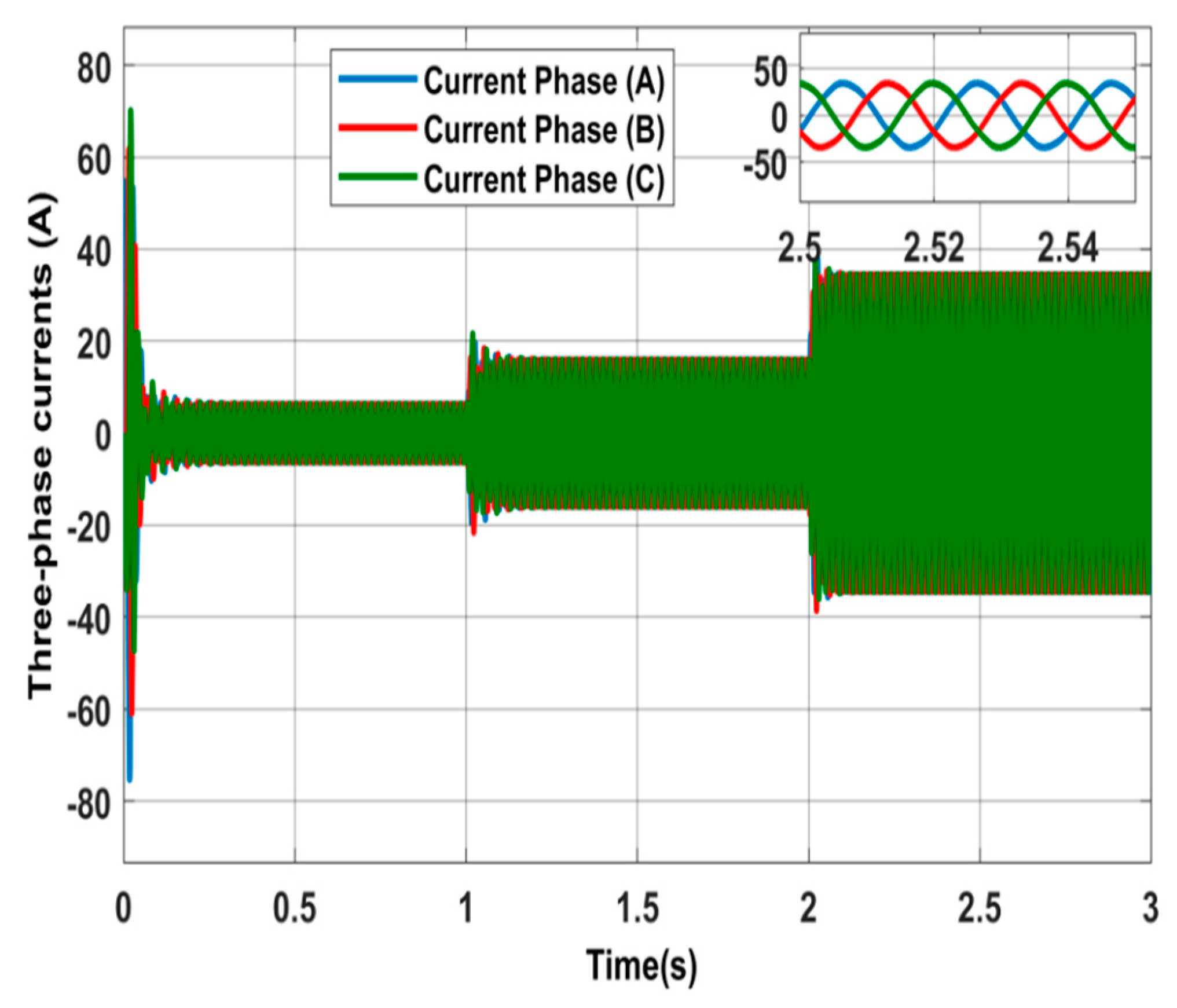
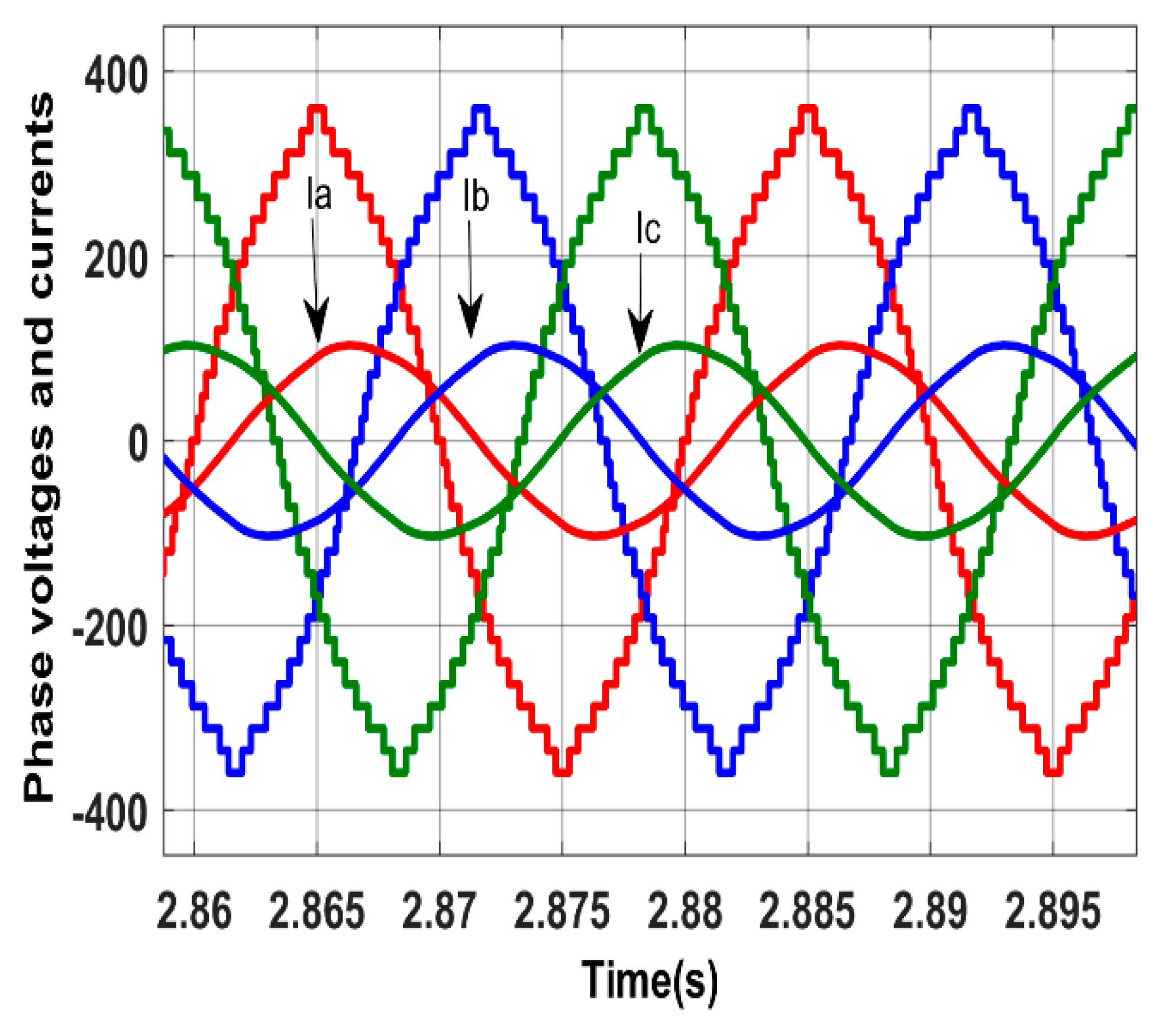
The phase currents supplied from 31-level MLI to the induction motor are shown in Figure 7. The current from 0 to 1 sec is about 4.25Arms when the motor is operating at no load. When the motor is subjected to external 20 N.m load at the instance from 1sec to 2 sec the current increases to 11.3Arms. And finally, from 2s to 3sec the current increases to about 24Arms when the motor is subjected to 40 N.m load. A phase shift of about 36° is observed between supply voltages and currents as shown in Figure 8 indicating a lagging power factor of 0.81.

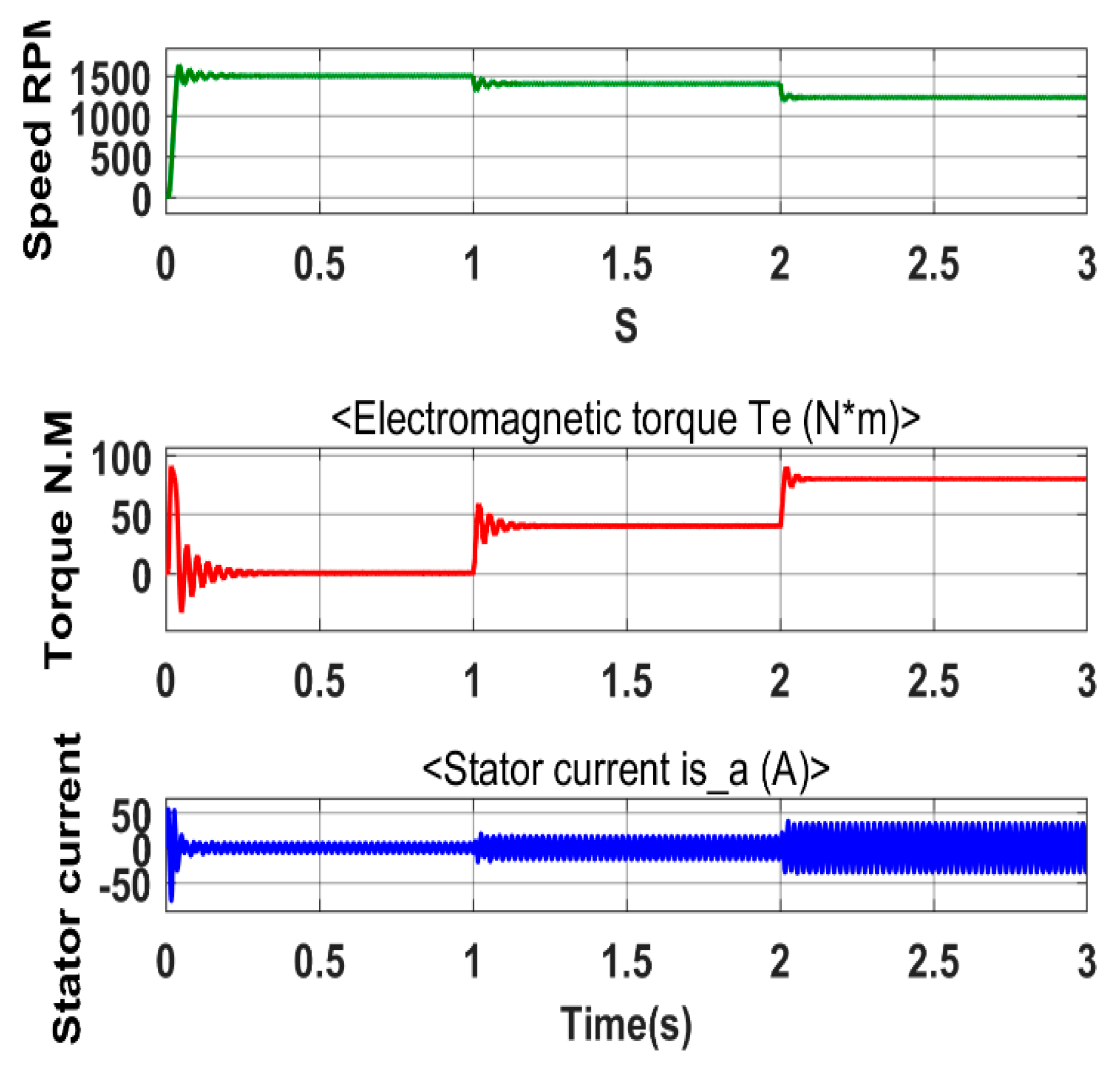
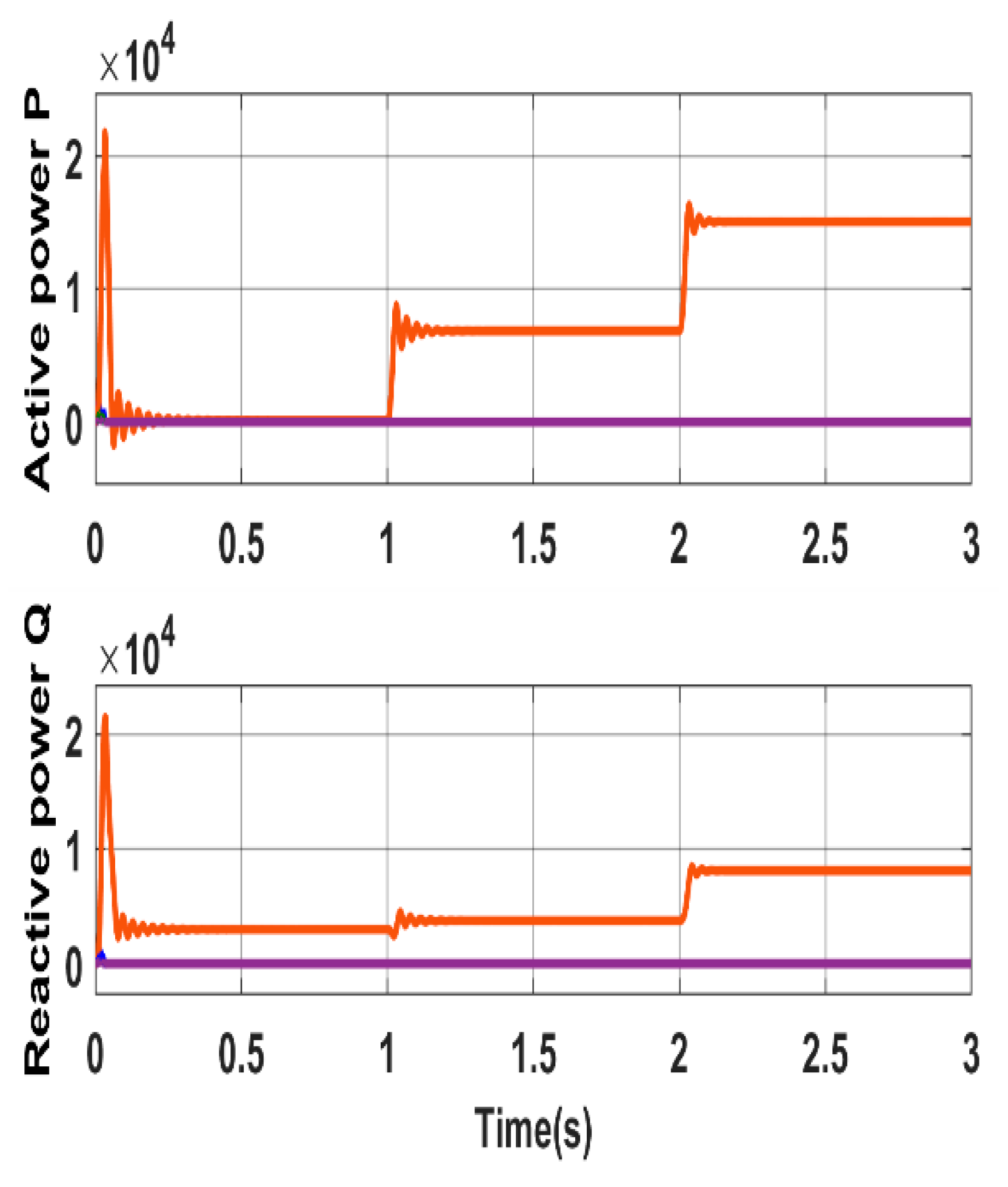
The measurement of the three-phase squirrel cage induction motor consisting of motor speed, electromagnetic torque, and stator current of phase A are shown in Figure 9. The motor reaches its base speed of about 1500 rpm at no load. This speed is then reduced due to the external load subjected at the instance between 1s and 2s. The stator current increases from no load values to higher values to reflect the applied load torque. The power consumed consists of active power P and reactive power Q are shown in Figure 10.

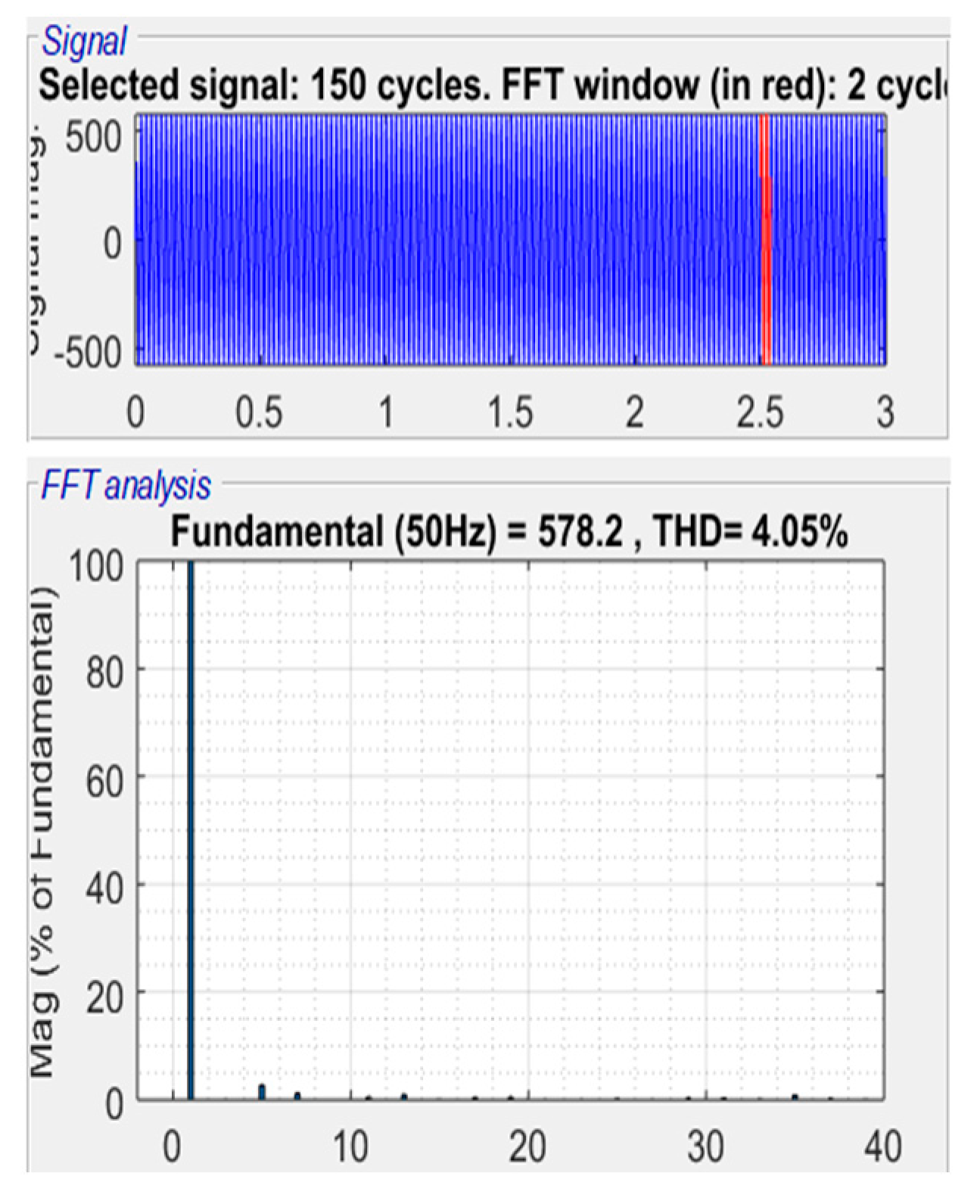
The fast Fourier toolbox set in MATLAB software shows that the harmonics contents in the inverter phase voltages are relatively low and the total harmonic distortion THD is about 4.69% and the recorded value of the line voltage THD is 4.05% as shown in Figure 11 and Figure 12 respectively.

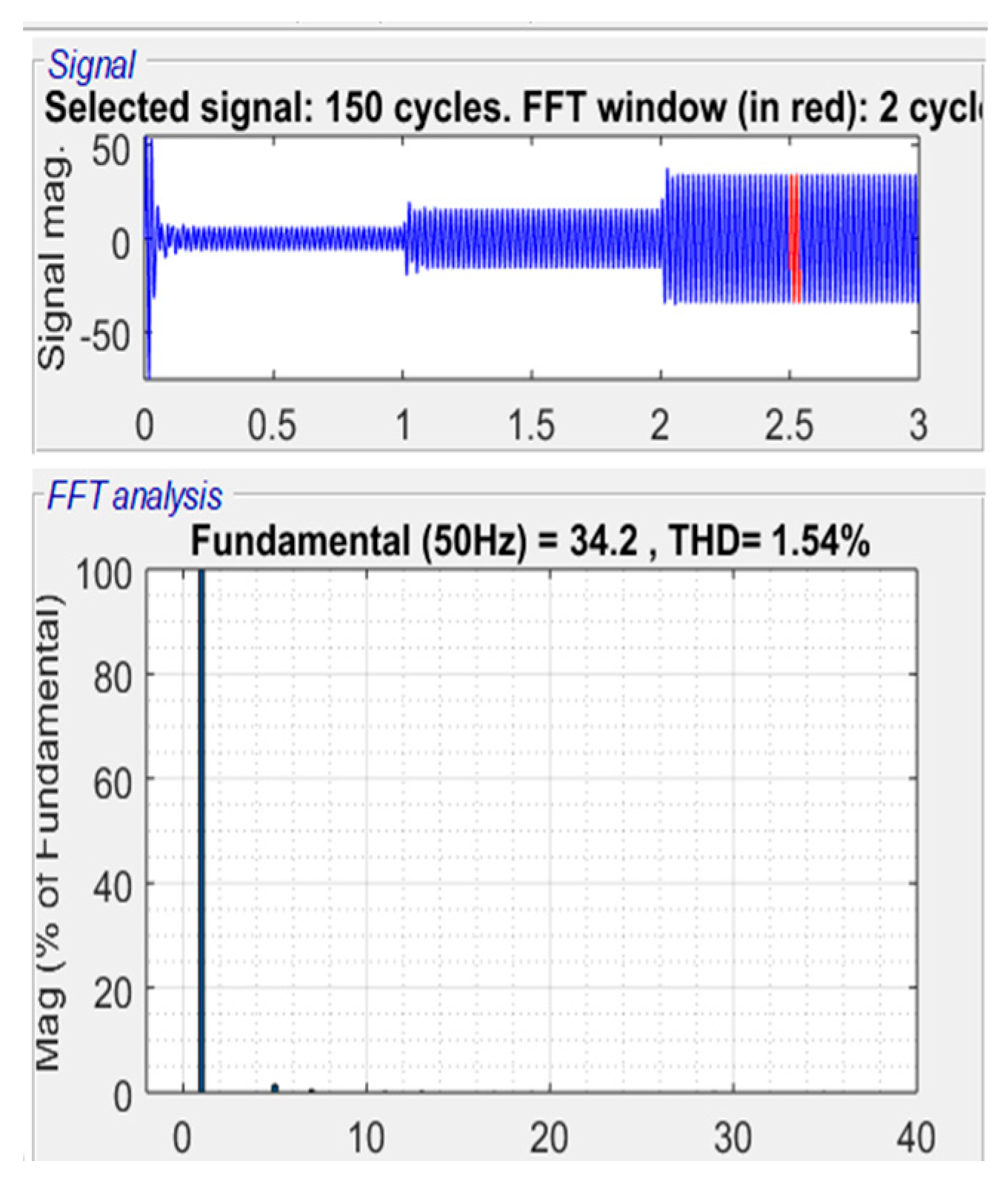
The motor is considered as inductive load which filters some harmonics, and resulting in a low harmonics distortion THD of 1.54% of motor current as shown in Figure 13.

4.2. Practical results

4.2.1 Generating gating pulses

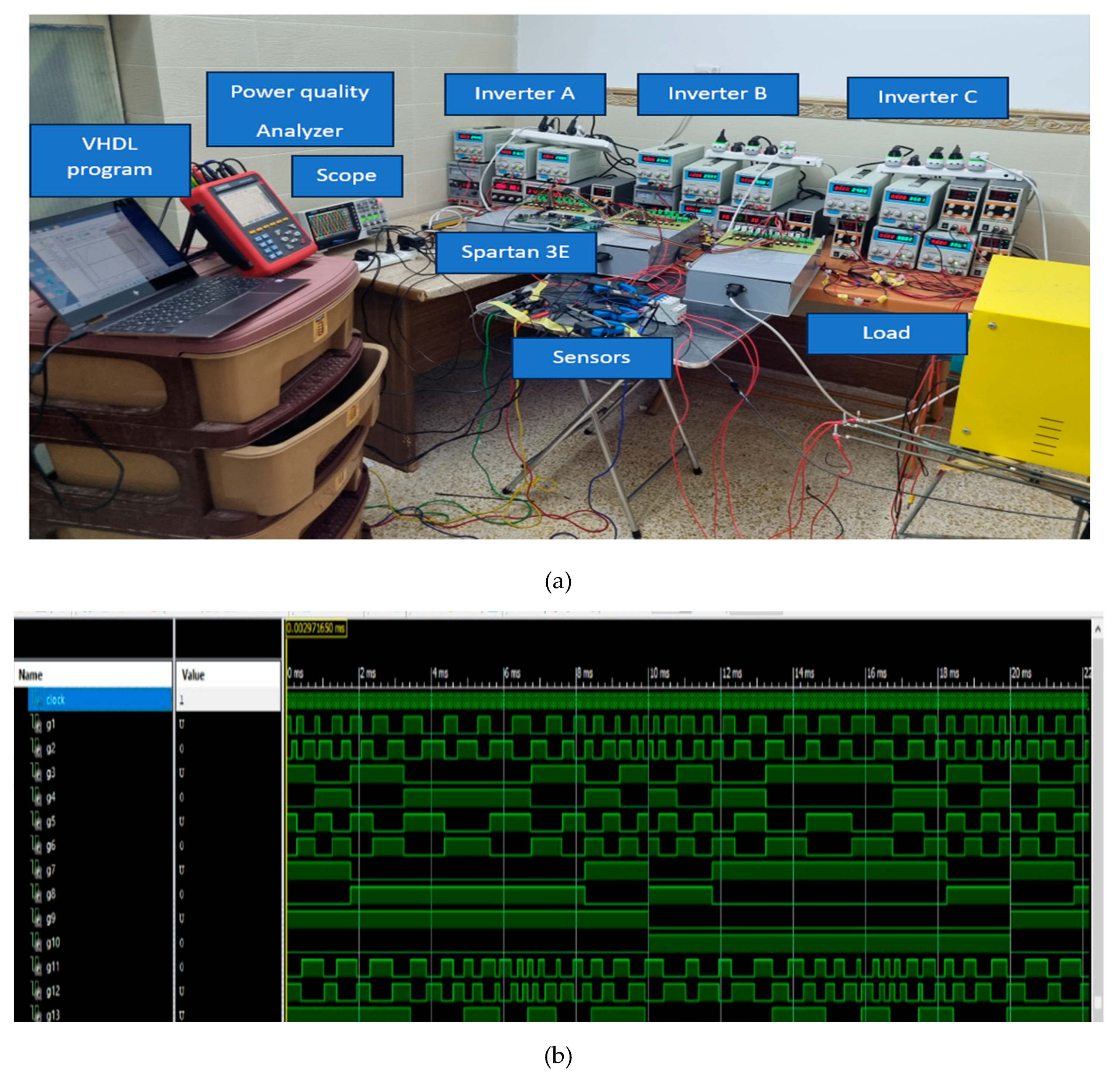
The Spartan 3E controller is used as the processor unit in the experiment. The clock frequency of the controller is 50MHz, there for the period of each clock is 20ns. To cover one cycle of 50Hz ac supply at the inverter output, a total of 20ms/20ns = 1000000 clocks from Spartan 3E controller is required. A prototype of the proposed three-phase, 31-level MLI is designed and built as shown in Figure 14a. The operation of 30 switches is programmed using Sparta 3E by writing a program in the VHDL language and then simulating it for the appropriate pulses to operate the switches. The simulated pulses are shown in Figure 14b for one cycle of operation.

The corresponding number of pulses for each optimized angle in Table 1 is calculated in Table 3.

Table 4 shows IGBTs states for the positive half -cycle for phase A. The states of IGBTs for Phases B and C are determined by taking into consideration the 120° phase shift between the three phases.

A VHDL file based on Table 4 to get 31-level MLI is uploaded to SPARTAN 3E controller. The controller outputs 30 gating signals. These gating signals are fed to the appropriate 30 power switches. The 10 power switches in each phase circuitry are designed to work in complementary mode as shown in Figure 15 for phase A. Also shown are the 120° phase shifts between phases A, B and C. A dead time of 4µsec is added between outgoing and incoming switches to avoid any possible short circuits.

4.2.2. The proposed 31-level MLI operating at no load

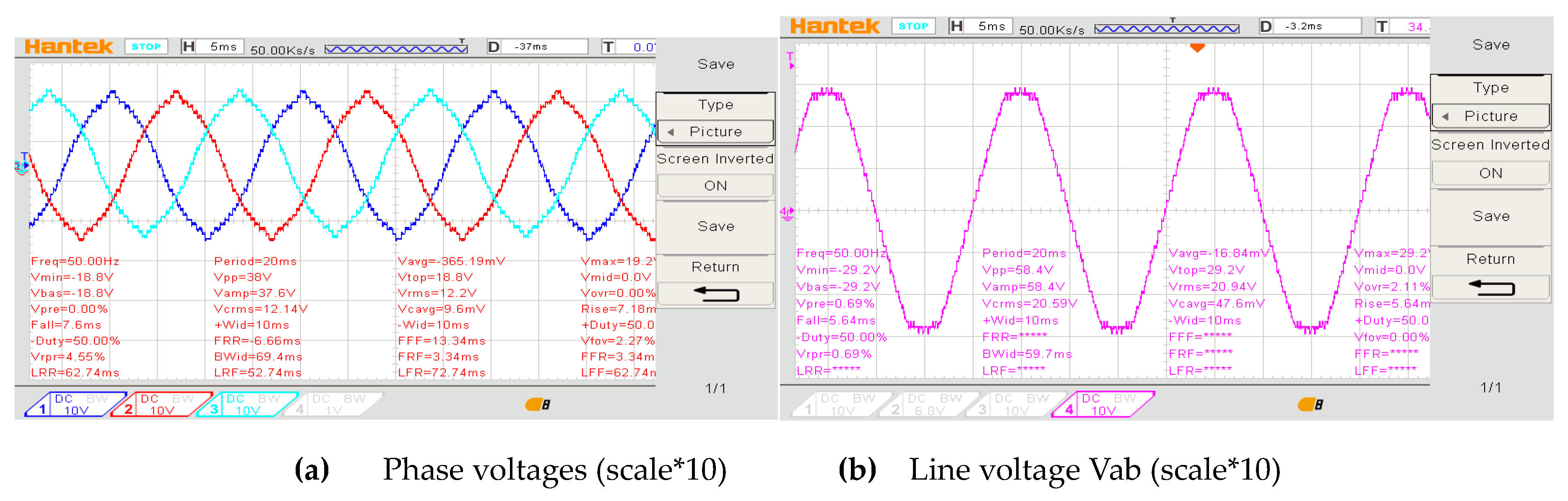
The system is operated at no load to monitor phase and line voltages. Figure 16a shows three-phase output voltages at 50Hz and 122Vrms. The line voltage (Vab) is shown in Figure 16b at 50Hz and 210Vrms.

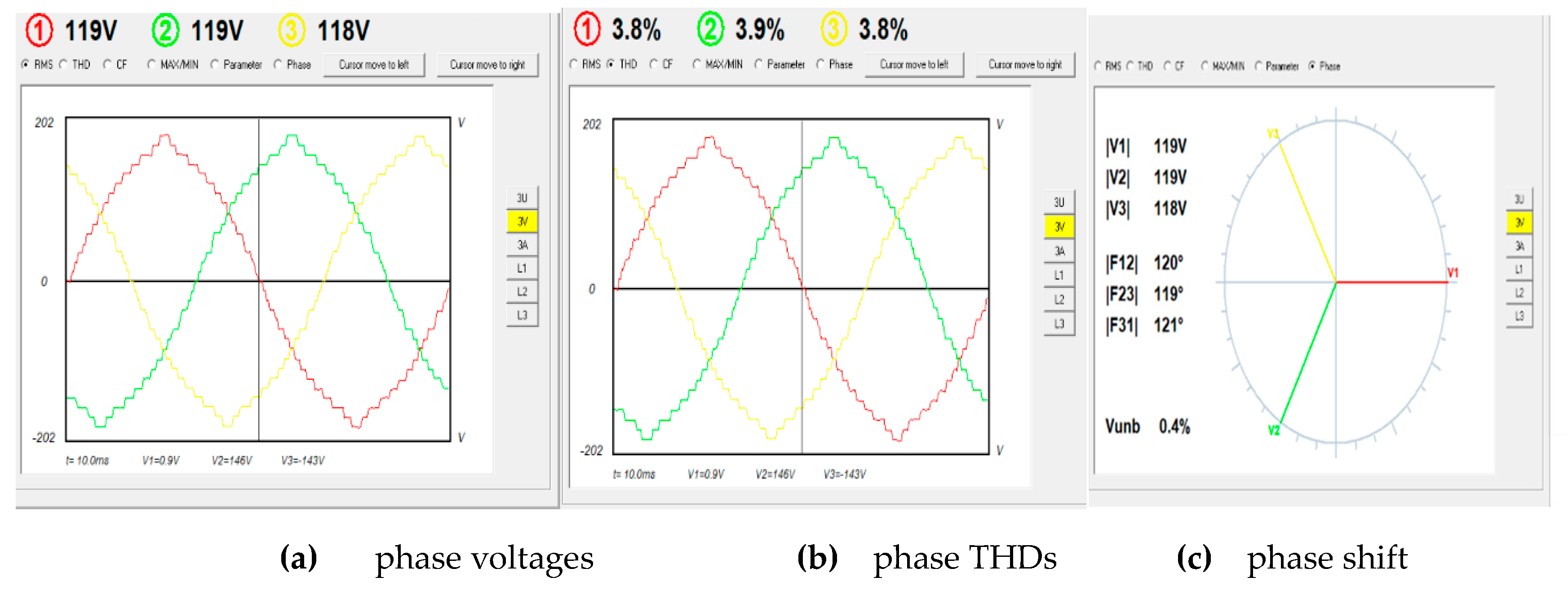
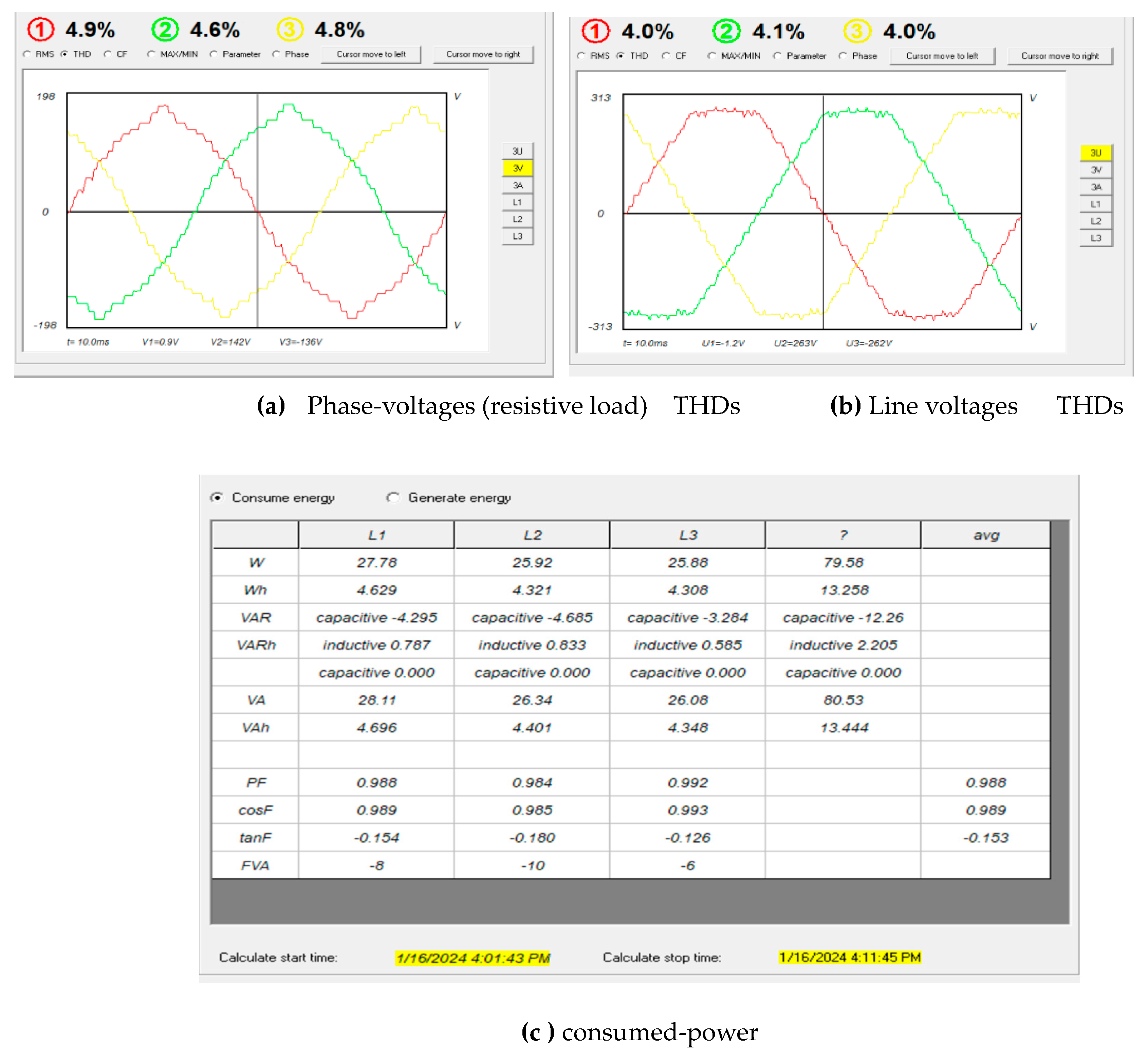
The power and quality analyzer HZCR-5000 are used to record the results. The three-phase voltages, THDs and phase shift between phases are shown in Figure 17a–c respectively.

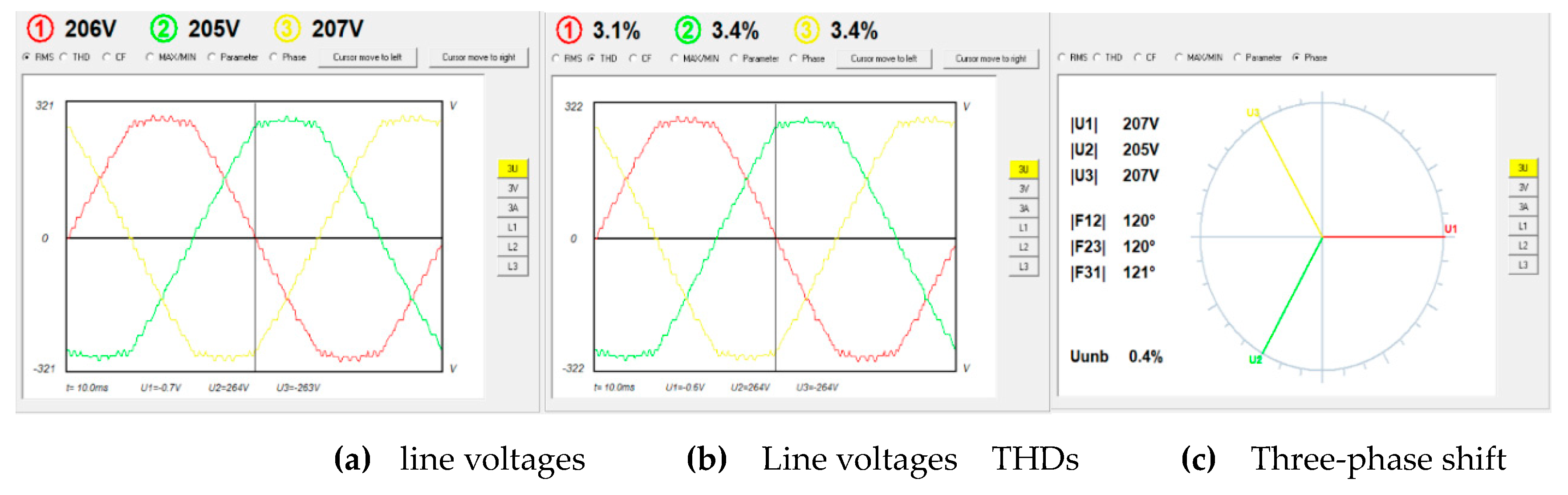
The line voltages, THDs and phase shift between phases are shown in Figure 18a–c respectively.

4.2.3. load test

The load test is divided into two parts, static load using three-phase resistive load and dynamic load using three-phase squirrel-cage induction motor. In the static load test, a Ү-connected resistive load connected to the output terminals of the 31-level MLI. From the results measured, THDs of the phase and line voltages are well below 5% limit as shown in Figure 19a,b respectively. The details of the consumed power are shown in Figure 19c where the power factor is almost unity due to purely resistive load.

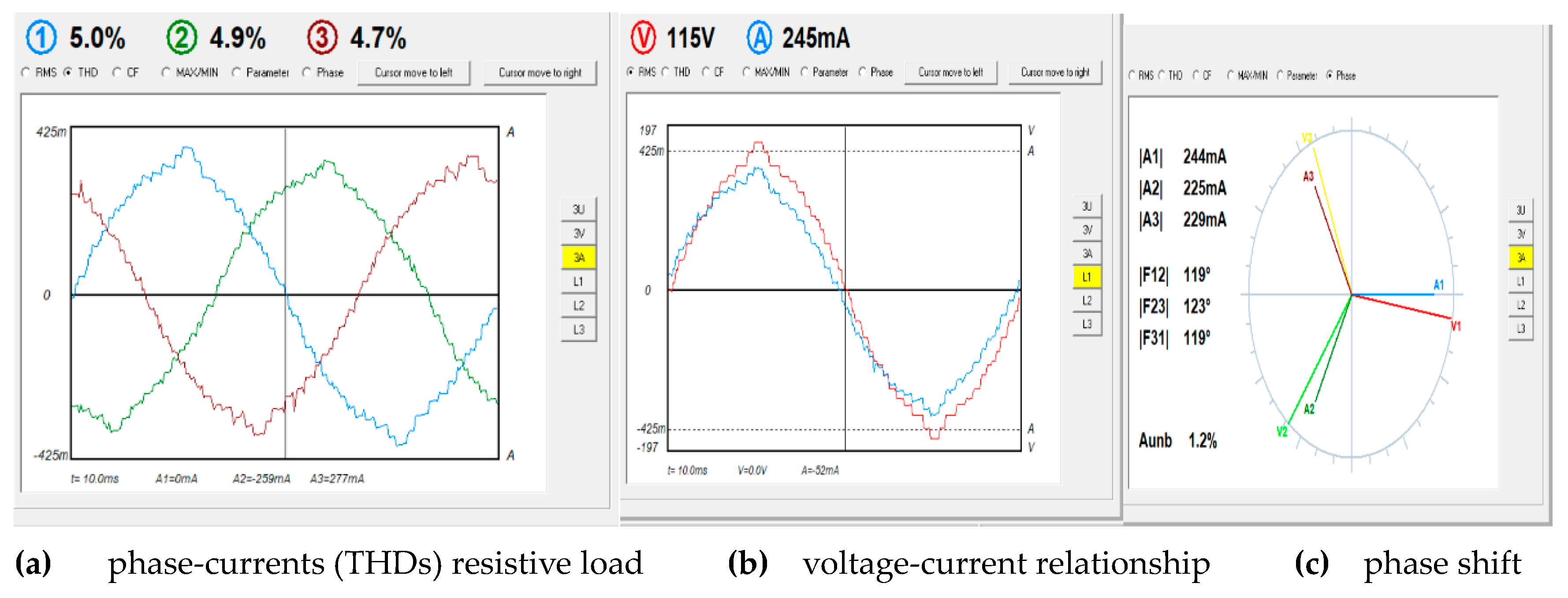
The three-phase currents shown in Figure 20a shows average THDs value below 5% which is compatible with their respective voltages. The relation between phase-voltage and current in phase A supply is shown in Figure 20b. Other phases respond in very similar characteristics. Figure 20c shows the phase difference between the three-phase currents. Although the load is resistive, there is a small value of phase difference between voltages and currents, and this is normal in practical work. The unbalance is recorded as 1.2% which is considered as low value.

A three-phase squirrel- motor is used in the dynamic load test. The motor has the following specifications:

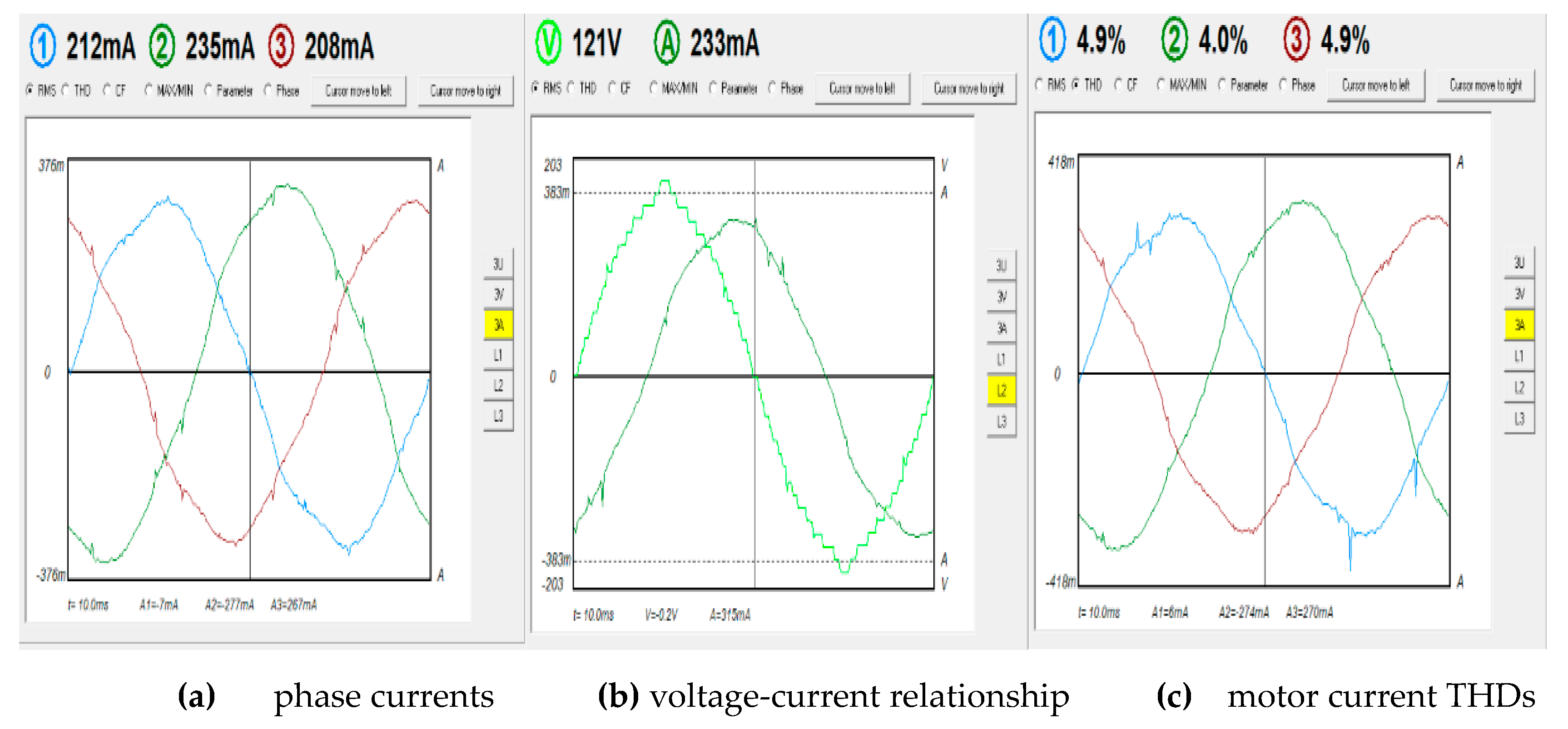
Three-phase induction motor (SIEMENS) 220/380 Δ/Ү, 0.18 kW, 1315 rpm, 50Hz. When the motor is at no load, the 31-level MLI supplies a relatively small three-phase current of about 0.25A per phase as shown in Figure 21a. The relation between phase voltage and current in phase B is shown in Figure 21b. The current lags the voltage since as the load is now inductive. The recorded THDs are less than 5% and shown in in Figure 21c.

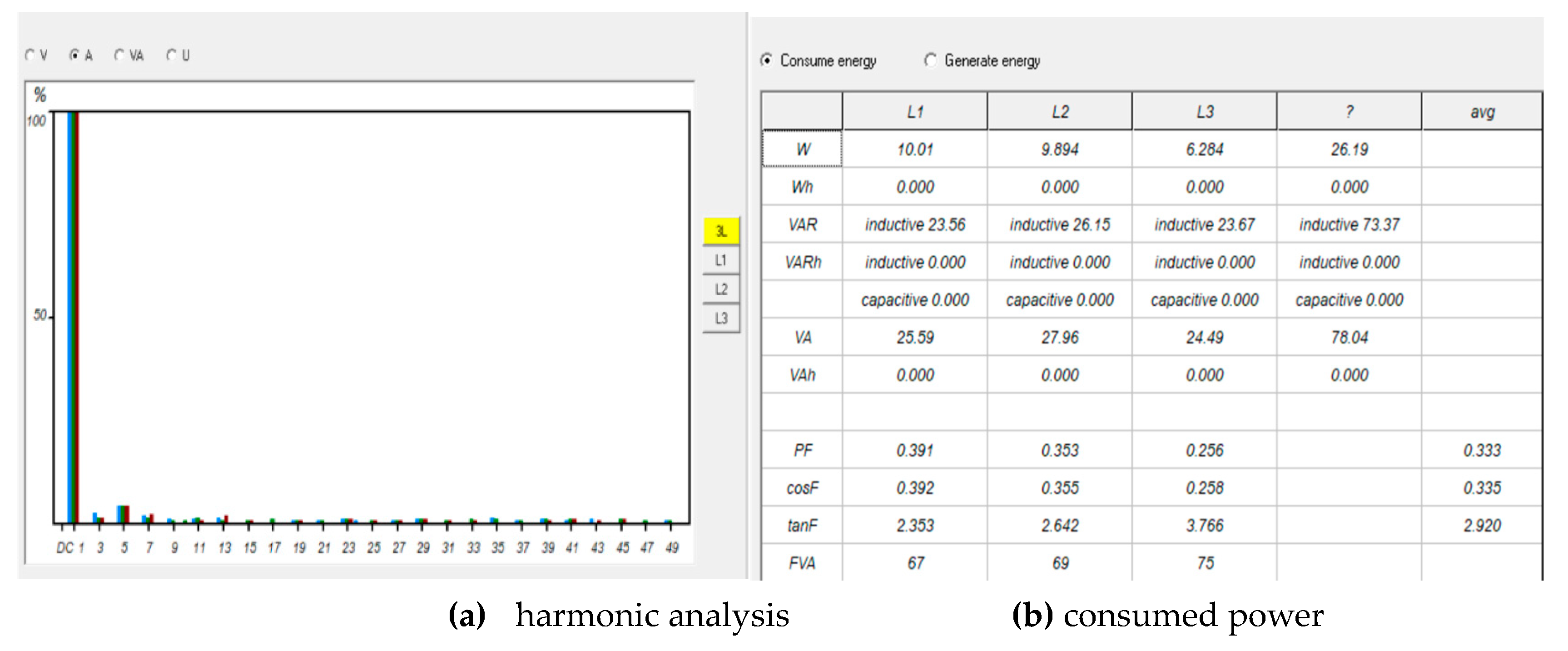
The harmonic analysis is shown in Figure 22a where most of the triple harmonics were either eliminated or at low values. The power consumed by the motor in Figure 22b clearly shows the effect of the inductive load in the total VAR power.

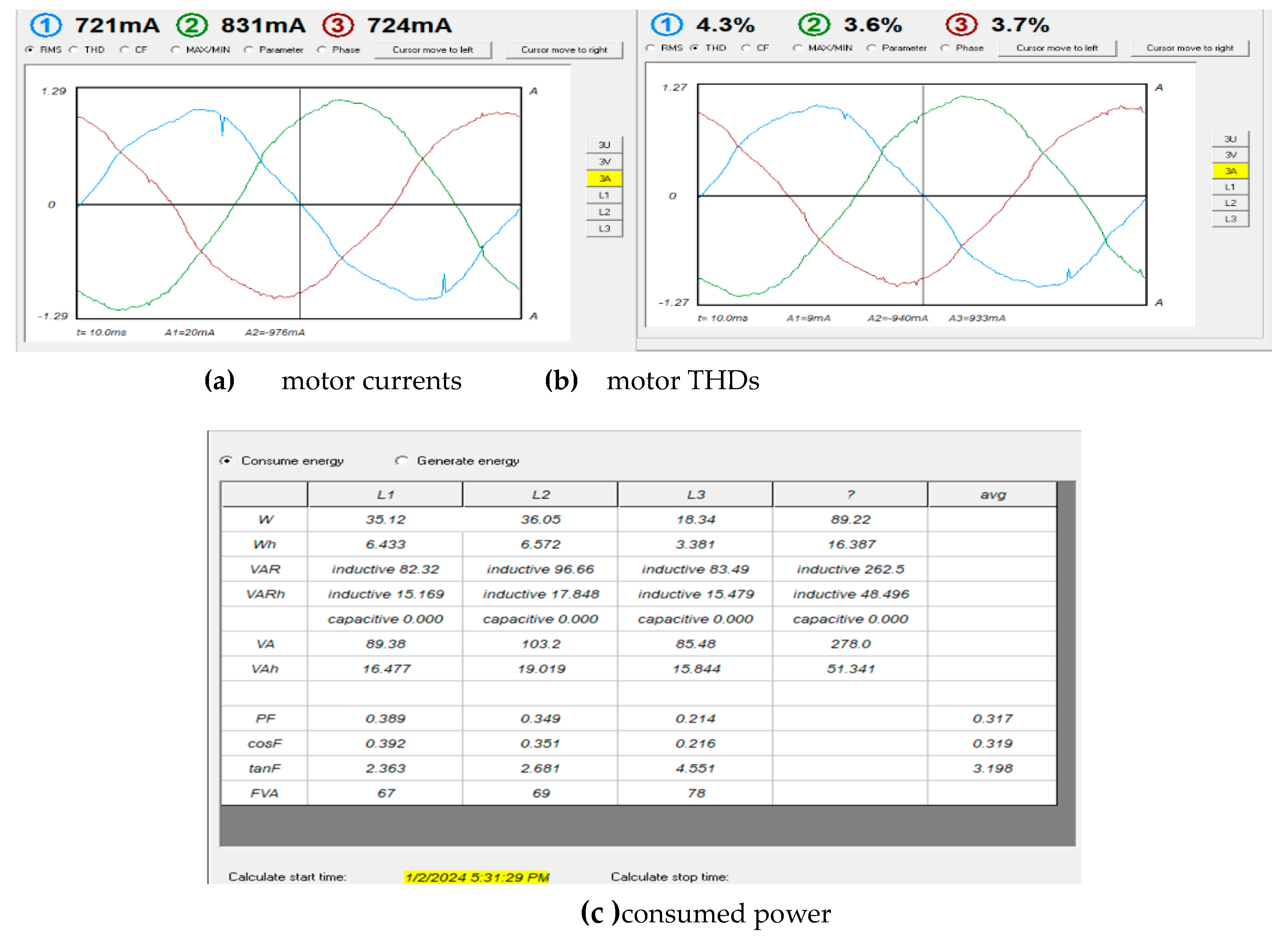
The motor is later subjected to fan load. As can be observed, the 31-level MLI supplies current about 0.75A per phase more to the motor to compensate for the applied load torque as shown in Figure 23a. The THDs is still low, averaging about 3.8% as shown in Figure 23b. The power consumed by the motor at load is shown in Figure 23c.

5. Conclusion

A three-phase, 31- level MLI has been designed, modeled, and experimentally tested as described in this paper. The genetic algorithm and gray wolf optimization algorithms are used to solve the trigonometric equations resulting from Fourier analysis of the inverter voltages for the purpose of finding the ideal angles to cancel many triple harmonics. The optimal angles are then chosen from among the ideal angles between the two algorithms by curve fitting. The inverter is loaded with a resistive load and a three-phase induction motor. It was observed that the THD values do not exceed 5% for all operating conditions for phase and line voltages as well as for load currents. Frequency analysis showed that many triple harmonics have been eliminated. The simulation of the three-phase MLI system is investigated in MATLAB Simulink model, and the simulation results are in good agreement with the practical results. This indicates that the 31-level MLI system can potentially become an efficient and reliable three-phase inverter supply for various static and dynamic loads.

6. Future suggestions

The THD value has a fundamental impact on the efficiency and utility of the inverter. There are two main factors that significantly reduce the amount of FAD. First, use optimal values for the operating angles of the power switches. This is done by choosing the best angles from a group of algorithms more than the algorithms used in this research. Secondly, reducing the number of switches used by deriving a topology that ensures smooth paths of current while at the same time obtaining a larger number of inverter levels and a contributing to reducing the number of DC sources needed by the inverter.

References

K.T. Maheswari, R. Bharanikumar, V. Arjun, R. Amrish, M. Bhuvanesh, “A comprehensive review on cascaded H-bridge multilevel inverter for medium voltage high power applications”, Materials Today: Proceedings, Volume 45, Part 2,2021, Pages 2666-2670, ISSN 2214-7853. [CrossRef]
L. Xing, Q. Wei and Y. Li, "A Practical Current Source Inverter-Based High-Power Medium-Voltage PV System," in IEEE Transactions on Power Electronics, vol. 38, no. 2, pp. 2617-2625, Feb. 2023. [CrossRef]
Ramesh, Adireddy & Sekhar, Obbu & Kumar, M. (2018). “A Novel Three Phase Multilevel Inverter with Single Dc Link for Induction Motor Drive Applications”. International Journal of Electrical and Computer Engineering. 81. 763-770. [CrossRef]
first_page.
settings.
$Order Article Reprints$ .
Usha Sengamalai, Geetha Anbazhagan, T. M. Thamizh Thentral, Pradeep Vishnuram “Three Phase Induction Motor Drive: A Systematic Review on Dynamic Modelling, Parameter Estimation and control schemes ”, Energies 2022, 15(21), 8260. [CrossRef]
K. Durgalakshmi, P. Anbarasu, V. Karpagam, A. Venkatesh, B. Kannapiran and V. Sharma, "Utilization of Reduced Switch Components with Different Topologies In Multi-Level Inverter For Renewable Energy Applications-A Detailed Review," 2022 5th International Conference on Contemporary Computing and Informatics (IC3I), Uttar Pradesh, India, 2022, pp. 913-920. [CrossRef]
Bughneda, A.; Salem, M.; Richelli, A.; Ishak, D.; Alatai, S. Review of Multilevel Inverters for PV Energy System Applications. Energies 2021, 14, 1585. [Google Scholar] [CrossRef]
Peeyush Kala, Sudha Arora, “A comprehensive study of classical and hybrid multilevel inverter topologies for renewable energy applications”. Renewable and Sustainable Energy Reviews 2017, 76, 905–931. [CrossRef]
Poorfakhraei, M. Narimani and A. Emadi, "A Review of Multilevel Inverter Topologies in Electric Vehicles: Current Status and Future Trends," in IEEE Open Journal of Power Electronics, vol. 2, pp. 155-170, 2021. [CrossRef]
Srinivasan, G.K.; Rivera, M.; Loganathan, V.; Ravikumar, D.; Mohan, B. “Trends and Challenges in Multi-Level Inverter with Reduced Switches”. Electronics 2021, 10, 368. [Google Scholar] [CrossRef]
H. P. Vemuganti, D. Sreenivasarao, S. K. Ganjikunta, H. M. Suryawanshi and H. Abu-Rub, "A Survey on Reduced Switch Count Multilevel Inverters," in IEEE Open Journal of the Industrial Electronics Society, vol. 2, pp. 80-111, 2021. [CrossRef]
M. D. Siddique, A. Iqbal, M. A. Memon and S. Mekhilef, "A New Configurable Topology for Multilevel Inverter with Reduced Switching Components," in IEEE Access, vol. 8, pp. 188726-188741, 2020. [CrossRef]
Rakan Khalil Antar, Taha Ahmed Hussein, Abdallah Mohamed Abdullah “Design and implementation of reduced number of switches for new multilevel inverter topology without zero-level state”, international journal of power electronics and drive systems (IJPEDS), Vol 13, No. 1, March 2022, pp. 401-410. [CrossRef]
T. A. Hussein and D. Ishak, "Three-phase MLI with Reduced Number of Switches and Hybrid Optimized Switching," 2023 International Conference on Energy, Power, Environment, Control, and Computing (ICEPECC), Gujrat, Pakistan, 2023, pp. 1-6. [CrossRef]
Sardar, M.U.; Vaimann, T.; Kütt, L.; Kallaste, A.; Asad, B.; Akbar, S.; Kudelina, K. Inverter-Fed Motor Drive System: A Systematic Analysis of Condition Monitoring and Practical Diagnostic Techniques. Energies 2023, 16, 5628. [Google Scholar] [CrossRef]
Katoch, S., Chauhan, S.S. & Kumar, V. A review on genetic algorithm: past, present, and future. Multimed Tools Appl 80, 8091–8126 (2021). [CrossRef]
Lambora, K. Gupta and K. Chopra, "Genetic Algorithm- A Literature Review," 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 2019, pp. 380-384. [CrossRef]
Mohammad H. Nadimi-Shahraki, Shokooh Taghian, Seyedali Mirjalili, “An improved grey wolf optimizer for solving engineering problems”,Expert Systems with Applications”,Volume 166, 2021. [CrossRef]
Bansal, J.C., Singh, S. “A better exploration strategy in Grey Wolf Optimizer”. J Ambient Intell Human Comput 12, 1099–1118 (2021). [CrossRef]
Mohmmad H. Rashid “ Power Electronics , Devices, Circuits and Applications”, Published by Pearson Education Limited , 2014.
Almomani, O. A Feature Selection Model for Network Intrusion Detection System Based on PSO, GWO, FFA and GA Algorithms. Symmetry 2020, 12, 1046. [Google Scholar] [CrossRef]

Figure 1. Proposed topology for the three-phase 31-level MLI.

Figure 2. Five level Inverter and its timing instants.

Figure 3. Three-phase 31- MLI Simulink model with squirrel cage motor load.

Figure 4. Fabrication of gating periods for Phase A.

Figure 5. Phase voltages from simulation.

Figure 6. Line voltages from simulation.

Figure 7. Squirrel cage motor currents.

Figure 8. Phase shift between voltages and currents.

Figure 9. Motor measurments at different loads.

Figure 10. Power consumed by the load.

Figure 11. Phase voltage.

Figure 12. Line voltage harmonics.

Figure 13. Current Harmonics.

Figure 14. (a) Experemental set up for the implementation of the proposed three-phase 31-level MLI. (b) Spartan 3E simulated pulses for IGBTs.

Figure 15. Gating pulses for IGBTs in phase A and the phase shift between phases.

Figure 16. Phase and line voltages of the proposed three-phase 31-level MLI at noload.

Figure 17. The three-phase voltages , THDs and phase shifts at no load.

Figure 18. Line voltages , THDs and phase shift at no load.

Figure 19. phase and line voltages THDs and consumed power for resistive load.

Figure 20. phase currents result for resistive load.

Figure 21. Motor currents at no-load.

Figure 22. Motor currents harmonics and consumed power at noload.

Figure 23. Motor currents , THDs and consumed power at load.

Table 1. Switching angles for 31 levels inverter.

Angle	$α_{1}$	$α_{2}$	$α_{3}$	$α_{4}$	$α_{5}$	$α_{6}$	$α_{7}$	$α_{8}$	$α_{9}$	$α_{10}$	$α_{11}$	$α_{12}$	$α_{13}$	$α_{14}$	$α_{15}$
GA	3.3	6.1	13.1	16.7	23.1	27.2	33.5	38.7	45.5	52.2	58.5	66.2	74.7	83.8	85
GWO	1.2	11.8	23.3	32.2	42.2	50.6	58.9	67.4	71.2	79.6	80.4	85.1	85.9	86	86
Optimum	2.4	5.21	8.42	14.2	16.3	22.6	27.4	31.6	37.1	42.9	50.5	58.4	67.4	78.6	85

Table 2. Switches states for the positive half period.

T1 T2*	T3 T4*	T5 T6*	T7 T8*	T9 T10*	Level	Duration	Shift
1	1	1	1	1	0	$α_{1}$	0
0	1	1	1	1	1	$α_{2} - α_{1}$	$α_{1}$
1	1	0	1	1	2	$α_{3} - α_{2}$	$α_{2}$
0	1	0	1	1	3	$α_{4} - α_{3}$	$α_{3}$
1	0	1	1	1	4	$α_{5} - α_{4}$	$α_{4}$
0	0	1	1	1	5	$α_{6} - α_{5}$	$α_{5}$
1	0	0	1	1	6	$α_{7} - α_{6}$	$α_{6}$
0	0	0	1	1	7	$α_{8} - α_{7}$	$α_{7}$
1	1	1	0	1	8	$α_{9} - α_{8}$	$α_{8}$
0	1	1	0	1	9	$α_{10} - α_{9}$	$α_{9}$
1	1	0	0	1	10	$α_{11} - α_{10}$	$α_{10}$
0	1	0	0	1	11	$α_{12} - α_{11}$	$α_{11}$
1	0	1	0	1	12	$α_{13} - α_{12}$	$α_{12}$
0	0	1	0	1	13	$α_{14} - α_{13}$	$α_{13}$
1	0	0	0	1	14	$α_{15} - α_{14}$	$α_{14}$
0	0	0	0	1	15	$π - 2 α_{15}$	$α_{15}$
1	0	0	0	1	14	$α_{15} - α_{14}$	$π - α_{15}$
0	0	1	0	1	13	$α_{14} - α_{13}$	$π - α_{14}$
1	0	1	0	1	12	$α_{13} - α_{12}$	$π - α_{13}$
0	1	0	0	1	11	$α_{12} - α_{11}$	$π - α_{12}$
1	1	0	0	1	10	$α_{11} - α_{10}$	$π - α_{11}$
0	1	1	0	1	9	$α_{10} - α_{9}$	$π - α_{10}$
1	1	1	0	1	8	$α_{9} - α_{8}$	$π - α_{9}$
0	0	0	1	1	7	$α_{8} - α_{7}$	$π - α_{8}$
1	0	0	1	1	6	$α_{7} - α_{6}$	$π - α_{7}$
0	0	1	1	1	5	$α_{6} - α_{5}$	$π - α_{6}$
1	0	1	1	1	4	$α_{5} - α_{4}$	$π - α_{5}$
0	1	0	1	1	3	$α_{4} - α_{3}$	$π - α_{4}$
1	1	0	1	1	2	$α_{3} - α_{2}$	$π - α_{3}$
0	1	1	1	1	1	$α_{2} - α_{1}$	$π - α_{2}$
1	1	1	1	1	0	$α_{1}$	$π - α_{1}$

Table 3. Corresponding pulses count of Spartan 3E clock for the 15 angles .

$α_{1}$ ₌6778	$α_{2}$ =14472	$α_{3}$ =23389	$α_{4}$ =39472	$α_{5}$ =45445	$α_{6}$ =62889	$α_{7}$ =76278	$α_{8}$ =87917
$α_{9}$ =103056	$α_{10}$ =119222	$α_{11}$ =140361	$α_{12}$ =162278	$α_{13}$ =187389	$α_{14}$ =218445	$α_{15}$ =236111

Table 4. shows IGBTs states for the positive half- cycle for phase A.

	T1	T3	T5	T7	T9	Duration
	T2*	T4*	T6*	T8*	T10*		PHASE A
1	1	1	1	1	1	$α_{1}$	0→6778
2	0	1	1	1	1	$α_{2} - α_{1}$	6779 → 14472
3	1	1	0	1	1	$α_{3} - α_{2}$	14473→ 23389
4	0	1	0	1	1	$α_{4} - α_{3}$	23390 → 39472
5	1	0	1	1	1	$α_{5} - α_{4}$	39473 → 45445
6	0	0	1	1	1	$α_{6} - α_{5}$	45446 → 62889
7	1	0	0	1	1	$α_{7} - α_{6}$	62890 → 76278
8	0	0	0	1	1	$α_{8} - α_{7}$	76279 → 87917
9	1	1	1	0	1	$α_{9} - α_{8}$	87918 → 103056
10	0	1	1	0	1	$α_{10} - α_{9}$	103057 → 119222
11	1	1	0	0	1	$α_{11} - α_{10}$	119223 → 140361
12	0	1	0	0	1	$α_{12} - α_{11}$	140362 → 162278
13	1	0	1	0	1	$α_{13} - α_{12}$	162279 → 187389
14	0	0	1	0	1	$α_{14} - α_{13}$	187390 → 218445
15	1	0	0	0	1	$α_{15} - α_{14}$	218446 → 236111
16	0	0	0	0	1	$π - 2 α_{15}$	236112 → 263890
17	1	0	0	0	1	$α_{15} - α_{14}$	263891 → 281557
18	0	0	1	0	1	$α_{14} - α_{13}$	281558 → 312613
19	1	0	1	0	1	$α_{13} - α_{12}$	312,614 →337725
20	0	1	0	0	1	$α_{12} - α_{11}$	337726 → 359643
21	1	1	0	0	1	$α_{11} - α_{10}$	359644 → 380783
22	0	1	1	0	1	$α_{10} - α_{9}$	380784 → 396950
23	1	1	1	0	1	$α_{9} - α_{8}$	396951 → 412089
24	0	0	0	1	1	$α_{8} - α_{7}$	412090 → 423729
25	1	0	0	1	1	$α_{7} - α_{6}$	423730 → 437120
26	0	0	1	1	1	$α_{6} - α_{5}$	437121 → 454564
27	1	0	1	1	1	$α_{5} - α_{4}$	454565 → 460538
28	0	1	0	1	1	$α_{4} - α_{3}$	460539 → 476622
29	1	1	0	1	1	$α_{3} - α_{2}$	476623 → 485540
30	0	1	1	1	1	$α_{2} - α_{1}$	485541 → 493235
31	1	1	1	1	1	$α_{1}$	493236 → 500000

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer