Fixed-Time Aperiodic Intermittent Control for Quasi-bipartite Synchronization of Competitive Neural Networks

1. Introduction

Since neural networks are widely used in computer science [1], remote sensing [2], autonomous control systems [3], and other fields, their dynamic behaviors have been extensively studied over the past several decades. It is worth noting that neural networks (NNs) only consider the dynamic level of neural activity. However, it is essential to recognize that synaptic weights between neurons change over time [4]. Consequently, $Meyer-b\ddot{a}se$ et al. [5] developed competitive neural networks (CNNs) with different time scales in 1996, which can be viewed as an extension of Hopfield neural networks and cellular networks [6,7]. CNNs are defined using two types of state variables: short-term memory (STM) describes the rapid neural activity, while long-term memory (LTM) depicts the slow, unsupervised synaptic modifications. On the other hand, coupled competitive neural networks(CCNNs) consist of several interconnected subsystems, and due to their complex dynamic behavior, they have garnered significant attention [8,9].

The activation functions of NNs are widely recognized for describing the connection between the input and output of a single neuron. They are commonly considered to be continuous. When the activation function is believed to be at the high gain limit, however, the activation function approaches discontinuity. As a result, an increasing number of scholars have been conducting considerable research on NNs with discontinuous activation functions [10,11,12,13]. On the other hand, the dynamic behaviors of NNs are frequently impacted by external disturbances, such as changs in network structure, hardware facilities and environmental noise. As far as we are aware, there are few studies take both discontinuous activation functions and external disturbances into account when discussing CCNNs. Therefore, it is both intriguing and challenging to research discontinuous activation functions and external disturbances in CCNNs.

Synchronization means that two or more dynamical systems adjust themselves to exhibit a common dynamical behavior. The synchronization problem of NNs has garnered significant attention recently due to its wide applicability in communication systems, biological sciences, mechanical engineering and other domains [14,15,16,17]. However, the synchronization of the aforementioned NNs only considers the cooperative relationships between network nodes. In many practical systems, relationships of competition and cooperation coexist. Therefore, the synchronization issue of NNs with both competitive and cooperative connections between nodes, known as bipartite synchronization, is of crucial importance and has been researched in [18,19]. On the other hand, due to inherent network constraints, complete synchronization may not be achievable, and instead, quasi-synchronization is observed. Quasi-synchronization implies that the synchronization error no longer approaches zero but rather converges to a bounded set. To our knowledge, few papers have addressed the quasi-bipartite synchronization problem of CCNNs.

In addition to asymptotic synchronization or exponential synchronization, finite-time (FET) synchronization has gained widespread attention as a more practical form of network synchronization in recent years. In FET synchronization, the synchronization time is bounded, but it is dependent on the initial state of the node. To eliminate this dependence on the initial state, fixed-time synchronization is proposed based on the fixed-time (FXT) stability [20], and its synchronization time only depends on the system or control parameters. Compared with the rich results of NNs [21,22], it is extremely scarce at present to explore the FXT synchronization of CCNNs. In [23], authors studied the FET bipartite synchronization of delayed CCNNs under quantized control. Whereas, to our knowledge, there are limited reports on FXT quasi-bipartite synchronization of CCNNs, and further research is needed.

Over the past few decades, the control problem of networks has been one of the most widely studied topics, and many useful control methods have been developed, such as adaptive control, sliding mode control, impulse control, and intermittent control, among others. Intermittent control involves alternating periods of applying control input and periods of no control input, making it a more economical choice compared to continuous control schemes. Hence, the intermittent control strategy has received extensive attention [24,25,26,27]. In [28], the FXT synchronization problem of time-delay complex networks under intermittent pinning control is studied. The author in [29] solved the FXT and predefined-time cluster lag synchronization of stochastic multi-weighted complex networks via intermittent quantized control. To our knowledge, there is currently no existing literature that addresses the challenging problem of FXT quasi-bipartite synchronization of CCNNs under intermittent control.

Motivated by the analysis provided above, the primary objective of this paper is to investigate FXT quasi-bipartite synchronization in coupled competitive neural networks. Firstly, the model under consideration incorporates time-varying delays, discontinuous activation functions, and external disturbances simultaneously, rendering it more comprehensive. Secondly, we introduce an innovative FXT aperiodic intermittent control scheme, making the pioneering endeavor to explore quasi-bipartite synchronization in CCNNs. Furthermore, some robust criterion are established for FXT quasi-bipartite synchronization based on the theory of practical FXT stability. Finally, we provide estimations for error bounds and settling times.

Below are shown the remaining contents. Section 2 gives some necessary preliminary knowledge and model description. Section 3 introduces the main theoretical conclusions. Section 4 provides numerical examples to validate the theoretical conclusions. Section 5 finishes our study and discusses future research.

Notations: R represents the set of real numbers. The n-dimensional Euclidean space is represented by the $R^n$. $R^{n\times m}$ is the set of $n\times m$ real matrices. ${\mathcal{N}}_{+}=\{1,2,...,N\}$. $I_n$ is identity matrix. ${\mathbf{0}}_n$ denotes zero matrix. $\left|P\right|=\left(\right|p_{ij}{\left|\right)}_{n\times n}$. For a symmetric matrix B, ${\lambda }_{max}\left(B\right)$ represents the maximum eigenvalue of matrix B. $diag(·)$ represents the diagonal matrix. ${\mathbf{1}}_n$ denotes that all elements of a column vector are 1. For any $p={(p_1,...,p_n)}^T\in R^n$, $sgn\left(p\right)=diag(sign\left(p_1\right),...,sign\left(p_n\right))$, $sign(·)$ represents the $sign$ function. $Sign\left(D\right)={\left(sign\left(d_{ij}\right)\right)}_{n\times n}$. The 2-norm of the vector p is denoted by ${\parallel p\parallel }_2$. For vector $\mathbf{w}>0$$(<,\ge ,\le )$, all of the components of $\mathbf{w}$ are positive (negative, non-negative, non-positive). For vectors ${\mathbf{q}}_1$ and ${\mathbf{q}}_2$, ${\mathbf{q}}_1<{\mathbf{q}}_2$$({\mathbf{q}}_1\le {\mathbf{q}}_2)$ implies ${\mathbf{q}}_1-{\mathbf{q}}_2<0$$({\mathbf{q}}_1-{\mathbf{q}}_2\le 0)$. Notation ⊗ denotes Kronecker product. $k>0$, $\mathcal{C}([-k,0],R^n)$ denotes the set of continuous function from $[-k,0]$ to $R^n$.

2. Model description and preliminaries

Consider the following competitive neural networks with time-varying delay:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill \epsilon {\dot{z}}_k\left(t\right)=& -c_k{z}_k\left(t\right)+\sum _{q=1}^n{a}_{kq}{f}_q\left(z_q\left(t\right)\right)+\sum _{q=1}^n{b}_{kq}{f}_q\left(z_q(t-\tau \left(t\right))\right)\hfill \\ \hfill & +E_k\sum _{l=1}^p{\omega }_l{m}_{kl}\left(t\right),k=1,...,n,\hfill \\ \hfill {\dot{m}}_{kl}\left(t\right)=& -{\overline{c}}_k{m}_{kl}\left(t\right)+{\overline{a}}_k{\omega }_l{f}_k\left(z_k\left(t\right)\right),l=1,...,p,\hfill \end{array}\hfill \end{array}\right.$$

(1)

where $z_k\left(t\right)$ is the state variable. $m_{kl}\left(t\right)$ represents synaptic efficiency. $c_k>0$ represents the self-feedback coefficient. Connection weights and delay connection weights, respectively, are represented by $a_{kq}$ and $b_{kq}$. $f_q(·)$ is the output of neuron which is discontinuous. ${\omega }_l$ is the weight of an external stimulus. ${\overline{c}}_k$ and ${\overline{a}}_k$ are given constants. $E_k$ is the intensity of the external stimulus. $\epsilon$ is the time scale of $STM$. Where $\tau$ is a known constant, $\tau \left(t\right)$ is the time-varying delay that satisfies $0\le \tau \left(t\right)\le \tau$.

Let $s\left(t\right)={\left(s_1\left(t\right),...,s_n\left(t\right)\right)}^T$, $s_k\left(t\right)={\sum }_{l=1}^p{\omega }_l{m}_{kl}\left(t\right)$ and $\omega ={({\omega }_1,...,{\omega }_p)}^T$. Without losing generality, suppose ${\parallel \omega \parallel }_2^2=1$, then network (1) can be written as

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill \dot{z}\left(t\right)=& -Cz\left(t\right)+Af\left(z\right(t\left)\right)+Bf\left(z\right(t-\tau \left(t\right)\left)\right)+Es\left(t\right),\hfill \\ \hfill \dot{s}\left(t\right)=& -\overline{C}s\left(t\right)+\overline{A}f\left(z\left(t\right)\right),\hfill \end{array}\hfill \end{array}\right.$$

(2)

where $z\left(t\right)={\left(z_1\left(t\right),...,z_n\left(t\right)\right)}^T$, $f\left(z\left(t\right)\right)={\left(f_1\left(z_1\left(t\right)\right),...,f_n\left(z_n\left(t\right)\right)\right)}^T$, ${\displaystyle A=(\frac{a_{kq}}{\epsilon }{)}_{n\times n}}$, ${\displaystyle B=(\frac{b_{kq}}{\epsilon }{)}_{n\times n}}$, ${\displaystyle C=diag\left(\frac{c_1}{\epsilon },...,\frac{c_n}{\epsilon }\right)}$, $\overline{C}=diag({\overline{c}}_1,...,{\overline{c}}_n)$, $\overline{A}=diag({\overline{a}}_1,...,{\overline{a}}_n)$, ${\displaystyle E=diag(\frac{E_1}{\epsilon },...,}$

${\displaystyle \frac{E_n}{\epsilon })}$. The initial value of system (2) is given by $z\left(t\right)={\varphi }_z\left(t\right)\in \mathcal{C}([-\tau ,0],R^n)$ and $s\left(t\right)={\varphi }_s\left(t\right)\in \mathcal{C}([-\tau ,0],R^n)$.

A class of CCNNs with external disturbances are modeled as follows:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill {\dot{Z}}_i\left(t\right)=& -C{Z}_i\left(t\right)+Af\left(Z_i\left(t\right)\right)+Bf\left(Z_i(t-\tau \left(t\right))\right)+E{S}_i\left(t\right)\hfill \\ \hfill & +\sum _{j=1}^N\left|d_{ij}\right|\left(sign\left(d_{ij}\right)Z_j\left(t\right)-Z_i\left(t\right)\right)+R_i\left(t\right)+{\Xi }_i\left(t\right),\hfill \\ \hfill {\dot{S}}_i\left(t\right)=& -\overline{C}{S}_i\left(t\right)+\overline{A}f\left(Z_i\left(t\right)\right)+\sum _{j=1}^N\left|u_{ij}\right|\left(sign\left(u_{ij}\right)S_j\left(t\right)-S_i\left(t\right)\right)\hfill \\ \hfill & +{\overline{R}}_i\left(t\right)+{\Xi }_i\left(t\right),i\in {\mathcal{N}}_{+},\hfill \end{array}\hfill \end{array}\right.$$

(3)

where $Z_i\left(t\right)={\left(Z_{i1}\left(t\right),...,Z_{in}\left(t\right)\right)}^T\in R^n$ and $S_i\left(t\right)={\left(S_{i1}\left(t\right),...,S_{in}\left(t\right)\right)}^T\in R^n$ are the state variables of $STM$ and $LTM$, respectively; ${\Xi }_i\left(t\right)={\left({\Xi }_{i1}\left(t\right),...,{\Xi }_{in}\left(t\right)\right)}^T$ indicates the external disturbance vector. $D=\left(d_{ij}\right)$ and $U=\left(u_{ij}\right)\in R^{N\times N}$ are the adjacency matrix associated with the signed graph $G\left(D\right)$ and $G\left(U\right)$ of the CCNNs, satisfying $d_{ii}=0$$\left(u_{ii}=0\right)$ for $i\in {\mathcal{N}}_{+}$; for $i\ne j$, $d_{ij}\ne 0$$\left(u_{ij}\ne 0\right)$ if there is a directed communication link from node j to node i, otherwise $d_{ij}=0$$\left(u_{ij}=0\right)$. $R_i\left(t\right)$ and ${\overline{R}}_i\left(t\right)$ are controllers to be designed. The initial conditions of network (3) meet: $Z_i\left(t\right)={\phi }_i\left(t\right)\in \mathcal{C}([-\tau ,0],R^n)$ and $S_i\left(t\right)={\overline{\phi }}_i\left(t\right)\in \mathcal{C}([-\tau ,0],R^n)$.

Remark 1. 

When $d_{ij}>0$$\left(u_{ij}>0\right)$, then the connection between nodes i and j is cooperative, the coupling term is given as $d_{ij}\left(Z_j\left(t\right)-Z_i\left(t\right)\right)$$\left(u_{ij}\left(S_j\left(t\right)-S_i\left(t\right)\right)\right)$. When $d_{ij}<0$$\left(u_{ij}<0\right)$, the connection between nodes i and j is competitive, the coupling term is presented as $-d_{ij}\left(Z_j\left(t\right)+Z_i\left(t\right)\right)$$\left(-u_{ij}\left(S_j\left(t\right)+S_i\left(t\right)\right)\right)$.

For the convenience of discussion, define ${\mathbf{x}}_i\left(t\right)=\left(Z_i^T\left(t\right),S_i^T\left(t\right)\right)$, $A_1={\left(A^T,{\overline{A}}^T\right)}^T$, $B_1={\left(B^T,{\mathbf{0}}_n\right)}^T$, $W_i\left(t\right)={\left({\Xi }_i^T\left(t\right),{\Xi }_i^T\left(t\right)\right)}^T$, $K_i\left(t\right)={\left(R_i^T\left(t\right),{\overline{R}}_i^T\left(t\right)\right)}^T$, $\mathbf{I}=\left(I_n,{\mathbf{0}}_n\right)$, $C_1=\left[\begin{array}{ccc}C& & -E\\ 0_n& & \overline{C}\end{array}\right]$, ${\mathbf{d}}_{ij}=\left[\begin{array}{ccc}{d}_{ij}& & 0\\ 0& & u_{ij}\end{array}\right]\otimes I_n$ and $D_1={\left({\mathbf{d}}_{ij}\right)}_{2nN\times 2nN}$.

Therefore, the coupled competitive neural networks (3) become:

$$\begin{array}{cc}\hfill {\dot{\mathbf{x}}}_i\left(t\right)=& -C_1{\mathbf{x}}_i\left(t\right)+A_{1}f\left(\mathbf{I}{\mathbf{x}}_i\left(t\right)\right)+B_{1}f\left(\mathbf{I}{\mathbf{x}}_i(t-\tau \left(t\right))\right)+K_i\left(t\right)\hfill \\ \hfill & +\sum _{j=1}^N\left|{\mathbf{d}}_{ij}\right|\left[Sign\left({\mathbf{d}}_{ij}\right){\mathbf{x}}_j\left(t\right)-{\mathbf{x}}_i\left(t\right)\right]+W_i\left(t\right).\hfill \end{array}$$

(4)

From (2), the tracking target can be described as follows:

$$\dot{\mathbf{y}}\left(t\right)=-C_1\mathbf{y}\left(t\right)+A_{1}f\left(\mathbf{I}\mathbf{y}\left(t\right)\right)+B_{1}f\left(\mathbf{I}\mathbf{y}(t-\tau \left(t\right))\right),$$

(5)

where $\mathbf{y}\left(t\right)={\left(z^T\left(t\right),s^T\left(t\right)\right)}^T$ is the state vector.

The necessary definitions, lemmas and assumptions are given below.

Definition 1 

([33]). Considering a system with discontinuous right-hand sides in the form of

$$\dot{\zeta }\left(t\right)=F\left(\zeta \left(t\right)\right),\zeta \left(0\right)=0,$$

where $\zeta \in R^n$, $F\left(\zeta \right):R^n\to R^n$ is locally bounded and Lebesgue measurable. The function $\zeta \left(t\right)$ is said to be the solution in Filippov sense which defined in the interval $[0,t_{*}),t_{*}\in [0,+\infty )$, if $\zeta \left(t\right)$ is absolutely continuous and satisfies the below differential inclusion

$$\dot{\zeta }\left(t\right)\in K\left[F\right]\left(\zeta \left(t\right)\right),a.e.t\in [0,t_{*}),$$

where the set-valued map $K\left[F\right]:R^n\to R^n$ is defined as

$$K\left[F\right]\left(\zeta \left(t\right)\right)\triangleq \bigcap _{\delta >0}\bigcap _{\mu \left(\Omega \right)>0}\overline{co}\{F(B(\zeta \left(t\right),\delta )\setminus \Omega \},$$

where $\overline{co}$ stands for the convex closure, $\mu \left(\Omega \right)$ is the Lebesgue measure of the set Ω, $B\left(\zeta \right(t),\delta )$ denotes the open ball centered at $\zeta \left(t\right)$ with radius δ.

Definition 2. 

The network (4) is said to achieve FXT quasi-bipartite synchronization with network (5) if there is a constant $T_1>0$, such that

$$\left\{\begin{array}{c}\underset{t\to T_1}{lim}{\parallel {\mathbf{x}}_i\left(t\right)-w_i\mathbf{y}\left(t\right)\parallel }_2\le \theta ,\hfill \\ \parallel {\mathbf{x}}_i\left(t\right)-w_i{\mathbf{y}\left(t\right)\parallel }_2\le \theta ,\forall t\ge T_1,i\in {\mathcal{N}}_{+},\hfill \end{array}\right.$$

(6)

where θ is a nonnegative constant.

Definition 3 

([34]). Aperiodically intermittent control is said to have an average control rate $\gamma \in (0,1)$, if there is $T_{\gamma }\ge 0$ such that

$$T_{con}(t,s)\ge \gamma (t-s)-T_{\gamma },\forall t>s>t_0,$$

where $T_{con}(t,s)$ denotes the total control interval length on $[s,t)$, $T_{\gamma }$ is called the elasticity number.

Lemma 1 

([30]). If $x_i\ge 0,i=1,...,n$, $0<\xi \le 1$ and $\eta >1$, then

$$\sum _{i=1}^n{x}_i^{\xi }\ge {\left(\sum _{i=1}^n{x}_i\right)}^{\xi },\sum _{i=1}^n{x_i}^{\eta }\ge n^{1-\eta }{\left(\sum _{i=1}^n{x}_i\right)}^{\eta }.$$

Lemma 2 

([35]). For any $x,y\in R^n$, and positive-definite matrix $\partial \in R^{n\times n}$, such that

$$2x^{T}y\le x^T\partial x+y^T{\partial }^{-1}y.$$

Lemma 3 

([36]). Assume that there is a Lyapunov function $V\left(t\right)\ge 0$ that satisfies

$$\left\{\begin{array}{c}\dot{V}\left(t\right)\le -a_1{V}^q\left(t\right)-a_2{V}^p\left(t\right)-a_{3}V\left(t\right)+{\wp }_1,t\in [{\zeta }_k,{\mu }_k),\hfill \\ \dot{V}\left(t\right)\le a_{4}V\left(t\right)+{\wp }_2,t\in [{\mu }_k,{\zeta }_{k+1}),\hfill \end{array}\right.$$

(7)

in which $a_1,a_2,a_3,a_4,{\wp }_1,{\wp }_2$ are positive constants and $0<p<1$, $q>1$. It is said system practical fixed time stable if $a_4-\gamma d<0$ and $(1-\gamma )d-a_3<0$, in which $d>0$. And the setting time $T^{*}$ satisfies

$$T^{*}\le \frac{1+a_5(q-1)T_{\gamma }}{a_5(q-1)\gamma }+\frac{1+a_6(1-p)T_{\gamma }}{a_6(1-p)\gamma },$$

where $a_5=a_1(1-\varphi )exp\left\{T_{\gamma }(1-q)d\right\}$, $a_6=a_2(1-\varphi )$ and $0<\varphi <1$. γ and $T_{\gamma }$ are defined in Definition 3. When $t>T^{*}$, there is

$$V\left(t\right)\le max\left\{{\delta }_1,{\delta }_2,{\delta }_3\right\},$$

where ${\delta }_1={\left(\frac{{\displaystyle {\wp }_1}}{{\displaystyle \varphi a_1}}\right)}^{\frac{1}{q}}$, ${\delta }_2={\left(\frac{{\displaystyle {\wp }_1}}{{\displaystyle \varphi a_2}}\right)}^{\frac{1}{p}}$, ${\delta }_3=\frac{{\displaystyle {\wp }_2}}{{\displaystyle d\gamma -a_4}}$.

For each $q=1,...,n$, the following assumptions are introduced:

Assumption 1 

([32]). $f_q(·):R\to R$ is continuous except on a countable set of isolated points $\left\{{\theta }_r^q\right\}$, where both the left limit $f_q^{-}\left({\theta }_r^q\right)$ and right limit $f_q^{+}\left({\theta }_r^q\right)$ exist. In addition, $f_q(·)$ has at most finite discontinuous jump points in each bounded compact set.

Assumption 2 

([32]). There exist positive constants $l_q$ and $h_q$ such that

$$|{\xi }_q-{\varsigma }_q|\le l_q|u-\nu |+h_q,\forall u,\nu \in R,$$

where ${\xi }_q\in K\left[f_q\left(u\right)\right]$, ${\varsigma }_q\in K\left[f_q\left(\nu \right)\right]$ with $K\left[f_q(·)\right]=\overline{co}\left[f_q(·)\right]=[min\left\{f_q^{-}(·),f_q^{+}(·)\right\},max\left\{f_q^{-}(·),f_q^{+}(·)\right\}]$.

Assumption 3 

([23]). The signed graphs are structurally balanced. In other words, the node sets $\mathcal{V}$ of G can be divided into two unsigned subgraphs ${\mathcal{V}}_1$ and ${\mathcal{V}}_2$, respectively. It satisfies $\mathcal{V}={\mathcal{V}}_1\cup {\mathcal{V}}_2$ and ${\mathcal{V}}_1\cap {\mathcal{V}}_2=⌀$. In addition, the links inside each subgraph are nonnegative, while the links between two unsigned subgraphs are negative.

Assumption 4. 

The activation functions $f_q(·)$ satisfies

$$f_q(-z)=-f_q\left(z\right),\forall z\in R.$$

Assumption 5. 

There exists a positive constant $M_q$ such that $|f_q\left(x\right)|\le M_q$.

Assumption 6. 

The external disturbance ${\Xi }_{ik}\left(t\right)(k=1,...,2n)$ is bounded. That is, there is a positive constant $W_k$ such that $|{\Xi }_{ik}\left(t\right)|\le W_k$.

Assumption 3 implies that there exists a diagonal matrix $\omega =diag(w_1,...,w_N)$, where $w_i=1$ if node $v_i\in {\mathcal{V}}_1$, otherwise $w_i=-1$. To achieve the FXT quasi-bipartite synchronization of CCNNs, the intermittent controller is designed as follows:

$$R_i\left(t\right)=\left\{\begin{array}{c}-\lambda \left({\mathbf{x}}_i\left(t\right)-w_i\mathbf{y}\left(t\right)\right)-{\sigma }_{1}sgn\left({\mathbf{x}}_i\left(t\right)-w_i\mathbf{y}\left(t\right)\right){|{\mathbf{x}}_i\left(t\right)-w_i\mathbf{y}\left(t\right)|}^{\alpha }\hfill \\ -{\sigma }_{2}sgn\left({\mathbf{x}}_i\left(t\right)-w_i\mathbf{y}\left(t\right)\right){|{\mathbf{x}}_i\left(t\right)-w_i\mathbf{y}\left(t\right)|}^{\beta },t\in [{\zeta }_k,{\mu }_k),\hfill \\ 0,t\in [{\mu }_k,{\zeta }_{k+1}),\hfill \end{array}\right.$$

(8)

where $i\in {\mathcal{N}}_{+}$, $0<\alpha <1$, $\beta >1$, $\lambda$, ${\sigma }_1$, ${\sigma }_2$ are positive constants.

Remark 2. 

The intermittent control proposed in this study can be accomplished in a fixed time, unlike the previous intermittent control, which can only achieve asymptotic results. Moreover, the aperiodic intermittent controller proposed in this study is different from the controller in [26,27] as follows:

$$R_i\left(t\right)=\left\{\begin{array}{c}{\displaystyle -\frac{r}{2}q\left(e_i\left(t\right)\right)-\frac{k}{2}sgn\left(q\left(e_i\left(t\right)\right)\right)(\mid e_i\left(t\right){\mid }^{\alpha }+\mid e_i\left(t\right){\mid }^{\beta })}\hfill \\ {\displaystyle -\frac{k}{2}({\left({\int }_{t-\tau }^t{e}_i^T\left(s\right)e_i\left(s\right)ds\right)}^{\frac{1+\alpha }{2}}+({\int }_{t-\tau }^t{e}_i^T\left(s\right)}\hfill \\ {\displaystyle \times e_i{\left(s\right)ds)}^{\frac{1+\beta }{2}})\frac{e_i\left(t\right)}{\Vert e_i{\left(t\right)\Vert }^2},mT\le t<(m+\theta )T,}\hfill \\ {\displaystyle -\frac{r}{2}q\left(e_i\left(t\right)\right),(m+\theta )T\le t<(m+1)T,}\hfill \end{array}\right.$$

and

$$R_i\left(t\right)=\left\{\begin{array}{c}{\displaystyle -k_i{e}_i\left(t\right)-\alpha \sum _{r=1}^3{\left(\frac{{\xi }_r}{1-{\sigma }_r}{\int }_{t-{\tau }_r\left(t\right)}^t{e}_i^T\left(s\right)e_i\left(s\right)ds\right)}^{\frac{p+1}{2}}\frac{e_i\left(t\right)}{\Vert e_i{\left(t\right)\Vert }^2}}\hfill \\ {\displaystyle -\beta \sum _{r=1}^3{\left(\frac{{\xi }_r}{1-{\sigma }_r}{\int }_{t-{\tau }_r\left(t\right)}^t{e}_i^T\left(s\right)e_i\left(s\right)ds\right)}^{\frac{q+1}{2}}\frac{e_i\left(t\right)}{\Vert e_i{\left(t\right)\Vert }^2}}\hfill \\ -\alpha sign\left(e_i\left(t\right)\right)\mid e_i\left(t\right){\mid }^p-\beta sign\left(e_i\left(t\right)\right)\mid e_i\left(t\right){\mid }^q,mT\le t<(m+\theta )T,\hfill \\ -k_i{e}_i\left(t\right),(m+\theta )T\le t<(m+1)T.\hfill \end{array}\right.$$

A linear term does not need to be set in the rest interval. This approach is proposed first to achieve FXT quasi-bipartite synchronization for coupled competitive neural networks. Furthermore, aperiodic intermittent control can be degenerated into periodic intermittent control and continuous control. It is particularly suitable for complex systems that require dynamic and flexible control.

Combined with controller (8), when $t\in [{\zeta }_k,{\mu }_k)$, the CCNNs (4) is rewritten as follows:

$$\begin{array}{cc}\hfill {\dot{\mathbf{x}}}_i\left(t\right)=& -C_1{\mathbf{x}}_i\left(t\right)+A_{1}f\left(\mathbf{I}{\mathbf{x}}_i\left(t\right)\right)+B_{1}f\left(\mathbf{I}{\mathbf{x}}_i(t-\tau \left(t\right))\right)+\sum _{j=1}^N{\overline{\mathbf{d}}}_{ij}{\mathbf{x}}_j\left(t\right)+W_i\left(t\right)\hfill \\ \hfill & -\lambda \left({\mathbf{x}}_i\left(t\right)-w_i\mathbf{y}\left(t\right)\right)-{\sigma }_{1}sgn\left({\mathbf{x}}_i\left(t\right)-w_i\mathbf{y}\left(t\right)\right){|{\mathbf{x}}_i\left(t\right)-w_i\mathbf{y}\left(t\right)|}^{\alpha }\hfill \\ \hfill & -{\sigma }_{2}sgn\left({\mathbf{x}}_i\left(t\right)-w_i\mathbf{y}\left(t\right)\right){|{\mathbf{x}}_i\left(t\right)-w_i\mathbf{y}\left(t\right)|}^{\beta },\hfill \end{array}$$

(9)

where ${\overline{D}}_1={\left({\overline{\mathbf{d}}}_{ij}\right)}_{2nN\times 2nN}$, ${\overline{\mathbf{d}}}_{ij}={\mathbf{d}}_{ij}$ for $i\ne j$ and ${\overline{\mathbf{d}}}_{ii}=-{\sum }_{j=1,j\ne i}^N\left|{\mathbf{d}}_{ij}\right|$. Then, according to Assumption 3, the CCNNs (9) can be transformed into:

$$\begin{array}{cc}\hfill {\dot{\tilde{\mathbf{x}}}}_i\left(t\right)=& -C_1{\tilde{\mathbf{x}}}_i\left(t\right)+A_{1}f\left(\mathbf{I}{\tilde{\mathbf{x}}}_i\left(t\right)\right)+B_{1}f\left(\mathbf{I}{\tilde{\mathbf{x}}}_i(t-\tau \left(t\right))\right)+\sum _{j=1}^N{\tilde{\mathbf{d}}}_{ij}{\tilde{\mathbf{x}}}_j\left(t\right)\hfill \\ \hfill & -\lambda \left({\tilde{\mathbf{x}}}_i\left(t\right)-\mathbf{y}\left(t\right)\right)-{\sigma }_{1}sgn\left({\tilde{\mathbf{x}}}_i\left(t\right)-\mathbf{y}\left(t\right)\right){|{\tilde{\mathbf{x}}}_i\left(t\right)-\mathbf{y}\left(t\right)|}^{\alpha }\hfill \\ \hfill & -{\sigma }_{2}sgn\left({\tilde{\mathbf{x}}}_i\left(t\right)-\mathbf{y}\left(t\right)\right){|{\tilde{\mathbf{x}}}_i\left(t\right)-\mathbf{y}\left(t\right)|}^{\beta }+w_i{W}_i\left(t\right),\hfill \end{array}$$

(10)

where ${\tilde{\mathbf{x}}}_i\left(t\right)=w_i{\mathbf{x}}_i\left(t\right)$, ${\tilde{\mathbf{d}}}_{ij}=w_i{\overline{\mathbf{d}}}_{ij}{w}_j=\left|{\mathbf{d}}_{ij}\right|$ for $i\ne j$ and ${\tilde{\mathbf{d}}}_{ii}=-{\sum }_{j=1,j\ne i}^N\left|{\mathbf{d}}_{ij}\right|$, $i\in {\mathcal{N}}_{+}$.

Similar analysis, for $t\in [{\mu }_k,{\zeta }_{k+1})$, one has

$$\begin{array}{cc}\hfill {\dot{\tilde{\mathbf{x}}}}_i\left(t\right)=& -C_1{\tilde{\mathbf{x}}}_i\left(t\right)+A_{1}f\left(\mathbf{I}{\tilde{\mathbf{x}}}_i\left(t\right)\right)+B_{1}f\left(\mathbf{I}{\tilde{\mathbf{x}}}_i(t-\tau \left(t\right))\right)\hfill \\ \hfill & +\sum _{j=1}^N{\tilde{\mathbf{d}}}_{ij}{\tilde{\mathbf{x}}}_j\left(t\right)+w_i{W}_i\left(t\right).\hfill \end{array}$$

(11)

By definition 1, there is $\varpi \left(t\right)={\left({\varpi }_1\left(t\right),...,{\varpi }_n\left(t\right)\right)}^T\in K\left[f\right(\mathbf{I}\mathbf{y}\left)\right]$ such that

$$\dot{\mathbf{y}}\left(t\right)=-C_1\mathbf{y}\left(t\right)+A_1\varpi \left(t\right)+B_1\varpi (t-\tau \left(t\right)).$$

(12)

Similarly, there exists at least one measurable function ${\hslash }_i\left(t\right)=({\hslash }_{i1}\left(t\right),...,$ ${\hslash }_{in}\left(t\right){)}^T\in K\left[f\left(\mathbf{I}{\tilde{\mathbf{x}}}_i\right)\right]$ such that

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill {\dot{\tilde{\mathbf{x}}}}_i\left(t\right)=& -C_1{\tilde{\mathbf{x}}}_i\left(t\right)+A_1{\hslash }_i\left(t\right)+B_1{\hslash }_i(t-\tau \left(t\right))+\sum _{j=1}^N{\tilde{\mathbf{d}}}_{ij}{\tilde{\mathbf{x}}}_j\left(t\right)+w_i{W}_i\left(t\right)\hfill \\ \hfill & -\lambda \left({\tilde{\mathbf{x}}}_i\left(t\right)-\mathbf{y}\left(t\right)\right)-{\sigma }_{1}sgn\left({\tilde{\mathbf{x}}}_i\left(t\right)-\mathbf{y}\left(t\right)\right){|{\tilde{\mathbf{x}}}_i\left(t\right)-\mathbf{y}\left(t\right)|}^{\alpha }\hfill \\ \hfill & -{\sigma }_{2}sgn\left({\tilde{\mathbf{x}}}_i\left(t\right)-\mathbf{y}\left(t\right)\right){|{\tilde{\mathbf{x}}}_i\left(t\right)-\mathbf{y}\left(t\right)|}^{\beta },t\in [{\zeta }_k,{\mu }_k),\hfill \\ \hfill {\dot{\tilde{\mathbf{x}}}}_i\left(t\right)=& -C_1{\tilde{\mathbf{x}}}_i\left(t\right)+A_1{\hslash }_i\left(t\right)+B_1{\hslash }_i(t-\tau \left(t\right))\hfill \\ \hfill & +\sum _{j=1}^N{\tilde{\mathbf{d}}}_{ij}{\tilde{\mathbf{x}}}_j\left(t\right)+w_i{W}_i\left(t\right),t\in [{\mu }_k,{\zeta }_{k+1}).\hfill \end{array}\hfill \end{array}\right.$$

(13)

3. Main result

In this part, we will consider the case of $W_i\left(t\right)=0$ and $W_i\left(t\right)\ne 0$. The Fixed-time quasi-bipartite synchronization criterion is derived by designing intermittent controller.

Define the synchronization error $e_i\left(t\right)={\tilde{\mathbf{x}}}_i\left(t\right)-\mathbf{y}\left(t\right)$, then the error dynamical system is:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill {\dot{e}}_i\left(t\right)=& -C_1{e}_i\left(t\right)+A_1{g}_i\left(t\right)+B_1{g}_i(t-\tau \left(t\right))+\sum _{j=1}^N{\tilde{\mathbf{d}}}_{ij}{e}_j\left(t\right)+w_i{W}_i\left(t\right)\hfill \\ \hfill & -{\sigma }_{1}sgn\left(e_i\left(t\right)\right)|e_i{\left(t\right)|}^{\alpha }-{\sigma }_{2}sgn\left(e_i\left(t\right)\right){\left|e_i\left(t\right)\right|}^{\beta }\hfill \\ \hfill & -\lambda \left(e_i\left(t\right)\right),t\in [{\zeta }_k,{\mu }_k)\hfill \\ \hfill {\dot{e}}_i\left(t\right)=& -C_1{e}_i\left(t\right)+A_1{g}_i\left(t\right)+B_1{g}_i(t-\tau \left(t\right))+\sum _{j=1}^N{\tilde{\mathbf{d}}}_{ij}{e}_j\left(t\right)\hfill \\ \hfill & +w_i{W}_i\left(t\right),t\in [{\mu }_k,{\zeta }_{k+1}),\hfill \end{array}\hfill \end{array}\right.$$

(14)

where $g_i\left(t\right)={\hslash }_i\left(t\right)-\varpi \left(t\right)$, $g_i(t-\tau \left(t\right))={\hslash }_i(t-\tau \left(t\right))-\varpi (t-\tau \left(t\right))$.

3.1. Fixed-time quasi-bipartite synchronization without disturbances

This section gives the results without external disturbances. Firstly, Theorem 1 gives a sufficient condition for the quasi-bipartite synchronization of networks (12) and (13) in fixed time.

Theorem 1. 

Based on Assumptions 1-5 and the controller (8), if

$$\begin{array}{cc}\hfill & 2\lambda -{\lambda }_{max}\left(\mathrm{\Phi }\right)-\kappa >0,\hfill \\ \hfill & {\varrho }_1+{\lambda }_{max}\left(\mathrm{\Phi }\right)+\kappa >0,\hfill \\ \hfill & {\varrho }_1+{\lambda }_{max}\left(\mathrm{\Phi }\right)+\kappa -\gamma d<0,\hfill \\ \hfill & (1-\gamma )d-2\lambda +{\lambda }_{max}\left(\mathrm{\Phi }\right)+\kappa <0,\hfill \end{array}$$

where $\mathrm{\Phi }=-I_N\otimes \left(C_1+C_1^T\right)+I_N\otimes \left(|A_1|L\mathbf{I}+(|A_1{\left|L\mathbf{I}\right)}^T\right)+\left({\tilde{D}}_1+{\tilde{D}}_1^T\right)$, $\kappa ={\kappa }_1+2{\kappa }_2$, λ, ${\varrho }_1$, d are positive constants, $\gamma \in (0,1)$ stands for the average control rate, then the quasi-bipartite synchronization can be ensured between networks (12) and (13) in fixed time. The settling time satisfies

$$T\le \frac{2+a_5\left(\beta -1\right)T_{\gamma }}{a_5\left(\beta -1\right)\gamma }+\frac{2+a_6\left(1-\alpha \right)T_{\gamma }}{a_6\left(1-\alpha \right)\gamma },$$

here $a_5=2{\sigma }_2{\left(2nN\right)}^{\frac{1-\beta }{2}}\left(1-\varphi \right)exp\left\{\frac{{\displaystyle 1}}{{\displaystyle 2}}{T}_{\gamma }\left(1-\beta \right)d\right\}$, $a_6=2{\sigma }_1\left(1-\varphi \right)$, $T_{\gamma }$ represents the elasticity number, $0<\varphi <1$. The state trajectory of (14) converges to a compact set $\Omega =\left\{e\left(t\right)\mid {\parallel e\left(t\right)\parallel }_2\le \sqrt{max\{{\delta }_1,{\delta }_2,{\delta }_3\}}\right\}$, ${\delta }_1={\left(\frac{{\displaystyle \aleph }}{{\displaystyle 2\varphi {\sigma }_2{\left(nN\right)}^{\frac{1-\beta }{2}}}}\right)}^{\frac{2}{\beta +1}}$, ${\delta }_2={\left(\frac{{\displaystyle \aleph }}{{\displaystyle 2\varphi {\sigma }_1}}\right)}^{\frac{2}{\alpha +1}}$, ${\delta }_3=\frac{{\displaystyle \aleph }}{{\displaystyle d\gamma -\varrho }}$, $\varrho ={\varrho }_1+{\lambda }_{max}\left(\mathrm{\Phi }\right)+\kappa$, $\aleph =\frac{{\displaystyle N}}{{\displaystyle {\kappa }_1}}{\left(|A_1\left|h\right)\right)}^T|A_1|h+\frac{{\displaystyle 2N}}{{\displaystyle {\kappa }_2}}{\left(|B_1|M\right)}^T\left|B_1\right|M$.

Proof. 

Consider the following Lyapunov function

$$V\left(t\right)=e^T\left(t\right)e\left(t\right),$$

where $e\left(t\right)={\left(e_1^T\left(t\right),...,e_N^T\left(t\right)\right)}^T$.

For $t\in [{\zeta }_k,{\mu }_k)$, calculate the derivative of $V\left(t\right)$ along the trajectory of the error system (14), one has

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)=& 2\sum _{i=1}^N{e}_i^T\left(t\right)(-C_1{e}_i\left(t\right)+A_1{g}_i\left(t\right)+B_1{g}_i(t-\tau \left(t\right))+\sum _{j=1}^N{\tilde{\mathbf{d}}}_{ij}{e}_j\left(t\right)\hfill \\ \hfill & -\lambda \left(e_i\left(t\right)\right)-{\sigma }_{1}sgn\left(e_i\left(t\right)\right)|e_i{\left(t\right)|}^{\alpha }-{\sigma }_{2}sgn\left(e_i\left(t\right)\right){\left|e_i\left(t\right)\right|}^{\beta }).\hfill \end{array}$$

Based on Assumption 2, we get

$$\begin{array}{cc}\hfill 2\sum _{i=1}^N{e}_i^T\left(t\right)A_1{g}_i\left(t\right)& \le 2\sum _{i=1}^N|e_i^T\left(t\right)\left|\right|A_1\left|\right|{\hslash }_i\left(t\right)-\varpi \left(t\right)|\hfill \\ \hfill & \le 2\sum _{i=1}^N|e_i^T\left(t\right)\left|\right|A_1\left|\right[L\mathbf{I}|e_i\left(t\right)|+h],\hfill \end{array}$$

(15)

where $L=diag\{l_1,...,l_n\}$, $h={(h_1,...,h_n)}^T$.

By Assumption 5, there is

$$\begin{array}{cc}\hfill 2\sum _{i=1}^N{e}_i^T\left(t\right)B_1{g}_i(t-\tau \left(t\right))& \le 2\sum _{i=1}^N|e_i^T\left(t\right)\left|\right|B_1\left|\right|{\hslash }_i(t-\tau \left(t\right))-\varpi (t-\tau \left(t\right))|\hfill \\ \hfill & \le 4\sum _{i=1}^N|e_i^T\left(t\right)\left|\right|B_1\left|\right|M,\hfill \end{array}$$

(16)

where $M={(M_1,...,M_n)}^T$.

From (15) and (16), one has

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)\le & -2\sum _{i=1}^N{e}_i^T\left(t\right)C_1{e}_i\left(t\right)+2\sum _{i=1}^N|e_i^T\left(t\right)\left|\right|A_1\left|L\mathbf{I}\right|e_i\left(t\right)|+2\sum _{i=1}^N|e_i^T\left(t\right)\left|\right|A_1|h\hfill \\ \hfill & +2\sum _{i=1}^N{e}_i^T\left(t\right)\sum _{j=1}^N{\tilde{\mathbf{d}}}_{ij}{e}_j\left(t\right)-2\lambda \sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)+4\sum _{i=1}^N|e_i^T\left(t\right)\left|\right|B_1|M\hfill \\ \hfill & -2{\sigma }_1\sum _{i=1}^N{e}_i^T\left(t\right)sgn\left(e_i\left(t\right)\right)|e_i{\left(t\right)|}^{\alpha }-2{\sigma }_2\sum _{i=1}^N{e}_i^T\left(t\right)sgn\left(e_i\left(t\right)\right){\left|e_i\left(t\right)\right|}^{\beta }.\hfill \\ \hfill \end{array}$$

According to Lemma 1, one has

$$\begin{array}{cc}\hfill -2{\sigma }_1\sum _{i=1}^N{e}_i^T\left(t\right)sgn\left(e_i\left(t\right)\right){\left|e_i\left(t\right)\right|}^{\alpha }& =-2{\sigma }_1\sum _{i=1}^N\sum _{k=1}^{2n}{\left|e_{ik}\left(t\right)\right|}^{\alpha +1}\hfill \\ \hfill & \le -2{\sigma }_1\sum _{i=1}^N{\left(\sum _{k=1}^{2n}{e}_{ik}^2\left(t\right)\right)}^{\frac{\alpha +1}{2}}\hfill \\ \hfill & \le -2{\sigma }_1{\left(\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)\right)}^{\frac{\alpha +1}{2}},\hfill \end{array}$$

(17)

and

$$\begin{array}{cc}\hfill -2{\sigma }_2\sum _{i=1}^N{e}_i^T\left(t\right)sgn\left(e_i\left(t\right)\right){\left|e_i\left(t\right)\right|}^{\beta }& =-2{\sigma }_2\sum _{i=1}^N\sum _{k=1}^{2n}{\left|e_{ik}\left(t\right)\right|}^{\beta +1}\hfill \\ \hfill & \le -2{\sigma }_2\sum _{i=1}^N\sum _{k=1}^{2n}(e_{ik}^2\left(t\right){)}^{\frac{\beta +1}{2}}\hfill \\ \hfill & \le -2{\left(2nN\right)}^{\frac{1-\beta }{2}}{\sigma }_2{\left(\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)\right)}^{\frac{\beta +1}{2}}.\hfill \end{array}$$

(18)

From Lemma 2, it follows that

$$\begin{array}{c}\hfill 2\sum _{i=1}^N|e_i^T\left(t\right)\left|\right|A_1|h\le {\kappa }_1\sum _{i=1}^N|e_i^T\left(t\right)\left|\right|e_i\left(t\right)|+\frac{N}{{\kappa }_1}\left(\right|A_1|h{)}^T\left|A_1\right|h,\end{array}$$

(19)

and

$$\begin{array}{c}\hfill 4\sum _{i=1}^N|e_i^T\left(t\right)\left|\right|B_1|M\le 2{\kappa }_2\sum _{i=1}^N|e_i^T\left(t\right)\left|\right|e_i\left(t\right)|+\frac{2N}{{\kappa }_2}\left(\right|B_1|M{)}^T\left|B_1\right|M.\end{array}$$

(20)

It follows from (17)-(20) that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \dot{V}\left(t\right)\le & -2\sum _{i=1}^N{e}_i^T\left(t\right)C_1{e}_i\left(t\right)+2\sum _{i=1}^N|e_i^T\left(t\right)\left|\right|A_1\left|L\mathbf{I}\right|e_i\left(t\right)|+{\kappa }_1\sum _{i=1}^N|e_i^T\left(t\right)\left|\right|e_i\left(t\right)|\hfill \\ \hfill & +2\sum _{i=1}^N\sum _{j=1}^N{e}_i^T\left(t\right){\tilde{\mathbf{d}}}_{ij}{e}_j\left(t\right)+2{\kappa }_2\sum _{i=1}^N|e_i^T\left(t\right)\left|\right|e_i\left(t\right)|+\frac{N}{{\kappa }_1}\left(\right|A_1|h{)}^T\left|A_1\right|h\hfill \\ \hfill & +\frac{2N}{{\kappa }_2}\left(\right|B_1|M{)}^T\left|B_1\right|M-2\lambda \sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)-2{\sigma }_1(\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right){)}^{\frac{\alpha +1}{2}}\hfill \\ \hfill & -2{\sigma }_2\left(2nN{)}^{\frac{1-\beta }{2}}\right(\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right){)}^{\frac{\beta +1}{2}}\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \le & -2e^T\left(t\right)(I_N\otimes C_1)e\left(t\right)+2e^T\left(t\right)(I_N\otimes \left|A_1\right|L\mathbf{I})e\left(t\right)+{\kappa }_1{e}^T\left(t\right)e\left(t\right)\hfill \\ \hfill & +2e^T\left(t\right){\tilde{D}}_{1}e\left(t\right)+2{\kappa }_2{e}^T\left(t\right)e\left(t\right)-2\lambda e^T\left(t\right)e\left(t\right)-2{\sigma }_1(e^T\left(t\right)e\left(t\right){)}^{\frac{\alpha +1}{2}}\hfill \\ \hfill & -2{\sigma }_2{\left(2nN\right)}^{\frac{1-\beta }{2}}{\left(e^T\left(t\right)e\left(t\right)\right)}^{\frac{\beta +1}{2}}+\frac{N}{{\kappa }_1}\left(\right|A_1|h{)}^T\left|A_1\right|h\hfill \\ \hfill & +\frac{2N}{{\kappa }_2}\left(\right|B_1|M{)}^T\left|B_1\right|M\hfill \\ \hfill \le & \left({\lambda }_{max}\left(\mathrm{\Phi }\right)+{\kappa }_1+2{\kappa }_2-2\lambda \right)e^T\left(t\right)e\left(t\right)-2{\sigma }_1{\left(e^T\left(t\right)e\left(t\right)\right)}^{\frac{\alpha +1}{2}}\hfill \\ \hfill & -2{\sigma }_2{\left(2nN\right)}^{\frac{1-\beta }{2}}{\left(e^T\left(t\right)e\left(t\right)\right)}^{\frac{\beta +1}{2}}+\frac{N}{{\kappa }_1}\left(\right|A_1|h{)}^T\left|A_1\right|h\hfill \\ \hfill & +\frac{2N}{{\kappa }_2}\left(\right|B_1|M{)}^T\left|B_1\right|M,\hfill \end{array}\end{array}$$

where $\mathrm{\Phi }=-I_N\otimes (C_1+C_1^T)+I_N\otimes \left(\right|A_1|L\mathbf{I}+(|A_1{\left|L\mathbf{I}\right)}^T)+({\tilde{D}}_1+{\tilde{D}}_1^T)$.

Therefore,

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)\le & -{\lambda }_{1}V\left(t\right)-2{\sigma }_{1}V{\left(t\right)}^{\frac{\alpha +1}{2}}-2{\sigma }_2{\left(2nN\right)}^{\frac{1-\beta }{2}}V{\left(t\right)}^{\frac{\beta +1}{2}}+\aleph \hfill \end{array}$$

for $t\in [{\zeta }_k,{\mu }_k)$, ${\lambda }_1=2\lambda -{\lambda }_{max}\left(\mathrm{\Phi }\right)-\kappa$, $\aleph =\frac{{\displaystyle N}}{{\displaystyle {\kappa }_1}}\left(\right|A_1|h{)}^T|A_1|h+\frac{{\displaystyle 2N}}{{\displaystyle {\kappa }_2}}\left(\right|B_1|M{)}^T\left|B_1\right|M$, and $\kappa ={\kappa }_1+2{\kappa }_2$.

Then, for $t\in [{\mu }_k,{\zeta }_{k+1})$, we have

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)\le & 2e^T\left(t\right)[-I_N\otimes C_1+I_N\otimes \left|A_1\right|L\mathbf{I}+{\tilde{D}}_1]e\left(t\right)+\left({\varrho }_1+\kappa \right)e^T\left(t\right)e\left(t\right)\hfill \\ \hfill & +\frac{N}{{\kappa }_1}\left(\right|A_1|h{)}^T|A_1|h+\frac{2N}{{\kappa }_2}\left(\right|B_1|M{)}^T\left|B_1\right|M\hfill \\ \hfill \le & \varrho V\left(t\right)+\aleph ,\hfill \end{array}$$

where $\varrho ={\lambda }_{max}\left(\mathrm{\Phi }\right)+{\varrho }_1+\kappa$.

Based on Lemma 3, the networks (12) and (13) achieve FXT quasi-bipartite synchronization and the settling time is estimated as T. Moreover, the system error $e\left(t\right)$ will converge to $\Omega =\left\{e\left(t\right)\mid {\parallel e\left(t\right)\parallel }_2\le \sqrt{max\{{\delta }_1,{\delta }_2,{\delta }_3\}}\right\}$ within T, where ${\delta }_1={\left(\frac{{\displaystyle \aleph }}{{\displaystyle 2\varphi {\sigma }_2{\left(nN\right)}^{\frac{1-\beta }{2}}}}\right)}^{\frac{2}{\beta +1}}$, ${\delta }_2={\left(\frac{{\displaystyle \aleph }}{{\displaystyle 2\varphi {\sigma }_1}}\right)}^{\frac{2}{\alpha +1}}$, ${\delta }_3=\frac{{\displaystyle \aleph }}{{\displaystyle d\gamma -\varrho }}$.

The theorem is proven. □

Remark 3. 

A previous study [23] focused on studying FET bipartite synchronization in competitive neural networks, whereby the settling time was dependent on the initial state. In contrast, Theorem 1 provides a sufficient condition for achieving FXT quasi-bipartite synchronization in CCNNs where the settling time is no longer dependent on the initial state, but rather on the adjustable controller parameters and the average control rate. Furthermore, our study utilizes a more practical intermittent controller compared to the one used in [23].

3.2. Fixed-time quasi-bipartite synchronization with disturbances

This section considers external disturbances. Theorem 2 gives sufficient conditions for quasi-bipartite synchronization of systems (12) and (13) in fixed time.

Theorem 2. 

Based on Assumptions 1-6 and the controller (8), if

$$\begin{array}{cc}\hfill & 2\lambda -{\lambda }_{max}\left(\mathrm{\Phi }\right)-\tilde{\kappa }>0,\hfill \\ \hfill & \psi +{\lambda }_{max}\left(\mathrm{\Phi }\right)+\tilde{\kappa }>0,\hfill \\ \hfill & \psi +{\lambda }_{max}\left(\mathrm{\Phi }\right)+\tilde{\kappa }-\gamma \tilde{d}<0,\hfill \\ \hfill & (1-\gamma )\tilde{d}-2\lambda +{\lambda }_{max}\left(\mathrm{\Phi }\right)+\tilde{\kappa }<0,\hfill \end{array}$$

where $\mathrm{\Phi }=-I_N\otimes \left(C_1+C_1^T\right)+I_N\otimes \left(|A_1|L\mathbf{I}+(|A_1{\left|L\mathbf{I}\right)}^T\right)+({\tilde{D}}_1+{\tilde{D}}_1^T)$, $\tilde{\kappa }={\kappa }_1+2{\kappa }_2+{\kappa }_3$, ψ, λ, $\tilde{d}$ are positive constants, $\gamma \in \left(0,1\right)$ stands for the average control rate, then the quasi-bipartite synchronization can be ensured between networks (12) and (13) in fixed time. The settling time satisfies

$$T^{*}\le \frac{2+{\tilde{a}}_5\left(\beta -1\right)T_{\gamma }}{{\tilde{a}}_5\left(\beta -1\right)\gamma }+\frac{2+{\tilde{a}}_6\left(1-\alpha \right)T_{\gamma }}{{\tilde{a}}_6\left(1-\alpha \right)\gamma },$$

here ${\tilde{a}}_5=2{\sigma }_2{\left(2nN\right)}^{\frac{1-\beta }{2}}\left(1-\varphi \right)exp\left\{\frac{{\displaystyle 1}}{{\displaystyle 2}}{T}_{\gamma }\left(1-\beta \right)\tilde{d}\right\}$, $a_6=2{\sigma }_1\left(1-\varphi \right)$, $T_{\gamma }$ represents the elasticity number, $0<\varphi <1$. The state trajectory of (14) converges to a compact set $\tilde{\Omega }=\left\{e\left(t\right)\mid {\parallel e\left(t\right)\parallel }_2\le \sqrt{max\{{\tilde{\delta }}_1,{\tilde{\delta }}_2,{\tilde{\delta }}_3\}}\right\}$ within $T^{*}$, ${\tilde{\delta }}_1={\left(\frac{{\displaystyle \tilde{\aleph }}}{{\displaystyle 2\varphi {\sigma }_2{\left(nN\right)}^{\frac{1-\beta }{2}}}}\right)}^{\frac{2}{\beta +1}}$, ${\tilde{\delta }}_2={\left(\frac{{\displaystyle \tilde{\aleph }}}{{\displaystyle 2\varphi {\sigma }_1}}\right)}^{\frac{2}{\alpha +1}}$, ${\tilde{\delta }}_3=\frac{{\displaystyle \tilde{\aleph }}}{{\displaystyle \tilde{d}\gamma -\tilde{\psi }}}$, $\tilde{\psi }=\psi +{\lambda }_{max}\left(\mathrm{\Phi }\right)+\tilde{\kappa }$, $\tilde{\aleph }=\frac{{\displaystyle N}}{{\displaystyle {\kappa }_1}}{\left(|A_1|h\right)}^T|A_1|h+\frac{{\displaystyle 2N}}{{\displaystyle {\kappa }_2}}{\left(|B_1|M\right)}^T\left|B_1\right|M+\frac{{\displaystyle N}}{{\displaystyle {\kappa }_3}}{W}^{T}W$.

Proof. 

Construct the following Lyapunov function

$$V\left(t\right)=e^T\left(t\right)e\left(t\right),$$

where $e\left(t\right)={\left(e_1^T\left(t\right),...,e_N^T\left(t\right)\right)}^T$.

For $t\in [{\zeta }_k,{\mu }_k)$, one obtains

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)=& 2\sum _{i=1}^N{e}_i^T\left(t\right)(-C_1{e}_i\left(t\right)+A_1{g}_i\left(t\right)+B_1{g}_i(t-\tau \left(t\right))+\sum _{j=1}^N{\tilde{\mathbf{d}}}_{ij}{e}_j\left(t\right)\hfill \\ \hfill & +w_i{W}_i\left(t\right)-\lambda \left(e_i\left(t\right)\right)-{\sigma }_{1}sgn\left(e_i\left(t\right)\right)|e_i{\left(t\right)|}^{\alpha }-{\sigma }_{2}sgn\left(e_i\left(t\right)\right){\left|e_i\left(t\right)\right|}^{\beta })\hfill \\ \hfill \le & 2\sum _{i=1}^N{e}_i^T\left(t\right)(-C_1{e}_i\left(t\right)+A_1{g}_i\left(t\right)+B_1{g}_i(t-\tau \left(t\right))+\sum _{j=1}^N{\tilde{\mathbf{d}}}_{ij}{e}_j\left(t\right)\hfill \\ \hfill & +|W_i\left(t\right)|-\lambda \left(e_i\left(t\right)\right)-{\sigma }_{1}sgn\left(e_i\left(t\right)\right)|e_i{\left(t\right)|}^{\alpha }-{\sigma }_{2}sgn\left(e_i\left(t\right)\right){\left|e_i\left(t\right)\right|}^{\beta }).\hfill \end{array}$$

(21)

Based on Assumption 2 and Assumption 5, it is clear that there are

$$\begin{array}{cc}\hfill 2\sum _{i=1}^N{e}_i^T\left(t\right)A_1{g}_i\left(t\right)& \le 2\sum _{i=1}^N|e_i^T\left(t\right)\left|\right|A_1\left|\right[L\mathbf{I}|e_i\left(t\right)+h],\hfill \\ \hfill 2\sum _{i=1}^N{e}_i^T\left(t\right)B_1{g}_i(t& -\tau \left(t\right))\le 4\sum _{i=1}^N|e_i^T\left(t\right)\left|\right|B_1|M,\hfill \end{array}$$

(22)

where $L=diag\{l_1,...,l_n\}$, $h={(h_1,...,h_n)}^T$, $M={(M_1,...,M_n)}^T$.

Combining (21) and (22), one has

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)\le & -2\sum _{i=1}^N{e}_i^T\left(t\right)C_1{e}_i\left(t\right)+2\sum _{i=1}^N{e}_i^T\left(t\right)|A_1\left|L\mathbf{I}\right|e_i\left(t\right)|+2\sum _{i=1}^N{e}_i^T\left(t\right)\left|A_1\right|h\hfill \\ \hfill & +2\sum _{i=1}^N{e}_i^T\left(t\right)\sum _{j=1}^N{\tilde{\mathbf{d}}}_{ij}{e}_j\left(t\right)-2\lambda \sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)+4\sum _{i=1}^N{e}_i^T\left(t\right)\left|B_1\right|M\hfill \\ \hfill & -2{\sigma }_1\sum _{i=1}^N{e}_i^T\left(t\right)sgn\left(e_i\left(t\right)\right)|e_i{\left(t\right)|}^{\alpha }-2{\sigma }_2\sum _{i=1}^N{e}_i^T\left(t\right)sgn\left(e_i\left(t\right)\right){\left|e_i\left(t\right)\right|}^{\beta }\hfill \\ \hfill & +2\sum _{i=1}^N{e}_i^T\left(t\right)\left|W_i\left(t\right)\right|.\hfill \end{array}$$

By Assumption 6, then

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)\le & -2\sum _{i=1}^N{e}_i^T\left(t\right)C_1{e}_i\left(t\right)+2\sum _{i=1}^N{e}_i^T\left(t\right)|A_1\left|L\mathbf{I}\right|e_i\left(t\right)|+2\sum _{i=1}^N{e}_i^T\left(t\right)\left|A_1\right|h\hfill \\ \hfill & +2\sum _{i=1}^N{e}_i^T\left(t\right)\sum _{j=1}^N{\tilde{\mathbf{d}}}_{ij}{e}_j\left(t\right)-2\lambda \sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)+4\sum _{i=1}^N{e}_i^T\left(t\right)\left|B_1\right|M\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & -2{\sigma }_1\sum _{i=1}^N{e}_i^T\left(t\right)sgn\left(e_i\left(t\right)\right)|e_i{\left(t\right)|}^{\alpha }-2{\sigma }_2\sum _{i=1}^N{e}_i^T\left(t\right)sgn\left(e_i\left(t\right)\right){\left|e_i\left(t\right)\right|}^{\beta }\hfill \\ \hfill & +2\sum _{i=1}^N{e}_i^T\left(t\right)W.\hfill \end{array}$$

By Lemma 1, it is easy to get

$$\begin{array}{cc}\hfill -2{\sigma }_1\sum _{i=1}^N{e}_i^T\left(t\right)sgn\left(e_i\left(t\right)\right){\left|e_i\left(t\right)\right|}^{\alpha }& \le -2{\sigma }_1{\left(\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)\right)}^{\frac{\alpha +1}{2}},\hfill \\ \hfill -2{\sigma }_2\sum _{i=1}^N{e}_i^T\left(t\right)sgn\left(e_i\left(t\right)\right){\left|e_i\left(t\right)\right|}^{\beta }& \le -2{\left(2nN\right)}^{\frac{1-\beta }{2}}{\sigma }_2{\left(\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)\right)}^{\frac{\beta +1}{2}}.\hfill \end{array}$$

(24)

Based on Lemma 2, we obtain

$$\begin{array}{cc}\hfill 2\sum _{i=1}^N{e}_i^T\left(t\right)W\le & {\kappa }_3\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)+\frac{N}{{\kappa }_3}{W}^{T}W,\hfill \\ \hfill 2\sum _{i=1}^N|e_i^T\left(t\right)\left|\right|A_1|h\le & {\kappa }_1\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)+\frac{N}{{\kappa }_1}{\left(|A_1|h\right)}^T\left|A_1\right|h,\hfill \\ \hfill 4\sum _{i=1}^N|e_i^T\left(t\right)\left|\right|B_1|M\le & 2{\kappa }_2\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)+\frac{2N}{{\kappa }_2}{\left(|B_1|M\right)}^T\left|B_1\right|M.\hfill \end{array}$$

(25)

Submitting (24) and (25) into (23), we obtain

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)\le & -2\sum _{i=1}^N{e}_i^T\left(t\right)C_1{e}_i\left(t\right)+2\sum _{i=1}^N{e}_i^T\left(t\right)|A_1\left|L\mathbf{I}\right|e_i\left(t\right)|+\frac{N}{{\kappa }_1}{\left(|A_1|h\right)}^T\left|A_1\right|h\hfill \\ \hfill & +{\kappa }_1\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)+2{\kappa }_2\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)+2\sum _{i=1}^N\sum _{j=1}^N{e}_i^T\left(t\right){\tilde{\mathbf{d}}}_{ij}{e}_j\left(t\right)\hfill \\ \hfill & -2\lambda \sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)+{\kappa }_3\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)-2{\sigma }_1{\left(\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)\right)}^{\frac{\alpha +1}{2}}\hfill \\ \hfill & -2{\sigma }_2{\left(2nN\right)}^{\frac{1-\beta }{2}}{\left(\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)\right)}^{\frac{\beta +1}{2}}+\frac{2N}{{\kappa }_2}{\left(|B_1|M\right)}^T\left|B_1\right|M\hfill \\ \hfill & +\frac{N}{{\kappa }_3}{W}^{T}W\hfill \\ \hfill =& -2e^T\left(t\right)(I_N\otimes C_1)e\left(t\right)+2e^T\left(t\right)(I_N\otimes \left|A_1\right|L\mathbf{I})e\left(t\right)+{\kappa }_1{e}^T\left(t\right)e\left(t\right)\hfill \\ \hfill & +2e^T\left(t\right){\tilde{D}}_{1}e\left(t\right)+2{\kappa }_2{e}^T\left(t\right)e\left(t\right)+{\kappa }_3{e}^T\left(t\right)e\left(t\right)+\frac{N}{{\kappa }_1}{\left(|A_1|h\right)}^T\left|A_1\right|h\hfill \\ \hfill & -2{\sigma }_1(e^T\left(t\right)e\left(t\right){)}^{\frac{\alpha +1}{2}}-2{\sigma }_2{\left(2nN\right)}^{\frac{1-\beta }{2}}{\left(e^T\left(t\right)e\left(t\right)\right)}^{\frac{\beta +1}{2}}+\frac{N}{{\kappa }_3}{W}^{T}W\hfill \\ \hfill & -2\lambda e^T\left(t\right)e\left(t\right)+\frac{2N}{{\kappa }_2}{\left(|B_1|M\right)}^T\left|B_1\right|M\hfill \\ \hfill \le & -{\lambda }_{2}V\left(t\right)-2{\sigma }_{1}V{\left(t\right)}^{\frac{\alpha +1}{2}}-2{\sigma }_2{\left(2nN\right)}^{\frac{1-\beta }{2}}V{\left(t\right)}^{\frac{\beta +1}{2}}+\tilde{\aleph },\hfill \end{array}$$

where $\mathrm{\Phi }=-I_N\otimes (C_1+C_1^T)+I_N\otimes \left(\right|A_1|L\mathbf{I}+(|A_1{\left|L\mathbf{I}\right)}^T)+({\tilde{D}}_1+{\tilde{D}}_1^T)$, ${\lambda }_2=2\lambda -{\lambda }_{max}\left(\mathrm{\Phi }\right)-\tilde{\kappa }$, $\tilde{\kappa }={\kappa }_1+2{\kappa }_2+{\kappa }_3$, $\tilde{\aleph }=\frac{{\displaystyle N}}{{\displaystyle {\kappa }_1}}{\left(|A_1|h\right)}^T|A_1|h+\frac{{\displaystyle 2N}}{{\displaystyle {\kappa }_2}}{\left(|B_1|M\right)}^T\left|B_1\right|M+\frac{{\displaystyle N}}{{\displaystyle {\kappa }_3}}{W}^{T}W$.

For $t\in [{\mu }_k,{\zeta }_{k+1})$, we obtain

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)\le & 2e^T\left(t\right)\left[-I_N\otimes C_1+I_N\otimes \left|A_1\right|L\mathbf{I}+{\tilde{D}}_1\right]e\left(t\right)+\psi e^T\left(t\right)e\left(t\right)+\tilde{\kappa }{e}^T\left(t\right)e\left(t\right)\hfill \\ \hfill & +\frac{N}{{\kappa }_1}{\left(|A_1|h\right)}^T|A_1|h+\frac{2N}{{\kappa }_2}{\left(|B_1|M\right)}^T\left|B_1\right|M+\frac{N}{{\kappa }_3}{W}^{T}W\hfill \\ \hfill =& \tilde{\psi }V\left(t\right)+\tilde{\aleph },\hfill \end{array}$$

where $\tilde{\psi }=\psi +{\lambda }_{max}\left(\mathrm{\Phi }\right)+\tilde{\kappa }$.

Based on Lemma 3, the FXT quasi-bipartite synchronization can be realized and the settling time is estimated as $T^{*}$. Moreover, the system error $e\left(t\right)$ will converge to $\tilde{\Omega }=\left\{e\left(t\right)\mid {\parallel e\left(t\right)\parallel }_2\le \sqrt{max\{{\tilde{\delta }}_1,{\tilde{\delta }}_2,{\tilde{\delta }}_3\}}\right\}$ within $T^{*}$, where ${\tilde{\delta }}_1={\left(\frac{{\displaystyle \tilde{\aleph }}}{{\displaystyle 2\varphi {\sigma }_2{\left(nN\right)}^{\frac{1-\beta }{2}}}}\right)}^{\frac{2}{\beta +1}}$, ${\tilde{\delta }}_2={\left(\frac{{\displaystyle \tilde{\aleph }}}{{\displaystyle 2\varphi {\sigma }_1}}\right)}^{\frac{2}{\alpha +1}}$, ${\tilde{\delta }}_3=\frac{{\displaystyle \tilde{\aleph }}}{{\displaystyle \tilde{d}\gamma -\tilde{\psi }}}$.

The theorem is proven. □

Remark 4. 

Unlike prior studies [31,36], our research takes into account the impact of discontinuous activation functions, external disturbances, and competitive relationships between nodes, which more closely mimics real-world networks. Specifically, due to the competitive nature among nodes and the presence of external disturbances, the synchronization method employed in [36] is not directly applicable to achieve FXT quasi-bipartite synchronization. Consequently, our main theorem extends the prior findings of FXT bipartite synchronization and is tailored to suit the aforementioned conditions.

Remark 5. 

Predefined time control has emerged as a promising method that allows synchronization time to be pre-set independently of system parameters. Due to its potential in various applications, predefined time synchronization has become a highly topical research area. However, there is still insufficient research into the predefined time bipartite synchronization of CCNNs, therefore further investigation is necessary.

4. Numerical examples

Two numerical examples are given in this part to demonstrate the validity of the derived theoretical conclusions.

Consider the following networks:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill \dot{z}\left(t\right)=& -\frac{1}{\epsilon }Cz\left(t\right)+\frac{1}{\epsilon }Af\left(z\left(t\right)\right)+\frac{1}{\epsilon }Bf\left(z(t-\tau \left(t\right))\right)+\frac{1}{\epsilon }Es\left(t\right),\hfill \\ \hfill \dot{s}\left(t\right)=& -\overline{C}s\left(t\right)+\overline{A}f\left(z\left(t\right)\right),\hfill \end{array}\hfill \end{array}\right.$$

(26)

where $z\left(t\right)={(z_1\left(t\right),z_2\left(t\right))}^T$, $s\left(t\right)={(s_1\left(t\right),s_2\left(t\right))}^T$, $\mathbf{y}\left(t\right)={\left(z^T\left(t\right),s^T\left(t\right)\right)}^T$, $\epsilon =0.83$, $\tau \left(t\right)=\frac{{\displaystyle 2e^t}}{{\displaystyle 2(1+e^t)}}$, $f\left(z\left(t\right)\right)={\left(sin\left(z_1\left(t\right)\right)+0.01sign\left(z_1\left(t\right)\right),sin\left(z_2\left(t\right)\right)+0.01sign\left(z_2\left(t\right)\right)\right)}^T$, $C=diag(2,2)$, $\overline{C}=diag(0.5,0.6)$, $\overline{A}=diag(1.2,1)$, $E=diag(0.01,0.01)$, $A=[1,2;-5.2,3.2]$, $B=[-4,2.1;2,3.5]$. 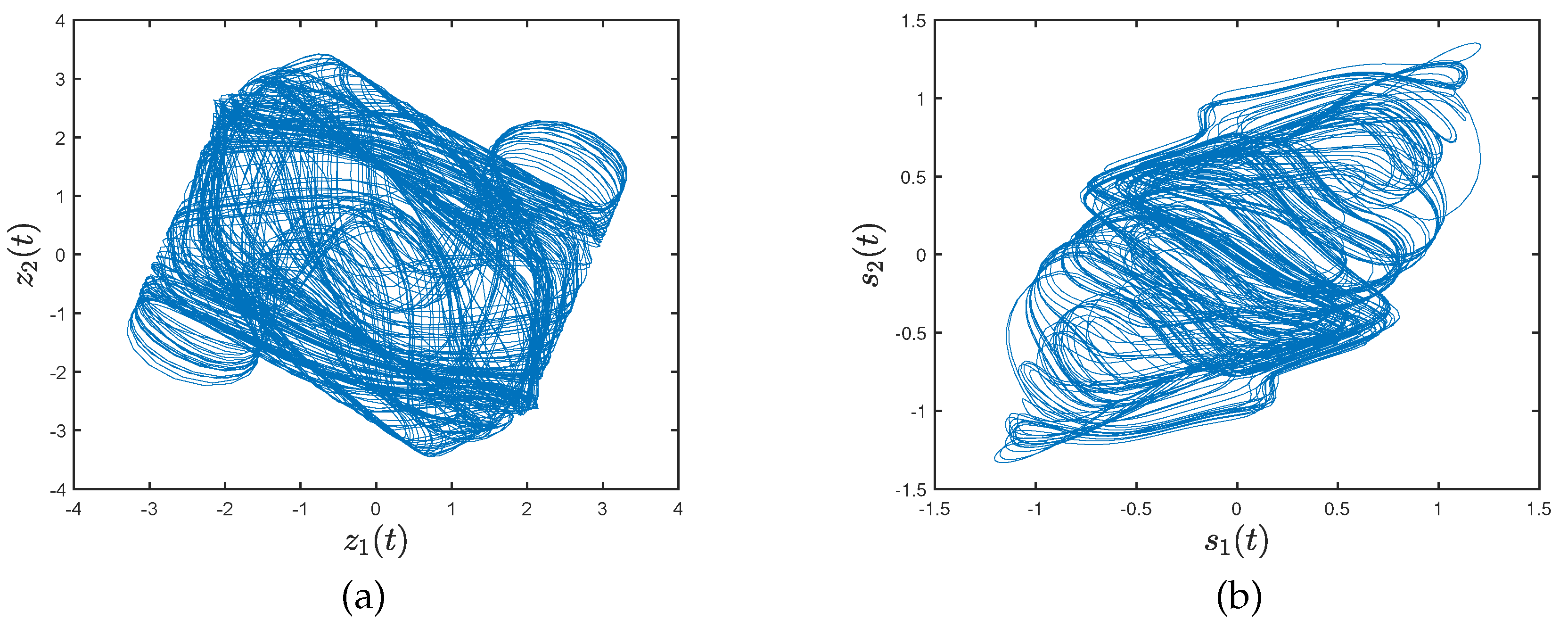Figure 1 shows the chaotic trajectories of network (26) with initial values $z\left(0\right)={(-0.4,0.6)}^T$, $s\left(0\right)={(-0.7,0.1)}^T$.

4.1. Fixed-time quasi-bipartite synchronization without disturbances

Now, consider CCNNs with 7 nodes as follows:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill {\dot{x}}_i\left(t\right)=& -\frac{1}{\epsilon }C{x}_i\left(t\right)+\frac{1}{\epsilon }Af\left(x_i\left(t\right)\right)+\frac{1}{\epsilon }Bf\left(x_i(t-\tau \left(t\right))\right)+\frac{1}{\epsilon }E{y}_i\left(t\right)\hfill \\ \hfill & +\sum _{j=1}^7\left|d_{ij}\right|\left(sign\left(d_{ij}\right)x_j\left(t\right)-x_i\left(t\right)\right)+R_i\left(t\right),\hfill \\ \hfill {\dot{y}}_i\left(t\right)=& -\overline{C}{y}_i\left(t\right)+\overline{A}f\left(x_i\left(t\right)\right)+\sum _{j=1}^7\left|u_{ij}\right|\left(sign\left(u_{ij}\right)y_j\left(t\right)-y_i\left(t\right)\right)\hfill \\ \hfill & +{\overline{R}}_i\left(t\right),i=1,2,...,7,\hfill \end{array}\hfill \end{array}\right.$$

(27)

where $x_i\left(t\right)={\left(x_{i1}\left(t\right),x_{i2}\left(t\right)\right)}^T$, $y_i\left(t\right)={\left(y_{i1}\left(t\right),y_{i2}\left(t\right)\right)}^T$, ${\mathbf{x}}_i\left(t\right)={\left(x_i^T\left(t\right),y_i^T\left(t\right)\right)}^T$. Set the initial values of network (27) to be $x_1\left(v\right)={(-1.9,2.8)}^T$, $x_2\left(v\right)={(-1.3,-1.4)}^T$, $x_3\left(v\right)={(2.2,1.4)}^T$, $x_4\left(v\right)={(-2.1,-2.9)}^T$, $x_5\left(v\right)={(2.4,-1.8)}^T$, $x_6\left(v\right)={(-1.2,0.9)}^T$, $x_7\left(v\right)={(-1.3,0.2)}^T$, $y_1\left(v\right)={(-2.6,0.1)}^T$, $y_2\left(v\right)={(0.4,-0.1)}^T$, $y_3\left(v\right)={(0.1,-0.9)}^T$, $y_4\left(v\right)={(-0.4,-1.6)}^T$, $y_5\left(v\right)={(0.5,1.6)}^T$, $y_6\left(v\right)={(0.1,0.8)}^T$, $y_7\left(v\right)={(-1.7,0.7)}^T$, $v\in [-1,0]$.

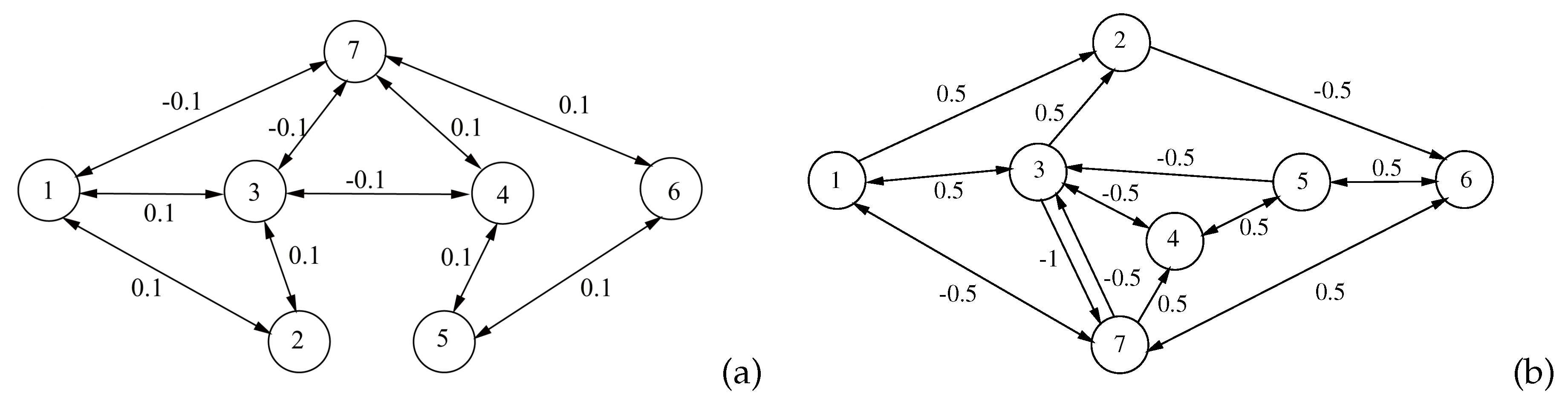
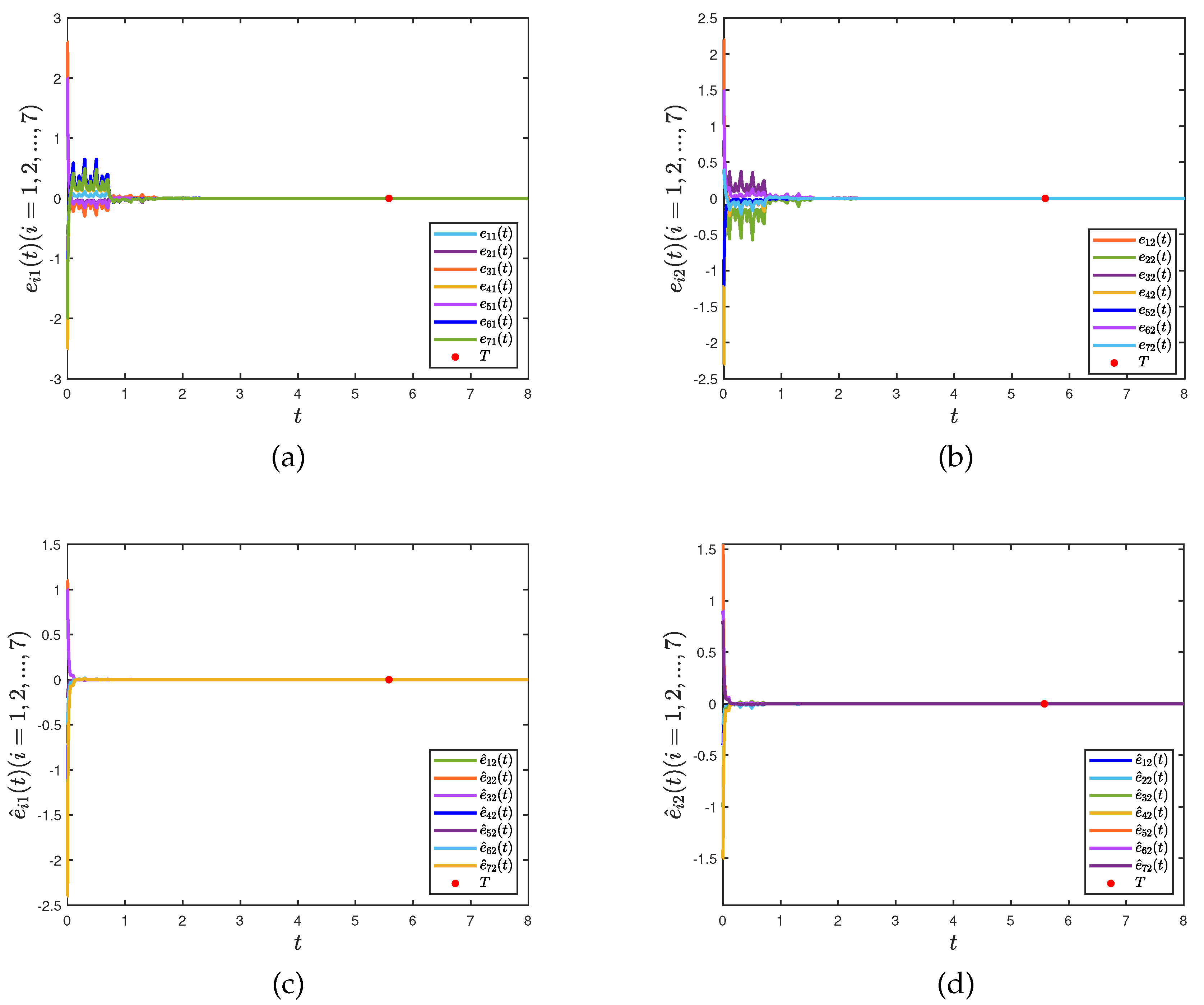
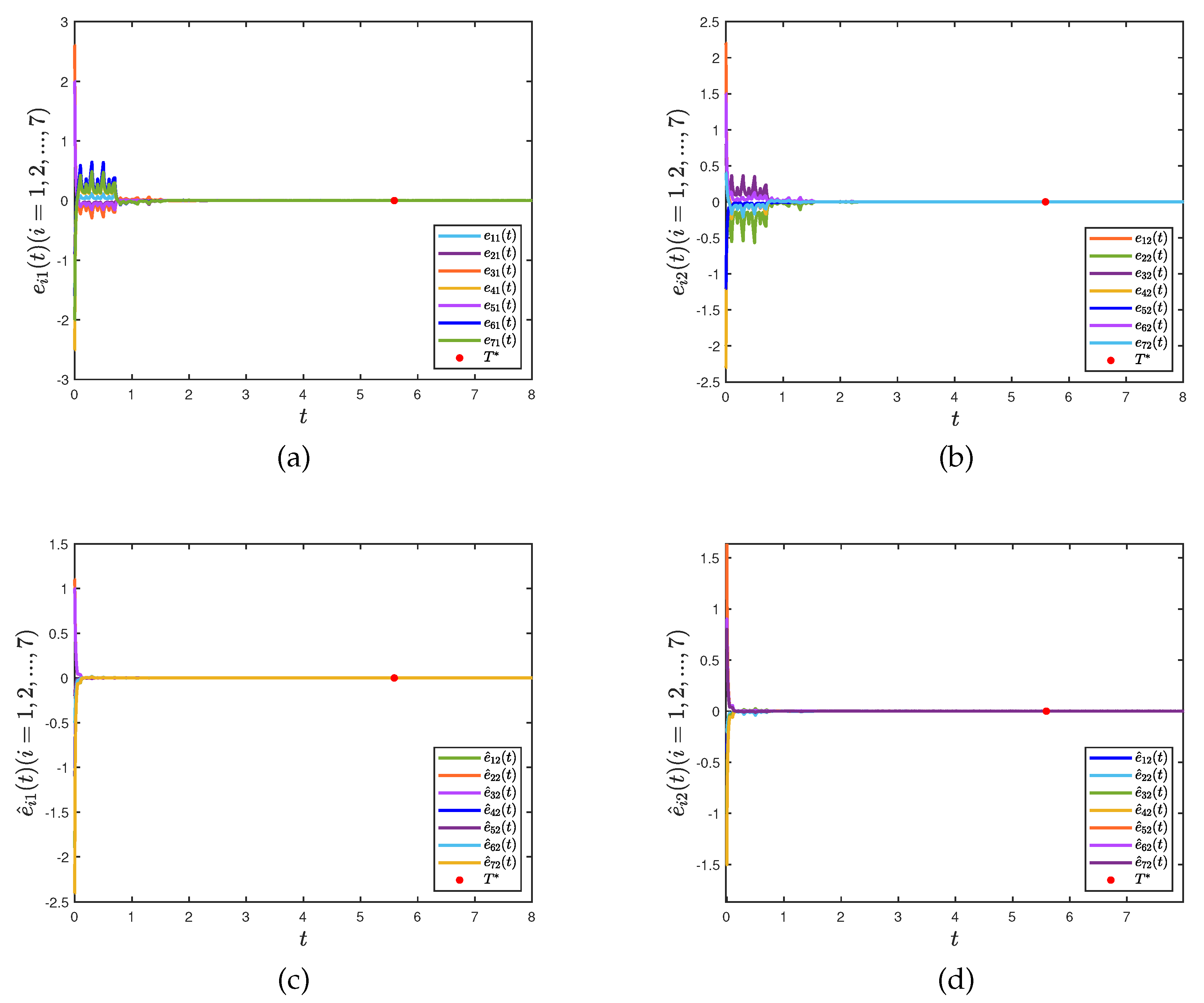
The topology of the networks (27) are presented in Figure 2. Let ${\mathcal{V}}_1=\{1,2,3\}$, ${\mathcal{V}}_2=\{4,5,6,7\}$, and take $\omega =diag(1,1,1,-1,-1,-1,-1)$, ${\left(e_i^T\left(t\right),{\widehat{e}}^T\left(t\right)\right)}^T={\mathbf{x}}_i\left(t\right)-w_i\mathbf{y}\left(t\right)$. Figure 3 depicts the trajectories of networks (26) and (27) under controller (8).

The control intervals of the intermittent controller is designed as follows:

$$\bigcup _{k=0}^{+\infty }[{\zeta }_k,{\mu }_k)=\bigcup _{l=0}^{+\infty }[0.2l,0.2l+0.05)\cup [0.2l+0.1,0.2l+0.18).$$

By simple calculation, $\gamma =0.65$ and $\lambda =32$. Choose $\alpha =0.96$, $\beta =3$, ${\sigma }_1=20$, ${\sigma }_2=25$, ${\kappa }_1=0.01$, ${\kappa }_2=10$, $\varphi =0.5$ , $d=98$ and $T_{\gamma }=0.0001$. By Theorem 1, the networks (26) and (27) are FXT quasi-bipartite synchronization and it is obtained that $T=5.58s$ and error bound is 2.96. The simulation results are presented in Figure 4 and 5.

4.2. Fixed-time quasi-bipartite synchronization with disturbances

Consider the CCNNs with 7 nodes as follows:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill {\dot{x}}_i\left(t\right)=& -C{x}_i\left(t\right)+Af\left(x_i\left(t\right)\right)+Bf\left(x_i(t-\tau \left(t\right))\right)+E{y}_i\left(t\right)\hfill \\ \hfill & +\sum _{j=1}^7|d_{ij}\left|\right(sign\left(d_{ij})x_j\left(t\right)-x_i\left(t\right)\right)+R_i\left(t\right)+{\Xi }_i\left(t\right),\hfill \\ \hfill {\dot{y}}_i\left(t\right)=& -\overline{C}{y}_i\left(t\right)+\overline{A}f\left(x_i\left(t\right)\right)+\sum _{j=1}^7\left|u_{ij}\right|\left(sign\left(u_{ij}\right)y_j\left(t\right)-y_i\left(t\right)\right)\hfill \\ \hfill & +{\overline{R}}_i\left(t\right)+{\Xi }_i\left(t\right),i=1,2,...,7,\hfill \end{array}\hfill \end{array}\right.$$

(28)

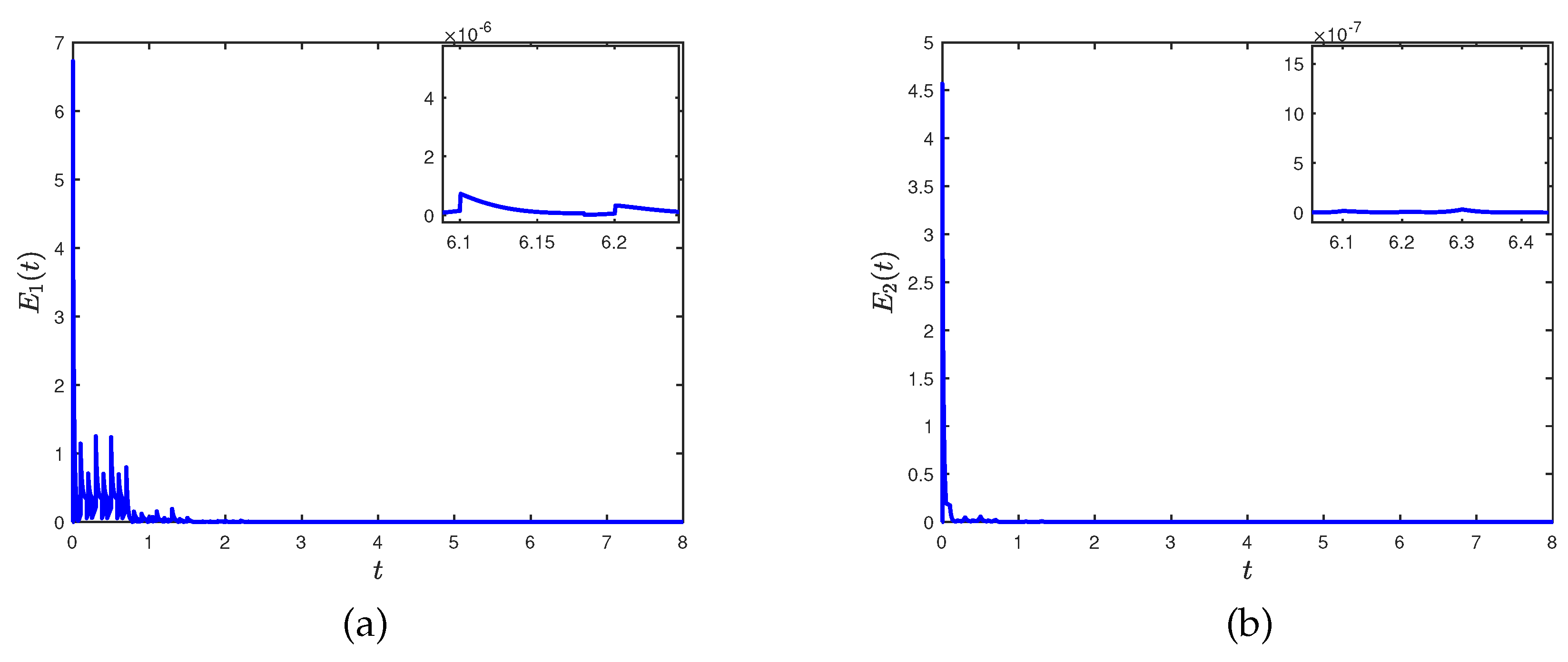
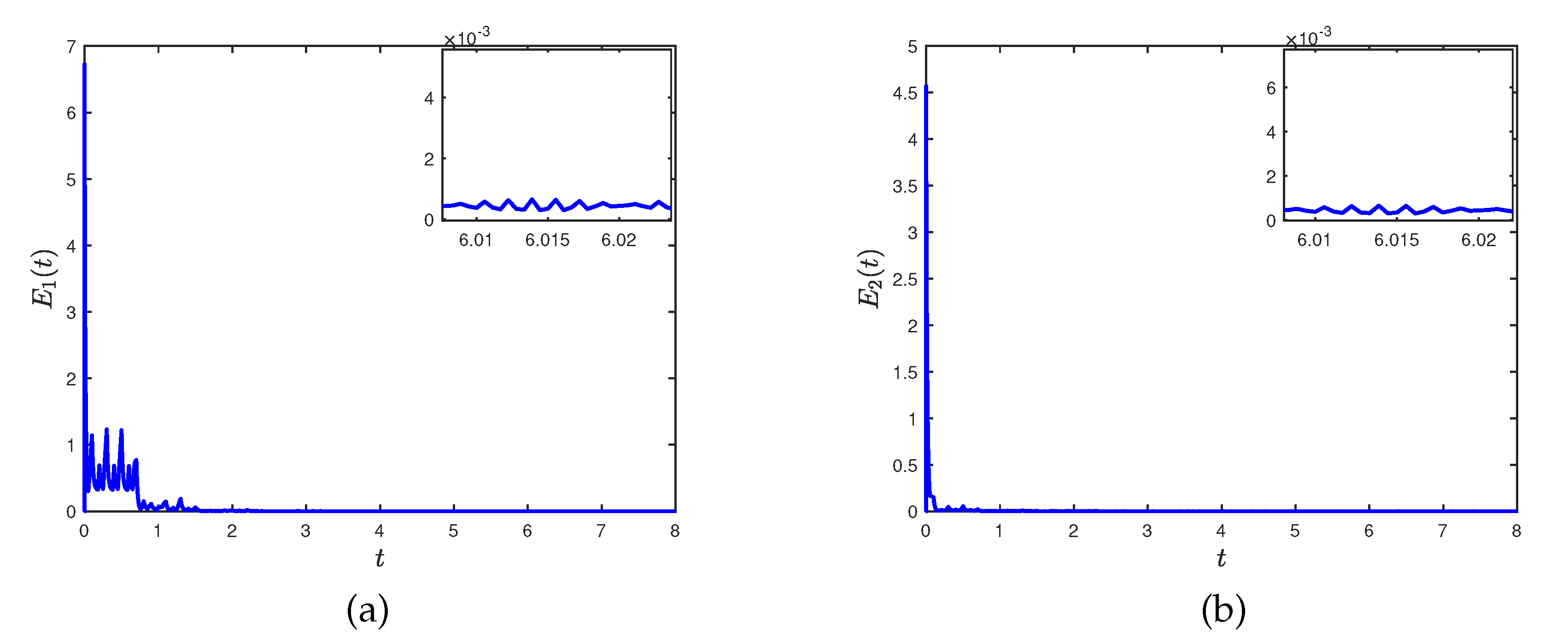
the model parameters are selected in section 4.1, where ${\Xi }_{i1}\left(t\right)=0.2cos\left(t\right)$, ${\Xi }_{i2}\left(t\right)=0.1sin\left(2t\right)$. Figure 6 presents the trajectories of (26) and (28) with controller (8).

In the following, the FXT quasi-bipartite synchronization of the networks (26) and (28) will be verified. According to the parameters in section 4.1, $\gamma =0.65$, $T_{\gamma }=0.0001$ and $\varphi =0.5$. Select $\alpha =0.96$, $\beta =3$, ${\sigma }_1=20$, ${\sigma }_2=25$, ${\kappa }_1=0.01$, ${\kappa }_2=10$, ${\kappa }_3=1$, $\lambda =35$. Evidently, all conditions in Theorem 2 are satisfied and the networks (28) with controller (8) is synchronized with (26) within settling time $T^{*}=5.59s$. Theoretical error bound is 2.97. The corresponding numerical results are illustrated in Figure 7 and 8.

5. Conclusion

In this study, the problem of FXT quasi-bipartite synchronization for CCNNs is considered by intermittent control strategy. Compared with the existing FXT intermittent control strategy, the linear term on the rest interval is removed, which makes our control method simpler and more economical. In addition, the influence of discontinuous activation functions, external disturbances and competitive relationships between nodes are considered in synchronous analysis, which makes the obtained criteria more general. Note that we can implement control measures on all nodes to achieve FXT synchronization when network topology is known. In practical scenarios, it is often either infeasible or unnecessary to control every single node. Therefore, the intermittent pinning control will be considered in forthcoming research.