Optimal Design of Group Orthogonal Phase Coded Waveforms for MIMO Radar

Preprint

Article

Optimal Design of Group Orthogonal Phase Coded Waveforms for MIMO Radar

Altmetrics

Downloads

104

Views

Comments

A peer-reviewed article of this preprint also exists.

Tianqu Liu

Jinping Sun

,Guohua Wang,

Xianxun Yao^*,Yaqiong Qiao

Tianqu Liu

Jinping Sun

,Guohua Wang,

Xianxun Yao^*,Yaqiong Qiao

This version is not peer-reviewed

Submitted:

10 January 2024

Posted:

10 January 2024

You are already at the latest version

Alerts

Abstract

Digital-Radio-Frequency-Memory (DRFM) has emerged as an advanced technique to achieve diverse jamming signals, due to its capability of intercepting waveforms within a short time. Multiple-Input Multiple-Output (MIMO) radars can transmit agile orthogonal waveform sets for different pulses to combat the DRFM-based jamming, where any two groups of waveform sets are also orthogonal. In order to design multiple groups of orthogonal waveform sets at the same time, this article formulates a group orthogonal waveforms optimal design model, whose objec-tive function is the weighted sum of the intra- and inter-group orthogonal performances metrics. To solve this optimization problem, this article proposes a group orthogonal waveforms design algorithm. Based on a primal-dual type method and proper relaxations, the proposed algorithm transforms the original problem into a series of simple sub-problems. Numerical results demonstrate that the proposed algorithm has the ability to balance the intra- and inter-group orthogonal performances by adjusting the weighting factors, which is not available using other state-of-the-art orthogonal waveform design algorithms.

Keywords:

Subject: Engineering - Telecommunications

1. Introduction

Multiple-Input Multiple-Output (MIMO) radar utilizes waveform diversity and multi-antenna technologies to improve its angular resolution, anti-jamming ability and other target detection performances [1,2,3,4]. By transmitting orthogonal waveform sets, MIMO radar can separate the received waveforms transmitted by different antennas. Generally, MIMO radar uses matched filter bank to process the echoes. Thus, the cross-correlation functions among the orthogonal waveforms should be as low as possible. Meanwhile, in order to achieve good pulse compression performance, the auto-correlation functions side-lobes should also be as low as possible.

Designing multiple different phase coding sequences with low cross-correlation is one of the most common ways to realize orthogonal waveform set [5,6,7]. With a large number of transmit waveforms, the phase coded waveform set is difficult to be intercepted by traditional jammers. Integrated Side-lobe Level (ISL) and Peak Side-lobe Level (PSL) are two commonly used metrics for orthogonal MIMO radar phase coded waveform set [9,10,11]. Aiming at ISL minimization, the researchers proposed Multi-CAN, MM-Corr, ISL-New, ADMM and other optimization algorithms [12,13,14,15], which cannot minimize the PSL. The PSL minimization is more complex and harder than ISL minimization. So far, some researchers have proposed effective PSL optimization algorithms [16,17,18,19,20], where the method based on Primal-Dual has the best performance [18]. All the above-mentioned ISL and PSL optimization algorithms design a single set of orthogonal waveforms. With the well-designed orthogonal phase coded waveform set, MIMO radar is able to obtain high waveform diversity gain and low probability of intercept.

With the advent of Digital-Radio-Frequency-Memory (DRFM) [21,22], more advanced jamming technologies have been developed rapidly. The DRFM-based jammers pose a great threat to MIMO radar, which can carry out read, copy and diverse parameters modulation (like delay, Doppler, etc.) within a short time. Therefore, the DRFM-based jammers would seriously affect the operational capabilities of MIMO radar in the future.

Transmitting agile waveform is an effective way to combat modern DRFM-based jamming [23,24]. Although the DRFM-based jammers have a strong ability of intercepting waveforms, they must delay at least one pulse repetition time (PRT) to complete jamming signal generation steps. So, if the correlation between adjacent pulses is low, it is difficult for the DRFM-based jammers to interfere with the waveforms. From the perspective of orthogonality, MIMO radar should transmit orthogonal waveform set intra each pulse. In different pulse intervals, the waveform sets should also be orthogonal to each other. Thus, even though the jammers have intercepted the waveforms in the previous pulse, it cannot interfere with the subsequent pulses. Therefore, this article models the MIMO radar anti-jamming agile waveform as multiple groups of orthogonal waveform sets.

In practice, above-mentioned PSL and ISL optimization algorithms can be used to design all groups of waveforms directly. However, they could not finely control the intra- and inter-group orthogonal performances. In order to overcome the shortcomings of the existing methods, this article proposes an optimal model for designing group orthogonal waveforms. Considering that the target detection is based on the judgment of the correlation peak, the proposed model formulates the objective function considering the following two aspects. One is to minimize the cross-correlation peak and auto-correlation side-lobe peak within each group of orthogonal waveform set, which can be evaluated by the traditional PSL metric. The other is to minimize the cross-correlation peak among the different groups of orthogonal waveforms, which can be evaluated by the peak cross-correlation level (PCL) metric. The objective function of the proposed model is the weighted sum of PSL and PCL metrics.

Minimizing the correlation function peak in the proposed model is difficult. Based on some relaxations, literature [18] divides the origin PSL minimization problem into a series of convex sub-problems. Inspired by the relaxation approach in [18], this article processes the intra- and inter-group correlation functions separately and transforms the proposed optimization model into series solvable sub-problems. After deriving the solutions of each sub-problem, this article proposes a group orthogonal waveforms optimal design algorithm. Numerical results show that the proposed algorithm can effectively design multiple groups of orthogonal waveform sets. The cross-correlation functions between the waveform sets are also low. The anti-jamming simulation results demonstrate that the designed group orthogonal waveforms can balance the DRFM-based deceptive jamming suppression and range compression performances of MIMO radar by adjusting the weighting factors.

2. Problem Formulation

The optimization variables of the group orthogonal waveforms design are G groups of waveforms with each group consisting of M waveforms. Considering phase coded waveform design, the group orthogonal waveforms with intra- and inter-group orthogonality can be realized by assigning different waveforms with different phase coded sequences. Since the pulse length, chip length, carrier frequency and other radar system parameters have little effect on the correlation function side-lobe level, this article models the group orthogonal waveforms

{x_{i}}_{i = 1}^{G M}

x_{i} [n] = \exp (j φ_{i, n}), i = 1, 2, ..., G M, n = 1, 2, ..., N

(1)

where N is sequence length. The phase value is continuous satisfying

φ_{i, n} \in [- π, π)

. The correlation functions of

{x_{i}}_{i = 1}^{G M}

are defined as

r_{i j} [k] = \sum_{n = 1}^{N} x_{i} [n + k] {\bar{x}}_{j} [n], k = - N + 1, ..., N - 1

(2)

where r_ij[k] is auto- or cross-correlation function and

\bar{(\cdot)}

represents complex conjugate. The set of the indexes of intra- and inter-group correlation functions values is defined as

{i, j, k | i, j = 1, 2, ..., G M, k = - N + 1, ..., N - 1}

To evaluate the correlation properties of the group orthogonal waveforms, we consider the intra- and inter-group correlation functions separately. We use the traditional Peak Side-lobe Level (PSL) metric [9,10,11] to evaluate the waveforms intra each group. The PSL metric for the g-th group is defined as

{PSL}_{g} ≜ \frac{1}{N^{2}} \max_{(i, j, k) \in 𝒦_{g}} | r_{i j} [k] |^{2}, g = 1, 2, ..., G

(3)

𝒦_{g} = {i, j, k | i, j \in [M (g - 1) + 1, M g], i \neq j or k \neq 0}

(4)

where set

𝒦_{g}

contains the correlation functions indexes intra the g-th group of waveforms, except the indexes of auto-correlation peak values that identically equal to N. Because there are only cross-correlation functions between different groups of waveforms, the following Peak Cross-correlation Level (PCL) is defined for evaluating the inter-group cross-correlation peak.

PCL ≜ \frac{1}{N^{2}} \max_{(i, j, k) \in 𝒢} {| r_{i j} [k] |}^{2}

(5)

𝒢 = {i, j, k | (i, j, k) \notin \cup_{g = 1}^{G} 𝒦_{g}, i \neq j}

(6)

The set

𝒢

in equation (6) contains all the indexes of inter-group cross-correlation functions.

The object of the group orthogonal waveforms design is to minimize the PSL₁, PSL₂,…, PSL_G and PCL metrics, which are the functions of the optimization variables

{x_{i}}_{i = 1}^{G M}

. Thus, the optimization model can be expressed as

\begin{array}{l} \min f ({x_{i}}_{i = 1}^{G M}) = ({PSL}_{1}, {PSL}_{2}, \dots, {PSL}_{G}, PCL) \\ s . t . | x_{i} [n] | = 1, i = 1, 2, ..., G M, n = 1, 2, ..., N \end{array}

(7)

where f represents the objective function vector, which contains the convolution and max(·) operations. Besides, the waveforms

{x_{i}}_{i = 1}^{G M}

have constant modulus constraints. The optimization model (7) is a complex minimax problem with non-convex constraints. In order to simplify the problem (7), we introduce the variables ε₁, ε₂,…, ε_G and γ to constrain the PSL₁, PSL₂,…, PSL_G and PCL metrics values respectively. Meanwhile, in order to balance the intra- and inter-group orthogonal performances, we introduce a weighting factor w, thereby transforming the origin problem into the following single objective problem.

\begin{array}{l} \min w \cdot (\sum_{g = 1}^{G} ε_{g}^{2} / G) + (1 - w) \cdot γ^{2} \\ s . t . ε_{g} \geq {| r_{i j} [k] |}^{2} / N^{2}, \forall (i, j, k) \in 𝒦_{g}, g = 1, 2, ..., G \\ γ \geq {| r_{i j} [k] |}^{2} / N^{2}, \forall (i, j, k) \in 𝒢 \\ r_{i j} (k) = \sum_{n} x_{i} [n + k] {\bar{x}}_{j} [n], \forall (i, j, k) \\ | x_{i} [n] | = 1, \forall (i, n) \end{array}

(8)

Note that the convolution operations and constant modulus constraints in problem (8) are not conducive to solving this problem. Inspired by literature [18], we introduce the auxiliary variables

{h_{i}}_{i = 1}^{G M}

and ρ_ij(k) to decompose the complex nonlinear convolutions. Then, the correlation functions constraints are replaced by the following linear equality constraints.

{\begin{cases} ρ_{i j} (k) = \sum_{n} x_{i} [n + k] {\bar{h}}_{j} [n], \forall (i, j, k) \\ h_{i}^{H} x_{i} = N, {‖ h_{i} ‖}_{2}^{2} \leq N, \forall i \end{cases}

(9)

In equation (9), if h_i=x_i holds for all i=1, 2,…, GM, then ρ_ij(k) are equal to the correlation functions r_ij(k). This equivalent constraint condition in equation (9) is correct according to the proposition below.

Proposition 1.

The constraints

h_{i}^{H} x_{i} = N, {‖ h_{i} ‖}_{2}^{2} \leq N

are equivalent to the constraint h_i= x _i for all i=1, 2,…, GM.

Proof of Proposition 1.

According to the Cauchy-Schwartz inequality

h_{i}^{H} x_{i} = N = | h_{i}^{H} x_{i} | \leq {‖ h_{i} ‖}_{2} {‖ x_{i} ‖}_{2} = \sqrt{N} {‖ h_{i} ‖}_{2}

(10)

Meanwhile,

{‖ h_{i} ‖}_{2} \leq \sqrt{N}

holds, then inequality (10) implies

{‖ h_{i} ‖}_{2} = \sqrt{N}

. Using the equality condition of the Cauchy-Schwartz inequality, we get

x_{i} = κ h_{i}, κ \in ℂ

(11)

According to equation (11) and

h_{i}^{H} x_{i} = N

, it is not difficult to find

κ = 1

. Thus, h_i=x_i is obtained and the proof is complete. □

By introducing the variables

{h_{i}}_{i = 1}^{G M}

, ρ_ij(k), the nonlinear constraints are relaxed to linear convex constraints. However, the constant modulus constraints of

{x_{i}}_{i = 1}^{G M}

in problem (8) are still coupled with its other constraints, which poses difficulties of solving for

{x_{i}}_{i = 1}^{G M}

. Therefore, we introduce the variables

{y_{i}}_{i = 1}^{G M}

to simplify the sub-problem about

{x_{i}}_{i = 1}^{G M}

. The following conditions are added to ensure the obtained waveforms are constant modulus.

x_{i} [n] = y_{i} [n], | y_{i} [n] | = 1, \forall (i, n)

(12)

Then, the constant modulus constraints are transferred to the sub-problem about

{y_{i}}_{i = 1}^{G M}

, which is easy to be solved even with the constant modulus constraints. The sub-problem about

{x_{i}}_{i = 1}^{G M}

becomes an unconstrained convex problem.

After introducing series auxiliary variables into the optimization model (8), we formulate the following group orthogonal waveforms optimal design model.

\begin{array}{l} \min w \cdot (\sum_{g = 1}^{G} ε_{g}^{2} / G) + (1 - w) \cdot γ^{2} \\ s . t . | ρ_{i j} (k) | \leq ε_{g}, \forall (i, j, k) \in 𝒦_{g}, g = 1, 2, ..., G \\ | ρ_{i j} (k) | \leq γ, \forall (i, j, k) \in 𝒢 \\ ρ_{i j} (k) = \sum_{n} x_{i} [n + k] {\bar{h}}_{j} [n], \forall (i, j, k) \\ h_{i}^{H} x_{i} = N, {‖ h_{i} ‖}_{2}^{2} \leq N, \forall i \\ x_{i} [n] = y_{i} [n], | y_{i} [n] | = 1, \forall (i, n) \end{array}

(13)

The weighting factor w can balance the intra- and inter-group correlation peak values. The optimization variables include

{x_{i}}_{i = 1}^{G M}

{y_{i}}_{i = 1}^{G M}

{h_{i}}_{i = 1}^{G M}

, ρ_ij(k), γ and ε_g, g=1, 2,…, G. Although the dimension of the optimization variables is increased, the intractable nonlinear and non-convex constraints in the optimization model (8) are relaxed into a series of linear and convex constraints.

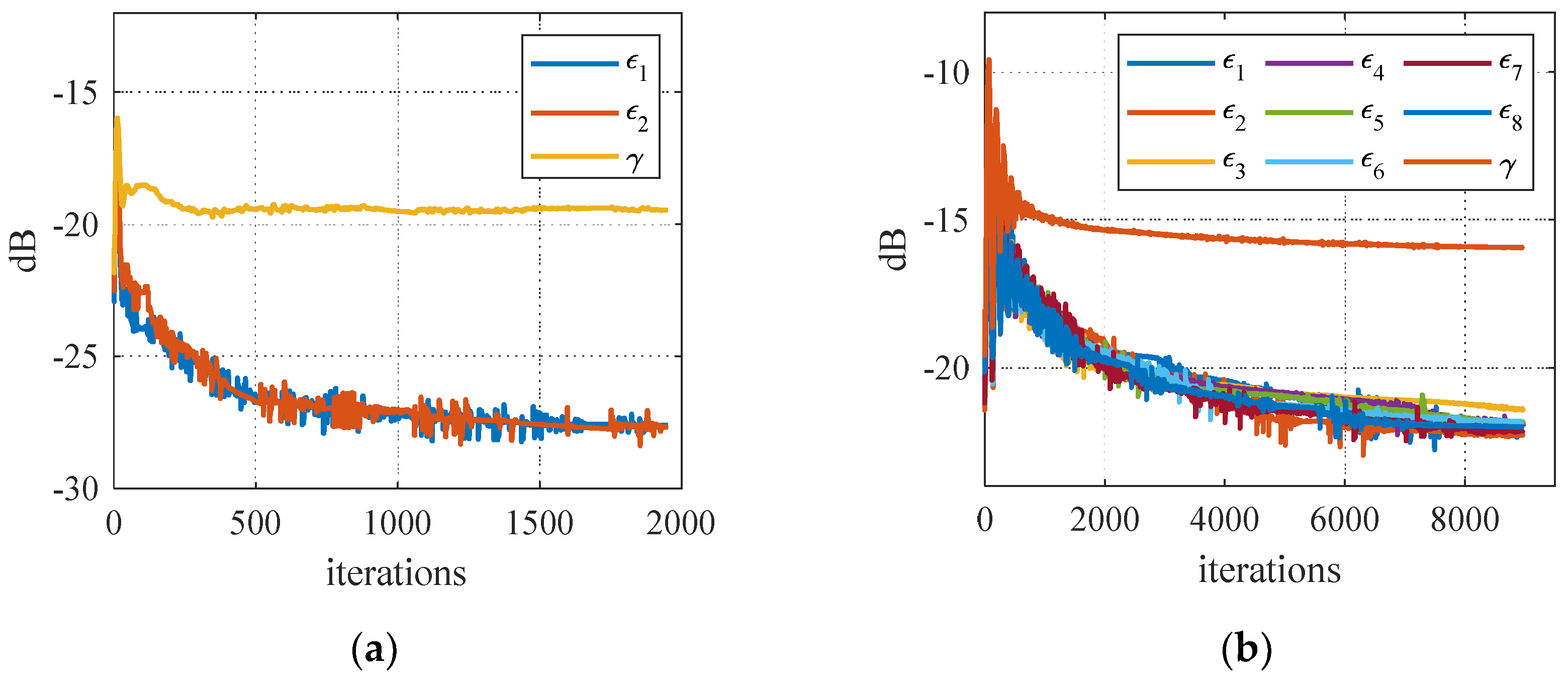
3. Proposed Group Orthogonal Waveform Design Algorithm

Based on the characteristics of the objective function and constraints in the optimization model (13), we formulate an augmented Lagrange function [25] and transform the problem (13) into the following constrained minimization problem.

\begin{array}{l} \min L (ε_{1}, ..., ε_{G}, γ, {ρ_{i j} (k)}, {x_{i}}, {y_{i}}, {h_{i}}, {λ_{i}}, {α_{i j k}}, {β_{i n}}) \\ s . t . | ρ_{i j} (k) | \leq ε_{g}, \forall (i, j, k) \in 𝒦_{g}, g = 1, 2, ..., G \\ | ρ_{i j} (k) | \leq γ, \forall (i, j, k) \in 𝒢 \\ {‖ h_{i} ‖}_{2}^{2} \leq N, \forall i \\ | y_{i} [n] | = 1, \forall (i, n) \end{array}

(14)

The augmented Lagrange function L can be expressed as

\begin{array}{l} L = w \cdot (\sum_{g = 1}^{G} ε_{g}^{2} / G) + (1 - w) \cdot γ^{2} + Re [\sum_{i} {\bar{λ}}_{i} (h_{i}^{H} x_{i} - N)] \\ + Re [\sum_{(i, j, k) \in (\cup_{g = 1}^{G} 𝒦_{g}) \cup 𝒢} {\bar{α}}_{i j k} (ρ_{i j} (k) - \sum_{n} x_{i} [n + k] {\bar{h}}_{j} [n])] \\ + Re [\sum_{i, n} {\bar{β}}_{i n} (x_{i} [n] - y_{i} [n])] + \frac{θ_{1}}{2} (\sum_{i} {| h_{i}^{H} x_{i} - N |}^{2}) \\ + \frac{θ_{2}}{2} (\sum_{(i, j, k) \in (\cup_{g = 1}^{G} 𝒦_{g}) \cup 𝒢} {| ρ_{i j} (k) - \sum_{n} x_{i} [n + k] {\bar{h}}_{j} [n] |}^{2}) \\ + \frac{θ_{3}}{2} (\sum_{i, n} {| x_{i} [n] - y_{i} [n] |}^{2}) \end{array}

(15)

where Re[·] represents the real part of a complex number. θ₁, θ₂, θ₃ are penalty parameters. {λ_i}, {α_ijk}, {β_in} are Lagrangian multipliers, also dual variables. To solve the problem (14), we propose a group orthogonal waveforms design algorithm based on a primal-dual type method. The proposed algorithm decomposes the problem (14) into series simple sub-problems. By sequentially updating the optimization variables and dual variables, the proposed algorithm minimizes the augmented Lagrange function L in equation (15) after iterations. According to the optimization model (13), the variables

{x_{i}^{(l)}}_{i = 1}^{G M}

{y_{i}}_{i = 1}^{G M}

and

{h_{i}^{(l)}}_{i = 1}^{G M}

will converge to the same point. The convergence condition is

\sum_{i} {‖ h_{i}^{(l)} - x_{i}^{(l)} ‖}_{2}^{2} / \sum_{i} {‖ x_{i}^{(l)} ‖}_{2}^{2} < η

. Algorithm 1 summarizes the proposed algorithm. The sub-problems of the proposed group orthogonal waveforms design algorithm can be expressed as follows.

{ε_{1}, \dots, ε_{G}, γ, \underset{\begin{array}{l} | ρ_{i j} (k) | \leq ε_{g}, \forall (i, j, k) \in 𝒦_{g}, g = 1, 2, ..., G \\ | ρ_{i j} (k) | \leq γ, \forall (i, j, k) \in 𝒢 \end{array}}{ρ_{i j} (k)}^{(l + 1)} = \arg \min L} (\begin{array}{l} ε_{1}, \dots, ε_{G}, γ, ρ_{i j} (k) \\ {x_{i}, y_{i}, h_{i}, λ_{i}, α_{i j k}, β_{i n}}^{(l)} \end{array})

(16)

{h_{i}}^{(l + 1)} = \underset{{‖ h_{i} ‖}_{2}^{2} \leq N, \forall i}{\arg \min} L (\begin{array}{l} {ε_{1}, \dots, ε_{G}, γ, ρ_{i j} (k)}^{(l + 1)}, \\ {h_{i}}, {x_{i}, y_{i}, λ_{i}, α_{i j k}, β_{i n}}^{(l)} \end{array})

(17)

{x_{i}}^{(l + 1)} = \arg \min L (..., {x_{i}}, ...)

(18)

{y_{i}}^{(l + 1)} = \underset{| y_{i} [n] | = 1, \forall (i, n)}{\arg \min} L (..., {y_{i}}, ...)

(19)

{\begin{cases} λ_{i}^{(l + 1)} = λ_{i}^{(l)} + c θ_{1} ({(h_{i}^{(l + 1)})}^{H} x_{i}^{(l + 1)} - N) \\ α_{i j k}^{(l + 1)} = α_{i j k}^{(l)} + c θ_{2} (ρ_{i j}^{(l + 1)} (k) - \sum_{n} x_{i}^{(l + 1)} [n + k] {\bar{h}}_{j}^{(l + 1)} [n]) \\ β_{i n}^{(l + 1)} = β_{i n}^{(l)} + c θ_{3} (x_{i}^{(l + 1)} [n] - y_{i}^{(l + 1)} [n]) \end{cases}

(20)

The parameter c in equation (20) is the step length. The superscript (l) represents the values of variables at the l-th iteration. Except for the sub-problem (16), the sub-problems (17-19) are actually the same as the Primal-Dual algorithm [18], which can be solved using similar methods as Primal-Dual. The rest of this section introduces the methods to solve the sub-problems.

Algorithm 1 Group Orthogonal Waveforms Design Algorithm

Initialization
Select randomly

{x_{i}^{(0)}}_{i = 1}^{G M}

(Constant modulus is not required).
Set constant modulus

{y_{i}^{(0)}}_{i = 1}^{G M}

using the phases of

{x_{i}^{(0)}}_{i = 1}^{G M}

.
Select randomly {λ_i}, {α_ijk}, {β_in} and

{h_{i}^{(0)}}_{i = 1}^{G M}

, set l=0.
Repeat
Compute

{ε_{1}, \dots, ε_{G}, γ, ρ_{i j} (k)}^{(l + 1)}

by solving sub-problem (16).
Compute

{h_{i}}^{(l + 1)}

by solving sub-problem (17).
Compute

{x_{i}}^{(l + 1)}

by solving sub-problem (18).
Compute

{y_{i}}^{(l + 1)}

by solving sub-problem (19).
Compute

λ_{i}^{(l + 1)}, α_{i j k}^{(l + 1)}, β_{i n}^{(l + 1)}

using (20), l=l+1.
Until

\sum_{i} {‖ h_{i}^{(l)} - x_{i}^{(l)} ‖}_{2}^{2} / \sum_{i} {‖ x_{i}^{(l)} ‖}_{2}^{2} < η

3.1. Solving sub-problem (16)

According to the augmented Lagrange function (15), the sub-problem (16) can be separated into two independent parts as follow.

\begin{matrix} \min_{| ρ_{i j} (k) | \leq ε_{g}} w ε_{g}^{2} / G + \sum_{(i, j, k) \in 𝒦_{g}} [a_{i j k} {| ρ_{i j} (k) |}^{2} + Re ({\bar{b}}_{i j k} ρ_{i j} (k))] \\ g = 1, 2, ..., G \end{matrix}

(21)

\min_{| ρ_{i j} (k) | \leq γ} (1 - w) γ^{2} + \sum_{(i, j, k) \in 𝒢} [a_{i j k} {| ρ_{i j} (k) |}^{2} + Re ({\bar{b}}_{i j k} ρ_{i j} (k))]

(22)

where

a_{i j k} = θ_{2} / 2, b_{i j k} = α_{i j k}^{(l)} - θ_{2} \cdot \sum_{n} x_{i}^{(l)} [n + k] {\bar{h}}_{j}^{(l)} [n]

. Considering the problem (21), when ε_g is fixed, the optimal solution of ρ_ij(k) for every index (i,j,k) can be expressed as

ρ_{i j k}^{*} (ε_{g}) = {\begin{cases} - b_{i j k} / (2 a_{i j k}), | b_{i j k} / (2 a_{i j k}) | \leq ε_{g} \\ - (b_{i j k} / | b_{i j k} |) ε_{g}, others \end{cases}

(23)

where

ρ_{i j k}^{*} (ε_{g})

is a function of ε_g. According to equation (23), the problem (21) is equivalent to

\min_{ε_{g} \geq 0} f (ε_{g}) ≜ w ε_{g}^{2} / G + \sum_{(i, j, k) \in 𝒦_{g}} f_{i j k}^{*} (ε_{g}), g = 1, 2, ..., G

(24)

where

\begin{matrix} f_{i j k}^{*} (ε_{g}) = a_{i j k} {| ρ_{i j k}^{*} (ε_{g}) |}^{2} + Re ({\bar{b}}_{i j k} ρ_{i j k}^{*} (ε_{g})) \\ = {\begin{cases} - {| b_{i j k} |}^{2} / (4 a_{i j k}), | b_{i j k} / (2 a_{i j k}) | \leq ε_{g} \\ a_{i j k} ε_{g}^{2} - | b_{i j k} | ε_{g}, others \end{cases} \end{matrix}

(25)

Because

f (ε_{g}) \leq f (- ε_{g})

, the condition

ε_{g} \geq 0

can be ignored. The optimal

ε_{g}^{*}

can be determined by solving the following equation.

\nabla f (ε_{g}) = 2 w ε_{g} + \sum_{(i, j, k) \in 𝒦_{g}} \min {2 a_{i j k} ε_{g} - | b_{i j k} |, 0} = 0

(26)

Because

a_{i j k} = θ_{2} / 2 > 0

\nabla f (ε_{g})

is a monotonically increasing function of ε_g. The optimal

ε_{g}^{(l + 1)} = ε_{g}^{*}

can be obtained efficiently by bisection method. Similarly, the optimal solution

γ^{(l + 1)} = γ^{*}

of problem (22) can be obtained by solving the following equation.

2 (1 - w) γ + \sum_{(i, j, k) \in 𝒢} \min {2 a_{i j k} γ - | b_{i j k} |, 0} = 0

(27)

3.2. Solving sub-problem (17)

According to equation (15), sub-problem (17) is separable for each h_i, i=1, 2,..., GM. The minimization problem can be expressed as

\min_{{‖ h_{i} ‖}_{2}^{2} < N} f (h_{i}) ≜ h_{i}^{H} A_{i} h_{i} + Re (t_{i}^{H} h_{i})

(28)

where

A_{i} = (θ_{2} / 2) \cdot \sum_{j, k} x_{j, (- k)}^{(l)} x_{j, (- k)}^{(l) H}

(29)

t_{i} = {\bar{λ}}_{i}^{(l)} x_{i}^{(l)} - θ_{1} N x_{i}^{(l)} - \sum_{j, k} ({\bar{α}}_{j i k}^{(l)} + θ_{2} {\bar{ρ}}_{j i}^{(l + 1)} (k)) x_{j, (- k)}^{(l)}

(30)

where x_j_,k represents the aperiodic delayed copy of the discrete signal x_j. For

k \geq 0

x_{j, k} = {(x_{j} [k + 1], x_{j} [k + 2], \dots, x_{j} [N], 0_{1 \times k})}^{T}

, for

k \leq 0

x_{j, k} = {(0_{1 \times | k |}, x_{j} [1], x_{j} [2], \dots, x_{j} [N - | k |])}^{T}

. The augmented Lagrange function of problem (28) can be expressed as follows.

L_{i} (h_{i}, λ) = h_{i}^{H} A_{i} h_{i} + Re (t_{i}^{H} h_{i}) + λ ({‖ h_{i} ‖}_{2}^{2} - N)

(31)

The Karush-Kuhn-Tucker (KKT) conditions for problem (28) are as follows.

{\begin{matrix} {‖ h_{i}^{*} ‖}_{2}^{2} \leq N, 2 A_{i} h_{i}^{*} + t_{i} + 2 λ^{*} h_{i}^{*} = 0 \\ λ^{*} \geq 0, λ^{*} ({‖ h_{i}^{*} ‖}_{2}^{2} - N) = 0 \end{matrix}

(32)

Obviously, when

λ^{*} = 0

, the KKT conditions (32) is equivalent to

{‖ h_{i}^{*} ‖}_{2}^{2} \leq N ， h_{i}^{*} = - A_{i}^{- 1} t_{i} / 2

(33)

If condition (33) is true, then

h_{i}^{(l + 1)} = h_{i}^{*}

, otherwise, the optimal solution should solved under the condition of

λ^{*} > 0

When

λ^{*} > 0

, condition (32) is equivalent to

{‖ h_{i}^{*} ‖}_{2}^{2} = N, h_{i}^{*} = - {(A_{i} + 2 λ^{*} I)}^{- 1} t_{i} / 2

(34)

In order to solve equation (34), the value of λ^* should be determined. According to equation (31), for any fixed value of

λ > 0

, the optimal v(λ) with minimal L_i(v(λ), λ) is below.

v (λ) = - {(A_{i} + 2 λ I)}^{- 1} t_{i} / 2

(35)

0 < λ^{'} < λ

, then

{\begin{cases} L_{i} (v (λ), λ) \leq L_{i} (v (λ^{'}), λ) \\ L_{i} (v (λ^{'}), λ^{'}) \leq L_{i} (v (λ), λ^{'}) \end{cases}

(36)

According to the function (31), and sum the two inequalities in (36), then

(λ^{'} - λ) {‖ v (λ^{'}) ‖}_{2}^{2} \leq (λ^{'} - λ) {‖ v (λ) ‖}_{2}^{2}

(37)

Therefore,

{‖ v (λ) ‖}_{2}^{2}

is a monotone decreasing function of λ. Solving the KKT conditions when

λ^{*} > 0

is equivalent to find the zero of the function

{‖ v (λ) ‖}_{2}^{2} - N

, which can be solved by the bisection method.

3.3. Solving sub-problem (18)

According to equation (15), sub-problem (18) can be separated into following unconstrained convex problem for each x_i, i=1, 2,…, GM.

\min_{x_{i}} f (h_{i}) ≜ x_{i}^{H} C_{i} x_{i} + Re (d_{i}^{H} x_{i})

(38)

where

C_{i} = (θ_{2} / 2) \cdot \sum_{j, k} h_{j, k}^{(l + 1)} h_{j, k}^{(l + 1) H} + (θ_{3} / 2) I

(39)

d_{i} = λ_{i}^{(l)} h_{i}^{(l + 1)} + β_{i}^{(l)} - θ_{1} N h_{i}^{(l + 1)} - \sum_{j, k} (α_{i j k}^{(l)} + θ_{2} ρ_{i j}^{(l + 1)} (k)) h_{j, k}^{(l + 1)} - θ_{3} y_{i}^{(l)}

(40)

where h_j_,k represents the periodic delayed copy of h_j, similar to the x_j_,k in equation (29) and (30). It is easy to find that the C_i in equation (39) is an N×N positive definite matrix. Therefore, the sub-problem (38) is an unconstrained quadratic optimization problem, whose optimal solution is

x_{i}^{(l + 1)} = x_{i}^{*} = - C_{i}^{- 1} d_{i} / 2

and can be found efficiently by conjugate gradient methods.

3.4. Solving sub-problem (19)

According to equation (15), sub-problem (19) can be separated for each y_i[n], i=1, 2,…, GM, n=1, 2,…, N, as follow.

\min_{| y_{i} [n] | = 1} Re [{\bar{u}}_{i n} y_{i} [n]]

(41)

where

u_{i n} = - β_{i n}^{(l)} - θ_{3} x_{i}^{(l + 1)} [n]

(42)

Define

{\bar{u}}_{i n} = | {\bar{u}}_{i n} | \cdot \exp (j ϕ_{i n})

, then the solution of the sub-problem (41) can be expressed as

y_{i}^{(l + 1)} [n] = y_{i}^{*} [n] = \exp (j \cdot (π - ϕ_{i n}))

4. Numerical Results

In order to demonstrate the effectiveness of Algorithm 1, this section performs a series of numerical simulations. The parameters are initialized as c=0.5, θ₁=θ₂=10. The parameter is set as

θ_{3} = \max {10, \min {2 (l + 1), 10^{5}}}

, where l is the current iteration. The parameter of the convergence condition is η=0.5×10⁻³. All experiments are implemented with MATLAB that runs on a PC with one Intel Core i7-7700 CPU and 16 GB RAM. All the obtained correlation function values and PSL, PCL metrics values in dB are calculated as 10log₁₀(|r_ij(k)|²/N²).

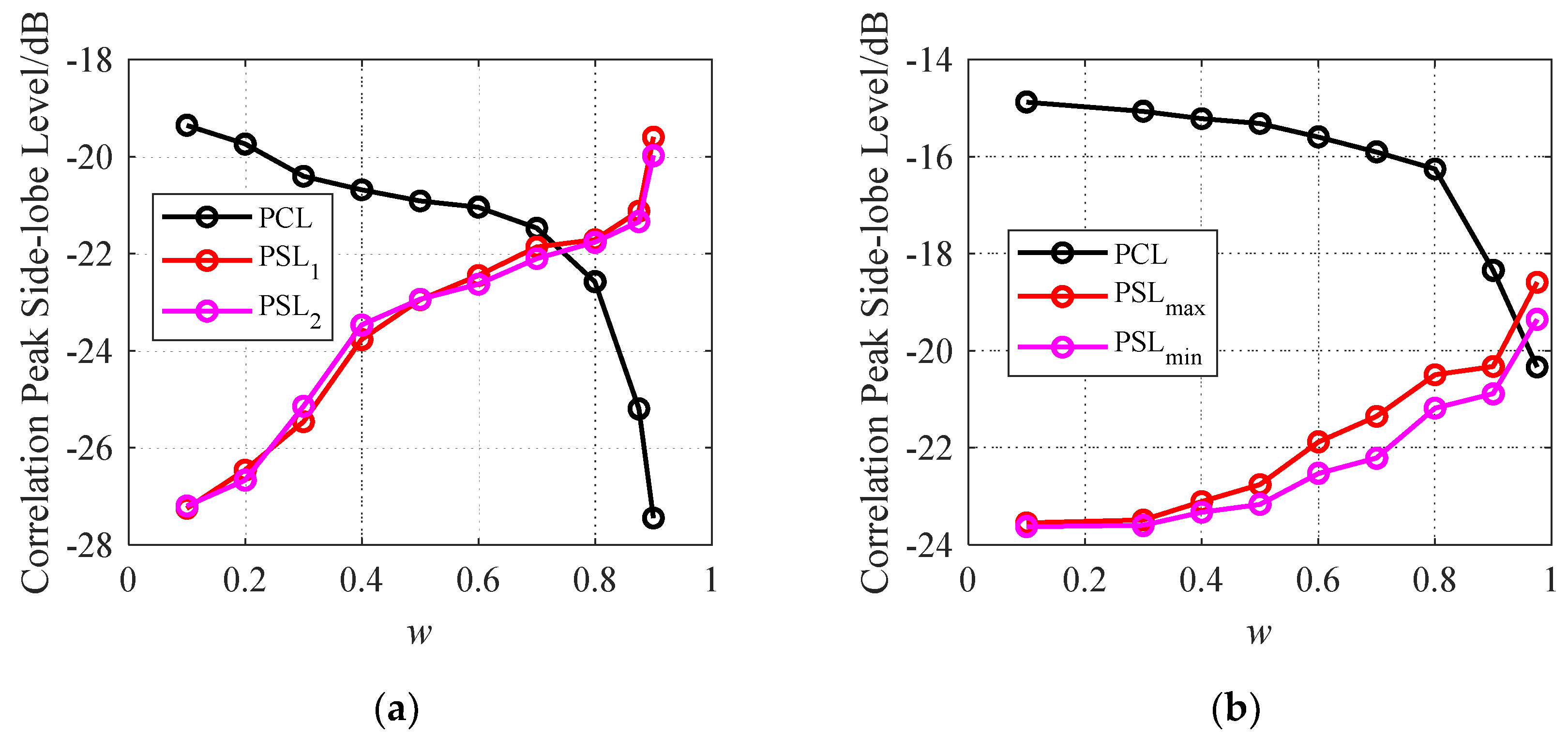
4.1. Effect of weighting factor w

Under different parameters, Figure 1 shows the convergence curves of the variables γ and ε_g, g=1, 2,…, G. The computational complexity per iteration of the proposed algorithm is

𝒪 (M G N^{2} + M^{2} G^{2} N \log N)

. The algorithm running time under M=2, G=2, N=256 is around 700 seconds on average. The convergence curves of the variables γ and ε_g are not monotonically decreasing because the proposed algorithm minimizes the augmented Lagrange function L in equation (15). When the convergence condition is satisfied, the variables

{x_{i}^{(l)}}_{i = 1}^{G M}

and

{h_{i}^{(l)}}_{i = 1}^{G M}

are almost the same, and the correlation function r_ij(k) of the optimal waveforms

{x_{i}}_{i = 1}^{G M}

satisfies r_ij(k)=ρ_ij(k). Thus, the PCL, PSL₁, PSL₂,…, PSL_G metrics are minimized effectively with the help of the auxiliary variables.

In order to analyze the effect of the weighting factor w on the metrics values, Figure 2(a) shows the PSL₁, PSL₂, and PCL metrics values obtained under different values of w, with fixed parameters of M=2, G=2 and N=256. Figure 2(b) performs the similar results under M=8, G=8 and N=256. Because the number of waveforms is large, the maximum and minimum values among PSL₁, PSL₂,…, PSL_G are shown, denoted by PSL_max and PSL_min respectively. It can be seen that the smaller the value of w, the lower the obtained intra-group PSL metrics values, and the higher the obtained inter-group PCL metric value. The results in Figure 2 demonstrate that the proposed algorithm is able to adjust the weighting factor w to balance the intra- and inter-group correlation functions performances for different requirements in MIMO radar applications.

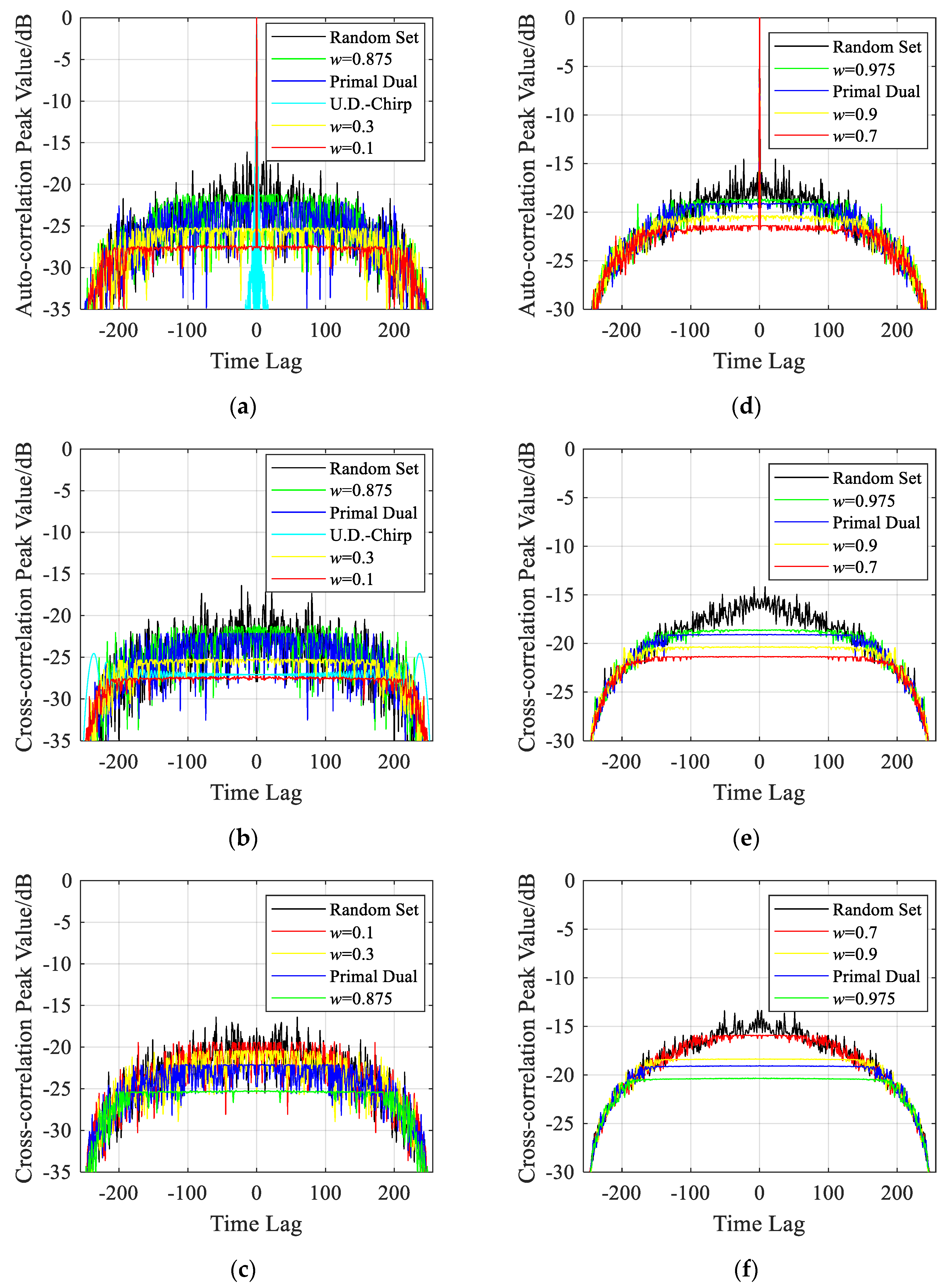
4.2. Obtained correlation functions

This subsection plots the intra- and inter-group correlation functions curves. Under different parameters, the obtained waveforms by the proposed group orthogonal waveforms algorithm are compared to other advanced orthogonal waveforms. In Figure 3, the Random-Set represents the waveforms generated directly by random numbers. The Primal-Dual algorithm is the current best PSL optimization algorithm for single orthogonal waveform set. The Up- and Down-Chirp signals have the lowest cross-correlation function when M=2. Therefore, by setting the same time-bandwidth product equal to N=256, the Up- and Down-Chirp signals can be compared to the intra-group orthogonal performance of the waveforms when M=2.

Under M=2, G=2 and N=256, Figure 3(a) shows the auto-correlation function peak value of the GM waveforms. Figure 3(b) shows the intra-group cross-correlation function peak value. Figure 3(c) shows the inter-group cross-correlation function peak value. Obviously, when w=0.1, the intra-group correlation side-lobe peak value obtained by the proposed algorithm is the lowest, compared to other waveforms, with relatively higher inter-group cross-correlation function peak value. When w=0.875, although the intra-group auto- and cross-correlation functions of the waveforms obtained by the proposed algorithm are relatively high, its inter-group cross-correlation functions are the lowest. The results under w=0.3 lie between those under w=0.1 and w=0.875. Figure 3(d), 3(e), 3(f) show the results under M=8, G=8, N=256.

The results in Figure 3 demonstrate that, under typical parameters, the proposed group orthogonal waveforms design algorithm is able to balance the intra- and inter-group correlation functions performances effectively. To brief sum up, compared with designing all the GM waveforms directly using the Primal-Dual algorithm, the proposed group orthogonal waveforms design algorithm is able to obtaining the lower intra-group PSL metrics by sacrificing a small quantity of inter-group cross-correlation performance, or vice versa. Therefore, for the applications of anti-jamming agile waveform, the proposed algorithm is more flexible. The proposed group orthogonal waveform design algorithm is able to design multiple groups of orthogonal waveform sets at the same time.

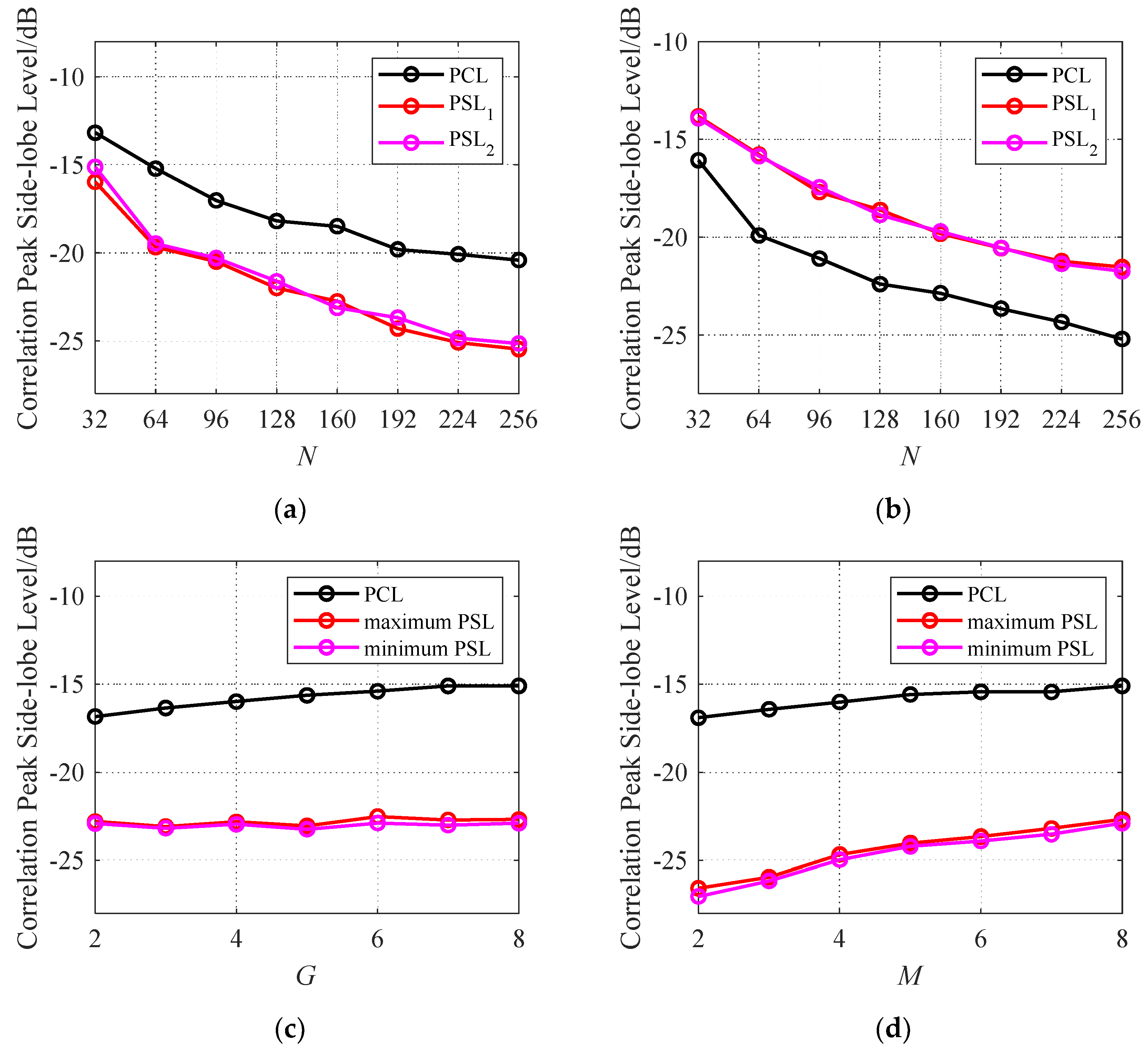
4.3. Effect of parameters M, N, G

Figure 4(a), 4(b) analyzes the effect of phase coding sequence length N on the results. The simulation keeps the weighting factor w and the waveform parameters M=2, G=2 unchanged. The waveforms are obtained by the proposed algorithm under N=32, 64, 96, 128, 160, 192, 224, 256. After calculating the PCL and intra-group PSL metrics (The PSL metrics are denoted by PSL₁ and PSL₂ because G=2), Figure 4(a), 4(b) show the obtained metrics values under w=0.3 and w=0.875 respectively. The results demonstrate that the larger the sequence length, the lower the obtained PCL and PSL metrics values.

Figure 4(c), 4(d) analyzes the effects of the number of groups G and the number of intra-group waveforms M on the results. Firstly, set the weighting factor as w=0.5 and the parameters as M=8, N=256. Then, perform the proposed algorithm to obtain the waveforms under G=2, 3, 4, 5, 6, 7, 8. Finally, calculate the PCL metric value and the maximum and minimum values among the PSL₁, PSL₂,…, PSL_G. The results are shown in Figure 4(c). It can be seen that the PCL is higher with the increase of G, because the total number of waveforms GM increases. Meanwhile, the obtained intra-group PSL metrics values change little with the increase of G, because the number of intra-group waveforms M=8 remains unchanged. Figure 4(d) keeps the parameter G=8 unchanged and performs the proposed algorithm under parameters M=2, 3, 4, 5, 6, 7, 8. It can be seen that the intra-group PSL metrics values are higher with the increase of M. Overall, the PCL metric value mainly depends on the total number of waveforms GM. The intra-group PSL metric values mainly depend on the parameter M.

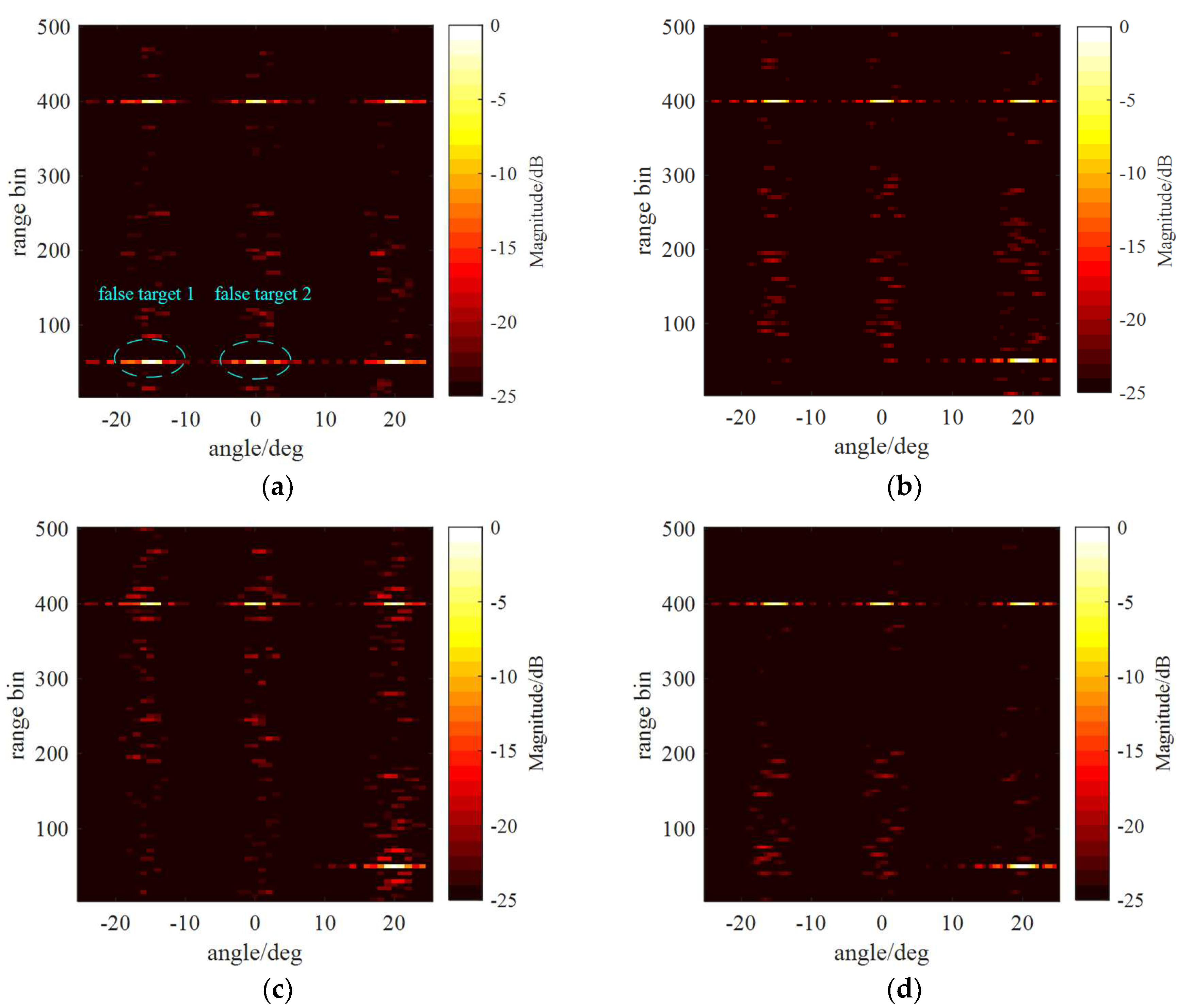
4.4. Anti-jamming simulation

In this section, the deceptive jamming suppression performances of MIMO radar using different waveforms in Table 1 are simulated. The radar is located at the origin of coordinates, whose carrier wavelength λ is 1 m and size of range bins is 100 m. The range corresponding to the first bin is 50 km. The angles, ranges and signal-to-noise ratios of the simulated four true targets are (−15°, 400, 3 dB), (0°, 400, 3 dB) (20°, 400, 3 dB) and (20°, 50, 5 dB), where the range parameters are in unit of range bin. The DRFM-based deceptive jamming causes 2 false targets, whose angles, ranges and jamming-to-noise ratios are (−15°, 50, 5 dB) and (0°, 50, 5 dB). The noise is Gaussian random white noise. The uniform linear array consists of 3 transmit elements spaced at 16λ apart, and 16 receive elements spaced at 0.5λ apart. Assumed that one pulse of the waveform has been intercepted, Figure 5 shows the angle-range images formed with MIMO radar using the adjacent pulse echoes. The results show that the proposed algorithm is able to balance the anti-jamming and range compression performances by adjusting the weighing factor. On this basis, MIMO radar could maximize the waveform diversity gain by selecting proper waveform set as a best response to flexible adaptive deceptive jamming [26].

5. Conclusions

Transmitting agile group orthogonal waveforms is an effective way for MIMO radar to combat DRFM jamming. Aiming at designing group orthogonal waveforms, the proposed model in this article formulates a weighted sum objective function, which separates the waveforms performances into two parts. One is the peak value of intra-group auto- and cross-correlation functions. The other is the peak value of the inter-group cross-correlation functions. To solve this optimization problem, after proper relaxations, the proposed algorithm in this article transforms the minimization of the augmented Lagrange function into series sub-problems. The numerical results showed the proposed algorithm can minimizes the intra- and inter-group correlation functions effectively. The anti-jamming simulation results showed that the proposed algorithm is able to trade-off the DRFM-based deceptive jamming suppression and range compression performances. The proposed algorithm is flexible and has the potential in adaptive anti-jamming applications for MIMO radar.

Author Contributions

Conceptualization, T.L. and J.S.; methodology, T.L.; software, T.L.; validation, J.S., G.W., X.Y. and Y.Q.; formal analysis, T.L.; investigation, T.L.; resources, J.S.; data curation, T.L.; writing—original draft preparation, T.L.; writing—review and editing, J.S., G.W., X.Y. and Y.Q.; visualization, T.L.; supervision, J.S.; project administration, X.Y.; funding acquisition, J.S. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported in part by National Natural Science Foundation of China under Grant 62131001 and Grant 62171029, Key R&D Plan of Zhejiang Province (2023C01148) and the Hangzhou Leading Innovation and Entrepreneurship Team (TD2022006).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Li, J.; Stoica, P. MIMO Radar with Colocated Antennas. IEEE Signal Process. Mag. 2007, 24, 106–114. [Google Scholar] [CrossRef]
Fishler, E.; Haimovich, A.; Blum, R.S.; Cimini, L.J.; Chizhik, D.; Valenzuela, R.A. Spatial Diversity in Radars—Models and Detection Performance. IEEE Trans. Signal Process. 2006, 54, 823–838. [Google Scholar] [CrossRef]
Haimovich, A.M.; Blum, R.S.; Cimini, L.J. MIMO Radar with Widely Separated Antennas. IEEE Signal Process. Mag. 2008, 25, 116–129. [Google Scholar] [CrossRef]
Bergin, J.; Guerci, J.R. MIMO Radar: Theory and Application; Artech House: Boston, USA, 2018; pp. 45–49. [Google Scholar]
Friedlander, B. Waveform Design for MIMO Radars. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1227–1238. [Google Scholar] [CrossRef]
Kajenski, P.J. Design of Low-Sidelobe Phase-Coded Waveforms. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 2891–2898. [Google Scholar] [CrossRef]
Hassan, A.K.; Al-Saggaf, U.M.; Moinuddin, M.; Alshoubaki, M.K. Statistical Method Based Waveform Optimization in Collocated MIMO Radar Systems. Mathematics 2023, 11, 680. [Google Scholar] [CrossRef]
Pace, P. Detecting and Classifying Low Probability of Intercept Radar, 2nd ed.; Artech House: Boston, USA, 2008; pp. 358–377. [Google Scholar]
Keel, B.M.; Baden, J.M.; Heath, T.H. A Comprehensive Review of Quasi-Orthogonal Waveforms. In Proceedings of the 2007 IEEE Radar Conference, Waltham, USA, 17-20 April 2007. [Google Scholar]
Liu, H.; Zhou, S.; Zang, H.; Cao, Y. Two Waveform Design Criteria for Colocated MIMO Radar. In Proceedings of the 2014 International Radar Conference, Lille, France, 13-17 October 2014. [Google Scholar]
Gini, F.; Maio, A.D.; Patton, L. Waveform Design and Diversity for Advanced Radar Systems; IET: London, UK, 2012; pp. 89–117. [Google Scholar]
He, H.; Stoica, P.; Li, J. Designing Unimodular Sequence Sets with Good Correlations—Including an Application to MIMO Radar. IEEE Trans. Signal Process. 2009, 57, 4391–4405. [Google Scholar] [CrossRef]
Song, J.; Babu, P.; Palomar, D.P. Sequence Set Design with Good Correlation Properties via Majorization-Minimization. IEEE Trans. Signal Process. 2016, 64, 2866–2879. [Google Scholar] [CrossRef]
Li, Y.; Vorobyov, S.A. Fast Algorithms for Designing Unimodular Waveform(s) with Good Correlation Properties. IEEE Trans. Signal Process. 2018, 66, 1197–1212. [Google Scholar] [CrossRef]
Wang, J.; Wang, Y. Designing Unimodular Sequences with Optimized Auto/Cross-Correlation Properties via Consensus-ADMM/PDMM Approaches. IEEE Trans. Signal Process. 2021, 69, 2987–2999. [Google Scholar] [CrossRef]
Esmaeili-Najafabadi, H.; Ataei, M.; Sabahi, M.F. Designing Sequence with Minimum PSL Using Chebyshev Distance and its Application for Chaotic MIMO Radar Waveform Design. IEEE Trans. Signal Process. 2017, 65, 690–704. [Google Scholar] [CrossRef]
Alaee-Kerahroodi, M.; Modarres-Hashemi, M.; Naghsh, M. M. Designing Sets of Binary Sequences for MIMO Radar Systems. IEEE Trans. Signal Process. 2019, 67, 3347–3360. [Google Scholar] [CrossRef]
Lin, Z.; Pu, W.; Luo, Z.Q. Minimax Design of Constant Modulus MIMO Waveforms for Active Sensing. IEEE Signal Process. Lett. 2019, 26, 1531–1535. [Google Scholar] [CrossRef]
Sankuru, S.P.; Jyothi, R.; Babu, P.; Alaee-Kerahroodi, M. Designing Sequence Set with Minimal Peak Side-Lobe Level for Applications in High Resolution RADAR Imaging. IEEE Open J. Signal Process. 2020, 2, 17–32. [Google Scholar] [CrossRef]
Hu, J.; Wei, Z.; Li, Y.; Li, H.; Wu, J. Designing Unimodular Waveform(s) for MIMO Radar by Deep Learning Method. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1184–1196. [Google Scholar] [CrossRef]
Feng, D.; Xu, L.; Pan, X.; Wang, X. Jamming Wideband Radar Using Interrupted-Sampling Repeater. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1341–1354. [Google Scholar] [CrossRef]
Pace, P. Developing Digital RF Memories and Transceiver Technologies for Electromagnetic Warfare; Artech House: Boston, USA, 2022. [Google Scholar]
Akhtar, J. Orthogonal Block Coded ECCM Schemes against Repeat Radar Jammers. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1218–1226. [Google Scholar] [CrossRef]
Zhang, J.; Xu, N. Discrete Phase Coded Sequence Set Design for Waveform-Agile Radar Based on Alternating Direction Method of Multipliers. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4238–4252. [Google Scholar] [CrossRef]
Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2009; pp. 215–271. [Google Scholar]
Panoui, A.; Lambotharan, S.; Chambers, J.A. Game Theoretic Distributed Waveform Design for Multistatic Radar Networks. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1855–1865. [Google Scholar] [CrossRef]

Figure 1. The convergence curves of γ and ε_g, g=1,2,…,G. (a) w=0.1, M=2, G=2, N=256; (b) w=0.7, M=8, G=8, N=256.

Figure 2. The convergence curves of γ and ε_g, g=1,2,…,G. (a) M=2, G=2, N=256; (b) M=8, G=8, N=256.

Figure 3. The correlation peak value obtained by the proposed algorithm. When M=2, G=2, N=256: (a) auto-correlation; (b) intra-group cross-correlation; (c) inter-group cross-correlation. When M=8, G=8, N=256: (d) auto-correlation; (e) intra-group cross-correlation; (f) inter-group cross-correlation.

Figure 4. The effect of parameters M, N, G on the obtained metrics values. (a) w=0.3, M=2, G=2; (b) w=0.875, M=2, G=2; (c) w=0.5, M=8, N=256; (d) w=0.5, G=8, N=256.

Figure 5. Angle-range images formed with MIMO radar using fixed and agile waveforms under DRFM-based deceptive jamming. (a) Fixed waveform; (b) Primal-Dual; (c) w=0.9, M=3, G=2, N=256; (d) w=0.1, M=3, G=2, N=256.

Table 1. Parameters and performance metrics of the simulated waveforms.

Waveforms Design methods	Title 2	Title 3
Fixed Waveform	M=3, N=256	PSL=−23.22 dB
Primal-Dual [18]	MG=6, N=256	PSL=−20.18 dB
Proposed methods when w=0.9	M=3, G=2, N=256	PSL₁=−19.18 dB PSL₂=−19.39 dB PCL=−25.56 dB
Proposed methods when w=0.1	M=3, G=2, N=256	PSL₁=−25.64 dB PSL₂=−25.88 dB PCL=−18.51 dB

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Optimal Design of Group Orthogonal Phase Coded Waveforms for MIMO Radar

Abstract

1. Introduction

2. Problem Formulation

3. Proposed Group Orthogonal Waveform Design Algorithm

3.1. Solving sub-problem (16)

3.2. Solving sub-problem (17)

3.3. Solving sub-problem (18)

3.4. Solving sub-problem (19)

4. Numerical Results

4.1. Effect of weighting factor w

4.2. Obtained correlation functions

4.3. Effect of parameters M, N, G

4.4. Anti-jamming simulation

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe