Submitted:
01 January 2024
Posted:
03 January 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
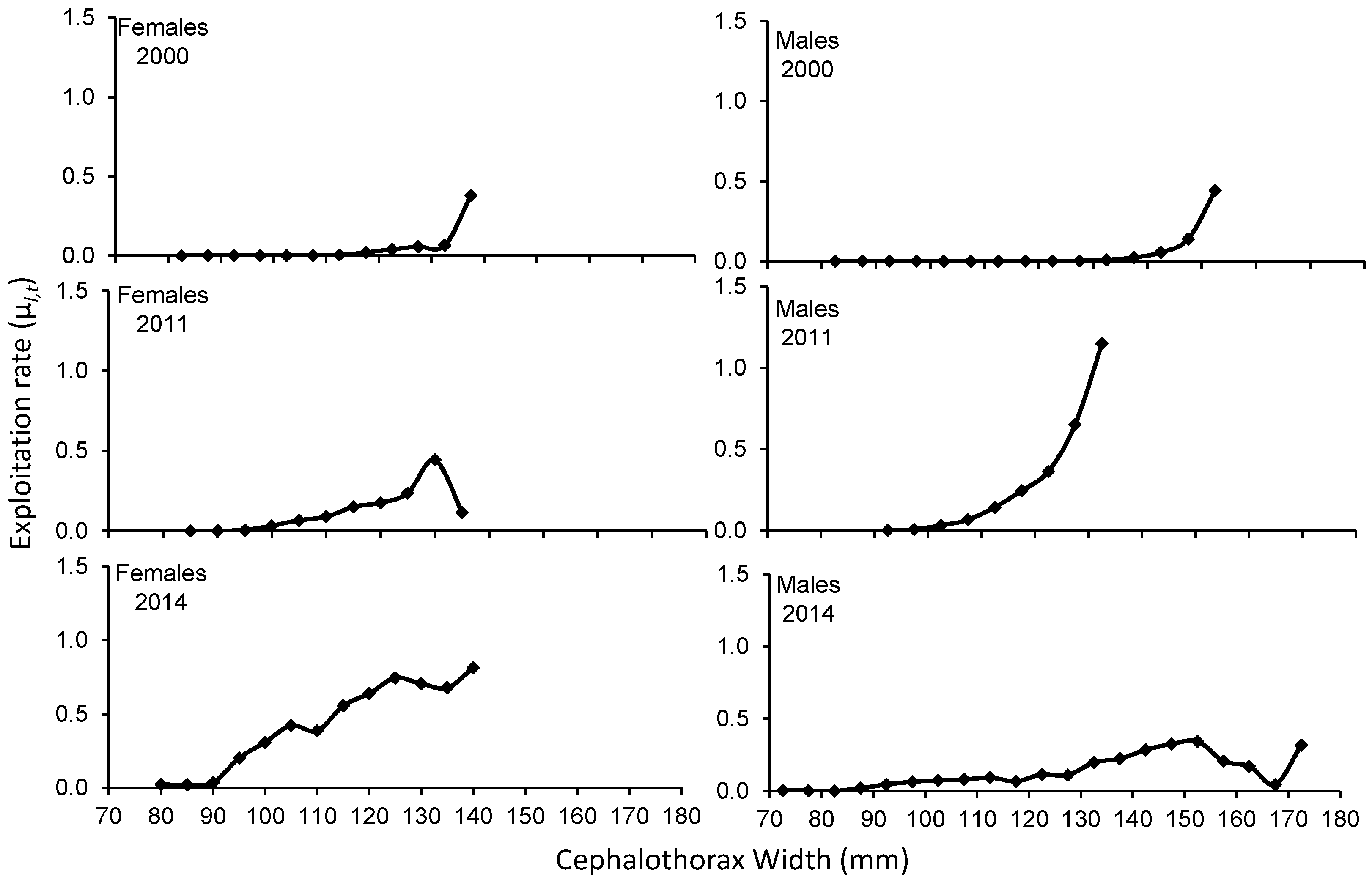
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Conflicts of Interest
References
- Ramos-Cruz, S. Estructura y parámetros poblacionales de Callinectes arcuatus Ordway, 1863 (Decapoda: Portunidae), en el sistema lagunar La Joya-Buenavista, Chiapas, México. Pan-Am. J. Aquat. Sci. 2008, 3, 259–268. [Google Scholar] [CrossRef]
- CONAPESCA. Anuario Estadístico de Acuacultura y Pesca Edición 2013; CONAPESCA: Mazatlán, Mexico, 2013; pp. 1–295. [Google Scholar]
- Heredia-Delgadillo, C.A.; Rodríguez-Domínguez, G.; Pérez-González, R.; Castañeda-Lomas, N.; Castillo-Vargasmachuca, S.G.; Aragón-Noriega, E.A. Analysis of crab size structure and the fishing effort applied to a crab fishery in northwest Mexico. Crustaceana 2018, 91, 225–237. [Google Scholar] [CrossRef]
- Cisneros-Mata, M.A.; Ramírez-Félix, E.; García-Borbón, J.A.; Castañeda-Fernández de Lara, V.; Labastida-Che, A.; Gómez-Rojo, C.; Madrid-Vera, J. Pesca de jaiba en el litoral del Pacífico mexicano; INAPESCA: Ciudad de Mexico, Mexico, 2014; pp. 1–86. [Google Scholar]
- Ramírez-Félix, E.; Singh-Cabanillas, J.; Gil-López, H.A.; Sarmiento-Náfate, S.; Salazar-Navarro, I.; Montemayor-López, G.; García-Borbón, J.A.; Rodríguez-Domínguez, G.; Castañeda-Lomas, N. La pesquería de jaiba (Callinectes spp.) en el Pacífico mexicano: Diagnóstico y propuesta de regulación; SAGARPA-INP: Mazatlán, Mexico, 2003; pp. 1–54. [Google Scholar]
- Ortega-Lizárraga, G.G.; Rodríguez-Domínguez, G. Sinaloa y su valor en jaiba. Cienc. Desarro. 2016, 285, 64–68. [Google Scholar]
- Sullivan, P.J.; Lai, H.L.; Gallucci, V.F. A catch-at-length analysis that incorporates a stochastic model of growth. Can. J. Fish. Aquat. Sci. 1990, 47, 184–198. [Google Scholar] [CrossRef]
- Álvarez-Arellano, A.D.; Gaitán-Moran, J. 1994. Lagunas costeras y el litoral mexicano. In Lagunas costeras y el litoral mexicano, 1st ed.; De la Lanza-Espino, G., Cáceres-Martínez, C., Eds.; Universidad Autónoma de Baja California Sur: La Paz, Mexico, 1994; pp. 13–74. [Google Scholar]
- Baranov FI. 1918. On the question of the biological basis of fisheries. Nauchnyi Issledovatelskii Ikhtiologicheskii Institut, Izvestiia 1: 81-128.
- Ricker, W.E. Computation and interpretation of biological statistics of fish populations. Bull. Fish. Res. Board Can. 1975, 191, 1–382. [Google Scholar]
- Doubleday, W.G. A least squares approach to analyzing catch at age data. ICNAF, Res. Bull. 1976, 12, 69–81. [Google Scholar]
- Hampton, J.; Kleiber, P.; Langley, A.; Hiramatsu, K. Stock assessment of yellowfin tuna in the western and central Pacific Ocean. WCPFC–SC1, Noumea, New Caledonia pp. 1–76.
- von Bertalanffy, L. A quantitative theory of organic growth (Inquiries on growth laws II). Hum. Biol. 1938, 10, 181–213. [Google Scholar]
- Rodríguez-Domínguez, G.; Castillo-Vargasmachuca, S.G.; Ramírez-Pérez, J.S.; Pérez-González, R.; Aragón-Noriega, E.A. Modelos múltiples para determinar el crecimiento de organismos juveniles de jaiba azul Callinectes arcuatus en cautiverio. Cienc Pesq 2014, 22, 29–35. [Google Scholar]
- Hogg, R.V.; Craig, A.T. Introduction to mathematical statistics; MacMillan: London, UK, 1970; pp. 1–438. [Google Scholar]
- Quinn, T.J.; Deriso, R.B. Quantitative fish dynamics; Oxford University Press: Oxford, 1999; pp. 1–542. [Google Scholar]
- Cerdenares-Ladrón De Guevara, G. Biología del pez vela Istiophorus platypterus (Shaw y Nodder, 1792) en el Golfo de Tehuantepec. Ph Thesis, Centro Interdisciplinario de Ciencias Marinas-Instituto Politécnico Nacional, La Paz, Mexico, 2011. [Google Scholar]
- Neter, J.; Kutner, M.H.; Nachtsheim, C.J.; Wasserman, W. Applied linear statistical models; McGraw-Hill: New York, 1996; pp. 1–1408. [Google Scholar]
- Rodríguez-Domínguez, G.; Castillo-Vargasmachuca, S.; Pérez-González, R.; Aragón-Noriega, E.A. Catch-maximum sustainable yield method applied to the crab fishery (Callinectes spp.) in the Gulf of California. J. Shell. Res. 2014, 33, 45–51. [Google Scholar] [CrossRef]
- Beverton, R.J.H.; Holt, S.J. On the Dynamics of Exploited Fish Populations, 1st ed.; Chapman and Hall: London, UK, 1957. [Google Scholar]
- Hernández, L.; Arreola-Lizárraga, J.A. Estructura de tallas y crecimiento de los cangrejos Callinectes arcuatus y C. bellicosus (Decapoda: Portunidae) en la laguna costera Las Guásimas, México. Rev.Biol. Trop. 2007, 55, 225–233. [Google Scholar] [CrossRef] [PubMed]
- Ulibarría-Valenzuela, J.J. Aplicación de un modelo predictivo a la pesquería de la jaiba café Callinectes bellicosus en la bahía Santa María de la Reforma. Bachelor Thesis, Facultad de Ciencias del Mar, Universidad Autónoma de Sinaloa, Mazatlán, Mexico, 2003. [Google Scholar]
- Sharpe, D.M.T.; Hendry, A.P. Life history change in commercially exploited fish stocks: an analysis of trends across studies. Evol. Appl. 2009, 2, 260–275. [Google Scholar] [CrossRef] [PubMed]
- Policansky, D. Fishing as a cause of evolution in fishes. In The Exploitation of Evolving Resources, 1st ed.; Stokes, T.K., McGlade, J.M., Law, R., Eds.; Springer-Verlag: Berlin, Germany, 1993; pp. 8–18. [Google Scholar] [CrossRef]
- Martell, S.; Froese, R. A simple method for estimating MSY from catch and Resilience. Fish. Fish. 2012, 14, 504–514. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




