Prerpints.org logo
Preprint
Review

Review of Machine Learning Methods for River Flood Routing

Altmetrics

Downloads

131

Views

38

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

30 December 2023

Posted:

03 January 2024

You are already at the latest version

Alerts
Abstract
River flood routing computes changes in shape of a flood wave over time as it travels downstream along a river. Conventional flood routing models, especially hydrodynamic models require high quality and quantity of input data such as measured hydrologic time series, geometric data, hydraulic structures and hydrological parameters. Unlike physically based models, machine learning algorithms, which are data driven models, do not require much knowledge about underlying physical processes and can identify complex nonlinearity between inputs and outputs. Due to the higher performance, less complexity, and low computation cost, novel machine learning methods as a single application or hybrid application were introduced by researchers to achieve more accurate and efficient flood routing. This paper reviews the recent application of machine learning methods in river flood routing.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Floods are one of the most devastating disasters that cause damages to human lives, society and ecosystem. Accurate simulation of flood flow is significantly important for flood control and reduction of flood losses. Physically based models and data-driven models are two main categories of existing flood routing models. Physically based model can be divided into hydraulic and hydrologic flood routing models constructed based on empirical or theoretical governing equations describing the propagation of a flood wave along a river to estimate the changes in streamflow (depth and discharge) with time. Various physical characteristics and boundary conditions are required to be determined to construct physically based models, which requires in-depth (extensive) knowledge in physical process. Widely used physically based models involve Muskingum model [1,2,3], and the hydrodynamic model based on Saint-Venant equations which is solved by various numerical methods [4,5,6,7,8,9,10].
Data-driven models map relationships between hydrological variables to describe hydrological processes without requiring extensive knowledge of underlying physical principles. Simple data-driven models based on linear assumptions for regression fitting include the auto-regressive moving average (ARMA) model [11], and the autoregressive integrated moving average (ARIMA) model [12]. In recent decades, machine learning (ML) methods have gained popularity along with the development of artificial intelligence. ML methods can deal with more complex hydrological processes by mapping nonlinear relationships between hydrological variables. Commonly applied ML methods in river flood routing computation include support vector regression (SVR) [13,14], artificial neural networks (ANNs) [15,16], multilayer perceptron (MLP) [14], gated recurrent units (GRUs) [14,17], long short-term memory (LSTM) [14,18], and so on. Machine learning methods have been widely applied in hydrological field such as rainfall-runoff models, and flood forecasting. However, the applications for river flood routing are relatively limited.
This paper mainly reviews the single application and hybrid application of ML methods for river flood routing as shown in Figure 1. The hybrid application of ML methods is divided into two categories: one is for optimization of physically based flood routing model and the other is for combined usage with a physically based flood routing model to improve prediction accuracy.

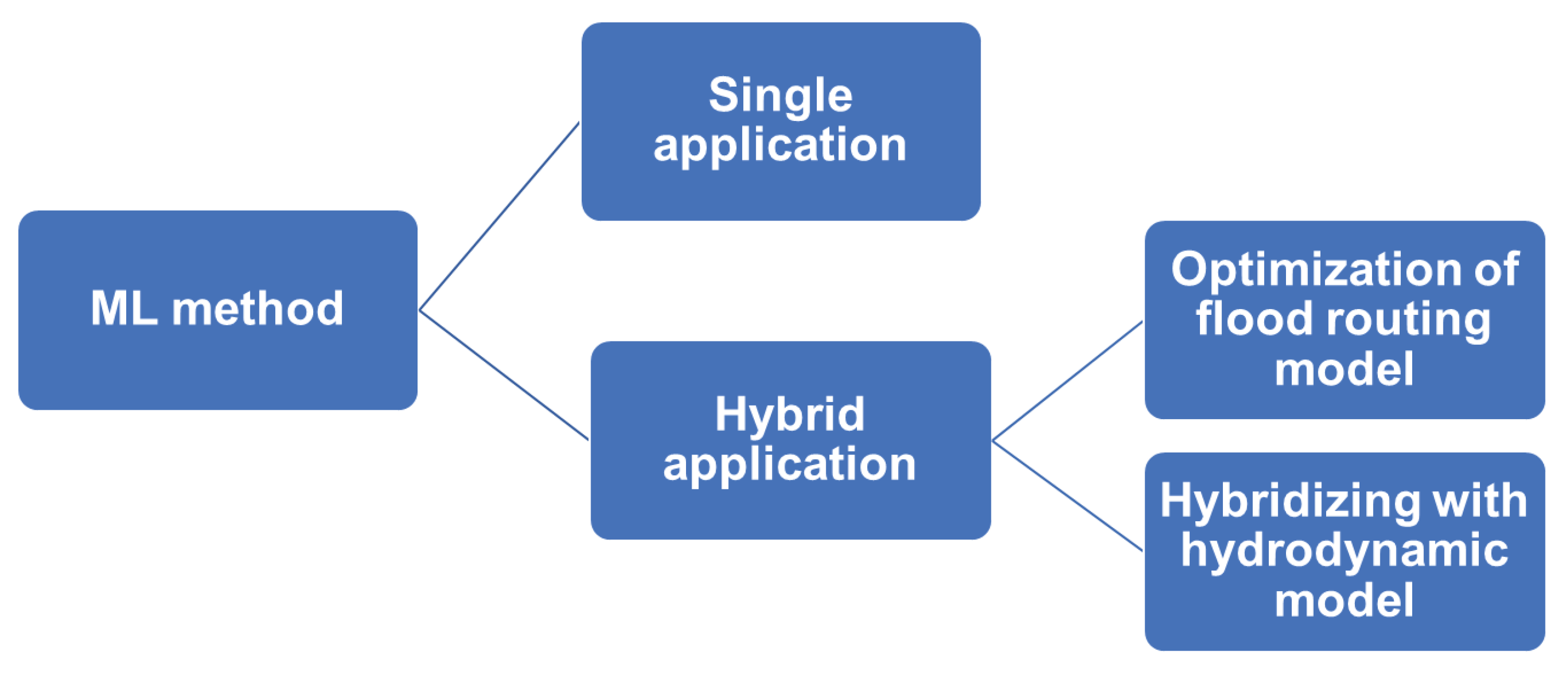
2. ML methods

2.1. Single application

Numerous studies applied ML models for flood routing simulation. Physically based models require physical parameters and river geometry data, while machine learning methods only use the time series data from upstream gauging stations to estimate the water level or discharge at the downstream locations of a river reach. Reviewed papers regarding the single application of ML methods for flood routing computation are presented in Table 1.

2.1.1. Support vector regression (SVR)

SVR is a ML technique based on structural risk minimization theory and statistical learning hypothesis [29]. The idea of SVR is that an entire sample set can be represented by a small number of support vectors [30]. In SVR, a kernel function is used to create a linearly divisible space by converting the sample space, then predictive analysis on the new samples is performed using the maximum interval partition line and support vectors [14]. The learning ability of a SVR model is highly affected by the selected kernel function. The commonly used kernel functions are the linear kernel, polynomial kernel, precomputed kernel, and radial basis function kernel. [13] used SVM in three different flood routing problems. In this study, the dynamics of the studied floods were captured by applying the SVM from observed data, and the model showed good performance for flood routing modeling. [27] compared the performance of various machine learning models including SVM for flood routing prediction in Eskisehir, Ankara and Sivas, and [14] used linear kernel in a SVR for flood routing in the Yangtze River.

2.1.2. Artificial neural network (ANN)

ANN is a nonlinear modeling approach which mimic the human brain function [31]. The nonlinear relationship between input and output variables in an ANN model is estimated by neurons, weights and biases. In an ANN, it is important to properly determine the number of hidden neurons, the number of hidden layers, and the activation functions. [32] showed that one hidden layer is adequate for an ANN to solve hydrological problems. Therefore, many studies in hydrological field used one hidden layer to estimate the nonlinear relationships [10,30]. The size of hidden nodes is usually defined by performing a trial-and-error method [30]. However, [33] proposed that the number of hidden nodes can be determined based on the number of samples. The most widely used training method for ANNs is the Levenberg-Marquardt (LM) algorithm as it is fast and the most efficient technique [34].
In the last few years, ANN has been applied to river flood routing problems including estimation at ungauged sites. [15] compared the performance of a MIKE11 hydrodynamic model and ANN technique, and found that the trained ANN model performs much better than MIKE11HD results. In this study, an ANN with one hidden layer including 8 neurons was applied to predict downstream water levels using measured hourly water level data at upstream gauging stations as inputs.
[16] used an ANN to simulate flows at a downstream location of the River Nile in Sudan based on flows measured at upstream locations. This study examined four scenarios for which data from different stations were used as inputs, and compared their performance in flood forecasting.
[23] trained an ANN to predict the downstream hydrograph and the results of the ANN were compared to the nonlinear Muskingum models optimized by particle swarm optimization (PSO), ant colony optimization (ACO), and GA, and numerical solutions of Saint-Venant equations. The results of this study showed that the performance of flood routing applying machine learning algorithms is as good as that of the Saint-Venant model.
ANNs combined with meta-heuristic algorithms have been investigated by many researchers. [21] presented an ANN optimized by social-based algorithm (SBA) to simulate flood routing. SBA is one of the meta-heuristic approaches which combines evolutionary algorithm (EA) and imperialist competitive algorithm (ICA) [35]. This paper showed that the hybrid optimization approach can achieve better results in efficiency and performance. In addition, [22] optimized ANN flood routing model with ICA, Bat algorithm (BA), PSO and GA, and their results showed that the ANN-ICA is the best prediction model.
The multilayer perceptron (MLP) is one of ANNs which is the most widely used feedforward model. A MLP consists of one input layer, at least one hidden layer, and one output layer, and the layers of a MLP are fully connected [36]. [20] investigated the feedforward ANNs to solve the complex nonlinear problems of Muskingum flood routing for a natural river in Myanmar. A feed forward multilayer perceptron (FMLP) structure was designed in this study based on the Muskingum routing equations. Therefore, the FMLP has the same input and output variables with a Muskingum routing approach. This study showed that the feedforward ANN is a promising alternative in Muskingum routing after comparing the FMLP to the nonlinear Muskingum models using other reported methods such as genetic algorithm (GA) [37], nelder-mead simplex (NMS) algorithm [38], broyden-fletcher-goldfarb-shanno (BFGS) method [39] in solving the parameter estimation. Besides, [14] applied a MLP with one hidden layer including 100 hidden neurons for the flood routing.

2.1.3. Recurrent neural network (RNN)

RNN is a neural network originated from the idea that human cognition is based on the past memory and experience [17]. The main difference compared to the MLP is that RNN can consider the input of the previous moment and involve a memory function of the previous content. Widely used hidden layer neurons are RNN, LSTM, and GRU.
LSTM is a recurrent neural network that uses the gated memory units to control input, memory, output, and other information, so that the problem of gradient disappearance and explosion of the RNN for long sequence data is solved [40]. [18] applied a LSTM for water level prediction using daily water levels observed at 12 gauging stations. The LSTM model was compared to the discrete linear cascade model (DLCM) in this study and it was shown that the LSTM model provides better results than the DLCM. This study noted that the encoder-decoder architecture of the LSTM is effective at solving multi-horizon forecasting problems.
GRU is a recurrent neural network which is similar to the structure of LSTM, but the number of gates used in the construction of the two models is different. It has been reported that GRU is simpler than LSTM, but has similar learning ability regarding long-term dependencies in time series data [17]. [14] constructed a GRU model for flood routing in the Yangtze River and compared the performance of the GRU with other machine learning models such as SVR, gaussian process regression (GRP), multilayer perceptron (MLP), random forest regression (RFR) and LSTM. It was demonstrated that the GRU model showed superior performance than other models. [17] adopted MLP and RNNs including LSTM and GRU to predict the water level of cascaded channels by mining the high-dimensional correlated hydrodynamic features considering the spatial and temporal window. This study compared the RNN-based prediction models with various methods such as MLP-based prediction model, ANN, SVM, and RF, and demonstrated that the RNN-based prediction model is more suitable for the water level prediction of cascade channels.

2.1.4. Random forest regression (RFR)

RFR is an ensemble machine learning proposed by [41]. It is based on the idea of integrated learning and the definition of several independent trees. The results from randomized and de-correlated decision trees are aggregated to obtain predictions [42]. The most important hyper-parameters of the RFR are the number of trees and randomly selected features. [14] and [27] used the RFR for flood routing and compared the performance of RFR to other various machine learning models. [14] noted that the RFR model showed overfitting for inflow hydrograph prediction of the Three Georges Reservoir.

2.1.5. K-nearest neighbor (KNN)

KNN is a non-parametric classification and regression algorithm [27]. It stores all of the available cases and creates new clusters by classifying them based on their similarity measure. The KNN finds the nearest neighbor using Euclidean distance and perform classification. [27] investigated the performance of the KNN algorithm compared with kernel-based and tree-based algorithms for flood routing prediction and concluded that the KNN can produce successful outputs for flood forecasting in Ankara.

2.1.6. Other ML methods

[43] designed a network-based Fuzzy Inference System (FIS) based on the Muskingum formula for describing the relationship between inflows and outflows. [24] applied the gene expression programming (GEP) and ANN as alternative approaches of the Muskingum model to predict the downstream outflow hydrograph. This study investigated inflow hydrographs at different time steps for GEP and ANN models. The results showed that the GEP model presents better performance compared with ANN and Muskingum model for multiple inflows system. [25] developed a new model applying ensemble empirical mode decomposition (EEMD) and stepwise regression for water level forecasting in a tidal river. Only water level data were used in the proposed model, and it was found that the model is simple and highly accurate.
The genetic programming (GP) was derived from Darwin’s principle of natural evolution. GP operates on parse trees to describe the relationship between input and output variables [19]. Control parameters have to be set before applying the GP algorithm such as population size, maximum number of generations, and crossover and mutation probability. [19] proposed a GP model as an alternative to the non-linear Muskingum model. This study demonstrated that the GP model can route complex flood hydrographs in natural channels and perform better than the non-linear Muskingum model. Other machine learning method applied for flood routing includes GPR [14], gradient-boosted machine (GBM) [27], bagged tree (BT) [27], and extreme gradient boosting (XGBoost) [27].
Machine learning methods have been applied combining with mathematical techniques such as wavelet packet decomposition [44] which divides an input time series into two components: approximation and detail. [44] applied the hybrid models named wavelet packet-based artificial neural network (WPANN) and wavelet packet-based adaptive neuro-fuzzy inference system (WPANFIS) to forecast the downstream river stage using upstream observed river stage and lags. The results of this study indicated that the ANN and ANFIS models for river stage forecasting improved after combining wavelet packet decomposition. A hybrid approach applying empirical model decomposition (EMD) and neural networks was proposed by [28] for flood routing prediction. This study hybridized the EMD signal decomposition technique with the feed-forward backpropagation neural network (FFBNN) and cascade forward backpropagation neural network (CFBNN) algorithms. The results of this study showed that the EMD signal decomposition technique can improve the performance of ML models, and the EMD-FFBNN model was the most successful algorithm in the flood routing calculation. Besides, hybrid machine learning models including least squares support vector machine (LSSVM), PSO-LSSVM, EMD-LSSVM, Wavelet-LSSVM, and variational model decomposition (VMD)-LSSVM were investigated by [26]. This research compared the performance of the five flood routing methods and found that the PSO-LSSVM is the most successful model.

2.2. Hybrid application

2.2.1. ML-based optimization technique

Intelligent optimization algorithms become popular due to their flexibility, simplicity to use, effective handling of discrete problems, no need for differentiation, and the ability to find global optima [45]. Muskingum routing, which is a hydrological method developed by [46], has been widely used for river flood routing with the parameter estimation for linear and nonlinear forms [20]. In order to improve the accuracy of the Muskingum model, numerous meta-heuristic algorithms have been used in the optimization of the model parameters, whose results have been reported more accurate than the outputs of the conventional method such as the Lagrange multiplier (LMM) and segmented least square method (S-LSM) [47]. The inspiration of meta-heuristic algorithms originated from natural concepts. For example, GA was proposed based on the Darwin’s “survival of the fittest”; PSO simulates the collective behavior of birds; and clonal selection algorithm (CSA) comes from the cuckoo nesting behavior. Table 2 shows the machine learning methods used for the estimation of parameters of Muskingum models.
[37] applied genetic algorithm (GA) and found that GA is efficient to estimate the parameters of nonlinear Muskingum routing models. [48] used a heuristic algorithm, harmony search (HS), and demonstrated that HS performs better in the parameter determination of the nonlinear Muskingum model than GA. The GA approach creates a new vector from only two vectors, while a new vector is originated from every single existing vector in the HS algorithm, which allows the HS to find better solutions with greater flexibility [48]. [43] compared the PSO algorithm to the GA and HS, and showed that HS algorithm produces the most precise results. An improved backtracking search algorithm (BSA) proposed by [1] was demonstrated to outperform PSO, GA, and differential evolution (DE) [51] for parameter estimation of nonlinear Muskingum model. Other algorithms such as immune clonal selection algorithm (ICSA) [49], parameter setting free-harmony search (PSF-HS) algorithm [50], Nelder-Mead simplex (NMS) algorithm [38], harmony search-Broyden-Fletcher-Goldfarb-Shanno (HS-BFGS) algorithm [52], modified honey-bee mating optimization (MHBMO) algorithm [58] have been proposed due to their efficiency and fast convergence.
[64] proposed a hybrid cuckoo quantum-behavior particle swarm optimization (C-QPSO) and demonstrated the global optimization ability of the algorithm in the application to the parameter estimation of a nonlinear Muskingum model. Other hybrid optimization algorithms combining two approaches include HS-BFGS [52], SFLA-NMS [54], and MHBMO-GRG [58]. These hybrid techniques can provide appropriate initial guess for Muskingum parameters and reduce the uncertainties to cause different results for different runs [58]. [53] presented a hybrid particle swarm optimization (HPSO) by combining PSO with NMS method to estimate the Muskingum model parameters. This study firstly used PSO algorithm to conduct the global optimization, then applied NMS method to perform the local search of optimum. Similarly, [59] developed hybrid bat-swarm algorithm (HBSA), which is a hybrid of bat algorithm (BA) and PSO algorithm, for the optimal estimation of four parameters of the Muskingum model, so that a global optimum can be searched without trapping in the local minimums. Another attempt to find global solution was made by [63] using hybrid PSO-LM algorithm for the calibration of the nonlinear Muskingum model.
Efforts were also made to determine parameters of modified forms of nonlinear Muskingum models by applying meta-heuristic optimization techniques. [58] proposed MHBMO-GRG for a six-parameter Muskingum model. [56] applied weed optimization algorithm (WOA) in the estimation of parameters for an extended nonlinear Muskingum model with introducing a parameterized initial storage condition. [57] and [60] implemented PSO algorithm and Shark algorithm, respectively, for four-parameter non-linear Muskingum models. [47] used Grey Wolf Optimizer (GWO) algorithm to estimate the parameters of two nonlinear Muskingum models with three and four constant parameters.
[65] applied ML techniques in the parameter calibration of the Routing Application for Parallel computation of Discharge (RAPID) model without requiring measured streamflow. The RAPID model uses a linear Muskingum routing algorithm. This study explored four ML architectures including GPR, gaussian mixture copula (GMC), XGBoost, and random forest (RF) in learning the relationship between river features and model parameters. The first two methods perform probabilistic predictions, while XGBoost and RF yield a single-point prediction. It was shown that XGBoost performs best, followed by GPR, RF, and GMC.

2.2.2. Hybrid application of a hydraulic model and ML method

A number of simplifications and assumptions are involved for physically based river flood routing models. Hydrologic and hydraulic methods are two main classes of conventional flood routing methods. Hydrological models such as the Muskingum model solves the storage equation and continuity equation to estimate the downstream flow hydrograph. Examples of hydraulic models includes kinematic wave model and model based on Saint-Venant equations. The efficiency of hydraulic models can be restricted due to the high demands on computer resources, the quality and quantity of inputs [20]. In addition, a high resolution in space and small calculation time step lead to quite high computational efforts [66], which restricts the application of a hydrodynamic model in real time operation. Therefore, methodologies combining artificial intelligence and hydrodynamic models have been proposed by many studies due to their robustness and fast speed. Table 3 shows the studies on the hybrid application of a hydraulic model and a ML method for the flood routing prediction.
[67] integrated flows computed from a one-dimensional hydrodynamic numerical model, at a river section where measured data is not available, for ANN training and validation. In this study, the studied river reach was divided into sub-reaches, and different ANN blocks were used for individual sub-reaches. The integration of observations and results of numerical model into the ANN model training enhanced the overall model performance. This study used a hydrodynamic numerical model only to provide data for historical flood events. [66] applied the HEC-RAS, which simulates one-dimensional hydrodynamic flow by numerically solving the Saint-Venant equations, to generate a training data of a multilayer-feedforward network (MLFN) covering possible extreme flood events instead of only considering recorded floods. By combining the HEC-RAS and an ANN, this study tried to overcome both the high computational demands regarding to the application of a hydrodynamic model and the restricted extrapolation abilities of ANNs. Similarly, [68] used synthetic floods generated by the HEC-RAS model to train adaptive ANN models for flood routing in river systems. They applied a MLP, a RNN, a time delay neural network (TDNN) and a time delay recurrent neural network (TDRNN) and found that the TDNN and the TDRNN, that are dynamic networks, perform more accurately than the static MLP network. [69] used ANN and adaptive neuro-fuzzy inference system (ANFIS) for flood routing. These two models were trained using the upstream hydrographs generated by HEC-1 and routed hygrographs by the HEC-RAS at downstream end. The two models used data of up to 10 previous time intervals (approximately 2.5 h) as inputs. This study showed that the results of ANN and ANFIS models coincided with the results of the HEC-RAS, and suggested the application of the two machine learning models due to their stability and high speed. In addition, [72] performed sensitivity analysis using HEC-RAS to identify effective parameters on the shape and the peak discharge of the downstream hydrograph. Then synthetic realizations generated by the HEC-RAS were used to train, validate, and test the ANNs to estimate peak discharge and the outflow hydrograph at a downstream section. The first ANN was trained to predict the peak discharge from base time of the upstream hydrograph, peak of this hydrograph, length of the reach, bed slope of the channel, and Manning’s coefficient of the channel. The second ANN was trained to estimate the outflow hydrograph from the inflow hydrograph at the upstream section. The ANN showed better performance compared to the Muskingum method in the prediction of outflow hydrograph.
[70] presented a new real-time updating approach named KN2K for a one-dimensional hydraulic model by coupling the k-nearest neighbor (KNN) procedure and the Kalman filter (KF). This study used the KNN procedure to improve the robustness and accuracy of the KF. The updating performance of KN2K was compared to that of the KF method, and it was turned out that the KN2K method is more reliable then the KF method.
[71] applied a deep convolutional neural network (CNN) model to rapidly predict fluvial flood inundation. The modeling approach based on a CNN method was proposed to solve the problem of high computational demand of two-dimensional (2D) hydraulic models in real-time application. The inputs of the CNN include discharge time-series with lags and observation time, and the outputs of the model are water depths. The inputs of the CNN are generated from the LISFLOOD-FP, which is a 2D hydraulic model. The results of this study showed high accuracy in capturing flooded cells and that the CNN model performs better than a SVR method.
[10] hybridized a hydrodynamic model based on the Saint-Venant equations with ANNs to improve the accuracy of the flood forecasting for the Han River. This study applied ANNs to correct the errors of the hydrodynamic model using the observed discharge and flow, and outputs of the hydrodynamic model. When the lead time of flood forecasting increases, the hybrid model showed improved accuracy compared to a single ANN model, which indicates that the hybrid approach presents less deterioration in forecasting accuracy at higher lead times. The results of this study showed that the hybrid model performs better than the single application of the hydrodynamic model or an ANN in flood forecasting.

3. Conclusions

This paper provides a comprehensive review on the application of machine learning techniques for river flood routing prediction. The application of ML models demonstrated outstanding performance in modeling flood routing with high accuracy. The advancement of the novel ML methods is determined by properly designing learning algorithms and the performance of ML models could be improved through coupling with other physically-based models, ML methods, and soft computing techniques. Such hybrid applications were demonstrated to provide more efficient and robust models that can effectively learn more complex flood routing prediction. In real-time application, ML models can overcome the problems of stability and long computational time of conventional flood routing models such as hydrodynamic models. The difficulties of applying hydrodynamic models in real-time operations were discussed by [66] who overcome such problems by using ANNs. However, one of the main limitations of ML models is that the trained models are difficult to be generalized due to the limited prediction ability when the inputs of the model beyond the data used to train them. ML models can be highly sensitive to the input data [10,14]. The effect of training data on the performance of ML models have not been fully studied as mentioned by [73].

Author Contributions

Conceptualization, L.L. and K.S.J.; investigation, L.L. and K.S.J.; resources, L.L. and K.S.J.; writing—original draft preparation, L.L.; writing—review and editing, K.S.J; supervision, K.S.J.; funding acquisition, K.S.J. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Korea Environmental Industry and Technology Institute (KEITI) (Grant number: 2022003460001).

Conflicts of Interest

The authors declare no conflicts of interest.

Nomenclature

ACO Ant colony optimization
ANFIS Adaptive neuro-fuzzy inference system
ANN Artificial neural network
ANSE Arithmetic mean
ARIMA Autoregressive integrated moving average
ARMA Auto-regressive moving averageo-regressive m
BA Bat algorithm
BFGS Broyden-fletcher-goldfarb-shanno
BSA Backtracking search algorithm
BT Bagged tree
CC Coefficient of correlation
CE Coefficient of efficiency
CFBNN Cascade forward backpropagation neural network
CNN Convolutional neural network
C-QPSO Cuckoo quantum-behaviour particle swarm optimization
CSA Clonal selection algorithm
DE Differential evolution
DE Differential evolution
DLCM Discrete linear cascade model
DP Difference in peak
DPF Difference in peak flow
EA Evolutionary algorithm
EEMD Ensemble empirical mode decomposition
EMD Empirical model decomposition
EQp Error of peak discharge
ETp Error of time to peak
FFBNN Feed-forward backpropagation neural network
FMLP Feed forward multilayer percetptron
GA Genetic algorithm
GBM Gradient-boosted machine
GEP Gene expression programming
GMC Gaussian mixture copula
GP Genetic programming
GPR Gaussian process regression
GRG Generalized reduced gradient
GRP Gaussian process regression
GRU Gated recurrent unit
GWO Grey wolf optimizer
HBSA Hybrid bat-swarm algorithm
HPSO Hybrid particle swarm optimization
HS Harmony search
ICA Imperialist competitive algorithm
ICSA Immune clonal selectio algorithm
IOA Index of agreement
KF Kalman filter
KGE Kling-Gupta efficiency
KN2K KNN-KF
KNN K-nearest neighbor
LM Levenberg-Marquardt
LMM Lagrange multiplier
LSSVM Least squares support vector machine
LSTM Long short-term memory
MAE Mean absolute error
MAPE Mean absolute percentage error
MBE Mean bias error
MHBMO Modified honey bee mating optimization
ML Mahine Learning
MLFN Multilayer-feedforward network
MLP Multilayer perceptron
MRE Mean relative error
MSE Mean square error
MWLP MLP-based water level prediction
NMM Nonlinear Muskingum model
NMS Nelder-mead simplex
NSE Nash-Sutcliffe Coefficient
PCC Pearson correlation coefficient
PI Persistence index
PSF-HS Parameter setting free-harmony search
PSO Particle swarm optimization
PWRMSE Peak-weighted root mean square error
R2 Coefficient of determination
RAPID Routing application for parallel computation of discharge
RCM Rating curve method
RF Random forest
RFR Random forest regression
RMSE Root mean square error
RNN Recurrent neural network
RWLP RNN-based water level prediction
SA Shark algorithm
SBA Social-based algorithm
SDE Standard deviation of the NSE
SFLA Shuffled frog leaping algorithm
SI Scatter index
S-LSM segmented least square method
SSE Sum of squared error
SSQ Sum of the square of the deviations between the observed and routed outflows
SVM Support vector machine
SVR Support vector regression
TDNN Time delay neural network
TDRNN Time delay recurrent neural network
TSS Taylor skill score
VMD Variational model decomposition
WI Willmott’s index of agreement
WOA Weed optimizatio algorithm
WPANFIS Wavelet packet-based adaptive neuro-fuzzy inference system
WPANN Wavelet packet-based artificial neural network
XGBoost Extream gradient boosting

References

  1. Yuan, X.; Wu, X.; Tian, H.; Yuan, Y.; Adnan, R.M. Parameter identification of nonlinear Muskingum model with Backtracking Search Algorithm. Water Resour. Manag. 2016, 30, 2767–2783. [Google Scholar] [CrossRef]
  2. Gong, Y.; Liu, P.; Cheng, L.; Chen, G.; Zhou, Y.; Zhang, X.; Xu, W. Determining dynamic water level control boundaries for a multi-reservoir system during flood seasons with considering channel storage. J. Flood Risk Manag. 2020, 13, e12586. [Google Scholar] [CrossRef]
  3. Chao, L.; Zhang, K.; Yang, Z.-L.; Wang, J.; Lin, P.; Liang, J.; Li, Z.; Gu, Z. Improving flood simulation capability of the WRF-Hydro-RAPID model using a multi-source precipitation merging method. J. Hydrol. 2021, 592, 125814. [Google Scholar] [CrossRef]
  4. Dhote, P.R.; Thakur, P.K.; Domeneghetti, A.; Chouksey, A.; Garg, V.; Aggarwal, S.P.; Chauhan, P. The use of SARAL/AltiKa altimeter measurements for multi-site hydrodynamic model validation and rating curves estimation: An application to Brahmaputra River. Adv. Space Res. 2021, 68, 691–702. [Google Scholar] [CrossRef]
  5. Singh, R.K.; Kumar Villuri, V.G.; Pasupuleti, S.; Nune, R. Hydrodynamic modeling for identifying flood vulnerability zones in lower Damodar river of eastern India. Ain Shams Eng. J. 2020, 11, 1035–1046. [Google Scholar] [CrossRef]
  6. Chatterjee, C.; Förster, S.; Bronstert, A. Comparison of hydrodynamic models of different complexities to model floods with emergency storage areas. Hydrol. Process. 2008, 22, 4695–4709. [Google Scholar] [CrossRef]
  7. Ping, F.; Jia-chun, L.; Qing-quan, L. Flood routing models in confluent and dividing channels. Appl. Math. Mech. 2004, 25, 1333–1343. [Google Scholar] [CrossRef]
  8. Wang, K.; Wang, Z.; Liu, K.; Cheng, L.; Bai, Y.; Jin, G. Optimizing flood diversion siting and its control strategy of detention basins: A case study of the Yangtze River, China. J. Hydrol. 2021, 597, 126201. [Google Scholar] [CrossRef]
  9. Li, L.; Jun, K.S. Distributed parameter unsteady flow model for the Han River. J. Hydro-environ. Research 2018, 21, 86–95. [Google Scholar] [CrossRef]
  10. Li, L.; Jun, K.S. A hybrid approach to improve flood forecasting by combining a hydrodynamic flow model and artificial neural networks. Water 2022, 14, 1393. [Google Scholar] [CrossRef]
  11. Zhang, J.; Xiao, H.; Fang, H. Component-based Reconstruction Prediction of Runoff at Multi-time Scales in the Source Area of the Yellow River Based on the ARMA Model. Water Resour. Manag. 2022, 36, 433–448. [Google Scholar] [CrossRef]
  12. Yan, B.; Mu, R.; Guo, J.; Liu, Y.; Tang, J.; Wang, H. Flood risk analysis of reservoirs based on full-series ARIMA model under climate change. J. Hydrol. 2022, 610, 127979. [Google Scholar] [CrossRef]
  13. Karahan, H.; Iplikci, S.; Yasar, M.; Gurarslan, G. River flow estimation from upstream flow records using support vector machines. J. Appl. Math. 2014, 714213. [Google Scholar] [CrossRef]
  14. Zhou, L.; Kang, L. Comparative analysis of multiple machine learning methods for flood routing in the Yangtze River. Water 2023, 15, 1556. [Google Scholar] [CrossRef]
  15. Panda, R.K.; Pramanik, N.; Bala, B. Simulation of river stage using artificial neural network and MIKE 11 hydrodynamic model. Computers & Geosciences 2010, 36, 735-745.
  16. Elsafi, S.H. Artificial neural networks (ANNs) for flood forecasting at Dongola Station in the River Nile, Sudan. Alexandria Eng. J. 2014, 53, 655–662. [Google Scholar] [CrossRef]
  17. Ren, T.; Liu, X.; Niu, J.; Lei, X.; Zhang, Z. Real-time water level prediction of cascaded channels based on multilayer perception and recurrent neural network. J. Hydrol. 2020, 585, 124783. [Google Scholar] [CrossRef]
  18. Vizi, Z.; Batki, B.; Ratki, L.; Szalanczi, S.; Rehevary, I.; Kozak, P.; Kiss, T. Water level prediction using long short-term memory neural network model for a lowland river: a case study on the Tisza River, Central Europe. Environ. Sci. Eur. 2023, 35, 92. [Google Scholar] [CrossRef]
  19. Sivapragasam, C.; Maheswaran, R.; Venkatesh, V. Genetic programming approach for flood routing in natural channels. Hydrol. Process 2008, 22(5), 623–628. [Google Scholar] [CrossRef]
  20. Latt, Z.Z. Application of feedforward artificial neural network in Muskingum flood routing: a black-box forecasting approach for a natural river system. Water Resour. Manage. 2015, 29, 4995–5014. [Google Scholar] [CrossRef]
  21. Nikoo, M.; Ramezani, F.; Hadzima-Nyarko, M.; Nyarko, E.K.; Nikoo, M. Flood-routing modeling with neural network optimized by social-based algorithm. Nat. Hazards. 2016, 82, 1–24. [Google Scholar] [CrossRef]
  22. Hassanvand, M.R.; Karami, H.; Mousavi, S.-F. Investigation of neural network and fuzzy inference neural network and their optimization using meta-algorithms in river flood routing. Nat. Hazards 2018, 94, 1057–1080. [Google Scholar] [CrossRef]
  23. Tayfur, G.; Singh, V.P.; Moramarco, T.; Barbetta, S. Flood hydrograph prediction using machine learning methods. Water 2018, 10(8), 968. [Google Scholar] [CrossRef]
  24. Pashazadeh, A.; Javan, M. Comparison of the gen expression programming, artificial neural network (ANN), and equivalent Muskingum inflow models in the flood routing of multiple branched rivers. Theor. Appl. Climatol. 2020, 139, 1349–1362. [Google Scholar] [CrossRef]
  25. Chen, Y.-C.; Yeh, H.-C.; Kao, S.-P.; Wei, C.; Su, P.-Y. Water level forecasting in tidal rivers during typhoon periods through ensemble empirical model decomposition. Hydrology 2023, 10(2), 47. [Google Scholar] [CrossRef]
  26. Katipoglu, O.M.; Sarigo, M. Coupling machine learning with signal process techniques and particle swarm optimization for forecasting flood routing calculations in the Eastern Black Sea Basin, Turkiye. Environ. Sci. Pollut. Res. 30, 46074–46091. [CrossRef] [PubMed]
  27. Katipoglu, O.M.; Sarigol, M. Prediction of flood routing results in the Central Anatolian region of Turkiye with various machine learning models. Stoch. Environ. Res. Risk Assess. 37, 1–20.
  28. Katipoglu, O.M.; Sarigol, M. Boosting flood routing prediction performance through a hybrid approach using empirical model decomposition and neural networks: a case of the Mera River in Ankara. Water Supply 2023c, 288.
  29. Safavi, H.R.; Esmikhani, M. Conjunctive use of surface water and groundwater: application of support vector machines (SVMs) and generic algorithms. Water Resour. Manage. 2013, 27, 2623–2644. [Google Scholar] [CrossRef]
  30. Rahbar, A.; Mirarabi, A.; Nakhaei, M.; Talkhabi, M.; Jamali, M. A Comparative Analysis of Data-Driven Models (SVR, ANFIS, and ANNs) for Daily Karst Spring Discharge Prediction. Water Resour. Manag. 2022, 36, 589–609. [Google Scholar] [CrossRef]
  31. Mokhtarzad, M.; Eskandari, F.; Vanjani, N.J.; Arabasadi, A. Drought forecasting by ANN, ANFIS and SVM and comparison of the models. Environ. Earth Sci. 2017, 76, 729. [Google Scholar] [CrossRef]
  32. Coulibaly, P.; Anctil, F.; Rasmussen, P.; Bobee, B. A recurrent neural networks approach using indices of low-frequency climatic variability to forecast regional annual runoff. Hydrol. Process 2000, 14, 2755–2777. [Google Scholar] [CrossRef]
  33. Huang, G.-B. Learning capability and storage capacity of two-hidden-layer feedforward networks. IEEE Trans. Neural Netw. 2003, 14(2), 274–281. [Google Scholar] [CrossRef] [PubMed]
  34. Maiti, S.; Tiwari, R.K. A comparative study of artificial neural networks Bayesian neural networks and adaptive neuro-fuzzy inference system in groundwater level prediction. Environ. Earth Sci. 2013, 71, 3147–3160. [Google Scholar] [CrossRef]
  35. Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: an algorithm for optimization inspired by imperialistic competition. IEEE congress on evolutionary computation 2007, 4661–4666. [Google Scholar]
  36. Rumelhart, D.E.; McClelland, J.L.; James, L. Parallel distribution processing: exploration in the microstructure of cognition. MIT Press, Cambridge, MA, 1986.
  37. Mohan, S. Parameter estimation of nonlinear Muskingum models using genetic algorithm. J. Hydraul. Eng. 1997, 123(2), 137–142. [Google Scholar] [CrossRef]
  38. Barati, R. Parameter estimation of nonlinear Muskingum models using the Nelder-Mead simplex algorithm. J. Hydrol. Eng. 2011, 16(11), 946–954. [Google Scholar] [CrossRef]
  39. Geem, Z.W. Parameter estimation for the nonlinear Muskingum model using the BFGS techniques. J. Irrig. Drain. Eng. 2006, 132(5), 474–478. [Google Scholar] [CrossRef]
  40. Li, Z.; Kang, L.; Zhou, L.; Zhu, M. Deep Learning Framework with Time Series Analysis Methods for Runoff Prediction. Water 2021, 13, 575. [Google Scholar] [CrossRef]
  41. Breiman, L. Random forests. Machine learning. 2001, 45(1), 5–32. [Google Scholar] [CrossRef]
  42. Svetnik, V.; Liaw, A.; Tong, C.; Culberson, J.C.; Sheridan, R.P.; Feuston, B.P. Random forest: a classification and regression tool for compound classification and QSAR modeling. J. Chem. Inf. Comput. Sci. 2003, 43(6), 1947–1958. [Google Scholar] [CrossRef] [PubMed]
  43. Chu, H.J.; Chang, L.C. Applying particle swarm optimization to parameter estimation of the nonlinear Muskingum model. J. Hydrol. Eng. 2009, 14(9), 1024–1027. [Google Scholar] [CrossRef]
  44. Seo, Y.; Kim, S. River stage forecasting using wavelet packet decomposition and data-driven models. Procedia Engineering 2016, 154, 1225–1230. [Google Scholar] [CrossRef]
  45. Kumar, N.; Shaikh, A.A.; Mahato, S.K.; Bhunia, A.K. Applications of new hybrid algorithm based on advanced cuckoo search and adaptive Gaussian quantum behaved particle swarm optimization in solving ordinary differential equations. Expert Syst. Appl. 2021, 172(15), 114646. [Google Scholar] [CrossRef]
  46. McCarthy G.T. The unit hydrograph and flood routing. Proc., Conference of the North Atlantic Division, U.S. Army Corps of Engineers, New London, CT, 1938.
  47. Akbari, K.; Hessami-kermani, M.-R. Parameter estimation of Muskingum model using grey wolf optimizer algorithm. MethodsX 2021, 101589. [Google Scholar] [CrossRef]
  48. Kim, J.H.; Geem, Z.W.; Kim, E.S. Parameter estimation of the nonlinear Muskingum model using harmony search. J. Am. Water Resour. Assoc. 2001, 37(5), 1131–1138. [Google Scholar] [CrossRef]
  49. Luo, J.; Xie, J. Parameter estimation for nonlinear Muskingum model based on immune clonal selection algorithm. J. Hydrol. Eng. 2010, 15(10), 844–851. [Google Scholar] [CrossRef]
  50. Geem, Z.W. Parameter estimation of the nonlinear Muskingum model using parameter-setting-free harmony search. J. Hydrol. Eng. 2011, 16(8), 684–688. [Google Scholar] [CrossRef]
  51. Xu, D.M.; Qiu, L.; Chen, S.Y. Estimation of nonlinear Muskingum model parameter using Differential Evolution. J. Hydrol. Eng. 2012, 17(2), 348–353. [Google Scholar] [CrossRef]
  52. Karahan, H.; Gurarslan, G.; Aff.M.ASCE; Geem, Z.W. Parameter estimation of the nonlinear Muskingum flood-routing model using a hybrid harmony search algorithm. J. Hydro. Eng. 2013, 18, 352-360.
  53. Ouyang, A.; Li, K.; Truong, T.K.; Sallam, A.; Sha, E.H.M. Hybrid particle swarm optimization for parameter estimation of Muskingum model. Neural Comput. Appl. 2014, 25, 1785–1799. [Google Scholar] [CrossRef]
  54. Haddad, O.B.; Hamedi, F.; Fallah-Mehdipour, E.; Orouji, H.; Marino, M.A. Application of a hybrid optimization method in Muskingum parameter estimation. Irrig. Drain. Eng. 2015, 141(12), 482-489.
  55. Niazkar, M.; Afzali, S.H. Assessment of modified honey bee mating optimization for parameter estimation of nonlinear Muskingum models. J. Hydrol. Eng. 2015, 20(4), 04014055. [Google Scholar] [CrossRef]
  56. Hamedi, F.; Bozorg-Haddad, O.; Pazoki, M.; Asgari, H.R.; Parsa, M.; Loaiciga, H.A. Parameter estimation of extended nonlinear Muskingum models with the weed optimization algorithm. J. Irrig. Drain. Eng. 2016, 142(12), 1–11. [Google Scholar] [CrossRef]
  57. Moghaddam, A.; Behmanesh, J.; Farsijani, A. Parameter estimation for the new four-parameter nonlinear Muskingum model using the particle swarm optimization. Water Resour. Manage. 2016, 30(7), 2143–2160. [Google Scholar] [CrossRef]
  58. Niazkar, M.; Afzali, S.H. Application of new hybrid optimization technique for parameter estimation of new improved version of Muskingum model. Water Resour. Manage. 2016, 30(13), 4713–4730. [Google Scholar] [CrossRef]
  59. Ehteram, M.; Othman, F.B.; Yaseen, Z.M.; Afan, H.A.; Allawi, M.F.; Malek, M.B.A.; Ahmed, A.N.; Shahid, S.; Singh, V.P.; EI-Shafie, A. Improving the Muskingum flood routing method using a hybrid of particle swarm optimization and bat algorithm. Water 2018, 1(6), 807. [Google Scholar] [CrossRef]
  60. Farahani, N.; Karami, H.; Farzin, S.; Ehteram, M.; Kisi, O.; Shafie, A.El. A new method for flood routing utilizing four-parameter nonlinear Muskingum an Shark algorithm. Water Resour. Manage. 2019, 33, 4879–4893. [Google Scholar] [CrossRef]
  61. Akbari, R.; Hessami-Kermani, M.R.; Shojaee, S. Flood routing: improving outflow using a new nonlinear muskingum model with four variable parameters coupled with PSO-GA algorithm. Water Resour. Manage. 2020, 34(10), 3219–3316. [Google Scholar] [CrossRef]
  62. Norouzi, H.; Bazargan, J. Effects of uncertainty in determining the parameters of the linear Muskingum method using the particle swarm optimization (PSO) algorithm. J. Water and Climate Change 2021, 12(5), 2055–2067. [Google Scholar] [CrossRef]
  63. Okkan, U.; Kirdemir, U. Locally tuned hybridized particle swarm optimization for the calibration of the nonlinear Muskingum flood routing model. J. Water Clim. Change 2020, 11(S1), 343–358. [Google Scholar] [CrossRef]
  64. Mai, X.; Liu, H.-B.; Liu, L.-B. A new hybrid cuckoo quantum-behavior particle swarm optimization algorithm and its application in Muskingum model. Neural Processing Letters 2023, 55, 8309–8337. [Google Scholar] [CrossRef]
  65. Zhao, Y.; Chadha, M.; Olsen, N.; Yeates, E.; Turner, J.; Gugaratshan, G.; Qian, G.; Todd, M.D.; Hu, Z. Machine learning-enabled calibration of river routing model parameters. J. Hydroinformatics 2023, 25(5), 1799. [Google Scholar] [CrossRef]
  66. Peters, R.; Schmitz, G.; Cullmann, J. Flood routing modelling with Artificial Neural Network. Adv. Geosci. 2006, 9, 131–136. [Google Scholar] [CrossRef]
  67. Shrestha, R.R.; Theobald, S.; Nestmann, F. Simulation of flood flow in a river system using artificial neural networks. Hydrol. Earth Syst. Sci. 2005, 9(4), 313–321. [Google Scholar] [CrossRef]
  68. Razavi, S.; Karamouz, M. Adaptive neural networks for flood routing in river systems. Water Int. 2007, 32(3), 360–375. [Google Scholar] [CrossRef]
  69. Ghalkhani, H.; Golian, S.; Saghafian, B.; Farokhnia, A.; Shamseldin, A. Application of surrogate artificial intelligent models for real-time flood routing. Water Environ. J. 2013, 535, 548. [Google Scholar] [CrossRef]
  70. Liu, K.; Li, Z.; Yao, C.; Chen, J.; Zhang, K.; Saifullah, M. Coupling the k-nearest neighbor procedure with the Kalman filter for real-time updating of the hydraulic model in flood forecasting. Int. J. Sediment Res. 2016, 31, 146–158. [Google Scholar] [CrossRef]
  71. Kabir, S.; Patidar, S.; Xia, X.; Liang, Q.; Neal, J.; Pender, G. A deep convolutional neural network model for rapid prediction of fluvial flood inundation. J. Hydrol. 2020, 590, 125481. [Google Scholar] [CrossRef]
  72. Tawfik, A.M. River flood routing using artificial neural networks. Ain Shams Eng. J. 2023, 14, 101904. [Google Scholar] [CrossRef]
  73. Peng, A.; Zhang, X.; Xu, W.; Tian, Y. Effects of Training Data on the Learning Performance of LSTM Network for Runoff Simulation. Water Resour. Manag. 2022, 36, 2381–2394. [Google Scholar] [CrossRef]
Preprints 94993 g001
Figure 1. Application of ML methods for river flood routing.
Figure 1. Application of ML methods for river flood routing.
Preprints 94993 g001
Table 1. Single applications of ML method for flood routing simulation.
Table 1. Single applications of ML method for flood routing simulation.
Paper No. of citations Journal Impact factor Studied river Adopted method Compared models Modeling performance criteria
[19] 73 Hydrological Processes 3.2 Walla Walla River, USA GP NMM RMSE, CC
[15] 125 Computers & Geosciences 8.1 Kushabhadra River, India ANN MIKE 11 HD RMSE, R2, NSE, IOA, DP
[16] 164 Alexandria Engineering Journal 6.8 River Nile, Sudan ANN R2, RMSE
[13] 7 Journal of Applied Mathematics - River Wyre, UK SVM Muskingum model SSE
[20] 19 Water Resources Management 4.2 Chindwin River, Myanmar ANN CE, MRE, EQp, ETp
[21] 46 Natural Hazards 3.7 Kheir Abad River, Iran ANN (FF-SBA) FF-GA, FF-PSO, Linear regression, Non-linear regression R2, MSE
[22] 18 Natural Hazards 3.7 Maryam Negar River, Iran ANN, ANFIS MAE, RMSE, Bias, SI, SSQ
[23] 40 Water 3.4 Tiber River, Italy ANN RCM, GA_RCM, PSO_RCM, ACO_RCM, Saint-Venant, PSO_NMM, ACO_NMM, GA_NMM EQp, ETp, MAE, RMSE
[24] 10 Theoretical and Applied Climatology 3.4 Gharesoo River, Iran GEP, ANN Muskingum model R2, RMSE
[17] 53 Journal of Hydrology 6.4 South-to-North water Diversion Project channel, China MWLP, RWLP, LSTM, GRU SVM, ANN RMSE, MAE, NSE, PCC, PI
[25] 3 Hydrology 3.2 Tanshui River, Taiwan EEMD and stepwise regression CC, RMSE
[26] 4 Environmental Science and Pollution Research 5.8 Turnasuyu Stream, Turkey LSSVM, PSO-LSSVM, EMD-LSSVM, Wavelet-LSSVM, VMD-LSSVM MAPE, NSE, MBE, R2
[27] 1 Stochastic Environmental Research and Risk Assessment 4.2 Mera Stream, Sarisu Stream, Kizilirmak River, Turkey BT, GBM, KNN, RF, SVM, XGBoost R2, RMSE, MAE
[28] 0 Water Supply 1.7 Mera River, Turkey EMD-CFBNN, EME-FFBNN CFBNN, FFBNN CC
[18] 0 Environmental Sciences Europe 5.9 Tisza River, Central Europe LSTM DLCM, MLP, Linear model, MAE, RMSE, R2, WI
[14] 2 Water 3.4 Yangtze River, China SVR, GPR, RFR, MLP, LSTM, GRU MAPE, RMSE, NSE, TSS, KGE
Table 2. ML methods used for the parameter estimation of Muskingum models.
Table 2. ML methods used for the parameter estimation of Muskingum models.
Paper No. of citations Journal Impact factor Adopted method
[37] 261 Journal of Hydraulic Engineering 2.4 GA
[48] 278 Journal of the American Water Resources Association 2.4 HS
[39] 95 Journal of Irrigation and Drainage Engineering 2.6 BFGS
[19] 73 Hydrological Processes 3.2 GP
[43] 87 Journal of Hydrologic Engineering 2.4 PSO
[49] 55 Journal of Hydrologic Engineering 2.4 ICSA
[38] 218 Journal of Hydrologic Engineering 2.4 NMS algorithm
[50] 65 Journal of Hydrologic Engineering 2.4 Parameter-setting-free HS
[51] 55 Journal of Hydrologic Engineering 2.4 DE
[52] 157 Journal of Hydrologic Engineering 2.4 BFGS-HS
[53] 55 Neural Computing and Application 6 HPSO
[54] 15 Journal of Irrigation and Drainage Engineering 2.6 SFLA-NMS
[55] 65 Journal of Hydrologic Engineering 2.4 MHBMO algorithm
[56] 23 Journal of Irrigation and Drainage Engineering 2.6 WOA
[57] 42 Water Resources Management 4.3 PSO
[58] 37 Water Resources Management 4.3 MHBMO-GRG
[1] 33 Water Resources Management 4.3 BSA evolutionary algorithm
[59] 39 Water 3.4 HBSA
[23] 40 Water 3.4 PSO, ACO, GA
[60] 11 Water Resources Management 4.3 SA
[61] 13 Water Resources Management 4.3 PSO-GA
[62] 9 Water & Climate Change 2.8 PSO
[63] 13 Water & Climate Change 2.8 PSO-LM
[47] 4 MethodsX 1.9 GWO algorithm
[64] 0 Neural Processing Letters 3.1 C-QPSO
[65] 0 Hydroinformatics 2.7 GPR, GMC, RF, XGBoost
Table 3. Hybrid applications of a hydraulic model and ML method.
Table 3. Hybrid applications of a hydraulic model and ML method.
Paper No. of citations Journal Impact factor Studied river Adopted method Compared model Modeling performance criteria
[67] 88 Hydrology and Earth System Science 6.3 Neckar River, Germany ANN & a one-dimensional hydrodynamic numerical model - CE, R2, RMSE, DPF
[66] 40 Advances in Geosciences 1.6 Freiberger Mulde River, Germany HEC-RAS & ANN HEC-RAS R2
[68] 14 Water International 2.6 Karoon River, Iran HEC-RAS & adaptive ANNs HEC-RAS, Muskingum routing method CE, PWRMSE, mean error of time to peak, volume error of highest peaks
[69] 36 Water and Environment Journal 2 Doogh River, Iran HEC-RAS & ANN; HEC-RAS & ANFIS HEC-RAS NSE, MRE, RMSE
[70] 64 International Journal of Sediment Research 3.6 Huai River, China KN2K & one-dimensional hydraulic model KF & one-dimensional hydraulic model NSE, ANSE, SDE
[71] 101 Journal of Hydrology 6.4 Eden Catchment, UK LISFLOOD-FP & CNN LISFLOOD-FP, SVR NSE, RMSE
[10] 0 Water 3.4 Han River, South Korea HM-ANN HM, ANN RMSE, NSE
[72] 2 Ain Shams Engineering Journal 6 HEC-RAS & ANN HEC-RAS, Muskingum method Standard error, etc.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated