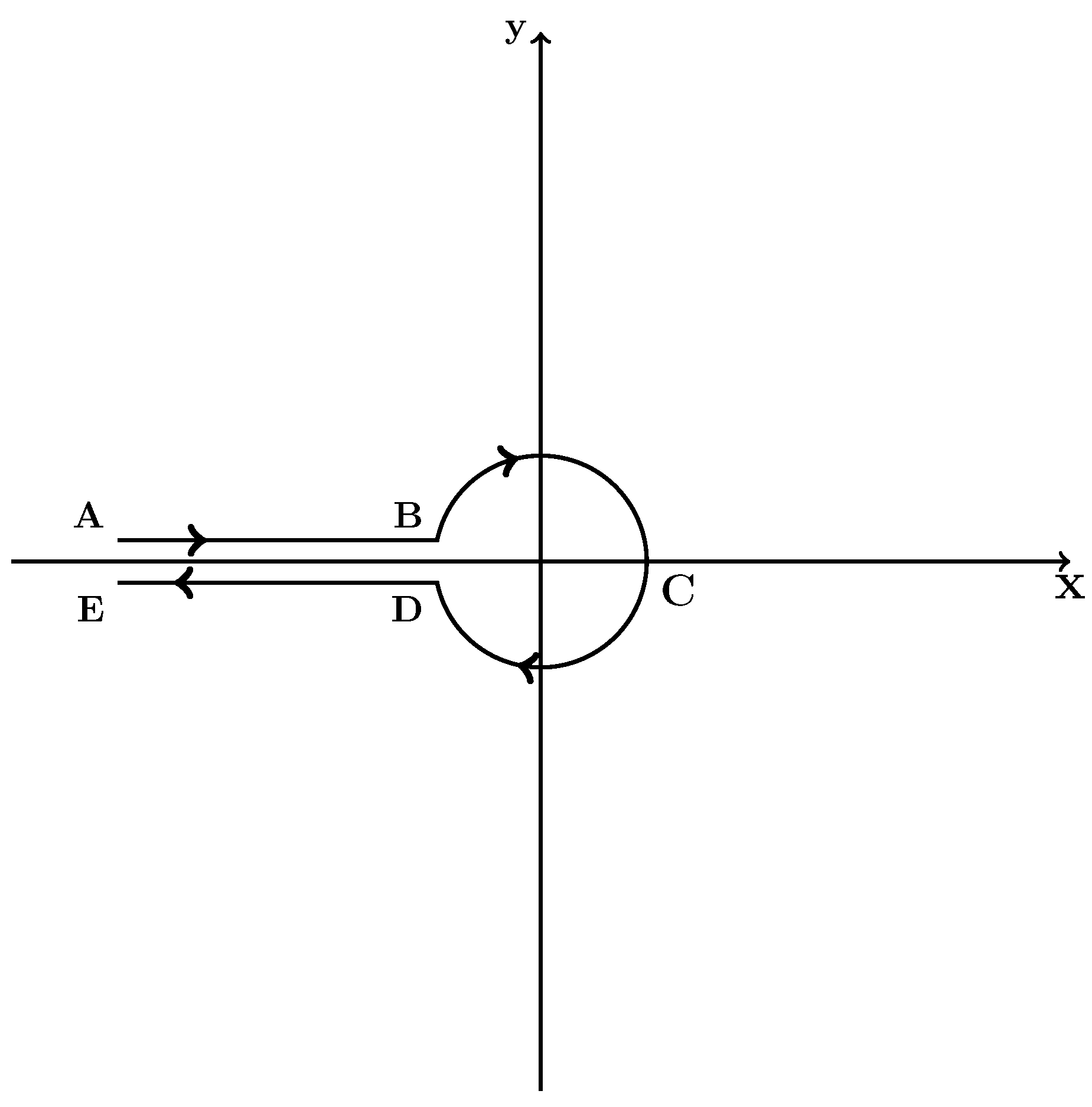Finite Representations of theWright Function

Preprint

Article

Finite Representations of theWright Function

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Dimiter Prodanov^*

This version is not peer-reviewed

Submitted:

20 December 2023

Posted:

25 December 2023

You are already at the latest version

Alerts

Abstract

The two-parameter Wright special function is an interesting mathematical object that arises in the theory of the space and time-fractional diffusion equations. Moreover, many other special functions are particular instantiations of the Wright function. The article demonstrates finite representations of the Wright function in terms of sums of generalized hypergeometric functions, which in turn provide connections with the theory of the Gaussian, Airy, Bessel, and Error functions, etc. The main application of the presented results is envisioned in computer algebra for testing numerical algorithms for the evaluation of the Wright function.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

The Wright function was introduced in two seminal publications by the British mathematician Sir E.M. Wright discussing the theory of partitions of numbers [1,2]. The function received renewed interest from the mathematical community when it was demonstrated that the space-time fractional diffusion equation with the temporal Caputo derivative can be solved in terms of Wright functions [3]. It was also discovered that the Wright function provides a unified treatment of several classes of special functions, notably the Bessel functions, the probability integral erf the Airy Ai, and the Whittaker function, among others. The Wright function was originally defined by the infinite series [1]:

W (a, b | z) : = \sum_{k = 0}^{\infty} \frac{z^{k}}{k! Γ (a k + b)}, z \in C,

under the conditions

b \in C

and

a > - 1

, where

Γ

denotes the Euler’s Gamma function. Later works on the function include the articles of Gorenflo, Luchko and Mainardi [4] and Luckko [5] among some others. Based on the sign of its first parameter, later, Mainardi classified the function into two types: the Wright function of the 1^st type if

a \geq 0

and the Wright function of 2^nd type for

- 1 < a < 0

[6,7]. This function fits into the more general theory of the Fox-Wright (FW) functions as will be discussed in Sec. 3.

The Wright function is closely related to the theory of the generalized hypergeometric (GHG) functions. Notably, for rational parameter values the Wright function can be represented as a finite sum of GHG functions. The link comes directly through the theory of the Euler’s Gamma function. Formulas for the Wright function representation of the 1^st type have been published in [4,8] and have been derived through its representation as a Meijer G function. Recently, Apelblat and Gonzales-Santander have tabulated representations in terms of GHG functions for many parameter combinations [9].

The contribution of the present article is twofold. On the first place, it extends the results of the above authors [9] for the cases wherever

a < 0

and

b > 1

and also demonstrates how the domain of the first parameter can be extended into the negative integers under certain conditions by explicitly constructing polynomial representations of the function. These representations allow us to distinguish a Wright function of 3^rd type (Sec. 4). Some of the present results have been presented in a preliminary form at the 2023 International Conference on Fractional Differentiation and Its Applications ICFDA 2023 [10]. On the second place, the article exhibits the link with the Mittag-Leffler function, which also has wide applications in fractional calculus. It is demonstrated that the theory of the Wright function is very rich and can produce many potentially useful integral identities. In a similar way, the domain of the Mittag-Leffler function can be analytically continued into negative integral values of its first parameter and integer values of its second parameter.

2. Some Applications of the Wright Function

Recent surveys about Wright function applications can be found in [7] and [11]. What makes the function useful for applications in calculus is the fact that it is closed under differentiation

\frac{d}{d z} W (a, b| z) = W (a, a + b| z)

(1)

which allows one to write

W (a, b| z) = \int_{0}^{z} W (a, a + b| z) + \frac{1}{Γ (b)}

(2)

and

\int W (a, b| z) d z = W (a, b - a| z) + C

(3)

The Wright function arises in the theory of the space-time fractional diffusion equation (FDE) with the temporal Caputo derivative [3]. We recall that the Caputo’s fractional derivative of order

β > 0

is defined for

β \notin N

as the differ-integral

D_{t}^{β} f (t) : = \frac{1}{Γ (m - β)} \int_{0}^{t} \frac{f^{(m)} (u) d u}{{(t - u)}^{β + 1 - m}}

(4)

where

m = ⌊ β ⌋

. The fractional differential equation in the Caputo sense with variable coefficients

D_{t}^{b} [t^{b} f^{'} (t)] = a t^{b - 1} f (t)

(5)

admits for a solution

f (t) = W (a, b| t^{a})

[12].

3. The Wright Function as a Simple Representative of the Fox-Wright Function Family

The generalized hypergeometric functions are defined by the infinite hypergeometric (HG) series

\begin{matrix} {}_{p}F_{q} (a_{1}, \dots, a_{p}; b_{1}, \dots, b_{q}, x) : = \\ \sum_{m = 0}^{\infty} \frac{x^{m}}{Γ (m + 1)} \prod_{k = 1}^{p} \frac{Γ (a_{k} + m)}{Γ (a_{k})} \prod_{k = 1}^{q} \frac{Γ (b_{k})}{Γ (b_{k} + m)} = \sum_{r = 0}^{\infty} \frac{x^{r}}{r!} \frac{\prod_{j = 0}^{p - 1} {(a_{j})}_{r}}{\prod_{j = 0}^{q - 1} {(b_{j})}_{r}} \end{matrix}

(6)

where

{(a)}_{r}

and

{(b)}_{r}

will denote rising factorials and

{(a)}_{0} = 1

, which assumes the normalization

{}_{p}F_{q} (\sim; \sim | 0) = 1

. By convention, equal parameters in the numerator and denominator will cancel out. Unless stated otherwise it will be always assumed that the infinite series converge in some domain

x \in R

The defining property fo HG series is that the coefficients are rational functions of the index variable (i.e. k). In the present article we will use the parametric notation similar to the one adopted by Oldham and Spanier [13].

{}_{p}F_{q} (a_{1}, \dots, a_{p}; b_{1}, \dots, b_{q}, x) \equiv [\begin{matrix} \begin{matrix} a_{1}, \dots, a_{p} \\ b_{1}, \dots, b_{q} \end{matrix} & ∣ & \begin{matrix} x \end{matrix} \end{matrix}]

The FW functions are further generalizations of the hypergeometric (HG) functions. It can be defined by the infinite series

\begin{matrix} {}_{p}{\bar{Ψ}}_{q} (x) \equiv \bar{Ψ} [\begin{matrix} \begin{matrix} (A_{1}, a_{1}) \dots, (A_{p}, a_{p}) \\ (B_{1}, b_{1}) \dots, (B_{q}, b_{q}) \end{matrix} & ∣ & \begin{matrix} x \end{matrix} \end{matrix}] : = \\ \sum_{m = 0}^{\infty} \frac{x^{m}}{Γ (m + 1)} \prod_{k = 1}^{p} \frac{Γ (a_{k} m + A_{k})}{Γ (A_{k})} \prod_{k = 1}^{q} \frac{Γ (B_{k})}{Γ (b_{k} m + B_{k})} \end{matrix}

whenever it converges.

At this point the following extended notation is introduced under the convention

{}_{p + 1}{\bar{Ψ}}_{q} (z) \equiv [\begin{matrix} \begin{matrix} a_{1}, \dots, a_{p} \\ b_{1}, \dots, b_{q} \end{matrix} & ∣ & \begin{matrix} (A, a) \\ - \end{matrix} & ∣ & \begin{matrix} z \end{matrix} \end{matrix}], {}_{p + 1}{\bar{Ψ}}_{q} (0) = 1,

In this notation, the hypergeometric parameters of the function are written first while the composite parameters are left second. The right parameters result in factors of the form

\frac{Γ (k a + A)}{Γ (A)}

or their reciprocals, respectively, while the left parameters result is Pochhammer multipliers (i.e.

A \in N

). The non-simplified parameters follow the usual convention established in literature. The order in the parametric convention for the arguments of the Gamma function follows the usual convention.

The following simplifying convention will be used further:

[\begin{matrix} \begin{matrix} a_{1}, \dots \\ b_{1}, \dots \end{matrix} & ∣ & \begin{matrix} - \\ - \end{matrix} & ∣ & \begin{matrix} x \end{matrix} \end{matrix}] \equiv [\begin{matrix} \begin{matrix} a_{1}, \dots \\ b_{1}, \dots \end{matrix} & ∣ & \begin{matrix} z \end{matrix} \end{matrix}]

(7)

and

[\begin{matrix} \begin{matrix} a_{1}, \dots, a_{p} \\ b_{1}, \dots, b_{q} \end{matrix} & ∣ & \begin{matrix} (A, 1) \\ - \end{matrix} & ∣ & \begin{matrix} z \end{matrix} \end{matrix}] \equiv [\begin{matrix} \begin{matrix} a_{1}, \dots, a_{p}, A \\ b_{1}, \dots, b_{q} \end{matrix} & ∣ & \begin{matrix} z \end{matrix} \end{matrix}]

(8)

This example shows different ways to write a hypergeometric function. Under this notation

W (a, b| z) = \frac{1}{Γ (b)} [\begin{matrix} \begin{matrix} - \\ - \end{matrix} & ∣ & \begin{matrix} - \\ (b, a) \end{matrix} & ∣ & \begin{matrix} z \end{matrix} \end{matrix}]

(9)

In this way one could appreciate that the Wright function is the simplest member of the class of the Fox-Wright functions. Other examples are the Bessel J function:

J_{ν} (z) = \frac{1}{Γ (ν + 1)} {(\frac{z}{2})}^{ν} [\begin{matrix} \begin{matrix} - \\ ν + 1 \end{matrix} & ∣ & \begin{matrix} - \frac{z^{2}}{4} \end{matrix} \end{matrix}]

The Struve H function:

H_{ν} (z) = \frac{1}{Γ (ν + 3 / 2) Γ (3 / 2)} {(\frac{z}{2})}^{ν + 1} [\begin{matrix} \begin{matrix} 1 \\ 3 / 2, ν + 3 / 2 \end{matrix} & ∣ & \begin{matrix} - \frac{z^{2}}{4} \end{matrix} \end{matrix}]

Furthermore, the following integral representation can be derived (see for example [14]):

\begin{matrix} [\begin{matrix} \begin{matrix} a_{1}, \dots, a_{p} \\ b_{1}, \dots, b_{q} \end{matrix} & ∣ & \begin{matrix} \dots \\ (B, b) \end{matrix} & ∣ & \begin{matrix} z \end{matrix} \end{matrix}] = \frac{Γ (B)}{2 π i} \int_{H a^{-}} \frac{e^{τ}}{τ^{B}} [\begin{matrix} \begin{matrix} a_{1}, \dots, a_{p} \\ b_{1}, \dots, b_{q} \end{matrix} & ∣ & \begin{matrix} \dots \\ \dots \end{matrix} & ∣ & \begin{matrix} \frac{z}{τ^{b}} \end{matrix} \end{matrix}] d τ \end{matrix}

(10)

where

H a^{-}

denotes the Hankel contour, which surrounds all poles of the GHG function from the left. Applied to the Wright function, where

B \mapsto a; b \mapsto a

this gives the integral

W (a, b| z) = \frac{1}{2 π i} \int_{H a^{-}} \frac{e^{ξ + z ξ^{- a}}}{ξ^{b}} d ξ, z \in C

(11)

along a Hankel contour, which surrounds the negative real semi-axis and the pole at the origin. Said contour can be deformed in a extreme was as depicted in Figure 1. This contour consists of the rays

A B

and

D E

as well as the arc

B C D

. For integral values of b and a the path of integration closes around the origin O so that the rays collapse and can be used to extend the domain of the function into the negative integer parameters.

4. Polynomial Reduction

In particular, let us consider the case when a is a negative integer and denote it by

- n

. Trivially, if b is a negative integer, say

b = - m

, then the above integral vanishes and

W (- n, - n| z) = 0

In contrast, if

n = - a

and

b = m, m

, such that

n \in N

then

W (- n, m| z) = Res (k e r (ξ), ξ = 0) = \frac{1}{Γ (m)} \{{(\frac{d}{d ξ})}^{m - 1} e^{ξ + z ξ^{n}}\} |_{ξ = 0}

Therefore, we can conclude that

W (- n, m| z)

is a polynomial in z. This is a novel result, which was not anticipated by Wright and allows for the extension of the domain of the parameters of the function. This polynomial can be computed explicitly by application of Faá di Bruno’s formula using the complete exponential Bell polynomials. For the natural numbers n and m:

W (- n, m| z) = \frac{1}{Γ (m)} B_{m - 1} (g^{'} (0), \dots, g^{(m - 1)} (0))

(12)

where

g (ξ) = ξ + z ξ^{n}

is the exponent of the kernel and it can be computed by the determinant

\begin{matrix} B_{m} (g^{'} (0), \dots, g^{(m)} (0)) = |\begin{matrix} (\binom{m - 1}{0}) g^{'} (0) & (\binom{m - 2}{1}) g^{''} (0) & \dots & (\binom{m - 1}{m - 1}) g^{(m)} (0) \\ - 1 & (\binom{m - 2}{0}) g^{'} (0) & \dots & (\binom{m - 2}{m - 2}) g^{(m - 1)} (0) \\ 0 & - 1 & \dots & (\binom{m - 3}{m - 3}) g^{(m - 3)} (0) \\ \dots \\ 0 & \dots & - 1 & (\binom{0}{0}) g^{'} (0) \end{matrix}| \end{matrix}

Remark 1.

It should noted that the resulting matrix is a band matrix since already

g^{″} (0) = 0

. For example, for

n = 3

m = 8

we have

B_{7} (\dots) = |\begin{matrix} 1 & 0 & 90 z & 0 & 0 & 0 & 0 \\ - 1 & 1 & 0 & 60 z & 0 & 0 & 0 \\ 0 & - 1 & 1 & 0 & 36 z & 0 & 0 \\ 0 & 0 & - 1 & 1 & 0 & 18 z & 0 \\ 0 & 0 & 0 & - 1 & 1 & 0 & 6 z \\ 0 & 0 & 0 & 0 & - 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & - 1 & 1 \end{matrix}|

The polynomial reduction formulas allow us the claim that Mainardi’s classification can be extended to add also Wright functions of the third type, that is whenever

a, b \in Z^{-}

5. Finite Hypergeometric Representations

Wherever the a parameter is rational the Wright function can be represented by a finite sum of hypergeometric functions. For positive and rational a one could obtain the representation in terms of

{}_{0}F_{m + n - 1}

GHG functions [9]:

Theorem 1

(First HG Representation). Suppose that

a = n / m > 0

, where n and m are co-prime and

b \neq 0

. Then

W (n / m, b| z)

admits the finite representation

W (n / m, b| z) = \sum_{r = 0}^{m - 1} \frac{z^{r}}{r! Γ (b + a r)} [\begin{matrix} \begin{matrix} 1 \\ \vec{b}, \vec{c} \end{matrix} & ∣ & \begin{matrix} \frac{z^{m}}{n^{n} m^{m}} \end{matrix} \end{matrix}],

(13)

where

\vec{b}

has n components and

\vec{c}

has m components given by

b_{j} = r / m + (b + j) / n, c_{j} = (r + 1 + j) / m,

respectively.

The proof follows [8] and is given as a staring point for the proof of the Second Representation Theorem.

Proof.

Starting from

a = n / m

\begin{matrix} W (a, b| z) = \sum_{k = 0}^{\infty} \frac{z^{k}}{k! Γ (a k + b)} = \sum_{q = 0}^{m - 1} \sum_{p \geq q / m}^{\infty} \frac{z^{m p - q}}{Γ (m p - q + 1) Γ (a (m p - q) + b)} \end{matrix}

since the integer k can be partitioned as

k = m p - q

, where

q = 0, \dots m - 1

. After some algebra we obtain

W (n / m, b| z) = \frac{1}{Γ (b)} + \sum_{r = 1}^{m} z^{r} \sum_{p = 0}^{\infty} \frac{z^{m p}}{Γ (a p + r a + b) Γ (m p + r + 1)} .

Observe that for

p = 0

the inner series evaluates to

C_{r} = Γ (r a + b) Γ (r + 1),

which serves as its normalization factor. Therefore, the series transforms as

\begin{matrix} W (n / m, b| z) = \sum_{r = 0}^{m} \frac{z^{r}}{C_{r}} \cdot \sum_{p = 0}^{\infty} \frac{Γ (r a + b) Γ (r + 1)}{Γ (n (p + r / m + b / n))} \frac{z^{m p}}{Γ (m (p + (r + 1) / m))} \end{matrix}

(14)

Further, use Prop. A1 to obtain

\frac{Γ (n (p + r / m) + b)}{Γ (n r / m + b)} = n^{n p} \prod_{j = 0}^{n - 1} \underset{b_{j}}{\underset{︸}{{(\frac{r}{m} + \frac{b}{n} + \frac{j}{n})}_{p}}}

(15)

From where we read off the component

b_{0} = \frac{r}{m} + \frac{b}{n}

with an increment

1 / n

\frac{Γ (m p + r + 1)}{Γ (r + 1)} = m^{m p} \prod_{j = 0}^{m - 1} \underset{c_{j}}{\underset{︸}{{(\frac{r + 1}{m} + \frac{j}{m})}_{p}}}

(16)

From where we read off the component

c_{0} = \frac{r + 1}{m}

with an increment

1 / m

. □

Observe that

r = m - 1

results in

c_{1} = 1

therefore, the GHG functions reduce to

{}_{0}F_{m + n - 1}

. The formula for a negative rational

a < 0

needs some more work. Suppose first that

b < 1

. Let

\begin{matrix} W (- n / m, b| z) = \frac{1}{Γ (b)} + \sum_{r = 1}^{m} \frac{z^{r}}{C_{r}} \sum_{p = 0}^{\infty} \frac{C_{r}}{Γ (- n p - r n / m + b)} \frac{z^{m p}}{Γ (m p + r + 1)} \end{matrix}

First we use the Gamma reflection formula to obtain

\frac{1}{Γ (- n p - r n / m + b)} = \frac{{(- 1)}^{n p} Γ (\frac{n r}{m} + n p - b + 1)}{Γ (b - \frac{n r}{m}) Γ (\frac{n r}{m} - b + 1)}

(17)

Therefore,

\begin{matrix} W (- n / m, b| z) = \frac{1}{Γ (b)} + \\ \sum_{r = 1}^{m} \frac{z^{r}}{C_{r}} \sum_{p = 0}^{\infty} \frac{{(- 1)}^{n p} C_{r} Γ (\frac{n r}{m} + n p - b + 1) z^{m p}}{Γ (b - \frac{n r}{m}) Γ (\frac{n r}{m} - b + 1) Γ (m (p + (r + 1) / m))} = \\ \frac{1}{Γ (b)} + \sum_{r = 1}^{m} \frac{z^{r}}{C_{r}} \sum_{p = 0}^{\infty} \frac{{(- 1)}^{n p} Γ (\frac{n r}{m} + n p - b + 1) Γ (r + 1) z^{m p}}{Γ (\frac{n r}{m} - b + 1) Γ (m p + r + 1))} \end{matrix}

We use Prop. A1 to compute

\begin{matrix} \frac{Γ (n (r / m + p) - b + 1)}{Γ (\frac{n r}{m} - b + 1)} = n^{n p} \prod_{j = 0}^{n - 1} {(\frac{r}{m} + \frac{1 - b}{n} + \frac{j}{n})}_{p} = \\ n^{n p} \prod_{j = n - 1}^{0} \underset{b_{j}^{'}}{\underset{︸}{{(1 + \frac{r}{m} - \frac{j + b}{n})}_{p}}} \end{matrix}

Finally, we read off the parameters

b_{j}^{'} = 1 + r / m - (b + j) / n

with an increment

1 / n

. Then we can formulate the following

Theorem 2

(Second HG Representation). For

b \leq 1

and

n \leq m

non-negative co-prime integers,

a = - n / m

W (- n / m, b| z) = \sum_{r = 0}^{m - 1} \frac{z^{r}}{r! Γ (b + a r)} [\begin{matrix} \begin{matrix} 1, {\vec{b}}^{'} \\ \vec{c} \end{matrix} & ∣ & \begin{matrix} \frac{{(-)}^{n} z^{m}}{n^{n} m^{m}} \end{matrix} \end{matrix}]

(18)

where

{\vec{b}}^{'} = {b_{0}^{'} \dots b_{n - 1}^{'}}

\vec{c} = {c_{0} \dots c_{m - 1}}

and

b_{j}^{'} = 1 + r / m - (b + j) / n, c_{j} = (r + 1 + j) / m

Observe that for

r = m - 1

c_{1} = 1

therefore, the GHG functions reduce to

{}_{n}F_{m - 1}

. For

b \geq 1

a polynomial part P must be also added to the representation as follows.

Theorem 3

(Third HG representation). Suppose that a and b are rational parameters and

b \geq 1

and

| a | \leq 1

. Define the polynomial

P_{b} (- a, z)

by the integral recursion

P_{b} (- a, z) = \int_{0}^{z} P_{b - a} (- a, x) d x + c_{b - 1},

(19)

where

c_{b - 1} = 1 / (b - 1)!

if b is an integer and 0 otherwise. Furthermore, define

P_{0} (z, - a) : = 1

and for

b < 0

assign

P_{b} (z, - a) : = 0

identically. Then for

a = - n / m

and

b \neq 0

W (- n / m, b| z) = \sum_{r = 0}^{m - 1} \frac{z^{r}}{r! Γ (b + a r)} [\begin{matrix} \begin{matrix} 1, {\vec{b}}^{'} \\ \vec{c} \end{matrix} & ∣ & \begin{matrix} \frac{{(-)}^{n} z^{m}}{n^{n} m^{m}} \end{matrix} \end{matrix}] + P_{b} (- a, z)

(20)

where m and n are co-prime numbers.

Proof.

First we prove that the arc integral results in a polynomial in z. Suppose that

b \geq 1

is rational and

- a = n / m

as before. Consider the arc BCD. We change variables as

ξ = ϵ η^{m}

. Then the integral becomes

I = m \oint_{B C D} \frac{d η ϵ^{1 - b}}{η^{(b - 1) m + 1}} e^{ϵ^{\frac{n}{m}} η^{n} z + ϵ η^{m}}

Development of the kernel in infinite series results in

k e r = m \frac{d η ϵ^{1 - b}}{η^{(b - 1) m + 1}} \sum_{j = 0}^{\infty} \sum_{i = 0}^{j} \frac{ϵ^{\frac{i m + (j - i) n}{m}} η^{i m + (j - i) n} z^{j - i}}{i! (j - i)!}

The scale-invariant part of the series is given by the members

k_{j}

for which

ϵ^{\frac{i m + (j - i) n}{m} - b + 1} = 1

This is given by the constraint

i = \frac{(b - 1) m - j n}{m - n}

Therefore,

k_{j} = \frac{d η m z^{\frac{(j - b + 1) n}{n - m}}}{η (\frac{(b - 1) n - j m}{n - m})! (\frac{(j - b + 1) n}{n - m})!}

Changing again variables to

η = e^{i φ / m}

results in the integral

\begin{matrix} c_{j} = \frac{1}{2 π i} \frac{i z^{\frac{(j - b + 1) m}{m - n}}}{(\frac{(b - 1) m - j n}{m - n})! (\frac{(j - b + 1) m}{m - n})!} \cdot \int_{- π}^{π} e^{\frac{i (b n - 1) φ}{n} + \frac{i φ}{n} - i b φ} d φ = \\ \frac{z^{\frac{(j - b + 1) m}{m - n}}}{(\frac{(b - 1) m - j n}{m - n})! (\frac{(j - b + 1) m}{m - n})!} \end{matrix}

Furthermore, the valid indices are given by the set

j : (\frac{(j - b + 1) m}{m - n} \in N) \cup (\frac{(b - 1) m - j n}{m - n} \in N)

Equivalently, in the a-notation

c_{j} = \frac{z^{\frac{j - b + 1}{1 - a}}}{(\frac{j - b + 1}{1 - a})! (\frac{- a j + b - 1}{1 - a})!}

(21)

Therefore,

a < 1

must hold for

c_{j}

not to vanish.

On the other hand,

b - 1 \leq j \leq (b - 1) / a \cup j \in N

which is a finite set. Therefore, for a rational b the integral I is a polynomial in z.

To derive the polynomial recursion we proceed as follows. By eq. 2

W (- a, b| z) = \int_{0}^{z} W (- a, b - a| z) + \frac{1}{Γ (b)}

(22)

so that the equation defines a recursion relationship.

Observe that for

j = b - 1 \in N

the coefficient becomes

c_{b - 1} = \frac{1}{(b - 1)!} = \frac{1}{Γ (b)}

Therefore, for non-integer b there are no constant monomials. Furthermore, consider the monomial

c_{j}

as a function of b. Differentiating eq. 21 one obtains the recursion

\begin{matrix} \frac{d}{d z} c_{j} (b) = \frac{z^{\frac{j - b + 1}{1 - a} - 1}}{(\frac{j - b + 1}{1 - a} - 1)! (\frac{- a j + b - 1}{1 - a})!} = \frac{z^{\frac{j - (b - a)}{1 - a}}}{(\frac{j - (b - a)}{1 - a})! (\frac{a j - b + 1}{a - 1})!} = c_{j - 1} (b - a), \end{matrix}

which is also consistent with the integral eq. 22. Therefore, the polynomial

P_{b} (- a, z)

should obey the above recursion. The second argument of the Wright function mutates and therefore it is convenient that it indexes the polynomial. □

For integer values of a, that is, when

m = 1

, Th. 3 corresponds with the polynomial representation since the hypergeometric sum disappears.

6. The Special Case $b = 0$

The case whenever

b = 0

needs separate treatment. From the theory of the FW functions we can formulate the following proposition.

Proposition 1.

Whenever

b = 0

we have the special FW representation

W (a, 0| z) = \frac{z}{Γ (a)} [\begin{matrix} \begin{matrix} 1 \\ 2 \end{matrix} & ∣ & \begin{matrix} - \\ (a, a) \end{matrix} & ∣ & \begin{matrix} z \end{matrix} \end{matrix}]

(23)

Proof.

The proof follows by direct computation:

W (a, 0| z) = \sum_{k = 1}^{\infty} \frac{z^{k}}{Γ (a k) Γ (k + 1)} = \sum_{j = 0}^{\infty} \frac{z^{j + 1}}{Γ (a j + a) Γ (j + 2)} = \frac{z}{Γ (a)} [\begin{matrix} \begin{matrix} 1 \\ 2 \end{matrix} & ∣ & \begin{matrix} - \\ (a, a) \end{matrix} & ∣ & \begin{matrix} z \end{matrix} \end{matrix}]

□

This result can be represented for rational a using the theory developed so-far as follows.

Proposition 2.

Whenever

a = m / n > 0

with

n, m

co-prime natural numbers

W (a, 0| z) = \sum_{r = 0}^{m - 1} \frac{z^{r + 1}}{(r + 1)! Γ (a + a r)} [\begin{matrix} \begin{matrix} 1 \\ \vec{b}, \vec{c} \end{matrix} & ∣ & \begin{matrix} \frac{z^{m}}{n^{n} m^{m}} \end{matrix} \end{matrix}]

(24)

where

\vec{b}

has n components and

\vec{c}

has m components given by

b_{j} = (r + 1) / m + j / n, c_{j} = (r + 2 + j) / m,

respectively.

Proof.

Starting from eq. 14 we observe that

C_{r} = Γ (a r + a) Γ (r + 2)

Furthermore,

\frac{Γ (m p + r + 2)}{Γ (r + 2)} = m^{m p} \prod_{j = 0}^{m - 1} \underset{c_{j}}{\underset{︸}{{(\frac{r + 2}{m} + \frac{j}{m})}_{p}}}

(25)

by Prop. A1. From where we read off the component

c_{0} = \frac{r + 2}{m}

with an increment

1 / m

. □

In a similar way, we can state

Proposition 3.

Whenever

- 1 < a = n / m < 0

with

n, m

co-prime natural numbers

W (- n / m, 0| z) = \sum_{r = 0}^{m - 1} \frac{z^{r + 1}}{(r + 1)! Γ (a + a r)} [\begin{matrix} \begin{matrix} 1, {\vec{b}}^{'} \\ \vec{c} \end{matrix} & ∣ & \begin{matrix} \frac{{(-)}^{n} z^{m}}{n^{n} m^{m}} \end{matrix} \end{matrix}]

(26)

where

{\vec{b}}^{'} = {b_{0}^{'} \dots b_{n - 1}^{'}}

\vec{c} = {c_{0} \dots c_{m - 1}}

and

b_{j}^{'} = 1 + (r + 1) / m - j / n c_{j} = (r + 2 + j) / m

Proof.

Use the Gamma reflection formula to obtain

b_{j}^{'} = 1 - (- r / m + (- n / m + j) / n) = 1 + r / m - (- n / m + j) / n = 1 + (r + 1) / m - j / n

□

7. Representations of the Wright Function of the First Type

The following representations can be computed using Th. 2:

7.1. Representations for $a = 1 / 2$

The following representation holds.

\begin{matrix} W (1 / 2, b| z) = \frac{1}{Γ (b)} [\begin{matrix} \begin{matrix} - \\ b, 1 / 2 \end{matrix} & ∣ & \begin{matrix} - \frac{z^{2}}{4} \end{matrix} \end{matrix}] + \frac{z}{Γ (b + 1 / 2)} [\begin{matrix} \begin{matrix} - \\ b + 1 / 2, 3 / 2 \end{matrix} & ∣ & \begin{matrix} - \frac{z^{2}}{4} \end{matrix} \end{matrix}] \end{matrix}

(27)

Here it makes sense to discuss odd and even functions.

7.2. Representations for $a = 1 / 3$ and $a = 2 / 3$

\begin{matrix} W (1 / 3, b| z) = \frac{{}_{0}F_{3} (-; b + \frac{2}{3}, \frac{4}{3}, \frac{5}{3}; \frac{z^{3}}{27}) z^{2}}{2 Γ (b + \frac{2}{3})} + \\ \frac{{}_{0}F_{3} (-, b + \frac{1}{3}, \frac{2}{3}, \frac{4}{3}; \frac{z^{3}}{27}) z}{Γ (b + \frac{1}{3})} + \frac{{}_{0}F_{3} (-; b, \frac{1}{3}, \frac{2}{3}; \frac{z^{3}}{27})}{Γ (b)} \end{matrix}

(28)

\begin{matrix} W (2 / 3, b| z) = \frac{1}{Γ (b)} [\begin{matrix} \begin{matrix} - \\ b / 2, b / 2 + 1 / 2, 1 / 3, 2 / 3 \end{matrix} & ∣ & \begin{matrix} \frac{z^{3}}{108} \end{matrix} \end{matrix}] + \\ \frac{z}{Γ (b + 2 / 3)} [\begin{matrix} \begin{matrix} - \\ b / 2 + 1 / 3, b / 2 + 5 / 6, 2 / 3, 4 / 3 \end{matrix} & ∣ & \begin{matrix} \frac{z^{3}}{108} \end{matrix} \end{matrix}] + \\ \frac{z^{2}}{2 Γ (b + 4 / 3)} [\begin{matrix} \begin{matrix} - \\ b / 2 + 2 / 3, b / 2 + 7 / 6, 4 / 3, 5 / 3 \end{matrix} & ∣ & \begin{matrix} \frac{z^{3}}{108} \end{matrix} \end{matrix}] \end{matrix}

(29)

7.3. Relationship to Trigonometric and Bessel Functions

In a similar way as for the Bessel functions for half-integer values of the second parameter the Wright function can be represented by trigonometric functions as follows:

W (1, 1 / 2| \frac{x^{2}}{4}) = \frac{cosh (x)}{\sqrt{π}}

W (1, 1 / 2| - \frac{x^{2}}{4}) = \frac{cos (x)}{\sqrt{π}}

and

W (1, 3 / 2| \frac{x^{2}}{4}) = 2 \frac{sinh (x)}{\sqrt{π} x}

W (1, 3 / 2| - \frac{x^{2}}{4}) = 2 \frac{sin (x)}{\sqrt{π} x}

For

b = 0

according to eq. 23 we have the special cases

W (1, 0| x) = I_{1} (2 \sqrt{x}) \sqrt{x}

and

W (1, 0| - x) = J_{1} (2 \sqrt{x}) \sqrt{x}

8. Representations of the Wright Function of the Second Type

The main application of Th. 3 is the representation of the Mainardi’s function [15]

M_{a} (z) = W (- a, 1 - a| - z)

The integral of the function is

I M_{a} (z) = - W (- a, 1| - z)

and its n^th derivative is

M_{a}^{(n)} (z) = {(-)}^{n} W (- a, 1 - (n + 1) a| - z)

8.1. Representations for $a = - 1 / 4$

\begin{matrix} M_{1 / 4} (z) = W (- 1 / 4, 3 / 4| - z) = \frac{{}_{0}F_{2} (-; \frac{5}{4}, \frac{3}{2}; - \frac{z^{4}}{256}) z^{2}}{2 Γ (\frac{1}{4})} \\ - \frac{{}_{0}F_{2} (-; \frac{3}{4}, \frac{5}{4}; - \frac{z^{4}}{256}) z}{\sqrt{π}} + \frac{{}_{0}F_{2} (-; \frac{1}{2}, \frac{3}{4}; - \frac{z^{4}}{256})}{Γ (\frac{3}{4})} \end{matrix}

(30)

8.2. Representations for $a = - 1 / 3$

The general formula for

b \leq 1

reads

\begin{matrix} W (- 1 / 3, b| z) = \frac{{}_{1}F_{2} (\frac{5}{3} - b; \frac{4}{3}, \frac{5}{3}; - \frac{z^{3}}{27}) z^{2}}{2 Γ (b - \frac{2}{3})} + \\ \frac{{}_{1}F_{2} (\frac{4}{3} - b; \frac{2}{3}, \frac{4}{3}; - \frac{z^{3}}{27}) z}{Γ (b - \frac{1}{3})} + \frac{{}_{1}F_{2} (1 - b; \frac{1}{3}, \frac{2}{3}, - \frac{z^{3}}{27})}{Γ (b)} \end{matrix}

(31)

For

b = 1 / 3

and

z > 0

the equation for reduces to

\begin{matrix} W (- 1 / 3, 1 / 3| - z) = - \frac{z}{3} (I_{2 / 3} (\frac{2 z^{\frac{3}{2}}}{3^{\frac{3}{2}}}) - I_{- 2 / 3} (\frac{2 z^{\frac{3}{2}}}{3^{\frac{3}{2}}})) = \\ \frac{z}{\sqrt{3} π} K_{2 / 3} (\frac{2 z^{\frac{3}{2}}}{3^{\frac{3}{2}}}) = - \sqrt[3]{3} {Ai}^{'} (\frac{z}{\sqrt[3]{3}}) \end{matrix}

(32)

while

W (- 1 / 3, 1 / 3| z) = - \frac{z}{3} (J_{2 / 3} (\frac{2 z^{3 / 2}}{3^{3 / 2}}) - J_{- 2 / 3} (\frac{2 z^{3 / 2}}{3^{3 / 2}})) = - \sqrt[3]{3} {Ai}^{'} (- \frac{z}{\sqrt[3]{3}})

Regarding the Mainardi function

M_{1 / 3} = W (- 1 / 3, 2 / 3| - z)

eq. 31 simplifies as expected for

b = 2 / 3

to the Airy Aifunction, which can be represented as a weighted sum of Bessel J or I functions, respectively. That is, for

z > 0

\begin{matrix} W (- 1 / 3, 2 / 3| - z) = \frac{I_{- 1 / 3} (\frac{2 z^{\frac{3}{2}}}{3^{\frac{3}{2}}}) \sqrt{z}}{\sqrt{3}} - \frac{I_{1 / 3} (\frac{2 z^{\frac{3}{2}}}{3^{\frac{3}{2}}}) \sqrt{z}}{\sqrt{3}} = \\ \frac{K_{1 / 3} (\frac{2 z^{\frac{3}{2}}}{3^{\frac{3}{2}}}) \sqrt{z}}{π} = \sqrt[3]{3^{2}} Ai (- z / \sqrt[3]{3}) \end{matrix}

(33)

while for

z < 0

\begin{matrix} W (- 1 / 3, 2 / 3| z) = \frac{J_{- 1 / 3} (\frac{2 z^{\frac{3}{2}}}{3^{\frac{3}{2}}}) \sqrt{z}}{\sqrt{3}} + \frac{J_{1 / 3} (\frac{2 z^{\frac{3}{2}}}{3^{\frac{3}{2}}}) \sqrt{z}}{\sqrt{3}} = \sqrt[3]{3^{2}} Ai (- z / \sqrt[3]{3}) \end{matrix}

(34)

8.3. Representations for $a = - 1 / 2$

For

b \leq 1

we have the general representation

W (- 1 / 2, b| z) = \frac{{}_{1}F_{1} (\frac{3}{2} - b; \frac{3}{2}; - \frac{z^{2}}{4}) z}{Γ (b - \frac{1}{2})} + \frac{{}_{1}F_{1} (1 - b; \frac{1}{2}; - \frac{z^{2}}{4})}{Γ (b)}

(35)

For

b = 3 / 4

z > 0

W (- 1 / 2, 3 / 4| - z) = \frac{\sqrt{z}}{\sqrt{2} π} K_{1 / 4} (\frac{z^{2}}{8}) e^{- \frac{z^{2}}{8}}

In particular, for

b = 1

the above equation reduces to

W (- 1 / 2, 1| z) = 1 + \erf (\frac{z}{2}) = erfc (- \frac{z}{2})

in accordance with the polynomial reduction.

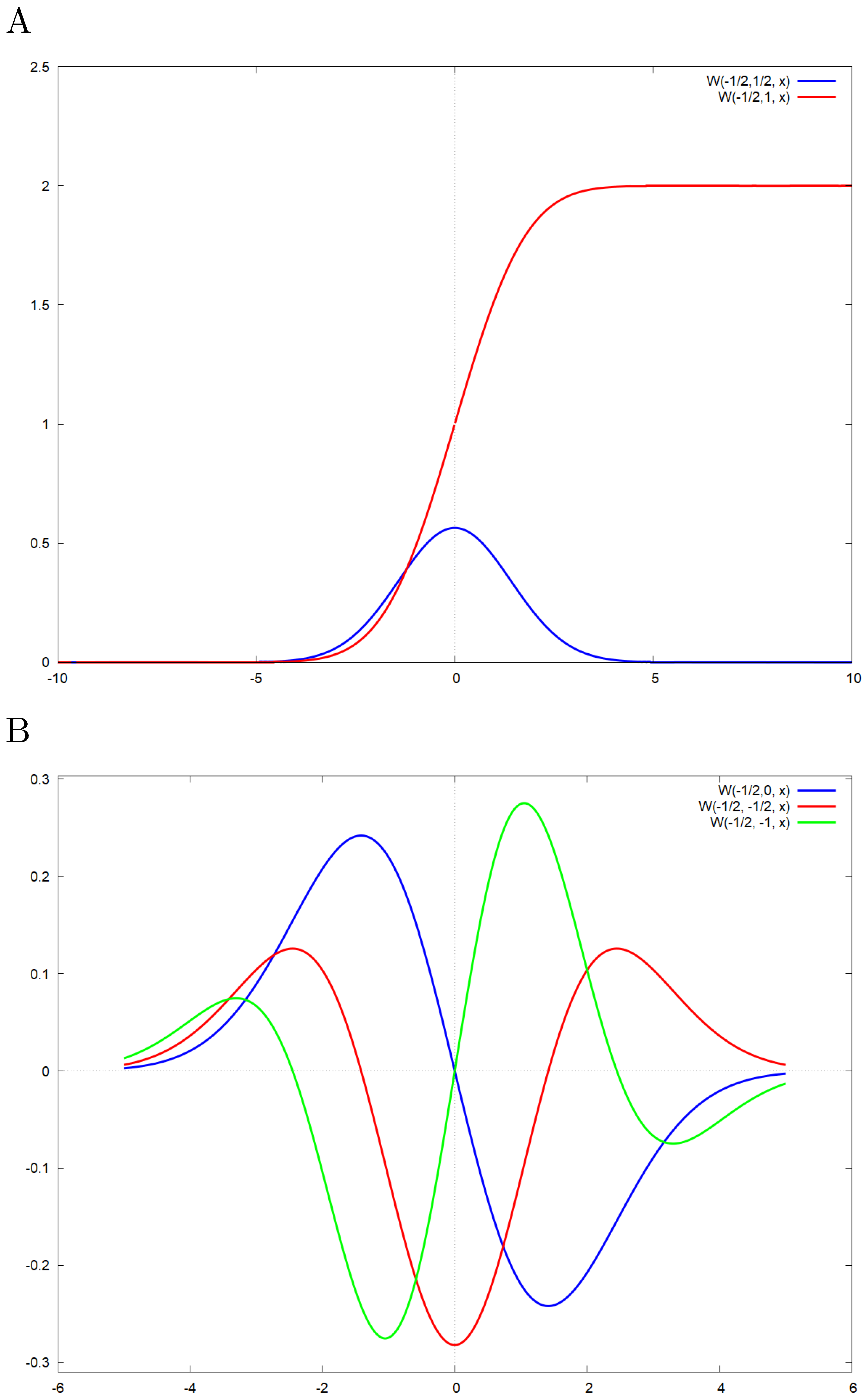
The Gaussian derivatives can be represented as

{(\frac{d}{d z})}^{n} \frac{e^{- z^{2} / 4}}{\sqrt{π}} = W (- \frac{1}{2}, \frac{1 - n}{2}| z)

(36)

Plots are presented in Figure 2. The anti-derivatives of the Gaussian kernel can be computed in a similar way using Th. 3. For example, for

b = 7 / 2

\begin{matrix} W (- 1 / 2, 7 / 2| z) = \frac{1}{\sqrt{π}} (\frac{z^{4}}{60} + \frac{3 z^{2}}{10} + \frac{8}{15}) e^{- \frac{z^{2}}{4}} \\ + (1 + \erf (\frac{z}{2})) (\frac{z^{5}}{120} + \frac{z^{3}}{6} + \frac{z}{2}) \end{matrix}

(37)

8.4. Representations for $a = - 2 / 3$

The Mainardi function for

a = 2 / 3

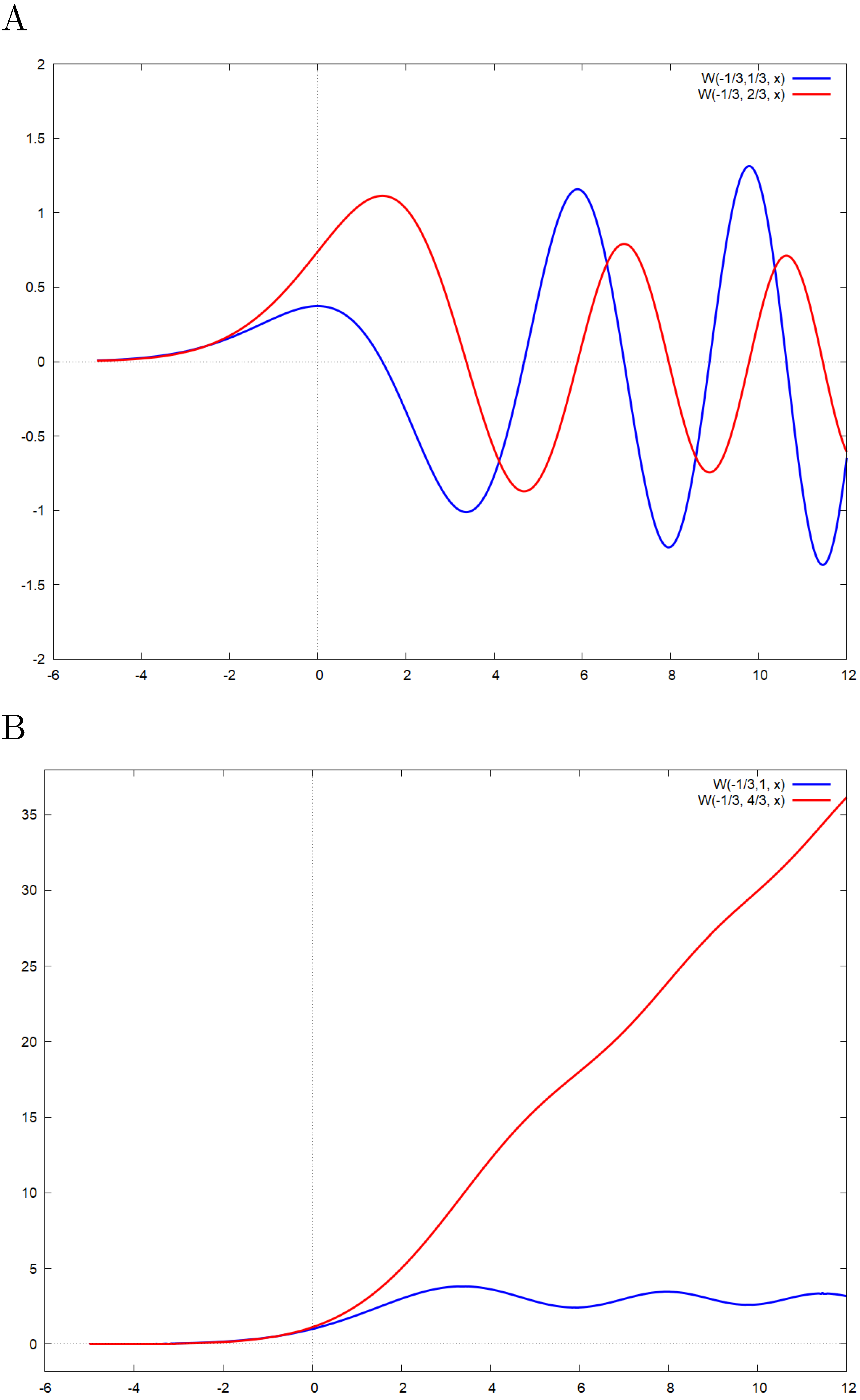
can be represented as the difference of two exponentially-weighted Bessel K functions on the entire real line:

\begin{matrix} W (- 2 / 3, 1 / 3| - z) = \frac{K_{2 / 3} (- \frac{2 z^{3}}{27}) z^{2} e^{- \frac{2 z^{3}}{27}}}{3^{\frac{3}{2}} π} - \frac{K_{1 / 3} (- \frac{2 z^{3}}{27}) z^{2} e^{- \frac{2 z^{3}}{27}}}{3^{\frac{3}{2}} π} \end{matrix}

(38)

On the other hand,

W (- 2 / 3, 1 / 3| z) = - \frac{e^{\frac{2 z^{3}}{27}} (3 {Ai}^{'} (\frac{z^{2}}{3^{\frac{4}{3}}}) + \sqrt[3]{3} z Ai (\frac{z^{2}}{3^{\frac{4}{3}}}))}{3^{\frac{2}{3}}}

in terms of the Airy function and its derivative. Plots are presented in Figure 3.

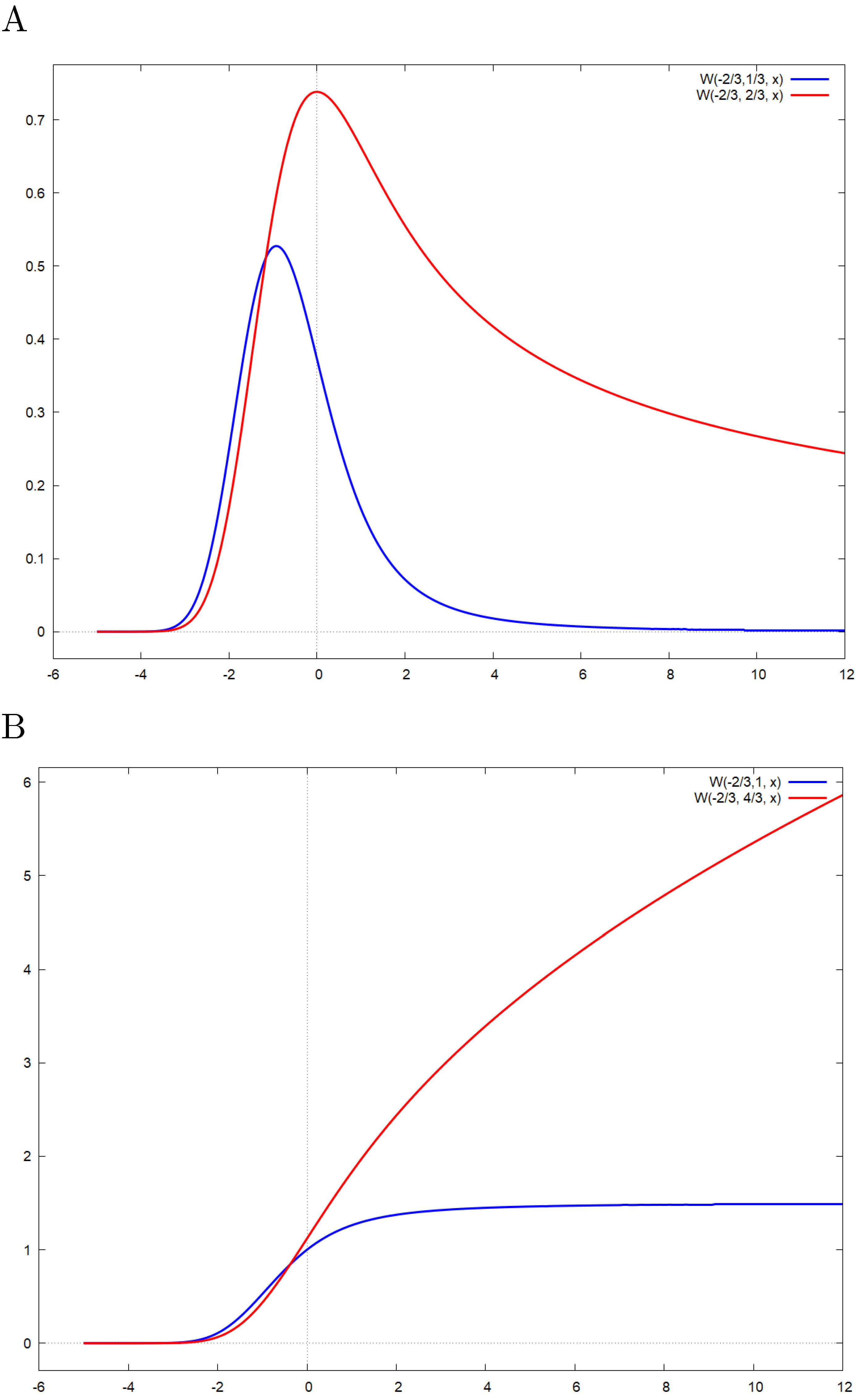
For

b = 2 / 3

W (- 2 / 3, 2 / 3| z) = \frac{K_{1 / 3} (\frac{2 z^{3}}{27}) z e^{\frac{2 z^{3}}{27}}}{\sqrt{3} π} = \sqrt[3]{9} e^{\frac{2 z^{3}}{27}} Ai (\frac{z^{2}}{3^{\frac{4}{3}}})

(39)

Plots are presented in Figure 4.

For

b = 4 / 3

W (- 2 / 3, 4 / 3| z) = - \frac{(I_{2 / 3} (\frac{2 z^{3}}{27}) + I_{1 / 3} (\frac{2 z^{3}}{27}) - I_{- 1 / 3} (\frac{2 z^{3}}{27}) - I_{- 2 / 3} (\frac{2 z^{3}}{27})) z^{2} e^{\frac{2 z^{3}}{27}}}{3}

This can be further represented as

W (- 2 / 3, 4 / 3| z) = 9^{\frac{1}{3}} z e^{\frac{2 z^{3}}{27}} Ai (\frac{z^{2}}{3^{\frac{4}{3}}}) - 3^{\frac{4}{3}} e^{\frac{2 z^{3}}{27}} {Ai}^{'} (\frac{z^{2}}{3^{\frac{4}{3}}})

(40)

9. Representations of the Wright Function of the Third Type

9.1. Representations for $a = - 1$

This formula was recently derived in [9] and is not anticipated in the previous literature since the parameter domain is customarily restricted to

a > - 1

W (- 1, b| z) = \frac{1}{Γ (b)} {}_{1}F_{0} (1 - b; -; z) = \frac{{(z + 1)}^{b - 1}}{Γ (b)}

(41)

9.2. Representations for $a \in Z^{-}$

For negative integers representations can be tabulated for some cases as follows. For

n = 1

1, z + 1

n = 2

\frac{1}{2}, \frac{2 z + 1}{2}, \frac{{(z + 1)}^{2}}{2}

n = 3

\frac{1}{6}, \frac{6 z + 1}{6}, \frac{6 z + 1}{6}, \frac{{(z + 1)}^{3}}{6}

n = 4

\frac{1}{24}, \frac{24 z + 1}{24}, \frac{24 z + 1}{24}, \frac{12 z^{2} + 12 z + 1}{24}, \frac{{(z + 1)}^{4}}{24}

n = 5

\frac{1}{120}, \frac{120 z + 1}{120}, \frac{120 z + 1}{120}, \frac{60 z + 1}{120}, \frac{60 z^{2} + 20 z + 1}{120}, \frac{{(z + 1)}^{5}}{120}

n = 6

\begin{matrix} \frac{1}{720}, \frac{720 z + 1}{720}, \frac{720 z + 1}{720}, \frac{360 z + 1}{720}, \frac{360 z^{2} + 120 z + 1}{720}, \\ \frac{120 z^{3} + 180 z^{2} + 30 z + 1}{720}, \frac{{(z + 1)}^{6}}{720} \end{matrix}

10. The Mittag-Leffler Function as a Laplace Transform of the Wright Function

The main application of the presented results so far is related to the Mittag-Leffler function

E_{a, b} (z)

. The 2 parameter Mittag-Leffler function [16,17] under the present convention will be denoted as

E_{a, b} (z) : = \sum_{k = 0}^{\infty} \frac{z^{k}}{Γ (a k + b)} = \frac{1}{Γ (b)} [\begin{matrix} \begin{matrix} 1 \\ - \end{matrix} & ∣ & \begin{matrix} - \\ (b, a) \end{matrix} & ∣ & \begin{matrix} z \end{matrix} \end{matrix}], a > 0, b \neq 0

This immediately gives the complex integral representation according to eq. 10

\begin{matrix} E_{a, b} (z) = \frac{1}{2 π i} \int_{H a^{-}} \frac{e^{τ}}{τ^{b}} [\begin{matrix} \begin{matrix} 1 \\ - \end{matrix} & ∣ & \begin{matrix} \frac{z}{τ^{a}} \end{matrix} \end{matrix}] d τ = \\ \frac{1}{2 π i} \int_{H a^{-}} \frac{e^{τ}}{τ^{b}} \frac{d τ}{1 - \frac{z}{τ^{a}}} = \frac{1}{2 π i} \int_{H a^{-}} \frac{τ^{a - b} e^{τ}}{τ^{a} - z} d τ \end{matrix}

(42)

For real indices

a_{i}

and

b_{i}

A > 0

and

a > 0

it was proven that [14]

\begin{matrix} [\begin{matrix} \begin{matrix} a_{1}, \dots, a_{p} \\ b_{1}, \dots, b_{q} \end{matrix} & ∣ & \begin{matrix} (A, a) \\ \dots \end{matrix} & ∣ & \begin{matrix} z \end{matrix} \end{matrix}] = \\ \frac{1}{Γ (A)} \int_{0}^{\infty} e^{- τ} τ^{A - 1} [\begin{matrix} \begin{matrix} a_{1}, \dots, a_{p} \\ b_{1}, \dots, b_{q} \end{matrix} & ∣ & \begin{matrix} \dots \\ \dots \end{matrix} & ∣ & \begin{matrix} z τ^{a} \end{matrix} \end{matrix}] d τ \end{matrix}

(43)

whenever the GHG function in the integral kernel converges. Then by eq. 43 for

A = 1, a = 1

it follows immediately that

E_{a, b} (z) = \int_{0}^{\infty} e^{- t} W (a, b| z t) d t

(44)

This representation can be used to derive also a Laplace transform pair:

\begin{matrix} \frac{1}{s} E_{a, b} (\frac{1}{s}) = \frac{1}{s} \int_{0}^{\infty} e^{- τ} W (a, b| \frac{τ}{s}) d τ = \\ \frac{1}{s} \int_{0}^{\infty} e^{- s t} W (a, b| \frac{s t}{s}) d (s t) = \int_{0}^{\infty} e^{- s t} W (a, b| t) d t \end{matrix}

for

s > 0

, since the integration variable

τ = s t

is positive. Therefore,

W (a, b| t) \div \frac{1}{s} E_{a, b} (\frac{1}{s}), a > 0

(45)

On the other hand, for the Wright function of the second type we have

\begin{matrix} \int_{0}^{\infty} e^{- s t} W (- a, b| t) d t = \frac{1}{2 π i} \int_{0}^{\infty} e^{- s t} d t \int_{H a^{-}} \frac{e^{ξ + t ξ^{a}}}{ξ^{b}} d ξ = \\ \frac{1}{2 π i} \int_{H a^{-}} \frac{e^{ξ}}{ξ^{b}} d ξ \int_{0}^{\infty} e^{t (ξ^{a} - s)} d t = \frac{1}{2 π i} \int_{H a^{-}} \frac{e^{ξ}}{ξ^{b} (ξ^{a} - s)} d ξ = \\ \frac{1}{2 π i} \int_{H a^{-}} \frac{e^{ξ} ξ^{a - (a + b)}}{ξ^{a} - s} d ξ = E_{a, a + b} (s) \end{matrix}

under the condition

Re (ξ^{a} - s) < 0

. Therefore, the corresponding Laplace transform pair is

W (- a, b| t) \div E_{a, a + b} (s), 0 \leq a \leq 1

(46)

This gives the relationship between the Wright and Mittag-Leffler functions.

For every rational parameter pair the ML function is reducible to a finite sum of HG functions as the following theorem [9]:

Theorem 4

(Mittag-Leffler HG Representation). Suppose that

a = n / m > 0

, where n and m are co-prime, and

b \neq 0

. Then

E_{a, b} (z) = \sum_{r = 0}^{m - 1} \frac{z^{r}}{Γ (b + a r)} [\begin{matrix} \begin{matrix} 1 \\ \vec{b} \end{matrix} & ∣ & \begin{matrix} \frac{z^{m}}{n^{n}} \end{matrix} \end{matrix}],

(47)

where

\vec{b}

has n components

b_{j} = r / m + (b + j) / n

Proof.

Starting from

E_{n / m, b} (z) = \sum_{k = 0}^{\infty} \frac{z^{k}}{Γ (a k + b)} = \sum_{q = 0}^{m - 1} \sum_{p \geq q / m}^{\infty} \frac{z^{m p - q}}{Γ (a (m p - q) + b)}

since the integer n can be partitioned as

k = m p - q

, where

q = 0, \dots m - 1

. After some algebra we obtain

E_{n / m, b} (z) = \frac{1}{Γ (b)} + \sum_{r = 1}^{m} z^{r} \sum_{p = 0}^{\infty} \frac{z^{m p}}{Γ (a p + r a + b)} .

Observe that for

p = 0

the inner series coefficient is

C_{r} = Γ (r a + b) = Γ (n r / m + b),

which serves as a normalization factor. Therefore, the series transforms as

E_{n / m, b} (z) = \sum_{r = 0}^{m} \frac{z^{r}}{C_{r}} \sum_{p = 0}^{\infty} \frac{C_{r}}{Γ (n (p + r / m) + b)} z^{m p}

(48)

Further, use Prop. A1 to obtain

\frac{Γ (n (p + r / m) + b)}{Γ (n r / m + b)} = n^{n p} \prod_{j = 0}^{n - 1} \underset{b_{j}}{\underset{︸}{{(r / m + b / n + j / n)}_{p}}}

(49)

Therefore,

E_{n / m, b} (z) = \sum_{r = 0}^{m} \frac{z^{r}}{Γ (r a + b)} \sum_{p = 0}^{\infty} \frac{z^{m p}}{n^{n p} \prod_{j = 0}^{n - 1} b_{j}}

From where we read off

b_{0} = \frac{r}{m} + \frac{b}{n}

with an increment

1 / n

so that

E_{n / m, b} (z) = \sum_{r = 0}^{m - 1} \frac{z^{r}}{Γ (b + a r)} [\begin{matrix} \begin{matrix} 1 \\ \vec{b} \end{matrix} & ∣ & \begin{matrix} \frac{z^{m}}{n^{n}} \end{matrix} \end{matrix}]

□

Observe that for

r = m - 1

c_{1} = 1

; therefore, the GHG functions reduce to

{}_{0}F_{m - 1}

. Unlike for the Wright function, whenever

b = 0

E_{a, 0} (z) = \sum_{k = 0}^{\infty} \frac{z^{k + 1}}{Γ (a k + a)} = \frac{z}{Γ (a)} [\begin{matrix} \begin{matrix} 1 \\ - \end{matrix} & ∣ & \begin{matrix} - \\ (a, a) \end{matrix} & ∣ & \begin{matrix} z \end{matrix} \end{matrix}] = z E_{a, a} (z)

Therefore, the previous case directly applies.

E_{n / m, 0} (z) = z \sum_{r = 0}^{m - 1} \frac{z^{r}}{Γ (a + a r)} [\begin{matrix} \begin{matrix} 1 \\ \vec{b} \end{matrix} & ∣ & \begin{matrix} \frac{z^{m}}{n^{n}} \end{matrix} \end{matrix}], a = n / m

(50)

where

\vec{b}

has n components

b_{j} = (r + 1) / m + j / n

10.1. Some Integral Identities Interlinking the ML and Wright Functions

This allows one to write the following sets of integrals by application of eq. 44: For

m, n > 0

according to the First Representation Theorem

\begin{matrix} E_{n / m, b} (z) = \sum_{r = 0}^{m - 1} \frac{z^{r}}{Γ (b + a r)} [\begin{matrix} \begin{matrix} 1 \\ \vec{b} \end{matrix} & ∣ & \begin{matrix} \frac{z^{m}}{n^{n}} \end{matrix} \end{matrix}] = \\ \int_{0}^{\infty} e^{- t} \sum_{r = 0}^{m - 1} \frac{z^{r} t^{r}}{r! Γ (b + a r)} [\begin{matrix} \begin{matrix} 1 \\ \vec{b}, \vec{c} \end{matrix} & ∣ & \begin{matrix} \frac{z^{m} t^{m}}{n^{n} m^{m}} \end{matrix} \end{matrix}] d t = \\ \sum_{r = 0}^{m - 1} \frac{z^{r}}{r! Γ (b + a r)} \int_{0}^{\infty} t^{r} e^{- t} [\begin{matrix} \begin{matrix} 1 \\ \vec{b}, \vec{c} \end{matrix} & ∣ & \begin{matrix} \frac{z^{m} t^{m}}{n^{n} m^{m}} \end{matrix} \end{matrix}] d t \end{matrix}

for

b \neq 0

. Therefore, after the substitution

y = z^{m} / n^{n}

we have

[\begin{matrix} \begin{matrix} 1 \\ \vec{b} \end{matrix} & ∣ & \begin{matrix} y \end{matrix} \end{matrix}] = \frac{1}{Γ (r + 1)} \int_{0}^{\infty} t^{r} e^{- t} [\begin{matrix} \begin{matrix} 1 \\ \vec{b}, \vec{c} \end{matrix} & ∣ & \begin{matrix} y \frac{t^{m}}{m^{m}} \end{matrix} \end{matrix}] d t,

(51)

where

\vec{b} = {r / m + (b + j) / n}

\vec{c} = {(r + 1 + j) / m}

as discussed above. The last formula can be used to produce many integral identities between GHG functions.

10.2. Analytical Continuation of the ML Function for Negative Parameters

The integral representation allows one to continue analytically the ML for negative first parameters Then one has

E_{- a, b} (z) : = \frac{1}{2 π i} \int_{H a^{-}} \frac{e^{τ}}{τ^{b}} \frac{d τ}{1 - z τ^{a}}, a > 0

Therefore, for rational parameters we can apply the Second and Third Representation theorems to obtain for

| a | < 1

E_{- n / m, b} (z) = \sum_{r = 0}^{m - 1} \frac{z^{r}}{r! Γ (b + a r)} \int_{0}^{\infty} e^{- t} t^{r} [\begin{matrix} \begin{matrix} 1, \vec{b} \\ \vec{c} \end{matrix} & ∣ & \begin{matrix} \frac{{(-)}^{n} z^{m} t^{m}}{n^{n} m^{m}} \end{matrix} \end{matrix}] d t

(52)

for

| b | < 1

and

\begin{matrix} E_{- n / m, b} (z) = \sum_{r = 0}^{m - 1} \frac{z^{r}}{r! Γ (b + a r)} \int_{0}^{\infty} e^{- t} t^{r} [\begin{matrix} \begin{matrix} 1, \vec{b} \\ \vec{c} \end{matrix} & ∣ & \begin{matrix} \frac{{(-)}^{n} z^{m} t^{m}}{n^{n} m^{m}} \end{matrix} \end{matrix}] d t + \\ \int_{0}^{\infty} e^{- t} P_{b} (n / m, z t) d t \end{matrix}

(53)

otherwise. From where we see that the integrals for non-natural parameters do not converge as they would involve kernels of

{}_{n + 1}F_{0}

according to eq. 51. Therefore, the analytical continuation is defined only for negative integers

a, b

like in the case for the Wright function. In such case, (i.e.

b = m \in N

)

E_{- n, m} (z) = \int_{0}^{\infty} e^{- t} P_{m} (n, z t) d t = 1 + \sum_{k = 1}^{m} c_{k} z^{k}

which is a polynomial in z. The coefficients of this polynomial can be evaluated from the formula

c_{k} = a_{k} \int_{0}^{\infty} e^{- t} t^{k} d t = k! a_{k}

Some examples can be presented as follows: For

n = 2

1, z + 1

For

n = 3

\frac{1}{2}, \frac{2 z + 1}{2}, \frac{2 z^{2} + 2 z + 1}{2}

For

n = 4

\frac{1}{6}, \frac{6 z + 1}{6}, \frac{6 z + 1}{6}, \frac{6 z^{3} + 6 z^{2} + 3 z + 1}{6}

For

n = 5

\frac{1}{24}, \frac{24 z + 1}{24}, \frac{24 z + 1}{24}, \frac{24 z^{2} + 12 z + 1}{24}, \frac{24 z^{4} + 24 z^{3} + 12 z^{2} + 4 z + 1}{24},

etc. These polynomials can be rightfully called Mittag-Leffler polynomials.

11. Discussion

The original goal of the present work was to to provide the ground truth for purely numerical algorithms for the evaluation of the Wright function. Such algorithms are a subject of continuous development [5,18,19,20].

The contributions of the present work can be discussed in several directions. On the first place, from a fundamental perspective, the existence of Wright function of the third type has been overlooked in the literature. This can be probably attributed to the extant focus on the Mainardi’s function, which is not defined for

a = 1

. On the second place, the present work completes all cases of finite representations of the Wright function. It should be noted that The Second and Third Representation theorems could not be traced to the literature prior to the preliminary presentation in [10]. Finally, one can also envision application in definite integration to be incorporated into different CAS integration – i.e. using eq. 51; and Inverse Laplace transform routines – i.e. using eq. 45 and 46.

Acknowledgments

The present work was funded by the European Union’s Horizon Europe program under grant agreement VIBraTE 101086815.

Appendix A. Euler Integrals

The Gamma integral i.e. the Euler integral of the second kind is

Γ (z) = \int_{0}^{\infty} e^{- τ} τ^{z - 1} d τ, Re z > 0

(A1)

The complex representation for the reciprocal Gamma function is given by the Heine’s contour integral as

\frac{1}{Γ (z)} = \frac{1}{2 π i} \int_{H a^{-}} \frac{e^{τ}}{τ^{z}} d τ

(A2)

Employing the last 2 formulas and the reflection formula of the Gamma function

Γ (z) Γ (1 - z) = \frac{π}{sin π z}, z \notin Z

(A3)

one could obtain the analytical continuation of the Gamma function valid on the entire complex plane for all

z \notin Z

Γ (z) = \frac{1}{2 i sin π z} \int_{H a^{-}} e^{τ} τ^{z - 1} d τ, τ \in C

(A4)

The Hankel contour is depicted in Figure 1. For non-integral arguments the branch cut is selected as the negative real axis.

Appendix B. Ratios of Gamma Factors

Proposition A1.

For non negative integers

n, m

Γ (m n + m b) = Γ (m b) m^{m n} \prod_{j = 0}^{m - 1} {(\frac{j}{m} + b)}_{n}

(A5)

Proof.

Using the Gauss-Legendre multiplication formula for the Gamma function

Γ (m x) = \frac{m^{m x - 1 / 2}}{{(2 π)}^{(m - 1) / 2}} \prod_{k = 0}^{m - 1} Γ (x + \frac{k}{m})

we substitute first

x = b

then

x = n + b / m

and divide the two identities. Thus, for a non negative integer n the formula can be expressed by a product of increasing factorials as

\frac{Γ (m n + m b)}{Γ (m b)} = m^{m n} \prod_{j = 0}^{m - 1} \frac{Γ (n + \frac{j}{m} + b)}{Γ (\frac{j}{m} + b)} = m^{m n} \prod_{j = 0}^{m - 1} {(\frac{j}{m} + b)}_{n}

□

References

Wright, E.M. The Asymptotic Expansion of the Generalized Hypergeometric Function. J London Math Soc 1935, s1-10, 286–293. [Google Scholar] [CrossRef]
Wright, E.M. The Asymptotic Expansion of Integral Functions Defined by Taylor Series. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 1940, 238, 423–451. [Google Scholar] [CrossRef]
Gorenflo, R.; Luchko, Y.; Mainardi, F. Wright functions as scale-invariant solutions of the diffusion-wave equation. Journal of Computational and Applied Mathematics 2000, 118, 175–191. [Google Scholar] [CrossRef]
Gorenflo, R.; Luchko, Y.; Mainardi, F. Analytical properties and applications of the Wright function. Fract Calc and Appl Anal 1999, 2, 383–414. [Google Scholar] [CrossRef]
Luchko, Y. Algorithms for evaluation of the Wright function for the real arguments’ values. Fract. Calc. Appl. Anal. 2008, 11, 57–75. [Google Scholar]
Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press, 2010. [CrossRef]
Mainardi, F.; Consiglio, A. The Wright Functions of the Second Kind in Mathematical Physics. Mathematics 2020, 8, 884. [Google Scholar] [CrossRef]
Miller, A.R.; Moskowitz, I.S. Reduction of a Class of Fox-Wright Ψ Functions for Certain Rational Parameters. Technical report, CHACS, 1995.
Apelblat, A.; González-Santander, J.L. The Integral Mittag-Leffler, Whittaker and Wright Functions. Mathematics 2021, 9, 3255. [Google Scholar] [CrossRef]
Prodanov, D. The Wright function – hypergeometric representation and symbolical evaluation. 2023 International Conference on Fractional Differentiation and Its Applications (ICFDA). IEEE, 2023. [CrossRef]
Povstenko, Y. Some Applications of the Wright Function in Continuum Physics: A Survey. Mathematics 2021, 9, 198. [Google Scholar] [CrossRef]
Garra, R.; Mainardi, F. Some applications of Wright functions in fractional differential equations. Reports on Mathematical Physics 2021, 87, 265–273. [Google Scholar] [CrossRef]
Oldham, K.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order; Academic Press: New York, 1974. [Google Scholar]
Prodanov, D. Integral Representations and Algebraic Decompositions of the Fox-Wright Type of Special Functions. Fractal and Fractional 2019, 3, 4. [Google Scholar] [CrossRef]
F. Mainardi.; Mura, A.; Pagnini, G. The M-Wright Function in Time-Fractional Diffusion Processes: A Tutorial Survey. Int. J. Diff. Equations 2010, 2010, 1–29. [Google Scholar] [CrossRef]
Mittag-Leffler, G.M. Sur la nouvelle fonction E_a(x) C. R. Acad. Sci. Paris 1903, pp. 554 – 558.
Wiman, A. Über den Fundamentalsatz in der Teorie der Funktionen E_a(x). Acta Mathematica 1905, 29, 191–201. [Google Scholar] [CrossRef]
Aceto, L.; Durastante, F. Efficient computation of the Wright function and its applications to fractional diffusion-wave equations. ESAIM: Mathematical Modelling and Numerical Analysis, 2022. [Google Scholar] [CrossRef]
Luchko, Y.; Trujillo, J.; Velasco, M. The Wright function and its numerical evaluation. Int J Pure Appl Math 2010, 64, 567–575. [Google Scholar]
Prodanov, D. Wright function approximation and representation, 2023. [CrossRef]

Figure 1. Partition of the Hankel contour

Figure 2. Plots of

W (a, b| x)

for

a = - 1 / 2

Figure 2. Plots of

W (a, b| x)

for

a = - 1 / 2

Figure 3. Plots of

W (a, b| x)

for

a = - 1 / 3

Figure 3. Plots of

W (a, b| x)

for

a = - 1 / 3

Figure 4. Plots of

W (a, b| x)

for

a = - 2 / 3

Figure 4. Plots of

W (a, b| x)

for

a = - 2 / 3

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Finite Representations of theWright Function

Abstract

1. Introduction

2. Some Applications of the Wright Function

3. The Wright Function as a Simple Representative of the Fox-Wright Function Family

4. Polynomial Reduction

5. Finite Hypergeometric Representations

6. The Special Case b = 0

7. Representations of the Wright Function of the First Type

7.1. Representations for a = 1 / 2

7.2. Representations for a = 1 / 3 and a = 2 / 3

7.3. Relationship to Trigonometric and Bessel Functions

8. Representations of the Wright Function of the Second Type

8.1. Representations for a = − 1 / 4

8.2. Representations for a = − 1 / 3

8.3. Representations for a = − 1 / 2

8.4. Representations for a = − 2 / 3

9. Representations of the Wright Function of the Third Type

9.1. Representations for a = − 1

9.2. Representations for a ∈ Z −

10. The Mittag-Leffler Function as a Laplace Transform of the Wright Function

10.1. Some Integral Identities Interlinking the ML and Wright Functions

10.2. Analytical Continuation of the ML Function for Negative Parameters

11. Discussion

Acknowledgments

Appendix A. Euler Integrals

Appendix B. Ratios of Gamma Factors

References

MDPI Initiatives

Important Links

Subscribe

6. The Special Case $b = 0$

7.1. Representations for $a = 1 / 2$

7.2. Representations for $a = 1 / 3$ and $a = 2 / 3$

8.1. Representations for $a = - 1 / 4$

8.2. Representations for $a = - 1 / 3$

8.3. Representations for $a = - 1 / 2$

8.4. Representations for $a = - 2 / 3$

9.1. Representations for $a = - 1$

9.2. Representations for $a \in Z^{-}$