Submitted:
12 December 2023
Posted:
14 December 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Modeling and identification of friction
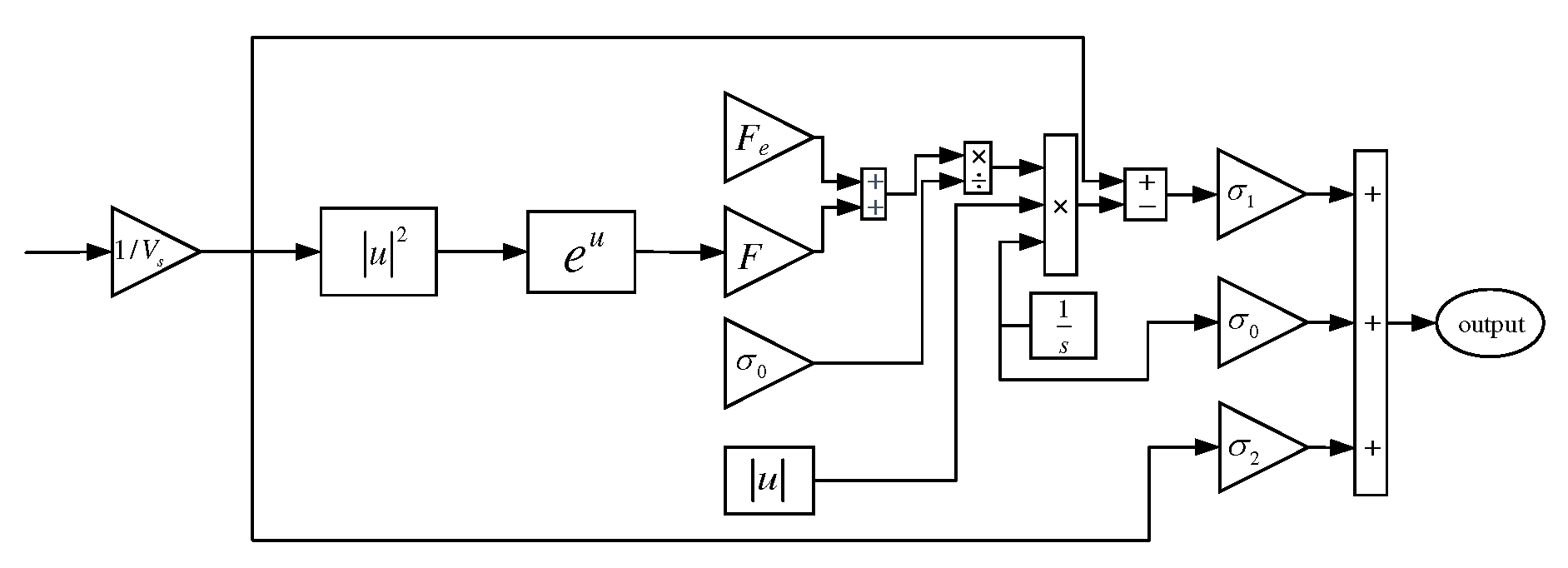
2.1. LuGre friction modeling
2.2. Multi-parameter identification of friction model
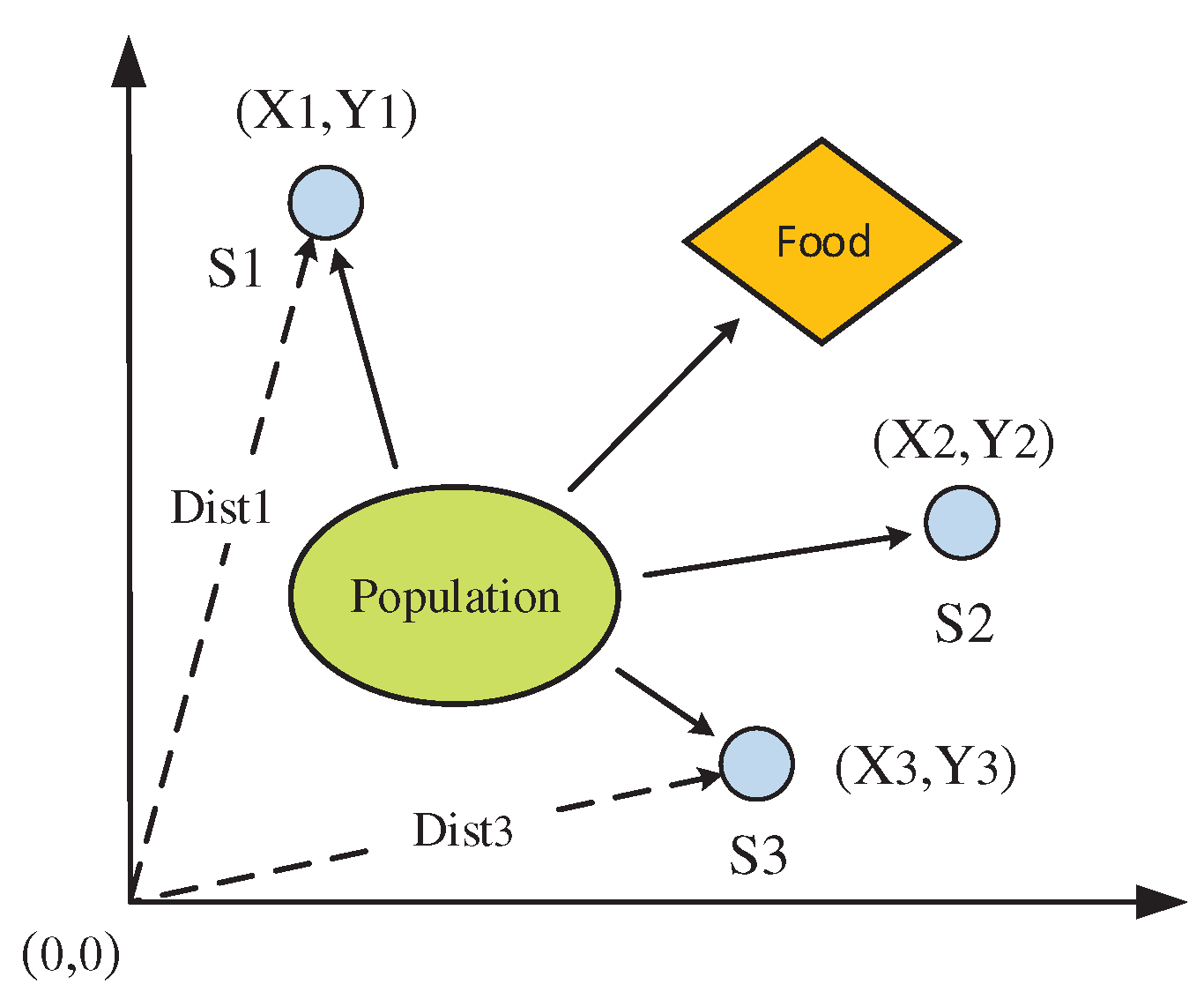
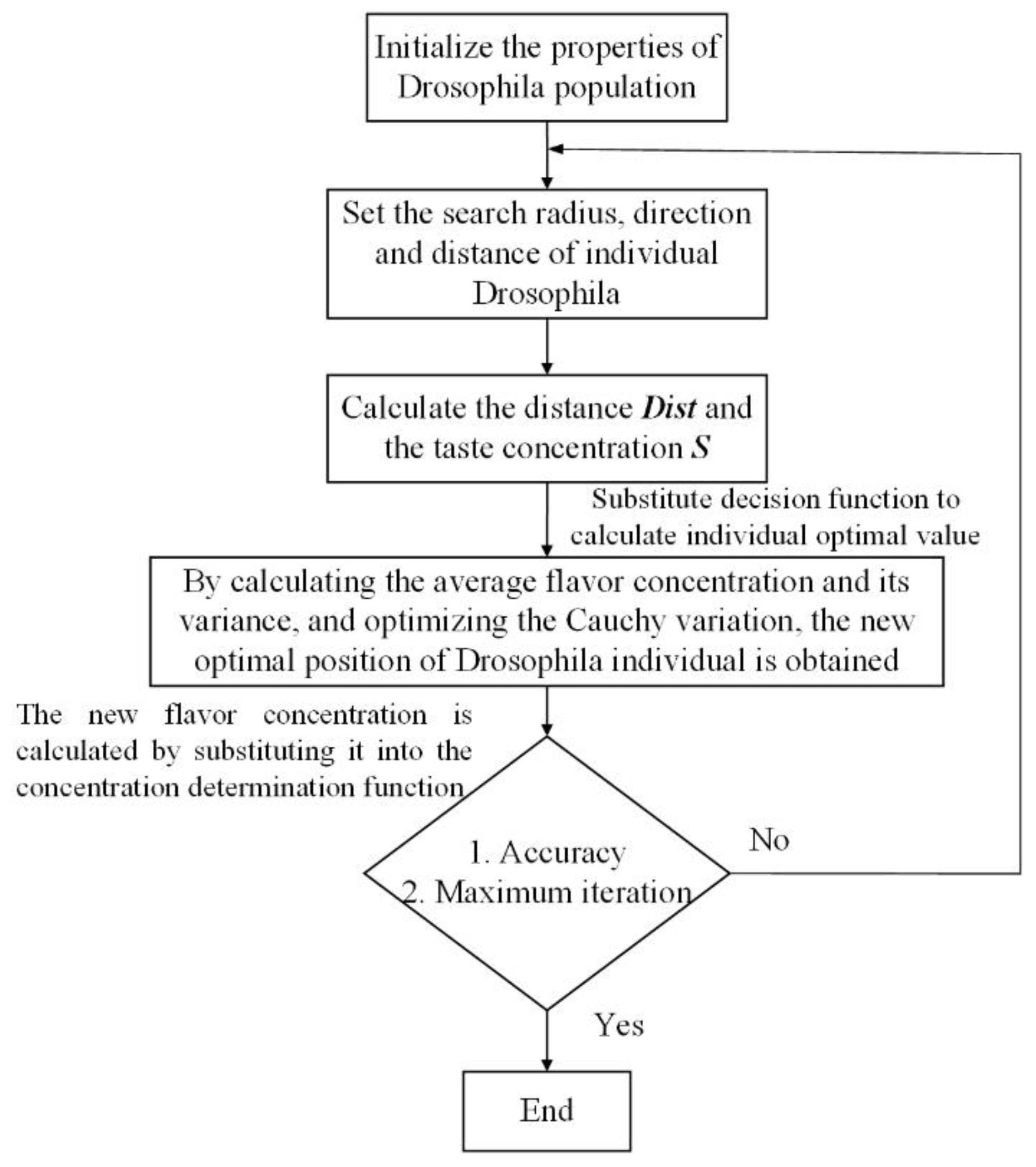
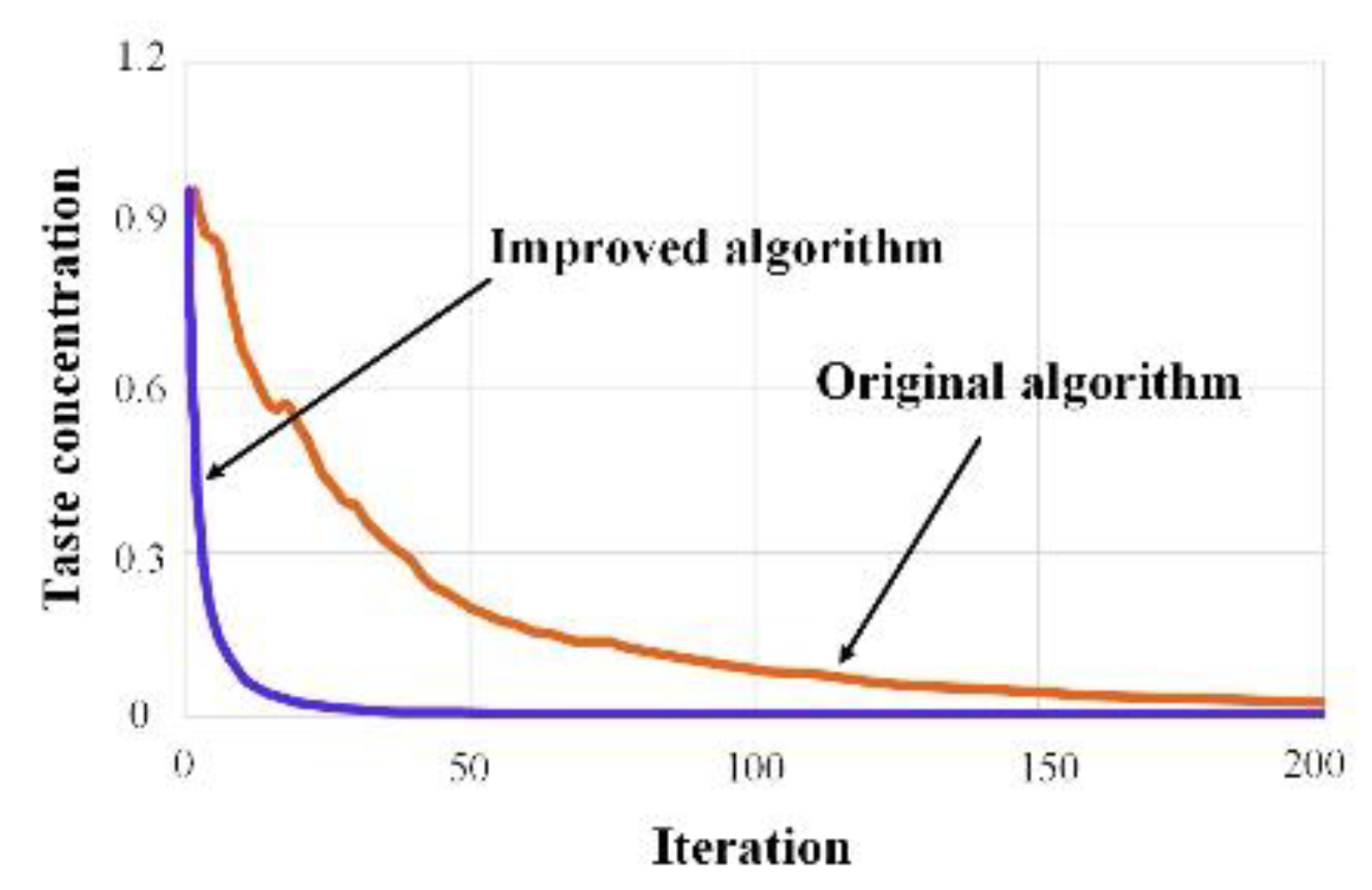
| Design values | Least square method | Genetic algorithm | Ant colony algorithm | Proposed algorithm |
|
| (N) | 30.00 | 30.51 | 30.63 | 30.21 | 30.12 |
| (rad/s) | 0.500 | 0.479 | 0.485 | 0.490 | 0.498 |
| (Nm/s) | 560.0 | 549.4 | 554.1 | 556.7 | 550.6 |
| (Nm/s) | 300.0 | 291.0 | 294.2 | 303 | 299.8 |
2.3. Tracking error modeling
3. Friction compensation and control strategy
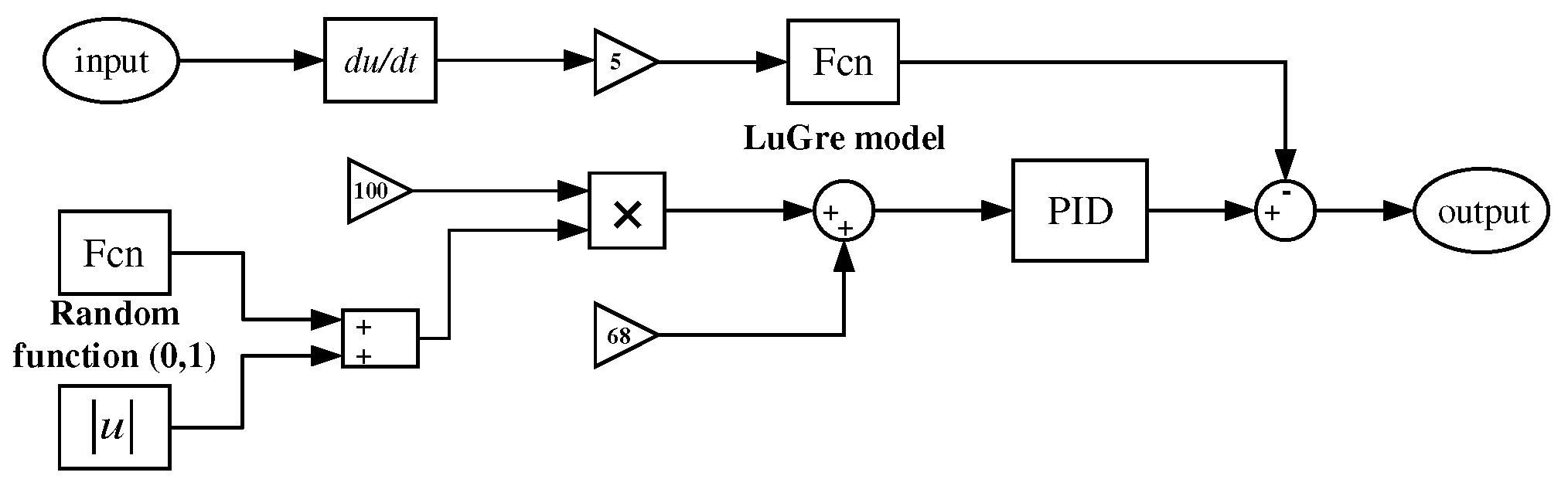
3.1. Friction feed-forward control design
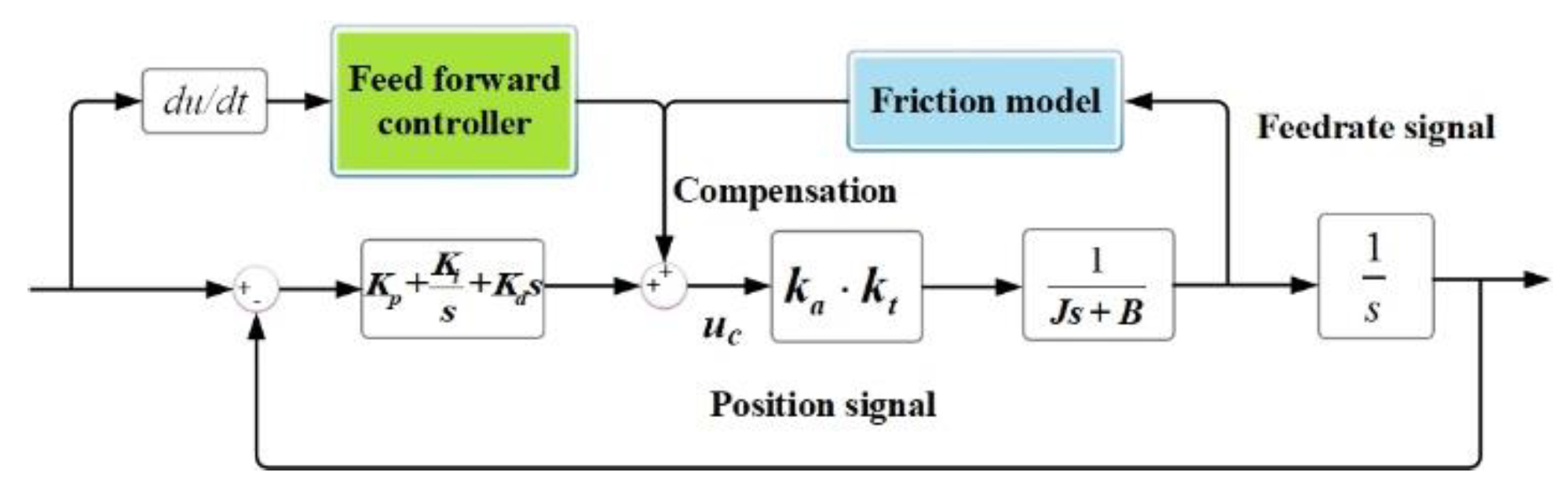
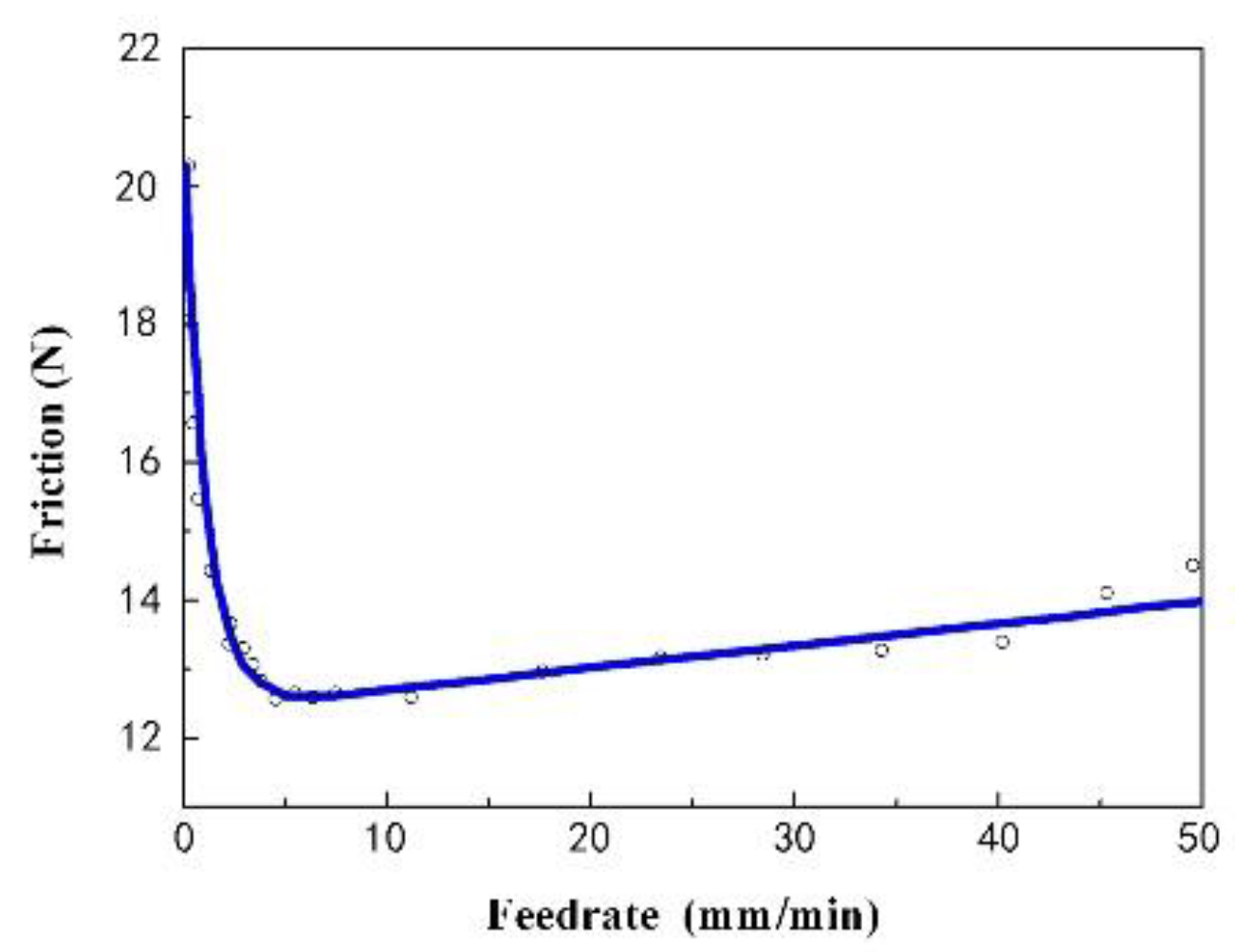
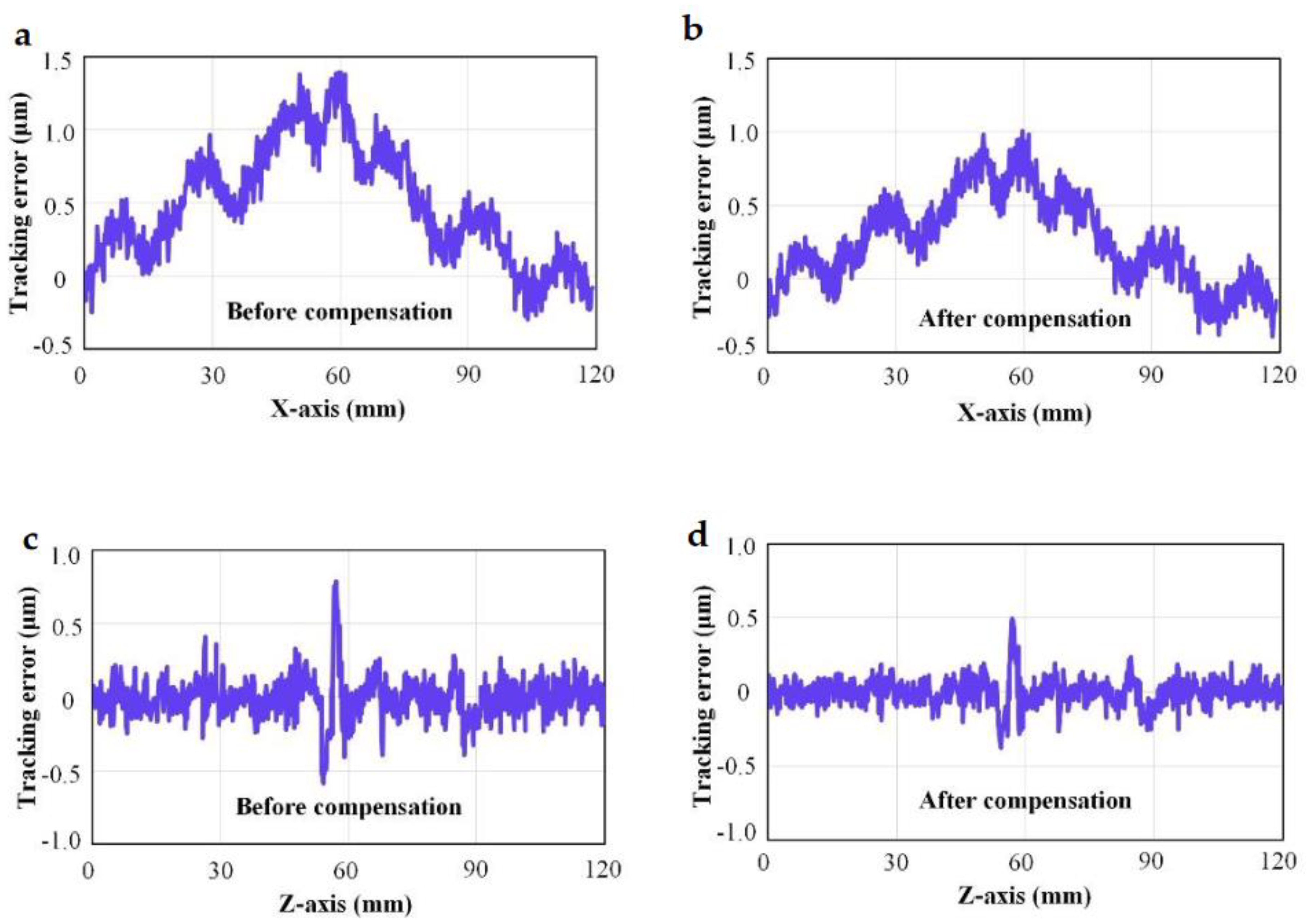
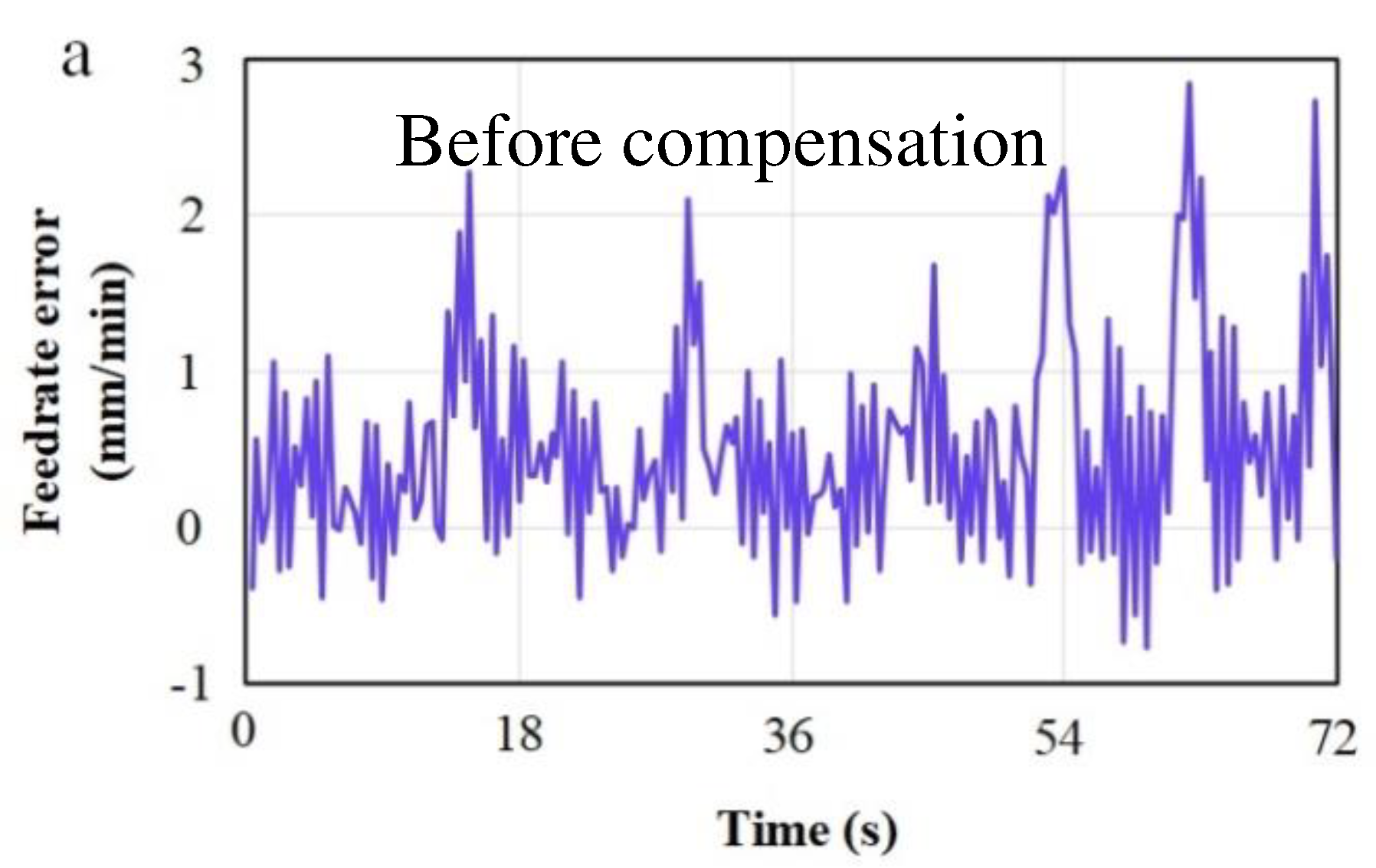
3.2. Experiment of friction compensation control
4. Contour error modeling and controlling
4.1. Contour error modeling
4.2. Influence of the dynamic parameter on contour error
- (1)
- When the motion time and dynamic gains of each axis are equal, the second and third terms of equation (27) become zero. Consequently, the error er is solely influenced by the first servo dynamic characteristics. In this scenario, the error is dependent on both the frequency of the servo bandwidth and the size of the design path.
- (2)
- When the motion time constants Tx and Ty of each axis are different, but the motion gains Kcx and Kcy are the same, the Eq. (27) can be rewritten as
- (3)
- Except for the first item, error er is affected by two parts based on (28). One part is constant and independent of time. The other part consists of elliptic trajectories that vary with time. These trajectories have a major axis distributed in the direction of 45° or 135°, and their radius is related to the system dynamic parameter ωt.
- (4)
- When the motion time constants Tx and Ty are equal, but the motion gains Kcx and Kcy are different, equation (27) can be rewritten as follows
- (5)
- When Tx, Ty and Kcx, Kcy are all different, Eq. (28) can be rewritten as
4.3. Design of cross-coupled control strategy

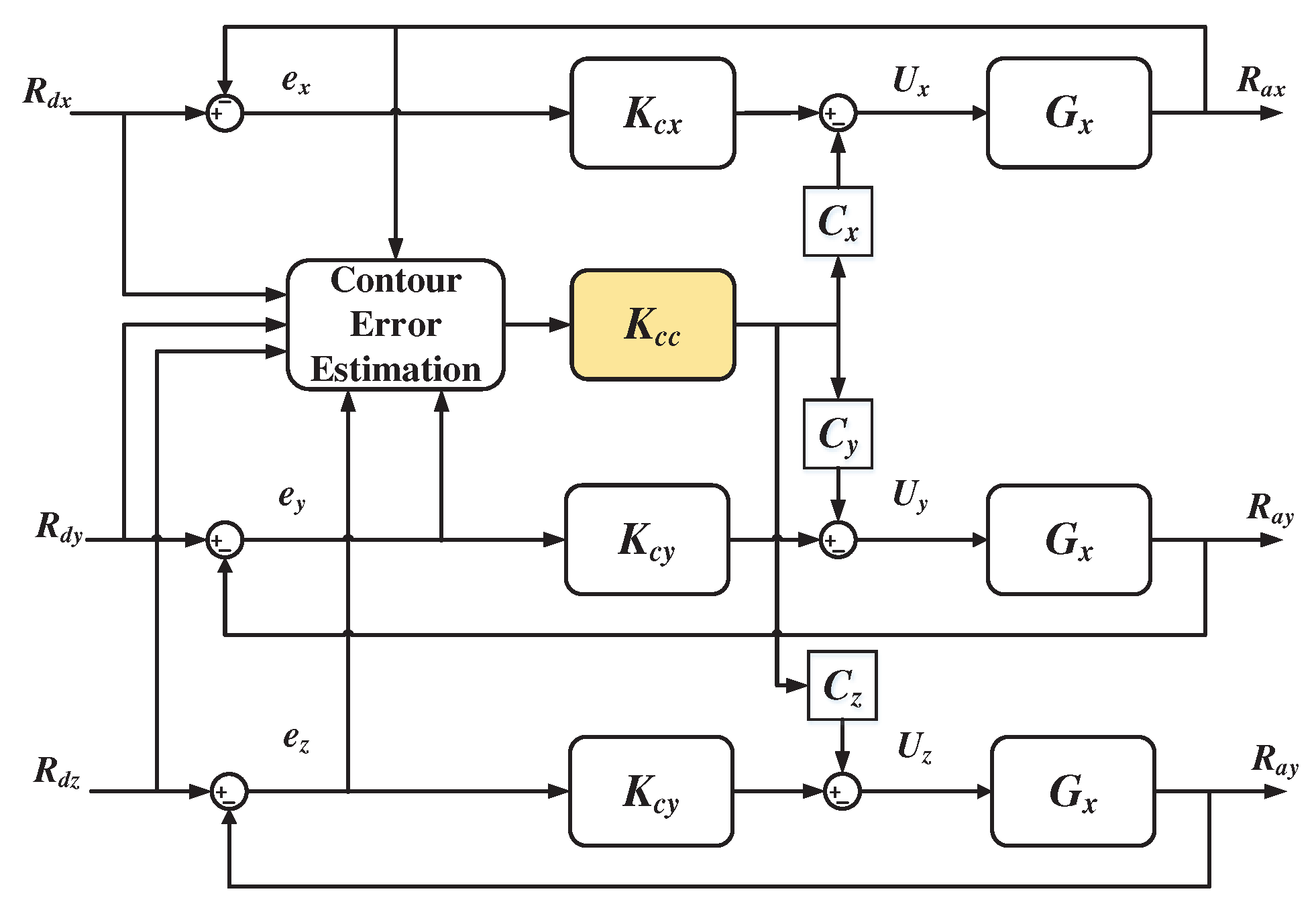
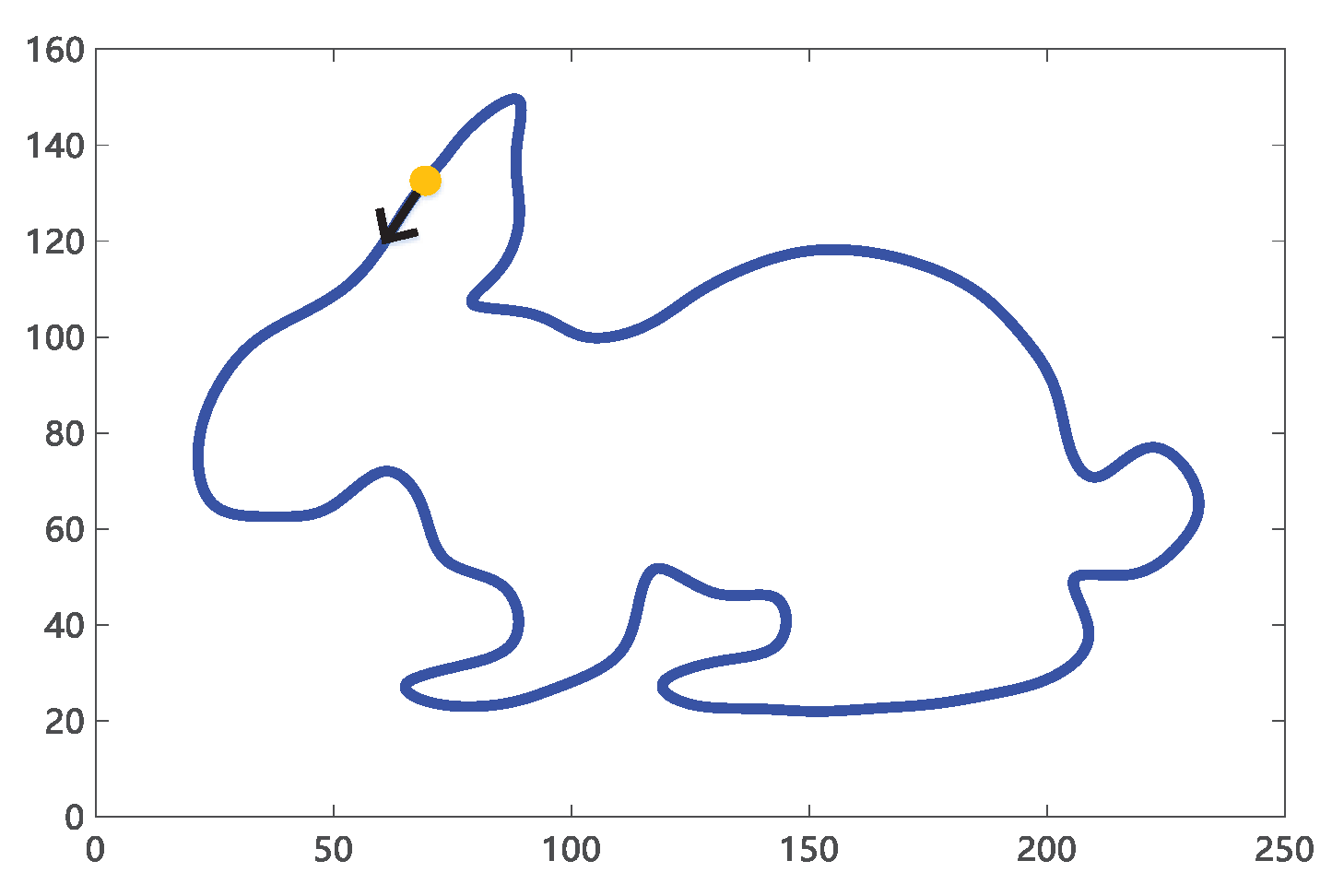
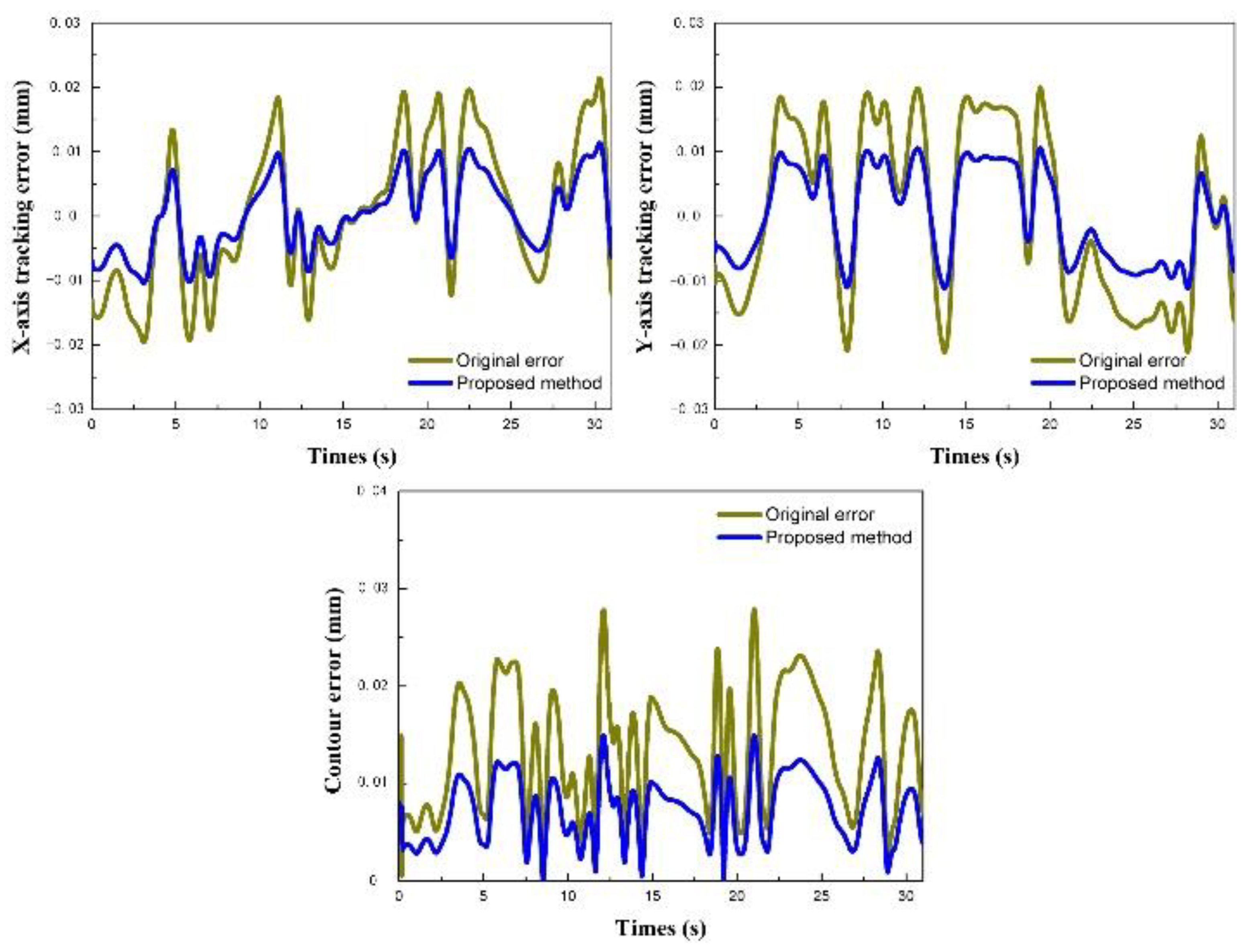
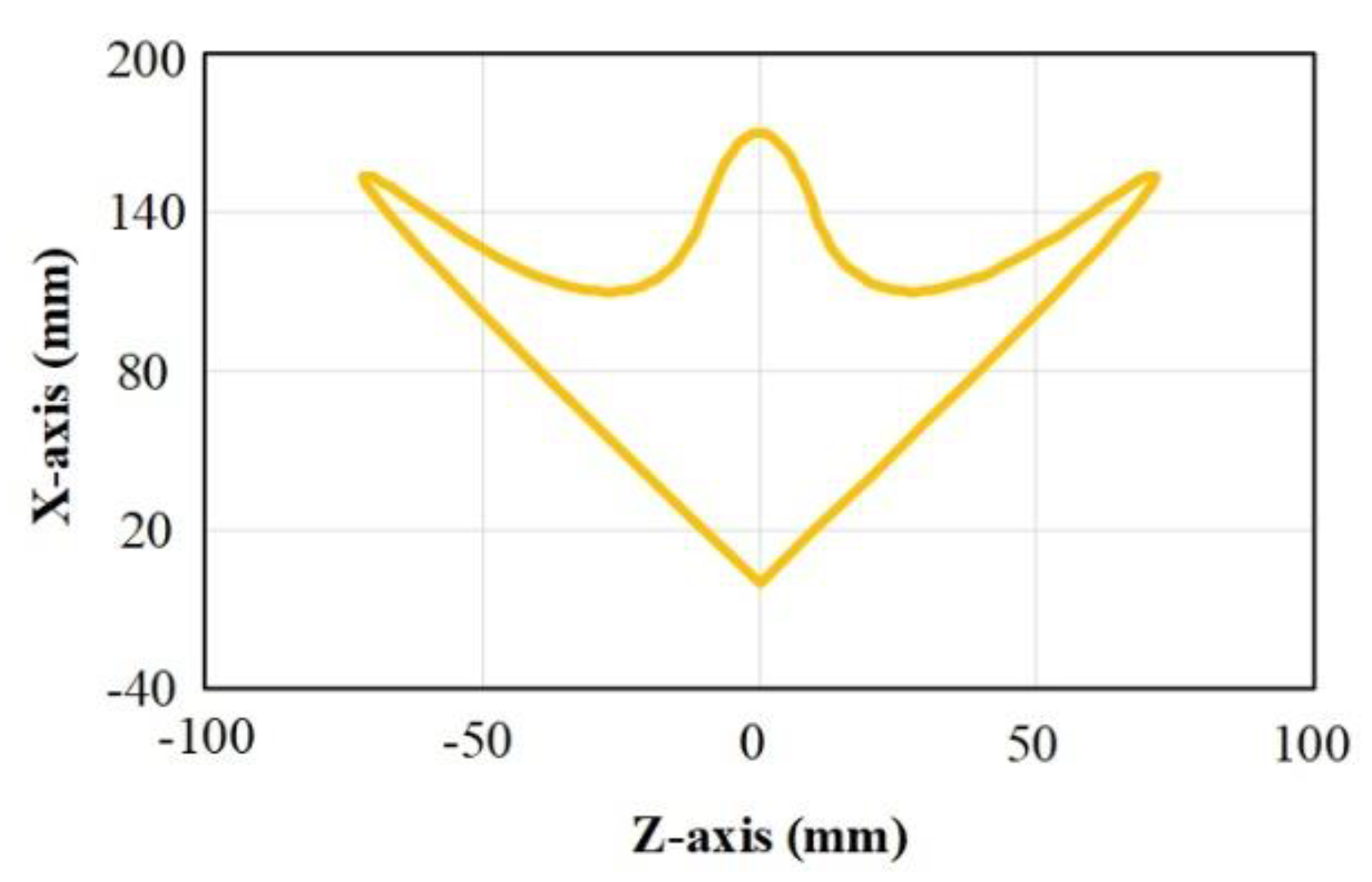
5. Machining experiment verification

6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang SL, Sun YW. Stability analysis for a milling system considering multi-point-contact cross-axis mode coupling and cutter run-out effects. Mechanical Systems and Signal Processing 2020, 141, 106452. [CrossRef]
- Quynh NV. The Fuzzy PI Controller for PMSM's Speed to Track the Standard Model[J]. Mathematical Problems in Engineering, 2020, 2020. [CrossRef]
- Xu JT, Zhang DY, Sun YW. Kinematics performance oriented smoothing method to plan tool orientations for 5-axis ball-end CNC machining. International Journal of Mechanical Sciences 2019, 157-158, 293–303. [CrossRef]
- Jiang Y, Guo Q. Simulation of multi-axis grinding considering runout based on envelope theory. Chinese Journal of Aeronautics 2020, 33, 3526–3534. [CrossRef]
- Zhao DM, Gao XJ, Wang Y. Design of Piezoelectric Ceramic Pliable Microgripper Based on Two Flexible Hinges. Journal of Liaoning Petrochemical University 2022, 42, 64–69.
- Dong H, Zhu XZ, Chen L. Analysis of Vibration Characteristic of Spindl⁃Bearing System of High Speed Grinding Machine. Journal of Liaoning Petrochemical University 2021, 41, 56–60.
- Wang S, Chen G, Cui Y. Design of Contour Error Coupling Controller Based on Neural Network Friction Compensation. Mathematical Problems in Engineering 2019. [CrossRef]
- Zhang S, Hao Q, Liu Y, et al. Simulation Study on Friction and Wear Law of Brake Pad in High-Power Disc Brake[J]. Mathematical Problems in Engineering. 2019. [CrossRef]
- Lu SK, Hua DX, Li Y, et al. Stiffness Calculation Model of Thread Connection Considering Friction Factors[J]. Mathematical Problems in Engineering, 2019, 2019:1-19.
- Sun YW, Jiang SL. Predictive modeling of chatter stability considering force-induced deformation effect in milling thin-walled parts [J]. International Journal of Machine Tools and Manufacture, 2018, 135: 38-52.
- Ding R, Xiao L. Quadratic Integral Sliding Mode Control for Nonlinear Harmonic Gear Drive Systems with Mismatched Uncertainties[J]. Mathematical Problems in Engineering, 2018, 2018(PT.9):1-18.
- Armstrong-Hélouvry B, Dupont P, Wit CCD. A survey of models, analysis tools and compensation methods for the control of machines with friction[J]. Automatica, 1994, 30(7):1083-1138.
- Simba KR, Bui BD, Msukwa MR, et al. Robust iterative learning contouring controller with disturbance observer for machine tool feed drives[J]. ISA Transactions, 2018: S0019057818300703.
- Li CB, Pavelescu D. The friction-speed relation and its influence on the critical velocity of stick-slip motion[J]. Wear, 1982, 82(3):277-289.
- Dahl, Philip R. Solid Friction Damping of Mechanical Vibrations[J]. AIAA Journal, 1976, 14(12):1675-1682.
- Canudasd WC, Olsson H, Astrom KJ, et al. A new model for control of systems with friction[J]. IEEE Transactions on Automatic Control, 1995, 40(3):419-425.
- Freidovich L, Robertsson A, Shiriaev A, et al. Friction compensation based on LuGre model[C]. IEEE Conference on Decision & Control. IEEE, 2006.
- Swevers J, Al-Bender F, Ganseman CG, et al. An integrated friction model structure with improved presliding behavior for accurate friction compensation[J]. IEEE Transactions on Automatic Control, 2000, 45(4):675-686.
- Chu H, Gao B, Gu W, et al. Low-Speed Control for Permanent-Magnet DC Torque Motor Using Observer-Based Nonlinear Triple-Step Controller[J]. IEEE Transactions on Industrial Electronics, 2017, 64(4):3286-3296.
- Cui P, Zhang D, Yang S, et al. Friction Compensation Based on Time-Delay Control and Internal Model Control for a Gimbal System in Magnetically Suspended CMG[J]. IEEE Transactions on Industrial Electronics, 2017, 64(5):3798-3807.
- Liu D, Tao T, Mei CS, et al. Study on the decoupling identification method of linear dynamic and nonlinear friction for servo driver system[J]. Chinese Journal of Scientific Instrument, 2010, 31(4):782-788.
- Ba DB, Simba KR, Uchiyama N. Contouring control for three-axis machine tools based on nonlinear friction compensation for lead screws[J]. International Journal of Machine Tools and Manufacture, 2016.
- Kim SJ, Ha IJ. A frequency-domain approach to identification of mechanical systems with friction[J]. IEEE Transactions on Automatic Control, 2001, 46(6):888-893.
- Du F, Li P, Wang Z, et al. Modeling, identification and analysis of a novel two-axis differential micro-feed system[J]. Precision Engineering, 2017: 320-327.
- Sanxiu W, Yunbo Z, Guang C. LuGre Friction Compensation Control of Servo Manipulator Based on Neural Network[J]. Journal of Beijing University of Technology, 2016.
- Zhu H, Fujimoto H. Mechanical deformation analysis and high-precision control for ball-screw-driven stages[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(2):956-966.
- Lin CJ, Yau HT, Tian YC. Identification and compensation of nonlinear friction characteristics and precision control for a linear motor stage[J]. IEEE/ASME Transactions on Mechatronics, 2012, 18(4):1385-1396.
- Iwasaki M, Shibata T, Matsui N. Disturbance-observer-based nonlinear friction compensation in table drive system[J]. IEEE/ASME Transactions on Mechatronics, 1999, 4(1):3-8.
- Rafan NA, Jamaludin Z, Chiew TH, et al. Contour error Analysis of precise positioning for ball screw driven stage using friction model feedforward[J]. Procedia CIRP, 2015, 26:712-717.
- Koren Y. Cross-coupled biaxial computer control for manufacturing systems[J]. Journal of Dynamic Systems, Measurement, and Control, 1980, 102(4):265-272.
- Koren Y, Lo C C. Variable-gain cross-coupling controller for contouring[J]. CIRP Annals-Manufacturing Technology, 1991, 40(1): 371-374.
- Su K H, Cheng M.Y. Contouring accuracy improvement using cross-coupled control and position error compensator[J]. International Journal of Machine Tools & Manufacture, 2008, 48(12-13):1444-1453.
- Huo F, Poo A N. Improving contouring accuracy by using generalized cross-coupled control[J]. International Journal of Machine Tools & Manufacture, 2012, 63: 49-57.


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




