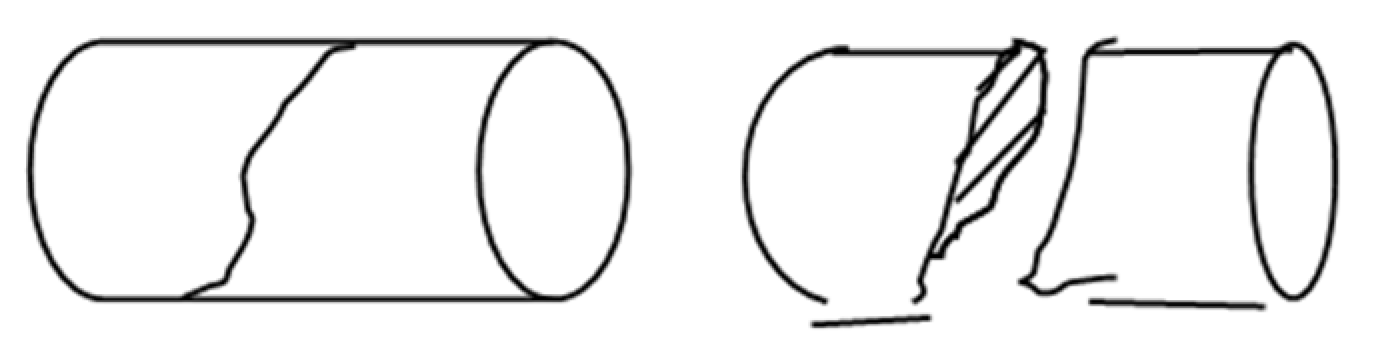Prerpints.org logo
Preprint
Article

Study on Failure Energy per Unit Area of Concrete Specimens Based on Minimum Energy Dissipation Theory

Altmetrics

Downloads

46

Views

9

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

08 December 2023

Posted:

08 December 2023

You are already at the latest version

Alerts
Abstract
In order to study the strength changes of concrete specimens under different loading conditions, based on the principle of minimum energy dissipation and from the Angle of concrete failure energy per unit area, the finite element numerical simulation software was applied to concrete specimens with different failure modes of tension, compression, bending and torsion, and the double-broken line damage constitutive model was adopted to simulate and analyze the failure forms of concrete specimens under different loading conditions. The failure area and failure energy of each specimen during loading were quantitatively calculated under each failure mode, and the relationship between the failure area and failure energy consumed under different failure modes was analyzed. The results show that under different failure modes, the failure area of concrete specimens is different, the energy consumed during failure is different, and the strength is different. However, in the process of failure, no matter how the failure mode changes, the failure energy W per unit area remains unchanged and is a constant, which is related to the physical properties of concrete itself.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

The finite element method is widely used to describe the deformation behavior and failure of rock from the perspective of energy[1,2,3,4,5,6,7,8,9]. However, due to the complex and multiphase nature of concrete materials, there are few researches on the deformation and failure of concrete materials based on energy method. In the process of studying the strength of concrete materials, the strength factor is used as a parameter to study and analyze the stress field and displacement field of macroscopic cracks[10]. The stress field and displacement field cannot be solved accurately and there are errors. The advantage of studying strength from the perspective of energy is that energy is a physical quantity that penetrates different structural levels, and it is more effective to study crack expansion or even fracture of concrete, a multiphase composite material.
Damage theory has been widely used in concrete research[11,12,13,14,15,16]. The damage process is considered as an irreversible energy conversion process. Based on the perspective of energy, it is effective and reasonable to establish the relationship between damage variables and dissipated energy as a method to provide solutions to the simulation analysis of concrete compressive damage.
In this paper, the strength failure, failure form and failure process of concrete materials are studied by using finite element numerical calculation from the perspective of energy. The process of crack generation and the formation of failure surface are numerically simulated. The calculation method of concrete failure area under different stress states is proposed, and the strength of concrete is characterized by the failure area from the side. In view of the discreteness of concrete strength and the different strength values under different loading conditions, this paper analyzes and studies the factors affecting the strength of concrete, explains the change mechanism of concrete strength, uses the macroscopic mechanical characteristics of fracture mechanics to study the dissipation energy and failure surface [17], and explores the theory of concrete strength. The reason for the different strength under various load conditions is explained from the Angle of damage area and energy.

2. Methods

Based on the principle of minimum energy dissipation[18], the finite element element of a unit volume of concrete specimen is taken as the consideration object, which produces deformation under the action of external force. Assuming that there is no heat exchange between the physical process and the outside world, the physical process is a closed system, and the total input energy generated by the external force is U, according to the first law of thermodynamics, it can be obtained as follows:
U = U d + U e .
The energy of each part of the concrete specimen unit in the principal stress space can be expressed as:
U d = ∫ 0 ε 1 σ 1 d ε 1 + ∫ 0 ε 2 σ 2 d ε 2 + ∫ 0 ε 3 σ 3 d ε 3 .
U e = 1 2 σ 1 ε 1 e + 1 2 σ 2 ε 2 e + 1 2 σ 2 ε 3 e .
ε i e = 1 E i [ σ i − λ ( σ j + σ k ) ] .
U is the total work done by the main stress, the unit dissipated energy Ud is used to form the internal damage and non-recoverable deformation of the unit, and Ue is the elastic strain energy that can be released by the unit.
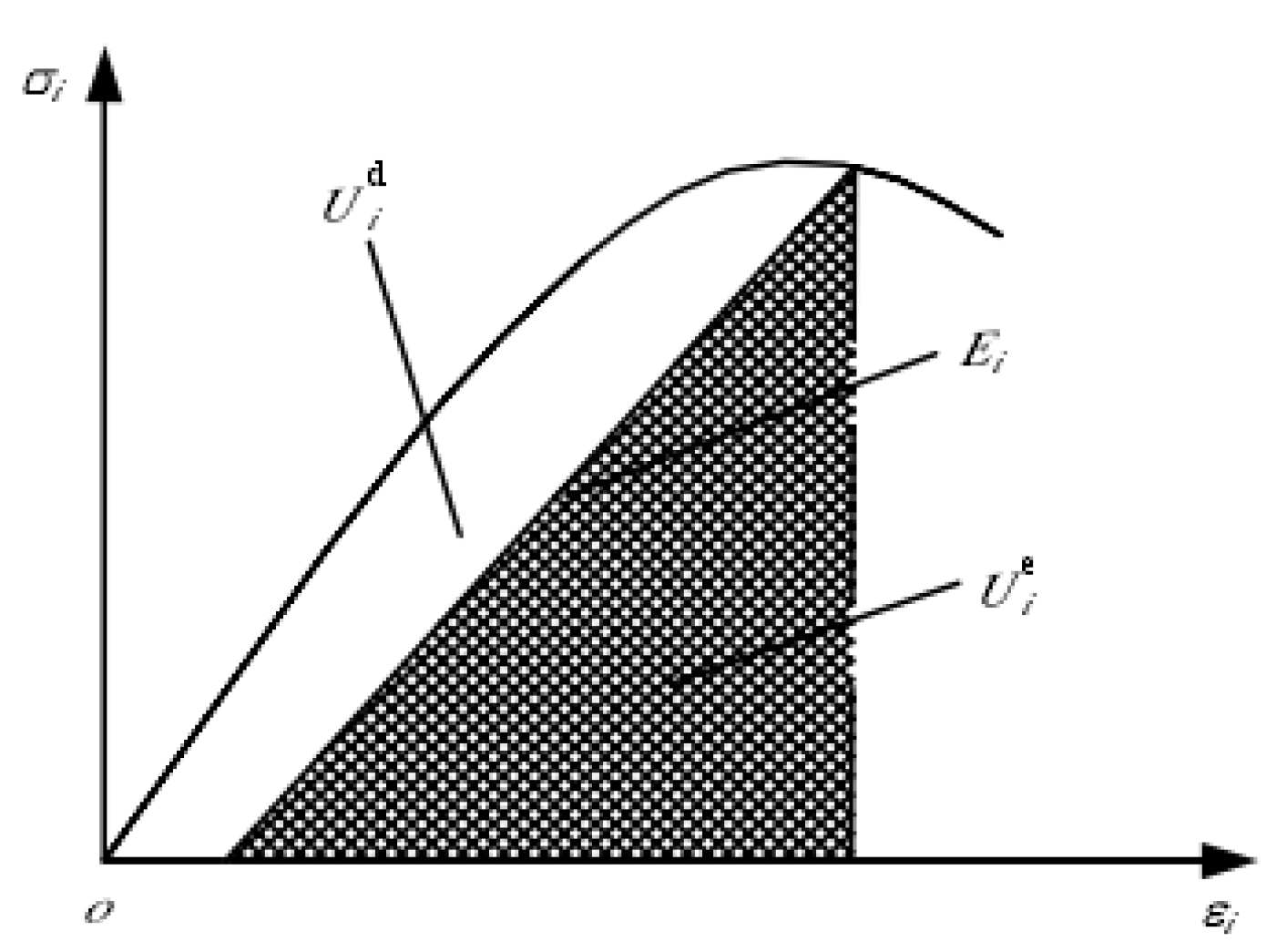
Figure 1 shows the stress-strain curve of the concrete specimen and the quantifiable relationship between the releasable strain energy and energy dissipation per unit volume. The area Udi is the energy consumed when the unit is damaged, and the shadow area Uei is the releasable strain energy stored in the unit, which is the elastic strain energy released by the unit after unloading. Ei is the unloading elastic modulus.
From the thermodynamic point of view, energy dissipation is irreversible, while energy release is two-way and reversible as long as certain conditions are met. The energy damage of the unit is defined as:
η = U d U c .
Uc is the critical value of energy dissipation when the element strength fails, and is the material constant. In a certain stress state, η=1 indicates loss of strength of concrete material.
The element "strength failure" is different from "failure". The element is gradually damaged with the increase of strain until the dissipation energy of the element is close to the critical energy dissipation value of the element, but the concrete specimen does not necessarily suffer from failure. When the strain energy of a certain element can reach the energy required for the failure of the element, the element is damaged. The elastic strain energy stored in the elements is released in the form of elastic surface energy, and the overall failure of the specimen occurs when the cumulative failure of the elements reaches a certain number.
The sum of strain energy dissipation of element damage and strain energy dissipation of element failure is determined as dissipation energy. In this paper, it is assumed that the concrete material is brittle and the failure is elastic fracture, that is, the energy provided by the outside world does not consider the energy dissipation caused by irrecoverable displacement, and dissipation energy is considered as failure energy.

3. Materials and experiment

3.1. Materials

This specimen is a C15 concrete cylindrical specimen with a water-cement ratio of 0.40. The aggregate is Jing River and pebble with a particle size of 5~20mm and the sand is middle sand from Xi 'an Zhuohe River. The test was conducted after 28 days of maintenance under standard conditions. The specific dimensions are shown in Table 1.

3.2. Experimental result

The failure form of specimen Pull-1 under tensile force is shown in Figure 2. Under the action of pure tensile stress, the specimen is damaged along the cross section, and the failure fracture is relatively flat. No matter how large or small the ratio of length to diameter, the failure surface is uniformly parallel to the cross section, and all of them show brittle failure.
The Bending moment causes the bending failure of the specimen, and the bending surface cracks along the cross section of the specimen, and the bending fracture is smooth and smooth.
The failure of specimen Twist-1 belongs to shear tensile failure, and the failure fracture is rough and uneven. As shown in Figure 3, its failure is from the outermost layer along the axis of the rod about 45 direction, and the failure surface is a spatial spiral twisted surface.
The concrete specimens subjected to pressure have various forms of failure, which are divided into long pressure, medium pressure and short pressure failure, in which the fixed lengthen diameter ratio λ≥10 is long pressure failure, 1<λ>10 is medium pressure failure, λ≤1 is short pressure failure. The failure surface of the specimen is shown in Table 2.

4. Numerical Simulation

4.1. Numerical model

The concrete is regarded as a random aggregate model of aggregate, mortar and interfacial three phase materials. The model adopts bottom Z-direction constraint and midpoint constraint.
The numerical test simulated the tensile, compressive (in which the compression length-diameter ratio H/R= 1,2,4,6,10), bending and torsional damage, and the calculated model dimensions were consistent with those in Table 1. Concrete specimen models Pre-1, Pre-3 and Pre-5 are short pressure, medium pressure and long pressure respectively, as shown in Figure 4.
When the short-pressure specimen is damaged under pressure, there are many cracks along the vertical direction, forming many longitudinal failure surfaces. After the specimen is damaged, it becomes fragmentary and the failure fracture is coarse. When the long-pressure specimen is under pressure, it belongs to the instability failure. The failure surface develops and fails along the cross section, and the shape of the failure surface is very similar to that of the tension specimen Pull-1. When the medium pressure specimen is under pressure, it is between the transition stage of long pressure and short pressure, and it belongs to shear failure. The failure surface gradually tilts along the cross section, forming a certain Angle α with the stress axis, and gradually tilts along the cross section. When the pure shear failure occurs, α=45°, the failure surface is elliptical, and the level of the failure surface is between the long pressure and the short pressure. The data simulation results of tensile specimens, bending specimens and torsion specimens are consistent with the experimental results.

4.2. Material model

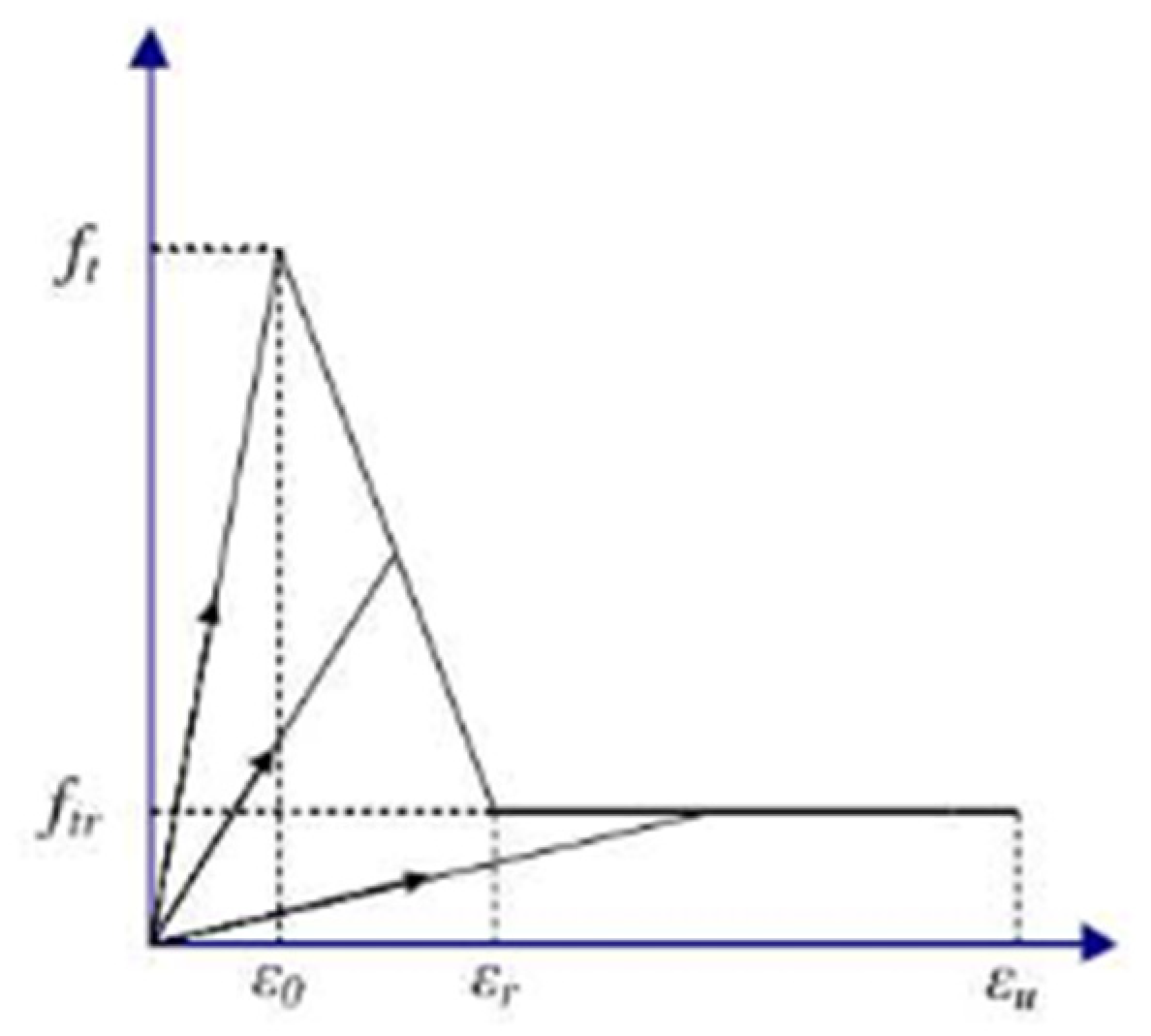
The double broken line damage evolution model is used in the numerical calculation. The influence of Poisson's ratio on material damage is not considered in the calculation, only the elastic modulus damage is considered. The damage variable D of the elastic modulus is introduced, and the elastic modulus after damage is E= (1-D) E0. The change law of the damage variable with the strain is shown in the elastic bifold damage model, as shown in Figure 5.
The initiation, development and penetration of cracks are simulated, and the strength and failure process are analyzed from the perspective of energy. In the calculation, the load is evenly distributed on the upper surface of the specimen, which is divided into seven steps. The degree of elastic modulus reduction reflects the damage degree of the meso-concrete specimen under continuous loading, and the damage process of various phase materials of the meso-concrete can be described. In the calculation, the maximum tensile strain failure criterion is selected to carry out numerical simulation calculation of the concrete cylinder specimen.
In the loading process, when the maximum tensile strain of the element exceeds the ultimate tensile strain of the material, the element stiffness fails, that is, with the increase of the load, the elastic modulus of the element changes with the damage law of the bifold line. The static equilibrium equation of the element is nonlinear, and the equation is solved by the incremental method. As the damage degree of elastic modulus varies with the increase of load, the solution process needs constant damage iteration, and the calculation amount is very large.
E ˜ = E 0 ( 1 − D )    ( 0 ≤ D ≤ 1 ) .
σ = E ˜ ε .
Where E0 is the initial elastic modulus, E ˜ is the residual elastic modulus, σ and ε are the nominal stress and nominal strain of the material, and the damage variable D is mainly determined by the double broken line damage evolution model. The expression of D is:
D = { 0 ( ε m a x < ε 0 ) 1 − η − λ η − 1 ε 0 ε m a x + 1 − λ η − 1 ( ε 0 < ε m a x ≤ ε r ) 1 − λ ε 0 ε m a x ( ε r < ε m a x ≤ ε u ) ( ε m a x > ε u )
f t r = λ f t .
ε = η ε 0 .
ε u = ξ ε 0 .
Where, ft is the tensile strength, ftr is the residual tensile strength, ε0 is the principal tensile strain of ft, εr is the residual strain when the unit tensile strength reaches the residual tensile strength. εu is the ultimate tensile strain, and εmax is the maximum tensile strain corresponding to a load value at loading. λ is the residual tensile strength coefficient, η is the residual strain coefficient, and ξ is the ultimate tensile strain coefficient.

3.3. Numerical simulation calculation

It is necessary to go through the intermediate damage stage from the initial stress to the final failure of the unit. From the initial loading to the final failure of the specimen, all the unit damage strain energy dissipation and unit damage strain energy dissipation are added together to obtain the overall damage strain energy dissipation and failure strain energy dissipation of the specimen, and the sum of the overall damage strain energy dissipation and failure strain energy dissipation is the total energy dissipation of the specimen from loading to failure.
The method for determining the energy consumption of damaged and damaged elements is as follows: According to the average stress-strain of the unit, the strain energy of each unit at each load step can be calculated. After each load step is applied, according to the maximum tensile strain criterion, which units enter the damage stage and which units enter the failure stage can be judged. The difference between the strain energy of the unit before entering the damage stage and the strain energy of the unit after entering the damage stage is defined as the damage strain energy of the unit. The difference between the strain energy of the unit before the failure stage and the strain energy of the unit after the failure stage is defined as the failure strain energy of the unit.
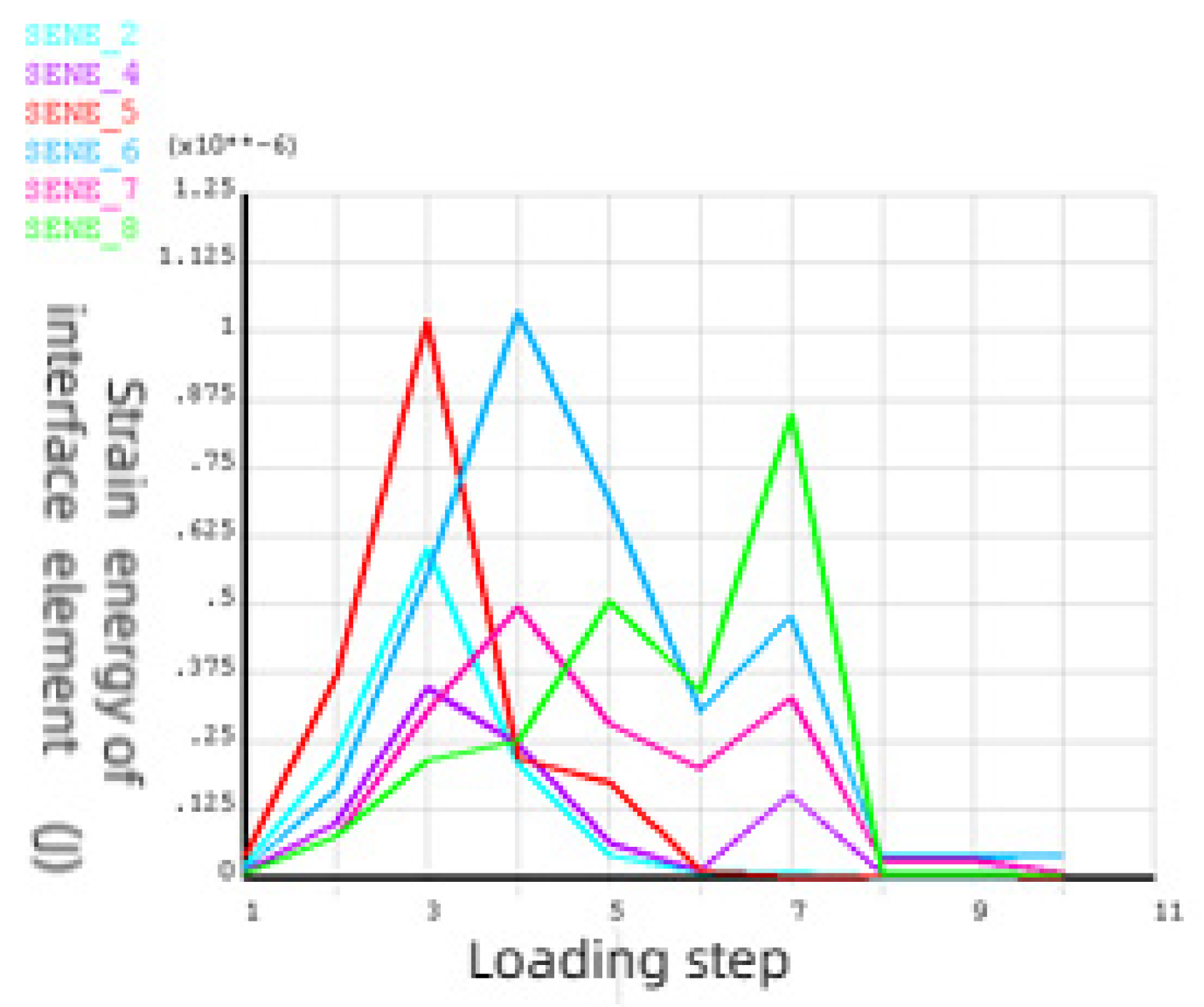
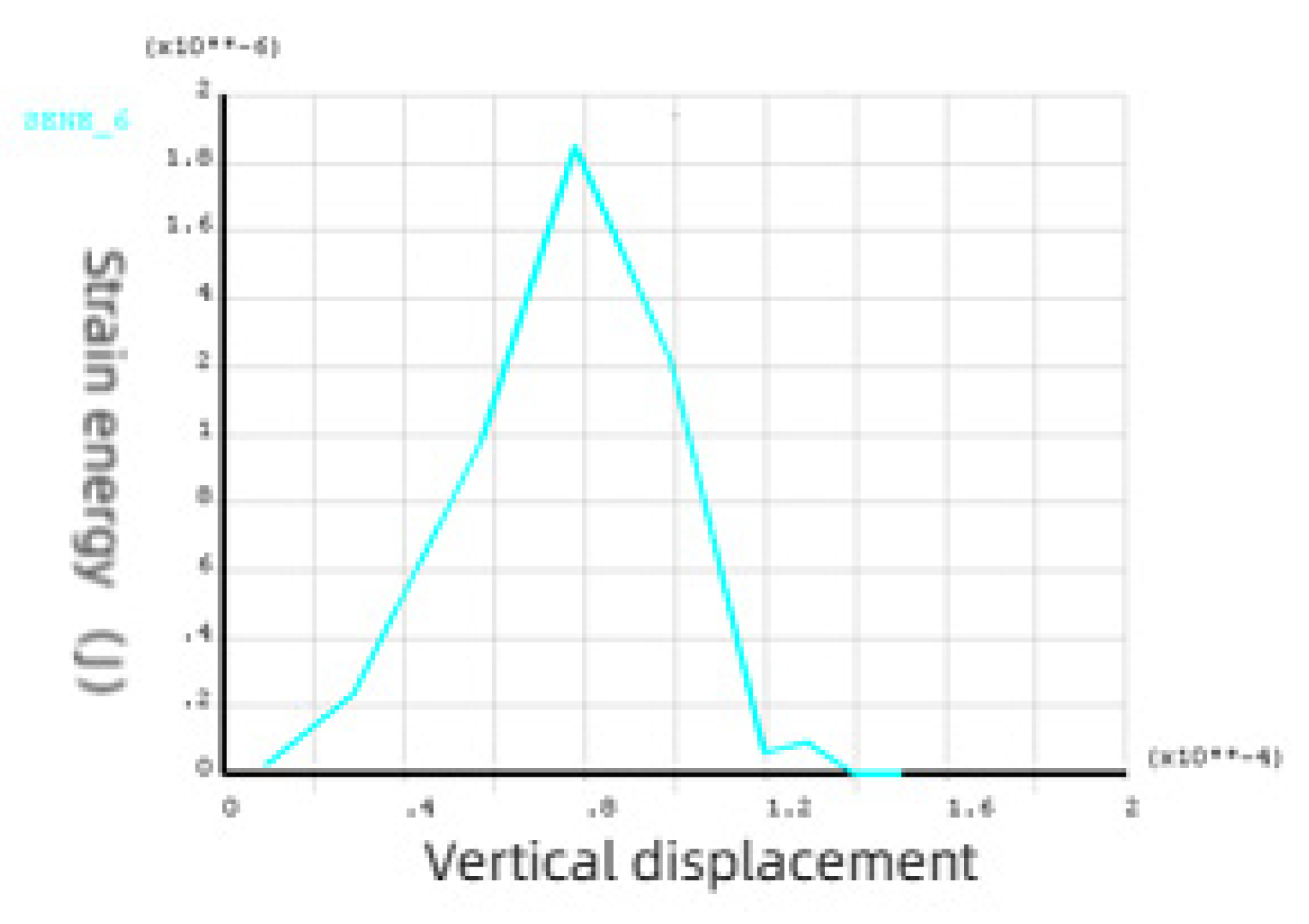
The strain energy of interface elements at different positions on the same section is respectively taken for analysis. With the increase of displacement, the strain energy increases first and then decreases. When different points reach the maximum strain energy, the displacement is different, and the change law of strain energy of elements at all surfaces is the same. It shows that the damage and consumption process of interfacial element strain energy with external force is complicated. With the damage of the elastic modulus, its energy consumption increases continuously. However, due to the different positions of the interface elements, the values of the stored elastic strain energy of each element are different, but the change law of the strain energy of each element is the same, and the fluctuation increases to the extreme value, and then all the strain energy stored in the unit is released, as shown in Figure 6.
The strain energy of mortar units at different positions on the same section is analyzed respectively. With the increase of displacement, the strain energy increases first and then decreases, but when the maximum strain energy is reached at different points, the displacement is very close, indicating that the strain energy of mortar in the same section is synchronized with the damage and consumption of external forces, as shown in Figure 7.
With the increasing load step, through the analysis of the changes in the stored strain energy of mortar and interfacial material units, the variation law of strain energy of specimens in the numerical calculation is basically the same, as shown in Figure 8: The strain energy of a unit increases with the increase of vertical displacement, and then the strain energy drops "abruptly" with the continuous increase of displacement, resulting in the failure of the unit.
The simulation of the numerical test calculated the tensile, compressive, bending and torsion damage, and calculated the number of interface and mortar kill elements, as well as the energy loss of interface and mortar. Since all model elements are divided into different sizes, the failure area of the specimen should be the number of mortar and interface kill elements multiplied by their respective surface area, the greater the failure area, the greater the failure energy.
This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.

5. Results and discussions

5.1. Failure area and failure energy

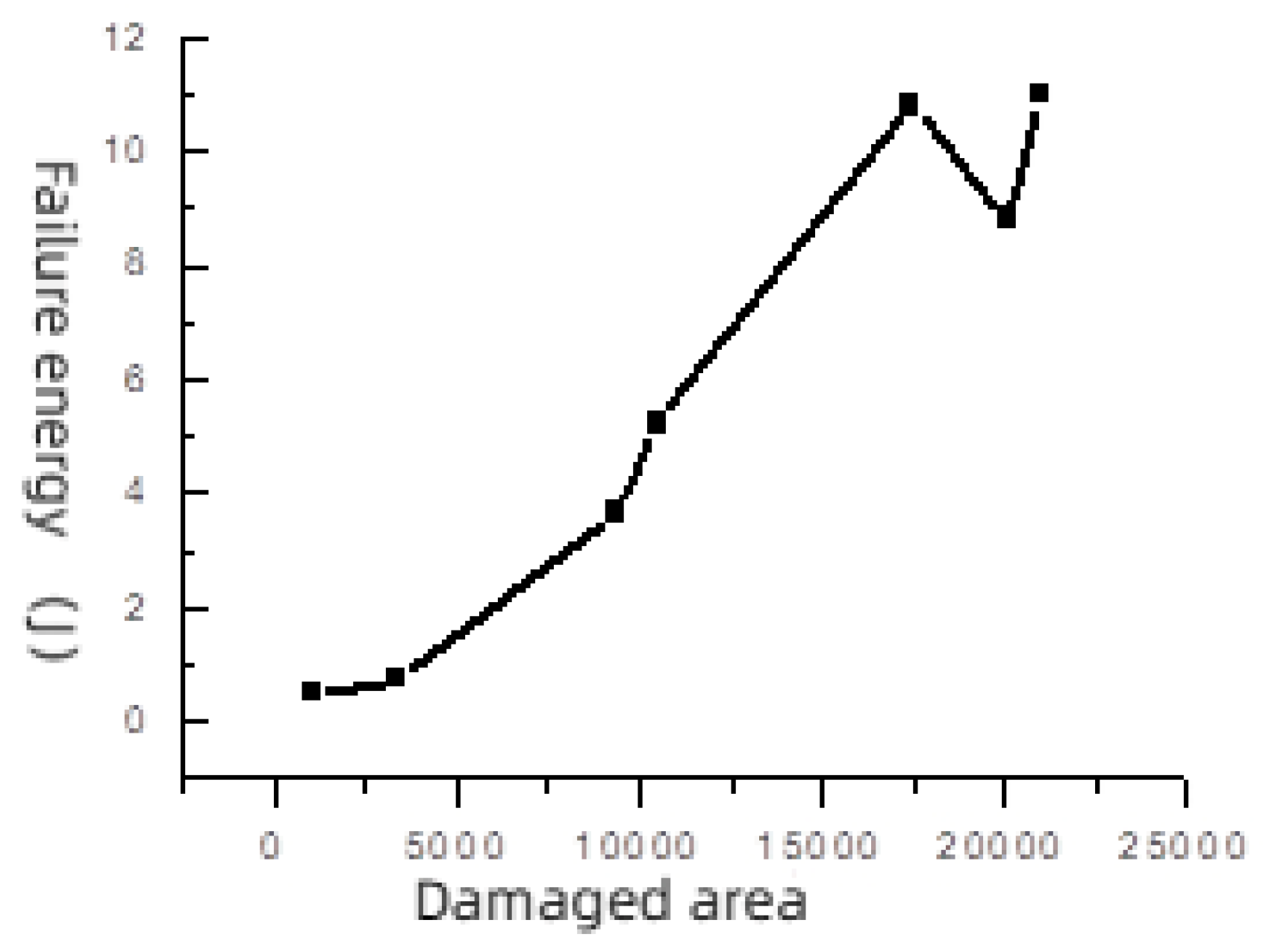
The relationship between failure area and energy is studied from the Angle of crack energy release rate, and it is found that the larger the failure area is, the larger the energy consumption is. Tensile damage area is the smallest, the bending, long pressure damage area is close to the tensile damage area, the medium pressure damage area is greater than the long pressure, the torsional damage area is greater than the medium pressure and less than the short pressure damage area, the corresponding damage can be from small to large in the order of tension, bending, long pressure, medium pressure, torsion and short pressure. It is concluded that the greater the strength of the specimen, the greater the area under stress, and the greater the energy of the external force to the surface energy of the specimen, that is, the more the failure area is, the greater the failure energy of the specimen.
The failure forms of concrete specimens under different stress conditions are different, and the crack cracking type and development direction are different, resulting in different failure areas and different failure energies when the specimens are damaged, such as Pull-1, Pre-1, Pre-5 and Twist-1. However, under different loading conditions, the failure form is the same, the crack cracking type, development path and failure area are the same, and the failure energy of the specimens is the same, which determines the same strength, such as Pull-1, Pre-5 and Bending-1. According to the failure area obtained under different loading conditions, the failure energy is obtained as shown in Table 3. It can be clearly seen from the above table that the relationship between the new surface generated under different loading conditions and the external input energy of the linear elastic concrete specimen. At the same time, the energy lost in the rupture process of the concrete specimen minus the energy required for the deformation of the concrete specimen should be proportional to the new surface area. Generally, the surface area per unit volume is inversely proportional to the current size. The smaller the block degree is, the larger the surface area per unit volume is. The development direction and richness of the crack, and even the roughness of the macroscopic failure surface are also related to the failure energy.

5.2. Study on failure energy per unit area of concrete specimens

Since the concrete specimen is a composite material, the energy dissipation per unit area is studied by studying the interface and mortar separately.
U i = U i n t e r f a c e + U m a t o r = ∑ i = A ω 1 + ∑ i = B ω 2 .
i is the number of calculation step; Uinterface is the interface energy; Umator is the mortar energy; ω1 is the strain energy of the interface element; ω2 is the strain energy of the mortar element; A is the number of interface elements; B is the number of mortar elements; Ui is the total energy of each calculation step.
Δ U i = U i − U i - 1 = Δ U i n t e r f a c e + Δ U m a t o r .
ΔUi is the energy loss between two loading steps when the load continues.
Δ u ¯ = ∑ i = n Δ U int e r f a c e （ ∑ i = n Δ U m a t o r ） ∑ i = n N ( ∑ i = n M ) .
Δ U ¯ is the unit destruction energy, N is the number of interface units killed per step, M is the number of mortar units killed per step, and n is the total number of loading steps.
Δ S ¯ = Δ U ¯ / S .
Through the above calculation, the total damage energy and the energy per unit damage area can be obtained as shown in Table 4. No matter how the loading mode and the height to diameter ratio of the specimen change, the loss per unit failure area is basically the same 2.0-6.0 mJ/cm2. Table 4 shows that when the specimen is damaged by force, the failure surface is caused by overcoming the surface energy of the specimen, and the ability of the specimen itself to resist external load is called its strength.
According to the theoretical calculation, the relationship between the failure area and failure energy of specimens under different loading methods is concluded:
JD=SD W.
JD is the destructive energy, SD is the destructive area, and W is the destructive energy per unit area.
In numerical calculation, due to the influence of specimen size effect, the influence of aggregate random position, the division of unit length in calculation, the difference of incremental steps, the selection of loading steps in displacement loading control, and the multiple splitting technology carried out in numerical calculation due to the thickness of interface elements, the failure energy of interface elements and mortar units of each model is different. The average unit failure energy of each model is also different, and the numerical calculation results are also different, but the failure energy per unit area is close, and W is taken as a range value.
As can be seen from Figure 8, the failure energy and failure area corresponding to different loading methods in numerical calculation are proportional to each other, and the slope of the curve of failure energy and failure area is the failure energy per unit area, that is, the failure energy per unit area is the same regardless of whether the loading method is pull, pressure (long pressure, medium pressure and short pressure) or other loading methods. Formula 16 is further verified.
This theory is also consistent with Rittinger's new surface energy theory, which holds that the physical and mechanical properties of rocks before and after crushing do not change, and only new surfaces are added after crushing. The surface energy of the new surface is proportional to the external energy input, and the energy lost during the crushing process is proportional to the new surface area.
The failure energy of concrete specimens varies linearly with the failure area regardless of the loading method, and the failure energy per unit area is related to the physical properties of concrete materials. Different mix ratios, different aggregates and different cement grades lead to different failure energy per unit area.

6. Conclusion

In order to study the strength changes of concrete specimens under different loading conditions, based on the principle of minimum energy dissipation and from the perspective of concrete failure energy per unit area, experiments and finite element numerical simulation were carried out on concrete specimens with different failure modes of tension, compression, bending and torsion, and the failure forms of concrete specimens under different loading conditions, as well as the failure area and failure energy of each specimen during loading were analyzed. The failure energy per unit area under each failure mode is quantitatively calculated. The main conclusions are as follows:
(1) In the numerical simulation process, the fracture process of concrete specimens is considered as elastic-brittle failure. By further studying the relationship between the failure energy consumed by each specimen under different loading conditions and the failure area, the relationship equation between the two is established, and it is concluded that the failure energy per unit of the failure area, that is, the unit fracture energy W, is a constant during the fracture process of concrete materials. The failure energy per unit area is related to the physical properties of concrete materials. Different mix ratios, different aggregates and different cement grades lead to different failure energy W per unit area, which is consistent with Rittinger's new surface energy theory.
(2) The failure process of concrete specimens is a process of overcoming material continuity and generating a new surface. When the concrete specimens break and break per unit area, a new surface of twice the area will be generated, and the surface energy inside the material overcome by the new surface is the energy consumed per unit area of damage. Therefore, the larger the failure area of the specimen, the more strain energy stored in the material is consumed, the more energy the specimen absorbs from the outside world, and the stronger the specimen is able to bear the external work, that is, the greater the bearing capacity and the greater the strength.

Author Contributions

Conceptualization, X.Y; Methodology, X.Y; Software; Writing—original draft, X.Y and Z.B.. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Natural Science Youth Foundation of China (51909204), Shanxi Natural Science Research Project (20220302121321)

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Xie H P, Ju Y. Preliminary study on damage mechanics in fractional dimensional space. Chinese Journal of Mechanics, 1999, 31(3): 300-310.
  2. You M Q, HUA A Z. Energy analysis on failure process of rock specimen. Chinese Journal of Rock Mechanics and Engineering. 2002, 21(6):778-781.
  3. Gao W X, Liu Y T. Energy dissipation of rock damage under impact loading. Chinese Journal of Rock Mechanics and Engineering. 2003, 22(11):1777-1780.
  4. Hua A Z. Energy analysis of rock mass around underground engineering. Chinese Journal of Rock Mechanics and Engineering 2003, 22(7):1054-1059.
  5. Yu Y, YIN J M.Energy Dissipation properties of three gorges granite under different loading modes.Chinese Journal of Rock Mechanics and Engineering. 2004, 23(2): 205-208.
  6. Hu F. Based on the theory of fracture mechanics and damage mechanism of fractured rock mass damage is studied. Chongqing: Chongqing University, 2015.
  7. Zhang G K, LI H B, WANG M Y, et al. Research on enery and damage evolution of rock under uniaxial compression. Chinese Journal of Geotechnical Engineering 2019, 41（06）:1074-1082.
  8. Song X F, Zhang B S, Lin X Y, et al. Energy evolution during uniaxial loading failure of sandstone. Coal engineering, 2021, 53（09）:132-137.
  9. Li J, Duan Y W. Mechanical Properties and Energy Evolution of Rock under Different Loading Methods. Value Engineering, 2022, 41（07）:125-127.
  10. Cai S W, Cai M. On the application of continuum damage theory to fiber reinforced concrete. Journal of HeFei University of Technology, 2000, 23(1):73-77.
  11. Zhao Y H, Xu S L, Wu Z M. A Dual-G criterion for crack propagation of concrete structures [J]. China Civil Engineering Journal. 2004.37.(10):13-18.
  12. Li S C, Diao B, Ye Y H, et al. Segment curve damage constitutive model of concrete based on energy method [J]. Industrial Architecture, 2007, 37(5):1-4.
  13. He J T, Ma H F, Chen H Q. Summarize on the concrete damage constitutive theory research [J]. Advances in Science and Technology of Water Resources, 2010, 30(3): 89-94.
  14. Shi J F, Yu T Q, Da J. Research on damage fracture coupling for mode Ⅰ crack of concrete material based on energy theory. Journal of Water Conservancy, 2012, 43(S1): 161-167.
  15. Qi H, Li Y G, Lv X L. A practical elastic plastic damage constitutive model based on energy. Engineering Mechanics, 2013, 30(5): 172-180. [CrossRef]
  16. Zheng S S, Qin Q, Ren M N, et al. Research on damage constitutive model of concrete based on Najar energy method. Functional Materials, 2015, 2 1 (4 6) : 21001-21006.
  17. Bai Z Z, MA R J, QU D G. Fracture mechanics of concrete. Shang hai :Tong ji University Press. 2020.
  18. Zhou Z B. Principle of minimum energy consumption and its application[M]. Beijing: Science Press. 2001.
Preprints 92697 g001
Figure 1. Quantity-value relationship between releashable strain energy and energy dissipation per unit volume.
Figure 1. Quantity-value relationship between releashable strain energy and energy dissipation per unit volume.
Preprints 92697 g001
Preprints 92697 g002
Figure 2. Failure under tensile stress.
Figure 2. Failure under tensile stress.
Preprints 92697 g002
Preprints 92697 g003
Figure 3. Twist-1 destruction diagram.
Figure 3. Twist-1 destruction diagram.
Preprints 92697 g003
Preprints 92697 g004
Figure 4. Failure diagram of the pressed specimen.
Figure 4. Failure diagram of the pressed specimen.
Preprints 92697 g004
Preprints 92697 g005
Figure 5. Bifold damage evolution model.
Figure 5. Bifold damage evolution model.
Preprints 92697 g005
Preprints 92697 g006
Figure 6. Strain energy variation diagram of interface element.
Figure 6. Strain energy variation diagram of interface element.
Preprints 92697 g006
Preprints 92697 g007
Figure 7. Strain energy variation diagram of mortar unit.
Figure 7. Strain energy variation diagram of mortar unit.
Preprints 92697 g007
Preprints 92697 g008
Figure 8. Strain energy variation diagram of the unit.
Figure 8. Strain energy variation diagram of the unit.
Preprints 92697 g008
Preprints 92697 g009
Figure 8. Curve of failure energy variation of specimen with failure area.
Figure 8. Curve of failure energy variation of specimen with failure area.
Preprints 92697 g009
Table 1. Concrete specimen model under loading condition.
Table 1. Concrete specimen model under loading condition.
model Pull-1 Pre-(1) Pre-(2) Pre-(3) Pre-(4) Pre-(5) Bending-1 Twist-1
(R×H)mm
(L×B×H)mm		 30×120 30×30 30×60 30×120 30×180 30×300 30×120 30×120
Table 2. Failure of compression specimens.
Table 2. Failure of compression specimens.
Aspect ratio λ ≤1 1～10 ≥10
failure mode brittle failure brittle failure brittle failure
Failure pattern of specimen Preprints 92697 i001 Preprints 92697 i002 Preprints 92697 i003
Failure mechanism Shear cable-stayed failure Shear failure predominates Bending failure
Table 3. Failure area and failure energy of specimens under different loading conditions.
Table 3. Failure area and failure energy of specimens under different loading conditions.
Different loading forms Pull-1 Pre-1 Pre-3 Pre-5 Twist-1 Bending-1
Damaged area SD（m2） 0.002 826 0.025 43 0.016 0.002 826 0.002 115 9 0.002 826
Failure energy U（J） 0.002 826 R 0.025 43 R 0.016 R 0.002 826 R 0.002 115 9 R 0.002 826 R
Table 4. Strength and failure energy of different specimens.
Table 4. Strength and failure energy of different specimens.
Model Strength
（MPa）		 Unit average
failure energy (J)		 Failure energy
（J）		 Number of
damaged elements		 Failure energy per
unit area
（MJ/cm2）
Pull-1 7.56 4.29E-5 0.5 Sj:340 69Jm:110 33452 12 2.02
Pre-1 29.78 2.78E-4 11 Sj:14892Jm:26356412 48 5.24
Pre-2 22.287 7 1.78E-4 10.8 Sj:120 41Jm:628 98749 39 5.38
Pre-3 18.409 1 1. 07E-4 8.82 Sj:130 02Jm:463 91593 93 5.06
Pre-4 14.098 4 2.03E-4 5.233 5 Sj:361 10Jm:27 792638 02 4.98
Pre-5 15.378 0 5.31E-5 3.671 96 Sj:120 41Jm:626 74747 15 4.93
Bending-1 6.2 3.25E-5 1.5 SJ:308 8Jm:144 42175 30 2.17
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated